A Brief Review of Some Recent Precision Casimir Force Measurements
Abstract
1. Introduction
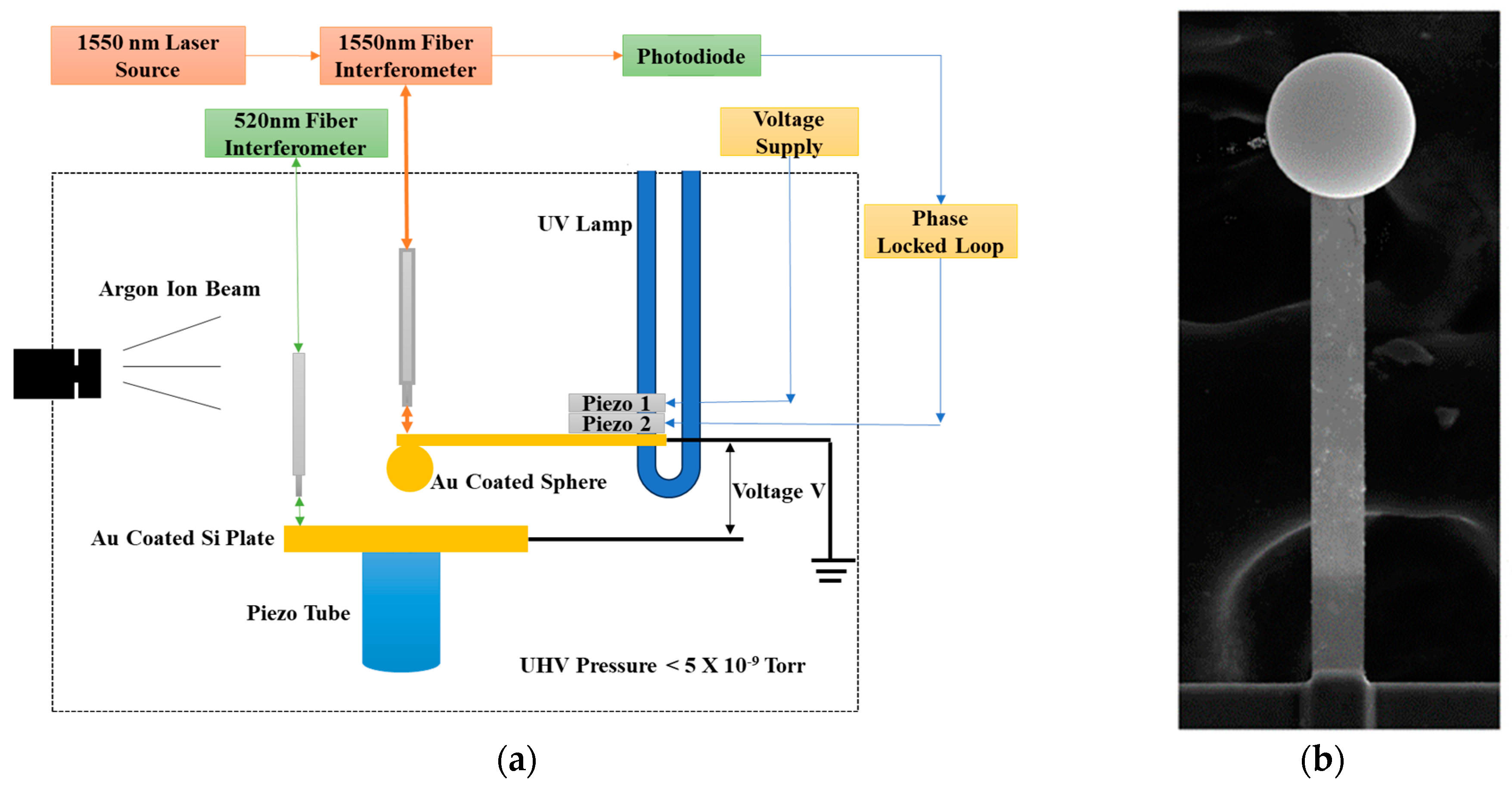
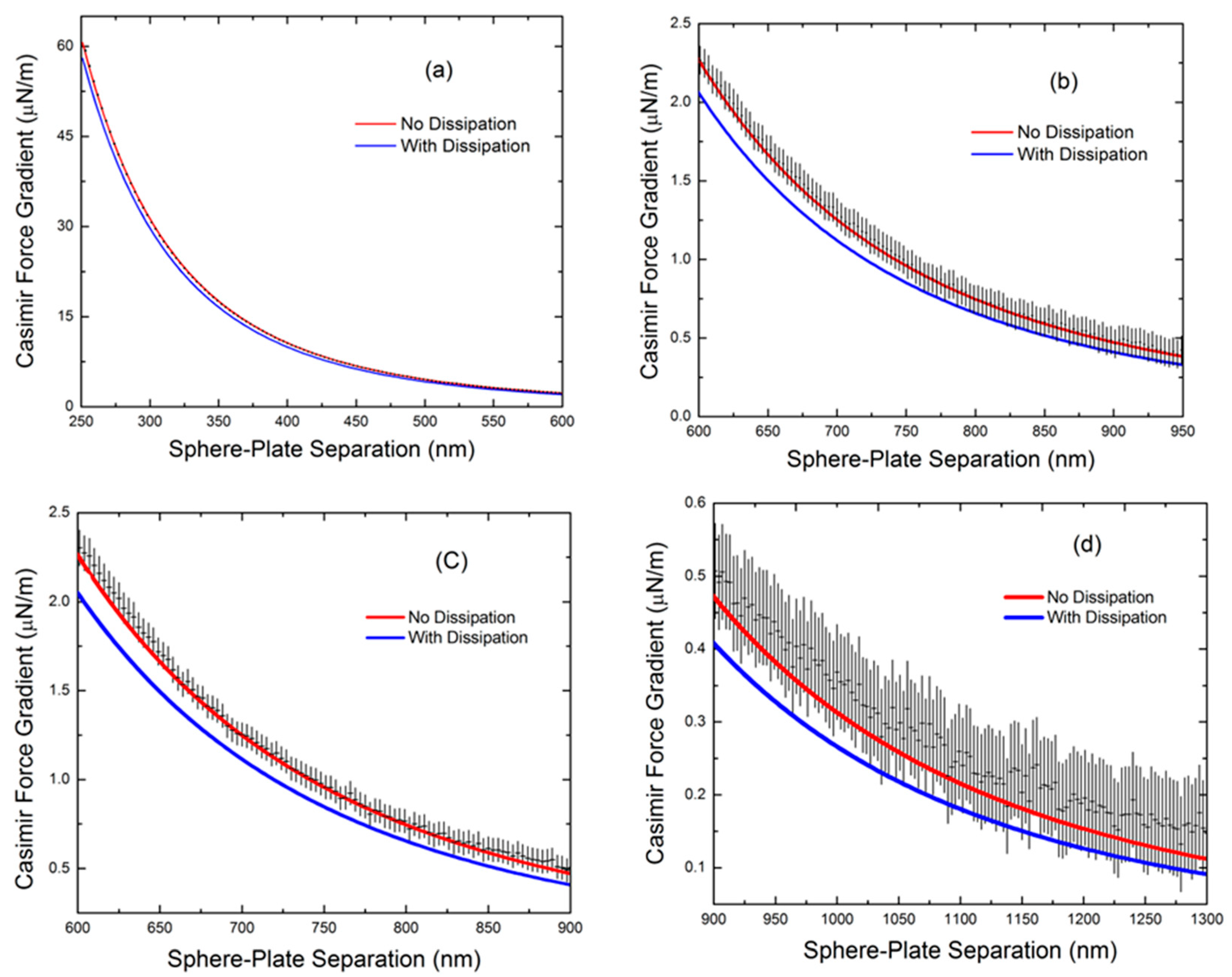
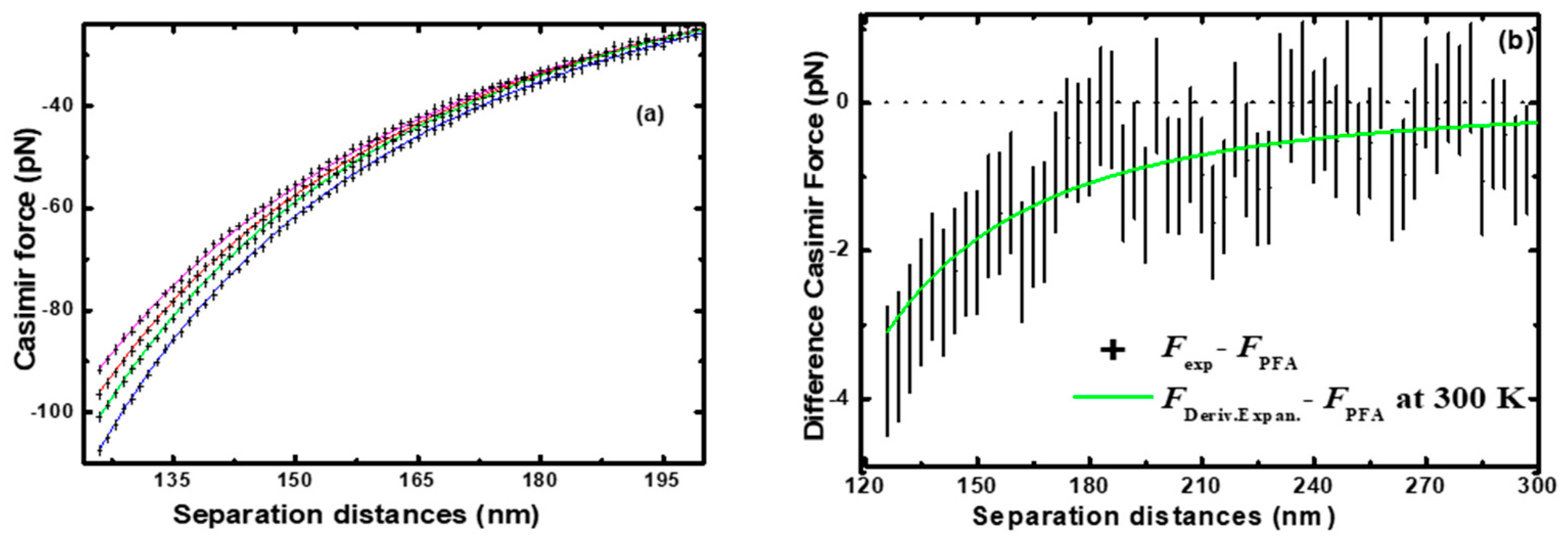
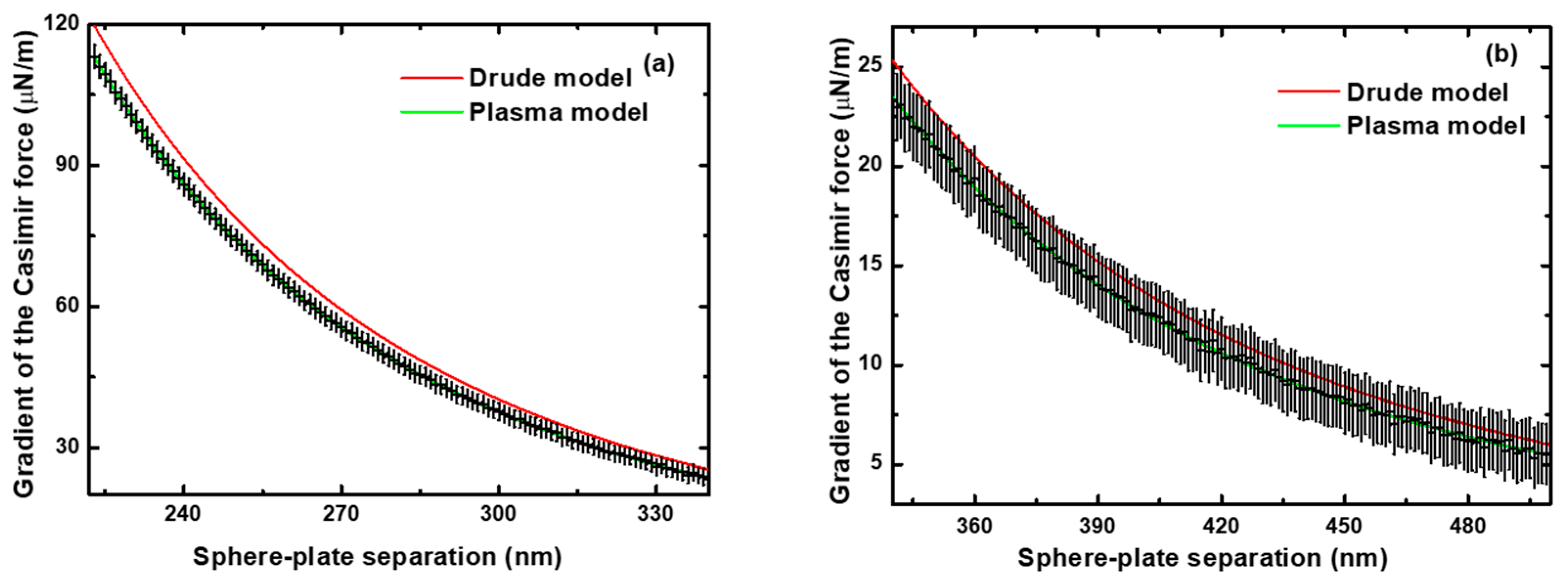
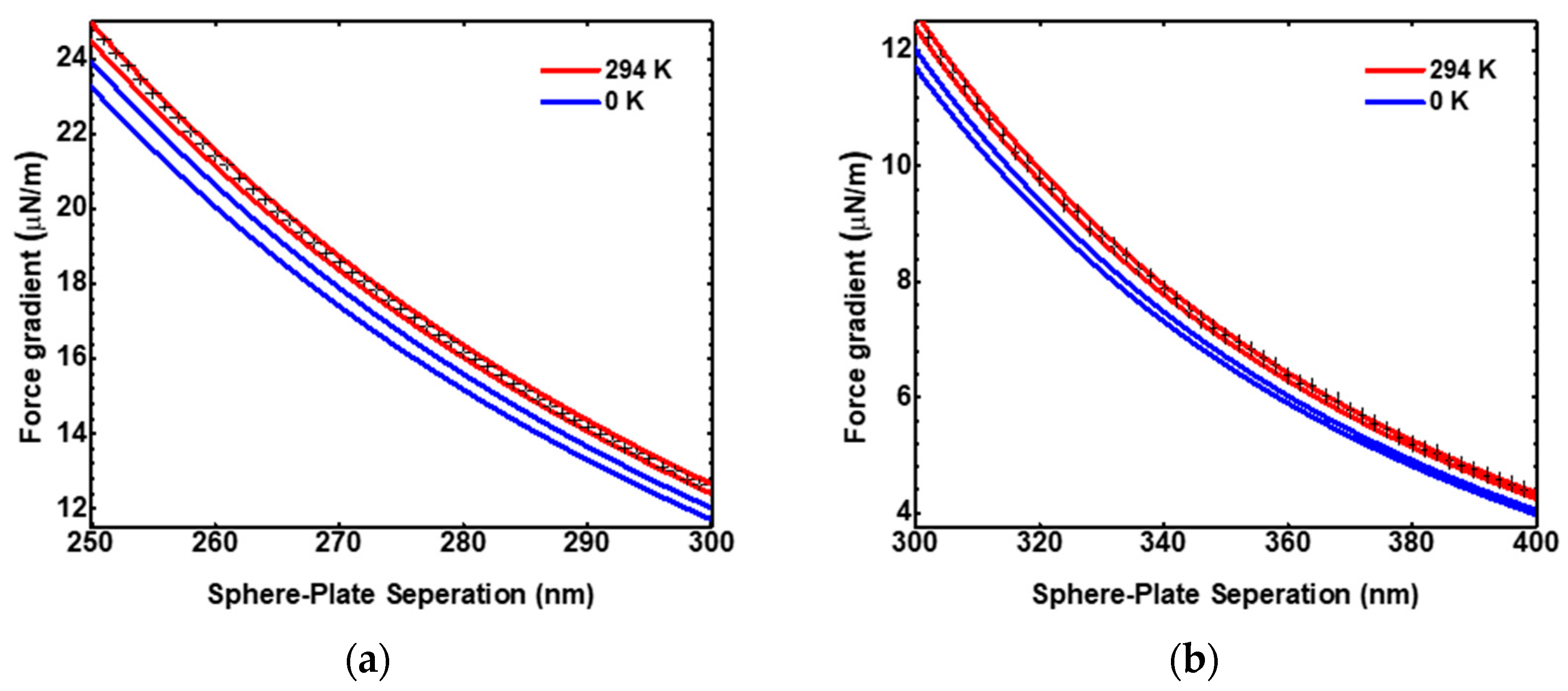
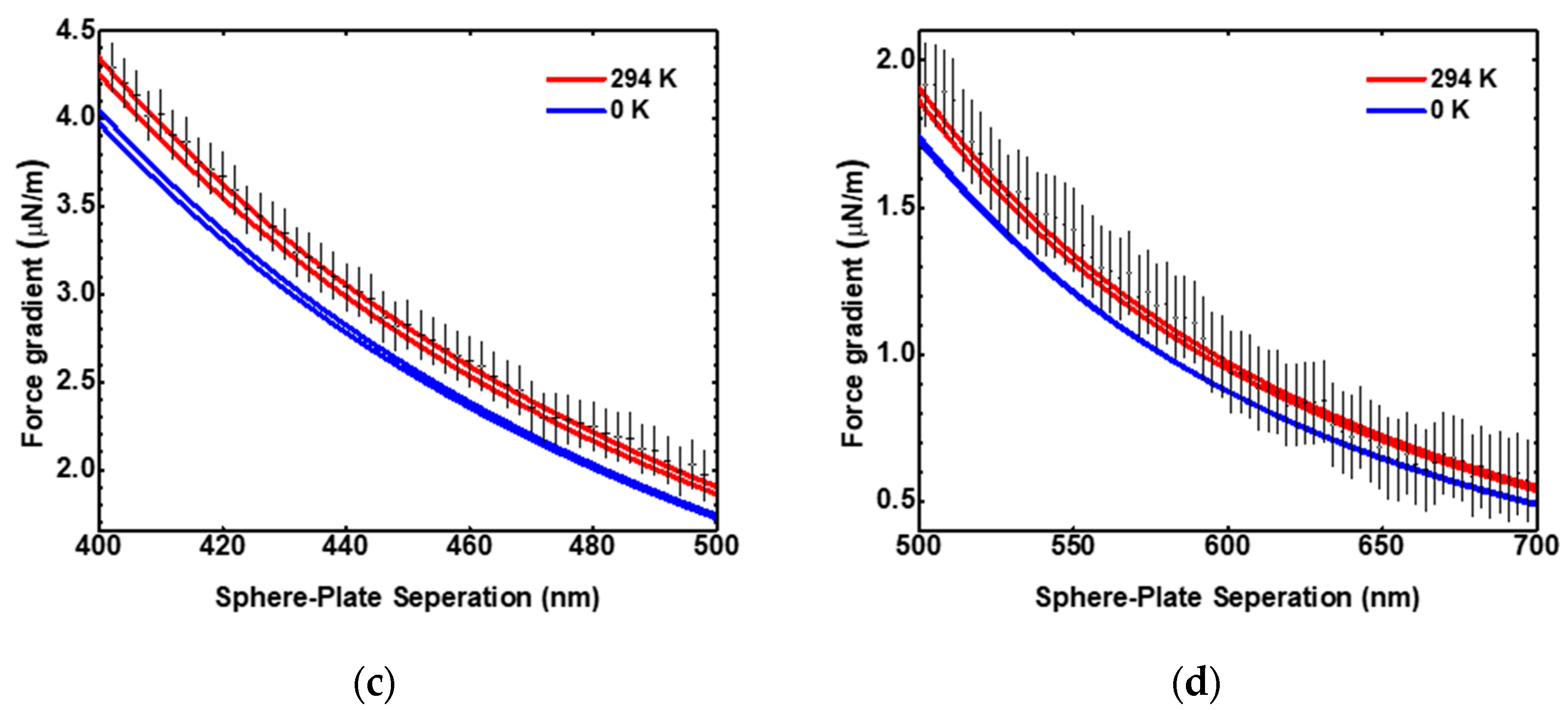
2. Recent Precision Casimir Force Measurements to 1.3 μm
- i.
- Force measurement sensitivity improved by a factor of 10.
- ii.
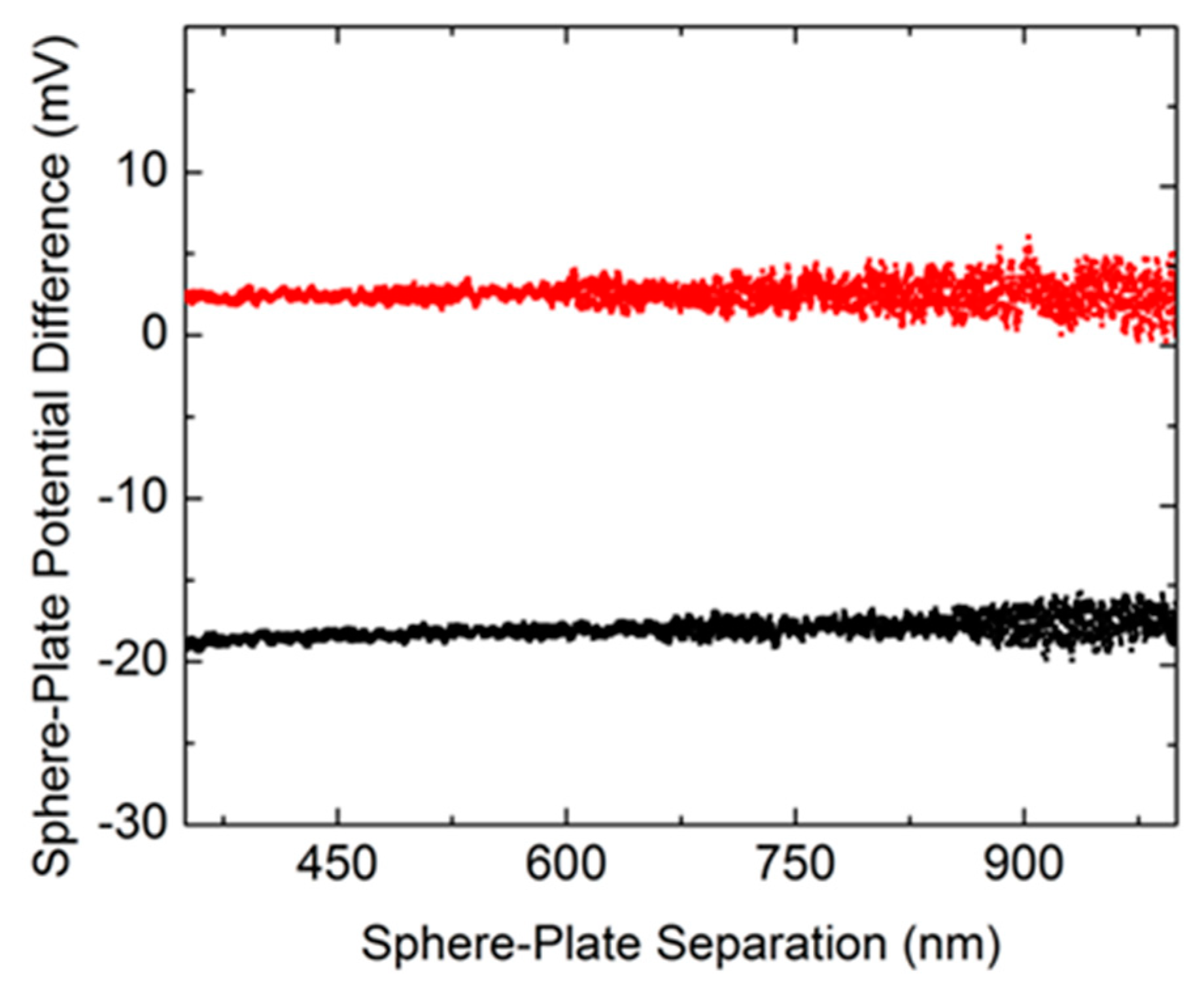
- An in situ Ar ion beam and UV cleaning procedure for the interacting surfaces were introduced, eliminating the effects of ambiguous electrostatic forces and achieving ultra-high vacuum.
- iii.
- The surface roughness of the plate was reduced by a factor of 2 to 1.08 nm through the use of polished Si wafer substrates and e-beam Au coating, which eliminated uncertainties in separation distance (reduced to a smaller than 10−4 effect).
- iv.
- Measurements were made to larger separation distances from 250 to 1300 nm (factor of 2 larger than previously).
Removing Ambiguity from Electrostatic Patches
3. Geometric Dependence of the Casimir Force with Sinusoidally Corrugated Surfaces
3.1. Demonstration of Asymmetry and Nonadditivity in Lateral Casimir Force
3.2. Role of Coherent Scattering in the Normal Casimir Force between Two Uniformly Corrugated Surfaces
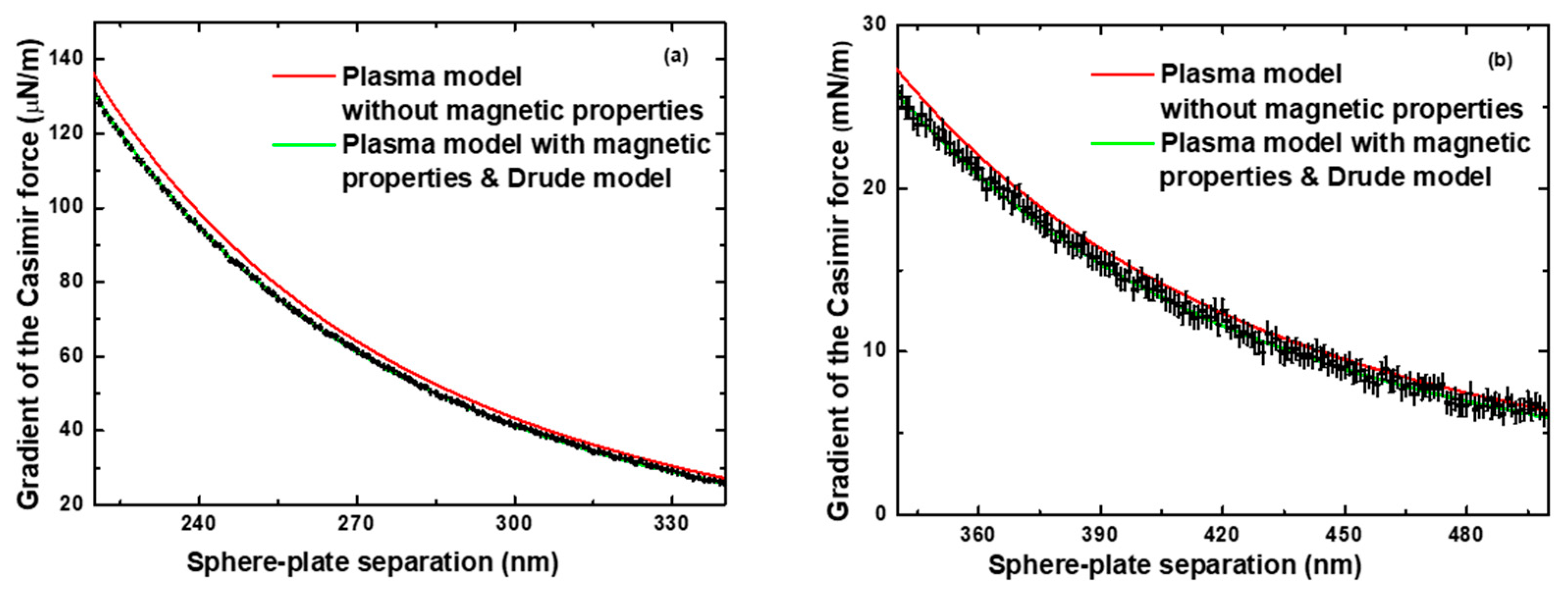
4. Role of Magnetic Fluctuations in the Casimir Force
Conclusion on Role of Electrostatic Patches
5. Precision Casimir Force Measurements with Graphene
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohideen, U.; Roy, A. Precision measurement of the Casimir force from 0.1 to 0.9 mm. Phys. Rev. Lett. 1998, 81, 4549–4552. [Google Scholar] [CrossRef]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Experimental and theoretical investigation of the lateral Casimir force between corrugated surfaces. Phys. Rev. A 2002, 66, 032113. [Google Scholar] [CrossRef]
- Harris, B.W.; Chen, F.; Mohideen, U. Precision measurement of the Casimir force using gold surfaces. Phys. Rev. A 2000, 62, 052109. [Google Scholar] [CrossRef]
- Decca, R.S.; Lopez, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise comparison of theory and new experiment for the Casimir force leads to stronger constraints on thermal quantum effects and long-range interactions. Ann. Phys. 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Decca, R.S.; Lopez, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Chang, C.-C.; Banishev, A.A.; Castillo-Garza, R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Gradient of the Casimir force between Au surfaces of a sphere and a plate measured using an atomic force microscope in a frequency-shift technique. Phys. Rev. B 2012, 85, 165443. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys. 2016, 88, 045003. [Google Scholar] [CrossRef]
- Bordag, M.; Mohideen, U.; Mostepanenko, V. New developments in the Casimir effect. Phys. Rep. 2001, 353, 1–205. [Google Scholar] [CrossRef]
- Palik, E.D. (Ed.) Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1985. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; Fong, K.Y.; Bhaskaran, H.; Lamoreaux, S.; Tang, H.X. Casimir force and in situ surface potential measurements on nanomembranes. Phys. Rev. Lett. 2012, 109, 027202. [Google Scholar] [CrossRef]
- Sushkov, A.O.; Kim, W.J.; Dalvit, D.A.R.; Lamoreaux, S.K. Observation of the thermal Casimir force. Nat. Phys. 2011, 7, 230–233. [Google Scholar] [CrossRef]
- Banishev, A.; Klimchitskaya, G.; Mostepanenko, V.; Mohideen, U. Demonstration of the Casimir force between ferromagnetic surfaces of a Ni-coated sphere and a Ni-coated plate. Phys. Rev. Lett. 2013, 110, 137401. [Google Scholar] [CrossRef] [PubMed]
- Banishev, A.A.; Chang, C.-C.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Measurement of the gradient of the Casimir force between a nonmagnetic gold sphere and a magnetic nickel plate. Phys. Rev. B 2012, 85, 195422. [Google Scholar] [CrossRef]
- Bimonte, G.; Lopez, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Reducing detrimental electrostatic effects in Casimir-force measurements and Casimir-force-based microdevices. Phys. Rev. A 2018, 97, 032501. [Google Scholar] [CrossRef]
- Liu, M.Y.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Precision measurement of the gradient of the Casimir force between ultraclean metallic surfaces at larger separations. Phys. Rev. A 2019, 100, 052511. [Google Scholar] [CrossRef]
- Liu, M.Y.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Examining the Casimir puzzle with an upgraded AFM-based technique and advanced surface cleaning. Phys. Rev. B 2019, 100, 081406. [Google Scholar] [CrossRef]
- Liu, M.Y.; Schafer, R.; Xu, J.; Mohideen, U. Elimination of electrostatic forces in precision Casimir force measurements using UV and Ar ion radiation. Mod. Phys. Lett. A 2020, 35, 2040001. [Google Scholar] [CrossRef]
- Behunin, R.; Intravaia, F.; Dalvit, D.; Neto, P.M.; Reynaud, S. Modeling electrostatic patch effects in Casimir force measurements. Phys. Rev. A 2012, 85, 012504. [Google Scholar] [CrossRef]
- Behunin, R.O.; Dalvit, D.A.R.; Decca, R.S.; Genet, C.; Jung, I.W.; Lambrecht, A.; Liscio, A.; Lopez, D.; Reynaud, S.; Schnoering, G.; et al. Kelvin probe force microscopy of metallic surfaces used in Casimir force measurements. Phys. Rev. A 2014, 90, 062115. [Google Scholar] [CrossRef]
- Behunin, R.O.; Zeng, Y.; Dalvit, D.A.R.; Reynaud, S. Electrostatic patch effects in Casimir-force experiments performed in the sphere-plane geometry. Phys. Rev. A 2012, 86, 052509. [Google Scholar] [CrossRef]
- Naji, A.; Dean, D.S.; Sarabadani, J.; Horgan, R.R.; Podgornik, R. Fluctuation-induced interaction between randomly charged dielectrics. Phys. Rev. Lett. 2010, 104, 060601. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Mohideen, U. Demonstration of the nontrivial boundary dependence of the Casimir force. Phys. Rev. Lett. 1999, 82, 4380–4383. [Google Scholar] [CrossRef]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Demonstration of the lateral Casimir force. Phys. Rev. Lett. 2002, 88, 101801. [Google Scholar] [CrossRef] [PubMed]
- Derjaguin, B. Untersuchungen über die Reibung und Adhäsion, IV. Theorie des Anhaftens kleiner Teilcher. Kolloid-Zeitschrift 1934, 69, 155–164. [Google Scholar] [CrossRef]
- Blocki, J.; Randrup, J.; Swiatecki, W.J.; Tsang, C.F. Proximity forces. Ann. Phys. 1977, 105, 427–462. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the asymmetric lateral Casimir force between corrugated surfaces in the nonadditive regime. Phys. Rev. B 2009, 80, 121402. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Lateral Casimir force between sinusoidally corrugated surfaces: Asymmetric profiles, deviations from the proximity force approximation, and comparison with exact theory. Phys. Rev. B 2010, 81, 115417. [Google Scholar] [CrossRef]
- Lord Rayleigh, Strutt, J.W. On the dynamical theory of gratings. Proc. R. Soc. Lond. A 1907, 79, 399–416. [Google Scholar] [CrossRef]
- Banishev, A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Demonstration of angle-dependent Casimir force between corrugations. Phys. Rev. Lett. 2013, 110, 250403. [Google Scholar] [CrossRef]
- Chan, H.B.; Bao, Y.; Zou, J.; Cirelli, R.; Klemens, F.; Mansfield, W.; Pai, C. Measurement of the Casimir force between a gold sphere and a silicon surface with nanoscale trench array. Phys. Rev. Lett. 2008, 101, 030401. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Gue’rout, R.; Lussange, J.; Lambrecht, A.; Cirelli, R.A.; Klemens, F.; Mansfield, W.M.; Pai, C.S.; Chan, H.B. Casimir force on a surface with shallow nanoscale corrugations: Geometry and finite conductivity effects. Phys. Rev. Lett. 2010, 105, 250402. [Google Scholar] [CrossRef]
- Golestanian, R.; Kardar, M. Mechanical Response of Vacuum. Phys. Rev. Lett. 1997, 78, 3421–3425. [Google Scholar] [CrossRef]
- Rodrigues, R.B.; Neto, P.A.M.; Lambrecht, A.; Reynaud, S. Lateral Casimir force beyond the proximity-force approximation. Phys. Rev. Lett. 2006, 96, 100402. [Google Scholar] [CrossRef]
- Canaguier-Durand, A.; Neto, P.A.M.; Lambrecht, A.; Reynaud, S. Thermal Casimir effect for Drude metals in the plane-sphere geometry. Phys. Rev. A 2010, 82, 012511. [Google Scholar] [CrossRef]
- Zandi, R.; Emig, T.; Mohideen, U. Quantum and thermal Casimir interaction between a sphere and a plate: Comparison of Drude and plasma models. Phys. Rev. B 2010, 81, 195423. [Google Scholar] [CrossRef]
- Rosa, F.S.S.; Dalvit, D.A.R.; Milonni, P.W. Casimir-Lifshitz theory and metamaterials. Phys. Rev. Lett. 2008, 100, 183602. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.B.; Neto, P.A.M.; Lambrecht, A.; Reynaud, S. Vacuum-induced torque between corrugated metallic plates. Europhys. Lett. 2006, 76, 822. [Google Scholar] [CrossRef][Green Version]
- Banishev, A.A.; Wagner, J.; Emig, T.; Zandi, R.; Mohideen, U. Experimental and theoretical investigation of the angular dependence of the Casimir force between sinusoidally corrugated surfaces. Phys. Rev. B 2014, 89, 235436. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Jaffe, R.L.; Kardar, M. Casimir forces beyond the proximity approximation. Europhys. Lett. 2012, 97, 50001. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Kardar, M. Material dependence of Casimir forces: Gradient expansion beyond proximity. Appl. Phys. Lett. 2012, 100, 074110. [Google Scholar] [CrossRef]
- Barash, Y.S.; Ginzburg, V.L. Electromagnetic fluctuations in matter and molecular (Van-der-Waals) forces between them. Sov. Phys. Usp. 1975, 18, 305–322. [Google Scholar] [CrossRef]
- Kenneth, O.; Klich, I.; Mann, A.; Revzen, M. Repulsive Casimir forces. Phys. Rev. Lett. 2002, 89, 033001. [Google Scholar] [CrossRef] [PubMed]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M.; Romero, C. Impact of surface imperfections on the Casimir force for lenses of centimeter-size curvature radii. Phys. Rev. B 2011, 83, 075417. [Google Scholar] [CrossRef]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Lopez, D.; Mohideen, U.; Mostepanenko, V.M. Capacitance measurements and electrostatic calibrations in experiments measuring the Casimir force. Int. J. Mod. Phys. A 2011, 26, 3930–3943. [Google Scholar] [CrossRef]
- Drosdoff, D.; Woods, L.M. Quantum and thermal dispersion forces: Application to graphene nanoribbons. Phys. Rev. Lett. 2014, 112, 025501. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Kort-Kamp, W.J.M.; Dalvit, D.A.R.; Woods, L.M. Casimir force phase transitions in the graphene family. Nat. Commun. 2017, 8, 14699. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Theory of the Casimir interaction from graphene-coated substrates using the polarization tensor and comparison with experiment. Phys. Rev. B 2014, 89, 115419. [Google Scholar] [CrossRef]
- Gomez-Santos, G. Thermal van der Waals interaction between graphene layers. Phys. Rev. B 2009, 80, 245424. [Google Scholar] [CrossRef]
- Sarabadani, J.; Naji, A.; Asgari, R.; Podgornik, R. Many-body effects in the van der Waals–Casimir interaction between grphene layers. Phys. Rev. B 2011, 84, 155407. [Google Scholar] [CrossRef]
- Banishev, A.A.; Wen, H.; Xu, J.; Kawakami, R.K.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Measuring the Casimir force gradient from graphene on a SiO2 substrate. Phys. Rev. B 2013, 87, 205433. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, L.; Mostepanenko, M.; Petrov, M. Quantum field theoretical description for the reflectivity of graphene. Phys. Rev. D 2016, 93, 089907. [Google Scholar] [CrossRef]
- Bimonte, G.; Klimchitskaya, G.L.; Mostepanenko, V.M. Thermal effect in the Casimir force for graphene and graphene-coated substrates: Impact of nonzero mass gap and chemical potential. Phys. Rev. B 2017, 96, 115430. [Google Scholar] [CrossRef]
- Sernelius, B.E. Retarded interactions in graphene systems. Phys. Rev. B 2014, 89, 079901. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sernelius, B.E. Two approaches for describing the Casimir interaction in graphene: Density-density correlation function versus polarization tensor. Phys. Rev. B 2014, 89, 125407. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of an unusual thermal effect in the casimir force from graphene. Phys. Rev. Lett. 2021, 126, 206802. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Experimental and theoretical investigation of the thermal effect in the Casimir interaction from graphene. Phys. Rev. B 2021, 104, 085436. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. (Eds.) Special Issue: 75 Years of the Casimir Effect: Advances and Prospects; Physics, in print; Available online: https://www.mdpi.com/journal/physics/special_issues/75yearsCasimir (accessed on 17 March 2024).
- Intravaia, F.; Koev, S.; Jung, I.W.; Talin, A.A.; Davids, P.S.; Decca, R.S.; Aksyuk, V.A.; Dalvit, D.A.R.; López, D. Strong Casimir force reduction through metallic surface nanostructuring. Nat. Commun. 2013, 4, 2515. [Google Scholar] [CrossRef]
- Tang, L.; Wang, M.; Ng, C.Y.; Nikolic, M.; Chan, C.T.; Rodriguez, A.W.; Chan, H.B. Measurement of non-monotonic Casimir forces between silicon nanostructures. Nat. Photon. 2017, 11, 97–101. [Google Scholar] [CrossRef]
- Rahi, S.J.; Emig, T.; Graham, N.; Jaffe, R.L.; Kardar, M. Scattering theory approach to electrodynamic Casimir forces. Phys. Rev. D 2009, 80, 085021. [Google Scholar] [CrossRef]
- Lambrecht, A.; Neto, P.A.; Reynaud, S. The Casimir effect within scattering theory. New J. Phys. 2006, 8, 243. [Google Scholar] [CrossRef]
- Maghrebi, M.F.; Rahi, S.J.; Emig, T.; Graham, N.; Jaffe, R.L.; Kardara, M. Analytical results on Casimir forces for conductors with edges and tips. Proc. Natl. Acad. Sci. USA 2011, 108, 6867–6871. [Google Scholar] [CrossRef]
- Milton, K.A.; Wagner, J. Multiple scattering methods in Casimir calculations. J. Phys. A Math. Theor. 2008, 41, 155402. [Google Scholar] [CrossRef]
- Grushin, A.G.; Cortijo, A. Tunable Casimir repulsion with three-dimensional topological insulators. Phys. Rev. Lett. 2011, 106, 020403. [Google Scholar] [CrossRef]
- Jiang, Q.; Wilczek, F. Chiral Casimir forces: Repulsive, enhanced, tunable. Phys. Rev. B 2019, 99, 125403. [Google Scholar] [CrossRef]
- Somers, D.A.; Munday, J.N. Conditions for repulsive Casimir forces between identical birefringent materials. Phys. Rev. A 2017, 95, 022509. [Google Scholar] [CrossRef]
- Tajik, F.; Palasantzas, G. Sensitivity of actuation dynamics of Casimir oscillators on finite temperature with topological insulator materials: Response of repulsive vs attractive interactions. Phys. Lett. A 2023, 481, 129032. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Graham, N.; Kardar, M.; Krüger, M. Equilibrium forces on nonreciprocal materials. Phys. Rev. B 2022, 106, 115106. [Google Scholar] [CrossRef]
- Rodriguez, A.W.; Capasso, F.; Johnson, S.G. The Casimir effect in microstructured geometries. Nat. Photon. 2011, 5, 211–221. [Google Scholar] [CrossRef]
- Javor, J.; Yao, Z.; Imboden, M.; Campbell, D.K.; Bishop, D.J. Analysis of a Casimir-driven parametric amplifier with resilience to Casimir pull-in for MEMS single-point magnetic gradiometry. Microsyst. Nanoeng. 2021, 7, 73. [Google Scholar] [CrossRef] [PubMed]
- Munday, J.N.; Iannuzzi, D.; Barash, Y.; Capasso, F. Torque on birefringent plates induced by quantum fluctuations. Phys. Rev. A 2005, 71, 042102. [Google Scholar] [CrossRef]
- Broer, W.; Lu, B.; Podgornik, R. Qualitative chirality effects on the Casimir-Lifshitz torque with liquid crystals. Phys. Rev. Res. 2021, 3, 033238. [Google Scholar] [CrossRef]
- Boström, M.; Sernelius, B.E. Thermal effects on the Casimir force in the 0.1–5 μm range. Phys. Rev. Lett. 2000, 84, 4757–4760. [Google Scholar] [CrossRef] [PubMed]
- Genet, C.; Lambrecht, A.; Reynaud, S. Temperature dependence of the Casimir effect between metallic mirrors. Phys. Rev. A 2000, 62, 012110. [Google Scholar] [CrossRef]
- Bordag, M.; Geyer, B.; Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir force at both nonzero temperature and finite conductivity. Phys. Rev. Lett. 2000, 85, 503–506. [Google Scholar] [CrossRef] [PubMed]
- Milton, K.A. The Casimir effect: Recent controversies and progress. J. Phys. A Math. Gen. 2004, 37, R209–R277. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Svetovoy, V.B. Probing the response of metals to low-frequency s-polarized evanescent fields. Europhys. Lett. 2022, 139, 66001. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhital, M.; Mohideen, U. A Brief Review of Some Recent Precision Casimir Force Measurements. Physics 2024, 6, 891-904. https://doi.org/10.3390/physics6020055
Dhital M, Mohideen U. A Brief Review of Some Recent Precision Casimir Force Measurements. Physics. 2024; 6(2):891-904. https://doi.org/10.3390/physics6020055
Chicago/Turabian StyleDhital, Madhav, and Umar Mohideen. 2024. "A Brief Review of Some Recent Precision Casimir Force Measurements" Physics 6, no. 2: 891-904. https://doi.org/10.3390/physics6020055
APA StyleDhital, M., & Mohideen, U. (2024). A Brief Review of Some Recent Precision Casimir Force Measurements. Physics, 6(2), 891-904. https://doi.org/10.3390/physics6020055




