Present Status of Spectroscopy of the Hyperfine Structure and Repolarization of Muonic Helium Atoms at J-PARC
Abstract
1. Introduction
2. Theoretical Backgrounds of the Experiment
2.1. Breit–Rabi Equation
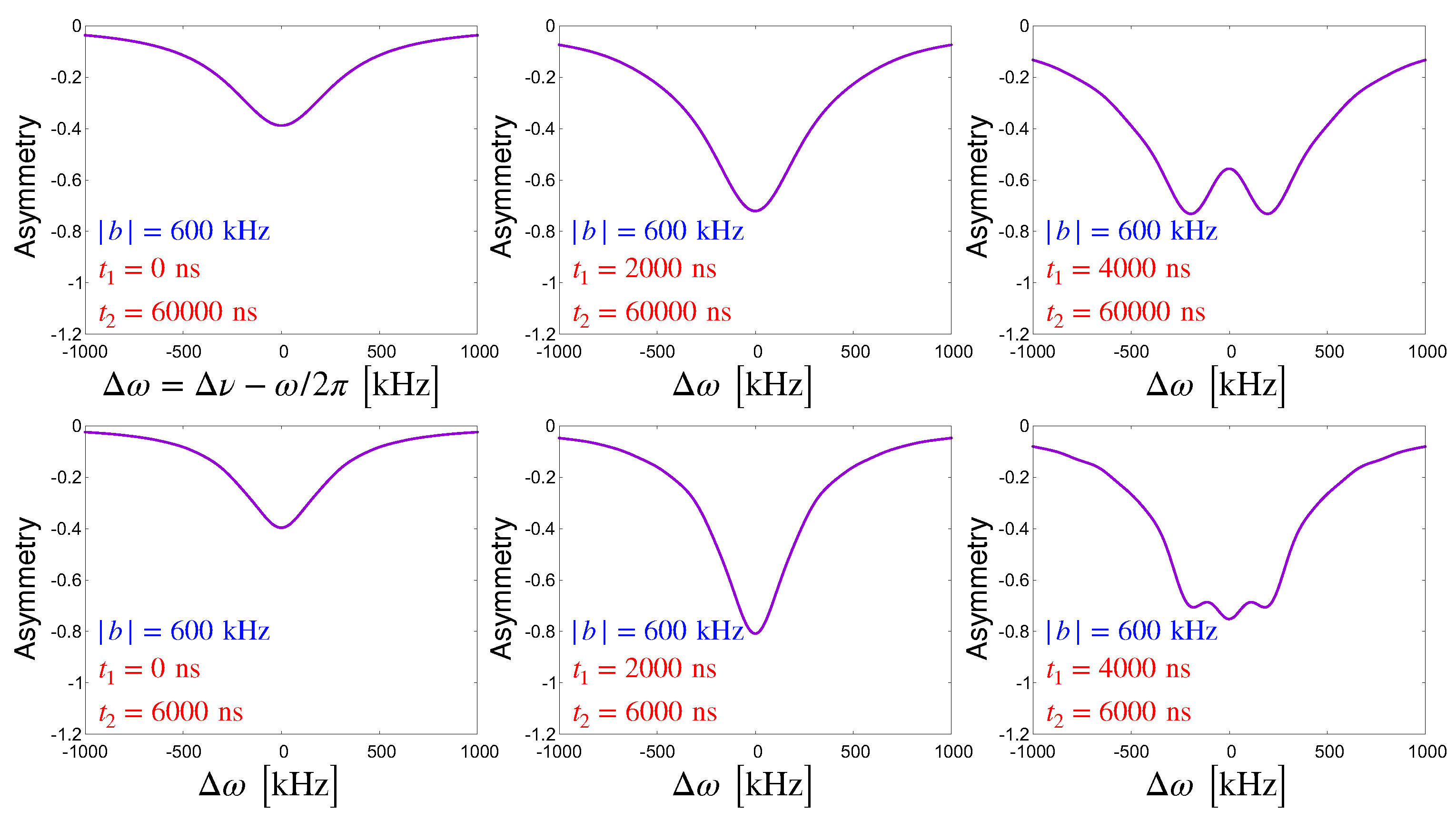
2.2. Resonance Curve
2.3. Pressure Shift
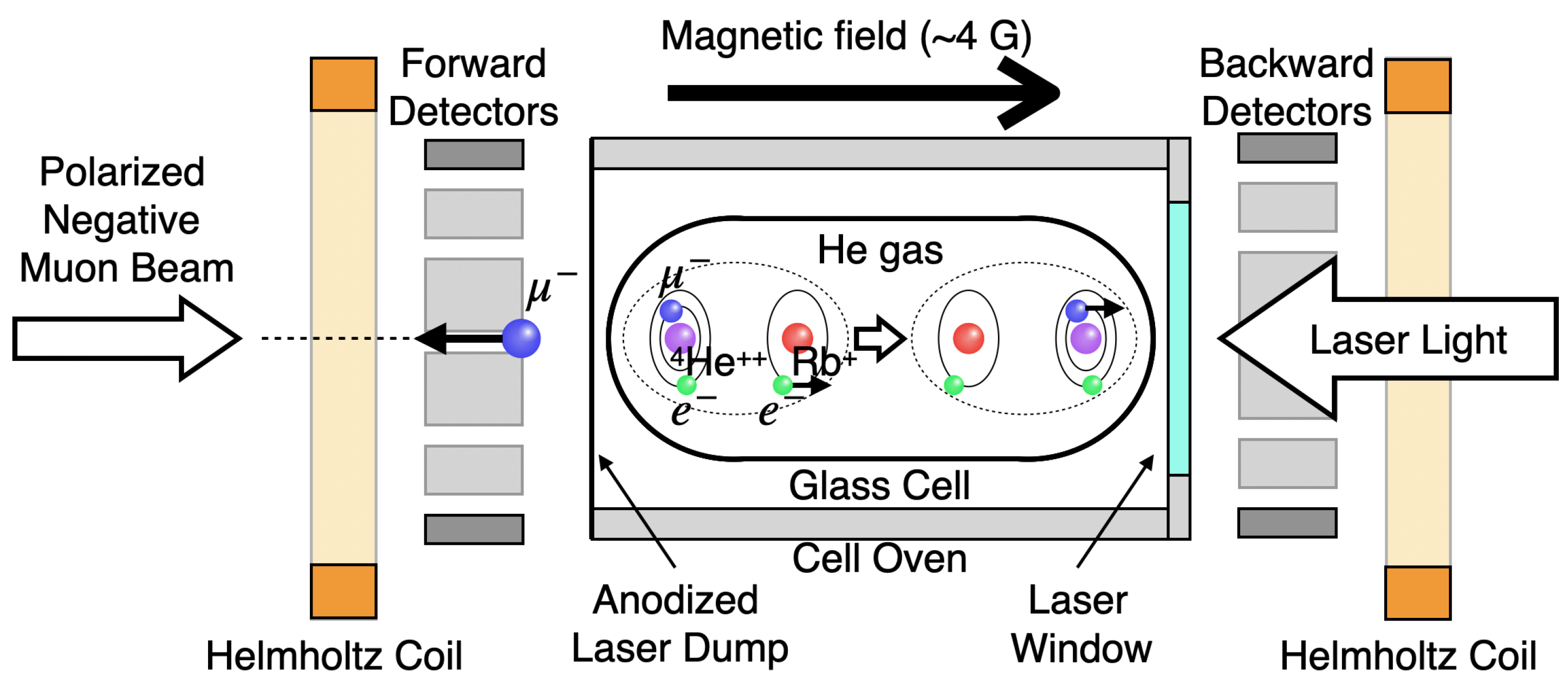
3. HFS Measurement
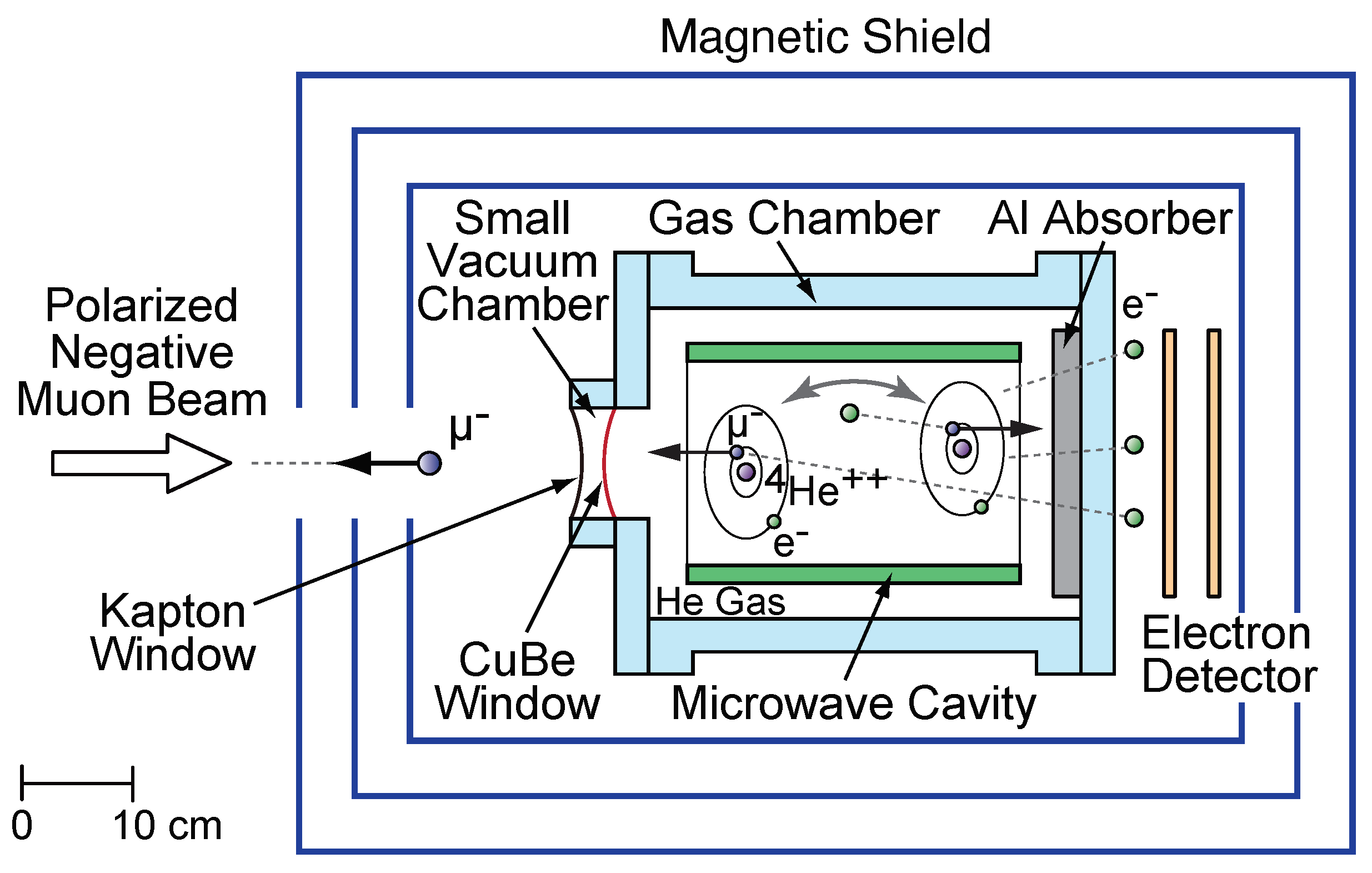
3.1. Apparatus
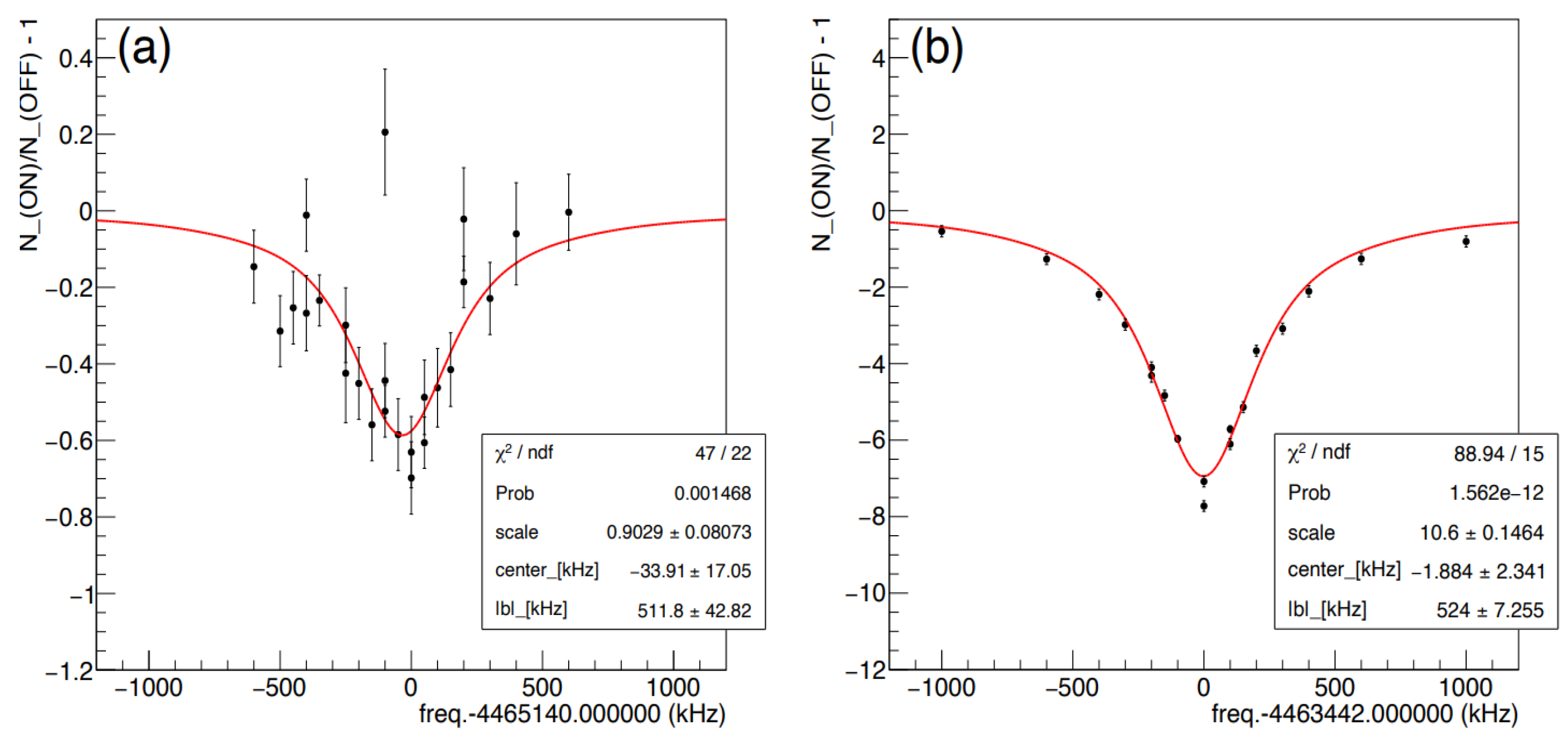
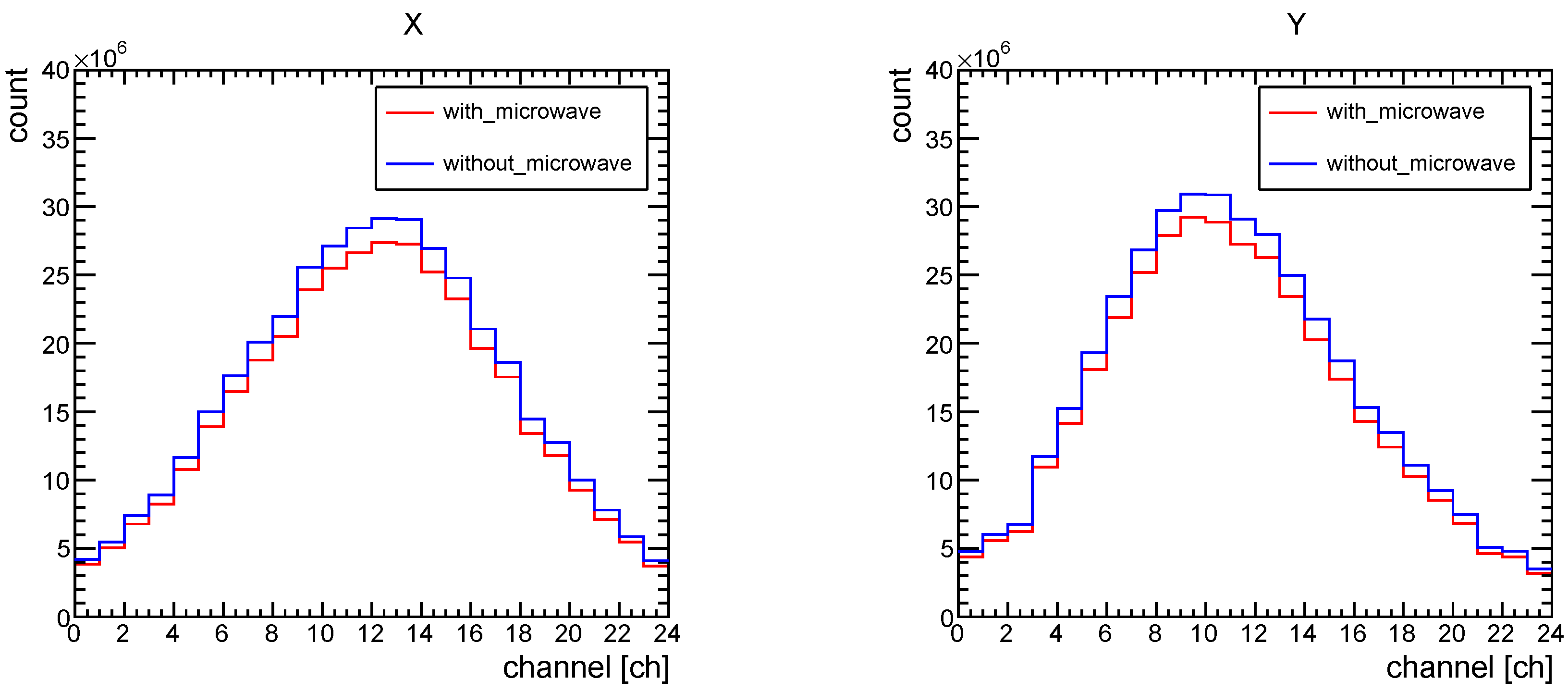
3.2. Analysis
4. Discussion
- to determine whether the particle decays every 1 ns;
- if the particle it does not decay, to determine whether spin exchange with alkali metals occurs;
- if the decay or spin exchange occurs, to determine the current state of the particle;
- if the spin exchange occurs, in subsequent calculations, the current time is considered to be , and the spin-exchange probability and the existence probability of each state are considered been determined.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BWD | backward (downstream) |
| CPT | charge–parity–time |
| CW | continuous wave |
| EDM | electric dipole moment |
| FWD | forward (upstream) |
| GE | General Electric |
| HFS | hyperfine structure |
| J-PARC | Japan Proton Accelerator Research Complex |
| MC | Monte Carlo |
| MRI | magnetic resonance imaging |
| MUSE | Muon Science Establishment |
| MuSEUM | Muonium Spectroscopy Experiment Using Microwave |
| NMR | nuclear magnetic resonance |
| ppb | parts per billion () |
| ppm | parts per million () |
| QED | quantum electrodynamics |
| SEOP | spin exchange optical pumping |
References
- Souder, P.A.; Crane, T.W.; Hughes, V.W.; Lu, D.C.; Orth, H.; Reist, H.W.; Yam, M.H.; Putlitz, G.z. Formation of the muonic helium atom. Phys. Rev. A 1980, 22, 33–50. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data; CRC Press, Inc.: Boca Raton, FL, USA, 1992; pp. 10-211–10-213. Available online: https://archive.org/details/hdbkofchemistryp00unse (accessed on 27 April 2024).
- Strasser, P. et al. [MuSEUM Collaboration] Improved measurements of muonic helium ground-state hyperfine structure at a near-zero magnetic field. Phys. Rev. Lett. 2023, 131, 253003. [Google Scholar] [CrossRef] [PubMed]
- Kanda, S.; Fukao, Y.; Ikedo, Y.; Ishida, K.; Iwasaki, M.; Kawall, D.; Kawamura, N.; Kojima, K.M.; Kurosawa, N.; Matsuda, Y.; et al. New precise spectroscopy of the hyperfine structure in muonium with a high-intensity pulsed muon beam. Phys. Lett. B 2021, 815, 136154. [Google Scholar] [CrossRef]
- Nishimura, S. et al. [MuSEUM Collaboration] Rabi-oscillation spectroscopy of the hyperfine structure of muonium atoms. Phys. Rev. A 2021, 104, L020801. [Google Scholar] [CrossRef]
- Tanaka, K.S.; Iwasaki, M.; Kamigaito, O.; Kanda, S.; Kawamura, N.; Matsuda, Y.; Mibe, T.; Nishimura, S.; Saito, N.; Sakamoto, N.; et al. Development of microwave cavities for measurement of muonium hyperfine structure at J-PARC. Prog. Theor. Exp. Phys. 2021, 2021, 053C01. [Google Scholar] [CrossRef]
- Schmid, E.W.; Ziegelmann, H. The Quantum Mechanical Three-Body Problem; Friedr. Vieweg + Sohn: Braunschweig, Germany; Pergamon Press: Oxford, UK, 1974. [Google Scholar] [CrossRef]
- Mann, R.A.; Rose, M.E. Depolarization of negative μ mesons. Phys. Rev. 1961, 121, 293–301. [Google Scholar] [CrossRef]
- Shmushkevich, I.M. Depolarization of μ−-mesons in μ-mesic atom formation. Nucl. Phys. 1959, 11, 419–431. [Google Scholar] [CrossRef]
- Mukhopadhyay, N.C. Nuclear muon capture. Phys. Rep. 1977, 30, 1–144. [Google Scholar] [CrossRef]
- Koike, T.; Akaishi, Y. Stark mixing in the exotic helium atom cascade process. Nucl. Phys. A 1998, 639, 521c–524c. [Google Scholar] [CrossRef]
- Hughes, V.W.; Putlitz, G.z. Muonium. In Quantum Electro-Dynamics; Kinoshita, T., Ed.; World Scientific: Singapore, 1990; pp. 822–904. [Google Scholar] [CrossRef]
- Bailey, J.M.; Cleland, W.E.; Hughes, V.W.; Prepost, R.; Ziock, K. Muonium. II. Observation of the muonium hyperfine-structure interval. Phys. Rev. A 1971, 3, 871–884. [Google Scholar] [CrossRef]
- Cleland, W.E.; Bailey, J.M.; Eckhause, M.; Hughes, V.W.; Prepost, R.; Rothberg, J.E.; Mobley, R.M. Muonium. III. Precision measurement of the muonium hyperfine-structure interval at strong magnetic field. Phys. Rev. A 1972, 5, 2338–2356. [Google Scholar] [CrossRef]
- Thompson, P.A.; Crane, P.; Crane, T.; Amato, J.J.; Hughes, V.W.; Putlitz, G.z.; Rothberg, J.E. Muonium. IV. Precision measurement of the muonium hyperfine-structure interval at weak and very weak magnetic fields. Phys. Rev. A 1973, 8, 86–112. [Google Scholar] [CrossRef]
- Sobel’man, I.I.; Vainshtein, L.A.; Yukov, E.A. Excitation of Atoms and Broadening of Spectral Lines; Springer: Berlin/Heidelberg, Germany, 1995; pp. 237–296. [Google Scholar] [CrossRef]
- Torii, H.A. Laser Spectroscopy of Antiprotonic Helium Atomcules-Collisional Shift and Broadening of Resonance Lines. Ph.D. Thesis, Tokyo University, Tokyo, Japan, 1997. [Google Scholar]
- Berkowitz, J.; Greene, J.P.; Cho, H.; Ruscić, B. The ionization potentials of CH4 and CD4. J. Chem. Phys. 1987, 86, 674–676. [Google Scholar] [CrossRef]
- Orth, H.; Arnold, K.-P.; Egan, P.O.; Gladisch, M.; Jacobs, W.; Vetter, J.; Wahl, W.; Wigand, M.; Hughes, V.W.; Putlitz, G.z. First observation of the ground-state hyperfine-structure resonance of the muonic helium atom. Phys. Rev. Lett. 1980, 45, 1483–1486. [Google Scholar] [CrossRef]
- Gardner, C.J.; Badertscher, A.; Beer, W.; Bolton, P.R.; Egan, P.O.; Gladisch, M.; Greene, M.; Hughes, V.W.; Lu, D.C.; Mariam, F.G.; et al. Precise measurement of the hyperfine-structure interval and Zeeman effect in the muonic helium atom. Phys. Rev. Lett. 1982, 48, 1168–1171. [Google Scholar] [CrossRef]
- Arseneau, D.J.; Fleming, D.G.; Li, Y.; Li, J.; Suleimanov, Y.V.; Guo, H. Rate coefficient for the 4Heμ++CH4 reaction at 500 K: Comparison between theory and experiment. J. Phys. Chem. B 2016, 120, 1641–1648. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.D.; Orth, C.J.; Schillaci, M.E.; Naumann, R.A.; Daniel, H.; Springer, K.; Knowles, H.B. Chemical effects in negative muon capture in some ionic and covalent solids and ionic aqueous solutions. Phys. Rev. A 1976, 13, 43–53. [Google Scholar] [CrossRef]
- Suzuki, T.; Measday, D.F.; Roalsvig, J.P. Total nuclear capture rates for negative muons. Phys. Rev. C 1987, 35, 2212–2224. [Google Scholar] [CrossRef] [PubMed]
- Aznabayev, D.T.; Bekbaev, A.K.; Korobov, V.I. The hyperfine structure of the ground state in the muonic helium atoms. Phys. Part. Nucl. Lett. 2018, 15, 236–239. [Google Scholar] [CrossRef]
- Krutov, A.A.; Martynenko, A.P. Ground-state hyperfine structure of the muonic helium atom. Phys. Rev. A 2008, 78, 032513. [Google Scholar] [CrossRef]
- Patkóš, V.; Yerokhin, V.A.; Pachucki, K. Higher-order QED corrections to the hyperfine splitting in 3He. Phys. Rev. Lett. 2023, 131, 183001. [Google Scholar] [CrossRef]
- Beltrami, I.; Aas, B.; Beer, W.; de Chambrier, G.; Goudsmit, P.F.A.; von Ledebur, T.; Leisi, H.J.; Ruckstuhl, W.; Sapp, W.W.; Strassner, G.; et al. New precision measurements of the muonic 3d5/2–2p3/2 X-ray transition in 24Mg and 28Si: Vacuum polarisation test and search for muon-hadron interactions beyond QED. Nucl. Phys. A 1986, 451, 679–700. [Google Scholar] [CrossRef]
- Liu, W.; Boshier, M.G.; Dhawan, S.; van Dyck, O.; Egan, P.; Fei, X.; Perdekamp, M.G.; Hughes, V.W.; Janousch, M.; Jungmann, K.; et al. High precision measurements of the ground state hyperfine structure interval of muonium and of the muon magnetic moment. Phys. Rev. Lett. 1999, 82, 711–714. [Google Scholar] [CrossRef]
- Kawamura, N.; Aoki, M.; Doornbos, J.; Mibe, T.; Miyake, Y.; Morimoto, F.; Nakatsugawa, Y.; Otani, M.; Saito, N.; Seiya, Y.; et al. New concept for a large-acceptance general-purpose muon beamline. Prog. Theor. Exp. Phys. 2018, 11, 113G01. [Google Scholar] [CrossRef]
- Yamazaki, T.; Kawamura, N.; Shimomura, K.; Miyake, Y.; Oishi, Y.; Adachi, T.; Strasser, P.; Koda, A.; Fujimori, H.; Yuasa, T.; et al. New beamlines and future prospects of the j-parc muon facility. EPJ Web Conf. 2023, 282, 01016. [Google Scholar] [CrossRef]
- Yamanaka, T.; Aoyagi, T.; Ikeda, H.; Ikeno, M.; Ito, T.; Ueno, K.; Uchida, T.; Kawagoe, K.; Kishishita, T.; Kume, T.; et al. Positron tracking detector for J-PARC muon g−2/EDM experiment. Nucl. Instrum. Meth. Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2020, 958, 162786. [Google Scholar] [CrossRef]
- Aoyagi, T.; Honda, Y.; Ikeda, H.; Ikeno, M.; Kawagoe, K.; Kohriki, T.; Kume, T.; Mibe, T.; Namba, K.; Nishimura, S.; et al. Performance evaluation of a silicon strip detector for positrons/electrons from a pulsed a muon beam. J. Instrum. 2020, 15, P04027. [Google Scholar] [CrossRef]
- Sasaki, K.; Sugita, M.; Abe, M.; Iinuma, H.; Ogane, C.; Mibe, T.; Shimomura, K.; Ogitsu, T. Development of precise shimming technique with materials having low saturation magnetization. IEEE Trans. Appl. Supercond. 2022, 32, 9002107. [Google Scholar] [CrossRef]
- Tada, H.; Yoshizu, F.; Oyama, S.; Tanaka, T.; Sasaki, K.I.; Shimomura, K. Development of magnetic field mapping system for the MuSEUM experiment with high precision using CW-NMR probes. IEEE Trans. Appl. Supercond. 2022, 32, 9002205. [Google Scholar] [CrossRef]
- Casperson, D.; Crane, T.W.; Hughes, V.W. DA new high precision measurement of the muonium hyperfine structure interval Δν. Phys. Lett. B 1975, 59, 397–400. [Google Scholar] [CrossRef]
- Barton, A.S.; Bogorad, P.; Cates, G.D.; Mabuchi, H.; Middleton, H.; Newbury, N.R.; Holmes, R.; McCracken, J.; Souder, P.A.; Xu, J.; et al. Highly polarized muonic he produced by collisions with laser optically pumped Rb. Phys. Rev. Lett. 1993, 70, 758–761. [Google Scholar] [CrossRef] [PubMed]
- Okudaira, T.; Oku, T.; Ino, T.; Hayashida, H.; Kira, H.; Sakai, K.; Hiroi, K.; Takahashi, S.; Aizawa, K.; Endo, H.; et al. Development and application of a 3He neutron spin filter at J-PARC. Nucl. Instrum. Meth. Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2020, 977, 164301. [Google Scholar] [CrossRef]
- Babcock, E.; Nelson, I.; Kadlecek, S.; Driehuys, B.; Anderson, L.W.; Hersman, F.W.; Walker, T.G. Hybrid spin-exchange optical pumping of 3He. Phys. Rev. Lett. 2003, 91, 123003. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fukumura, S.; Strasser, P.; Fushihara, M.; Goto, Y.; Ino, T.; Iwai, R.; Kanda, S.; Kawamura, S.; Kitaguchi, M.; Nishimura, S.; et al. Present Status of Spectroscopy of the Hyperfine Structure and Repolarization of Muonic Helium Atoms at J-PARC. Physics 2024, 6, 877-890. https://doi.org/10.3390/physics6020054
Fukumura S, Strasser P, Fushihara M, Goto Y, Ino T, Iwai R, Kanda S, Kawamura S, Kitaguchi M, Nishimura S, et al. Present Status of Spectroscopy of the Hyperfine Structure and Repolarization of Muonic Helium Atoms at J-PARC. Physics. 2024; 6(2):877-890. https://doi.org/10.3390/physics6020054
Chicago/Turabian StyleFukumura, Seiso, Patrick Strasser, Mahiro Fushihara, Yu Goto, Takashi Ino, Ryoto Iwai, Sohtaro Kanda, Shiori Kawamura, Masaaki Kitaguchi, Shoichiro Nishimura, and et al. 2024. "Present Status of Spectroscopy of the Hyperfine Structure and Repolarization of Muonic Helium Atoms at J-PARC" Physics 6, no. 2: 877-890. https://doi.org/10.3390/physics6020054
APA StyleFukumura, S., Strasser, P., Fushihara, M., Goto, Y., Ino, T., Iwai, R., Kanda, S., Kawamura, S., Kitaguchi, M., Nishimura, S., Oku, T., Okudaira, T., Shimizu, H. M., Shimomura, K., Tada, H., & Torii, H. A. (2024). Present Status of Spectroscopy of the Hyperfine Structure and Repolarization of Muonic Helium Atoms at J-PARC. Physics, 6(2), 877-890. https://doi.org/10.3390/physics6020054




