Avogadro and Planck Constants, Two Pillars of the International System of Units

Abstract

The International System of Units (SI), the current form of the metric system and the world’s most used system of units, has been continuously updated and refined since the Metre Convention of 1875 to ensure that it remains up to date with the latest scientific and technological advances. The General Conference on Weights and Measures, at its 26th meeting in 2018, decided to adopt stipulated values of seven physical constants linked to seven measurement units (the second, meter, kilogram, ampere, kelvin, mole, and candela). This paper reviews the technologies developed, in intense and long-standing work, to determine the Avogadro and Planck constants, which are now integral to realising the kilogram.

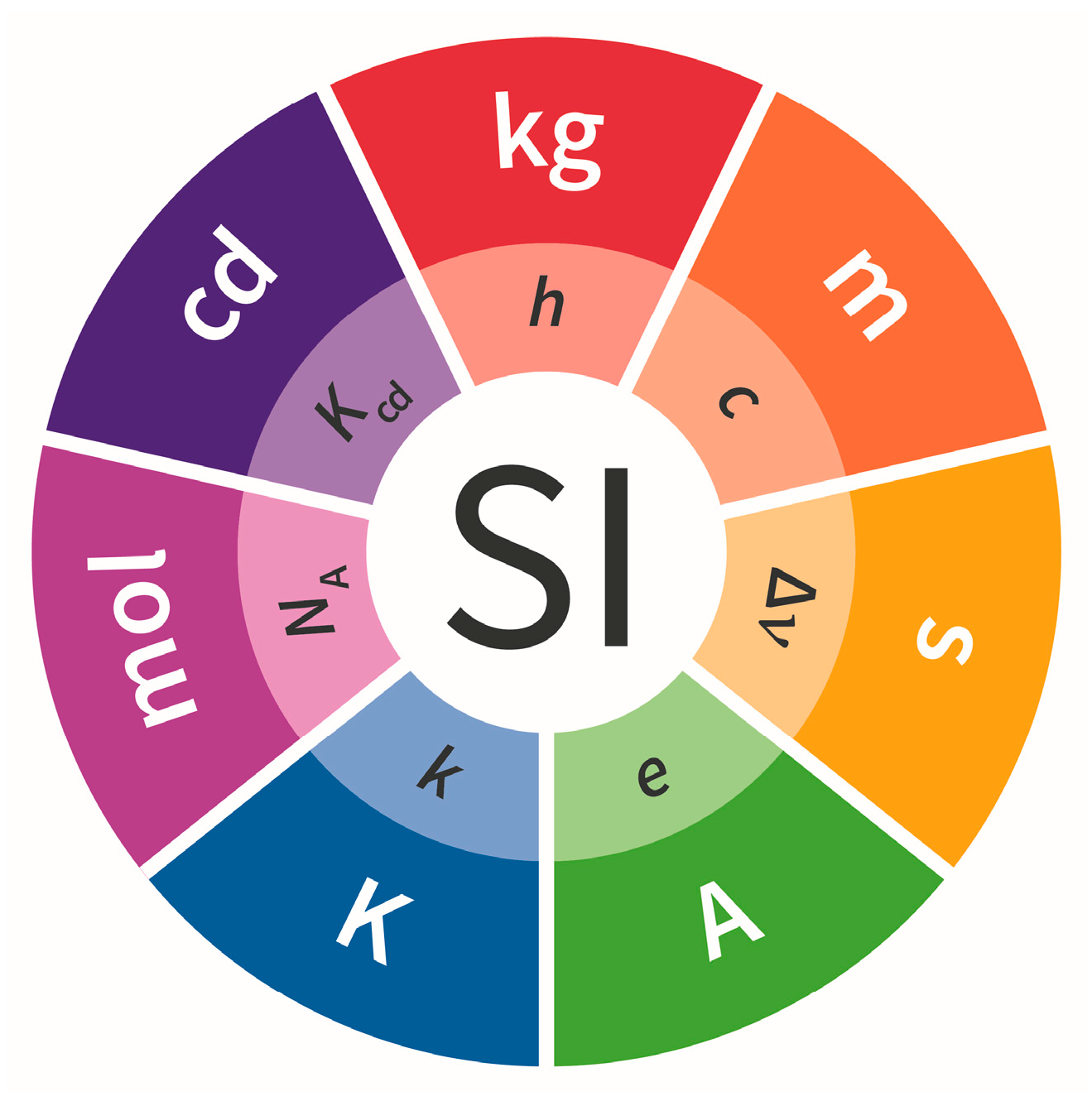
1. Introduction

In ancient times, various civilizations developed methods for measuring physical quantities, such as mass, length, volume, and time. The ancient Egyptians developed beam balances, which were depicted in the Book of the Dead [1]. This book describes the “weighing of the heart” or “judgment of Osiris”. According to Egyptian mythology, after a person dies, the fate in the afterlife is determined by weighing the heart against a feather, where the feather acts as the reference standard for the unit of measure. If the heart is heavier than the feather, Ammit (the swallower of the dead) will eat the heart, and the death will be forever. If the scale remains balanced, the soul will join Osiris, the king of the blessed dead, for eternity.

Outside of mythology, for unit systems to be usable in everyday life, trade, and science, the units need to be standardized. This process began by using locally available materials and artefacts, such as body parts like feet and hands, as length standards. The metric system, which was established during the French Revolution, used natural quantities to create a system of units that would apply to all people, for all time. The meter was defined as the length of a meridian arc, and the kilogram was defined as the mass of one cubic decimeter of pure water at its maximum density. To ensure stability and practical realization, platinum prototypes of the meter and kilogram were created in 1799 and stored as references in the Archives de la République in Paris.

To implement a worldwide common system of units, on the 20 May 1875, the representatives of seventeen nations signed an international treaty commonly known as the Metre Convention [2]. The Metre Convention established the International Bureau of Weights and Measures (commonly referred to as BIPM by its French name), in Sèvres, France, charged with maintaining new international prototypes, the meter, (which—as with the Metre of the Archives—was significantly easy to use and durable) and the kilogram and to act as the repository of the physical measurement standards. The new kilogram, whose mass was essentially the same as the Kilogram of the Archives, was made from an alloy of platinum and iridium from a batch of material provided by Johnson, Matthey & Co., London, UK in 1880 [3] and called the International Prototype of the Kilogram [4] (IPK, also referred to by the metrologists as Le Grand K).

Before 1889, there was no official definition for the kilogram. It was only in that year, during the 1st General Conference on Weights and Measures (CGPM, Conférence Générale des Poids et Mesures, in French), that the mass of the IPK was established as being equal to 1 kg. The CGPM sanctioned that “this prototype shall henceforth be considered to be the unit of mass” [5]. Since then, this prototype has defined the kilogram and is kept in a BIPM’s vault. In 1901, the 3rd CGPM confirmed that “the kilogram is the unit of mass; it is equal to the mass of the International Prototype of the Kilogram” [6]. This statement was intended to end the ambiguity of using the word weight for mass. Because of these definitions, the mass of the international prototype is exactly equal to 1 kg and raised to the status of a universal constant.

After three verifications were carried out in 1889, 1946, and 1991 [7], the mass difference between the international prototype and its official copies, known as ‘’témions”, has been observed to drift by about 50 μg per century. However, instead of all témions and many national copies drifting similarly, the observations pointed to the instability of the mass of the international prototype itself, despite being defined as invariant. The kilogram definition by an artefact caused concern among metrologists, who seek a new definition that allows for the measurement of the prototype mass’s changes.

The masses of témions were remeasured against the international prototype in 2014 [8] in anticipation of the redefinition of the kilogram (see Figure 1). This has resulted in the discovery of a 35 μg offset between the BIPM “as-maintained” mass unit and the mass of the international prototype. This offset further highlights the inadequacy of a definition based on a material artefact.

Although a variety of processes (e.g., surface contamination, alloying, and the diffusion of included hydrogen) might explain the mass drift, its reason is still experimentally unexplained. To tackle this issue, metrologists have come up with two (redundant and independent) methods of realizing the mass unit: the Kibble balance (KB, previously known as watt balance), linking the kilogram to the Planck constant; and the X-Ray Crystal Density (XRCD) method, linking the kilogram to the Avogadro constant. These two measurement methods have, since the 1980s, played a crucial role in the effort to redefine the International System of Units (SI, Système International d’unités, in French), aligning it with our understanding of how nature behaves.

2. From Mass Artefacts to Physical Constants

In 1870, following the footsteps of the French revolutionaries, James Clerk Maxwell [9] suggested that physical units should not be founded on macroscopic quantities but on the properties of these “imperishable and unalterable” molecules. Later in 1899, Max Planck proposed a system of units that relied solely on universal constants [10].

The vision of the French revolutionaries, Maxwell and Planck to have a system of units based on natural constants was finally realized on 20 May 2019. Quantum mechanics and the semiconductor industry are deeply involved in replacing the kilogram artefact with realizations based on fundamental constants of physics.

In 1963, Claudio Egidi [11] proposed the idea of a mass standard that could be established using a crystal made up of a known number of atoms. He envisioned a perfect cubic crystal where the atoms are arranged regularly in the crystal lattice. By calculating the ratio of the macroscopic volume to the volume of a single atom, it is possible to determine the number of atoms. Once the atom had been established as the mass standard, the mass of the cube could be determined.

In 1965, Ulrich Bonse and Michael Hart [12] operated the first X-ray interferometer and paved the way for the achievement of Egidi’s dream. Soon, Richard Deslattes and colleagues [13] used an X-ray interferometer to measure the lattice parameter of a silicon crystal, completed the first count of the atoms in a natural silicon crystal, and established a link between the kilogram and the Avogadro constant. To bypass limitations of the measurement accuracy due to the indirect determination of the silicon density and natural silicon [14] occurring in three isotopes, Gianfranco Zosi proposed to count the atoms in a sphere highly enriched with the isotope 28 and demonstrated that polishing perfect silicon spheres is possible [15,16].

To ensure that no discontinuity is produced to the 1901 definition, it was necessary for the mass of the ²⁸Si atom and, equivalently, for the Avogadro constant, to be more accurately measured in terms of the mass of the Pt–Ir prototype. Next, by reversing the experiment, the mass can be determined in terms of a (suitably) fixed value of the Avogadro constant.

In 2004, following Egidi and Zosi, a group of metrology laboratories, including the BIPM, INRiM (Italy), IRMM (Belgium), NMIA (Australia), NMIJ (Japan), NPL (UK), and PTB (Germany), combined their resources and expertise by launching an International Avogadro Coordination (IAC) to grow a silicon crystal enriched with ²⁸Si. The goal was twofold: firstly, to accurately determine the Avogadro constant, $N_A$ [17,18,19,20,21]; secondly, to demonstrate that realizing a mass standard by counting ²⁸Si atoms was technologically possible.

In addition to the enrichment and growth of a hyper-pure and perfect crystal, several critical technologies needed to be developed ex novo. X-ray and optical interferometry were pushed to their limits, first by Giovanni Mana and colleagues [22] and then by the author of the present paper and colleagues [23]. The PTB and NMIJ laboratories developed new ways to measure the volume of silicon balls and characterize their surface layers in terms of thickness and chemical compositions [24,25]. Eventually, to determine the isotopic composition of the enriched crystal, PTB laboratory invented a new procedure of trace element analysis [26]. The IAC results are reported in a special issue of Metrologia published in 2011 [27].

To link a physical constant, precisely the Planck one, to the unit of mass, there is a second method. In 1976, Bryan Kibble developed a new way to realize the SI ampere [28]. This apparatus allowed electrical metrology to be accurately based on conventional electrical units but set it apart from the SI. By operating the “ampere current balance” in the reverse mode, the Kibble apparatus was subsequently perfected and evolved by Ian Robinson at the NPL [29], by Stephan Schlamminger and colleagues at the NIST [30], by Carlos Sanchez and colleagues at the NRC [31], and by Matthieu Thomas and colleagues at the LNE [32] into a balance comparing mechanical and electrical powers. As in the case of the XRCD experiment, before a kilogram realization based on this balance was possible, it was used to measure the Planck constant, h, in terms of the 1901 definition of the kilogram. Nowadays, it is run in reverse, realizes the mass unit from the Planck constant, and was renamed, firstly, watt balance and, next, Kibble balance. It is worth noting that the Rydberg, fine structure, Planck, and Avogadro constants—$R_{\infty }$, α, $h$, and $N_A$, respectively,—the speed of light, $c$, and the molar mass, $M_e$, of the electron, are interrelated by [33]

$$2R_{\infty }hc=\frac{{\alpha }^2{M}_e{c}^2}{N_A} .$$

(1)

This relationship implies that the accurate determinations of $R_{\infty }$, α, and $M_e$ determine the molar Planck constant as

$$N_{A}h=\frac{{\alpha }^2{M}_{e}c}{2R_{\infty }} .$$

(2)

The result of the XRCD experiment delivered, de facto, also an accurate value of the Planck constant. Vice versa, the Kibble balance delivered, de facto, is also an accurate value of the Avogadro constant.

The ’’tour de force’’ for the determination of Avogadro and Planck constants sped up in 2005, after the publication of a paper [34] claiming that the “time for the redefinition of the kilogram had come”.

The CGPM was already looking at the redefinition of the kilogram. In 1999, the 21st CGPM recommended that metrologists “continue their efforts to refine experiments that link the unit of mass to fundamental or atomic constants…” (Resolution 7: The definition of the kilogram [35]). In 2007, the 23rd CGPM recommended that metrologists make it possible “to redefine the kg, the ampere, the kelvin, and the mole using fixed values of the fundamental constants at the time of the next 24th CGPM” (Resolution 12: On the possible redefinition of certain base units of the International System of Units (SI) [36]). At that time, the main impediment to redefining the kilogram was the discrepancy of about one part in 10⁶ between the results of the Planck and Avogadro constants measurements, which were compared via the well-measured molar Planck constant value.

After significant progress in Kibble balance technology and XRCD experiments, in 2011, the 24th CGPM established the bases of the revised SI and proposed wording for the definitions of the base units (Resolution 1: On the possible future revision of the International System of Units, the SI [37]). In 2014, the 25th CGPM asked “to complete all work necessary for the CGPM at its 26th Meeting to adopt a resolution that would replace the current SI with the revised SI, provided the amount of data, their uncertainties, and level of consistency are deemed satisfactory” (Resolution 1: On the future revision of the International System of Units, the SI [38]).

At the same time, the Consultative Committee for Mass and Related Quantities (CCM) defined the requirements and, jointly with the Consultative Committee for Units (CCU) of the International Committee for Weights and Measures (CIPM, Comité International des Poids et Mesures, in French), the roadmap to make the redefinition of the kilogram possible [39].

The metrologists and CCM aimed for both agreement and low uncertainties of the measured values of the Planck and Avogadro constants. To achieve this, the CCM made a recommendation “On a new definition of the kilogram” in its 14th Meeting [40]. This recommendation put forward four conditions.

The first condition is that at least three independent experiments, including the Kibble balance and XRCD one, should yield consistent results of the measurements of the Planck and Avogadro constants with relative standard uncertainties not larger than 5 parts in 10⁸.

The second condition states that the uncertainty associated with at least one measurement result should not be larger than 2 parts in 10⁸.

The third condition requires that the measurement results be traceable to the masses of the BIPM’s mass standards and the international prototype of the kilogram.

The fourth condition is to validate the ‘’mise en pratique’’ [41] of the new kilogram definition following the principles of the CIPM-MRA (Mutual Recognition Arrangement).

These requirements were successfully fulfilled at the time of the 16th Meeting of the CCM in 2017. As a result, the scientific work aimed at redefining the kilogram was concluded and the CGPM, at its 26th Meeting, rebuilt the SI. The redefinition led to the kilogram, ampere, kelvin, and mole, which were previously defined in terms of material artefacts or properties, being redefined through their linkage to stipulated values of fundamental constants of physics.

3. The Realization of the Kilogram

In the new SI, the kilogram is defined in terms of the Planck constant, which was previously determined (in terms of the 1901 definition of the kilogram) via the Kibble balance and XRCD experiment. The formal kilogram definition now reads [41]: “The kilogram, with the symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be h = 6.62607015 × 10⁻³⁴ when expressed in the unit J s, which is equal to m² kg s⁻¹, where the meter and the second are defined in terms of c and Δν_Cs’’.

Therefore, the Planck constant is conventionally stipulated to be h = 6.62607015 × 10⁻³⁴ J s, where c and Δν_Cs are the speed of light and the unperturbed ground-state hyperfine transition frequency of the ¹³³Cs atom, respectively. The numerical value of the Planck constant sets the size of the kilogram. It was accurately chosen so that no gap could be detected between the new and past realizations, within the associated uncertainties. This value was the result of a least-squares adjustment (LSA) of the values of the fundamental physical constants provided in 2017 by the Committee on Data for Science and Technology (CODATA) through its Task Group on Fundamental Physical Constants. Figure 2 summarizes the best determination of the Planck constant. It shows the results of the measurements carried out from 2011 to 2017 by both the Kibble balance and XRCD experiments. The black dot is the value recommended by the CODATA in 2017 [42,43] and was adopted by the 26th CGPM to redefine the kilogram.

The definition of the kilogram does not provide any practical way to realize it. To address this, the CCM issued a mise en pratique [41], which explains how the definition can be realized. However, any procedure that derives the mass value in a way that can be traced back to the set of defined fundamental constants, within the stated uncertainty, can be considered a realization of the kilogram. Currently, only the XRCD and the KB experiments can realize the kilogram with relative uncertainties of a few parts in 10⁸, corresponding to a few tens of micrograms.

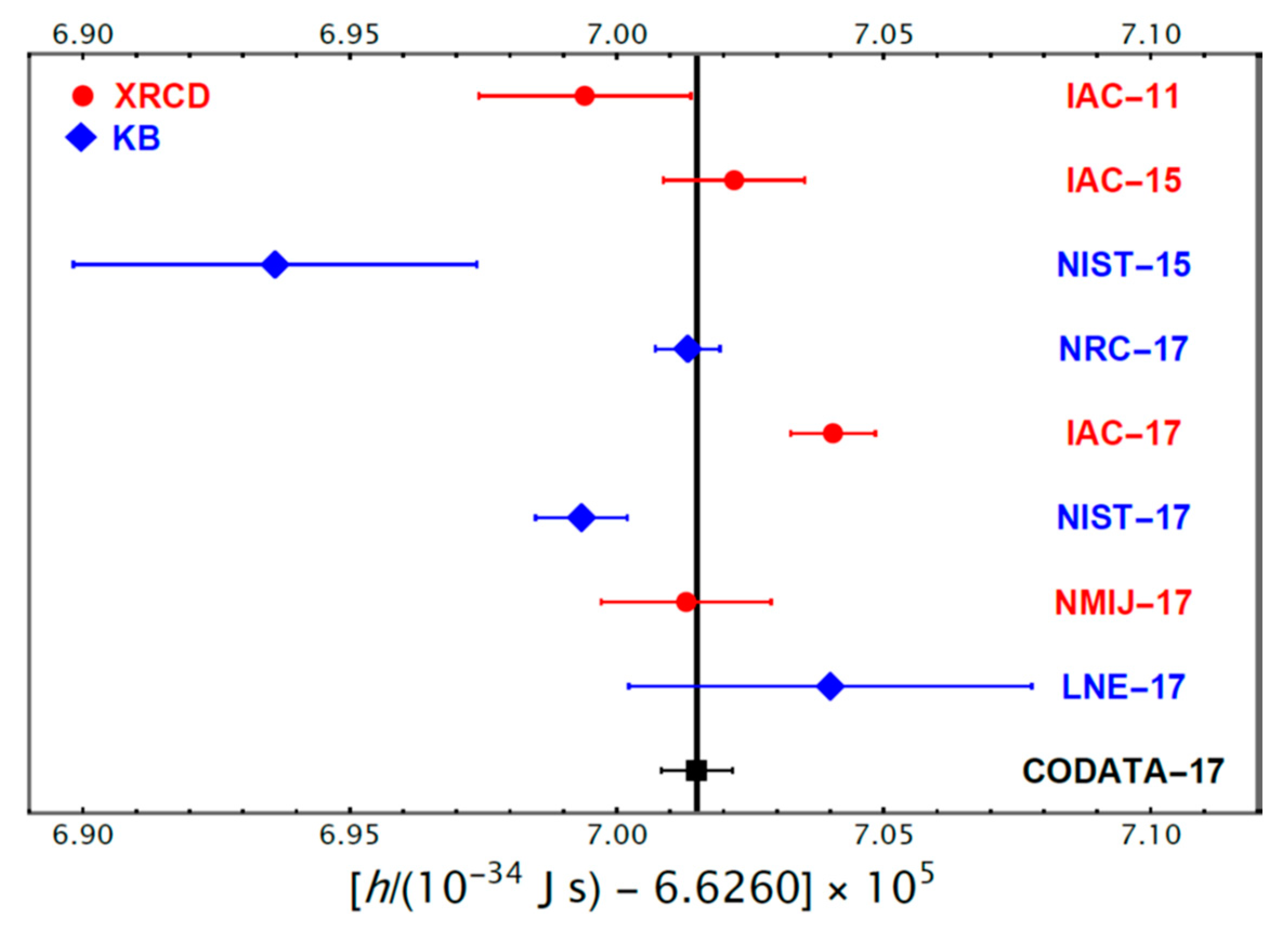
3.1. The XRCD Method

The XRCD method for the realization of the unit of mass is the reverse of the original experiment determining the Avogadro constant in terms of the kilogram prototype mass, where the measurement equation is solved for the mass of a perfect and hyper-pure Si crystal shaped as a nearly perfect sphere instead of for the Avogadro constant. The link to the Planck constant originates from the independent determination of the mass of the ²⁸Si atom, which is now needed.

According to this method, the measurement equation of the sphere mass is

$$m_{\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}}=Nm\left(\mathrm{S}\mathrm{i}\right)-m_{\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}}+m_{\mathrm{S}\mathrm{L}}=\frac{8V_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}}{a^3}m\left(\mathrm{S}\mathrm{i}\right)-m_{\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}}+m_{\mathrm{S}\mathrm{L}} ,$$

(3)

where N is the number of Si atoms in the Si core of the sphere, $m\left(\mathrm{S}\mathrm{i}\right)$ is the mass of the Si atom, $m_{\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}}$ is the mass defect or excess due to chemical impurities and crystal point defects (self-interstitials and vacancies), $m_{\mathrm{S}\mathrm{L}}$ is the mass of the surface layers (see Figure 3), $a^3$ is the (cubic) unit-cell volume, 8 is the number of Si atoms in the unit cell, and $V_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ is the volume of the Si core.

Since silicon occurs in three stable isotopes, $m\left(\mathrm{S}\mathrm{i}\right)$ is given by

$$m\left(\mathrm{S}\mathrm{i}\right)=\sum _{k=28}^{30}f\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)m\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right) ,$$

(4)

where $m\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)$ is the mass of the k-th isotope, and the amount-of-substance fractions, $f\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)$, of each isotope $\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)$ has to be measured. Taking the identity of the ratio of the masses of $\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)$ and the electron and the ratio of their relative masses, $A_r$, into account, the mass of $\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)$ can be obtained from the electron mass, $m\left(e\right)$, as

$$m\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)=\frac{A_r\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)}{A_r\left(e\right)}m\left(e\right) .$$

(5)

Ultimately, the electron mass is traced back to the Planck constant via the measurements of the Rydberg and fine-structure constants:

$$m\left(e\right)=\frac{{2hR}_{\infty }}{c{\alpha }^2} .$$

(6)

Combining Equations (3)–(6), the sphere mass is traced back to the Planck constant:

$$m_{\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}}=\frac{8V_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}}{a^3}\frac{2h{R}_{\infty }}{c{\alpha }^2}\left(\sum _{k=28}^{30}f\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)\frac{A_r\left({}^{\mathrm{k}}\mathrm{S}\mathrm{i}\right)}{A_r\left(e\right)}\right)-m_{\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}}+m_{\mathrm{S}\mathrm{L}} .$$

(7)

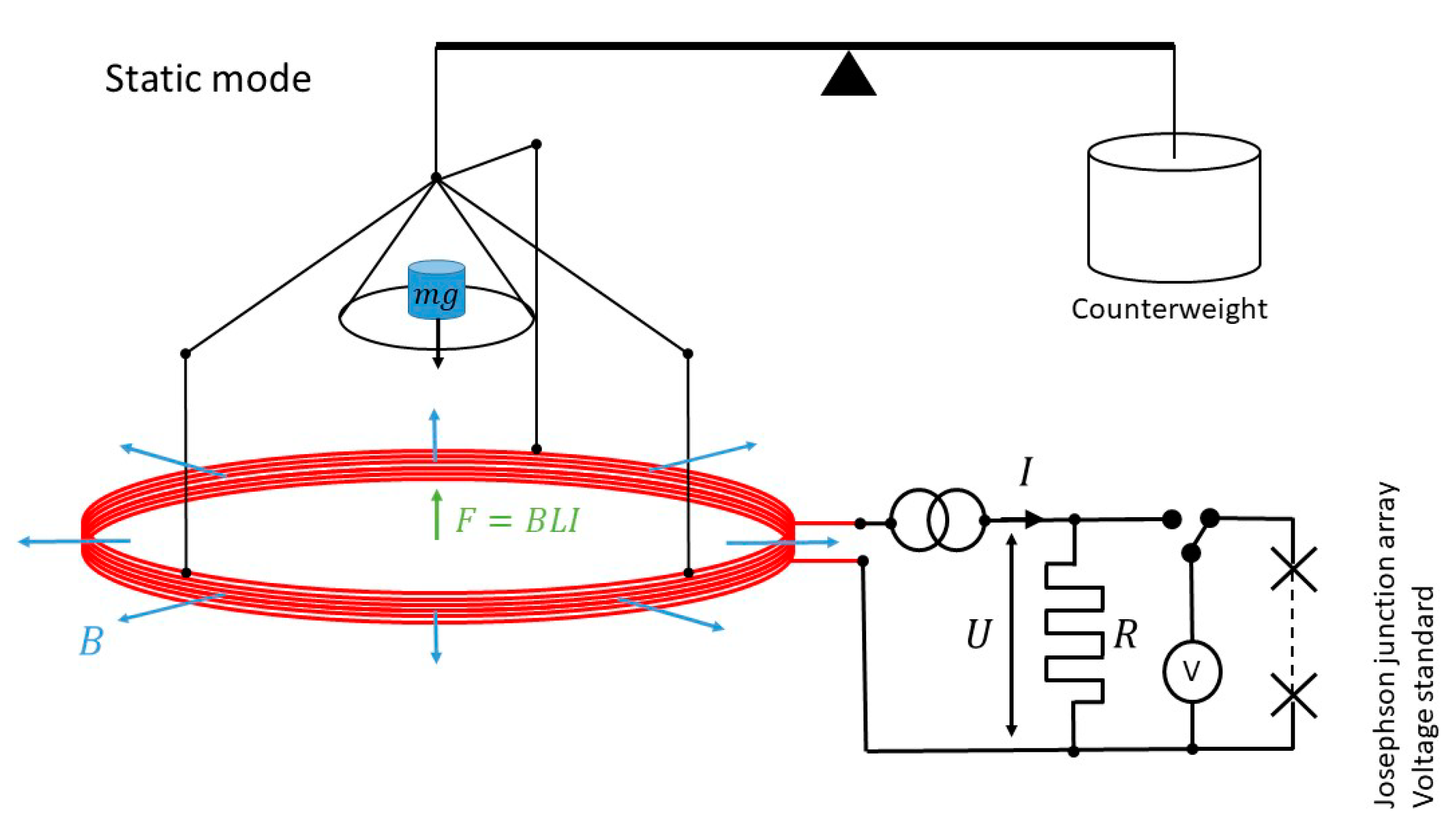
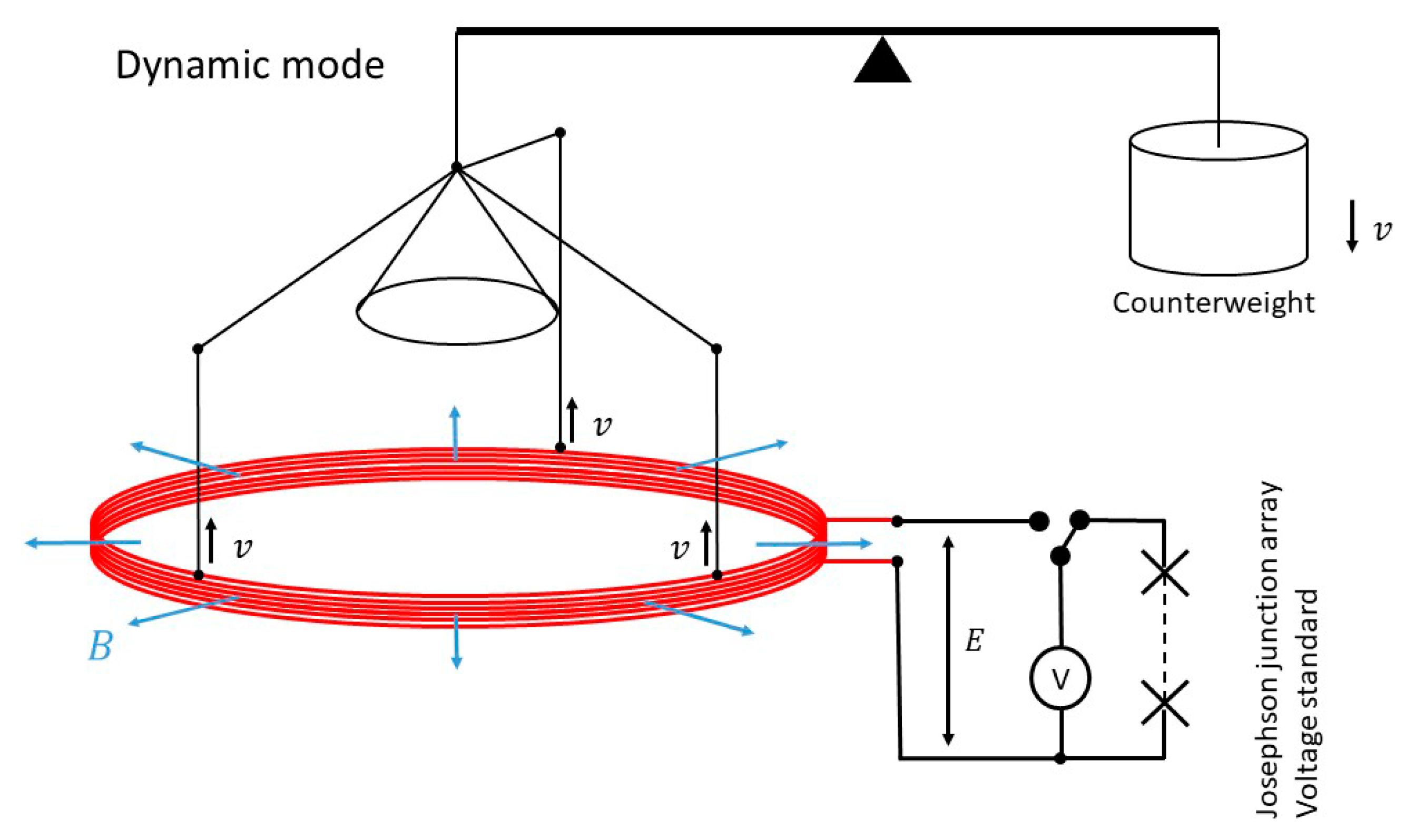
3.2. The Kibble Balance Method

The direct way to trace a mass to the Planck constant is by the Kibble balance. In this device, the mechanical and electrical powers produced by the mass motion in the Earth’s gravitational field and the motion of the supporting coil in a magnetic field are virtually compared. As shown in Figure 4, the comparison is carried out in two steps.

In the static or force mode, the balance comparesthe weight ($mg$, with $g$ the acceleration of gravity) and the Lorentz force $BLI$ are generated by the interaction of the electrical current $I$ flowing in the supporting coil of length $L$ and immersed in the magnetic field, $B$. Hence, by leaving out a vector notation,

$$mg=BLI.$$

(8)

In the dynamic or velocity mode, the coil is moved at constant velocity, $\nu$, and the induced electromotive force, $E$, is measured at its ends. Hence,

$$E=BL\nu .$$

(9)

The geometric term $BL$ appearing in both Equations (8) and (9) cannot be measured with the aimed 10⁻⁸ fractional accuracy. Therefore, it is eliminated to obtain the so-called watt equation (the name stems from both the mechanical and electrical powers being measured in the watt unit)

$$mg\nu =EI.$$

(10)

The electromotive force is measured via the Josephson effect as $E=n_1\left(h/2e\right)f_1$, where $n_1$ is an integer, $e$ is the elementary charge, and $f_1$ is the frequency irradiating the device. The current measurement, via the Ohm law, $I=U/R$, is based on both the Josephson effect (hence, $U=n_2\left(h/2e\right)f_2$), and the quantum Hall effect (hence, $R=r(h/e^2)$). Here, $n_2$ is an integer, $r$ is a unitless calibration factor, $f_2$ is a frequency irradiating the Josephson device, and the ratio, $R_k=h/e^2$, is known as the von Klitzing constant.

After using the above definitions in Equation (10), the $h/m$ ratio reads

$$\frac{h}{m}=\frac{4r}{{n_{1}n}_2}\frac{g\nu }{f_1{f}_2} .$$

(11)

This measurement equation, which was previously solved for $h$ (expressed in terms of the mass of the 1901 Pt-Ir prototype of the kilogram), expresses $m$ in terms of the stipulated values of the Planck constant, speed of light, and frequency splitting between the hyperfine levels of the ground state of the ¹³³Cs atom.

All the quantities on the right-hand side of Equation (11) are measured with uncertainties small enough to give $h/m$ with a relative uncertainty of 1 × 10⁻⁸. However, other sources of uncertainty, such as alignments, unwanted motion, and parasitic forces and torques, must be made harmless and still prevent this uncertainty from being reached. Detailed descriptions of the Kibble-balance experiments can be found in Refs. [29,30,31,32,45,46,47,48,49,50,51].

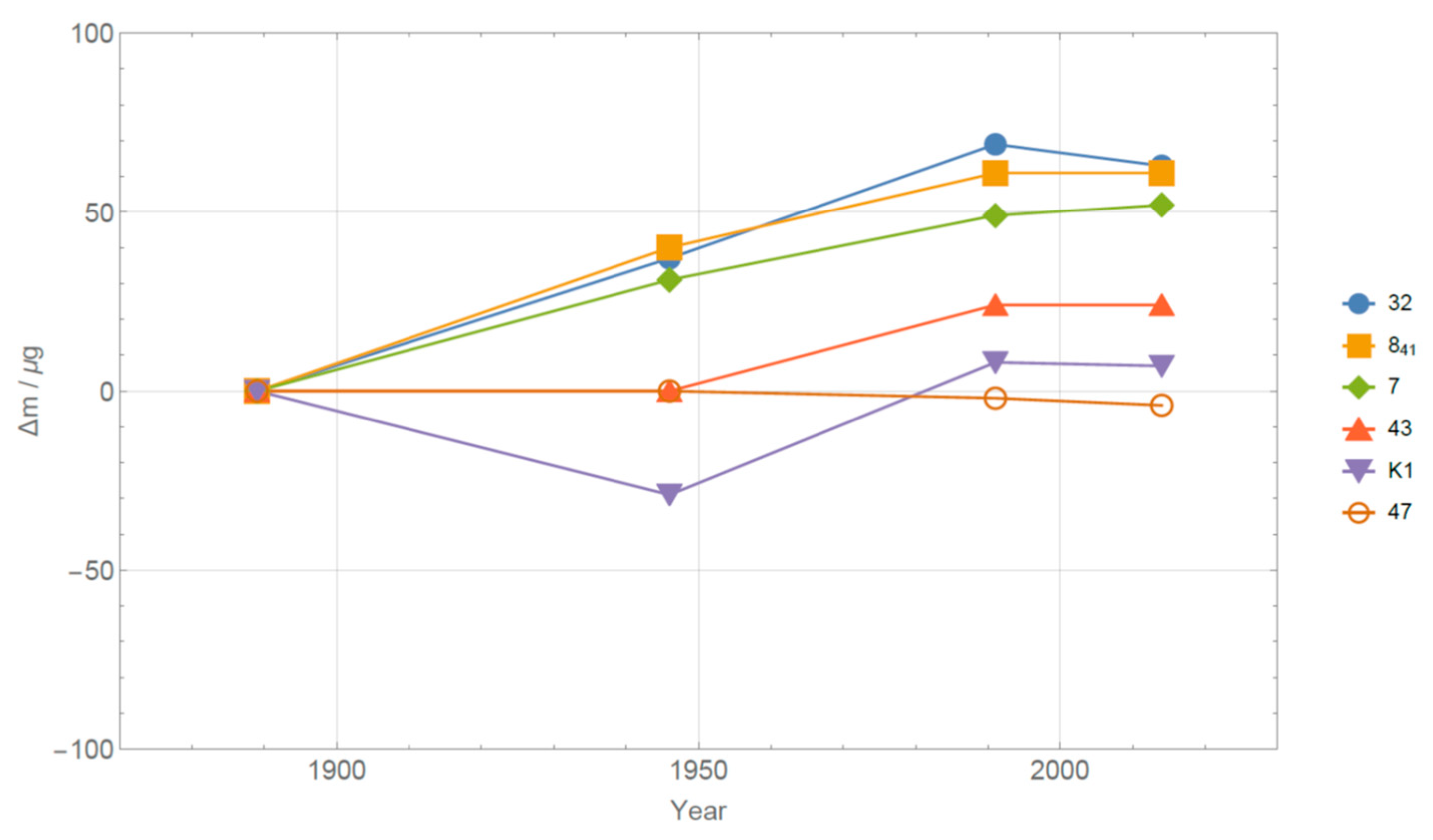
4. Dissemination of the Kilogram

On 20 May 2019, the kilogram was redefined to be based on the fixed numerical value of the Planck constant, rather than the international prototype’s mass. Actually, after the redefinition, any National Metrological Institute (NMI) could realize that the kilogram is traceable to the Planck constant.

The values measured by Kibble balances and the XRCD method submitted to CODATA for the 2017 special adjustment were not in perfect agreement. To achieve consistency, a multiplicative expansion factor of 1.7 was applied to the uncertainties of the data shown in Figure 2 [42]. This correction to the uncertainties of the data led to the implementation of a procedure for a smooth and reliable transition between the international prototype and the new SI realizations of the kilogram. Therefore, the CCM recommended [52] coordinated (rather than independent) realizations. The coordination key is a “consensus value” for the mass of the IPK resulting from international key comparisons of the realizations of the new kilogram definition. The consensus value is an offset from the BIPM as-maintained mass unit, which represents the mass of the IPK. It acts as a proxy for the realization experiments, and its uncertainty reflects a typical uncertainty of the experiments participating in the comparisons and the stability of the BIPM working standards.

The details were established by a CCM task group [53] as follows:

• Phase 0: traceability to the IPK, $m_{\mathrm{I}\mathrm{P}\mathrm{K}}=1$ kg, before the revision of the SI on 20 May 2019;
• Phase 1: traceability to the Planck constant via its known relationship with the IPK, $m_{\mathrm{I}\mathrm{P}\mathrm{K}}=1$ kg, with an additional uncertainty of $u_{m_{\mathrm{I}\mathrm{P}\mathrm{K}}}=10$ μg, from 20 May 2019 until a consensus value resulting from the first key comparison of primary realizations of the kilogram is published.
• Phase 2: dissemination from the consensus value, until the decision of the CCM.
• Phase 3: dissemination by individual realizations.

Three comparison exercises have been already performed: a pilot study [54] and two international key comparisons [55,56].

Table 1. Implementation of the traceability of the kilogram over the years 2019, 2021, and 2023 [54,55,56].

Date of Implementation	Basis for Dissemination	Uncertainty
20 May 2019	m(IPK) = 1 kg	10 μg
1 February 2021	Consensus value 2021 m(IPK) = 1 kg − 2 μg	20 μg
1 March 2023	Consensus value 2023 m(IPK) = 1 kg − 7 μg	20 μg

gives the consensus values of the mass of the international prototype following these exercises. The 2023 consensus value for the SI unit of mass, the kilogram, has been determined to be 1 kg − 7 μg, with a standard uncertainty of 20 μg to the mass value of the IPK, which is equal to the BIPM as-maintained mass unit. Since 1 March 2023, to achieve consistency with the consensus value, all NMIs would need to reduce the mass value of their national as-maintained mass unit by 7 μg with respect to the mass value based on the IPK.

It should be noted that, during the last key comparison, the difference between the two primary realizations with the lowest uncertainty using the Kibble balance (at the NRC) and the XRCD method (at the PTB) is 0.050 mg, which is about five times the stated uncertainty (coverage factor k = 1) of the individual experiments [56].

Considering the current uncertainty of the 2023 consensus value (which includes all primary realizations participating in the last three comparison exercises), it is possible that the Kibble balance and the count of atoms in the ²⁸Si realizations could detect any instability in the international prototype within a few decades.

5. Conclusions

This review focused on how the International System of Units (SI) has been redefined by establishing its units on stipulated values of a set of fundamental constants of physics. Redefining the measurement units required new technologies to realize them in practice and without introducing discontinuity of their value. Since 1990, the redefinition of electric units and the mole would have been possible based on the Planck and Avogadro constants and the elementary charge. Such redefinition would have implied a fixed value of the mass difference between the ground-state hyperfine energy levels of the ¹³³Cs atom, which, in turn, would have necessitated a redefinition of the unit of mass. However, there was no technology available to derive a kilogram from this very small mass difference in a manner competitive with the dissemination from the international prototype.

Hence, the central role played by the development of the technologies necessary to reliably realize the kilogram by reversing accurate measurements of the Planck and Avogadro constants (the pillars of today’s SI) was carried out by comparing electrical and mechanical powers and counting atoms. Thanks to the accuracy required, approaching 10⁻⁸ in fractional terms, these researches and developments have been quite a challenge [57] and, then, were at the top of the metrologist’s agenda for many decades; and engaged a multitude of those involved.

In the new system, any unit can be expressed by the fixed values of one or more of the seven defining constants. The links between the units historically identified as “base units” and the defining constants are displayed by the SI logo shown in Figure 5. However, the distinction between the second, meter, kilogram, ampere, kelvin, mole, and candela, conventionally chosen as base units, and the other derived units, apart from historical and educational values, no longer has any reason to exist.

In the new SI, any measurement procedure (no matter what its accuracy is) giving a result without relation to a standard, but relating it directly to defining constants, is a primary realization of the unit (or its multiples and submultiples) within the stated uncertainty. This answers the “for all times, for all peoples” request of the French revolutionaries and opens the way to realize, to mention a few, the mechanical units of mass, force, and torque—ranging from atomic to macroscopic scales—where needed, tailored on the actual accuracy needs, and, since independent of material artefacts, traceable to the system of units independently of national metrology institutes.

From this vantage, the KB and XRCD method are both primary realizations of the kilogram and, possibly, its multiples and submultiples. It is fortunate there exist independent, cross-checking, and top-level realizations relying on different aspects of nature’s developments. While the KB relies on solid-state physics (via the Josephson and quantum Hall effects), the XRCD realization ultimately relies on the measurement of the ratios between atoms or electron inertial masses and the Planck constant (via atomic interferometry and spectroscopy).

Practical considerations must also be taken into account. Through silicon crystallization, the XRCD method amplifies an atomic mass to macroscopic scales and allows material standards to be realized. This means that, once the realization has been completed, the well-established mass metrology can be unaffected by the redefinition. However, if one aims at achieving the smallest realization uncertainty at the one-kilogram level, isotopic enrichment is necessary and, consequently, the primary realization cost is exceptionally high given the (present) impossibility of determining the isotopic composition of natural silicon with the necessary accuracy.

The cost of building a KB with a comparable level of accuracy is less expensive and more widely affordable. However, the operation cost can be quite high. Dealing with the KB is a delicate matter, and keeping it operational requires a team of highly skilled and versatile professionals.