Damping and Dispersion of Non-Adiabatic Acoustic Waves in a High-Temperature Plasma: A Radiative-Loss Function
Abstract
1. Introduction
2. Method and Basic Equations
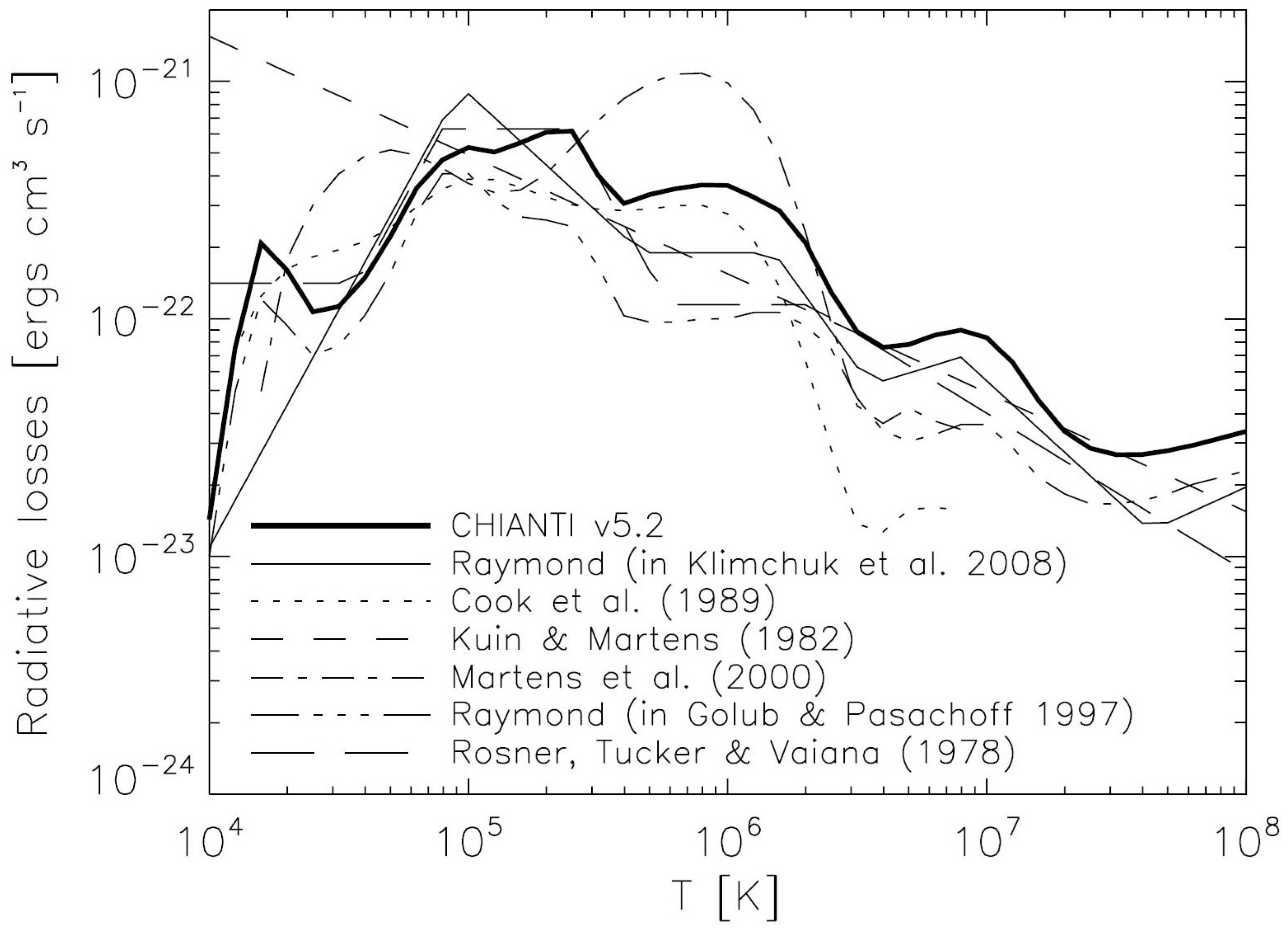
2.1. Heating/Cooling Function
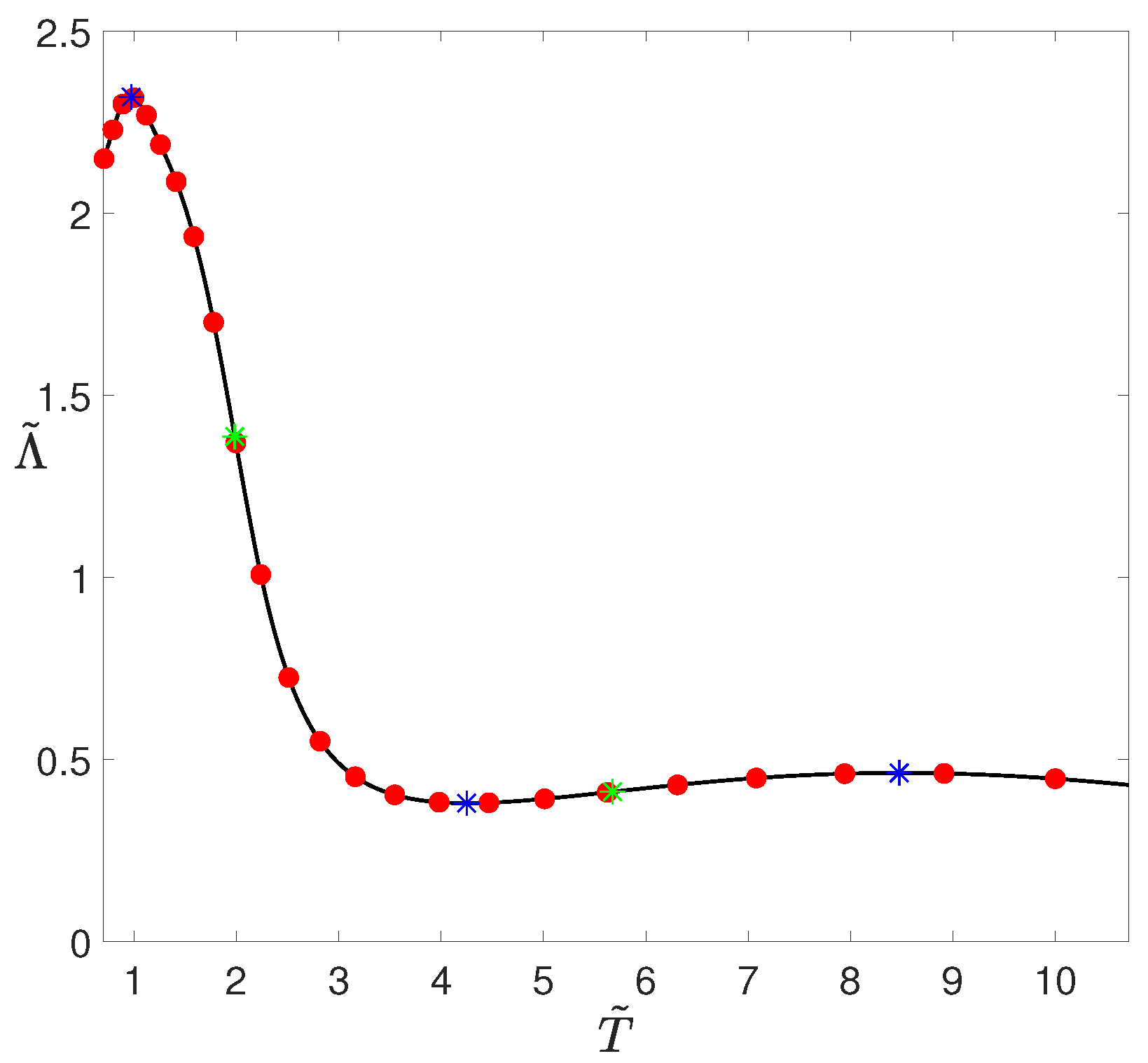
2.2. Interpolation of a Radiative-Loss Function
2.3. Basic Equations
3. Results
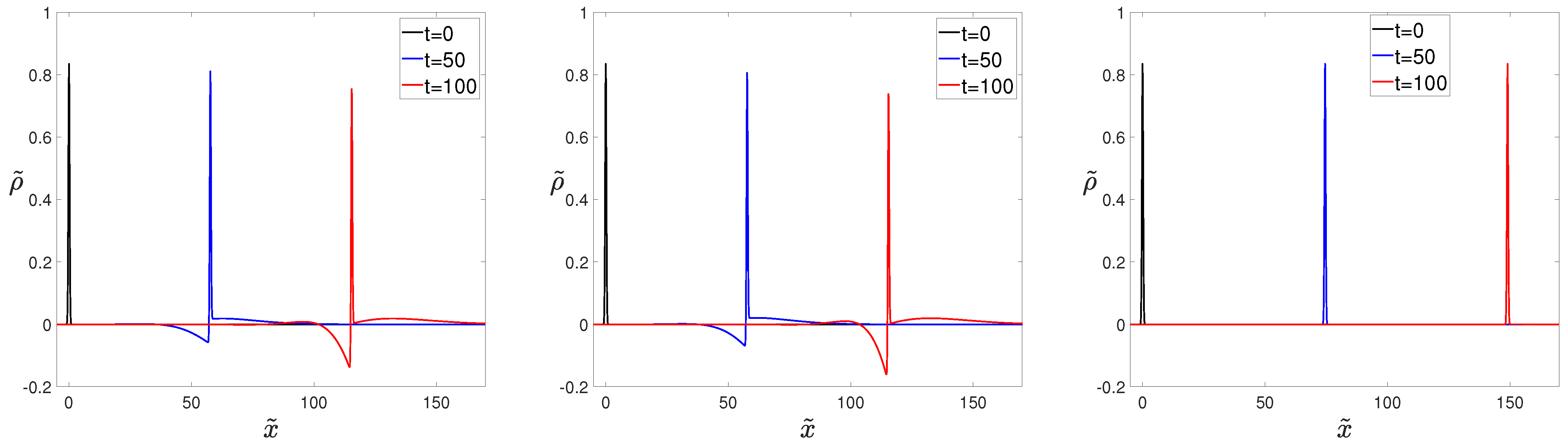
3.1. Wave Instability
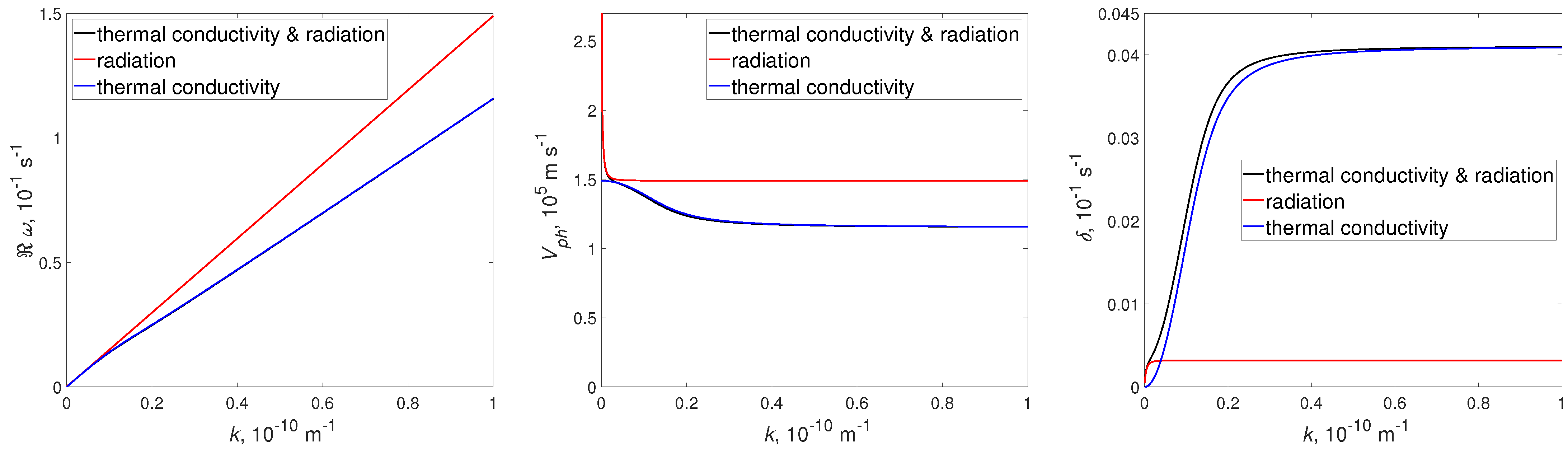
3.2. Wave Damping
3.3. Wave Dispersion
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Srivastava, A.K.; Kuridze, D.; Zaqarashvili, T.V.; Dwivedi, B.N. Intensity oscillations observed with Hinode near the south pole of the Sun: Leakage of low frequency magneto-acoustic waves into the solar corona. Astron. Astrophys. 2008, 481, L95–L98. [Google Scholar] [CrossRef]
- De Moortel, I. Longitudinal waves in coronal loops. Space Sci. Rev. 2009, 149, 65–81. [Google Scholar] [CrossRef]
- Banerjee, D.; Gupta, G.R.; Teriaca, L. Propagating MHD waves in coronal holes. Space Sci. Rev. 2011, 158, 267–288. [Google Scholar] [CrossRef]
- Banerjee, D.; Krishna Prasad, S. MHD waves in coronal holes. In Low-Frequency Waves in Space Plasmas; Keiling, A., Lee, D.-H., Nakariakov, V.M., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2016; pp. 419–430. [Google Scholar] [CrossRef]
- Krishna Prasad, S.; Van Doorsselaere, T. Compressive oscillations in hot coronal loops: Are sloshing oscillations and standing slow waves independent? Astrophys. J. 2021, 914, 81. [Google Scholar] [CrossRef]
- Wang, T.J. Standing slow-mode waves in hot coronal loops: Observations, modeling, and coronal seismology. Space Sci. Rev. 2011, 158, 397–419. [Google Scholar] [CrossRef]
- De Moortel, I.; Nakariakov, V.M. Magnetohydrodynamic waves and coronal seismology: An overview of recent results. Phil. Trans. Roy. Soc. A 2012, 370, 3193–3216. [Google Scholar] [CrossRef]
- Ofman, L.; Wang, T. Hot coronal loop oscillations observed by SUMER: Slow magnetosonic wave damping by thermal conduction. Astrophys. J. 2002, 580, L85–L88. [Google Scholar] [CrossRef]
- De Moortel, I.; Hood, A.W. The damping of slow MHD waves in solar coronal magnetic fields. Astron. Astrophys. 2003, 408, 755–765. [Google Scholar] [CrossRef]
- Priest, E.R.; Foley, C.R.; Heyvaerts, J.; Arber, T.D.; Culhane, J.L.; Acton, L.W. Nature of the heating mechanism for the diffuse solar corona. Nature 1998, 393, 545–547. [Google Scholar] [CrossRef]
- Aschwanden, M.J.; Terradas, J. The effect of radiative cooling on coronal loop oscillations. Astrophys. J. 2008, 686, L127–L130. [Google Scholar] [CrossRef]
- Mikhalyaev, B.B.; Veselovskii, I.S.; Khongorova, O.V. Radiation effects on the MHD wave behavior in the solar corona. Sol. Syst. Res. 2013, 47, 50–57. [Google Scholar] [CrossRef]
- Kolotkov, D.Y.; Nakariakov, V.M.; Zavershinskii, D.I. Damping of slow magnetoacoustic oscillations by the misbalance between heating and cooling processes in the solar corona. Astron. Astrophys. 2019, 628, A133. [Google Scholar] [CrossRef]
- Zavershinskii, D.I.; Kolotkov, D.Y.; Nakariakov, V.M.; Molevich, N.E.; Ryashchikov, D.S. Formation of quasi-periodic slow magnetoacoustic wave trains by the heating/cooling misbalance. Phys. Plasmas 2019, 26, 082113. [Google Scholar] [CrossRef]
- Belov, S.A.; Molevich, N.E.; Zavershinskii, D.L. Dispersion of slow magnetoacoustic waves in the active region fan loops introduced by thermal misbalance. Sol. Phys. 2021, 296, 122. [Google Scholar] [CrossRef]
- Ginzburg, V.L. Concerning the general relationship between absorption and dispersion of sound waves. Sov. Phys. - Acoustics 1955, 1, 32–41. [Google Scholar]
- Dere, K.P.; Landi, E.; Young, P.R.; Del Zanna, G.; Landini, M.; Mason, H.E. CHIANTI—An atomic database for emission lines IX. Ionization rates, recombination rates, ionization equilibria for the elements hydrogen through zinc and updated atomic data. Astron. Astrophys. 2009, 498, 915–929. [Google Scholar] [CrossRef]
- Dudík, J.; Dzifčáková, E.; Karlický, M.; Kulinová, A. The bound-bound and free-free radiative losses for the nonthermal distributions in solar and stellar coronae. Astron. Astrophys. 2011, 529, A103. [Google Scholar] [CrossRef]
- Del Zanna, G.; Dere, K.P.; Young, P.R.; Landi, E. CHIANTI—An atomic database for emission lines. XVI. Version 10, further extensions. Astrophys. J. 2021, 909, 38. [Google Scholar] [CrossRef]
- Field, G.B. Thermal instability. Astrophys. J. 1965, 142, 531–567. [Google Scholar] [CrossRef]
- Priest, E.R. Magnetohydrodynamics of the Sun; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Dere, K.P.; Landi, E.; Mason, H.E.; Monsignori Fossi, B.C.; Young, P.R. CHIANTI—An atomic database for emission lines. I. Wavelengths greater than 50 Å. Astron. Astrophys. Suppl. Ser. 1997, 125, 149–173. [Google Scholar] [CrossRef]
- Landi, E.; Landini, M. Radiative losses of optically thin coronal plasmas. Astron. Astrophys. 1999, 347, 401–408. Available online: https://ui.adsabs.harvard.edu/abs/1999A%26A...347..401L/ (accessed on 25 January 2023).
- Rosner, R.; Tucker, W.H.; Vaiana, G.S. Dynamics of the quiescent solar corona. Astrophys. J. 1978, 220, 643–665. [Google Scholar] [CrossRef]
- Carbonell, M.; Oliver, R.; Ballester, J.L. Time damping of linear non-adiabatic magnetohydrodynamic waves in an unbounded plasma with solar coronal properties. Astron. Astrophys. 2004, 45, 739–750. [Google Scholar] [CrossRef]
- Klimchuk, J.A.; Patsourakos, S.; Cargill, P.J. Highly efficient modeling of dynamic coronal loops. Astrophys. J. 2008, 682, 1351–1362. [Google Scholar] [CrossRef]
- Landi, E.; Del Zanna, G.; Young, P.R.; Dere, K.P.; Mason, H.E.; Landini, M. CHIANTI—An atomic database for emission lines. VII. New data for X-rays and other improvements. Astrophys. J. Supp. Ser. 2006, 162, 261–280. [Google Scholar] [CrossRef]
- Parker, E.N. Instability of thermal fields. Astrophys. J. 1953, 117, 431–436. [Google Scholar] [CrossRef]
- Weymann, R. Heating of stellar chromospheres by shock waves. Astrophys. J. 1960, 132, 452–460. [Google Scholar] [CrossRef]
- Kolotkov, D.Y.; Duckenfield, T.J.; Nakariakov, V.M. Seismological constraints on the solar coronal heating function. Astron. Astrophys. 2020, 644, A33. [Google Scholar] [CrossRef]
- Kolotkov, D.Y.; Zavershinskii, D.I.; Nakariakov, V.M. The solar corona as an active medium for magnetoacoustic waves. Plasma Phys. Control. Fusion 2021, 63, 124008. [Google Scholar] [CrossRef]
- CHIANTI: An Atomic Database for Spectroscopic Diagnostics of Astrophysical Plasmas. Available online: http://www.chiantidatabase.org (accessed on 25 January 2023).
- Reale, F. Coronal loops: Observations and modeling of onfined plasma. Living Rev. Sol. Phys. 2014, 11, 4. [Google Scholar] [CrossRef]
- Spitzer, L., Jr. Physics of Fully Ionized Gases; Dover Publications, Inc.: Mineola, NY, USA, 2006. [Google Scholar]
- Nakariakov, V.M.; Afanasyev, A.N.; Kumar, S.; Moon, Y.-J. Effect of local thermal equilibrium misbalance on long-wavelength slow magnetoacoustic waves. Astrophys. J. 2017, 849, 62. [Google Scholar] [CrossRef]


| i | (K), | , | , |
|---|---|---|---|
| 0 | 0.5011872 | 2.267829 | 2.108884 |
| 1 | 0.562341 | 2.367434 | 2.201509 |
| 2 | 0.630957 | 2.418156 | 2.248675 |
| 3 | 0.707946 | 2.469151 | 2.296096 |
| 4 | 0.794328 | 2.547926 | 2.369351 |
| 5 | 0.891251 | 2.622882 | 2.439053 |
| 6 | 1 | 2.646271 | 2.460803 |
| 7 | 1.122018 | 2.602311 | 2.419923 |
| 8 | 1.258925 | 2.523537 | 2.346671 |
| 9 | 1.412538 | 2.421656 | 2.25193 |
| 10 | 1.584893 | 2.266581 | 2.107724 |
| 11 | 1.778279 | 2.019601 | 1.878054 |
| 12 | 1.995262 | 1.665344 | 1.548626 |
| 13 | 2.238721 | 1.269071 | 1.180126 |
| 14 | 2.511886 | 0.946541 | 0.880201 |
| 15 | 2.818383 | 0.729857 | 0.678704 |
| 16 | 3.162278 | 0.59583 | 0.55407 |
| 17 | 3.548134 | 0.52004 | 0.483592 |
| 18 | 3.981072 | 0.483017 | 0.449164 |
| 19 | 4.466836 | 0.471106 | 0.438087 |
| 20 | 5.011872 | 0.474839 | 0.441559 |
| 21 | 5.623413 | 0.487475 | 0.45331 |
| 22 | 6.309573 | 0.504156 | 0.468822 |
| 23 | 7.079458 | 0.520485 | 0.484006 |
| 24 | 7.943282 | 0.531125 | 0.493901 |
| 25 | 8.912509 | 0.530389 | 0.493216 |
| 26 | 10 | 0.513176 | 0.47721 |
| 27 | 11.220185 | 0.476465 | 0.443071 |
| 28 | 12.589254 | 0.421238 | 0.391715 |
| 29 | 14.125375 | 0.357961 | 0.332873 |
| i | Ai | Bi | Ci | Di |
|---|---|---|---|---|
| 0 | −8.164325 | −6.655046 | 1.952125 | 2.108884 |
| 1 | 42.533874 | −8.152892 | 1.046559 | 2.201509 |
| 2 | 6.927944 | 0.602624 | 0.52849 | 2.248675 |
| 3 | −11.622274 | 2.202738 | 0.74447 | 2.296096 |
| 4 | −7.161141 | -0.809143 | 0.864853 | 2.36935 |
| 5 | 0.696996 | −2.891375 | 0.506189 | 2.439053 |
| 6 | 5.9093052 | −2.6639816 | −0.097951 | 2.4608027 |
| 7 | 0.940888 | −0.500849 | −0.484119 | 2.419923 |
| 8 | −1.306459 | −0.114406 | −0.568352 | 2.3466709 |
| 9 | −0.579185 | −0.71647 | −0.695985 | 2.25193 |
| 10 | 0.091538 | −1.015948 | −0.994577 | 2.107724 |
| 11 | 1.443157 | −0.962841 | −1.377247 | 1.878054 |
| 12 | 1.4062024 | −0.02342 | −1.591249 | 1.548626 |
| 13 | −0.261502 | 1.003637 | −1.352606 | 1.180126 |
| 14 | −0.388805 | 0.789338 | −0.862828 | 0.880201 |
| 15 | −0.189246 | 0.431835 | −0.488543 | 0.678704 |
| 16 | −0.102562 | 0.236593 | −0.258674 | 0.55407 |
| 17 | −0.046161 | 0.117871 | −0.121902 | 0.483592 |
| 18 | −0.021779 | 0.057916 | −0.045797 | 0.449164 |
| 19 | −0.009937 | 0.026178 | −0.004947 | 0.438087 |
| 20 | −0.004251 | 0.009929 | 0.0147325 | 0.044156 |
| 21 | −0.002043 | 0.002131 | 0.0221072 | 0.453309 |
| 22 | −0.001395 | −0.20738 | 0.022146 | 0.468822 |
| 23 | −0.000595 | −0.005296 | 0.0164728 | 0.484006 |
| 24 | −0.000074 | −0.006839 | 0.005991 | 0.4939 |
| 25 | 0.000361 | −0.007054 | −0.007474 | 0.493216 |
| 26 | 0.00049 | −0.005878 | −0.021536 | 0.47721 |
| 27 | 0.000944 | −0.004084 | −0.033691 | 0.443071 |
| 28 | 0.000667 | −0.000021 | −0.039563 | 0.391715 |
| i | |||||
|---|---|---|---|---|---|
| 0 | 0.501187 | 0.405448 | 1.952125 | 4.207778 | 5.509194 |
| 1 | 0.562341 | 0.540673 | 1.04656 | 3.9149 | 4.6126 |
| 2 | 0.63096 | 0.721 | 0.52849 | 3.5639 | 3.916237 |
| 3 | 0.707946 | 0.961468 | 0.744471 | 3.243322 | 3.739636 |
| 4 | 0.794328 | 1.282138 | 0.864853 | 2.982836 | 3.559404 |
| 5 | 0.891251 | 1.709759 | 0.506189 | 2.736663 | 3.074122 |
| 6 | 1 | 2.28 | −0.097951 | 2.460803 | 2.395502 |
| 7 | 1.122019 | 3.040429 | −0.484119 | 2.156759 | 1.834013 |
| 8 | 1.258925 | 4.054477 | −0.568352 | 1.864027 | 1.485126 |
| 9 | 1.412538 | 5.406732 | −0.695985 | 1.594244 | 1.130255 |
| 10 | 1.584893 | 7.209993 | −0.994577 | 1.329884 | 0.666833 |
| 11 | 1.778279 | 9.61468 | −1.377247 | 1.056107 | 0.137943 |
| 12 | 1.995262 | 12.821382 | −1.591249 | 0.776152 | −0.284681 |
| 13 | 2.238721 | 17.097588 | −1.352606 | 0.527143 | −0.374595 |
| 14 | 2.5118864 | 22.8 | −0.862828 | 0.350415 | −0.224804 |
| 15 | 2.818383 | 30.404289 | −0.488543 | 0.240813 | −0.084882 |
| 16 | 3.162278 | 40.544771 | −0.258674 | 0.175212 | 0.002763 |
| 17 | 3.548134 | 54.06732 | −0.121902 | 0.136295 | 0.055027 |
| 18 | 3.981072 | 72.099931 | −0.045797 | 0.112825 | 0.008229 |
| 19 | 4.466836 | 96.146803 | −0.004947 | 0.098076 | 0.094778 |
| 20 | 5.011872 | 128.21382 | 0.014733 | 0.088103 | 0.097924 |
| 21 | 5.623413 | 170.97588 | 0.022107 | 0.080611 | 0.095349 |
| 22 | 6.309573 | 228 | 0.022146 | 0.074303 | 0.089068 |
| 23 | 7.079458 | 304.04289 | 0.016473 | 0.068368 | 0.07935 |
| 24 | 7.943282 | 405.44771 | 0.005991 | 0.062178 | 0.066172 |
| 25 | 8.912509 | 540.6732 | −0.007474 | 0.05534 | 0.050357 |
| 26 | 10 | 720.9993 | −0.021536 | 0.047721 | 0.033363 |
| 27 | 11.220185 | 961.46803 | −0.033691 | 0.039489 | 0.017028 |
| 28 | 12.589254 | 1 282.1382 | −0.039563 | 0.031115 | 0.00474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derteev, S.; Shividov, N.; Bembitov, D.; Mikhalyaev, B. Damping and Dispersion of Non-Adiabatic Acoustic Waves in a High-Temperature Plasma: A Radiative-Loss Function. Physics 2023, 5, 215-228. https://doi.org/10.3390/physics5010017
Derteev S, Shividov N, Bembitov D, Mikhalyaev B. Damping and Dispersion of Non-Adiabatic Acoustic Waves in a High-Temperature Plasma: A Radiative-Loss Function. Physics. 2023; 5(1):215-228. https://doi.org/10.3390/physics5010017
Chicago/Turabian StyleDerteev, Sergei, Nikolai Shividov, Dzhirgal Bembitov, and Badma Mikhalyaev. 2023. "Damping and Dispersion of Non-Adiabatic Acoustic Waves in a High-Temperature Plasma: A Radiative-Loss Function" Physics 5, no. 1: 215-228. https://doi.org/10.3390/physics5010017
APA StyleDerteev, S., Shividov, N., Bembitov, D., & Mikhalyaev, B. (2023). Damping and Dispersion of Non-Adiabatic Acoustic Waves in a High-Temperature Plasma: A Radiative-Loss Function. Physics, 5(1), 215-228. https://doi.org/10.3390/physics5010017





