Laws of Spatially Structured Population Dynamics on a Lattice
Abstract
:1. Introduction
2. General Setup and Agent-Based Modeling of Population Dynamics
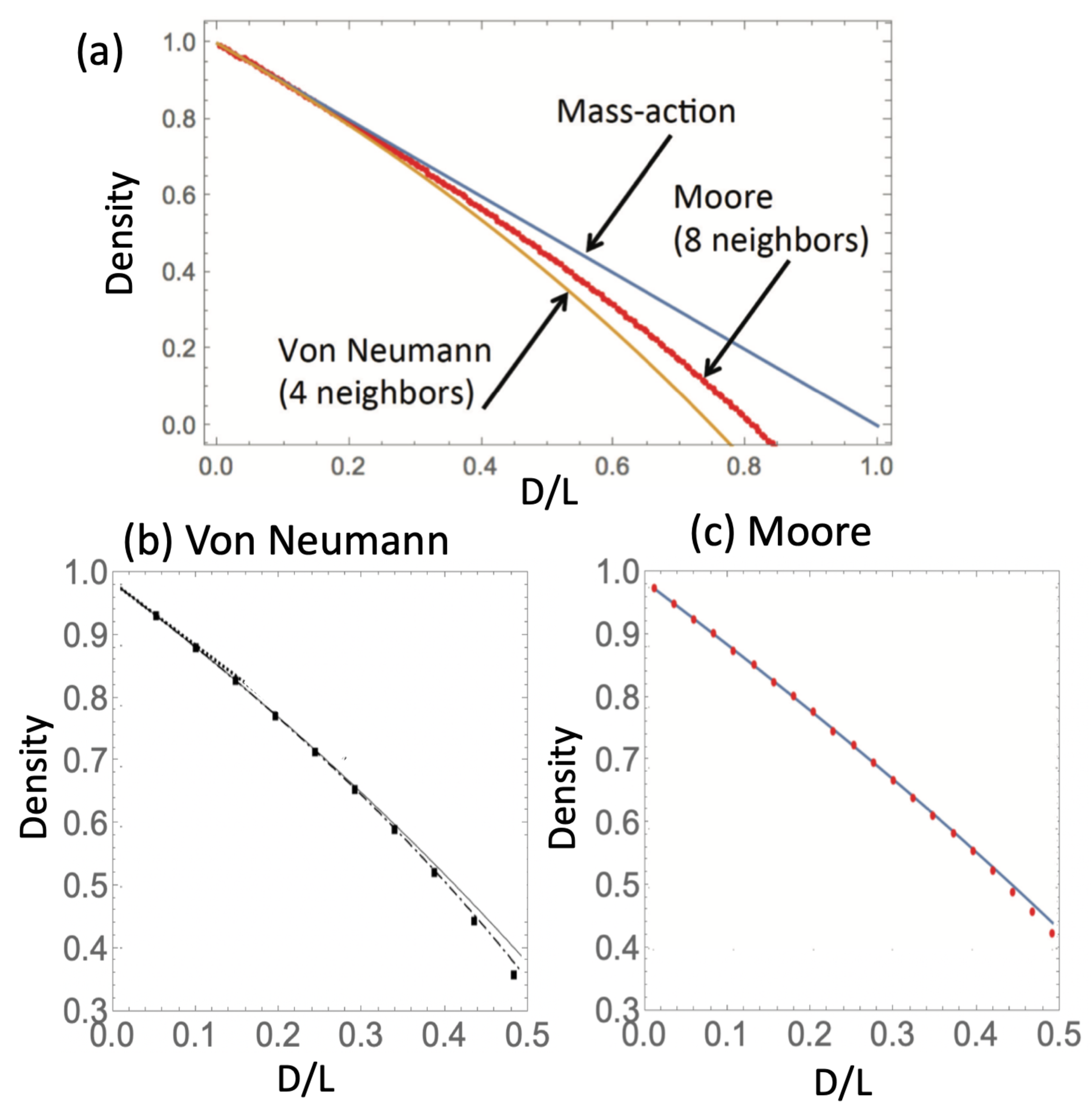
3. Analytical Approximations for Steady-State Density (A Single Type)
Equilibrium Density in Space: An Analytical Method
4. Disadvantageous Mutants and Selection–Mutation Balance in Spatial Models
4.1. A Basic ODE Formulation
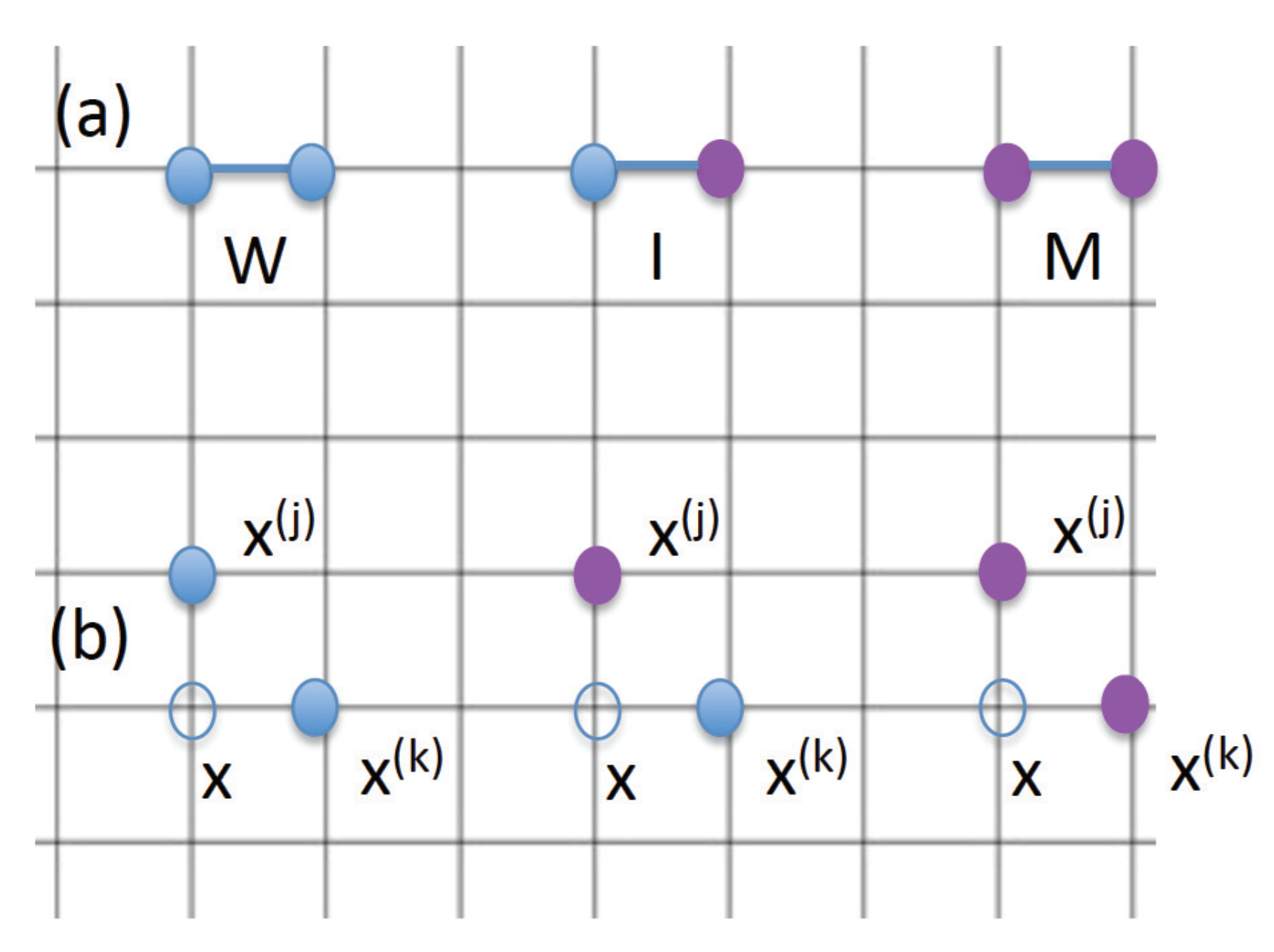
4.2. A Spatial Description: Equations for the Densities
- is the probability to have two wild-type cells at two neighboring locations;
- is the probability to have a wild-type cell and a mutant at two neighboring locations;
- is the probability to have two mutant cells at two neighboring locations.
4.3. Selection–Mutation Balance Solution
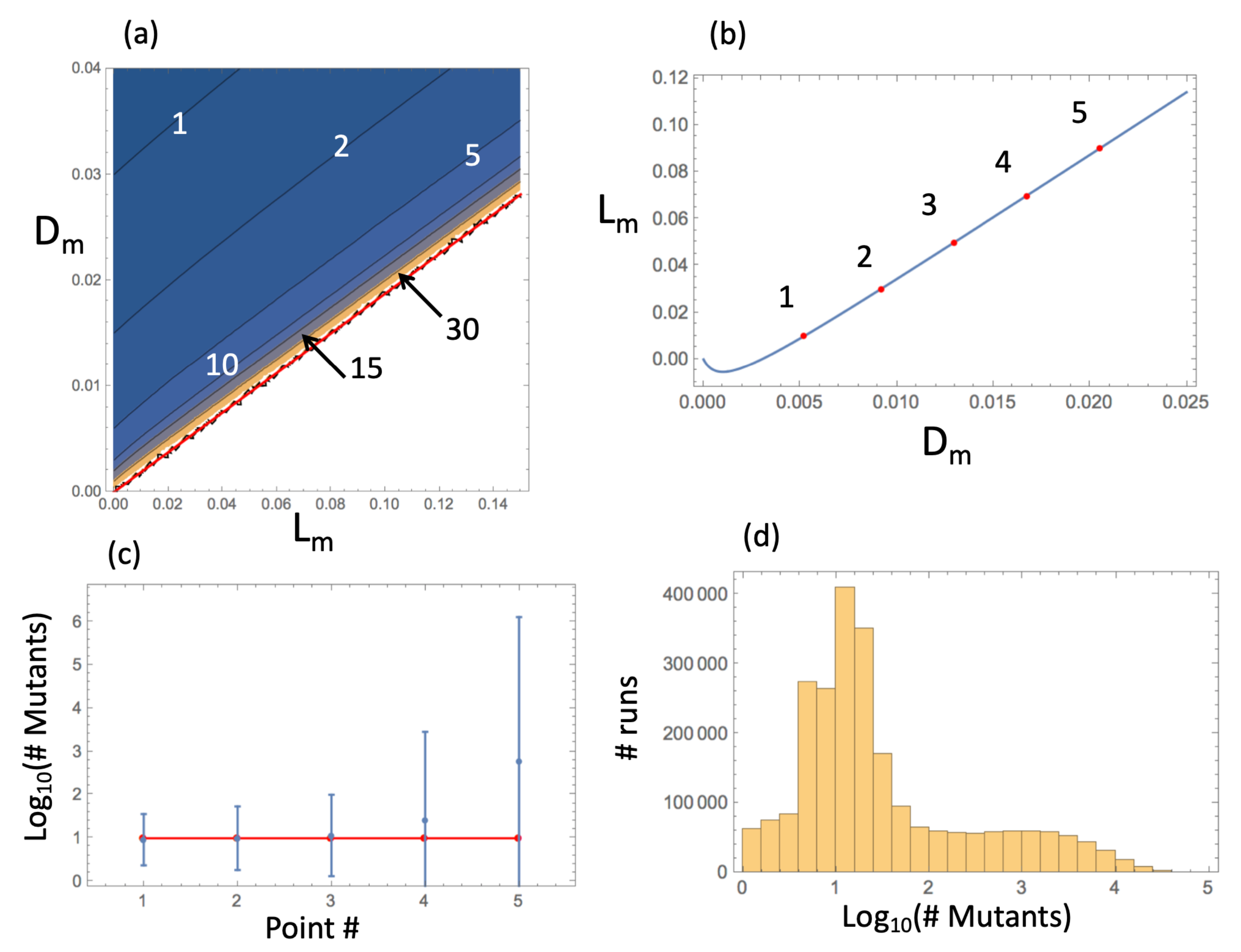
4.4. Applications and Comparison with Computations
- Quasi-equilibrium density in finite populations. If simulations are continued until a finite grid is filled, the population reaches a quasi-equilibrium state where wild-type and disadvantageous mutant cells coexist. For a 2D square grid under a von Neumann neighborhood, the density of the mutants is approximated by in Equation (28), while the density of wild-types is given by , Equation (27). The total numbers of mutant and wild-type cells are obtained by multiplying the quantities and by the total number of grid points, respectively. Note that this scenario is not interesting in the case of advantageous or neutral mutants, as the entire population will eventually consist of mutant cells.
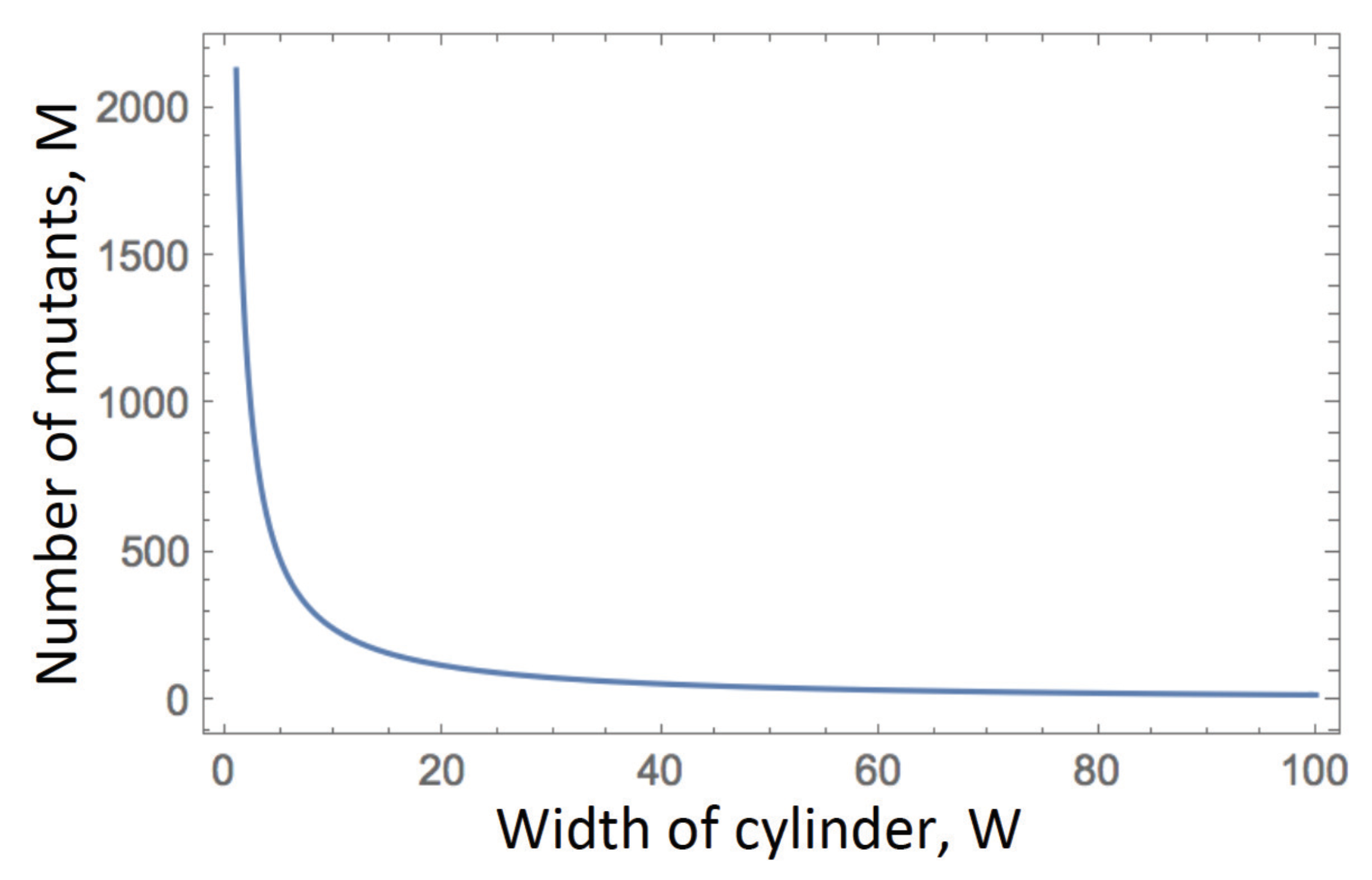
- Number of mutants in spatially expanding populations. Simulating a growing population (on a large grid where the boundaries are not reached), we can ask how the number of disadvantageous mutants scales with the total number of cells, N. Since the core of the expanding colony is in quasi-equilibrium, Equation (29) shows that the number of mutants grows as the first power of N. Results for the scaling laws for neutral and advantageous mutants are discussed in the next Section.
5. Laws of Neutral and Advantageous Mutant Spread in Different Geometries
5.1. Derivation of the Growth Laws
5.1.1. Two-Dimensional Flat Front
5.1.2. Two-Dimensional: Circular Range Expansion
5.1.3. Three-Dimensional Flat Front
5.1.4. Three-Dimensional Range Expansion
5.1.5. Exponential (Non-Spatial, Mass-Action) Growth
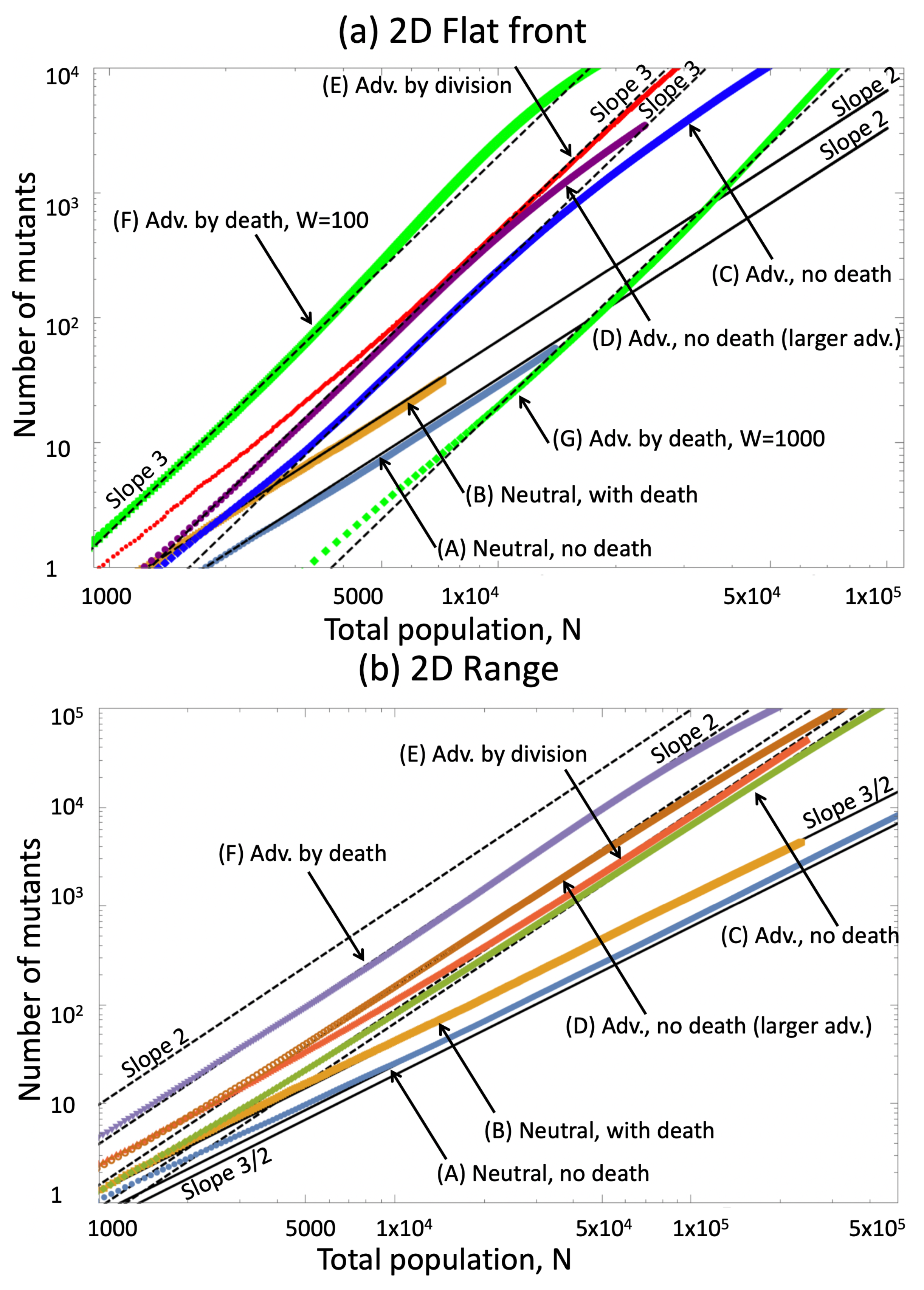
5.2. Comparison with Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kimura, M. On the probability of fixation of mutant genes in a population. Genetics 1962, 47, 713. [Google Scholar] [CrossRef] [PubMed]
- Patwa, Z.; Wahl, L.M. The fixation probability of beneficial mutations. J. R. Soc. Interface 2008, 5, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Kepler, T.B.; Oprea, M. Improved inference of mutation rates: I. An integral representation for the Luria–Delbrück distribution. Theor. Popul. Biol. 2001, 59, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Dewanji, A.; Luebeck, E.; Moolgavkar, S.H. A generalized Luria–Delbrück model. Math. Biosci. 2005, 197, 140–152. [Google Scholar] [CrossRef] [PubMed]
- Komarova, N.L.; Wu, L.; Baldi, P. The fixed-size Luria–Delbruck model with a nonzero death rate. Math. Biosci. 2007, 210, 253–290. [Google Scholar] [CrossRef]
- Zheng, Q. Progress of a half century in the study of the Luria–Delbrück distribution. Math. Biosci. 1999, 162, 1–32. [Google Scholar] [CrossRef]
- Bryder, D.; Rossi, D.J.; Weissman, I.L. Hematopoietic stem cells: The paradigmatic tissue-specific stem cell. Am. J. Pathol. 2006, 169, 338–346. [Google Scholar] [CrossRef]
- Gestel, J.V.; Vlamakis, H.; Kolter, R. Division of labor in biofilms: The ecology of cell differentiation. In Microbial Biofilms; Ghannoum, M., Parsek, M., Whiteley, M., Mukherjee, P.K., Eds.; AMS Press: Washington, DC, USA, 2015; pp. 67–97. [Google Scholar] [CrossRef]
- Webb, J.S.; Givskov, M.; Kjelleberg, S. Bacterial biofilms: Prokaryotic adventures in multicellularity. Curr. Opin. Microbiol. 2003, 6, 578–585. [Google Scholar] [CrossRef]
- Komarova, N.L. Spatial stochastic models for cancer initiation and progression. Bull. Math. Biol. 2006, 68, 1573–1599. [Google Scholar] [CrossRef]
- Durrett, R.; Moseley, S. Spatial Moran models I. Stochastic tunneling in the neutral case. Ann. Appl. Probab. 2015, 25, 104. [Google Scholar] [CrossRef]
- Durrett, R.; Foo, J.; Leder, K. Spatial Moran models, II: Cancer initiation in spatially structured tissue. J. Math. Biol. 2016, 72, 1369–1400. [Google Scholar] [CrossRef] [PubMed]
- Gralka, M.; Hallatschek, O. Environmental heterogeneity can tip the population genetics of range expansions. Elife 2019, 8, e44359. [Google Scholar] [CrossRef] [PubMed]
- Waclaw, B.; Bozic, I.; Pittman, M.E.; Hruban, R.H.; Vogelstein, B.; Nowak, M.A. A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity. Nature 2015, 525, 261–264. [Google Scholar] [CrossRef] [PubMed]
- Gralka, M.; Stiewe, F.; Farrell, F.; Möbius, W.; Waclaw, B.; Hallatschek, O. Allele surfing promotes microbial adaptation from standing variation. Ecol. Lett. 2016, 19, 889–898. [Google Scholar] [CrossRef] [PubMed]
- Otwinowski, J.; Krug, J. Clonal interference and Muller’s ratchet in spatial habitats. Phys. Biol. 2014, 11, 056003. [Google Scholar] [CrossRef]
- Lavrentovich, M.O.; Wahl, M.E.; Nelson, D.R.; Murray, A.W. Spatially constrained growth enhances conversional meltdown. Biophys. J. 2016, 110, 2800–2808. [Google Scholar] [CrossRef]
- Fusco, D.; Gralka, M.; Kayser, J.; Anderson, A.; Hallatschek, O. Excess of mutational jackpot events in expanding populations revealed by spatial Luria–Delbrück experiments. Nat. Commun. 2016, 7, 12760. [Google Scholar] [CrossRef]
- Wodarz, D.; Komarova, N.L. Mutant Evolution in Spatially Structured and Fragmented Expanding Populations. Genetics 2020, 216, 191–203. [Google Scholar] [CrossRef]
- Rodriguez-Brenes, I.A.; Wodarz, D.; Komarova, N.L. Beyond the pair approximation: Modeling colonization population dynamics. Phys. Rev. E 2020, 101, 032404. [Google Scholar] [CrossRef]
- Gerlee, P.; Anderson, A.R. An evolutionary hybrid cellular automaton model of solid tumour growth. J. Theor. Biol. 2007, 246, 583–603. [Google Scholar] [CrossRef]
- Wodarz, D.; Sun, Z.; Lau, J.W.; Komarova, N.L. Nearest-neighbor interactions, habitat fragmentation, and the persistence of host-pathogen systems. Am. Nat. 2013, 182, E94–E111. [Google Scholar] [CrossRef] [PubMed]
- Komarova, N.L.; Shahriyari, L.; Wodarz, D. Complex role of space in the crossing of fitness valleys by asexual populations. J. R. Soc. Interface 2014, 11, 20140014. [Google Scholar] [CrossRef] [PubMed]
- Kreger, J.; Brown, D.; Komarova, N.L.; Wodarz, D.; Pritchard, J. The role of migration in mutant evolution in fragmented populations. bioRxiv 2021. [Google Scholar] [CrossRef]
- Iwasa, Y.; Nowak, M.A.; Michor, F. Evolution of resistance during clonal expansion. Genetics 2006, 172, 2557–2566. [Google Scholar] [CrossRef]
- Horswell, S.; Matthews, N.; Swanton, C. Cancer heterogeneity and “the struggle for existence”: Diagnostic and analytical challenges. Cancer Lett. 2013, 340, 220–226. [Google Scholar] [CrossRef]
- Banin, E.; Hughes, D.; Kuipers, O.P. Bacterial pathogens, antibiotics and antibiotic resistance. FEMS Microbiol. Rev. 2017, 41, 450–452. [Google Scholar] [CrossRef]
- Karamched, B.; Ott, W.; Timofeyev, I.; Alnahhas, R.; Bennett, M.; Josić, K. Moran model of spatial alignment in microbial colonies. Phys. D Nonlinear Phenom. 2019, 395, 1–6. [Google Scholar] [CrossRef]
- van Vliet, S.; Hauert, C.; Fridberg, K.; Ackermann, M.; Dal Co, A. Global dynamics of microbial communities emerge from local interaction rules. PLoS Comput. Biol. 2022, 18, e1009877. [Google Scholar] [CrossRef]
- Koldaeva, A.; Tsai, H.F.; Shen, A.Q.; Pigolotti, S. Population genetics in microchannels. Proc. Natl. Acad. Sci. USA 2022, 119, e2120821119. [Google Scholar] [CrossRef]


| Lattice | Geometry | Density |
|---|---|---|
| von Neumann | 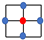 | |
| Moore | 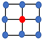 | |
| Hexagonal | 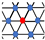 | |
| Mass-action |  | |
| neighbors |  |
| 2D Flat | 2D Range | 3D Flat | 3D Range | Exponential | |
|---|---|---|---|---|---|
| Mutant property |  |  |  |  |  |
| Disadvantageous | |||||
| Neutral | |||||
| Advantageous |
| Curve | Description | ||||
|---|---|---|---|---|---|
| A | Neutral, no death | 0.7 | 0.7 | 0 | 0 |
| B | Neutral, with death | 0.7 | 0.7 | 0.2 | 0.2 |
| C | Adv, no death | 0.7 | 0.9 | 0 | 0 |
| D | Adv, no death, larger advantage | 0.7 | 1.0 | 0 | 0 |
| E | Adv by division, with death | 0.7 | 0.8 | 0.2 | 0.2 |
| F | Adv by death | 0.7 | 0.7 | 0.2 | 0.1 |
| G | Adv by death, wider front | 0.7 | 0.7 | 0.2 | 0.1 |
| Curve | Description | u | ||||
|---|---|---|---|---|---|---|
| A | Neutral, range | 0.7 | 0.7 | 0.1 | 0.1 | |
| B, yellow | Adv by division, range | 0.4 | 0.8 | 0.1 | 0.1 | |
| B, red | Adv by division, range | 0.7 | 0.7 | 0.2 | 0.2 | |
| C | Adv by death, range | 0.7 | 0.7 | 0.2 | 0.1 | |
| D | Neutral, flat | 0.8 | 0.8 | 0.1 | 0.1 | |
| E | Adv by division, flat | 0.4 | 0.8 | 0.1 | 0.1 | |
| F | Adv by death, flat | 0.7 | 0.7 | 0.2 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komarova, N.L.; Rodriguez-Brenes, I.A.; Wodarz, D. Laws of Spatially Structured Population Dynamics on a Lattice. Physics 2022, 4, 812-832. https://doi.org/10.3390/physics4030052
Komarova NL, Rodriguez-Brenes IA, Wodarz D. Laws of Spatially Structured Population Dynamics on a Lattice. Physics. 2022; 4(3):812-832. https://doi.org/10.3390/physics4030052
Chicago/Turabian StyleKomarova, Natalia L., Ignacio A. Rodriguez-Brenes, and Dominik Wodarz. 2022. "Laws of Spatially Structured Population Dynamics on a Lattice" Physics 4, no. 3: 812-832. https://doi.org/10.3390/physics4030052
APA StyleKomarova, N. L., Rodriguez-Brenes, I. A., & Wodarz, D. (2022). Laws of Spatially Structured Population Dynamics on a Lattice. Physics, 4(3), 812-832. https://doi.org/10.3390/physics4030052





