Past and Present Trends in the Development of the Pattern-Formation Theory: Domain Walls and Quasicrystals
Abstract
:1. Introduction
1.1. The Objective of This Paper
1.2. Complex Ginzburg–Landau Equations: The Formulation, Plane Waves, and Dissipative Solitons
1.3. The Structure of This Paper
2. DW (Domain-Wall) Patterns
2.1. The Source Pattern Generated by the Single Complex GL Equation
2.1.1. The Generic Case
2.1.2. Domain Walls as Shock Waves in the Diffusion-Free Complex GL Equation
2.2. DWs in Systems of Real Coupled GL Equations: Old and New Solutions
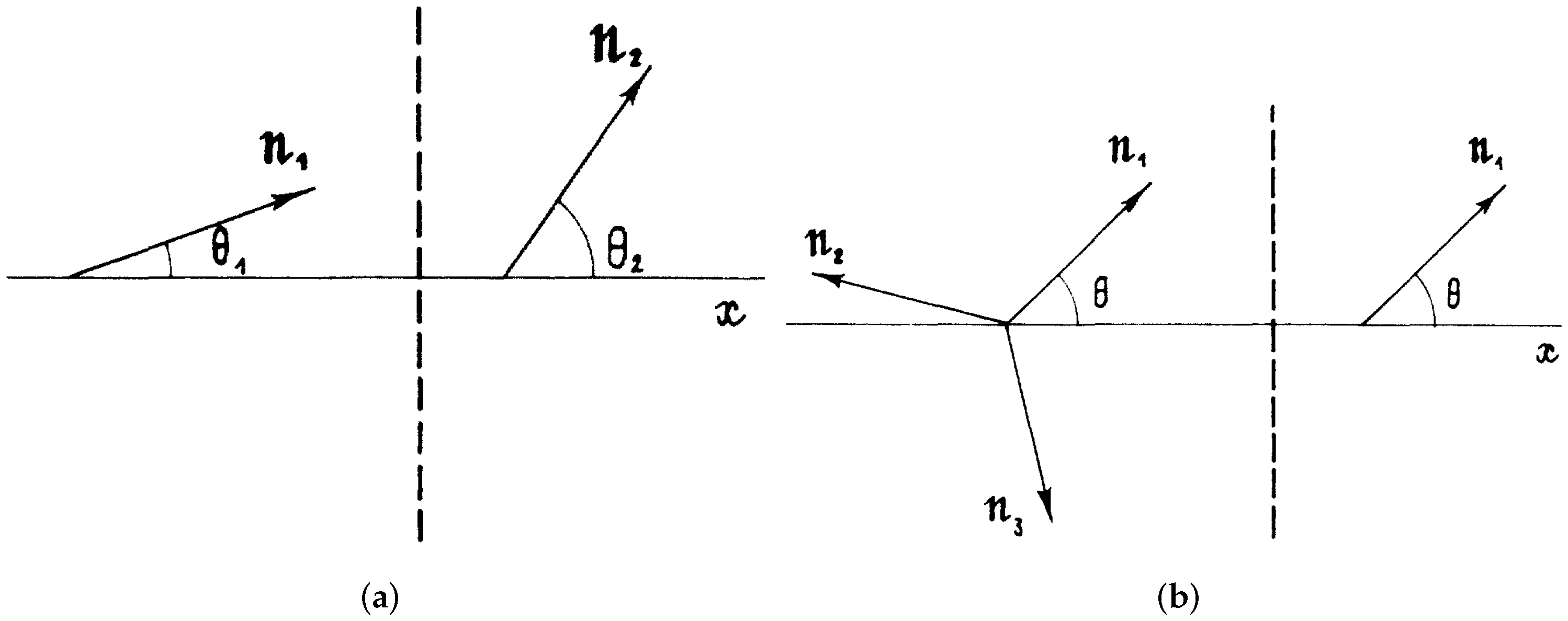
2.2.1. The Setting
2.2.2. Original Analytical Results
2.2.3. New Analytical Results
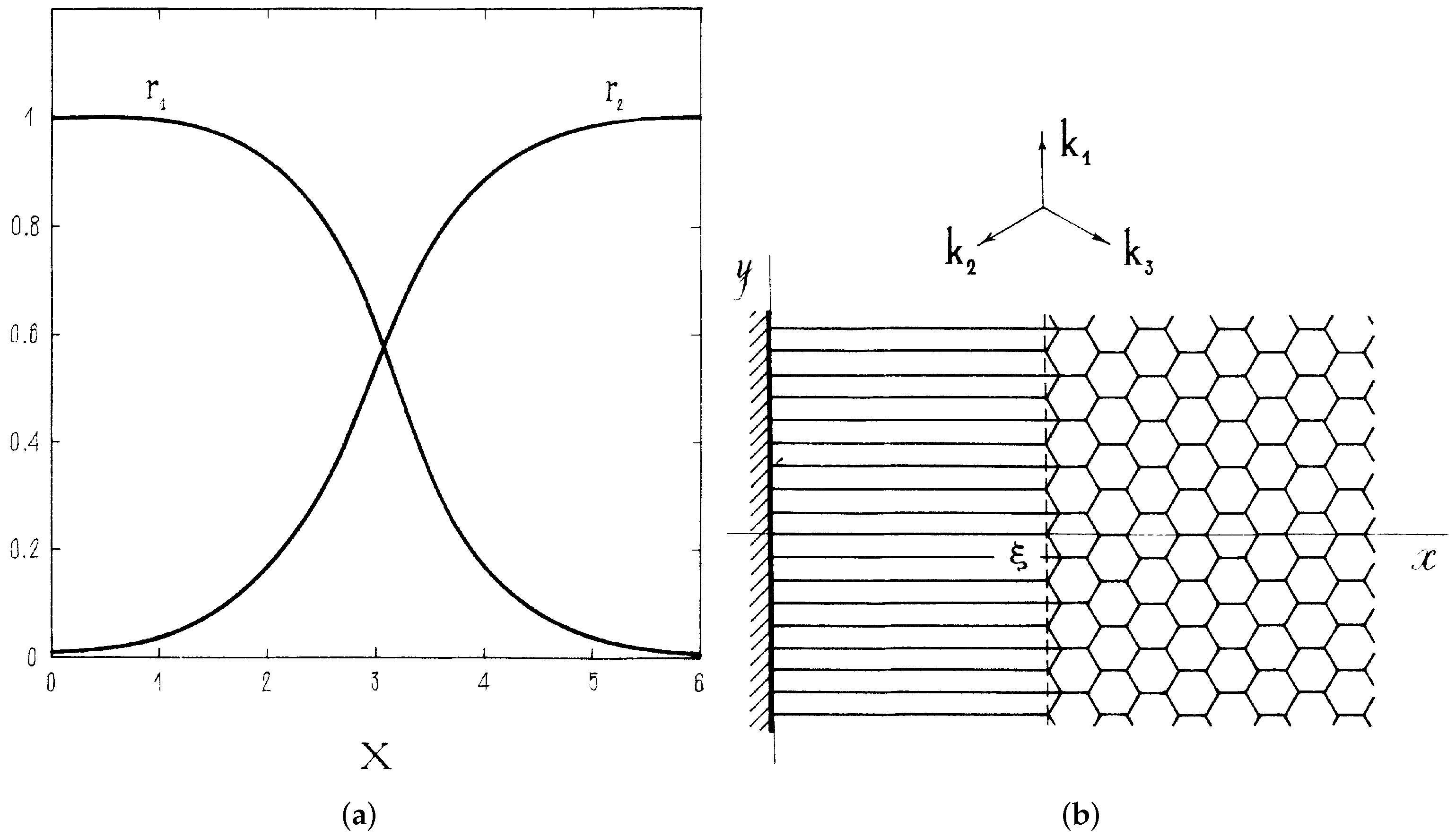
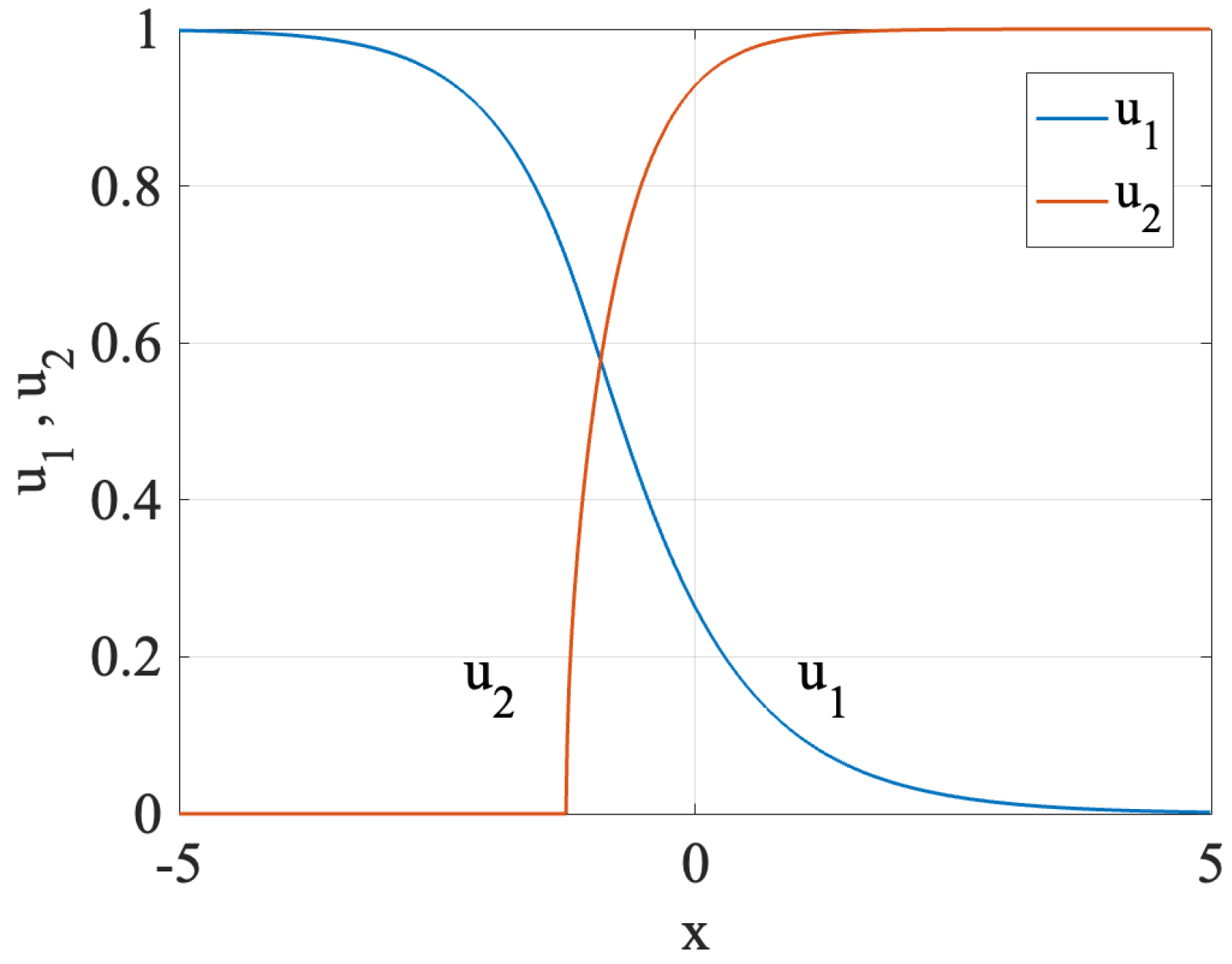
Symmetric DWs
The Effect of the Confining Potential
Exact Asymmetric DWs
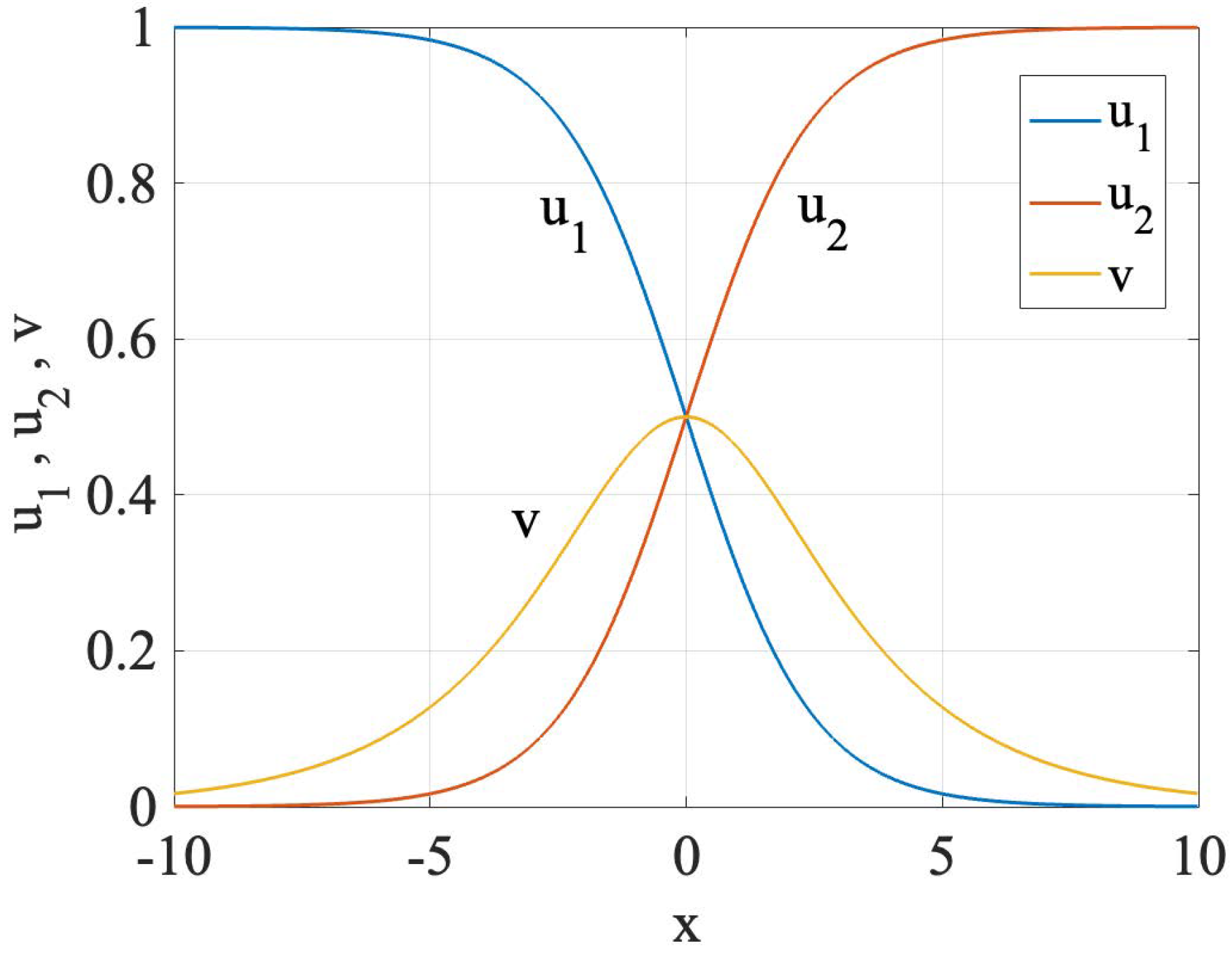
2.2.4. DW–Bright-Soliton Complexes
An Exact Solution for the Composite State
The Bifurcation of the Creation of the Composite State in the General Case
2.3. Domain Walls between Traveling Waves
2.3.1. The Setting
2.3.2. A (New) Exact Analytical Solution
2.3.3. The Sink or Source Coupled to a Bright Soliton in an Additional Component
3. Two- and Three-Dimensional Quasiperiodic Patterns
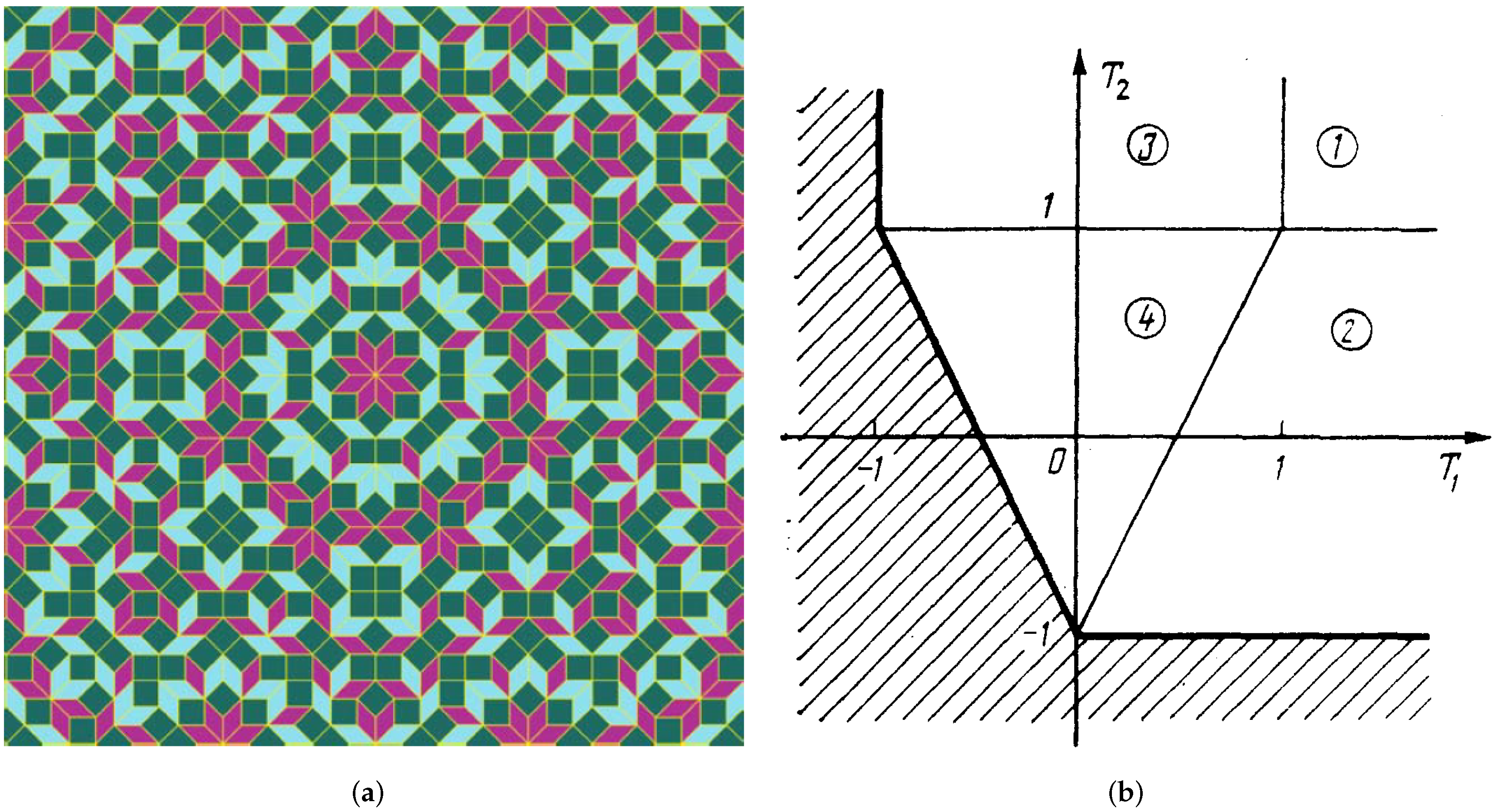
3.1. 2D Octagonal (Eight-Mode) and Decagonal (Ten-Mode) Quasicrystals
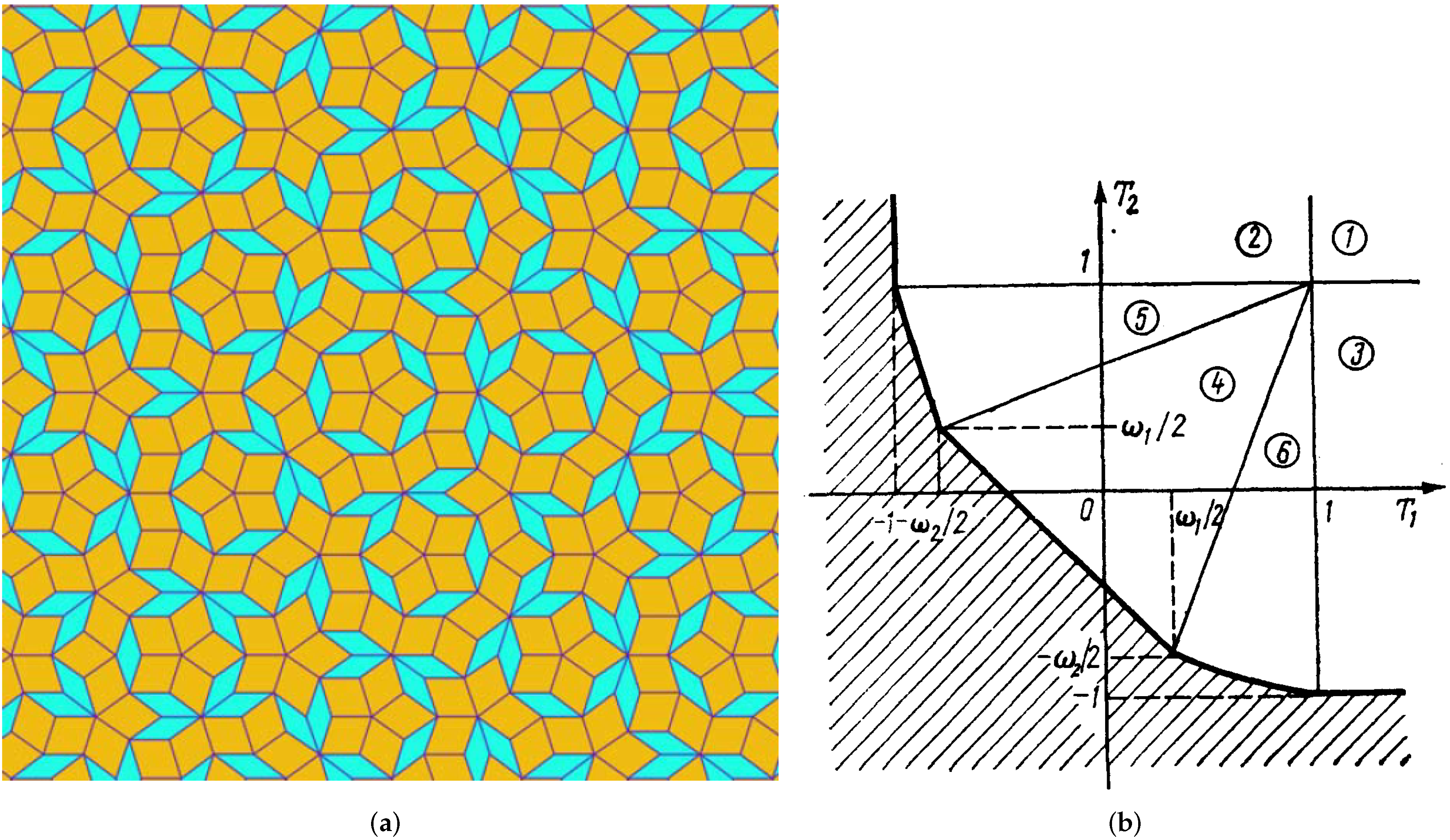
3.2. Dodecagonal Quasicrystals ()
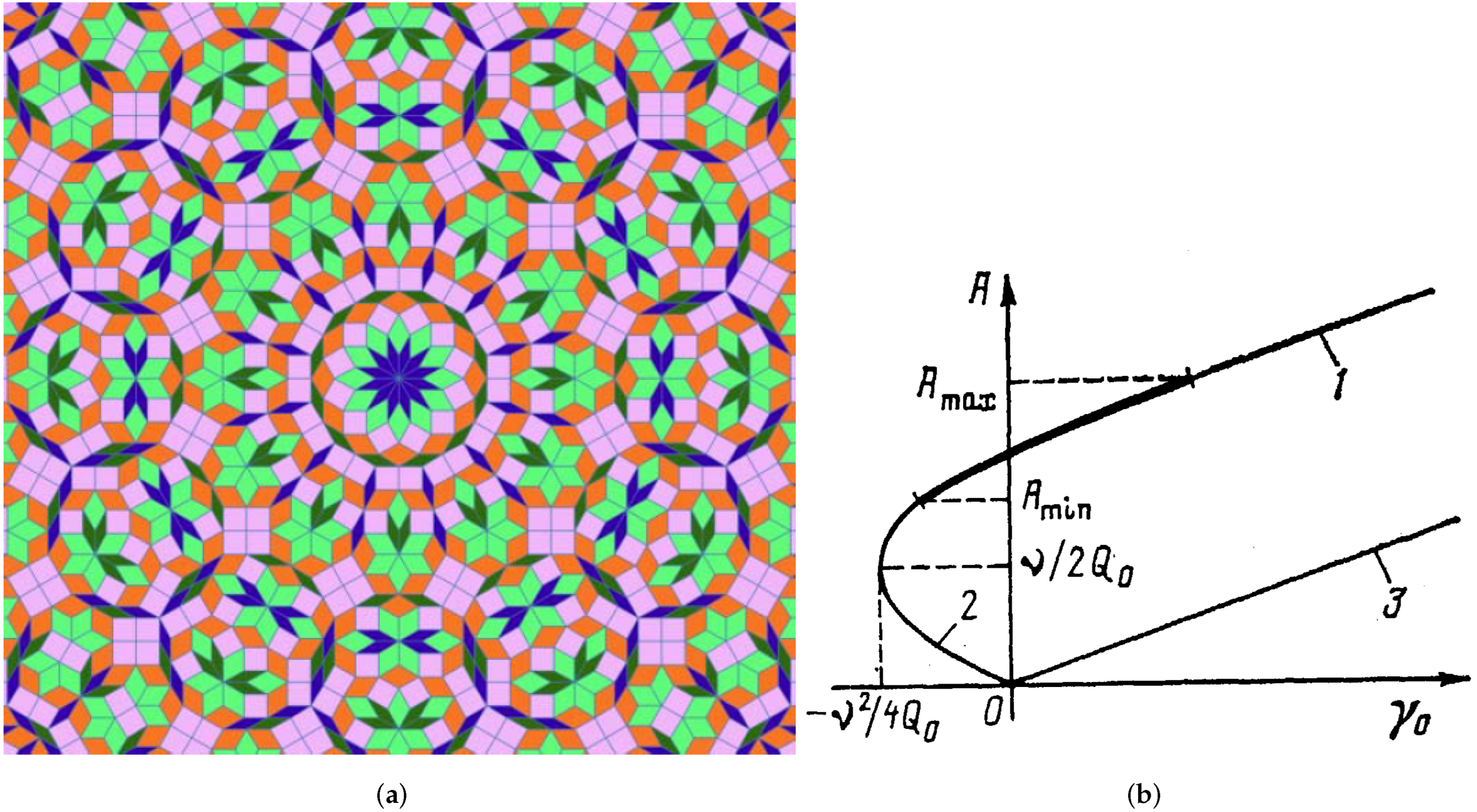
3.3. A Quasicrystalline Layer between Orthogonally Oriented Square-Lattice Patterns
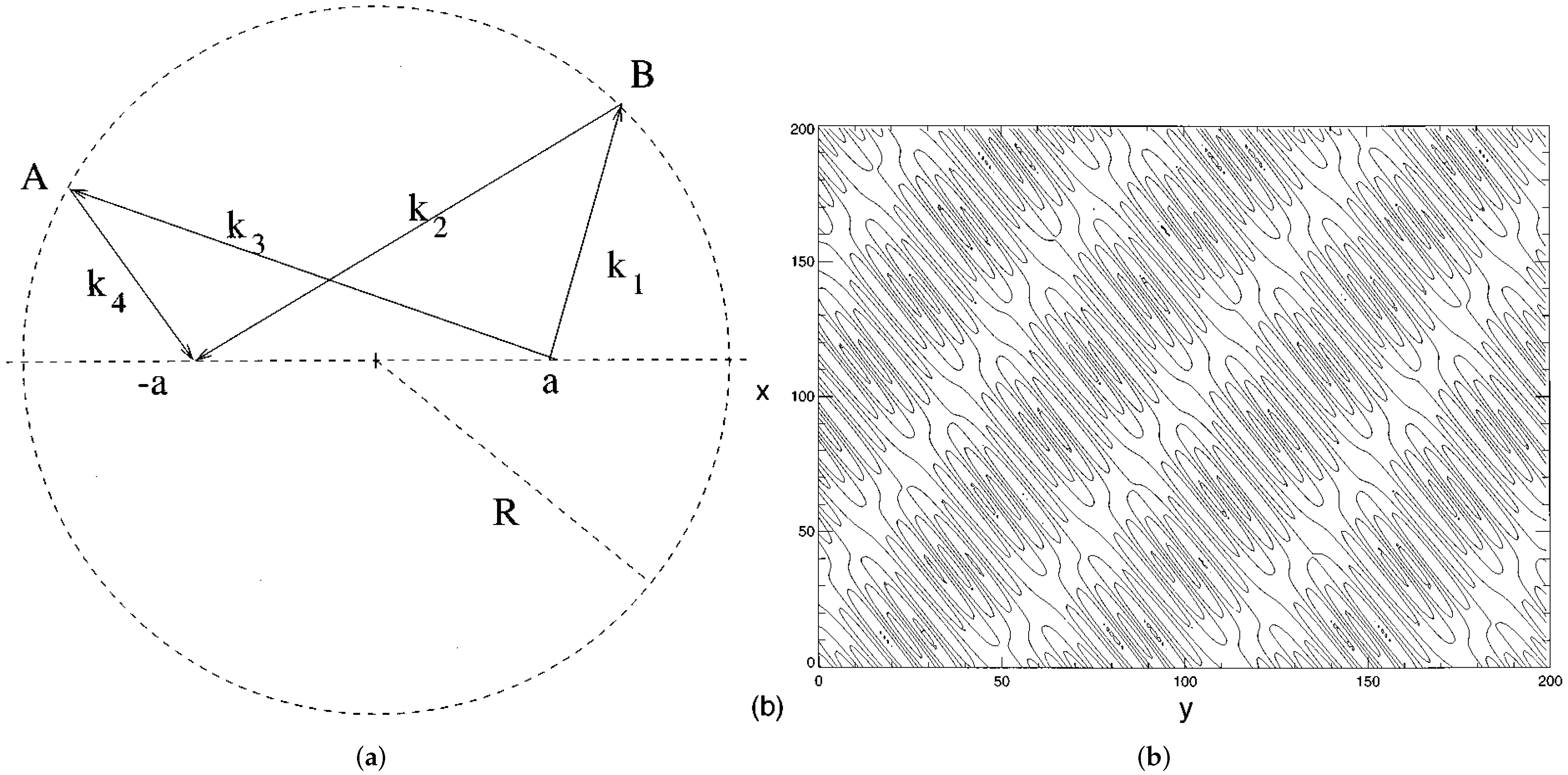
3.4. Three-Dimensional Quasicrystals
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anisimov, S.I.; Tribel’skiĭ, M.I.; Épel’baum, Y.G. Instability of Plane Evaporation Boundary in Interaction of Laser Radiation with Matter. Sov. Phys.—JETP 1980, 51, 802–806. Available online: http://jetp.ras.ru/cgi-bin/dn/e_051_04_0802.pdf (accessed on 1 November 2021).
- Bunkin, F.V.; Tribel’sky, M.I. Non-resonant interaction of high-power optical radiation with a liquid. Sov. Physics Uspekhi 1980, 130, 105–133. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.S.; Tribelsky, M.I. Anomalous light scattering by small particles. Phys. Rev. Lett. 2006, 97, 263902. [Google Scholar] [CrossRef] [Green Version]
- Tribelsky, M.I.; Flach, S.; Miroshnichenko, A.E.; Gorbach, A.V.; Kivshar, Y.S. Light scattering by a finite obstacle and Fano resonances. Phys. Rev. Lett. 2008, 100, 043903. [Google Scholar] [CrossRef] [Green Version]
- Tribelsky, M.I.; Geffrin, J.M.; Litman, A.; Eyraud, C.; Moreno, F. Small dielectric spheres with high refractive index as new multifunctional elements for optical devices. Sci. Rep. 2015, 5, 12288. [Google Scholar] [CrossRef] [Green Version]
- Miroshnichenko, A.E.; Tribelsky, M.I. Giant in-particle field concentration and Fano resonances at light scattering by high-refractive-index particles. Phys. Rev. A. 2016, 83, 053837. [Google Scholar] [CrossRef] [Green Version]
- Miroshnichenko, A.E.; Tribelsky, M.I. Ultimate absorption in light scattering by a finite obstacle. Phys. Rev. Lett. 2018, 120, 263902. [Google Scholar] [CrossRef] [Green Version]
- Malomed, B.A.; Nepomnyashchy, A.A.; Tribelsky, M.I. Domain boundaries in convection patterns. Phys. Rev. A 1990, 42, 7244–7263. [Google Scholar] [CrossRef]
- Malomed, B.A.; Nepomnyashchiĭ, A.A.; Tribel’skiĭ, M.I. Two-Dimensional Quasiperiodic Structures in Nonequilibrium Systems. Sov. Phys.—JETP 1989, 69, 388–396. Available online: http://jetp.ras.ru/cgi-bin/dn/e_069_02_0388.pdf (accessed on 1 November 2021).
- Malomed, B.A. New Findings for the Old Problem: Exact Solutions for Domain Walls in Coupled Real Ginzburg-Landau Equations. To be published.
- Malomed, B.A.; Tribelsky, M.I. Bifurcations in distributed kinetic systems with aperiodic instability. Phys. D 1984, 14, 67–87. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20, 1064–1082. (In Russian). English Translation: Collected Papers of L.D. Landau; Ter-Haar, D.; Pergamon Press: Oxford, UK, 1965; pp. 546–568 [Google Scholar] [CrossRef] [Green Version]
- Cross, M.C. Ingredients of a theory of convective textures close to onset. Phys. Rev. A 1982, 25, 1065–1076. [Google Scholar] [CrossRef] [Green Version]
- Eckhaus, W. Studies in Non-Linear Stability Theory; Springer: New York, NY, USA, 1965. [Google Scholar] [CrossRef]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef] [Green Version]
- Malomed, B.A. Complex Ginzburg-Landau equation. In Encyclopedia of Nonlinear Science; Scott, A., Ed.; Routledge: New York, NY, USA, 2005; pp. 157–160. [Google Scholar]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Boccaletti, S.; Ramazza, P. Pattern formation and competition in nonlinear optics. Phys. Rep. 1999, 318, 1–83. [Google Scholar] [CrossRef]
- Rosanov, N.N. Transverse patterns in wide-aperture nonlinear optical systems. Progr. Opt. 1996, 35, 1–60. [Google Scholar] [CrossRef]
- Rosanov, N.N. Spatial Hysteresis and Optical Patterns; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Lega, J. Traveling hole solutions of the complex Ginzburg-Landau equation: A review. Phys. D 2001, 152, 269–287. [Google Scholar] [CrossRef]
- Cross, M.C.; Hohenberg, P.C. Pattern-formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef] [Green Version]
- Ipsen, M.; Kramer, L.; Sorensen, P.G. Amplitude equations for description of chemical reaction-diffusion systems. Phys. Rep. 2000, 337, 193–235. [Google Scholar] [CrossRef]
- Hoyle, R. Pattern Formation: An Introduction to Methods; Cambridge University Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Malomed, B.A. Evolution of nonsoliton and “quasiclassical” wavetrains in nonlinear Schrödinger and Korteweg—de Vries equations with dissipative perturbations. Phys. D 1987, 29, 155–172. [Google Scholar] [CrossRef]
- Sakaguchi, H. Motion of pulses and vortices in the cubic-quintic complex Ginzburg-Landau equation without viscosity. Phys. D 2005, 210, 138–148. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. (Eds.) Dissipative Solitons: From Optics to Biology and Medicine; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef] [Green Version]
- Wise, F.W.; Chong, A.; Renninger, W.H. High-energy femtosecond fiber lasers based on pulse propagation at normal dispersion. Laser Phot. Rev. 2008, 2, 58–73. [Google Scholar] [CrossRef]
- Ackemann, T.; Firth, W.J.; Oppo, G.L. Fundamentals and applications of spatial dissipative solitons in photonic devices. Adv. At. Mol. Opt. Phys. 2009, 57, 323–421. [Google Scholar] [CrossRef] [Green Version]
- Leblond, H.; Mihalache, D. Models of few optical cycle solitons beyond the slowly varying envelope approximation. Phys. Rep. 2013, 523, 61–126. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.F.; Shi, X.J.; Wu, C.F.; Tang, D.Y.; Zhang, H. Recent progress of study on optical solitons in fiber lasers. Appl. Phys. Rev. 2019, 6, 0213139. [Google Scholar] [CrossRef]
- Hocking, L.M.; Stewartson, K. On the nonlinear response of a marginally unstable plane parallel flow to a two-dimensional disturbance. Proc. R. Soc. London Ser. A 1972, 326, 289–313. [Google Scholar] [CrossRef]
- Pereira, N.R.; Stenflo, L. Nonlinear Schrödinger equation including growth and damping. Phys. Fluids 1977, 20, 1733–1734. [Google Scholar] [CrossRef] [Green Version]
- Malomed, B.A. Strong periodic amplification of solitons in a lossy optical fiber: Analytical results. J. Opt. Soc. Am. B 1994, 11, 1261–1266. [Google Scholar] [CrossRef]
- Berntson, A.; Malomed, B.A. Dispersion-management with filtering. Opt. Lett. 1999, 24, 507–509. [Google Scholar] [CrossRef]
- Bekki, N.; Nozaki, K. Formation of spatial patterns and holes in the generalized Ginzburg-Landau equation. Phys. Lett. A 1985, 1985. 110, 133–135. [Google Scholar] [CrossRef]
- Petviashvili, V.I.; Sergeev, A.M. Spiral solitons in active media with an excitation threshold. Dokl. Akad. Nauk SSSR 1984, 276, 1380–1384. (In Russian). Available online: http://mi.mathnet.ru/dan46625 (accessed on 1 November 2021).
- Fauve, S.; Thual, O. Solitary waves generated by subcritical instabilities in dissipative systems. Phys. Rev. Lett. 1990, 64, 282–284. [Google Scholar] [CrossRef]
- van Saarloos, W.; Hohenberg, P.C. Pulses and fronts in the complex Ginzburg-Landau equation near a subcritical bifurcation. Phys. Rev. Lett. 1990, 84, 749–752. [Google Scholar] [CrossRef] [Green Version]
- Hakim, V.; Jakobsen, P.; Pomeau, Y. Fronts vs. solitary waves in nonequilibrium systems. Europhys. Lett. 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Malomed, B.A.; Nepomnyashchy, A.A. Kinks and solitons in the generalized Ginzburg-Landau equation. Phys. Rev. A 1990, 42, 6009–6014. [Google Scholar] [CrossRef] [PubMed]
- Kuramoto, Y.; Tsuzuki, T. Persistent propagation of concentration waves in dissipative media far from thermal equilibrium. Progr. Theor. Phys. 1976, 55, 356–369. [Google Scholar] [CrossRef] [Green Version]
- Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames—I. Derivation of basic equations. Acta Astronaut. 1977, 4, 1177–1206. [Google Scholar] [CrossRef]
- Kuramoto, Y. Diffusion-induced chaos in reaction systems. Progr. Theor. Phys. Suppl. 1978, 64, 346–367. [Google Scholar] [CrossRef]
- Cladis, P.E.; Fradin, C.; Finn, P.L.; Brand, H.R. A novel route to defect turbulence in nematics. Mol. Cryst. Liq. Cryst. Sci. Tech. A: Mol. Cryst. Liq. Cryst. 1998, 328, 513–521. [Google Scholar] [CrossRef]
- Manneville, P.; Pomeau, Y. A grain-boundary in cellular structures near the onset of convection. Phil. Mag. A 1983, 48, 607–621. [Google Scholar] [CrossRef]
- Haragus, M.; Iooss, G. Bifurcation of symmetric domain walls for the Bénard-Rayleigh convection problem. Arch. Ration. Mech. Anal. 2021, 239, 733–781. [Google Scholar] [CrossRef]
- Steinberg, V.; Ahlers, G.; Cannell, D.S. Pattern formation and wave-number selection by Rayleigh-Bénard convection in a cylindrical container. Phys. Scr. 1985, 32, 534–547. [Google Scholar] [CrossRef]
- Rohrer, G.S. Grain boundary energy anisotropy: A review. J. Mater. Sci. 2011, 46, 5881–5895. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.; Lee, M.G.; Wagoner, R.H. Simulation of polycrystal deformation with grain and grain boundary effects. Int. J. Plast. 2011, 27, 1328–1354. [Google Scholar] [CrossRef]
- Rudolph, P. Dislocation patterning and bunching in crystals and epitaxial layers—A review. Cryst. Res. Tech. 2017, 52, 1600171. [Google Scholar] [CrossRef] [Green Version]
- Atxitia, U.; Hinzke, D.; Nowak, U. Fundamentals and applications of the Landau-Lifshitz-Bloch equation. J. Phys. D Appl. Phys. 2017, 50, 033003. [Google Scholar] [CrossRef]
- Galkina, E.G.; Ivanov, B.A. Dynamic solitons in antiferromagnets. Low Temp. Phys. 2018, 44, 618–633. [Google Scholar] [CrossRef]
- Yao, W.; Wu, B.; Liu, Y. Growth and grain boundaries in 2D materials. ACS NANO 2020, 14, 9320–9346. [Google Scholar] [CrossRef] [PubMed]
- Yerin, Y.; Drechsler, S.-L. Phase solitons in a weakly coupled three-component superconductor. Phys. Rev. B 2021, 104, 014518. [Google Scholar] [CrossRef]
- Malomed, B.A. Optical domain walls. Phys. Rev. E 1994, 50, 1565–1571. [Google Scholar] [CrossRef] [PubMed]
- Trippenbach, M.; Góral, K.; Rzażewski, K.; Malomed, B.; Band, Y.B. Structure of binary Bose-Einstein condensates. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 4017–4031. [Google Scholar] [CrossRef]
- Malomed, B.A. Nonsteady waves in distributed dynamical systems. Phys. D 1983, 8, 353–359. [Google Scholar] [CrossRef]
- Malomed, B.A. Stability and grain boundaries in the dispersive Newell-Whitehead-Siegel equation. Phys. Scr. 1997, 57, 115–117. [Google Scholar] [CrossRef]
- Cross, M.C. Traveling and standing waves in binary-fluid convection in finite geometries. Phys. Rev. Lett. 1986, 57, 2935–2938. [Google Scholar] [CrossRef] [Green Version]
- Cross, M.C. Structure of nonlinear traveling-wave states in finite geometries. Phys. Rev. A 1988, 38, 3593–3600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coullet, P.; Frisch, T.; Plaza, F. Sources and sinks of wave patterns. Phys. D 1993, 62, 75–79. [Google Scholar] [CrossRef]
- Voss, H.U.; Kolodner, P.; Abel, M.; Kurths, J. Amplitude equations from spatiotemporal binary-fluid convection data. Phys. Rev. Lett. 1999, 83, 3422–3425. [Google Scholar] [CrossRef] [Green Version]
- Komarova, N.; Malomed, B.A.; Moloney, J.V.; Newell, A.C. Resonant quasiperiodic patterns in a three-dimensional lasing medium. Phys. Rev. A 1997, 56, 803–812. [Google Scholar] [CrossRef] [Green Version]
- Rotstein, H.; Malomed, B.A. A quasicrystallic domain wall in nonlinear dissipative patterns. Phys. Scr. 2000, 62, 164–168. [Google Scholar]
- Lugiato, A.A.; Lefever, R. Spatial dissipative structures in passive optical systems. Phys. Rev. Lett. 1987, 58, 2209–2211. [Google Scholar] [CrossRef]
- Oppo, G.-L.; Brambilla, M.; Lugiato, L. Formation and evolution of roll patterns in optical parametric oscillators. Phys. Rev. A 1994, 49, 2028–2032. [Google Scholar] [CrossRef]
- Chembo, Y.K.; Menyuk, C.R. Spatiotemporal Lugiato-Lefever formalism for Kerr-comb generation in whispering-gallery-mode resonators. Phys. Rev. A 2013, 87, 053852. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.W.; Yang, J.H.; Yang, S.H.; Yu, M.B.; Kwong, D.L.; Zelevinsky, T.; Jarrahi, M.; Wong, C.W. Globally stable microresonator Turing pattern formation for coherent high-power THz radiation on-chip. Phys. Rev. X 2017, 7, 041002. [Google Scholar] [CrossRef] [Green Version]
- de Valcarcel, G.J.; Staliunas, K. Phase-bistable Kerr cavity solitons and patterns. Phys. Rev. A 2013, 87, 043802. [Google Scholar] [CrossRef] [Green Version]
- Garbin, B.; Wang, Y.D.; Murdoch, S.G.; Oppo, G.L.; Coen, S.; Erkintalo, M. Experimental and numerical investigations of switching wave dynamics in a normally dispersive fibre ring resonator. Eur. Phys. J. D 2017, 71, 240. [Google Scholar] [CrossRef]
- Mineev, V.P. The theory of the solution of two near-ideal Bose gases. Sov. Phys.—JETP 1974, 40, 132–136. Available online: http://jetp.ras.ru/cgi-bin/dn/e_040_01_0132.pdf (accessed on 1 November 2021).
- Busse, F.H. The stability of finite amplitude cellular convection and its relation to an extremum principle. J. Fluid Mech. 1967, 30, 625–649. [Google Scholar] [CrossRef]
- Pomeau, Y. Front motion, metastability and subcritical bifurcations in hydrodynamics. Phys. D 1986, 23, 3–11. [Google Scholar] [CrossRef]
- van Hecke, M.; Malomed, B.A. A domain wall between single-mode and bimodal states and its transition to dynamical behavior in inhomogeneous systems. Phys. D 1997, 101, 131–156. [Google Scholar] [CrossRef] [Green Version]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Skorobogatiy, M.; Yang, J. Fundamentals of Photonic Crystal Guiding; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein Condensation and Superfluidity; Oxford University Press: Oxford, UK, 2016. [Google Scholar] [CrossRef]
- Ballagh, R.J.; Burnett, K.; Scott, T.F. Theory of an output coupler for Bose-Einstein condensed atoms. Phys. Rev. Lett. 1997, 78, 1608–1611. [Google Scholar] [CrossRef]
- Asghari, M.; White, I.H.; Penty, R.V. Wavelength conversion using semiconductor optical amplifiers. J. Light. Tech. 1997, 15, R3310–R3313. [Google Scholar] [CrossRef]
- Kim, J.; Laemmlin, M.; Meuer, C.; Bimberg, D.; Eisenstein, G. Theoretical and experimental study of high-speed small-signal cross-gain modulation of quantum-dot semiconductor optical amplifiers. IEEE J. Quant. Elect. 2009, 45, 240–248. [Google Scholar] [CrossRef]
- Merhasin, M.I.; Malomed, B.A.; Driben, R. Transition to miscibility in a binary Bose-Einstein condensate induced by linear coupling. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 877–892. [Google Scholar] [CrossRef]
- Alama, S.; Bronsard, L.; Contreras, A.; Pelinovsky, D.E. Domains walls in the coupled Gross-Pitaevskii equations. Arch. Rat. Mech. Appl. 2015, 215, 579–615. [Google Scholar] [CrossRef] [Green Version]
- Marzok, C.; Deh, B.; Courteille, P.W.; Zimmermann, C. Ultracold thermalization of 7Li and 87Rb. Phys. Rev. A 2007, 76, 052704. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, A.S.; Kabanov, V.V. Excitations and phase segregation in a two-component Bose–Einstein condensate with an arbitrary interaction. J. Phys. Condens. Matter 2002, 14, L327–L332. [Google Scholar] [CrossRef]
- Malomed, B.A. Domain wall between traveling waves. Phys. Rev. E 1994, 50, R3310–R3313. [Google Scholar] [CrossRef] [PubMed]
- Kai, Y.; Yin, Z. Asymptotic analysis to domain walls between traveling waves modeled by real coupled Ginzburg-Landau equations. Chaos Solitons Fractals 2021, 152, 111266. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Chen, H.; Kuo, K. Two-dimensional quasicrystal with eightfold rotational symmetry. Phys. Rev. Lett. 1987, 59, 1010–1013. [Google Scholar] [CrossRef] [Green Version]
- Barkan, K.; Diamant, H.; Lifshitz, R. Stability of quasicrystals composed of soft isotropic particles. Phys. Rev. B 2011, 83, 172201. [Google Scholar] [CrossRef] [Green Version]
- Torquato, S. Hyperuniform states of matter. Phys. Rep. 2018, 745, 1–95. [Google Scholar] [CrossRef] [Green Version]
- Steurer, W. Quasicrystals: What do we know? What do we want to know? What can we know? Acta Crystallogr. A 2018, 74, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Savitz, S.; Babadi, M.; Lifshitz, R. Multiple-scale structures: From Faraday waves to soft-matter quasicrystals. IUCrJ 2018, 5, 247–268. [Google Scholar] [CrossRef] [PubMed]
- Skjaervo, S.H.; Marrows, C.H.; Stamps, R.L.; Leyderman, L.J. Advances in artificial spin ice. Nat. Rev. Phys. 2020, 2, 13–28. [Google Scholar] [CrossRef] [Green Version]
- Lifshitz, R.; Petrich, D.M. Theoretical model for Faraday waves with multiple-frequency forcing. Phys. Rev. Lett. 1997, 79, 1261–1264. [Google Scholar] [CrossRef] [Green Version]
- von Freymann, G.; Ledermann, A.; Thiel, M.; Staude, I.; Essig, S.; Busch, K.; Wegener, M. Three-dimensional nanostructures for photonics. Adv. Funct. Mater. 2010, 20, 1038–1052. [Google Scholar] [CrossRef]
- Bellingeri, M.; Chiasera, A.; Kriegel, I.; Scotognella, F. Optical properties of periodic, quasi-periodic, and disordered one-dimensional photonic structures. Opt. Mater. 2017, 72, 403–421. [Google Scholar] [CrossRef] [Green Version]
- Vardeny, Z.V.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystals. Nat. Photonics 2013, 7, 177–187. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljacic, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef] [Green Version]
- Steurer, W.; Sutter-Widmer, D. Photonic and phononic quasicrystals. J. Phys. D: Appl. Phys. 2007, 40, R229–R247. [Google Scholar] [CrossRef]
- Malomed, B.A.; Tribelskiĭ, M.I. On the Stability of Stationary Weakly Overcritical Patterns in Convection and Allied Problems. Sov. Phys.—JETP 1987, 65, 305–310. Available online: http://jetp.ras.ru/cgi-bin/dn/e_065_02_0305.pdf (accessed on 1 November 2021).
- Malomed, B.A.; Nepomnyashchy, A.A.; Tribelsky, M.I. Two-dimensional dissipative structures with a quasicrystallic symmetry. Pis’ma Zh. Tekh. Fiz. (Sov. Phys. Tech. Phys. Lett.) 1987, 13, 1165–1167. [Google Scholar]
- Steurer, W. Twenty years of structure research on quasicrystals. Part I. Pentagonal, octagonal, decagonal and dodecagonal quasicrystals. Z. für Krist. 2004, 219, 391–446. [Google Scholar] [CrossRef]
- Socolar, J.E.S.; Lubensky, T.C.; Steinhardt, P.J. Phonons, phasons, and dislocations in quasi-crystals. Phys. Rev. B 1986, 34, 3345–3360. [Google Scholar] [CrossRef]
- Yamamoto, A. Crystallography of quasiperiodic crystals. Acta Crystallogr. A 1996, 52, 509–560. [Google Scholar] [CrossRef]
- Freedman, B.; Lifshitz, R.; Fleischer, J.W.; Segev, M. Phason dynamics in nonlinear photonic quasicrystals. Nat. Mater. 2007, 6, 776–781. [Google Scholar] [CrossRef]
- Iooss, G.; Joseph, D.D. Elementary Stability Bifurcation Theory; Springer: New York, NY, USA, 1980. [Google Scholar]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, K.-X.; Feng, L.; Hu, J.; Chin, C. Pattern formation in a driven Bose–Einstein condensate. Nat. Phys. 2020, 16, 652–656. [Google Scholar] [CrossRef]
- Wang, Z.; Navarrete-Benlloch, C.; Cai, Z. Pattern formation and exotic order in driven-dissipative Bose-Hubbard systems. Phys. Rev. Lett. 2020, 125, 115301. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malomed, B.A. Past and Present Trends in the Development of the Pattern-Formation Theory: Domain Walls and Quasicrystals. Physics 2021, 3, 1015-1045. https://doi.org/10.3390/physics3040064
Malomed BA. Past and Present Trends in the Development of the Pattern-Formation Theory: Domain Walls and Quasicrystals. Physics. 2021; 3(4):1015-1045. https://doi.org/10.3390/physics3040064
Chicago/Turabian StyleMalomed, Boris A. 2021. "Past and Present Trends in the Development of the Pattern-Formation Theory: Domain Walls and Quasicrystals" Physics 3, no. 4: 1015-1045. https://doi.org/10.3390/physics3040064
APA StyleMalomed, B. A. (2021). Past and Present Trends in the Development of the Pattern-Formation Theory: Domain Walls and Quasicrystals. Physics, 3(4), 1015-1045. https://doi.org/10.3390/physics3040064




