Dissipative Ion-Acoustic Solitary Waves in Magnetized κ-Distributed Non-Maxwellian Plasmas
Abstract
:1. Introduction
2. Basic Plasma-Fluid-Dynamic Formalism
3. A Schamel Equation for Damped Ion-Acoustic Waves (IAWs)
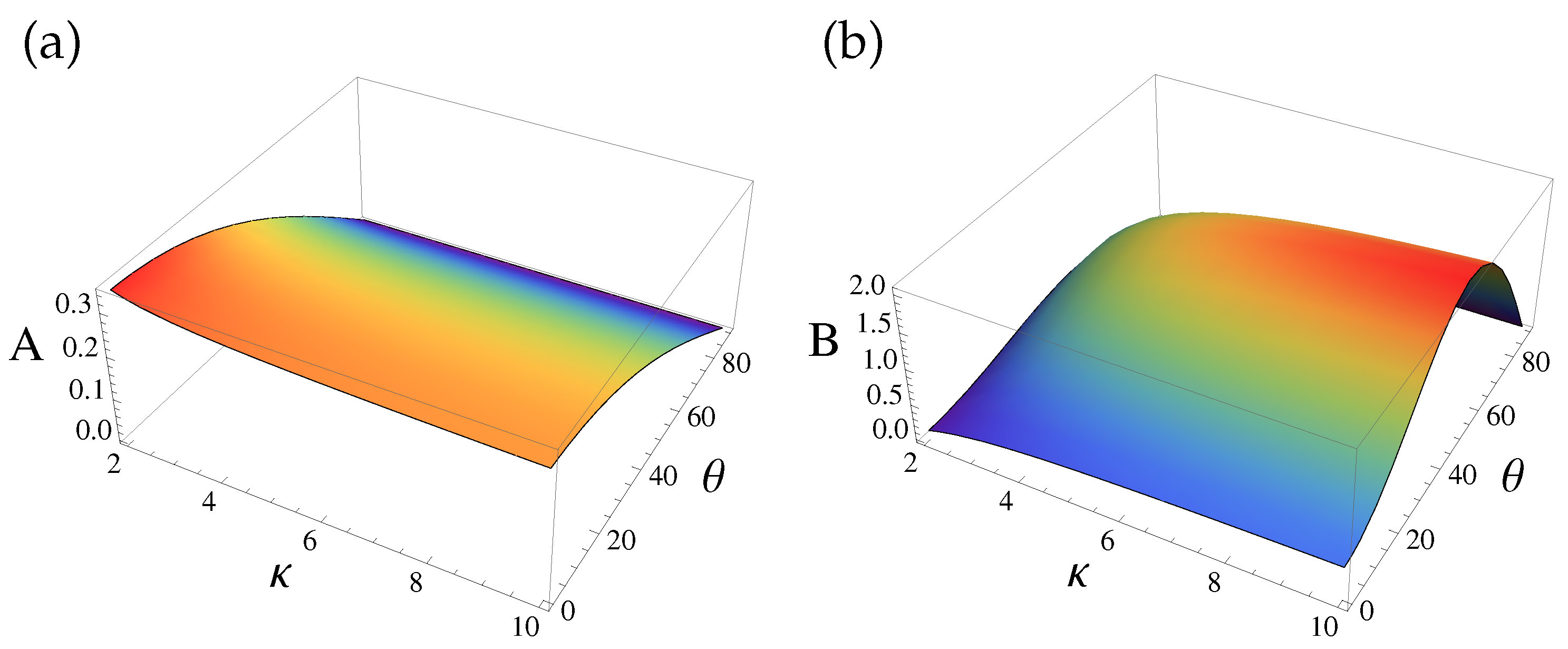
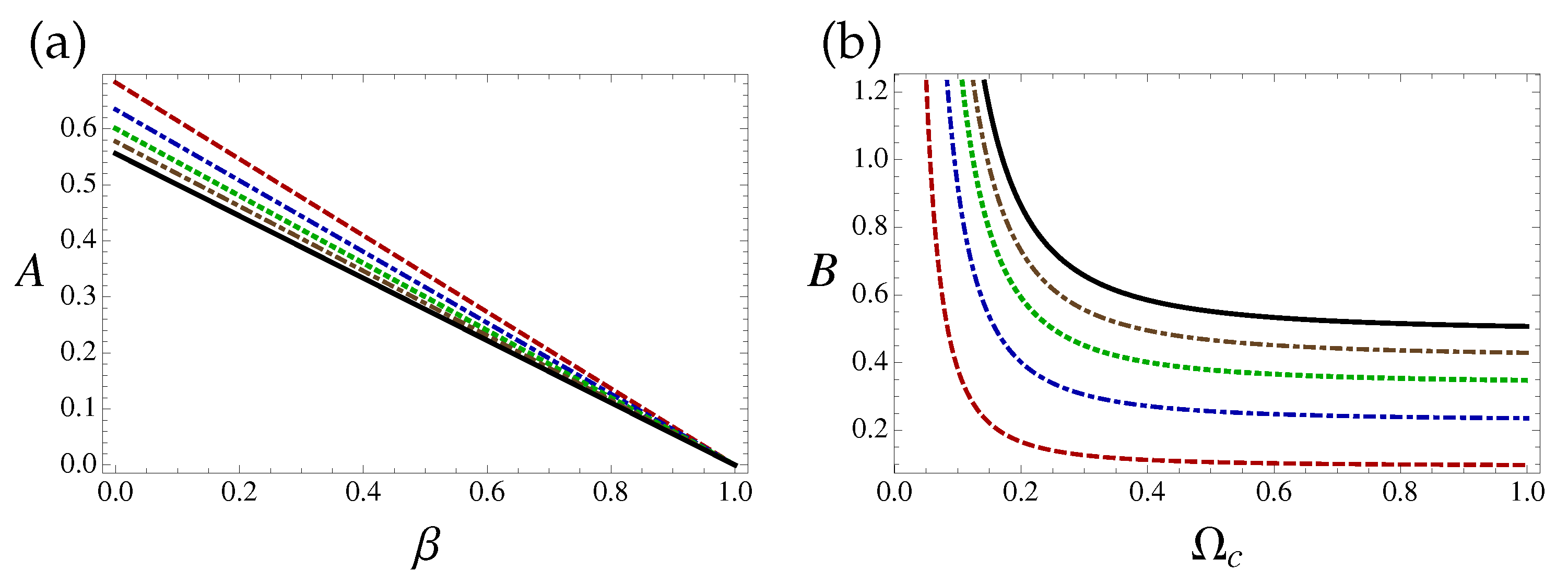
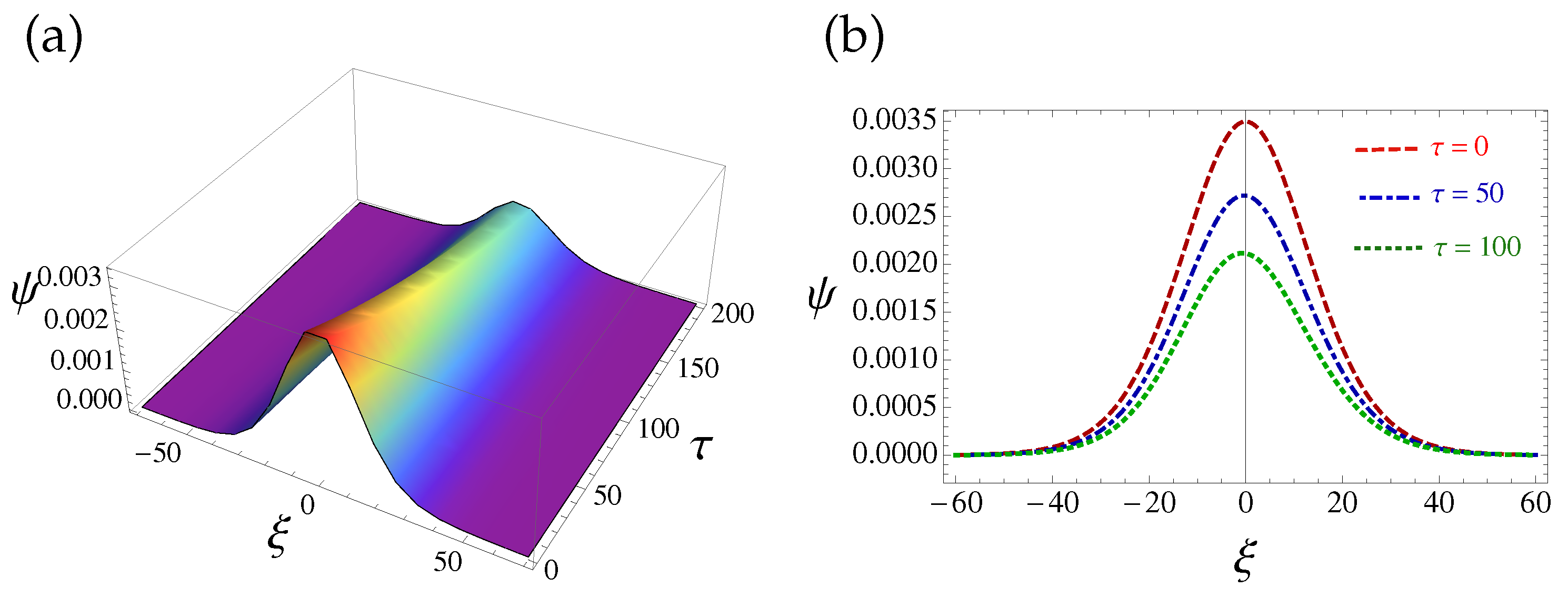
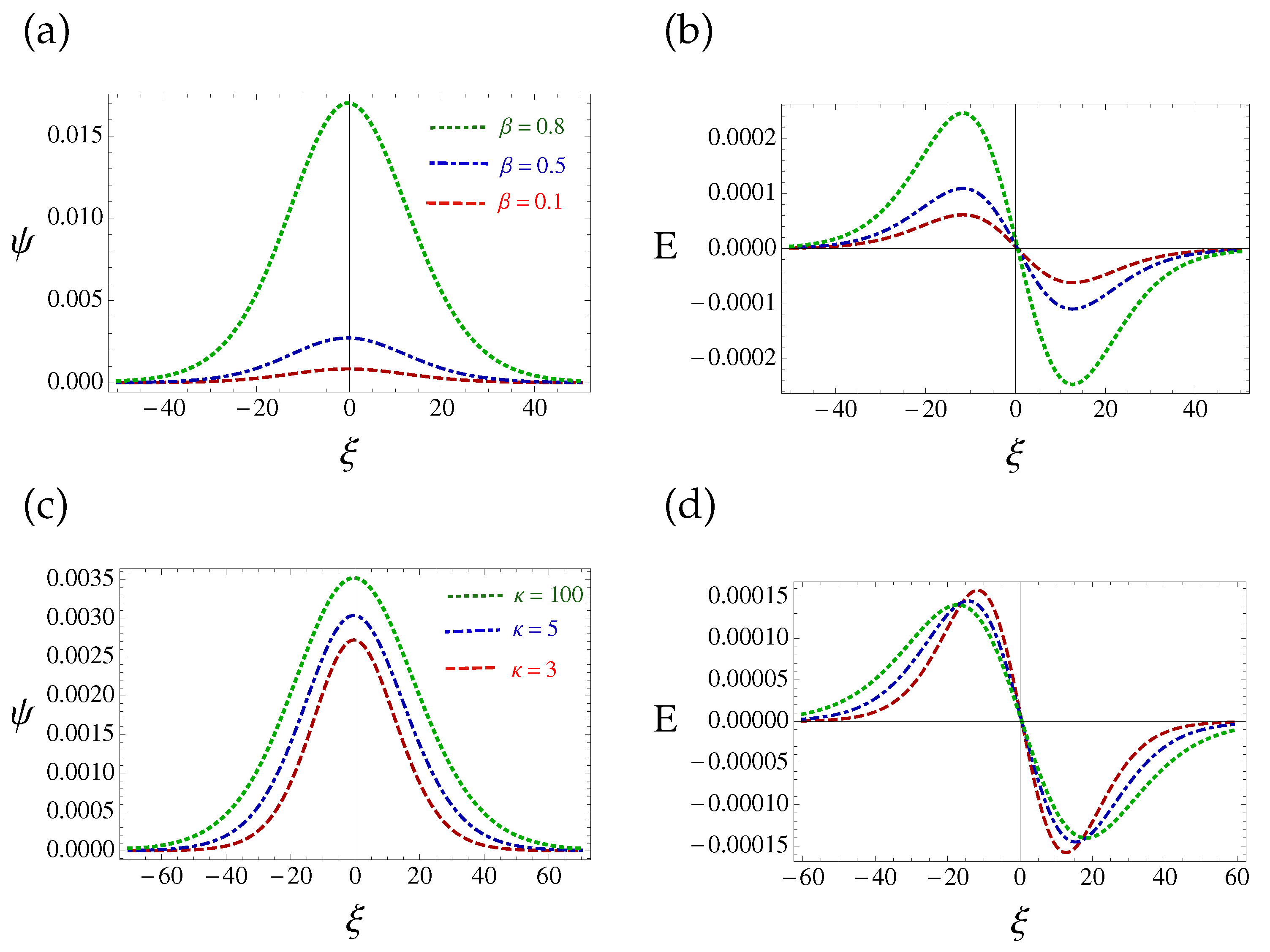
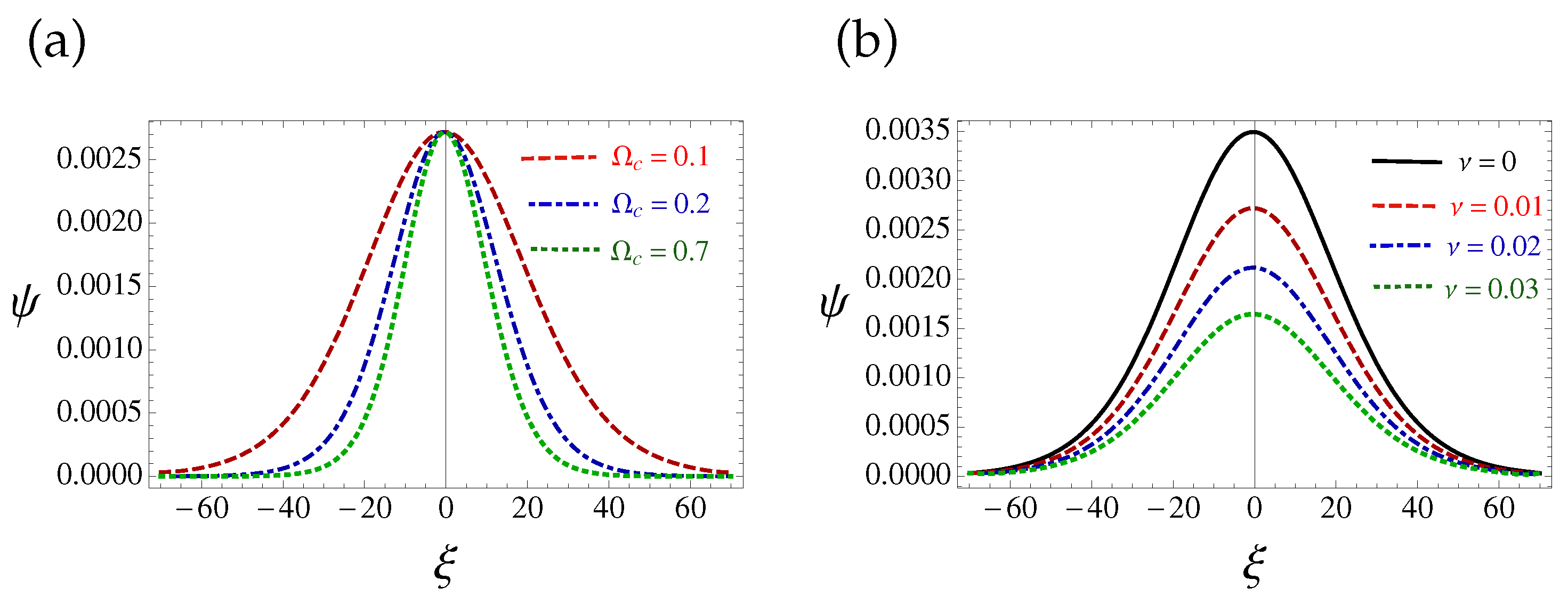
4. Parametric Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839–2884. [Google Scholar] [CrossRef]
- De Feiter, L.D.; De Jager, C. Superthermal plasma nodules and their relation to solar flares. Sol. Phys. 1973, 28, 183–186. [Google Scholar] [CrossRef]
- Scudder, J.D.; Sittler, E.C.; Bridge, H.S. A survey of the plasma electron environment of Jupiter: A view from Voyager. J. Geophys. Res. 1981, 86, 8157–8179. [Google Scholar] [CrossRef] [Green Version]
- Leubner, M.P. On Jupiter’s whistler emission. J. Geophys. Res. 1982, 87, 6335–6338. [Google Scholar] [CrossRef]
- Christon, S.P.; Williams, D.J.; Mitchell, D.G.; Frank, L.A.; Huang, C.Y. Spectral characteristics of plasma sheet ion and electron populations during undisturbed geomagnetic conditions. J. Geophys. Res. 1989, 94, 13409–13424. [Google Scholar] [CrossRef]
- Collier, M.R. On generating kappa-like distribution functions using velocity space Lévy flights. Geophys. Res. Lett. 1993, 20, 1531–1534. [Google Scholar] [CrossRef]
- Decker, D.T.; Basu, B.; Jasperse, J.R.; Strikland, D.J.; Sharber, J.R.; Winningham, J.D. Upgoing electrons produced in an electron-proton-hydrogen atom aurora. J. Geophys. Res. 1995, 100, 21409–21420. [Google Scholar] [CrossRef]
- Codrescu, M.V.; Fuller-Rowell, T.J.; Robble, R.G.; Evans, D.S. Medium energy particle precipitation influences on the mesosphere and lower thermosphere. J. Geophys. Res. 1997, 102, 19977–19987. [Google Scholar] [CrossRef]
- Maksimovic, M.; Gary, S.P.; Skoug, R.M. Solar wind electron suprathermal strength and temperature gradients: Ulysses observations. J. Geophys. Res. 2000, 105, 18337–18350. [Google Scholar] [CrossRef]
- Antonova, E.E.; Stepanova, M.V.; Teltzov, M.V.; Tverskoy, B.A. Multiple inverted-V structures and hot plasma pressure gradient mechanism of plasma stratification. J. Geophys. Res. 1998, 103, 9317–9332. [Google Scholar] [CrossRef] [Green Version]
- Mori, H.; Ishii, M.; Murayama, Y.; Kubota, M.; Sakanoi, K.; Yamamoto, M.Y.; Monzen, Y.; Lummerzheim, D.; Watkins, B.J. Energy distribution of precipitating electrons estimated from optical and cosmic noise absorption measurements. Ann. Geophys. 2004, 22, 1613–1622. [Google Scholar] [CrossRef] [Green Version]
- Livadiotis, G. (Ed.) Kappa Distributions. Theory and Applications in Plasmas; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Armstrong, T.P.; Paonessa, M.T.; Bell, E.V.; Krimigis, S.M. Voyager observations of Saturnian ion and electron phase space densities. J. Geophys. Res. 1983, 88, 8893–8904. [Google Scholar] [CrossRef]
- Hasegawa, A.; Mima, K.; Duong-van, M. Plasma Distribution function in a superthermal radiation field. Phys. Rev. Lett. 1985, 54, 2608–2611. [Google Scholar] [CrossRef]
- Hellberg, M.A.; Mace, R.L.; Armstrong, R.J.; Karlstad, G. Electron-acoustic waves in the laboratory: An experiment revisited. J. Plasma Phys. 2000, 64, 433–443. [Google Scholar] [CrossRef]
- Baluku, T.K.; Hellberg, M.A. Dust acoustic solitons in plasmas with kappa-distributed electrons and/or ions. Phys. Plasmas 2008, 15, 123705. [Google Scholar] [CrossRef]
- Hellberg, M.A.; Mace, R.L.; Baluku, T.K.; Kourakis, I.; Saini, N.S. Comment on “Mathematical and physical aspects of Kappa velocity distribution” [Phys. Plasmas 14, 110702 (2007)]. Phys. Plasmas 2009, 16, 094701. [Google Scholar] [CrossRef] [Green Version]
- Sultana, S.; Kourakis, I.; Saini, N.S.; Hellberg, M.A. Oblique electrostatic excitations in a magnetized plasma in the presence of excess superthermal electrons. Phys. Plasmas 2010, 17, 032310. [Google Scholar] [CrossRef] [Green Version]
- Sultana, S.; Kourakis, I. Electrostatic solitary waves in the presence of excess super-thermal electrons: Modulational instability and envelope soliton modes. Plasma Phys. Control. Fusion 2011, 53, 045003. [Google Scholar] [CrossRef] [Green Version]
- Mauk, B.H.; Mitchell, D.G.; McEntire, R.W.; Paranicas, C.P.; Roelof, E.C.; Williams, D.J.; Krimigis, S.M.; Lagg, A. Energetic ion characteristics and neutral gas interactions in Jupiter’s mag-netosphere. J. Geophys. Res. 2004, 109, A09S12. [Google Scholar]
- Hapgood, M.; Perry, C.; Davies, J.; Denton, M. The role of suprathermal particle meas-urements in CrossScale studies of collisionless plasma processes. Planet. Space Sci. 2011, 59, 618–629. [Google Scholar] [CrossRef]
- Kourakis, I.; Sultana, S.; Hellberg, M.A. Dynamical characteristics of solitary waves, shocks and envelope modes in kappa-distributed non-thermal plasmas: An overview. Plasma Phys. Control. Fusion 2012, 54, 124001. [Google Scholar] [CrossRef]
- Atteya, A.; Sultana, S.; Schlickeiser, R. Dust-ion-acoustic solitary waves in magnetized plasmas with positive and negative ions: The role of electrons superthermality. Chinese J. Phys. 2018, 56, 1931–1939. [Google Scholar] [CrossRef]
- Lotekar, A.; Kakad, A.; Kakad, B. Generation of ion acoustic solitary waves through wave breaking in superthermal plasmas. Phys. Plasma 2017, 24, 102127. [Google Scholar] [CrossRef]
- Goldman, M.V.; Newman, D.L.; Mangeney, A. Theory of weak bipolar fields and electron holes with applications to space plasmas. Phys. Rev. Lett. 2007, 99, 145002. [Google Scholar] [CrossRef]
- Sarri, G. Observation and characterization of laser-driven phase space electron holes. Phys. Plasmas 2010, 17, 010701. [Google Scholar] [CrossRef]
- Schamel, H. Stationary solitary, snoidal and sinusoidal ion acoustic waves. Plasma Phys. 1972, 14, 905–924. [Google Scholar] [CrossRef]
- Schamel, H. A modified Korteweg-de Vries equation for ion acoustic wavess due to resonant electrons. J. Plasma Phys. 1973, 9, 377–387. [Google Scholar] [CrossRef]
- Schamel, H. Cnoidal electron hole propagation: Trapping, the forgotten nonlinearity in plasma and fluid dynamics. Phys. Plasma 2012, 19, 020501. [Google Scholar] [CrossRef] [Green Version]
- Ergun, R.E.; Carlson, C.W.; McFadden, J.P.; Mozer, E.S.; Delory, G.T.; Peria, W.; Chaston, C.C.; Temerin, M.; Roth, I.; Muschietti, L.; et al. FAST satellite observations of large-amplitude solitary structures. Geophys. Res. Lett. 1998, 25, 2041–2044. [Google Scholar] [CrossRef]
- Ergun, R.E.; Andersson, L.; Main, D.S.; Su, Y.J.; Carlson, C.W.; McFadden, J.P.; Mozer, F.S. Parallel electric fields in the upward current region of the aurora: Numerical solutions. Phys. Plasmas 2002, 9, 3685–3694. [Google Scholar] [CrossRef] [Green Version]
- Andersson, L.; Ergun, R.E.; Newman, D.L.; McFadden, J.P.; Carlson, C.W.; Su, Y.J. Characteristics of parallel electric fields in the downward current region of the aurora. Phys. Plasmas 2002, 9, 3600–3609. [Google Scholar] [CrossRef]
- Cattell, C.; Neiman, C.; Dombeck, J.; Crumley, J.; Wygant, J.; Kletzing, C.A.; Peterson, W.K.; Mozer, F.S.; André, M. Large amplitude solitary waves in and near the Earth’s magnetosphere, magnetopause and bow shock: Polar and cluster observations. Nonlinear Proc. Geophys. 2003, 10, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Schippers, P.; Blanc, M.; André, N.; Dandouras, I.; Lewis, G.R.; Gilbert, L.K.; Persoon, A.M.; Krupp, N.; Gurnett, D.A.; Coates, A.J.; et al. Multi-instrument analysis of electron populations in Saturn’s magnetosphere. J. Geophys. Res. 2008, 113, A07208. [Google Scholar] [CrossRef]
- Lynov, J.P.; Michelsen, P.; Pecseli, H.L.; Rasmussen, J.J.; Saeki, K.; Turikov, V.A. Observations of solitary structures in a magnetized, plasma loaded waveguide. Phys. Scr. 1979, 20, 328–335. [Google Scholar] [CrossRef]
- Goldman, M.V.; Newman, D.L.; Ergun, R.E. Phase-space holes due to electron and ion beams accelerated by a current-driven potential ramp. Nonlinear Proc. Geophys. 2003, 10, 37–44. [Google Scholar] [CrossRef]
- Jenab, S.M.H.; Brodin, G.; Juno, J.; Kourakis, I. Ultrafast electron holes in plasma phase space dynamics. Sci. Rep. 2021, 11, 16358. [Google Scholar] [CrossRef]
- Simpson, J.A.; Bastian, T.S.; Chenette, D.L.; Lentz, G.A.; McKibben, R.B.; Pyle, K.R.; Tuzzolino, A.J. Saturnian trapped radiation and its absorption by satellites and rings: The first results from Pioneer 11. Science 1980, 207, 411–415. [Google Scholar] [CrossRef]
- Verheest, F.; Hereman, W. Conservations laws and solitary wave solutions for gen-eralized Schamel equations. Phys. Scr. 1994, 50, 611–614. [Google Scholar] [CrossRef]
- Williams, G.; Verheest, F.; Hellberg, M.A.; Anowar, A.G.M.; Kourakis, I. A Schamel equation for ion acoustic waves in superthermal plasmas. Phys. Plasmas 2014, 21, 092103. [Google Scholar] [CrossRef] [Green Version]
- Sultana, S.; Islam, S.; Mamun, A.A.; Schlickeiser, R. Oblique propagation of ion-acoustic solitary waves in a magnetized plasma with electrons following a generalized distribution function. Phys. Plasmas 2019, 26, 012107. [Google Scholar] [CrossRef]
- Sultana, S.; Mannan, A.; Schlickeiser, R. Obliquely propagating electron-acoustic solitary waves in magnetized plasmas: The role of trapped superthermal electrons. Eur. Phys. J. D 2019, 73, 220. [Google Scholar] [CrossRef]
- Mamun, A.A.; Cairns, R.A.; Shukla, P.K. Effects of vortex-like and non-thermal ion distributions on non-linear dust-acoustic waves. Phys. Plasmas 1996, 3, 2610–2614. [Google Scholar] [CrossRef]
- Nejoh, Y.-N. The dust charging effect on electrostatic ion waves in a dusty plasma with trapped electrons. Phys. Plasmas 1997, 4, 2813–2819. [Google Scholar] [CrossRef]
- Mamun, A.A. Nonlinear propagation of ion-acoustic waves in a hot magnetized plasma with vortexlike electron distribution. Phys. Plasmas 1998, 5, 322–324. [Google Scholar] [CrossRef] [Green Version]
- Mamun, A.A.; Shukla, P.K. Electron-acoustic solitary waves via vortex electron distribution. J. Geophys. Res. Space Phys. 2002, 107, 1135. [Google Scholar] [CrossRef] [Green Version]
- Mamun, A.A.; Shukla, P.K.; Stenflo, L. Obliquely propagating electron-acoustic solitary waves. Phys. Plasmas 2002, 9, 1474–1477. [Google Scholar] [CrossRef]
- Tribeche, M.; Djebarni, L.; Schamel, H. Solitary ion-acoustic wave propagation in the presence of electron trapping and background nonextensivity. Phys. Lett. A 2012, 376, 3164–3174. [Google Scholar] [CrossRef]
- Hafez, M.G.; Roy, N.C.; Talukder, M.R.; Ali, M.H.; Hafez, M.G.; Roy, N.C.; Talukder, M.R.; Ali, M.H. Effects of trapped electrons on the oblique propagation of ion acoustic solitary waves in elec-tron-positron-ion plasmas. Phys. Plasmas 2016, 23, 082904. [Google Scholar] [CrossRef]
- Hassan, M.R.; Rajib, T.I.; Sultana, S. Electron-acoustic solitons in magnetized collisional nonthermal lasmas. arXiv 2019, arXiv:1912.04756. [Google Scholar]
- Sultana, S.; Kourakis, I. Electron-scale electrostatic solitary waves and shocks: The role of superthermal electrons. Eur. Phys. J. D 2012, 66, 100. [Google Scholar] [CrossRef]
- Ferdousi, M.; Sultana, S.; Mamun, A.A. Oblique propagation of ion-acoustic solitary waves in a magnetized electron-positron-ion plasma. Phys. Plasmas 2015, 22, 032117. [Google Scholar] [CrossRef]
- Sultana, S.; Kourakis, I. Electron-scale dissipative electrostatic solitons in mul-ti-species plasmas. Phys. Plasmas 2015, 22, 102302. [Google Scholar] [CrossRef]
- Sultana, S. Ion acoustic solitons in magnetized collisional non-thermal dusty plasmas. Phys. Lett. A 2018, 382, 1368–1373. [Google Scholar] [CrossRef]
- Sultana, S.; Schlickeiser, R.; Elkamash, I.S.; Kourakis, I. Dissipative high-frequency envelope soliton modes in nonthermal plasmas. Phys. Rev. E 2018, 98, 033207. [Google Scholar] [CrossRef]
- Jovanoviç, D.; Shukla, P.K.; Stenflo, L.; Pegoraro, F. Nonlinear model for electron phase-space holes in magnetized space plasmas. J. Geophys. Res. Space Phys. 2002, 107, 1110. [Google Scholar] [CrossRef]
- Eliasson, B.; Shukla, P.K. Formation and dynamics of coherent structures involving phase-space vortices in plasmas. Phys. Rep. 2006, 422, 225–290. [Google Scholar] [CrossRef]
- Schamel, H. Two-parametric, mathematically undisclosed solitary electron holes and their evolution equation. Plasma 2020, 3, 166–179. [Google Scholar] [CrossRef]
- Schamel, H. Pattern formation in Vlasov-Poisson plasmas beyond Landau, as caused by the continuous spectra of electron and ion hole equilibria. arXiv 2021, arXiv:2110.01433. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultana, S.; Kourakis, I. Dissipative Ion-Acoustic Solitary Waves in Magnetized κ-Distributed Non-Maxwellian Plasmas. Physics 2022, 4, 68-79. https://doi.org/10.3390/physics4010007
Sultana S, Kourakis I. Dissipative Ion-Acoustic Solitary Waves in Magnetized κ-Distributed Non-Maxwellian Plasmas. Physics. 2022; 4(1):68-79. https://doi.org/10.3390/physics4010007
Chicago/Turabian StyleSultana, Sharmin, and Ioannis Kourakis. 2022. "Dissipative Ion-Acoustic Solitary Waves in Magnetized κ-Distributed Non-Maxwellian Plasmas" Physics 4, no. 1: 68-79. https://doi.org/10.3390/physics4010007
APA StyleSultana, S., & Kourakis, I. (2022). Dissipative Ion-Acoustic Solitary Waves in Magnetized κ-Distributed Non-Maxwellian Plasmas. Physics, 4(1), 68-79. https://doi.org/10.3390/physics4010007



