Vector Potential, Magnetic Field, Mutual Inductance, Magnetic Force, Torque and Stiffness Calculation between Current-Carrying Arc Segments with Inclined Axes in Air
Abstract
:1. Introduction
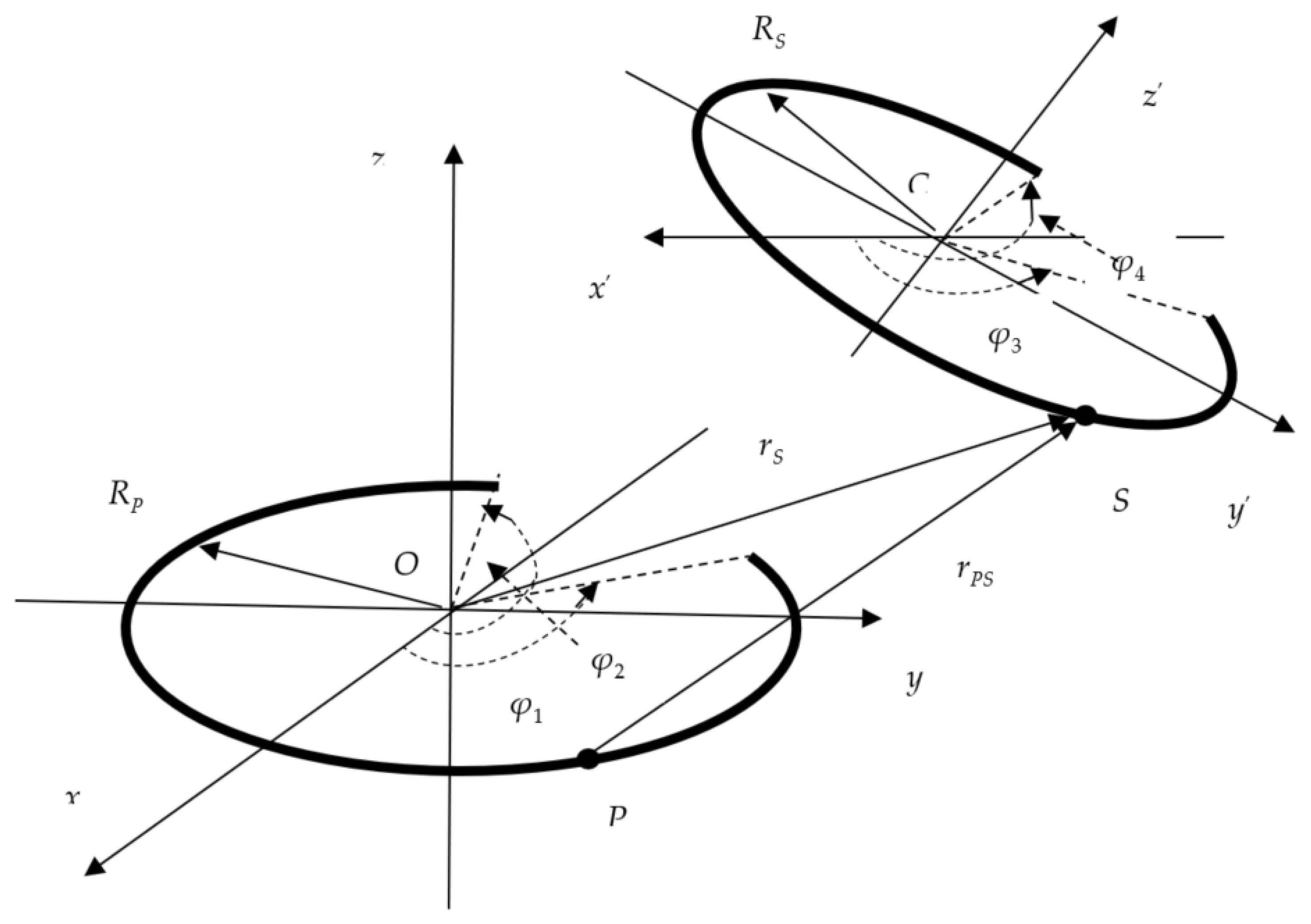
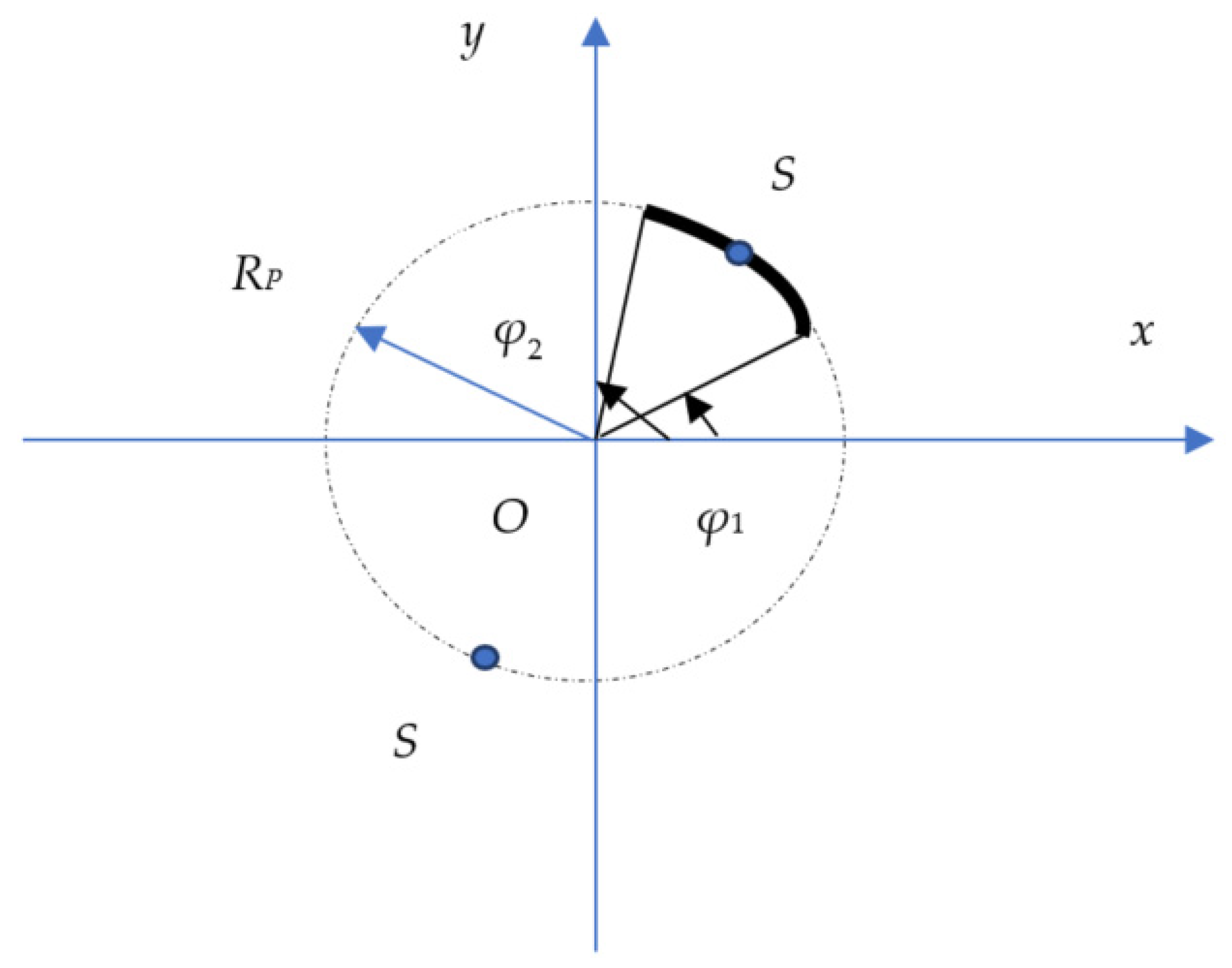
2. Basic Expressions
3. Magnetic Vector Potential Calculation at Point S (, , )
3.1. Special Cases
3.1.1.
3.1.2. Z-axis (
3.1.3.
3.1.4.
3.1.5. For , Plane x = 0. One Needs to Put and Use Equations (16)–(18)
4. Magnetic Field Calculation at the Point S (, , )
4.1. Special Cases
4.1.1.
4.1.2.
4.1.3.
4.1.4.
4.1.5.
4.1.6. For , Plane x = 0. One Needs to Put and Use Equations (35)–(37)
5. Magnetic Force Calculation between Two Inclined Current-Carrying Arc Segments
5.1. Special Cases
5.1.1.
5.1.2. ,
5.1.3. ,
6. Magnetic Torque Calculation between Two Inclined Current-Carrying Arc Segments
6.1. Special Cases
6.1.1.
6.1.2. ,
6.1.3. ,
7. Mutual Inductance Calculation between Two Current-Carrying Arc Segments with Inclined Axes
7.1. Special Cases
7.1.1.
7.1.2. ,
7.1.3. ,
8. Stiffness Calculation between Two Inclined Current-Carrying Arc Segments
8.1. Special Cases
8.1.1.
8.1.2. ,
8.1.3. ,
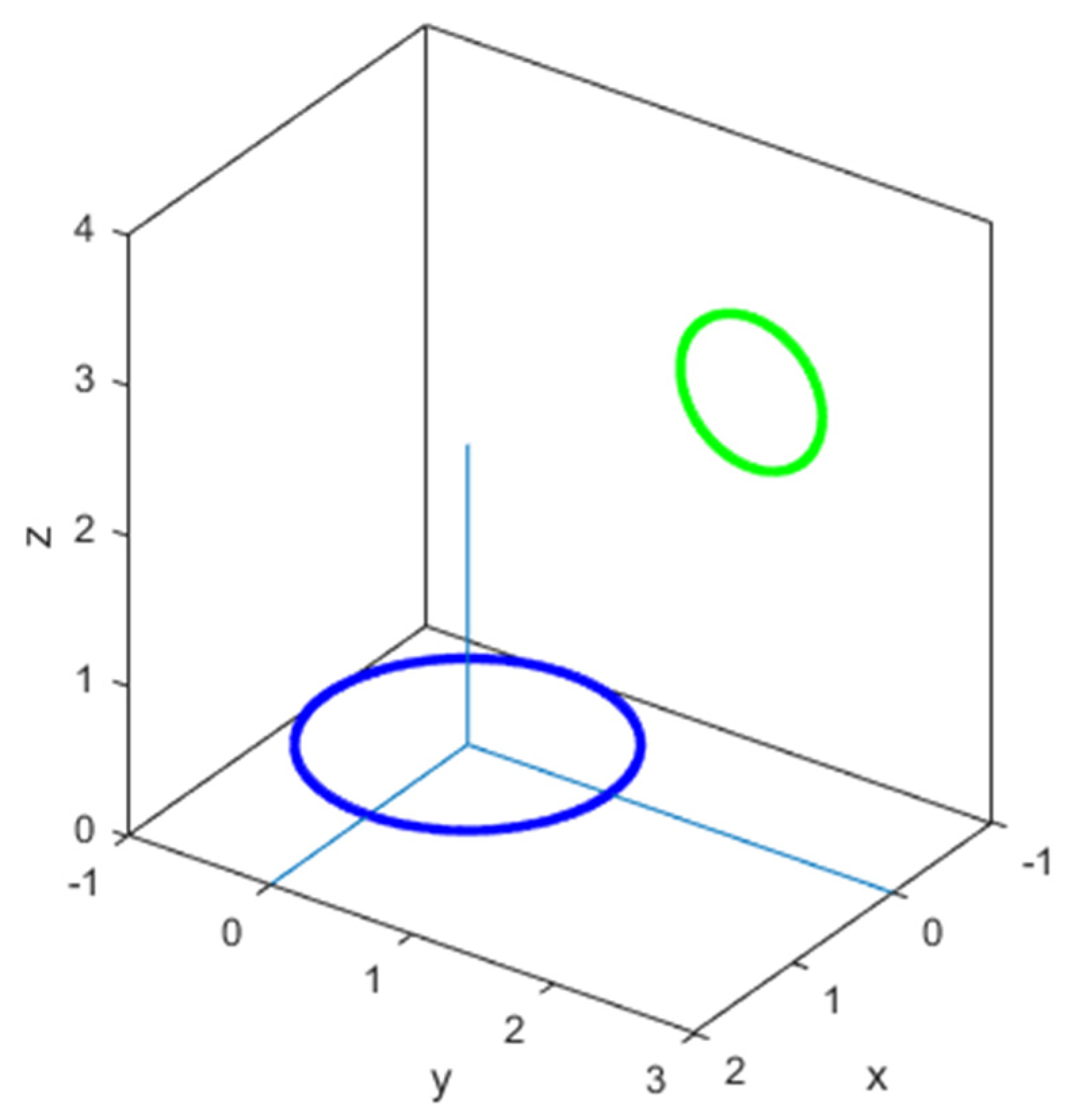
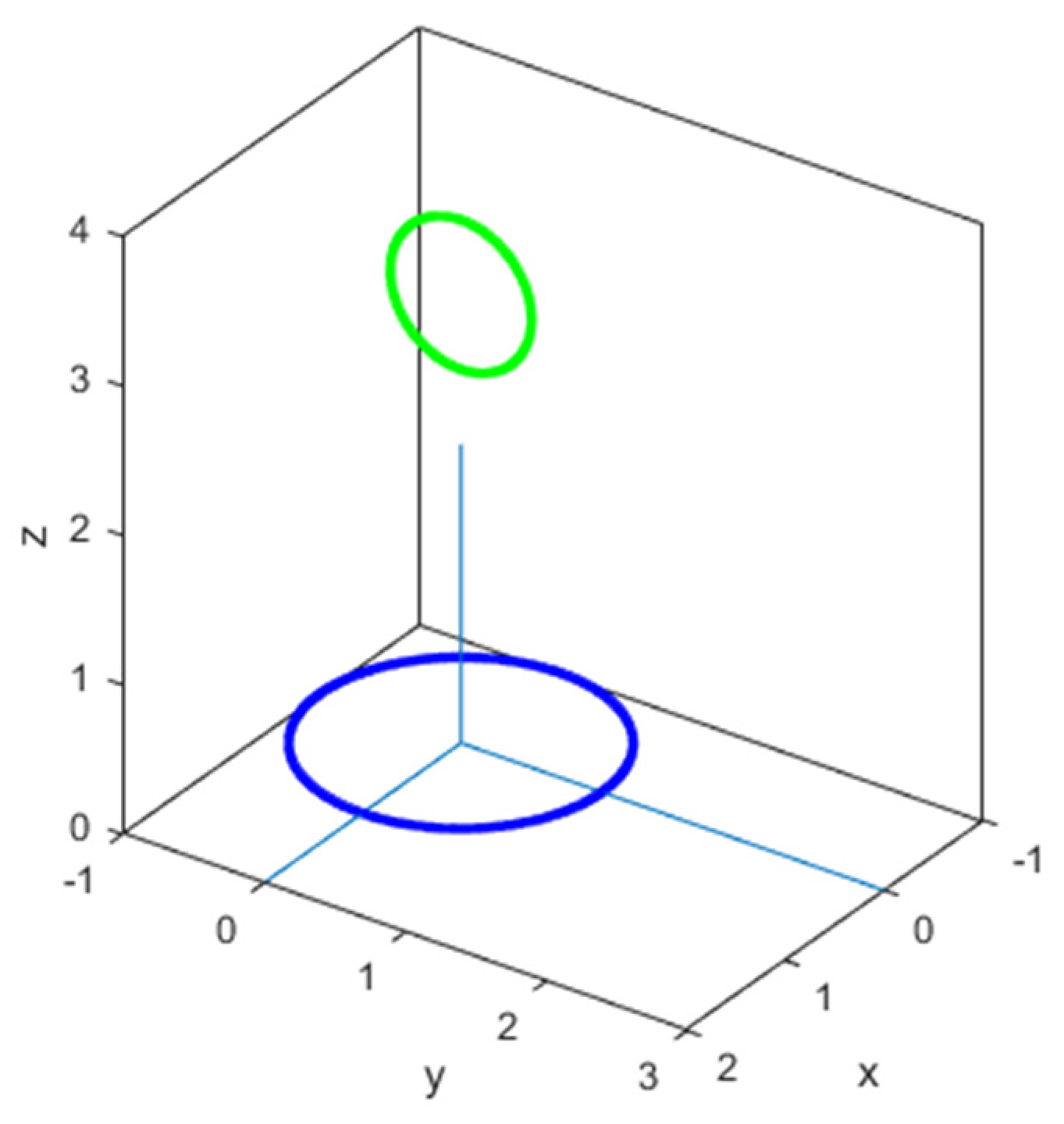
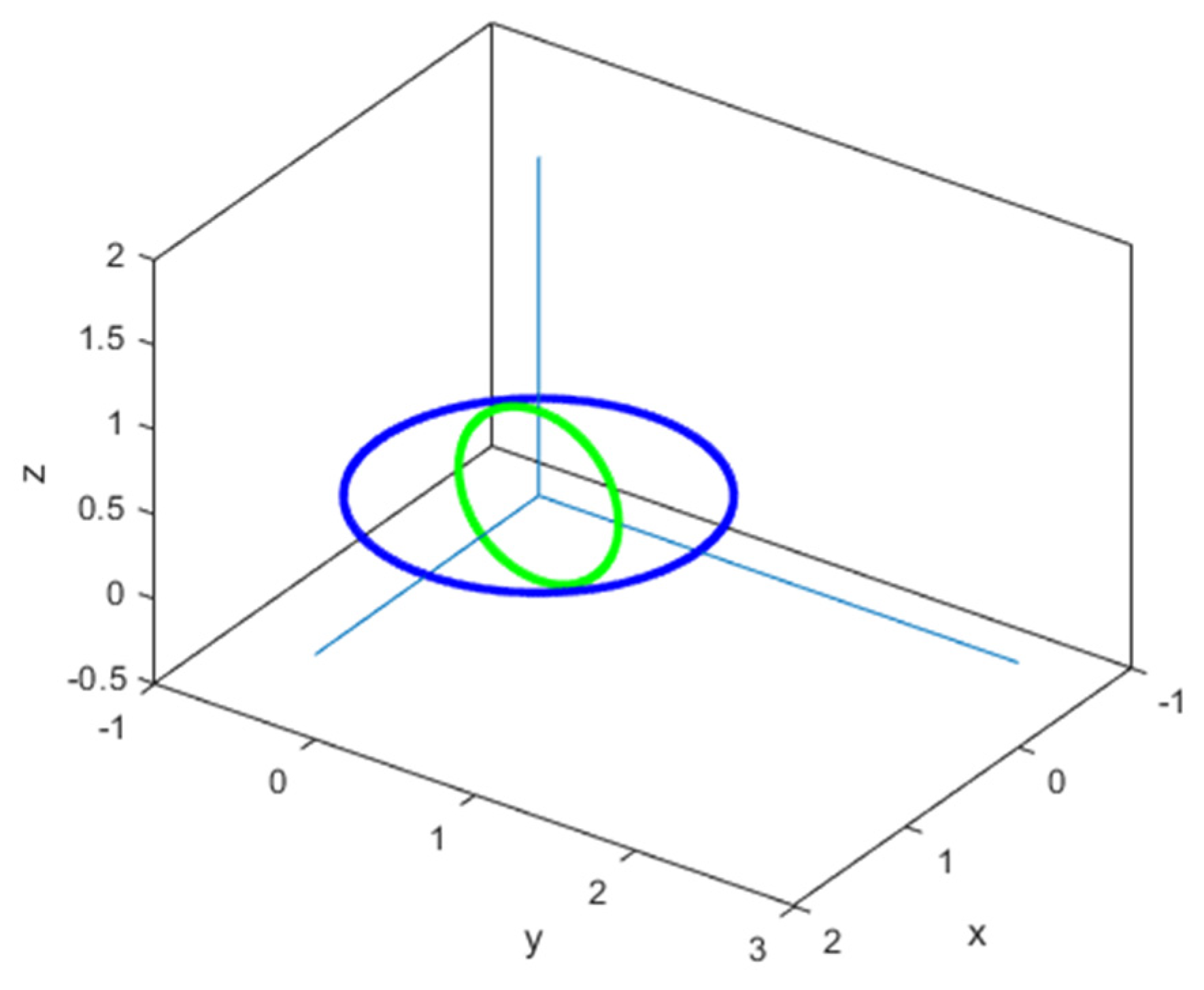
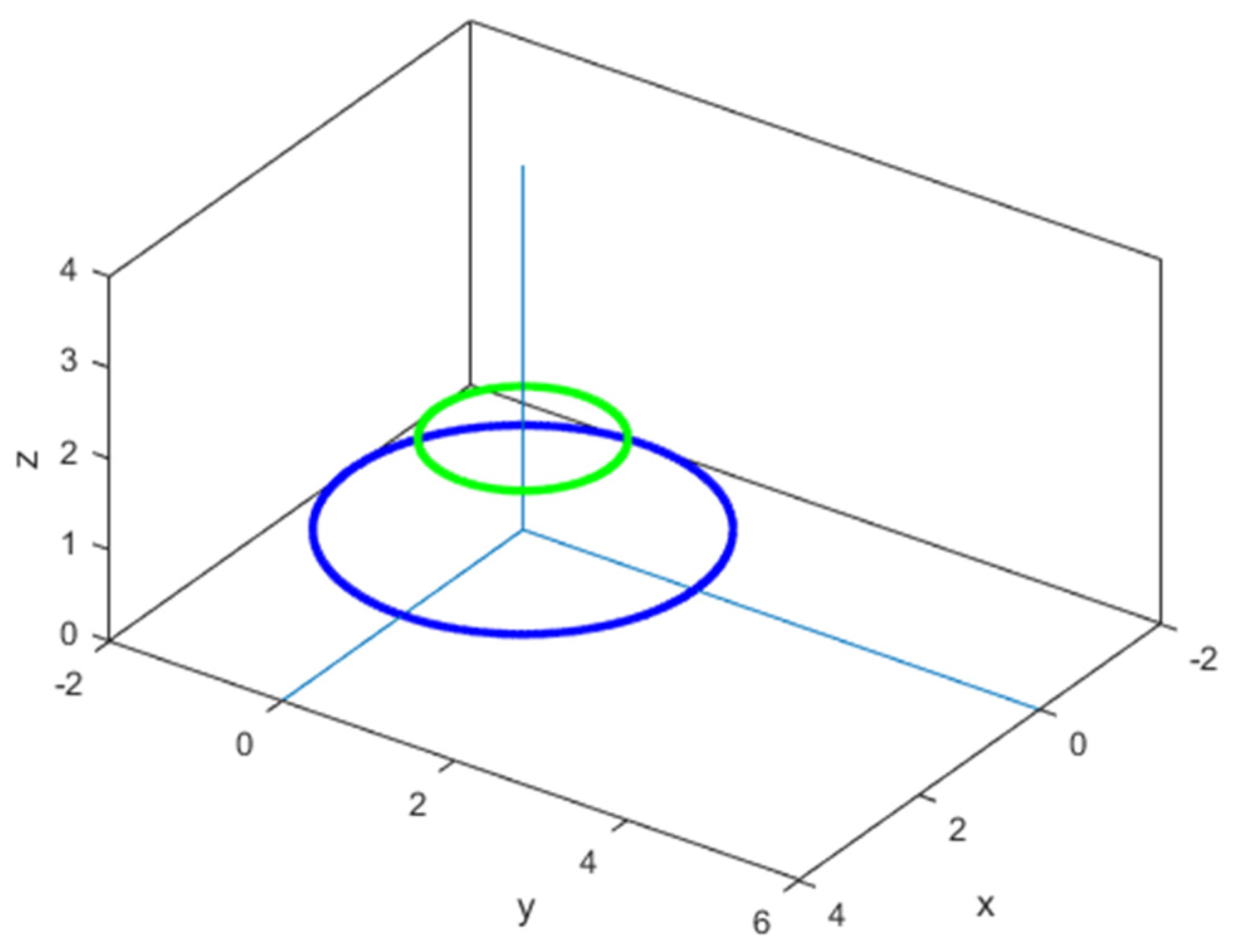
9. Numerical Validation
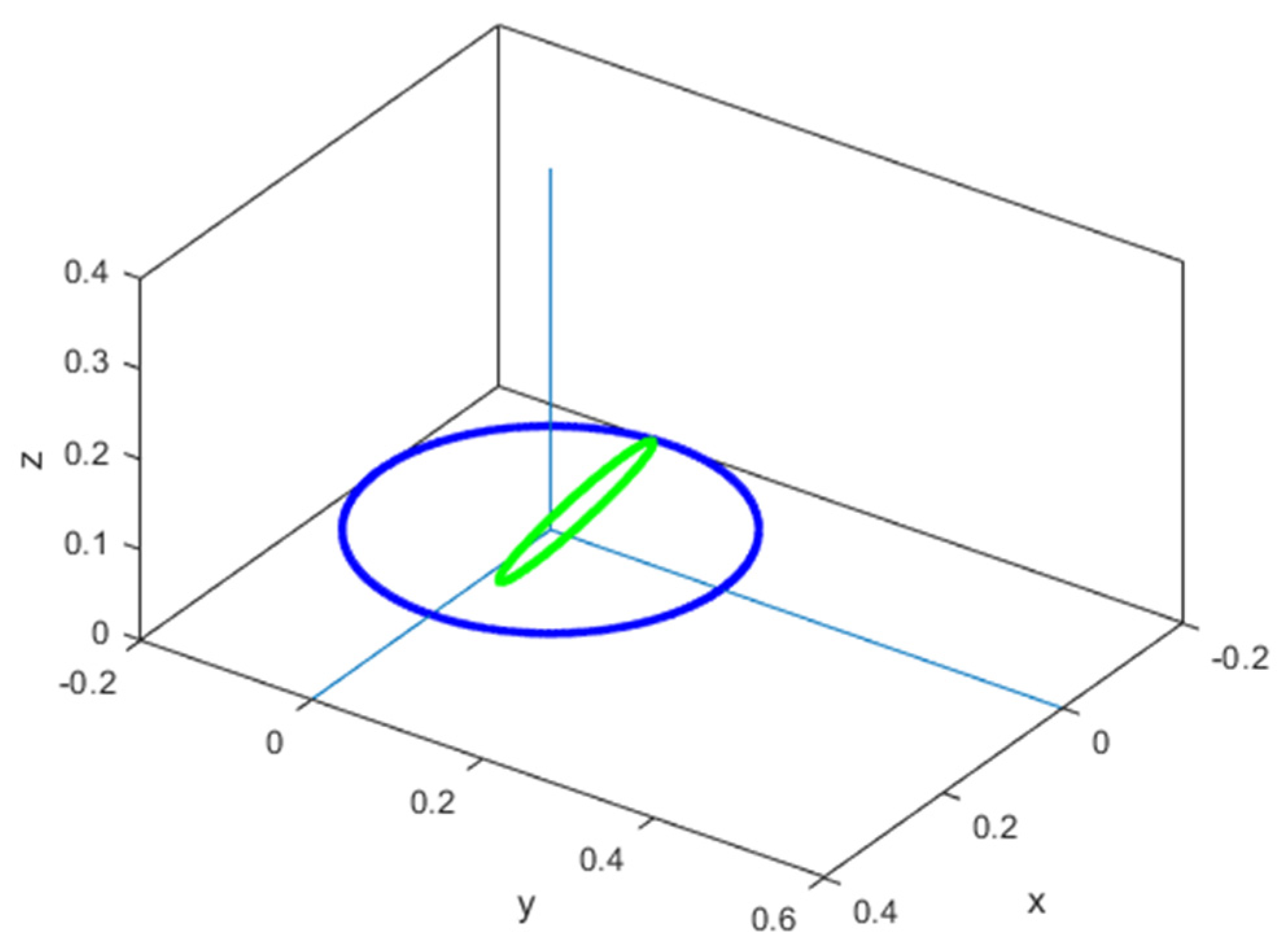


- (a)
- C (1 m; 2 m; 3 m)
- (b)
- C (1 m; 2 m; 0 m)
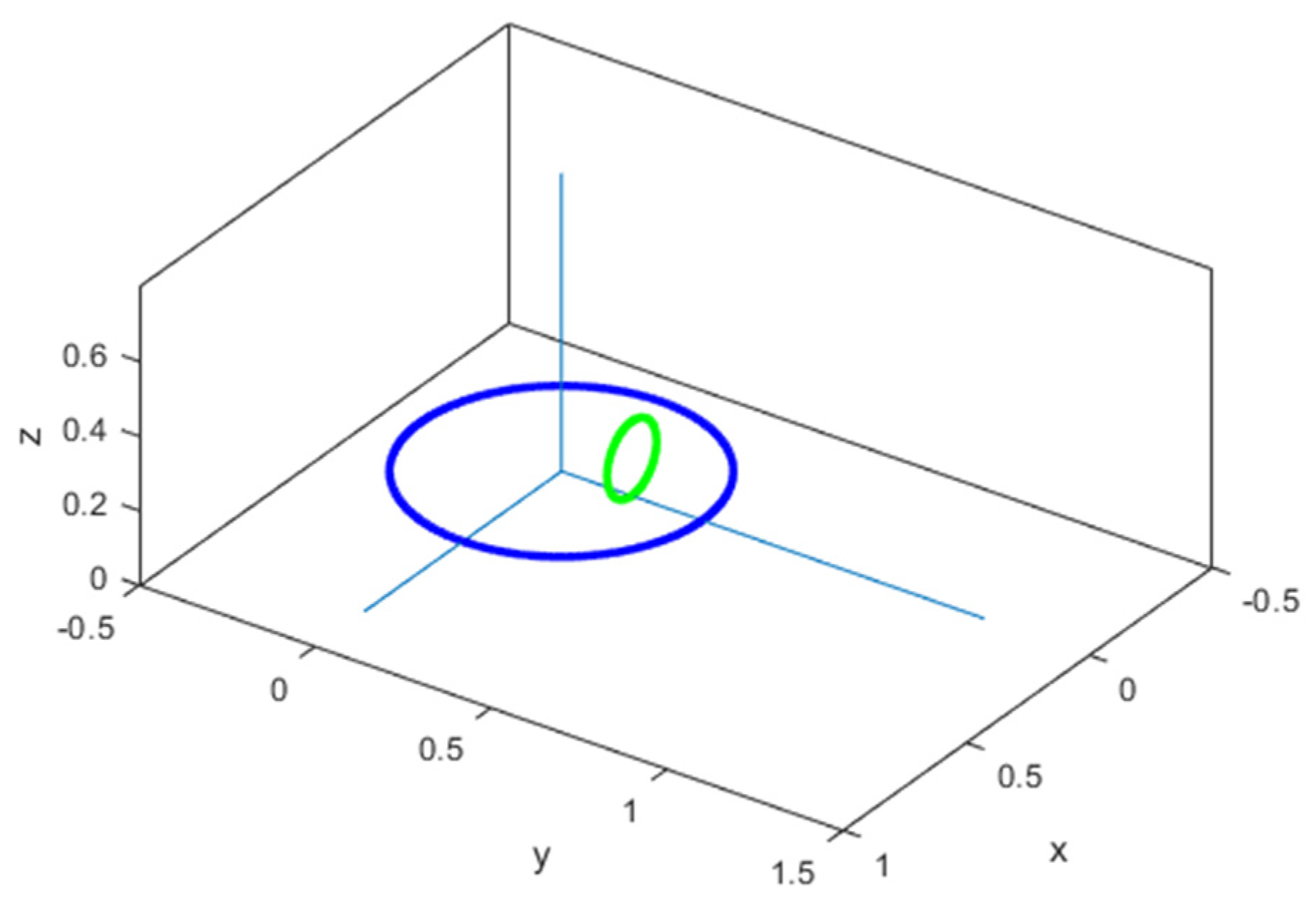
- (c)
- C (0 m; 0 m; 0 m)
- (d)
- C (1 m; 0 m; m)
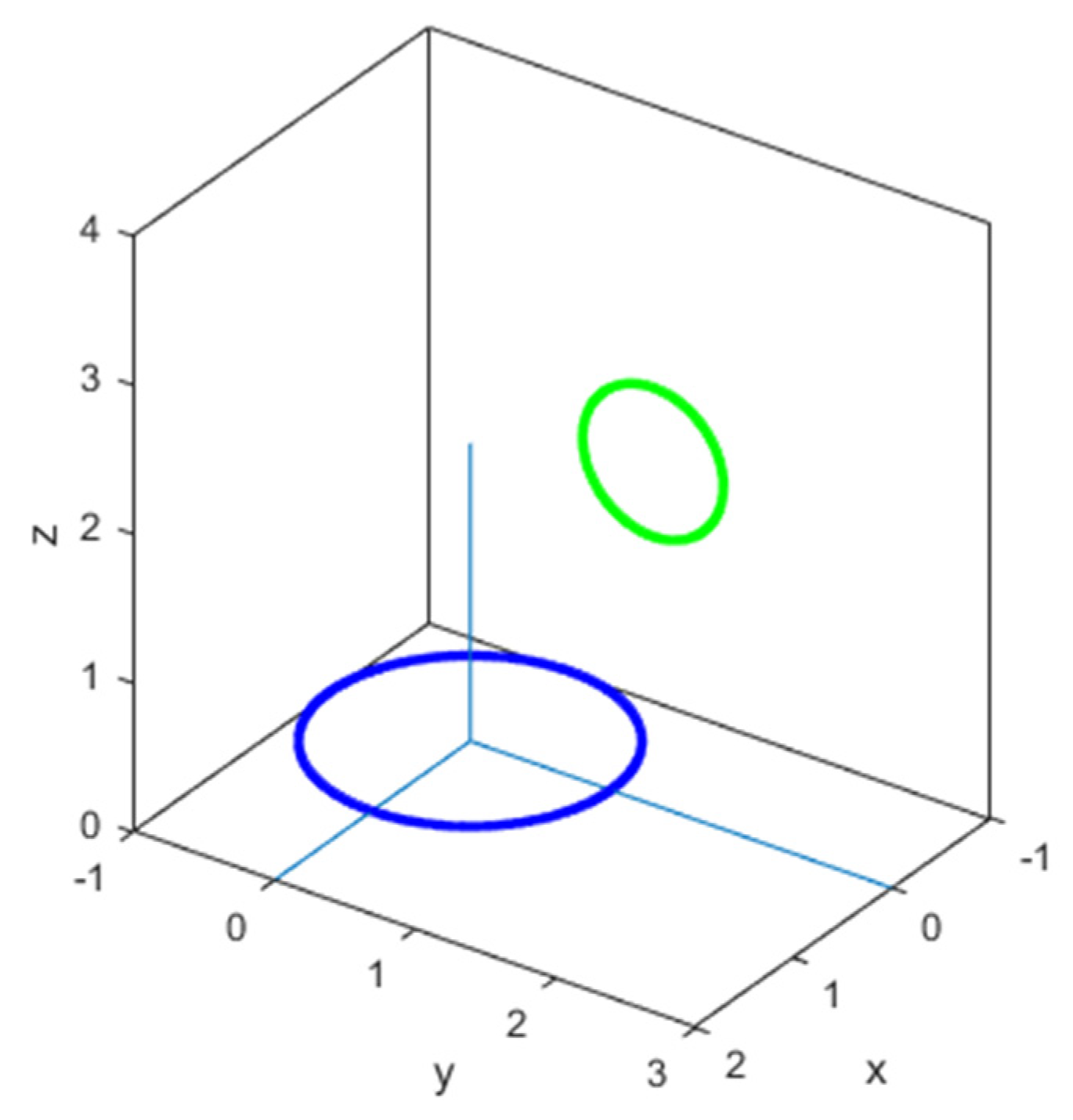
- (a)
- C (0 m; 2 m; 3 m)
- (b)
- C (0 m; 2 m; 0 m)
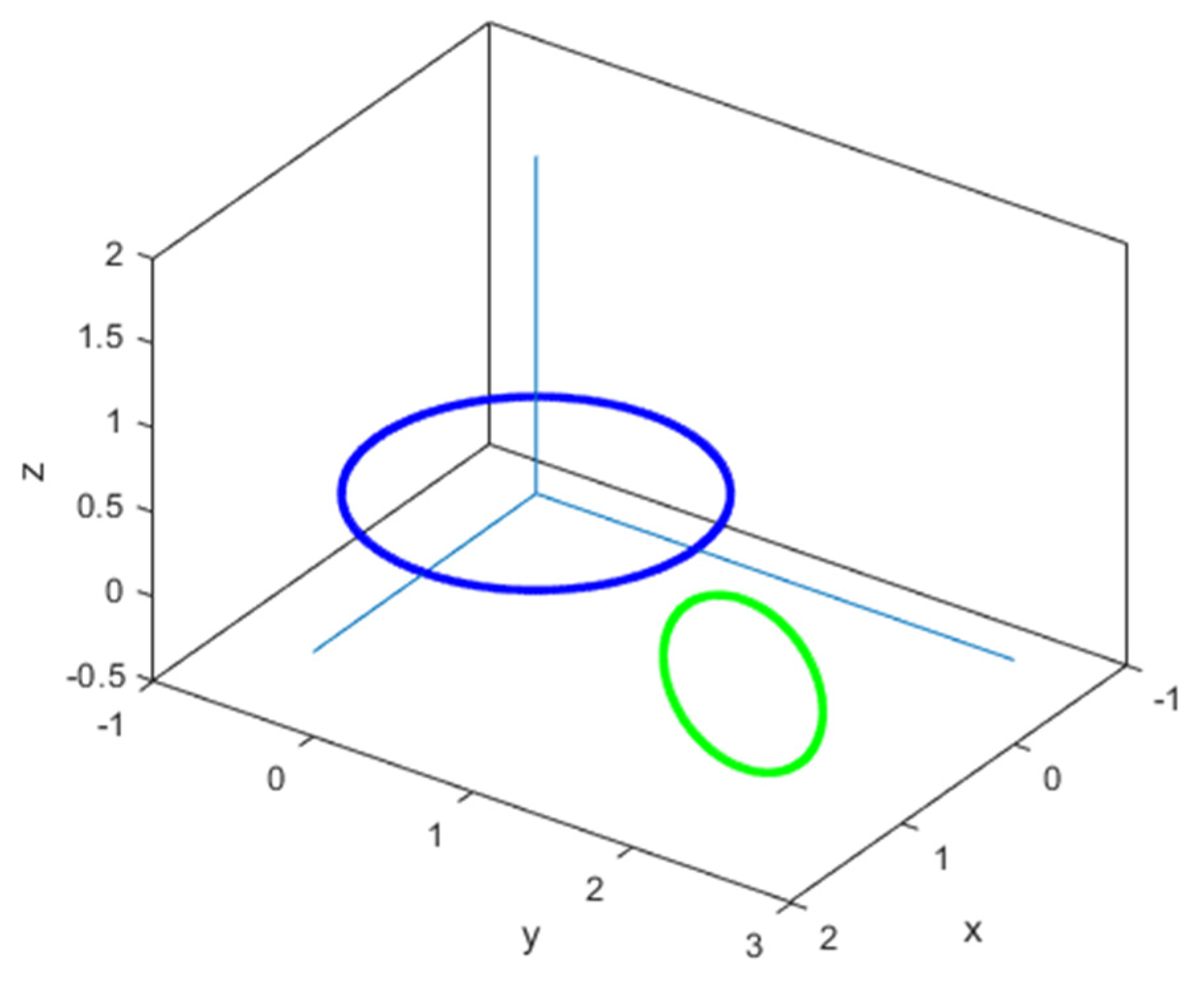
- (c)
- C (0 m; 0 m; 3 m)
- (d)
- C (0 m; 0 m; 0 m)
10. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Dover Publications Inc.: New York, NY, USA, 1954; Volume 2. [Google Scholar]
- Grover, F.W. Inductance Calculations; Dover: New York, NY, USA, 1964; Chapters 2 and 13. [Google Scholar]
- Snow, C. Formulas for Computing Capacitance, and Inductance; National Bureau of Standards Circular 544: Washington, DC, USA, 1954.
- Kalantarov, P.L. Inductance Calculations; National Power Press: Moscow, USSR, 1955. (In Russian) [Google Scholar]
- Kalantarov, P.L.; Zeitlin, L.A. Raschet Induktivnostey [Calculation of Inductances]; Energoatomizdat: Leningrad, USSR, 1986. (In Russian) [Google Scholar]
- Urankar, L. Vector potential and magnetic field of current-carrying finite arc segment in analytical form, part I: Filament approximation. IEEE Trans. Magn. 1980, 16, 1283–1288. [Google Scholar] [CrossRef]
- Urankar, L. Vector potential and magnetic field of current-carrying finite arc segment in analytical form, part II: Thin sheet approximation. IEEE Trans. Magn. 1982, 18, 911–917. [Google Scholar] [CrossRef]
- Urankar, L. Vector potential and magnetic field of current-carrying finite arc segment in analytical form, part III: Exact computation for rectangular cross section. IEEE Trans. Magn. 1982, 18, 1860–1867. [Google Scholar] [CrossRef]
- Urankar, L. Vector potential and magnetic field of current-carrying finite arc segment in analytical form, part IV: General three-dimensional current density. IEEE Trans. Magn. 1984, 20, 2145–2150. [Google Scholar] [CrossRef]
- Urankar, L. Vector potential and magnetic field of current-carrying circular finite arc segment in analytical form. V. Polygon cross section. IEEE Trans. Magn. 1990, 26, 1171–1180. [Google Scholar] [CrossRef]
- Walstrom, P.L. Algorithms for Computing the Magnetic Field, Vector Potential, and Field Derivatives for Circular Current Loops in Cylindrical Coordinates; National Laboratory: Los Alamos, NM, USA, 2017. [CrossRef]
- Christodoulides, C. Comparison of the Ampere and Biot-Savart magnetostatic force laws in their line-current-element forms. Am. J. Phys. 1988, 56, 357–362. [Google Scholar] [CrossRef]
- Babic, S.; Krstajic, B.; Milojkovic, S.; Andjelic, Z. Magnetostatic Field of Thin Current-Carrying Arc Filament. In Proceedings of the Fifth International Symposium on High Voltage Engineering, Braunshweige, Germany, 24–28 August 1987. [Google Scholar]
- Smith, M.; Fokas, N.; Hart, K.; Babic, S.I.; Selvaggi, J.P. The magnetic field produced from a conical current sheet and from a thin and tightly wound conical coil. Prog. Electromagn. Res. B 2021, 90, 1–20. [Google Scholar] [CrossRef]
- Conway, J. Exact solutions for the magnetic fields of axisymmetric solenoids and current distributions. IEEE Trans. Magn. 2001, 37, 2977–2988. [Google Scholar] [CrossRef]
- Conway, J.T. Trigonometric Integrals for the magnetic field of the coil of rectangular cross section. IEEE Trans. Magn. 2006, 42, 1538–1548. [Google Scholar] [CrossRef]
- Conway, J.T. Inductance calculations for circular coils of rectangular cross section and parallel axes using bessel and struve functions. IEEE Trans. Magn. 2009, 46, 75–81. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, F.; Kuang, G.; Chen, W.; Tan, Y.; Zhu, J.; He, P. Mutual inductance and force calculations between coaxial bitter coils and superconducting coils with rectangular cross section. J. Supercond. Nov. Magn. 2010, 24, 1687–1691. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, J.; Gao, X.; Shen, F.; Chen, S. Electromagnetic, mechanical, and thermal performance analysis of the CFETR magnet system. Nucl. Fusion 2015, 55, 093002. [Google Scholar] [CrossRef]
- Wang, Z.J.; Ren, Y. Magnetic force and torque calculation between circular coils with nonparallel axes. IEEE Trans. Appl. Supercond. 2014, 24, 4901505. [Google Scholar] [CrossRef]
- Babic, S.I.; Akyel, C. Torque calculation between circular coils with inclined axes in air. Int. J. Numer. Model. Electron. Netw. Devices Fields 2011, 24, 230–243. [Google Scholar] [CrossRef]
- Babic, S.; Akyel, C. New formulas for calculating torque between filamentary circular coil and thin wall solenoid with inclined axes whose axes are at the same plane. Prog. Electromagn. Res. M 2018, 73, 141–151. [Google Scholar] [CrossRef]
- Babic, S.; Akyel, C. Magnetic force between inclined circular filaments placed in any desired position. IEEE Trans. Magn. 2011, 48, 69–80. [Google Scholar] [CrossRef]
- Babic, S.; Sirois, F.; Akyel, C.; Girardi, C. Mutual inductance calculation between circular filaments arbitrarily positioned in space: alternative to Grover’s formula. IEEE Trans. Magn. 2010, 46, 3591–3600. [Google Scholar] [CrossRef]
- Babic, S.I.; Akyel, C. Magnetic force calculation between thin coaxial circular coils in air. IEEE Trans. Magn. 2008, 44, 445–452. [Google Scholar] [CrossRef]
- Babic, S.I.; Akyel, C. Magnetic force between inclined circular loops (Lorentz approach). Prog. Electromagn. Res. B 2012, 38, 333–349. [Google Scholar] [CrossRef] [Green Version]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V. Force and stiffness of passive magnetic bearings using permanent magnets. Part 1: Axial magnetization. IEEE Trans. Magn. 2009, 45, 2996–3302. [Google Scholar] [CrossRef] [Green Version]
- Ravaud, R.; Lemarquand, G. Force and stiffness of passive magnetic bearings using permanent magnets. Part 2: Radial magnetization. IEEE Trans. Magn. 2009, 45, 3334–3342. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.-B.; Levi, E.; Zabar, Z.; Birenbaum, L. Restoring force between two noncoaxial circular coils. IEEE Trans. Magn. 1996, 32, 478–484. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Korvink, J. Efficient calculation of the mutual inductance of arbitrarily oriented circular filaments via a generalisation of the Kalantarov-Zeitlin method. J. Magn. Magn. Mater. 2019, 483, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Poletkin, K.V. Calculation of force and torque between two arbitrarily oriented circular filaments using Kalantarov-Zeitlin’s method. arXiv 2021, arXiv:2106.09496. [Google Scholar]
- Poletkin, K.V.; Chernomorsky, A.I.; Shearwood, C.; Wallrabe, U. An Analytical Model of Micromachined Electromagnetic Inductive Contactless Suspension. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Poletkin, K.; Chernomorsky, A.I.; Shearwood, C.; Wallrabe, U. A qualitative analysis of designs of micromachined electromagnetic inductive contactless suspension. Int. J. Mech. Sci. 2014, 82, 110–121. [Google Scholar] [CrossRef]
- Lu, Z.; Poletkin, K.; Hartogh, B.D.; Wallrabe, U.; Badilita, V. 3D micro-machined inductive contactless suspension: Testing and modeling. Sens. Actuators A Phys. 2014, 220, 134–143. [Google Scholar] [CrossRef]
- Ferreira da Rocha Gama, M.B. Modelling and Simulation of Inductive Levitation Micro-Actuators. Mestrado Integrado em Engenharia Mecânica (Faculdade De Engenharia, Universidade Do Porto, Porto, Portugal, 2021). Available online: https://repositorio-aberto.up.pt/bitstream/10216/133306/2/453360.pdf (accessed on 20 September 2021).
- Poletkin, K.; Chernomorsky, A.; Shearwood, C. Proposal for Micromachined Accelerometer, Based on a Contactless Suspension with Zero Spring Constant. IEEE Sens. J. 2012, 12, 2407–2413. [Google Scholar] [CrossRef]
- Lubin, T.; Berger, K.; Rezzoug, A. Inductance and force calculation for axisymmetric coil systems including an iron core of finite length. Prog. Electromagn. Res. B 2012, 41, 377–396. [Google Scholar] [CrossRef] [Green Version]
- Theodoulidis, T.; Ditchburn, R.J. Mutual Impedance of Cylindrical Coils at an Arbitrary Position and Orientation above a Planar Conductor. IEEE Trans. Magn. 2007, 43, 3368–3370. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A.; Miller, D.A.B. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; (National Bureau of Standards Applied Mathematics Series No. 55). J. Appl. Mech. 1965, 32, 239. [Google Scholar] [CrossRef] [Green Version]
- Gradshteyn, I.S.; Rhyzik, I.M. Tables of Integrals, Series and Products; Dover: New York, NY, USA, 1972. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babic, S. Vector Potential, Magnetic Field, Mutual Inductance, Magnetic Force, Torque and Stiffness Calculation between Current-Carrying Arc Segments with Inclined Axes in Air. Physics 2021, 3, 1054-1087. https://doi.org/10.3390/physics3040067
Babic S. Vector Potential, Magnetic Field, Mutual Inductance, Magnetic Force, Torque and Stiffness Calculation between Current-Carrying Arc Segments with Inclined Axes in Air. Physics. 2021; 3(4):1054-1087. https://doi.org/10.3390/physics3040067
Chicago/Turabian StyleBabic, Slobodan. 2021. "Vector Potential, Magnetic Field, Mutual Inductance, Magnetic Force, Torque and Stiffness Calculation between Current-Carrying Arc Segments with Inclined Axes in Air" Physics 3, no. 4: 1054-1087. https://doi.org/10.3390/physics3040067
APA StyleBabic, S. (2021). Vector Potential, Magnetic Field, Mutual Inductance, Magnetic Force, Torque and Stiffness Calculation between Current-Carrying Arc Segments with Inclined Axes in Air. Physics, 3(4), 1054-1087. https://doi.org/10.3390/physics3040067




