Cylindrical and Spherical Nucleus-Acoustic Solitary and Shock Waves in Degenerate Electron-Nucleus Plasmas
Abstract
:1. Introduction
- The IAWs are driven by the electron thermal pressure depending on the electron temperature and number density, whereas the NAWs are driven by the electron degenerate pressure depending only on the electron number density.
- The non-degenerate plasmas at finite temperature allow the IAWs to exist, but do not allow the NAWs to exist.
- The degenerate plasmas at absolute zero temperature do not allow the IAWs to exist, but do allow the NAWs to exist.
- The NAWs and IAWs are completely different from the view of their length scale and phase speed.
2. Basic Equations
3. MK-dV Equation
4. MBurgers Equation
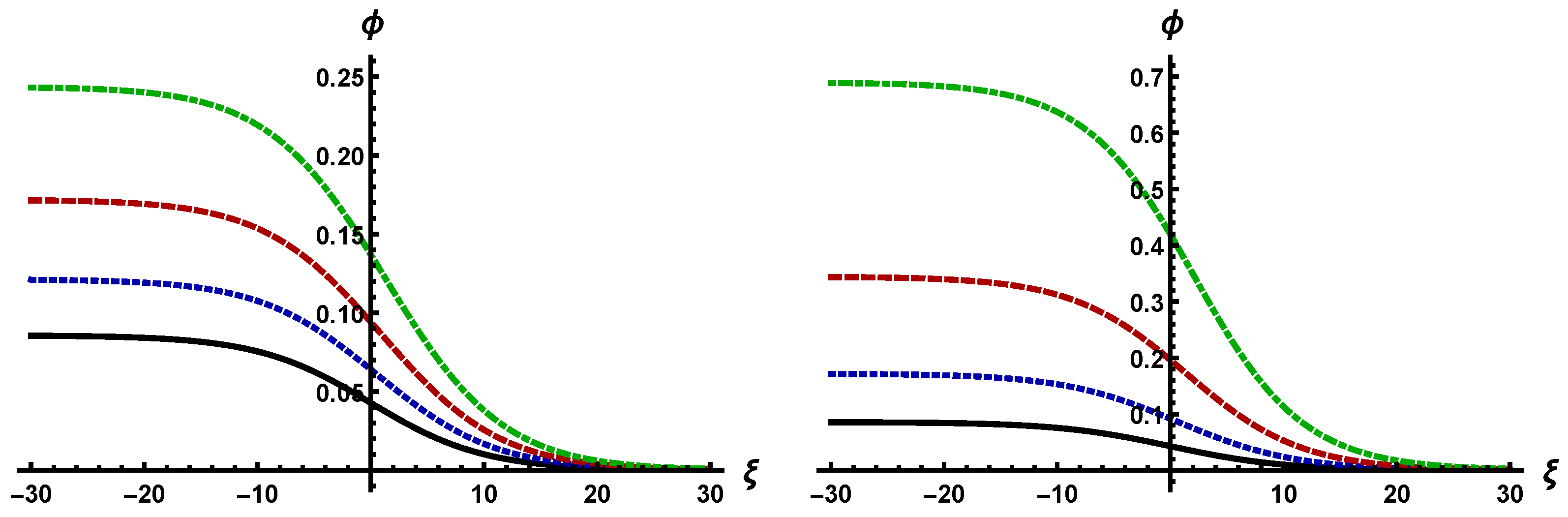
5. Discussion
- The phase speed of the NAWs is given bywhere Equation (3) is used, and is the inter-electron distance. This expression indicates that is inversely proportional to and the mass, m, of a nucleus species, but is directly proportional to the number of protons, , in the nucleus species. The phase speed does not depend on the temperature of the electron or nucleus species. This is an unique feature of the NAWs by which the NAWs appeared as new waves, and are completely different from the IAWs [23,24] which do not exist at absolute zero-temperature.
- The dimensional amplitudes of both types of nonlinear waves are determined by using Equations (3) and (38), and are expressed as:where is the dimensional speed of the frame of reference. These expressions imply that the amplitudes of the both types of nonlinear waves are directly proportional to , and to the square root of the mass of the nucleus species, , but inversely proportional to the square root of the inter-electron distance, , and the number of the proton, , in a nucleus species.
- The dimensional widths of both types of nonlinear waves are given byThese expressions imply that the width of the solitary waves is the order of a fraction of the length scale, , of the waves, since is a fraction of for the formation of the NA solitary waves. The width of the NA shock waves increases with the dynamical viscosity coefficient, , of the nucleus fluid, but decreases with the speed, .
- The amplitude (width) of the cylindrical NA solitary and shock waves is smaller (larger) than that of the spherical NA solitary and shock waves. The time evolution of the spherical solitary and shock waves is faster than that of the NA cylindrical solitary and shock waves.
- The amplitude (width) of the NA solitary waves is minimum (maximum) for a very large value of , which causes to neglect the effect of cylindrical and spherical geometries, and gives rise to one dimensional (1D) planar NA solitary and shock waves. Thus, for a large value of , 1D planar, cylindrical and spherical solitary and shock waves are found to be identical.
- The length scale as well as the phase speed, height, and thickness of the NA solitary and shock waves are completely independent of temperature. These are completely new linear and nonlinear features of the NAWs under consideration.
Funding
Acknowledgments
Conflicts of Interest
References
- Mamun, A.A.; Amina, M.; Schlickeiser, R. Nucleus-acoustic shock (waves in a strongly coupled self-gravitating degenerate quantum plasma. Phys. Plasmas 2016, 23, 094503. [Google Scholar] [CrossRef]
- Mamun, A.A.; Amina, M.; Schlickeiser, R. Heavy NA spherical solitons in self-gravitating super-dense plasmas. Phys. Plasmas 2017, 24, 042307. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The highly collapsed configurations of a stellar mass. Mon. Not. R. Astron. Soc. 1931, 91, 456–4566. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The pressure in the interior of a star. Mon. Not. R. Astron. Soc. 1936, 96, 644–646. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects, 1st ed.; Wiley-VCH Verlag: Weinheim, Germany, 1983; pp. 15–375. [Google Scholar]
- Potekhin, A.Y.; Chabrier, G. Thermodynamic functions of dense plasmas: Analytic approximations for astrophysical applications. Contrib. Plasma Phys. 2010, 50, 82–87. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, R.S.; Zhang, X.L.; Rolston, S.L. Observation of collective modes of ultracold plasmas. Phys. Rev. Lett. 2006, 96, 105003. [Google Scholar] [CrossRef] [Green Version]
- Glenzer, S.H.; Redmer, R. X-ray Thomson scattering in high energy density plasmas. Rev. Mod. Phys. 2009, 81, 1625. [Google Scholar] [CrossRef]
- Drake, R.P. Perspectives on high-energy-density physics. Phys. Plasmas 2009, 16, 055501. [Google Scholar] [CrossRef]
- Drake, R.P. High-energy-density physics. Phys. Today 2010, 63, 18. [Google Scholar] [CrossRef]
- Hu, S.X.; Collins, L.A.; Boehly, T.R.; Kress, J.D.; Goncharov, V.N.; Skupsky, S. First-principles thermal conductivity of warm-dense deuterium plasmas for inertial confinement fusion applications. Phys. Rev. E 2014, 89, 04105. [Google Scholar] [CrossRef]
- Shukla, P.K.; Mamun, A.A.; Mendis, D.A. Nonlinear ion modes in a dense plasma with strongly coupled ions and degenerate electron fluids. Phys. Rev. E 2011, 84, 026405. [Google Scholar] [CrossRef] [Green Version]
- Sultana, S.; Schlickeiser, R. Fully nonlinear heavy ion-acoustic solitary waves in astrophysical degenerate relativistic quantum plasmas. Astrophys. Space Sci. 2018, 363, 1–9. [Google Scholar] [CrossRef]
- Sultana, S.; Schlickeiser, R. Arbitrary amplitude nucleus-acoustic solitons in multi-ion quantum plasmas with relativistically degenerate electrons. Phys. Plasmas 2018, 25, 022110. [Google Scholar] [CrossRef]
- Sultana, S.; Islam, S.; Mamun, A.A.; Schlickeiser, R. Modulated heavy nucleus-acoustic waves and associated rogue waves in a degenerate relativistic quantum plasma system. Phys. Plasmas 2018, 25, 012113. [Google Scholar] [CrossRef]
- Chowdhury, N.A.; Hasan, M.M.; Mannan, A.; Mamun, A.A. Nucleus-acoustic envelope solitons and their modulational instability in a degenerate quantum plasma system. Vacuum 2018, 147, 31–37. [Google Scholar] [CrossRef] [Green Version]
- Karmakar, P.K.; Das, P. Nucleus-acoustic waves: Excitation, propagation, and stability. Phys. Plasmas 2018, 25, 082902. [Google Scholar] [CrossRef]
- Das, P.; Karmakar, P.K. Nonlinear nucleus-acoustic waves in strongly coupled degenerate quantum plasmas. Europhys. Lett. 2019, 126, 10001. [Google Scholar] [CrossRef]
- Mannan, A.; Sultana, S.; Mamun, A.A. Arbitrary amplitude heavy nucleus-acoustic solitary waves in thermally degenerate plasmas. IEEE Trans. Plasma Sci. 2020, 48, 4093–4102. [Google Scholar] [CrossRef]
- Kaur, R.; Singh, K.; Saini, N.S. Heavy-and light-nuclei acoustic dressed shock waves in white dwarfs. Chin. J. Phys. 2021, 72, 286–298. [Google Scholar] [CrossRef]
- Saini, N.S.; Kaur, R. Ion-acoustic solitary, breathers, and freak waves in a degenerate quantum plasma. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Tonks, L.; Langmuir, I. Oscillations in ionized gases. Phys. Rev. 1929, 33, 95–210. [Google Scholar] [CrossRef]
- Revans, R.W. The transmission of waves through an ionized gas. Phys. Rev. 1933, 44, 798–902. [Google Scholar] [CrossRef]
- Mamun, A.A. Degenerate pressure driven modified nucleus-acoustic waves in degenerate plasmas. Phys. Plasmas 2018, 25, 024502. [Google Scholar] [CrossRef]
- Koester, D.; Chanmugam, G. Physics of white dwarf stars. Rep. Prog. Phys. 1990, 53, 837–915. [Google Scholar] [CrossRef]
- Koester, D. White dwarfs: Recent developments. Astron. Astrophys. Rev. 2002, 11, 33–66. [Google Scholar] [CrossRef]
- Washimi, H.; Taniuti, T. Propagation of ion-acoustic solitary waves of small amplitude. Phys. Rev. Lett. 1966, 17, 996–997. [Google Scholar] [CrossRef]
- Mamun, A.A.; Shukla, P.K. Effects of nonthermal distribution of electrons and polarity of net dust-charge number density on nonplanar dust-ion-acoustic solitary waves. Phys. Rev. E 2009, 80, 037401. [Google Scholar] [CrossRef] [PubMed]
- Maxon, S.; Viecelli, J. Spherical solitons. Phys. Rev. Lett. 1974, 32, 4–6. [Google Scholar] [CrossRef]
- Mamun, A.A.; Cairns, R.A. Dust-acoustic shock waves due to strong correlation among arbitrarily charged dust. Phys. Rev. E 2009, 79, 055401. [Google Scholar] [CrossRef]
- Mamun, A.A. On stretching of plasma parameters and related open issues for the study of dust-ion-acoustic and dust-acoustic shock waves in dusty plasmas. Phys. Plasmas 2019, 26, 084501. [Google Scholar] [CrossRef]
- Hirota, R. Exact solutions to the equation describing “cylindrical solitons”. Phys. Lett. A 1979, 71, 393–394. [Google Scholar] [CrossRef]
- Mannan, A.; Fedele, R.; Onorato, M.; De Nicola, S.; Jovanović, D. Ring-type multi-soliton dynamics in shallow water. Phys. Rev. E 2015, 91, 012921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yokus, A.; Kaya, D. Comparison exact and numerical simulation of the traveling wave solution in nonlinear dynamics. Int. J. Modern Phys. B 2020, 34, 2050282. [Google Scholar] [CrossRef]
- Witze, A. Space-station science ramps up. Nature 2014, 510, 196–197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanderburg, A.; Johnson, J.A.; Rappaport, S.; Bieryla, A.; Irwin, J.; Lewis, J.A.; Kipping, D.; Brown, W.R.; Dufour, P.; Ciardi, D.R.; et al. A disintegrating minor planet transiting a white dwarf. Nature 2015, 526, 546–549. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamun, A.A. Cylindrical and Spherical Nucleus-Acoustic Solitary and Shock Waves in Degenerate Electron-Nucleus Plasmas. Physics 2021, 3, 1088-1097. https://doi.org/10.3390/physics3040068
Mamun AA. Cylindrical and Spherical Nucleus-Acoustic Solitary and Shock Waves in Degenerate Electron-Nucleus Plasmas. Physics. 2021; 3(4):1088-1097. https://doi.org/10.3390/physics3040068
Chicago/Turabian StyleMamun, A A. 2021. "Cylindrical and Spherical Nucleus-Acoustic Solitary and Shock Waves in Degenerate Electron-Nucleus Plasmas" Physics 3, no. 4: 1088-1097. https://doi.org/10.3390/physics3040068
APA StyleMamun, A. A. (2021). Cylindrical and Spherical Nucleus-Acoustic Solitary and Shock Waves in Degenerate Electron-Nucleus Plasmas. Physics, 3(4), 1088-1097. https://doi.org/10.3390/physics3040068




