Gain-Assisted Optical Pulling Force on Plasmonic Graded Nano-Shell with Equivalent Medium Theory

Abstract

The tunable optical pulling force on a graded plasmonic core-shell nanoparticle consisting of a gain dielectric core and graded plasmonic shell is investigated in the illumination of a plane wave. In this paper, the electrostatic polarizability and the equivalent permittivity of the core-shell sphere are derived and the plasmonic enhanced optical pulling force in the antibonding and bonding dipole modes of the graded nanoparticle are demonstrated. Additionally, the resonant pulling force occurring on the dipole mode is shown to be dependent on the aspect ratio of the core-shell particle, which is illustrated by the obtained equivalent permittivity. This shows that the gradation of the graded shell will influence the plasmonic feature of the particle, thus further shifting the resonant optical force peaks and strengthening the pulling force. The obtained results provide an additional degree of freedom to manipulate nanoparticles and give a deep insight into light–matter interaction.

1. Introduction

The change of the field gradients or linear momentum carried by photons will give rise to the optical force [1]. Radiation pressure induced by photon momentum exchange always pushes objects in the light flow direction, which is known as “optical pushing”. In contrast, if the light–matter momentum transfer leads to the backward motion of the objects, this phenomenon is named “optical pulling”. The optical pulling force is a more novel phenomenon than the pushing one because it requires many more critical conditions to realize it and has many more potential applications in nano-manipulation [2,3,4,5,6,7,8]. One possible way to obtain the optical pulling force to pull the object towards the light is by increasing the forward scattering via Gaussian beam [9,10], Bessel Beam [11], and other tractor beams. Recently, the optical pulling forces acting on a nano-object consisting of chiral [12,13,14], hyperbolic [15], and gain [16,17,18] materials have been widely investigated. The introduction of a gain material could provide additional forward scattering strength with the appropriate gain threshold to achieve the optical pulling force [17]; therefore, investigating the threshold gain for the pulling force in different gain-assist nanostructures constitutes another task for researchers. Actually, the threshold gain for the pulling force was analytically studied for nano-spheres, thin cylinders and thin slabs [18]. Moreover, the continuous modulation from the pushing to the pulling force was exhibited by controlling the incident angle of the interfering plane waves near the Fano resonance of the plasmonic nanoparticle [19]. The plasmonic enhanced optical force has been applied to quantum measurement, signal detection, and other fields [20,21,22,23,24]. Furthermore, tunable optical pulling forces originating from plasmon singularity and Fano resonance on plasmonic nanoparticles have been investigated in detail [25,26,27].

The approaches to realize and maximize the optical fulling force rely on designing a specific tractor beam [2,3,5,27,28,29,30], modifying the surroundings of the manipulated objects [31,32,33], or utilizing a gain-assist structure [15,18,25,34]. The resonant interplay between plasmonic structures and gain media and the coupling with a gain medium located in the core of a metallic nanoshell, when excited by means of an external pump, produces intense changes of the electromagnetic fields around the structure, thus producing novel features which can be useful for a variety of applications, such as photothermal therapy, enhanced spectroscopy, and spaser [35,36,37,38]. Graded materials are the materials whose material properties can vary continuously in space with a gradient coefficient, and graded core-shell spheres show a widely tunable plasmonic response band [39,40,41,42]. The near field distribution [43], far field scattering as well as nonlinear response [44] enhanced by plasmon resonances could be adjustable by changing the gradient coefficient and aspect ratio of the inner and outer radii of the sphere. More recently, the nonlinear optical properties of graded magnetite nanoparticles in a colloid were investigated experimentally as a sample of the extension from the electrical field to the magnetic field [45]. The gradient coefficient provides us with a new freedom to control the plasmonic feature of the graded core-shell particle and could thus be further adopted to tailor the optical pulling force on the core-shell structure. Recently, the optical trapping force on a gain-enriched metallic nanoshell by a Gaussian beam was investigated [38], which opened perspectives for gain-assisted optomechanics where nonlinear optical forces are finely tuned to efficiently trap, manipulate, channel, and deliver an externally controlled nanophotonic system. The aim of this paper is to explore the optical pulling force on a gain-assist graded core-shell sphere at the nanoscale and to investigate the dependence of the pulling force on the gain threshold and the degree of gradation. Moreover, the equivalent permittivity of the graded core-shell is adopted to explain the pulling force that occurs in different plasmon resonant modes in the cases of low and high aspect ratios.

2. Models and Methods

We consider a core-shell sphere consisting of a dielectric gain core and graded plasmonic shell illuminated by a plane electric field in the host medium with a relative permittivity, ${\epsilon }_{\mathrm{h}}$. Here, we make the assumption that the dielectric function of the graded materials varies along the radial direction, r, in the spherical coordinates $(r,\theta ,\phi )$ and can be written as ${\epsilon }_{\mathrm{s}}(r)$. The inner and outer radii are $a$ and $b$. For simplicity, the size of the particle is assumed to be much smaller than the incident wavelength, and therefore the retardation effect is neglected and a long-wavelength approximation could be adopted [46]. The electric potentials in whole space satisfy the following equation within the quasi-static approximation [43]:

$$\nabla ·\left[{\epsilon }_{\beta }(r)\nabla {\varphi }_{\beta }\right]=0,$$

(1)

where ${\varphi }_{\beta }$ is the electric potential in each area ($\beta =\mathrm{c},\mathrm{s},\mathrm{h}$ indicates the core, the shell and the host media, respectively) and could derivate the local electric field by:

$$E_{\beta }=-\nabla {\varphi }_{\beta }.$$

(2)

In the illumination of an external uniform electric field along the z-direction, it can be written as:

$$\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^2{\epsilon }_{\beta }\left(r\right)\frac{\partial {\varphi }_{\beta }}{\partial r}\right]+\frac{1}{r\sin \theta }\frac{\partial }{\partial \theta }\left[{\epsilon }_{\beta }\left(r\right)\frac{\sin \theta }{r}\frac{\partial {\varphi }_{\beta }}{\partial \theta }\right]=0,$$

(3)

The electric potentials in each region have the following general expressions:

$$\begin{array}{l}{\varphi }_{\mathrm{c}}(r,\theta )=-Ar{P}_1(\cos \theta )E_0,\begin{array}{cccc}& & & r\le a\end{array},\\ {\varphi }_{\mathrm{s}}(r,\theta )=[A_1{R}_1^{+}(r)+B_1{R}_1^{-}(r)]P_1(\cos \theta )E_0,\begin{array}{cc}& a<r\le b\end{array},\\ {\varphi }_{\mathrm{h}}(r,\theta )=(-r+b^{3}B{r}^{-2})P_1(\cos \theta )E_0,\begin{array}{ccc}& & r>b\end{array}\end{array}$$

(4)

where $A,B,A_1,B_1$ are four unknown coefficients to be determined, $P_n(\cos \varphi )$ is the n-th order Legendre polynomials, and the radial function, $R_n(r)$, in the shell region satisfies the following equation:

$$\frac{\partial }{\partial r}\left[r^2{\epsilon }_s\left(r\right)\frac{\partial R_n\left(r\right)}{\partial r}\right]-n(n+1)\left[{\epsilon }_s\left(r\right)R_n\left(r\right)\right]=0,$$

(5)

where $R_n^{+}(r)$ and $R_n^{-}(r)$ are the two solutions that are regular at the origin and infinity, respectively, and are the key to achieving the polarizability of the graded core-shell particle.

Considering the boundary condition, i.e., the continuity of the potentials and normal electric displacements:

$$\begin{array}{c}{{\varphi }_{\mathrm{c}}(r,\theta )|}_{r=a}={{\varphi }_{\mathrm{s}}(r,\theta )|}_{r=a},\\ {{\varphi }_{\mathrm{s}}(r,\theta )|}_{r=b}={{\varphi }_{\mathrm{h}}(r,\theta )|}_{r=b},\\ {-{\epsilon }_{\mathrm{c}}\frac{\partial {\varphi }_{\mathrm{c}}(r,\theta )}{\partial r}|}_{r=a}={-{\epsilon }_{\mathrm{s}}(r)\frac{\partial {\varphi }_{\mathrm{s}}(r,\theta )}{\partial r}|}_{r=a},\\ {-{\epsilon }_{\mathrm{s}}(r)\frac{\partial {\varphi }_{\mathrm{s}}(r,\theta )}{\partial r}|}_{r=b}={-{\epsilon }_{\mathrm{h}}\frac{\partial {\varphi }_{\mathrm{h}}(r,\theta )}{\partial r}|}_{r=b}.\end{array}$$

(6)

The coefficients are obtained as:

$$\begin{array}{l}{A}_1=-3b{T}_1^{-}(a)/T(a,b),\\ B_1=3b{T}_1^{+}(a)/T(a,b),\\ A=-a^{-1}[A_1{R}_1^{+}(a)+B_1{R}_1^{-}(a)],\\ B=[F(b)-{\epsilon }_{\mathrm{h}}]/[F(b)+2{\epsilon }_{\mathrm{h}}],\\ T(a,b)=T_2^{+}(b)T_1^{-}(a)-T_2^{-}(b)T_1^{+}(a),\\ T_1^{\pm }(a)=R_1^{\pm }(a)-a\frac{{\epsilon }_{\mathrm{s}}(a)}{{\epsilon }_{\mathrm{c}}}\frac{\partial }{\partial r}{R}_1^{\pm }(a),\\ T_2^{\pm }(b)=2R_1^{\pm }(b)+b\frac{{\epsilon }_{\mathrm{s}}(b)}{{\epsilon }_{\mathrm{h}}}\frac{\partial }{\partial r}{R}_1^{\pm }(b),\\ R_1(r)=A_1{R}_1^{+}(r)+B_1{R}_1^{-}(r),\\ F(b)=\frac{b{\epsilon }_{\mathrm{s}}(b)}{R_1(b)}\frac{\partial R_1(b)}{\partial r}.\end{array}$$

(7)

The spherical shell permittivity profile is given by the graded Drude model [43]:

$${\epsilon }_{\mathrm{s}}\left(r,\omega \right)={\epsilon }_{\mathrm{b}}-\frac{{\omega }_{\mathrm{p}}^2\left(r\right)}{\omega (\omega +i\mathsf{\Gamma })},$$

(8)

where ${\omega }_{\mathrm{p}}^{}\left(r\right)$ and $\mathsf{\Gamma }$ are the spatially varying plasmon frequency and the relaxation rate, respectively. $r$ We introduce a graded plasmon frequency ${\omega }_{\mathrm{p}}^2\left(r\right)={\omega }_{\mathrm{p}}^2(0)(1-h{r}^k)$ in the graded Drude model [47], where $h$ and $k$ are two gradient coefficients denoting the gradation of the shell. Without loss of generality, we further normalize the external field frequencies $\omega$ and the relaxation rate $\mathsf{\Gamma }$ by ${\omega }_p(0)$. Consequently, Equation (8) reduces to ${\epsilon }_{\mathrm{s}}\left(r,\omega \right)={\epsilon }_{\mathrm{b}}-\left(1-h{r}^k\right)/\left[\omega (\omega +i\mathsf{\Gamma })\right]$. In the case of $1-h{r}^k>0$, the graded Drude model has a positive imaginary part, indicating that it is a lossy material.

The gain effect of the dielectric core can be realized by using a semiconductor or dye molecules with pumping [48]. In the theoretical part, we describe the gain core with a relative permittivity function whose imaginary part has a negative value, i.e., ${\epsilon }_{\mathrm{c}}={\epsilon }_{\mathrm{c}0}+i{\epsilon }_{\mathrm{cg}}$ with ${\epsilon }_{\mathrm{cg}}<0$ corresponding to the material gain. The electrostatic polarizability including the radiation reaction of the graded core-shell sphere can be written as:

$$\alpha =\frac{{\alpha }_0}{1-i\frac{2}{3}\frac{k_{\mathrm{h}}^3{\alpha }_0}{4\pi {\epsilon }_0{\epsilon }_{\mathrm{h}}}}$$

(9)

with ${\alpha }_0=4\pi {\epsilon }_0{\epsilon }_{\mathrm{h}}{b}^{3}B,$ $k_{\mathrm{h}}=\frac{2\pi }{\lambda }\sqrt{{\epsilon }_h}$ and ${\epsilon }_0$ being the permittivity of vacuum. The time-averaged optical forces on the nonmagnetic Rayleigh nanoparticle for the incident wave are expressed as:

$$⟨F⟩=\frac{1}{2}{k}_{\mathrm{h}}{E}_0^2\mathrm{Im}(\alpha ).$$

(10)

We normalize the force with $F_0=\pi b^2{S}_{\mathrm{inc}}/c$ ($S_{\mathrm{inc}}$) is the power flow density of the incident wave and $c$ is the speed of light). In the long-wavelength approximation, the dipole contribution dominates the electric response of the dielectric particle. If the dipolar factor $B$ of the core-shell particle vanishes in Equation (4), this means that the core-shell particle and the host medium are the same in view of the dielectric response. Substituting ${\epsilon }_{\mathrm{eq}}$ for ${\epsilon }_{\mathrm{h}}$ in the dipolar factor $B$ and implying $B=0$ yield the self-consistency equation [49], which is solved to obtain the equivalent permittivity of the graded core-shell particle:

$${\epsilon }_{\mathrm{eq}}(b)=\frac{b{\epsilon }_{\mathrm{s}}(b)}{R_1(b)}\frac{\partial R_1(b)}{\partial r}.$$

(11)

If one considers the nongraded case and the gradient coefficient is set to $h=0$, then the equivalent permittivity of the graded core-shell particle is naturally reduced to the nongraded case:

$${\epsilon }_{\mathrm{eq}}(b)={\epsilon }_{\mathrm{s}}(0)\frac{2a^3\left[{\epsilon }_{\mathrm{c}}-{\epsilon }_{\mathrm{s}}(0)\right]+b^3\left[{\epsilon }_{\mathrm{c}}+2{\epsilon }_{\mathrm{s}}(0)\right]}{a^3\left[{\epsilon }_{\mathrm{s}}(0)-{\epsilon }_{\mathrm{c}}\right]+b^3\left[{\epsilon }_{\mathrm{c}}+2{\epsilon }_{\mathrm{s}}(0)\right]}.$$

(12)

3. Results and Discussion

The graded Drude model in Equation (8) shows that the gradient coefficient $h$ plays a more important role than $k$ within the present framework because the permittivity is independent of $k$ when the radius is fixed, especially for the dipole moment, which we mainly focus on in the following. Figure 1 illustrates the permittivity of the graded shell as a function of the gradient coefficient $h$ with the following parameter: ${\omega }_{\mathrm{p}}(0)=1.367\times {10}^{16}{ \mathrm{s}}^{-1}$, $\mathsf{\Gamma }=2.733\times {10}^{13}{ \mathrm{s}}^{-1}$, ${\epsilon }_{\mathrm{c}0}=2.1$ and ${\epsilon }_{\mathrm{h}}=1$. This shows that the graded shell can change from being dielectric-like to metallic-like with an increasing incident wavelength. On the other hand, the graded shell is more like a metal when $h$ is low within the present spectrum. Actually, from Equation (8) one concludes that the dielectric-like or metallic-like profile of the graded Drude model is dependent on the choice of $h$ and $k$, and for a plasmonic shell lower $h$ and lower $k$ values are needed. In what follows, the parameter range of $h$ is used as being from 0 to 0.3 to achieve the plasmonic profile of the shell.

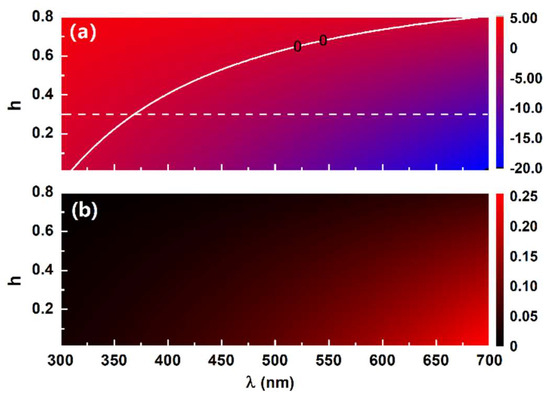
Figure 1. Real (a) and imaginary (b) parts of the graded shell permittivity ${\epsilon }_{\mathrm{s}}\left(b\right)$ as a function of the gradient coefficient, h, and the incident wavelength, λ. The white curve in (a) indicates a value of zero. Other parameters are the outer radius $b=10 \mathrm{nm}$ and the gradient coefficient $k=0.4$.

Figure 2 shows the normalized time-averaged optical force as a function of the incident wavelength with different gradient coefficients $h$ and gain coefficients ${\epsilon }_{\mathrm{cg}}$ for cases with a low aspect ratio ($a/b=0.2$) and high aspect ratio ($a/b=0.8$), respectively. The evolution of the optical force on the gradient coefficient $h$ in the non-gain case (${\epsilon }_{\mathrm{cg}}=0$) is well seen in Figure 2a. As it is a graded plasmonic core-shell sphere, one expects two surface plasmon resonant modes, i.e., the bonding dipole mode at the long wavelength ${\lambda }_{+}$ and the antibonding dipole mode at the short wavelength ${\lambda }_{-}$. These two resonant modes lead to enhanced optical forces, and meanwhile the resonant wavelength is blue-shifted and the magnitudes of the peak value are decreased when the gradient coefficient $h$ increases. It is easy to understand that both the real and imaginary parts of the permittivity of the graded shell are determined by $h$ (see Figure 1), especially the real part which dramatically influences the resonant wavelength. When the gain level is increased, an enhanced negative optical force occurs in the antibonding dipole mode. There exists a critical level of gain in order to achieve the maximal optical pulling force, and a further increase of the gain level could not give rise to a stronger optical pulling force. On the other hand, the absolute value of the resonant peak is dramatically decreased with an increasing $h$ for both the positive and negative forces. As for the optical force enhanced with the bonding dipole mode, it is not sensitive to the gain in the low aspect ratio case.

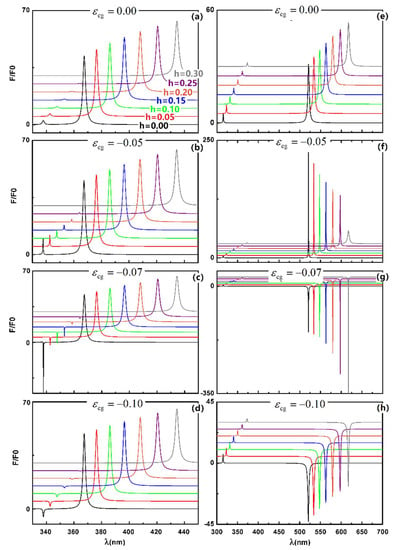
Figure 2. Normalized time-averaged optical force as a function of the incident wavelength $\lambda$ for low aspect ratio, $a/b=0.2$ (a–d), and high aspect ratio, $a/b=0.8$ (e–h) with different gain coefficients ${\epsilon }_{\mathrm{cg}}$ and gradient coefficients $h$. Other parameters are $b=10 \mathrm{nm}$ and $k=0.4$. For the normalization $F_0=\pi b^2{S}_{inc}/c$ ($S_{inc}$ is the power flow density of the incident wave) is used.

In contrast to the low aspect ratio case, the gain has a more dramatic influence on the bonding mode than on the antibonding mode in the high $a/b$ case. An extremely strong optical pushing force (see Figure 2f) and pulling force (see Figure 2g) are achieved with the same level of gain as in the previous case. In addition, the gradient coefficient is found to dramatically enhance the optical pulling force in the bonding dipole mode, as shown in Figure 2g. Up to now, the gain-assisted optical pulling force has been found in both the antibonding mode and bonding mode in the graded core-shell particle. However, it should be mentioned that these two kinds of negative forces arise from different origins in terms of the equivalent medium, which is considered in detail below.

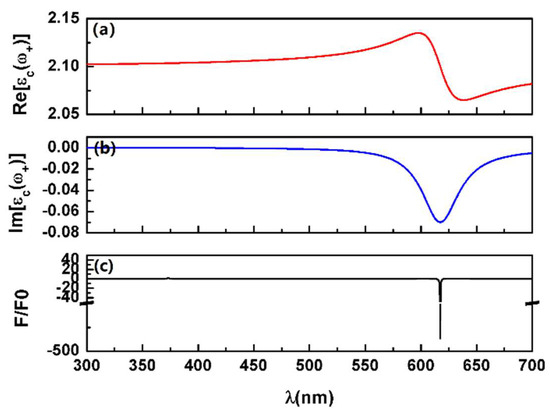
We now adopt the equivalent permittivity of the graded core-shell sphere, as shown in Equation (11), and plot the equivalent permittivity of the graded core-shell sphere for both low and high aspect ratio cases in Figure 3 and Figure 4. It is found that $\mathrm{Im}({\epsilon }_{\mathrm{eq}})$ could exceed −7 in the equivalent permittivity spectrum of the low aspect ratio case due to the surface plasmon resonance. Note that ${\epsilon }_{\mathrm{cg}}$ is merely −0.07 in the present model, which is not a high level of gain [50]; however, the equivalent sphere achieves an extremely high plasmonic enhanced effective gain level. As for the case of the high aspect ratio, the surface plasmon resonance leads to an extremely high loss peak in the equivalent permittivity spectrum. It should be mentioned that there exists only one resonant mode occurring in the inner surface of the core-shell sphere in the equivalent permittivity spectrum. This is because the equivalent permittivity obtained by the self-consistency method is independent of the host medium and this resonance is the intrinsic property of the core-shell sphere itself. Actually, the intrinsic plasmon resonance arises from the plasmonic singularity [25], and the resonant curve shapes vary with different ${\epsilon }_{\mathrm{cg}}$. If increases further, $\mathrm{Im}({\epsilon }_{\mathrm{eq}})$ in the high aspect ratio case will show a negative value peak.

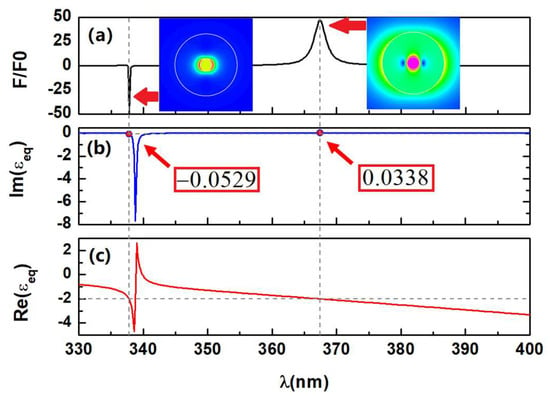
Figure 3. (a) Normalized optical force for the case of the low aspect ratio, as shown in Figure 2, with ${\epsilon }_{\mathrm{cg}}=-0.07$ and $h=0$. (b) The imaginary and (c) real parts of the equivalent permittivity. The insets in (a) indicate the near field intensity distributions at the resonant wavelengths.

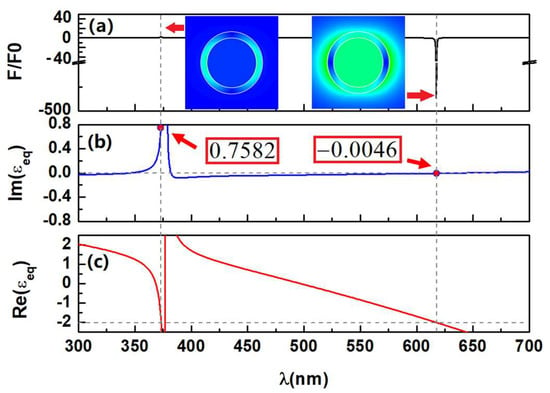
Figure 4. (a) Normalized optical force for the case of the high aspect ratio, as shown in Figure 2, with ${\epsilon }_{\mathrm{cg}}=-0.07$ and $h=0.3$. (b) The imaginary and (c) real parts of the equivalent permittivity. The insets in (a) indicate the near field intensity distributions at the resonant wavelengths.

To give a simple approach for finding the resonant optical force and, on other hand, to mathematically explain why the resonant optical pulling force exists in the bonding (or antibonding) resonant modes corresponding to a high (or low) aspect ratio, we now introduce the equivalent permittivity of the core-shell sphere as obtained in Equation (12). When the core-shell particle is modeled as a sphere with an equivalent permittivity, the optical force on the corresponding equivalent sphere in the long-wavelength approximation is:

$$⟨F⟩=2\pi {\epsilon }_0{\epsilon }_{\mathrm{h}}{k}_{\mathrm{h}}{b}^3{E}_0^2\frac{3\mathrm{Im}({\epsilon }_{\mathrm{eq}})+2{(k_{\mathrm{h}}b)}^3{\left[\mathrm{Re}({\epsilon }_{\mathrm{eq}})-{\epsilon }_{\mathrm{h}}\right]}^2/3}{{\left[\mathrm{Re}({\epsilon }_{\mathrm{eq}})+2{\epsilon }_{\mathrm{h}}\right]}^2+{\left[\mathrm{Im}({\epsilon }_{\mathrm{eq}})\right]}^2+4{(k_{\mathrm{h}}b)}^3\mathrm{Im}({\epsilon }_{\mathrm{eq}}){\epsilon }_{\mathrm{h}}}.$$

(13)

Equation (13) illustrates that the optical force can be enhanced by the surface plasmon resonances occurring when $\mathrm{Re}({\epsilon }_{\mathrm{eq}})=-2{\epsilon }_{\mathrm{h}}$, and the optical pulling force can be achieved when the numerator of Equation (13) has a negative value. Note that the second term of the numerator is always positive and that the potential negative optical force requires $\mathrm{Im}({\epsilon }_{\mathrm{eq}})$ to be negative and its absolute value to be larger than the second term. On the other hand, by substituting $\mathrm{Re}({\epsilon }_{\mathrm{eq}})=-2{\epsilon }_{\mathrm{h}}$ into Equation (13) and ignoring the second term for a sufficiently small $k_{\mathrm{h}}b$, Equation (13) reduces to a simple version as $⟨F⟩=6\pi {\epsilon }_0{\epsilon }_{\mathrm{h}}{k}_{\mathrm{h}}{b}^3{E}_0^2/\mathrm{Im}({\epsilon }_{\mathrm{eq}})$, which indicates that the absolute value of the negative optical force is inversely proportional to $\mathrm{Im}({\epsilon }_{\mathrm{eq}})$.

We highlight the values of $\mathrm{Im}({\epsilon }_{\mathrm{eq}})$ at resonant wavelengths in Figure 3 and Figure 4, and this explains why, mathematically, the optical pulling force occurs in different modes with the low and high aspect ratios in vacuum (${\epsilon }_{\mathrm{h}}=1$). In general, $F/F_0$ is negative when the equivalent sphere plays a role as the active gain medium with $\mathrm{Im}({\epsilon }_{\mathrm{eq}})<0$, and $F/F_0$ is positive when the equivalent sphere is lossy with $\mathrm{Im}({\epsilon }_{\mathrm{eq}})>0$. Moreover, it is concluded that the stronger optical pushing force can be achieved when the equivalent loss is low ($\mathrm{Im}({\epsilon }_{\mathrm{eq}})=0.0338$) (see Figure 3b), and one can realize a stronger optical pulling force when the equivalent gain is low ($\mathrm{Im}({\epsilon }_{\mathrm{eq}})=-0.0046$) (see Figure 4b). With the equivalent permittivity, one can predict where the pulling force occurs in a simpler way. The inserts indicate the near field intensity distributions of the graded core-shell sphere in the different resonant modes for both low and high aspect ratio cases. It is well seen that the antibonding mode is dominated by the surface plasmon resonant on the inner surface. In contrast, the bonding mode is more influenced by the plasma on the outer surface. A dramatically high concentrated local field intensity in the dielectric core is found in the low aspect ratio case, especially in the bonding mode.

To further demonstrate this, the phase diagrams of the equivalent permittivity as a function of $\lambda$ and $h$ for both cases are plotted in Figure 5. The parameter space for $\mathrm{Im}({\epsilon }_{\mathrm{eq}})<0$ is clearly plotted with a red–black color, and the pulling force peaks are located on the white lines that indicate the resonant conditions, $\mathrm{Re}({\epsilon }_{\mathrm{eq}})=-2{\epsilon }_{\mathrm{h}}$. Moreover, the pushing force peaks on the white lines lying in the gray region ($\mathrm{Im}({\epsilon }_{\mathrm{eq}})>0$) are indicated in Figure 5 as well. The resonant pulling forces in the high aspect ratio case are generally stronger than those in the low aspect ratio (see Figure 2c,g), as soon as $\left|\mathrm{Im}({\epsilon }_{\mathrm{eq}})\right|$ are much smaller on the pulling force line in Figure 5b, according to the previous analysis of Equation (13). Actually, in spite of the giant resonant pushing/pulling force on the white lines, in Figure 5b there exists a broader parameter space for a slight pulling force where $\mathrm{Im}({\epsilon }_{\mathrm{eq}})<0$. Let us remark here that $\mathrm{Re}({\epsilon }_{\mathrm{eq}})$ might not rigorously satisfy the resonant condition, i.e., $\mathrm{Re}({\epsilon }_{\mathrm{eq}})>-2{\epsilon }_{\mathrm{h}}$ with $h$ increasing since the loss of the graded shell is inversely proportional to $h$, as illustrated in Figure 1b; consequently, there exists a cut-off for the resonant white line in the low aspect ratio case when $h$ reaches $~0.24$. Still, a tiny pulling force peak occurs in the bonding mode in Figure 2c with a large $h$.

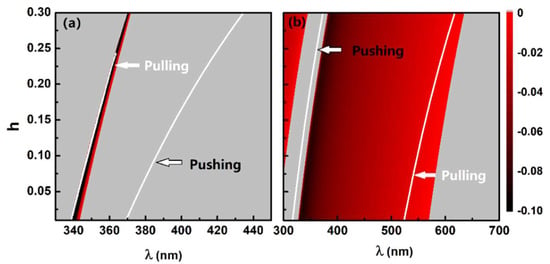
Figure 5. $\mathrm{Im}({\epsilon }_{\mathrm{eq}})$ versus incident wavelength, $\lambda$, and gradient coefficient, $h$, for the cases of (a) low aspect ratio ($a/b=0.2$) and (b) high aspect ratio ($a/b=0.8$). Gray regions indicate the parameter space for a positive value. The white lines show the positions of $\mathrm{Re}({\epsilon }_{\mathrm{eq}})=-2{\epsilon }_{\mathrm{h}}$. The gain coefficient is set as ${\epsilon }_{\mathrm{cg}}=-0.07$ for both cases.

Finally, we investigate the dependence of the pulling force on the aspect ratio of the graded core-shell particle in Figure 6. The resonant pulling force tends to occur in the gain-assisted core-shell sphere with either a low aspect ratio or high aspect ratio (see the rectangle), and in contrast the resonant pushing force exists in the case of a wider moderate aspect ratio. On the other hand, the resonant wavelength together with the resonant pulling force peak varies with the graded coefficient $h$. This gives rise to a broader parameter space in order to realize the resonant pulling force in the antibonding mode and, on the contrary, a smaller space in the bonding mode with a high $h$.

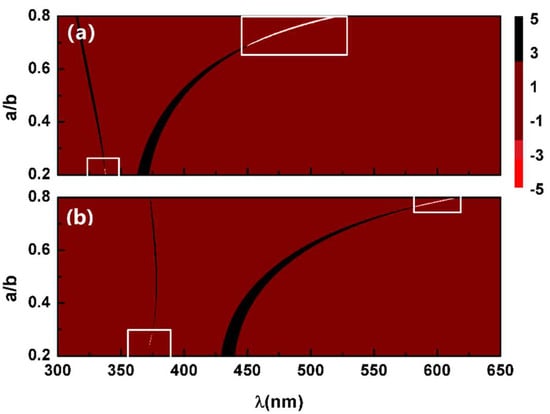
Figure 6. Normalized optical force, F/F₀, versus incident wavelength, $\lambda$, and aspect ratio, $a/b$, in the cases of (a) $h=0$ and (b) $h=0.3$ with ${\epsilon }_{\mathrm{cg}}=-0.07$. The white curves indicate a pulling force much stronger than $-5$, which is marked by a white rectangle.

It should be noted that, in this paper, we use a flat imaginary part of ${\epsilon }_{\mathrm{c}}$ instead of a more realistic frequency-dependent one [25,35,38]. In what follows, a brief comparison between the results with the Lorentzian dependent permittivity and those with a flat constant permittivity for the gain media are given in order to certify the validity of this study. Thus, the gain media is described by the permittivity with a Lorentzian shape [38] as:

$${\epsilon }_{\mathrm{c}}(\omega )={\epsilon }_{\mathrm{c}0}-\frac{{\epsilon }_{\mathrm{cg}}\Delta }{2(\omega -{\omega }_{\mathrm{g}})+i\Delta },$$

(14)

where ${\epsilon }_{\mathrm{c}0}$ is the background permittivity of the gain core, ${\omega }_{\mathrm{g}}$ is the emission centerline of the gain elements, and $\Delta =2/\tau$ is the width of the Lorentzian shape where $\tau$ is the energy relaxation time of the gain. ${\epsilon }_{\mathrm{cg}}$ is a dimensionless parameter measuring the amount of gain present in the system.

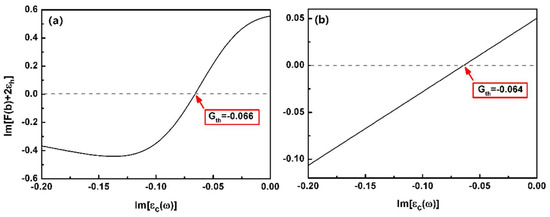
Figure 7 and Figure 8 illustrate that when the gain lines shape is centered exactly on the plasmon resonant frequency, the optical pulling force obtained by ${\epsilon }_{\mathrm{c}}(\omega )$ in Equation (14) is the same as that with a flat constant ${\epsilon }_{\mathrm{c}}$. It is worth noting that ${\epsilon }_{\mathrm{c}}(\omega )$ at the plasmon resonant position has the same real and imaginary values as the flat one. One of the goals in this study is to demonstrate the different behaviors of the optical force in plasmonic resonant modes of a graded nanoshell with different aspect ratios (i.e., a/b) on the same level of gain. Thus, what makes sense is the central gain amount at the resonant frequency. From this point of view, the conclusions made with the flat constant model are the same as those made with the frequency-dependent one. However, it is found that the overall gain amount (${\epsilon }_{\mathrm{cg}}=-0.07$) slightly exceeds the spaser threshold (see Figure 9) for both cases in Figure 7 and Figure 8, which might lead to a spaser instability [35].

Figure 7. Real (a) and imaginary (b) parts of ${\epsilon }_{\mathrm{c}}(\omega )$ in the case of a low aspect ratio (a/b = 0.2) of Figure 2c with ${\epsilon }_{\mathrm{cg}}=-0.07$ and $h=0$. (c) The same as Figure 3a but using the present ${\epsilon }_{\mathrm{c}}(\omega )$. Parameters: $\tau ={10}^{-14} \mathrm{s}$, ${\omega }_{\mathrm{g}}={\omega }_{-}=2\pi c/{\lambda }_{-}$, ${\lambda }_{-}=337.8 \mathrm{nm}$.

Figure 8. Real (a) and imaginary (b) parts of ${\epsilon }_{\mathrm{c}}(\omega )$ in the case of a high aspect ratio (a/b = 0.8) of Figure 2g with ${\epsilon }_{\mathrm{cg}}=-0.07$ and $h=0.3$. (c) The same as Figure 4a but using the present ${\epsilon }_{\mathrm{c}}(\omega )$. Parameters: $\tau ={10}^{-14} \mathrm{s}$, ${\omega }_{\mathrm{g}}={\omega }_{+}=2\pi c/{\lambda }_{+}$, ${\lambda }_{+}=617.4 \mathrm{nm}$.

Figure 9. Finding the spaser threshold gain $G_{\mathrm{th}}$ for the cases of (a) Figure 7 and (b) Figure 8.

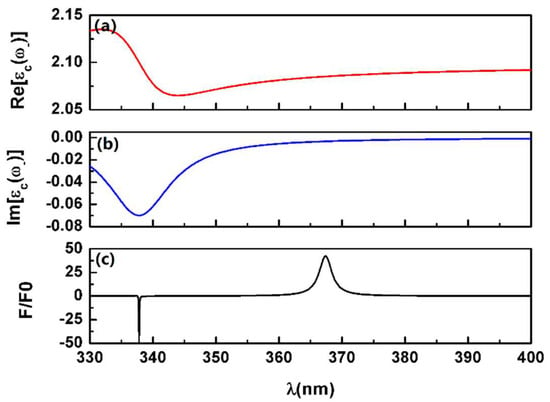
According to Ref. [35], a more complex model should be introduced. However, the analytical results for the coefficient $B$ in Equation (4) contain the hyper-geometric function $F(\alpha ,\beta ,\gamma ,z)$ in $R_1^{+}(r)$ and $R_1^{-}(r)$, i.e., $R_1^{+}(r)=rF({\alpha }_1,{\beta }_1,{\gamma }_1,z)$ and $R_1^{-}(r)=r^{-2}F({\alpha }_{-1},{\beta }_{-1},{\gamma }_{-1},z)$, where ${\alpha }_{\pm 1}=\left[k\pm 3-\sqrt{{(k+1)}^2+8}\right]/2k$, ${\beta }_{\pm 1}=\left[k\pm 3+\sqrt{{(k+1)}^2+8}\right]/2k$, ${\gamma }_{\pm 1}=(\pm 3+k)/k$ and $z=-h{r}^k/({\omega }^2+i\omega \mathsf{\Gamma }-1)$. Thus, it is not straight to analyze the temporal dynamic evolution of the dipole moments and study the condition of instability, especially for the case of the metallic nanoshell where more than one plasmonic resonant mode exists. The exact nature of this final state requires a thorough study dependent on the various model parameters, which is not within the scope of this paper.

4. Conclusions

In summary, in this paper, giant gain-assisted resonant pulling forces are demonstrated on a graded core-shell nanoparticle in a long-wavelength approximation. It is found that these plasmonic enhanced pulling forces can exist in either the antibonding or bonding modes based on the choice of the aspect ratio of the core-shell sphere. Generally, the antibonding mode in the low aspect ratio case and the bonding mode in the high aspect ratio would lead to the resonant pulling force, and this could be demonstrated by the obtained equivalent permittivity of the graded core-shell sphere. The gradation of the shell has a dramatic influence on the resonant wavelength of the pulling force and could strengthen the resonant pulling force with the same level of gain as in the nongraded case. Moreover, the parameter space for realizing the pulling force is broadened with a higher gradient coefficient. The present study may give a deep insight into the mechanism of the pulling force in gain systems and offer an effective way to obtain large negative forces for nano-manipulation.