1. Introduction
A measuring apparatus may consist of various components (magnets, cavities, crystals, detectors, and so on). In the literature, such a complex apparatus is often referred to as a detector. In the following, the word ”detector” will only be employed for the components of the measuring apparatus that can provide an output signal. Typical examples are ionisation chambers and scintillation counters. The output signal delivered by a detector indicates that a quantum object (particle or photon) has been detected. In the present study, only the action of the detector as a counter is of interest. The only task of a counter is to count the number of registered events. An individual measurement is completed when the detector has produced the output signal and the result has been registered. Detectors are highly important for experimental performance, because measurement results for single particles or photons are usually determined by means of detectors.
One problem is that quantum theory describes the interactions between quantum object and measuring apparatus in a highly simplified manner. The Copenhagen interpretation of quantum mechanics assumes that a measuring apparatus is a classical apparatus. However, it is not clear how a quantum mechanical system can interact with a classical one. John von Neumann [
1] has developed the mathematical foundations of the orthodox interpretation of quantum mechanics. An important prerequisite is the assumption that the measuring apparatus can be considered as a quantum mechanical system. An ideal measurement then describes an interaction between two quantum mechanical systems: a microscopic one (the incident quantum object) and a macroscopic one (the measuring apparatus). Unfortunately, the time evolution of the wave functions of both systems during the quantum measurement process cannot be described by the time-dependent Schrödinger equation. This is the measurement problem of quantum mechanics. In the literature, one finds a huge number of publications discussing this problem, which is still unresolved. Only the studies by R. Omnès [
2], D. Home and M.A.B. Whitaker [
3], and M. Schlosshauer [
4] are mentioned here as examples. The question of whether macroscopic objects can be treated as quantum mechanical systems has been discussed by W.H. Zurek [
5].
Following an ideal measurement, the incident object will be in a well-defined quantum mechanical state. Hence, an ideal measurement is repeatable, and the same object can interact a second time with an identical measuring apparatus. If one repeats the same measurement immediately, then one must obtain the same result as for the first measurement. According to R. Omnès [
2], this statement can be considered as the definition of an ideal measurement.
Most real measurements do not fulfil the conditions of ideal measurements. Either they cannot be repeated, or, if they are repeatable, one will not obtain the same outcome as in the first measurement. Neutrons and photons are often absorbed when they strike a detector. If one wants to measure the energy of a charged particle, this particle has to deposit its full energy in the detector. Hence, these measurements are not repeatable.
The probability distribution of measurement results is a highly important quantity that allows to compare measured and calculated results. This distribution is successfully described in the framework of quantum mechanics by means of two postulates, the reduction postulate and the Born rule. However, there remain the following open questions.
Why do experimenters find in each individual measurement a well-defined result while quantum mechanics provides only probability distributions?
Why does chance determine the result of an individual measurement?
When is a measurement completed? (This question is of special interest for Schrödingers cat [
6].)
During each measurement, a transition from the quantum mechanical to the classical state takes place. However, we still do not know when does this transition occur?
These questions cannot be answered in the framework of orthodox quantum mechanics. (Similar questions have been posed by M. Schlosshauer [
4].) One possible way out is to look for a better understanding of the interaction between particle and detector. Haake and Weidlich [
7], Hepp [
8], and M. Cini et al. [
9] have developed more realistic models to describe this interaction. However, these models do not reproduce the properties of real detectors.
Today, these properties are much better known than in the 1920s. In the present study, an attempt is made to use this knowledge as a starting point to describe the quantum mechanical measuring process. One aim is to see whether one can find answers to the questions posed above. First, one has to check whether it is possible to describe the interaction between particle and detector with the methods of quantum mechanics. As a first step, the time dependence of this interaction is studied in
Section 2.
2. The Interaction between Quantum Object and Detector
In a first step of an experiment, a large number of particles is prepared in a well-defined state
.
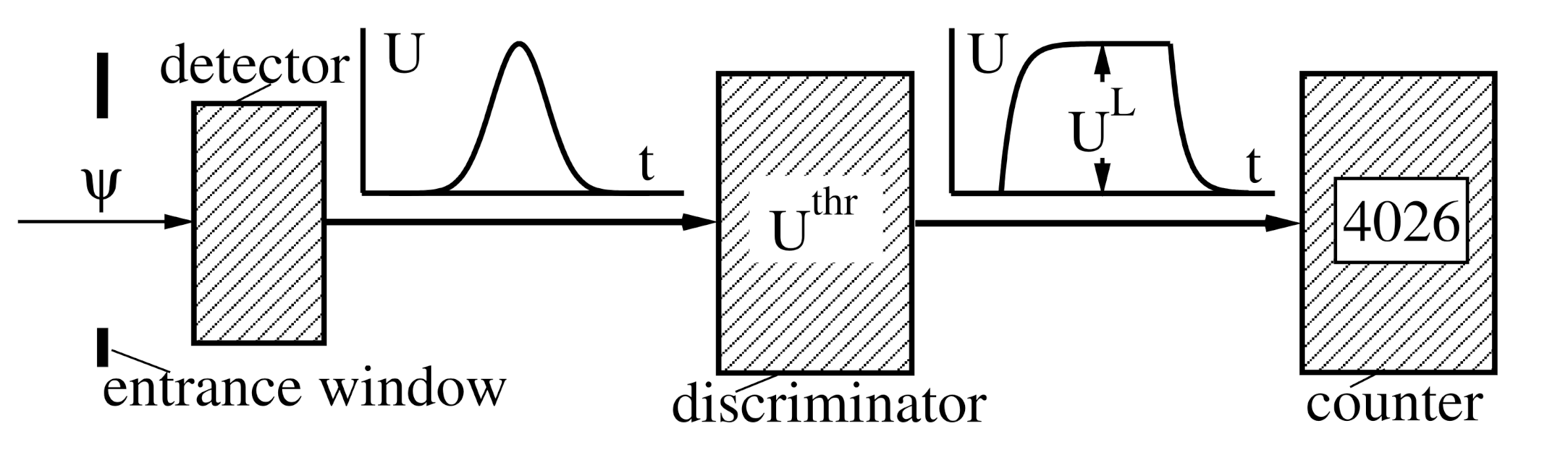
Figure 1 shows a simple electronic set-up that can detect a single quantum object and that counts the number of detected objects. An incident charged particle deposits a certain amount of energy in the detector. This energy is utilised to provide a voltage pulse,
, where
t denotes time. To suppress thermal noise, the experimenter will set a fixed threshold
. The discriminator in
Figure 1 will only deliver a logical output signal
if
exceeds the threshold. In most detectors, this means that an output signal
can only be generated if the energy
deposited in the detector is greater than a certain threshold energy
:
To generate an output signal, an incident particle usually triggers a large number of reactions in the detector medium. At any given time, the particle can only initiate a reaction with one other particle. During its passage through matter, a charged particle ”a” with sufficient energy can excite and ionise many atoms ”X”:
In a semiconducting detector, a large number of electrons (”e
”) are transferred from the valence band to the conduction band. In a scintillator, many photons are produced. These examples show that the numbers of charged objects and photons are vastly increased along the path of a charged particle. Thus, a single particle state becomes a many particle state. In the following, this effect will be called amplification. Such amplification processes are employed in various detectors to produce a logical output signal
(see
Figure 1).
Neutrons and photons do not ionise or excite atoms during their passage through matter. Hence, one utilises special detectors to detect such objects. In these detectors, reactions occur, in which one or two charged particles are released. Examples include nuclear reactions for neutrons, and pair production and the photoelectric and Compton effects for photons. In the following, these reactions will be called start reactions, because the released charged particles ionise and excite many atoms and initiate the amplification process mentioned above. If condition (
1) is fulfilled, then a logical output signal
will be produced.
In the next step, the time dependence of the interaction between a quantum object and an appropriate detector is considered. Successful measurements can often be divided into three phases:
In phase 1, the start reaction occurs. The incident object initiates a reaction with a microscopic part of the detector (atom, molecule, electron or nucleus), rather than with the whole detector.
Phase 2 is the amplification phase. An avalanche of secondary objects (charged particles or photons) is released.
Phase 3 is the readout phase. A fully operable detector will produce a detectable output signal.
As a first example, the detection of single photons from the visible light spectrum with a photomultiplier tube is considered. The photomultiplier tube consists of three parts: a photocathode, dynode system, and anode. In phase 1, the incident photon interacts with a single atom in the photocathode. In this case, the photoelectric effect is the start reaction. The photon will be absorbed, and a photoelectron will be ejected. The photoelectron will not fulfil condition (
1). Hence, this photoelectron will be accelerated to the first dynode in an electric field. Here, it will eject several secondary electrons, which are accelerated to the second dynode. In phase 2, many secondary electrons are released in the dynode system. In phase 3, a voltage pulse
is readout at the anode, and the discriminator in
Figure 1 will produce a detectable output signal
.
Thermal neutrons can be detected in a proportional chamber filled with boron trifluoride (BF
) gas enriched to 96%
B. Here, the reaction,
is the start reaction. The charged particles
and
Li ionise many molecules in phase 2. Electrons and ions move to the electrodes of the chamber in an external electric field and produce the output signal. Both examples show that the incident object (photon or neutron) triggers a reaction with a single atom or nucleus in phase 1, but not with the whole detector.
During the detection of a single particle, many reactions occur in phases 1 and 2. Although each reaction is a quantum mechanical process, the sum effect of these reactions (the production of incoherent light or an electric current in phase 3) can be described in the language of classical physics. A scintillation counter collects the light emitted by many excited atoms at the photocathode of a photomultiplier tube. In a semiconducting detector, electrons and holes are accelerated in an external electric field and produce a current pulse.
A start reaction initiates the amplification process in a detector, and with certainty produces a logical output signal . However, neutrons and photons can trigger various reactions that do not start an amplification process. Hence, the start reaction is defined as the first reaction occurring in a detector that fulfils the following two conditions:
- (I)
A start reaction is a reaction between the incident particle (or photon) and an object (atom, molecule, electron, or nucleus) in the detector.
- (II)
In the exit channel of a start reaction, there must be at least one or two charged particles. The kinetic energy of these particles should be so large that they can release a large number of secondary charged particles or photons in the detector medium.
When a charged particle interacts with a detector that is placed under vacuum conditions, its first reaction of the type (
2) or (
3) with an atom of the detector is defined as the start reaction if its kinetic energy is larger than the threshold energy
(see Equation (
1)). This definition fulfils conditions (I) and (II).
An experimenter who wants to detect particles of a special type will first choose an appropriate detector, and then bring it into an operable state. For the detection of thermal neutrons, he will choose a proportional chamber filled with BF
gas. Reaction (
4) is the only possible start reaction in this case. On the other hand, an incident photon can initiate various reactions that fulfil the conditions (I) and (II) such as pair production, the photoelectric and Compton effects. In what follows, the start reaction is defined as consisting of all reactions fulfilling both conditions (I) and (II). A particle that triggers the start reaction in an operable detector will certainly produce an output signal.
3. Detector Model for Position Measurements
One aim of the present study is to find out whether it is possible to describe the interaction between particle and detector with the methods of quantum mechanics. Interactions between particles and different types of detectors can be considered as sequences consisting of three phases: start reaction, amplification, and readout. This observation forms the basis of a detector model that is called here the three-phase model. The study performed is limited to the detection of heavy non-relativistic particles in a detector that is not position sensitive. (Presumably, a similar detector model can also be developed for photons.) The particles are detected without determining their energy and particle nature. The detection of a particle is also a position measurement, because at the moment of the measurement each detector has a well-defined position. The uncertainty of the measured position is defined by the size of the detector.
Only detectors that fulfil the following requirements are considered:
- (A)
The detector should be able to detect single particles.
- (B)
All reactions following after the start reaction should be of type (
2) or (
3).
These requirements are fulfilled when neutrons or charged particles (protons, -particles, etc.) interact with different types of detectors. Examples include ionisation chambers, semiconducting detectors, photomultiplier tubes, scintillation counters, and cloud and bubble chambers. (Detectors that use the Cherenkov effect do not fulfil requirement (B).) In all cases, the quantum mechanical state of the incident particle is destroyed when it is detected in a (macroscopic) detector.
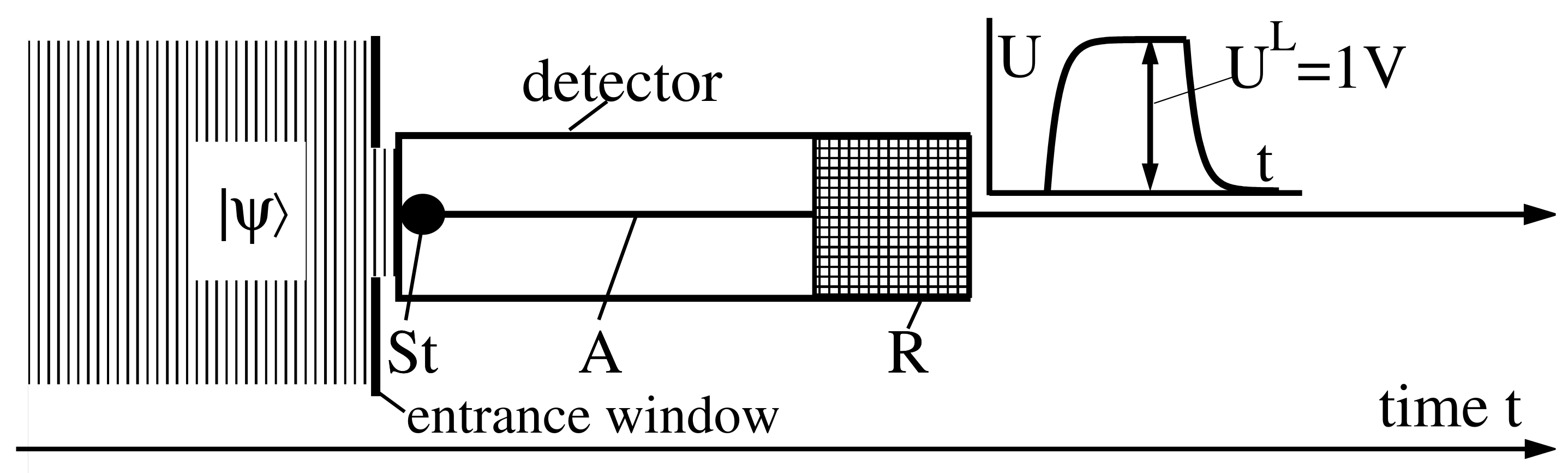
Figure 2 illustrates the time sequence of a position measurement according to the detector model. The start reaction (in phase 1) is represented by a black dot since the incident particle triggers a reaction with a single quantum object. The amplification mechanism (in phase 2) is plotted as a line. This is a reminder that the tracks of energetic charged particles are straight lines in cloud and bubble chambers. A macroscopic part of the detector and the discriminator (see
Figure 1) are involved in the readout process (in phase 3). The readout is, therefore, represented as a square box.
As a first example, a particle is considered that is in a plane wave state. (More general cases to be considered elsewhere [
10].) This particle interacts with a fully operable detector that fulfils the requirements (A) and (B). If this particle initiates the start reaction (one of the possible start reactions) in the detector medium, then the same detector will certainly provide a logical output signal
. The converse is also true: if the logical output signal delivered by the detector has been registered, then it is known that this signal has been caused by the start reaction in the same detector. Here, it is assumed that an output signal can only be generated by the incident particle. (Other sources such as cosmic radiation, radioactive decays in the environment, thermal noise of the electronics must be excluded by additional measures.) Here one concludes: there is a one-to-one correlation between a quantum mechanical event (the start reaction occurs in phase 1) and a classical event (the detector and discriminator produce a logical output signal
in phase 3).
In the case of a position measurement, an appropriate and fully operational detector provides a logical output signal if, and only if, the incident particle has previously triggered the start reaction in it.
The three-phase model reduces the complicated measurement process to an effective two-particle interaction. This result simplifies the theoretical analysis considerably, as is shown in
Section 4.
The reactions occurring in phase 2 appear to have no influence. However, this is not true. They are important if one measures the energies of charged particles or if one investigates tracks of charged particles in a bubble chamber. In the present work, we are only interested in the detection of particles. In this case, it is only important whether an output signal is generated or not. This ”yes” or ”no” decision depends only on the question of whether the start reaction has been initiated.
4. Angular Distribution of Diffracted Particles
So far, only the interactions between quantum objects and a single detector have been studied. In a second example, the passage of particles through a diffractive aperture (a small round opening) is considered in a thought experiment. The particles may be thermal neutrons or charged particles. They are detected with an array of
Z small (appropriate) detectors. The detectors are placed on a spherical surface whose centre coincides with the aperture. Diffracted particles are described by the wave function,
Here, denotes the scattering angle, denotes the (scattering) amplitude, k is the wave number, and r is the radius.
The angular distribution of the diffracted particles is measured. In a first experiment, the diffraction of charged particles is investigated. Small ionisation chambers are used as detectors. From the classical viewpoint, an ionisation chamber is a capacitor filled with argon gas. From the quantum mechanical viewpoint, the detector is a collection of atoms or molecules. In phase 1, the state of the projectile is described by the probability wave (
5). Hence, the projectile can interact with all atoms of all detectors. Each incident particle views the different detectors as one big target consisting of all the atoms of all the detectors. The spatial order of the detectors does not play an essential role in phase 1 of the measurement.
At an arbitrary time, the incident particle can only trigger a reaction with a single quantum object in one of the Z detectors. Let us assume that the first reaction, the start reaction, randomly occurs in detector D (with ). During a reaction, the state of the incident particle is changed. It is, therefore, excluded that the incident particle (in its initial state) triggers start reactions in more than one detector.
The mean free path length of a charged particle is considerably smaller than the size of a typical detector. Hence, all the reactions following in phase 2 will occur in the same detector D
. At this point, the spatial order of the detectors is important. In phase 3, the ionisation chamber D
can be considered as a capacitor in which clouds of positively and negatively charged particles move. Under the influence of an external electric field, a large number of electrons and ions move towards the capacitor plates. The uncorrelated movement of several tens of thousands of charged particles can be described as a classical electric current. This current generates a short voltage pulse in detector D
. Before measurement, the outputs of all discriminators (see
Figure 1) were in the ground state (
V for
). Immediately after the detection of the particle, for a short time one detector (D
) will be in an ”excited” state with a definite output voltage (
V):
Only one detector (D
) will produce a logical output signal. (In the literature, a similar effect is called wave packet reduction; see, e.g., Cini et al. [
9].) This is the result of an individual position measurement. According to the three-phase model, this result improves our knowledge: it is known now that the incident particle has initiated the first reaction, the start reaction, with a single atom in detector D
. Since the detector is not position sensitive, it is assumed that this first reaction took place in the centre of the detector surface corresponding to the scattering angle,
. This angle is the measurement result. A well-defined outcome will be obtained for each successful measurement. However, one cannot predict the detector in which the incident particle will be detected, as soon as it is impossible to predict the atom with which this particle will trigger the first reaction.
Probability Distribution of Measurement Results
The probability distribution of measurement results is determined for the experiment described in
Section 4. This distribution is determined in quite a different manner in experiment and theory. For the experimenter, the detectors and discriminators are classical apparatuses, which produce a ”yes” or ”no” decision for each particle that leaves the source. The discriminator (see
Figure 1) will either generate a logical output signal or deliver no signal. This decision is described in the language of classical physics. For each detector, the experimenter detects a large number of events and determines the probability,
, that detector D
and the corresponding discriminator generate a logical output signal,
. Each output signal
indicates the detection of a particle in detector D
.
From the theoretical viewpoint, there are two possibilities to calculate the probability distribution of measurement results. Orthodox quantum mechanics uses the Born rule, the detectors are not taken into account. The probability
that a particle has passed the entrance window (see
Figure 2) of detector D
is determined from the wave function (
5) of the particle:
Here, is the solid angle under which the entrance window of detector D is seen from the diffractive aperture, and is the scattering angle corresponding to the centre of that window. The constant factor depends on the diameter of the aperture and the thickness of the detector.
In the present work, the interaction between particle and detector is taken into account. An individual measurement is completed when one of the detectors (D
) has provided an output signal, i.e., when the incident particle has triggered
the start reaction (one of the possible start reactions) in the same detector. Hence, the probability,
, that the incident particle initiates the start reaction in detector D
is calculated. At least in simple cases, the calculation can be performed in the framework of quantum mechanics as shown below.
can be written as the product of the two terms:
with
defined in Equation (
6), and
representing the probability that a particle that passed the entrance window of detector D
triggers the start reaction in the same detector:
corresponds to the detection efficiency of the detector.
According to the three-phase model (see
Section 3), there is a one-to-one correlation between the start reaction in detector D
and the production of a logical output signal
. In an experiment, the number of start reactions initiated in detector D
is, therefore, equal to the number of output signals provided by detector D
. Under the conditions of the experiment, the probabilities
and
are equal:
It should be noted that is determined by the experimenter using methods of classical physics, while can be calculated with the methods of quantum mechanics.
Only two cases are considered here:
. This is the case when charged particles are detected in an ionisation chamber D
filled with argon gas. These particles will certainly initiate the start reaction (one of the reactions (
2) or (
3)) in detector D
, and produce a detectable output signal
, if the threshold condition (
1) is fulfilled. According to Equation (
7), the result
agrees with the result (
6) of orthodox quantum mechanics.
. This is the case when thermal neutrons that have passed the diffractive aperture are detected in a thin proportional chamber filled with BF
gas (see
Section 2). In this case, reaction (
4) is the start reaction. The detector can be considered as a thin target through which most neutrons pass without reaction.
is proportional to the total reaction cross section
for reaction (
4):
where
is the number of
B atoms per unit volume,
d is the thickness of the detector.
5. Summary
In the present work, interactions between particles and a small number of detectors have been studied. The incident object is in a quantum mechanical state. Conversely, the detector and discriminator provide classical information.
A detector is built up of a large number of quantum mechanical systems. To generate a detectable output signal, the incident particle must deposit energy in the detector medium. The particle must, therefore, trigger at least one reaction, in most cases a large number of reactions. At an arbitrary but fixed time, the incident particle can only initiate a reaction with a single quantum object (atom, molecule, nucleus, or electron) in the detector. The start reaction (the first reaction in most cases) is the most important reaction because it determines which detector provides the output signal.
For various types of detectors, such as ionisation chambers and scintillation counters, the quantum measurement process can be considered as a sequence of the three phases: start reaction (phase 1), amplification (phase 2), and readout (phase 3). This observation has been utilised to develop the three-phase model, which can describe individual position measurements for non-relativistic particles.
Detectors behave quite differently during the three phases. Let us assume that charged particles that are in a well-defined quantum mechanical state strike an array of Z ionisation chambers filled with argon gas. In phase 1, the Z detectors form one big target with a large number of atoms. During the first reaction, the start reaction, an incident particle initiates a reaction with one atom, but not with the whole detector. If the start reaction occurs in detector D, then all reactions following in phase 2 will occur in the same detector. All reactions are quantum mechanical processes. In phases 1 and 2, the incident particle ionises a large number of atoms and produces a cloud of charged particles in detector D. In phase 3, this cloud determines the properties of the output signal, while the incident particle does not play a role. At the beginning of a position measurement, the detector can be considered as a collection of many quantum mechanical systems, and at the end the detector behaves like a classical apparatus. The conclusion is that the detector is neither a quantum mechanical system nor a classical apparatus. The transition from the quantum mechanical to the classical description occurs in the detector.
The detection of a particle is a complicated process. A particle that is in a quantum mechanical state provides an output signal, i.e., classical information. So far, only one example has been discussed. However, this example shows that it is possible to describe the interaction between particle and detector with the methods of quantum mechanics.
Probability distributions are determined quite differently in experimental and theoretical physics. The experimenter employs methods of classical physics to determine the probability that detector D generates an output signal. This probability cannot be calculated in the framework of quantum physics. However, one can calculate the probability that the incident particle initiates the start reaction in detector D. According to the three-phase model, both probabilities are equal. Here, the one-to-one correlation between the start reaction and the logical output signal is utilised. Formally, the measurement process is replaced by a two-particle reaction between the incident particle and a single object in the detector medium.
In the present study, the interaction between particle and detector has been taken into account. The three-phase model describes the detection of a particle for a large class of detectors that fulfil the requirements (A) and (B) (in
Section 3). Taking the particle-detector interaction into account makes it possible to answer the questions posed in
Section 1:
Individual position measurements can be described with the methods of quantum mechanics. The quantum measurement process is reduced to an effective two-particle interaction. As additional information, we obtain the outcome of the measurement: If detector D provides an output signal, then we know that the incident particle has initiated the start reaction with a single atom in the same detector. This signal indicates the result of an individual measurement, comprising the position of the detected particle.
Chance determines the result of an individual measurement, because one cannot predict the detector in which the incident particle will initiate the first reaction. Only one of several detectors will provide an output signal. In the literature, this effect is called wave packet reduction.
A measurement is completed when the result has been registered.
The transition from the quantum mechanical to the classical state takes place in the detector.
This success does not mean that the measurement apparatus must be accounted for in each theoretical analysis. In most experiments, one is only interested in the probability distribution of the measurement results. This distribution is already fixed before the incident particles interact with the detector(s). It is excellently described in the framework of orthodox quantum mechanics.