Abstract
In this paper, a discussion of the Landau damping of Langmuir waves is presented together with a simple derivation which does not require the application of methods of complex analysis. A general dispersion relation is derived systematically which corresponds to a nonlinear equation. The latter equation is solved numerically but asymptotic limits are also discussed.
1. Introduction
In the current paper, the damping of plasma waves, also known as Langmuir waves [1], is explored. Plasma waves are related to electron oscillations and, thus, they are sometimes called plasma oscillations. The standard description of those waves is based on the momentum equation (Euler equation) for the electrons, their continuity equation, and Gauss’ law of electrodynamics. Furthermore, it is assumed that the electrons behave like an ideal gas. In order to find the dispersion relation of Langmuir waves, the aforementioned fluid equations are linearized leading to the Bohm–Gross dispersion relation (see [2,3,4]),
Therein, the wave number k, the plasma frequency
and the electron thermal speed
are used in terms of the electron particle density (particles per volume), , the elementary charge, e, the electron mass, , the permittivity of free space, , Boltzmann’s constant, , and the absolute temperature, T (in Kelvin). Note, the electron thermal speed comes straight from the equipartition theorem which states that each degree of freedom has the average kinetic energy . Therefore,
is a consequence of having only one degree of freedom due to the one-dimensional motion of the electrons. This relation can be straight rearranged to obtain Equation (3).
A useful parameter in the description of plasma waves is the Debye length corresponding to the distance over which significant charge separation occurs; it is given by
By considering linearized fluid and Maxwell equations, one can show that Langmuir waves are longitudinal in nature.
In this paper, Landau damping, describing the damping of plasma waves due to the interaction between the wave and the electrons in the plasma, is revisited. This is a special case of wave–particle interactions in a plasma. According to [5], the physical mechanism of Landau damping can be understood as follows: particles having velocities slightly less than the phase velocity of the wave are accelerated by the wave’s electric field to move with the wave phase velocity. Therefore, the group of particles moving slightly slower than the phase velocity gain energy from the wave. In a collisionless plasma characterized by a Maxwellian distribution (see Section 3), the number of slower particles is greater than the number of faster particles. Therefore, energy gained from the waves by slower particles is more than the energy given to the waves by faster particles, thus leading to net damping of the waves. An example plot is given in Figure 1.
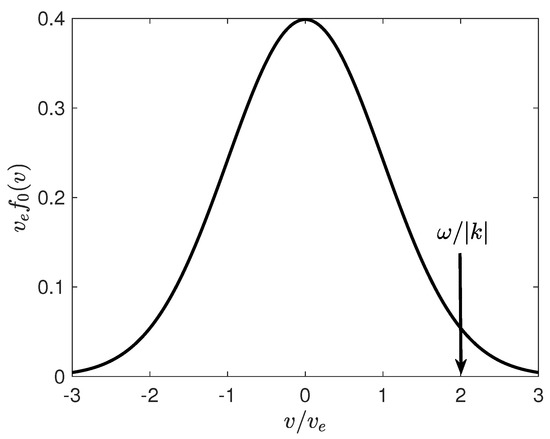
Figure 1.
Maxwellian distribution. The arrow points to the location of the phase speed of the Langmuir wave. In the considered case, the wave speed is larger than the electron thermal speed. Particles to the left of the arrow are slower, and particles to the right of the arrow are faster than the wave. Here we have used the wave number k, the frequency , the electron speed v, and the electron thermal speed .
The first theoretical description of Landau damping was presented in [6] and was based on the Vlasov equation [7]. Although Landau damping was originally derived for plasma waves, it can also be considered in the context of magnetohydrodynamic waves [8].
The derivation of traditional Landau damping, as provided in [6], is based on Laplace transforms and complex contour integrations. In [9], it was shown that Landau damping can also be described by using a Fourier transform and normal mode expansion. The latter modes are usually called van Kampen modes. In [10], it was demonstrated that Landau’s and van Kampen’s treatments of plasma oscillations are equivalent. Alternative and simpler derivations of Landau damping can be found in textbooks, see, e.g., [11]. However, all the aforementioned descriptions are based on contour integrals and other tools of complex analysis.
In order to avoid using tools of complex analysis, an alternative derivation of Landau damping is presented in the current article. This approach can be particularly useful for teaching this topic to undergraduate and graduate students in introductory plasma physics and magnetohydrodynamics courses.
The reminder of this paper is organized as follows. Section 2 lists the basic equations used to describe Landau damping. This includes the Vlasov equation, Gauss’ law, and linearizing those equations. Section 3 contains the derivation of a nonlinear equation for the dispersion relation, . Numerical and analytical solutions of this nonlinear relation are discussed in Section 4 and Section 5, respectively. Finally, Section 6 discusses and summarizes the findings.
2. Basic Equations
In order to describe the statistical behavior of a physical system not in a state of equilibrium the Boltzmann equation is used. Let us assume that the plasma electrons are described via the distribution function which depends on position, , and velocity, , of the particles, as well as the time, t. Furthermore, the considered particles experience an external force, , and collisions. With the help of Liouville’s theorem [12], one finds:
where describes the collisions. For the total time-derivative of the distribution function,
can be used. Here, the dot defines time derivative.
Equations (8) and (9) can be combined to find the Boltzmann equation. The collisionless Boltzmann equation, on the other hand, is given by
In what follows, only this collisionless case is considered. Furthermore, is replaced by using Newton’s second law, , to find:
with m being the particle mass.
For the case considered in this paper, where describes Coulomb interactions, Equation (11) is usually called the Vlasov equation [7]. The Vlasov equation, discussed here, is commonly used to investigate the interaction between particles and fields. In the case of Landau damping, this equation describes the interaction between Langmuir waves and the electrons of the plasma. However, the Vlasov equation is also used as a starting point to describe the interaction between magnetic turbulence and energetic particles such as cosmic rays (see, e.g., [13,14,15]).
For the investigations, presented here, it is sufficient to consider the one-dimensional case for which the Vlasov equation reads:
In the case considered, the force is just the electric force and, thus,
can be used, where q is the electric charge of the particle. The electric field, , therein is the wave field of the plasma wave. Using this in Equation (12) yields:
In order to solve the Vlasov equation, a perturbation approach of the form,
is employed.
Here, is the unperturbed distribution often assumed to be Maxwellian (see Section 3 below). The quantity describes the fluctuations corresponding to the deviations from the unperturbed distributions. These fluctuations are a consequence of the interactions with the electric field of the wave and are assumed to be small so that the perturbation approach can be justified. Using Equation (15) in Equation (14) yields in first-order:
Equation (16) is called the linearized Vlasov equation. As a second equation, Gauss’ law,
is employed.
Note that SI units are used here rather than Gaussian or cgs units. In the one-dimensional case considered, Equation (17) becomes:
where the electric charge density is replaced by the velocity integral over the fluctuations . In order to solve Vlasov and Gauss equations, a Fourier ansatz,
is used.
The first equation can be rearranged to read:
Using this in Equation (21) yields:
As the electric field does not depend on the particle velocity v, one can cancel in the latter equation. Therefore, the following dispersion relation,
is obtained.
The function therein corresponds to the unperturbed particle density per volume. In the following, the replacement is made and the plasma frequency, defined via Equation (2), is used. This leads Equation (24) to be rewritten as:
Note, is now the number of particles per velocity meaning that due to normalization, one needs:
which fixes constants in the distribution function .
3. The Dispersion Relation
Let us now discuss the obtained dispersion relation as given by Equation (25). In order to evaluate this further, the Maxwellian distribution,
is employed.
The latter function is visualized via Figure 1. Note, this is a Maxwellian distribution in one dimension and, therefore, it is in coincidence with a Gaussian distribution. The used form is correctly normalized meaning that it satisfies Equation (26). Furthermore, the electron thermal speed, given by Equation (3), is used. From Equation (27), it follows that:
Using this, Equation (25) reads:
Note that it looks like there is a singularity at . However, this is not so as long as is a complex number with non-vanishing imaginary part.
The aim here is to derive the dispersion relation . To this end, let us rewrite the integral occurring in Equation (29) as:
To continue,
is considered.
The integral on the left-hand-side of Equation (31) is a usual Gaussian integral which can be solved via
The second integral on the right-hand-side of Equation (31) is the desired integral as defined via Equation (30).
Thus, Equation (31) can be rewritten as:
Alternatively, this can be written as;
Therewith the dispersion relation (29) becomes:
In the remaining integral, the substitution,
is employed to derive
To continue, the parameter,
is defined.
Note that the latter parameter is a complex number in the general case. Therewith, one can write Equation (36) as:
In the result obtained, Equation (6) can be now used to finally arrive at
where the integral,
is used.
Let us solve this integral. First, the integral is generalized via
Note, we are looking for . One can derive that
Here, the symmetry of the integral is used and, at the end, one would only need to solve a Gaussian integral. With the help of Equation (32), one finally derives:
Note, here and above, is assumed to be a positive real number. To continue, the result is integrated over :
In the integral therein the substitution is used:
Therewith:
In Appendix A, it is demonstrated that
Furthermore, and, thus, Equation (46) reads:
Then, using the substitution :
The remaining integral corresponds to an imaginary error function (see, e.g., [16]):
Using this in Equation (49) finally yields:
After using Equation (51) in Equation (39), one finds for the dispersion relation:
where the parameter is given by Equation (37). Alternatively, the result obtained can be written as:
Furthermore, the parameter can be rewritten as:
4. Numerical Solution for the General Case
Instead of dealing with Equation (53), let us return and use Equation (39) as starting point for numerical investigations. Equation (48) can be written as:
where
is used.
Substituting these equations into Equation (39) gives:
For numerical investigations, it is useful to define the dimensionless quantities,
so that the parameter , defined via Equation (54), becomes:
Therewith, Equation (57) can be written as:
The solution of the latter equation is the complex quantity y as a function of the real variable x. It is straightforward to solve Equation (60) by using a standard Newton-solver in combination with MATLAB; the details are given in Appendix B. The numerical solutions are shown in Figure 2, where the analytical solution obtained for asymptotic limits is also given. This analytical solution is derived in Section 5 below.
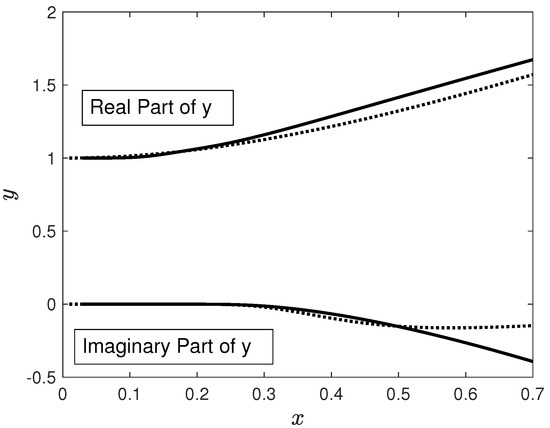
Figure 2.
Visualized is the numerical solution of Equation (60). Shown are the real part of (top two lines) as well as its imaginary part (bottom two lines) versus the variable . Compared are the numerical solution (solid lines) with the analytical limits (dotted lines) given by Equations (82) and (91), respectively. ωp is the plasma frequency and λD is the Debye length.
5. Analytical Solutions in Asymptotic Limits
In Section 3, the nonlinear Equation (53) was derived and solved numerically. In order to obtain pure analytical solutions, we consider the case of
meaning that the phase speed of the wave, , is assumed to be much larger than the electron thermal speed, . Due to this assumption, one can employ the following asymptotic expansion (see, e.g., [16]),
With the help of Equation (54) this equation can be rewritten as:
In the following, it is assumed that and are small. As corresponds to the imaginary part of , it describes the damping of the Langmuir wave. Thus, the assumption of small and corresponds to weak damping.
To continue, let us Taylor-expand and take into account only terms linear in :
Using the above equations in Equation (65) yields:
Taking the real part of the latter equation gives:
As soon as is focused on (see, e.g., Equation (61)), the term with the exponential function can be neglected. Thus, in the lowest-order:
Due to Equation (37), one gets:
Furthermore, one finds
as a consequence of Equation (6).
Combining all the above findings, allows us to finally derive from Equation (71):
This can be rewritten as:
which can be understood as a quadratic equation for . It has the solutions
Therein, taking the plus-sign and employing Equation (6), one finds:
So far it was assumed that the restriction, given by Equation (61), is valid. Furthermore, the damping effect was assumed to be small meaning that is small. This essentially means that . Furthermore, the condition, given by Equation (61), turns into
It is clear that this can only be valid if
One can find that the result obtained concides with the plasma wave dispersion relation of Equation (7). In dimensionless quantities (58):
Considering the imaginary part of Equation (69), one finds:
This equation can be rearranged:
As soon as :
From Equation (54) it follows that
Therefore, one finds:
Combining Equation (81) and condition (80), one gets in the lowest order. Therewith, the result obtained for reads:
In dimensionless quantities (58), one gets:
Equations (82) and (91) are visualized in Figure 2 together with the numerical solution discussed in Section 4. One can immediately see that the agreement between the numerical solution and the analytical one is much better for smaller values of x corresponding to small wave numbers. The assumption of small wave numbers is part of the analytical calculation presented above (see, e.g., Equation (80)) and, therefore, the deviation between the analytical and numerical solutions for larger wave numbers was predictable.
Note that as soon as the case is considered, one can further approximate Equation (90) by
which is in perfect agreement with Equation (17) of [6]. A discussion about the validity and possible improvements of asymptotic formulas for the Landau damping rates of electrostatic waves can be found in [17].
6. Discussion and Conclusions
The derivations and discussions, presented in the current paper, are based on lecture notes I have developed for a course about magnetohydrodynamics. The aim was to obtain a mathematically simpler description of Landau damping compared to what Landau originally developed in his seminal paper [6]. This means, in particular, that tools of complex analysis, such as contour integrals, are avoided and one just solves standard integrals in combination with imaginary error functions.
Although using methods of complex analysis was avoided throughout the current paper, one still arrives at the correct Langmuir dispersion relation as given by Equation (81) as well as the correct Landau damping rate as given by Equation (90). These results were obtained analytically by employing Equations (61) and (80). The more general dispersion relation is given by Equation (57) corresponding to a nonlinear equation. However, it can be solved by using standard tools of computational physics. All findings are visualized in Figure 2.
Although the main intention behind the current paper was to present a simpler derivation of known results, Equation (53) is quite general since it does not require to consider asymptotic limits. Therefore, the method, proposed in this paper, could lead to an improved understanding of Landau damping in some other limits. Furthermore, it could be possible that the method developed here can be used to explore other effects such as the dispersion relation of electron-acoustic waves.
It needs to be emphasized that the exploration of Landau damping is still an active field of research pursued both in mathematics and in theoretical physics. A comprehensive overviews of Landau damping which includes some historical remarks, derivations, and mathematical details can be found in [18,19].
Funding
This research was funded by the Natural Sciences and Engineering Research Council (NSERC) of Canada.
Data Availability Statement
This study does not report any data.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Some Mathematical Details
Equation (41) can be written as
Note that is a complex number, given by Equation (37), and is a positive real number. Equation (A1) can be rewritten as:
where the symmetry properties of one of the integrals is used. In the limit ,
The remaining integral can be solved via substitution:
and then,
in the integral. Furthermore, for the inverse hyperbolic tangent function, the relations,
and
are employed. Therefore, one gets:
and, thus:
Appendix B. The Newton-Solver
The task is to solve the nonlinear relation given by Equation (60). For convenience, let us write this equation down again:
In the latter, the function,
is used, as well as:
Therewith, one can write:
The nonlinear relation above is solved via a standard Newton method; see, e.g., in [20]. The task is to find y for a given x; therefore, it is needed to compute y for each x. This y is obtained via the iteration method,
where, in the case considered here,
Furthermore, one also needs to compute the derivative of the latter function with respect to y. One derives:
where
is used.
References
- Tonks, L.; Langmuir, I. Oscillations in ionized gases. Phys. Rev. 1929, 33, 195–210. [Google Scholar] [CrossRef]
- Bohm, D.; Gross, E.P. Theory of plasma oscillations. A. Origin of medium-like behavior. Phys. Rev. 1949, 75, 1851–1864. [Google Scholar] [CrossRef]
- Bohm, D.; Gross, E.P. Theory of plasma oscillations. B. Excitation and damping of oscillations. Phys. Rev. 1949, 75, 1864–1876. [Google Scholar] [CrossRef]
- Bohm, D.; Gross, E.P. Effects of plasma boundaries in plasma oscillations. Phys. Rev. 1950, 79, 992–1001. [Google Scholar] [CrossRef]
- Tsurutani, B.; Lakhina, G. Some basic concepts of wave-particle interactions in collisionless plasmas. Rev. Geophys. 1997, 35, 491–502. [Google Scholar] [CrossRef]
- Landau, L. On the vibration of the electronic plasma. J. Phys. (USSR) 1946, 10, 25–34, Reprinted in Collected Papers of L.D. Landau; Ter Haar, D.; Pergamon Press. Ltd.: Oxford, UK; 1965, pp. 445–460. [Google Scholar] [CrossRef]
- Vlasov, A.A. On vibration properties of electron gas. Zh. Exp. Teor. Fiz. 1938, 8, 291. (In Russian); English Translation in Sov. Phys. Uspekhi. 1968, 10, 721–733 [Google Scholar] [CrossRef]
- Schlickeiser, R.; Fichtner, H.; Kneller, M. Revised Landau damping rates of magnetohydrodynamics waves in hot magnetized equilibrium plasmas and its consequences for cosmic ray transport in the interplanetary medium. J. Geophys. Res. 1997, 102, 4725–4739. [Google Scholar] [CrossRef] [Green Version]
- van Kampen, N.G. On the theory of stationary waves in plasma. Physica 1955, 21, 949–963. [Google Scholar] [CrossRef]
- Case, K.M. Plasma oscillations. Ann. Phys. 1959, 7, 349–364. [Google Scholar] [CrossRef] [Green Version]
- Krall, N.A.; Trivelpiece, A.W. Principles of Plasma Physics; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Liouville, J. Sur la theorie de la variation des constantes arbitraires. J. Math. Pures Appl. 1838, 3, 342–349. [Google Scholar]
- Schlickeiser, R. Cosmic Ray Astrophysics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Shalchi, A. Nonlinear Cosmic Ray Diffusion Theories; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef] [Green Version]
- Zank, G.P. Transport Processes in Space Physics and Astrophysics: Lecture Notes in Physics; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- McKinstrie, C.J.; Giacone, R.E.; Startsev, E.A. Formulas for the Landau damping rates of electrostatic waves. Phys. Plasmas 1999, 6, 463–466. [Google Scholar] [CrossRef] [Green Version]
- Ryutov, D.D. Landau damping: Half a century with the great discovery. Plasma Phys. Control. Fusion 1999, 41, A1–A12. [Google Scholar] [CrossRef]
- Mouhot, C.; Villani, C. On Landau damping. Acta Math. 2011, 207, 29–201. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).