Adaptive Synchronization of Fractional-Order Complex-Valued Chaotic Neural Networks with Time-Delay and Unknown Parameters
Abstract
:1. Introduction
- (i)
- Most of the existing studies on the synchronization methods of fractional-order neural networks are about fractional-order real-valued neural networks. On the other hand, existing studies on fractional-order complex-valued neural networks are on the known parameters or with no time-delay or without identifying the parameters.
- (ii)
- A new adaptive controller and update laws are designed to synchronize the driving and response systems. This is the first study of synchronization of fractional-order complex-valued neural networks with time-delay and unknown complex parameters.
- (iii)
- Compared with previous synchronization models of fractional-order complex neural networks, the model proposed in this paper is more tractable and easier to be implemented in practical systems.
- (iv)
- For fractional-order complex neural networks with known parameters and time-delay or known parameters without time-delay, the synchronization model proposed in this paper is also applicable, and only the control strategies need to be adjusted accordingly.
- (v)
- This paper proposes the novel perspective that chaos occurs in fractional-order complex-valued neural networks as long as the parameters are suitable, and two new FOCVCNNs are given to broaden the application of fractional-order complex-valued neural networks.
2. Preliminaries
3. Main Results
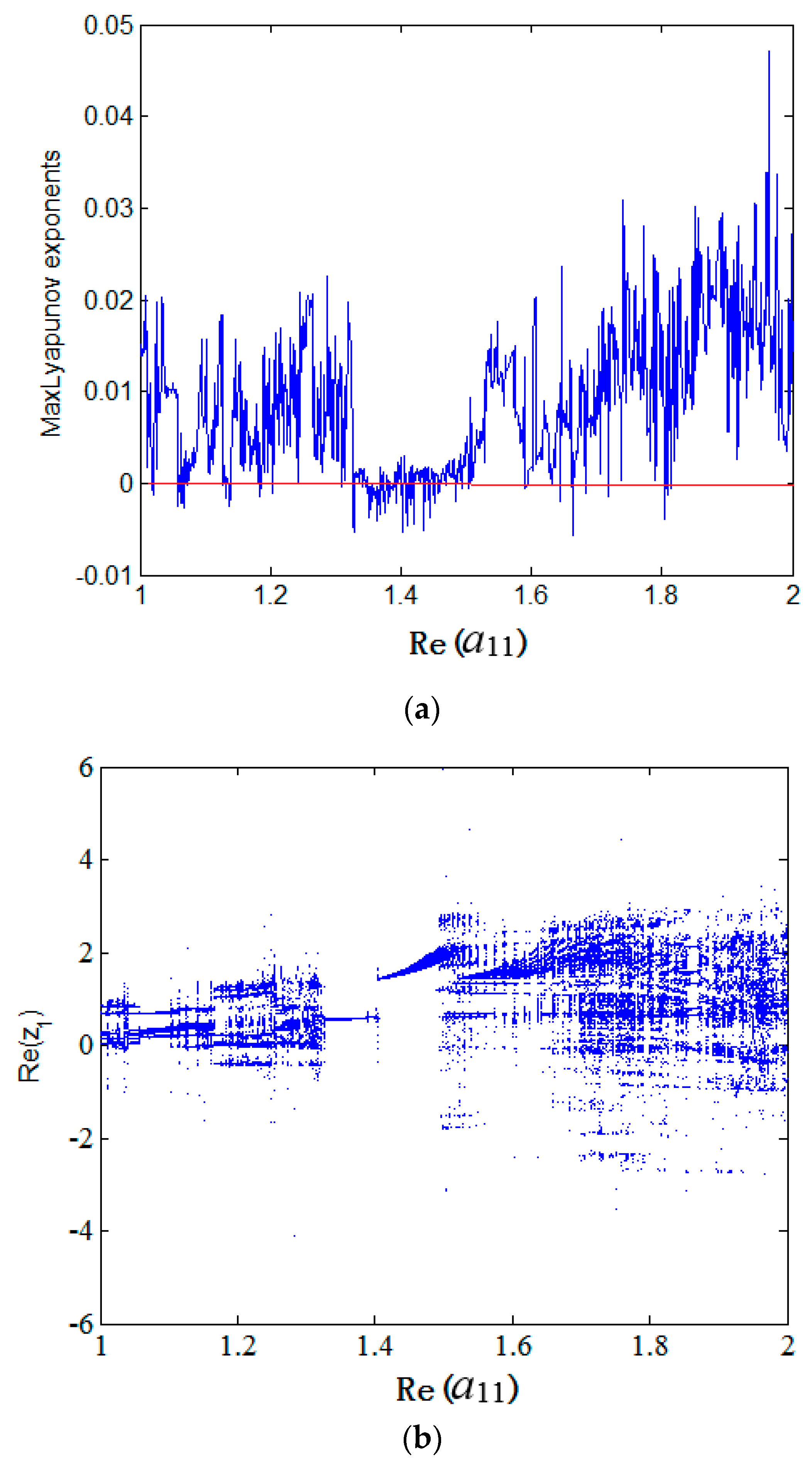
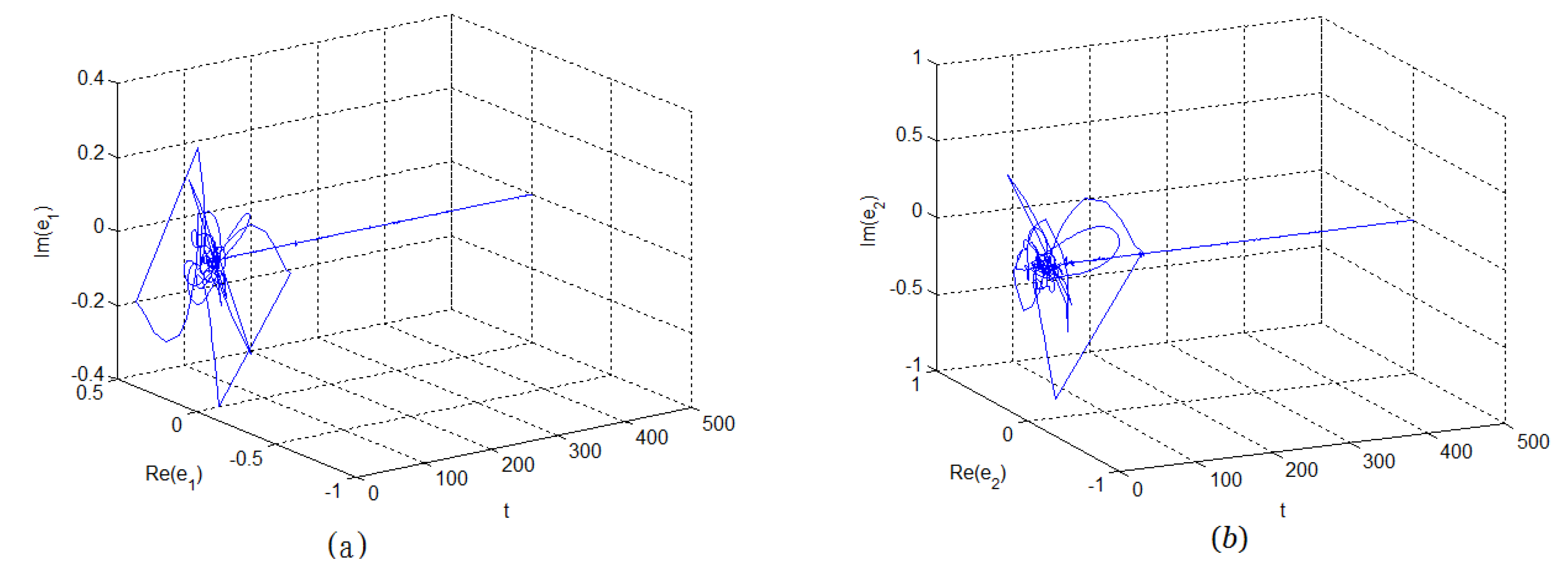
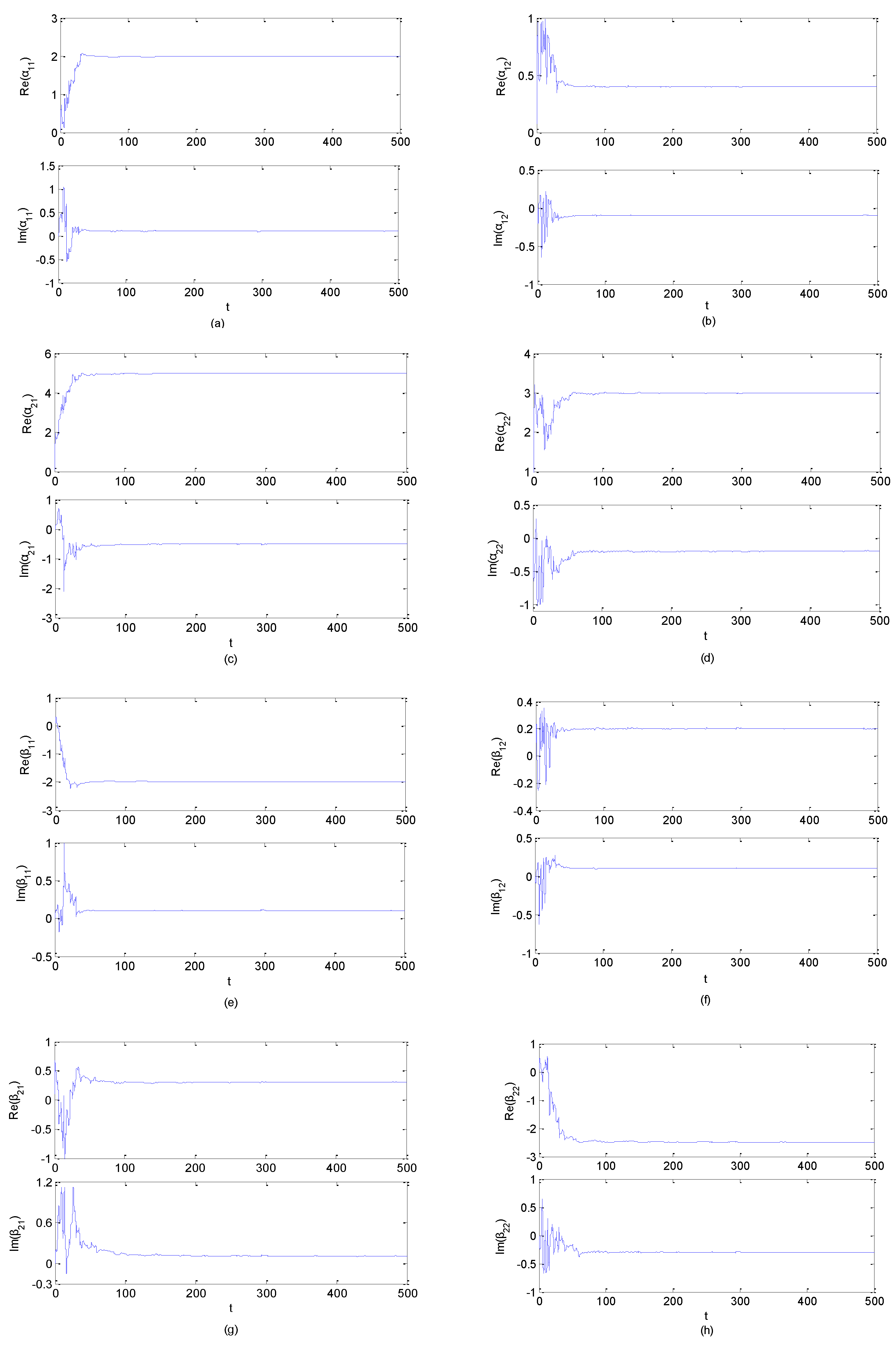
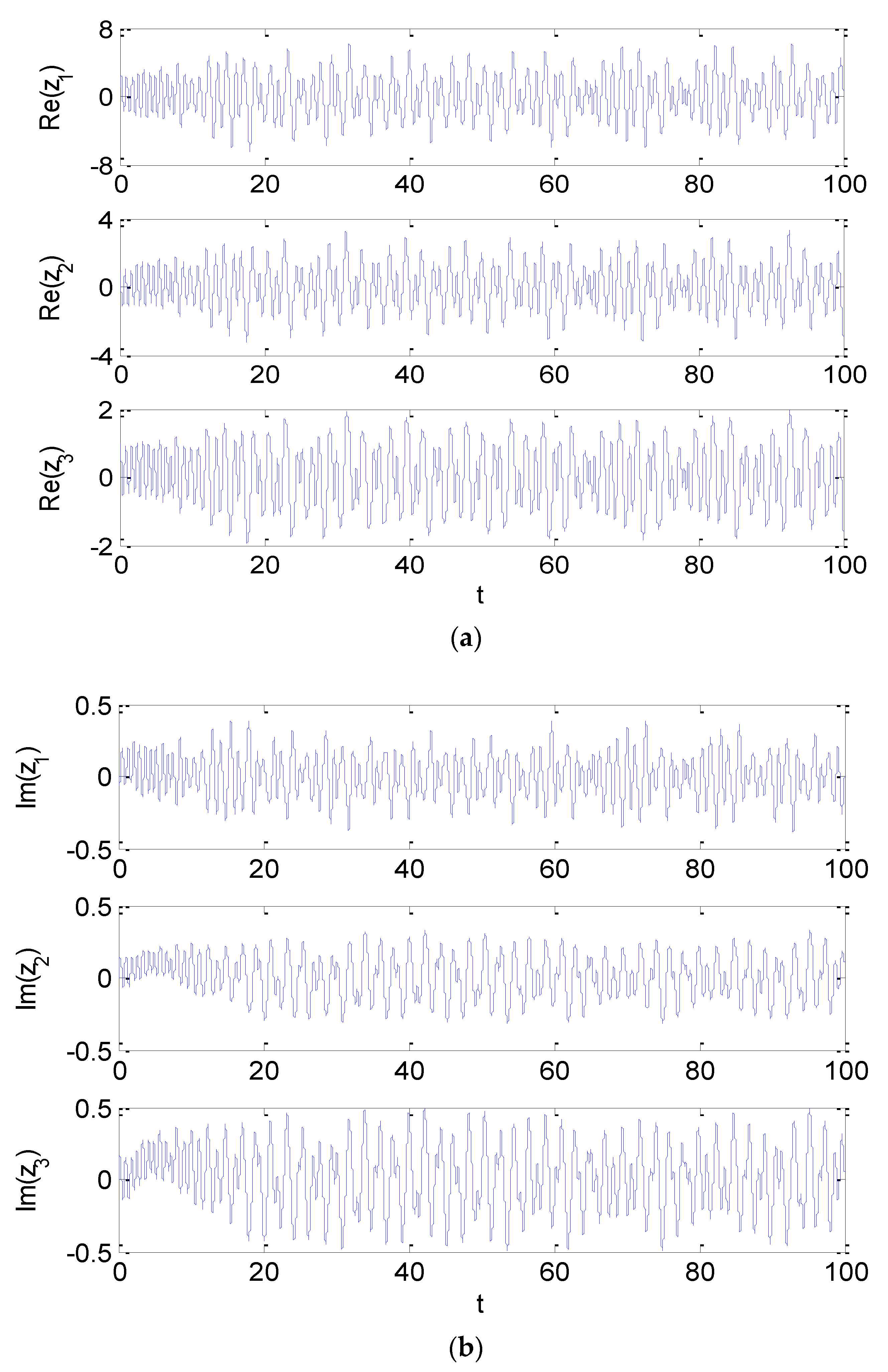
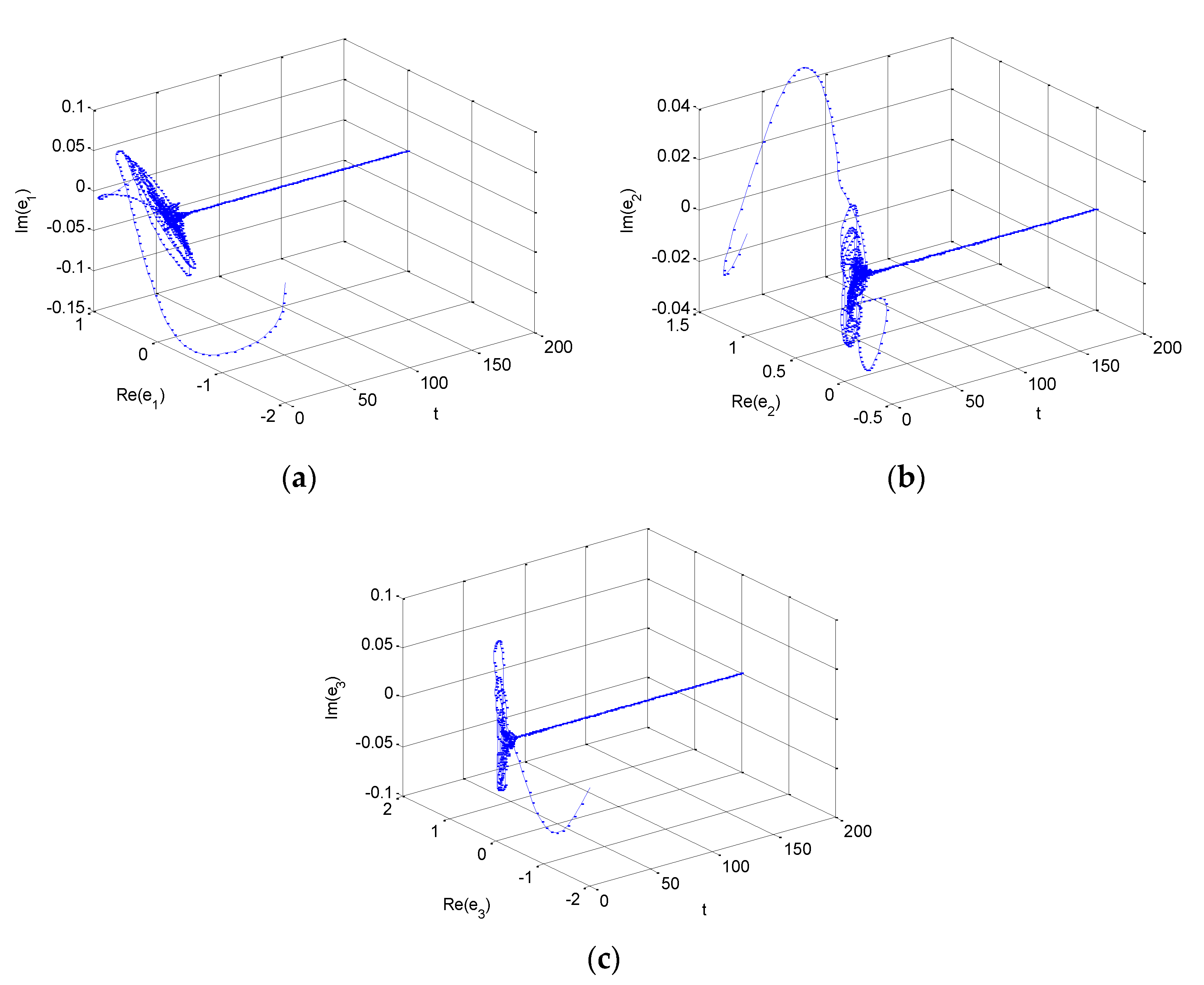
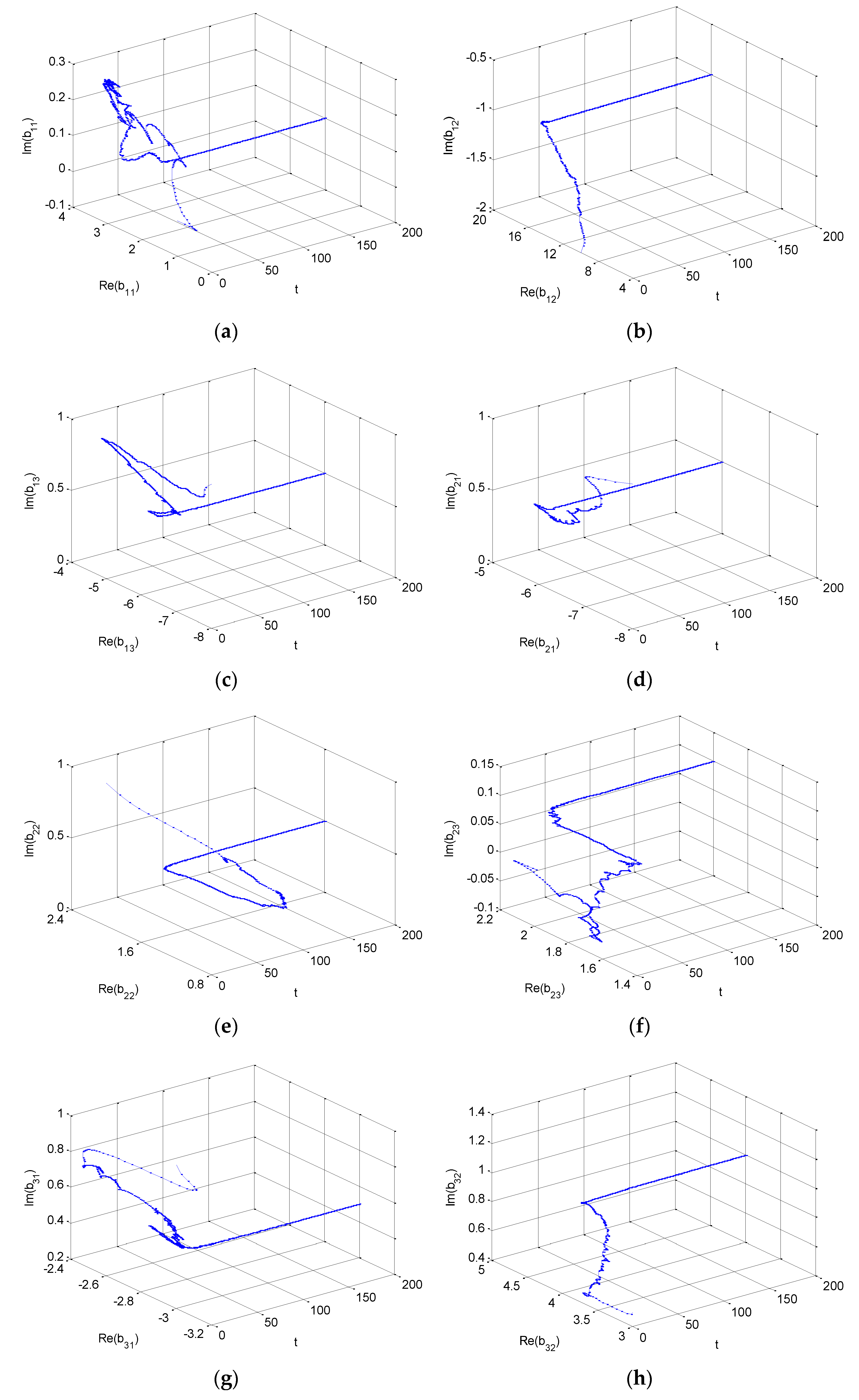
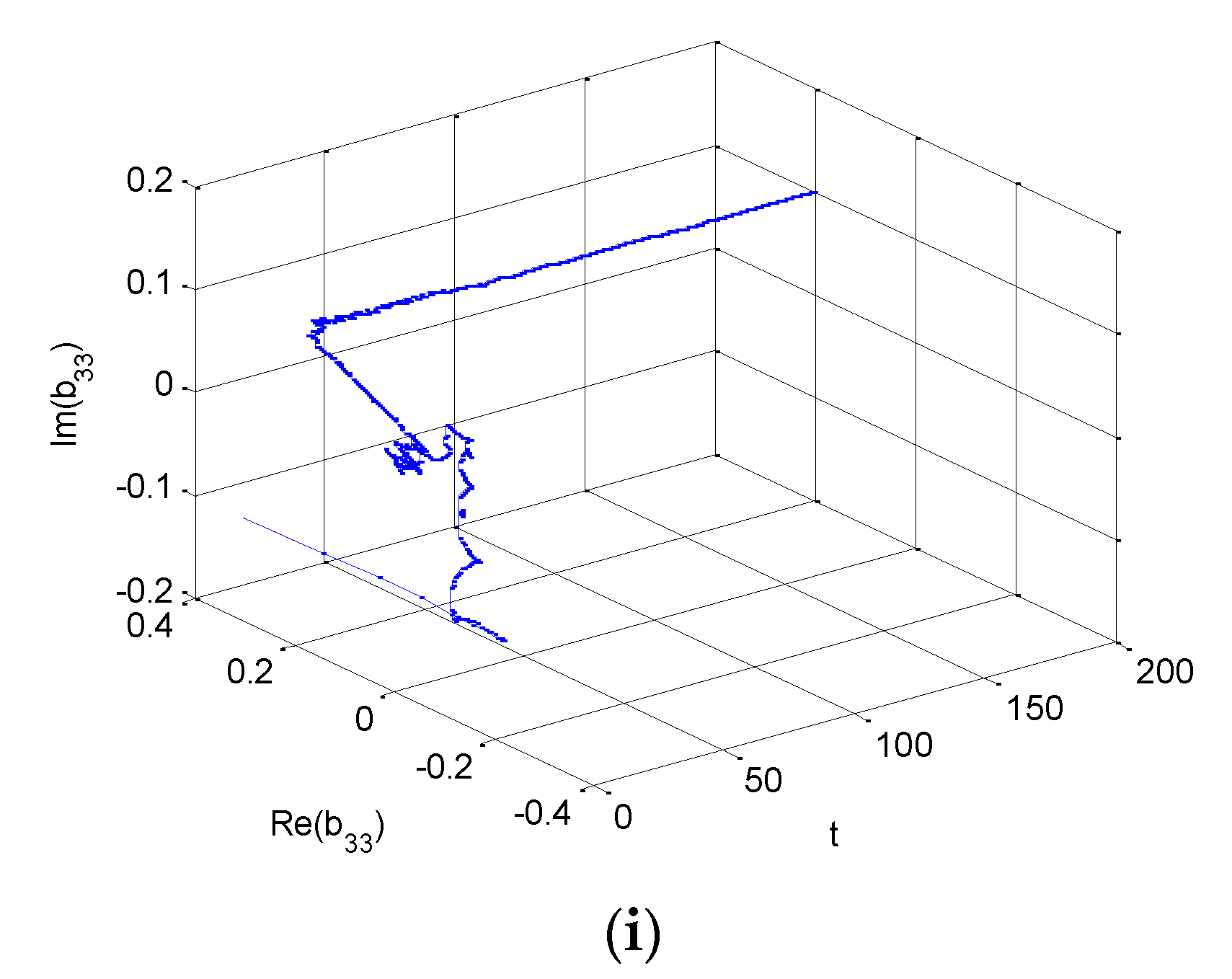
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nitta, T. Orthogonality of decision boundaries of complex-valued neural networks. Neural Comput. 2004, 16, 73–97. [Google Scholar] [CrossRef]
- Hirose, A. Complex-Valued Neural Networks: Theories and Applications; World Scientific Publishing Company: Singapore, 2003. [Google Scholar] [CrossRef] [Green Version]
- Tanak, G.; Aihara, K. Complex-valued multistate associative memory with nonlinear multilevel functions for gray-level image reconstruction. IEEE Trans. Neural Netw. 2009, 20, 1463–1473. [Google Scholar] [CrossRef]
- Amin, M.F.; Murase, K. Single-layered complex-valued neural network for real-valued classification problems. Neurocomputing 2009, 72, 945–955. [Google Scholar] [CrossRef] [Green Version]
- Rao, V.S.H.; Murthy, G. Global dynamics of a class of complex valued neural networks. Int. J. Neural Syst. 2008, 18, 165–171. [Google Scholar]
- Zhou, W.; Zurada, J.M. Discrete-time recurrent neural networks with complex-valued linear threshold neurons. IEEE Trans. Circuits Syst. II Express Briefs 2009, 56, 669–673. [Google Scholar] [CrossRef]
- Duan, C.; Song, Q. Boundedness and stability for discrete-time delayed neural network with complex-valued linear threshold neurons. Discret. Dyn. Nat. Soc. 2010, 19, 368–379. [Google Scholar] [CrossRef]
- Bohner, M.; Rao, V.S.H.; Sanyal, S. Global stability of complex-valued neural networks on time scales. Differ. Equ. Dyn. Syst. 2011, 19, 3–11. [Google Scholar] [CrossRef]
- Zeng, X.; Li, C.; Huang, T.; He, X. Stability analysis of complex-valued impulsive systems with time delay. Appl. Math. Comput. 2015, 256, 75–82. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.H.; Cao, J. Synchronization of fractional-order complex-valued neural networks with time delay. Neural Netw. 2016, 81, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Song, Q. Boundedness and complete stability of complex-valued neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1227–1238. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhang, H.; Wang, Z. Multistability of complex-valued recurrent neural networks with real-imaginary-type activation functions. Appl. Math. Comput. 2014, 229, 187–200. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Li, Y.; Shen, H.; Lu, J. Hopf bifurcation analysis of a complex-valued neural network model with discrete and distributed delays. Appl. Math. Comput. 2018, 330, 152–169. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, C.; Chen, B. Global stability criterion for delayed complex-valued recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1704–1708. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Global stability of complex-valued recurrent neural networks with time-delays. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 853–865. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Zhang, J.; Shi, J. Exponential stability of complex-valued neural networks with mixed delays. Neurocomputing 2014, 128, 483–490. [Google Scholar] [CrossRef]
- Wan, P.; Jian, J. Global Mittag-Leffler boundedness for fractional-order complex-valued Cohen-Grossberg neural networks. Neural Process. Lett. 2019, 49, 121–139. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Huang, T.; Song, Q.; Huang, J. Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays. Chaos Soliton Fractal 2018, 110, 105–123. [Google Scholar] [CrossRef]
- Lee, D.-L.; Wang, W.-J. A multivalued bidirectional associative memory operating on a complex domain. Neural Netw. 1998, 11, 1623–1635. [Google Scholar] [CrossRef]
- Bao, H.; Cao, J. Projective synchronization of fractional-order memristor-based neural networks. Neural Netw. 2015, 63, 1–9. [Google Scholar] [CrossRef]
- Bao, H.; Park, J.; Cao, J. Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 2015, 82, 1343–1354. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Z.; Jiang, P. Global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 2014, 51, 1–8. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Song, Q.; Huang, T.; Chen, X. Mittag–Leffler stability analysis on variable-time impulsive fractional-order neural networks. Neurocomputing 2016, 207, 276–286. [Google Scholar] [CrossRef]
- Ding, Z.; Shen, Y.; Wang, L. Global Mittag–Leffler synchronization of fractional-order neural networks with discontinuous activations. Neural Netw. 2016, 73, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Velmurugana, G.; Rakkiyappana, R.; Vembarasan, V.; Cao, J.; Alsaedi, A. Dissipativity and stability analysis of fractional-order complex-valued neural networks with time delay. Neural Netw. 2016, 86, 42–53. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Song, Q.K.; Zhao, Z.J. Stability analysis of fractional-order complex-valued neural networks with both leakage and discrete delays. Appl. Math. Comput. 2017, 298, 296–309. [Google Scholar] [CrossRef]
- Wang, L.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F.E. Global asymptotic stability of impulsive fractional-order complex-valued neural networks with time delay. Neurocomputing 2017, 243, 49–59. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Velmurugan, G.; Cao, J. Stability analysis of fractional-order complex-valued neural networks with time delays. Chaos Solitons Fractals 2015, 78, 297–316. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Velmurugan, G.; Cao, J. Finite-time stability analysis of fractional-order complex-valued memristor-based neural networks with time delays. Nonlinear Dyn. 2014, 78, 2823–2836. [Google Scholar] [CrossRef]
- Chang, W.; Zhu, S.; Li, J.; Sun, K. Global Mittag–Leffler stabilization of fractional-order complex-valued memristive neural networks. Appl. Math. Comput. 2018, 338, 346–362. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, S. Finite-time projective synchronization of fractional-order complex-valued memristor-based neural networks with delay. Chaos Solitons Fractals 2019, 128, 176–190. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Lu, J.; Li, Y. Adaptive Synchronization of Fractional-Order Complex-Valued Neural Networks with Discrete and Distributed Delays. Entropy 2018, 20, 124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niamsup, P.; Botmart, T.; Weera, W. Modified function projective synchronization of complex dynamical networks with mixed time-varying and asymmetric coupling delays via new hybrid pinning adaptive control. Adv. Differ. Equ. 2017, 1, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Chartbupapan, W.; Bagdasar, O.; Mukdasai, K. A novel delay-dependent asymptotic stability conditions for differential and Riemann-Liouville fractional differential neutral systems with constant delays and nonlinear perturbation. Mathematics 2020, 8, 82. [Google Scholar] [CrossRef] [Green Version]
- Dai, X.; Li, X.; Gutiérreze, R.; Guo, H. Explosive synchronization in populations of cooperative and competitive oscillators. Chaos Solitons Fractals 2020, 132, 109589. [Google Scholar] [CrossRef]
- Dai, X.; Li, X.; Jia, D.; Perc, M.; Manshour, P.; Wang, Z.; Boccaletti, S. Discontinuous Transitions and Rhythmic States in the D-Dimensional Kuramoto Model Induced by a Positive Feedback with the Global Order Parameter. Phys. Rev. Lett. 2020, 125, 194101. [Google Scholar] [CrossRef]
- Arslan, E.; Narayanan, G.; Ali, M.S.; Arik, S.; Saroha, M. Controller design for finite-time and fixed-time stabilization of fractional-order memristive complex-valued BAM neural networks with uncertain parameters and time-varying delays. Neural Netw. 2020, 130, 60–74. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.X.; Liu, Y.L. A new Barbalat’s lemma and Lyapunov stability theorem for fractional order systems. In Proceedings of the 29th Chinese control and decision conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 3676–3681. [Google Scholar]
- Zhang, R.X.; Liu, Y.L.; Yang, S.P. Adaptive synchronization of fractional-order complex chaotic system with unknown complex parameters. Entropy 2019, 21, 207. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.X.; Feng, S.W.; Yang, S.P. Complex Modified Projective Synchronization of Fractional-order Complex-Variable Chaotic System with Unknown Complex Parameters. Entropy 2019, 21, 407. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; Available online: https://www.sciencedirect.com/bookseries/mathematics-in-science-and-engineering/vol/198/suppl/C (accessed on 6 October 2021).
- Quan, X.; Zhuang, S.; Liu, S.; Xiao, J. Decentralized adaptive coupling synchronization of fractional-order complex-variable dynamical networks. Neurocomputing 2016, 186C, 119–126. [Google Scholar] [CrossRef]
- Li, H.L.; Hu, C.; Cao, J.D. Quasi-projective and complete synchronization of fractional-order complex-valued neural networks with time delays. Neural Netw. 2019, 118, 102–109. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Chen, G.R.; Fu, X.C. Synchronization of a network coupled with complex-variable chaotic systems. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 023127. [Google Scholar] [CrossRef] [PubMed]
- Kai, D.; Ford, D.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Gu, Y.; Yu, Y.; Wang, H. Synchronization-based parameter estimation of fractional-order neural networks. Phys. A Stat. Mech. Appl. 2017, 483, 351–361. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]


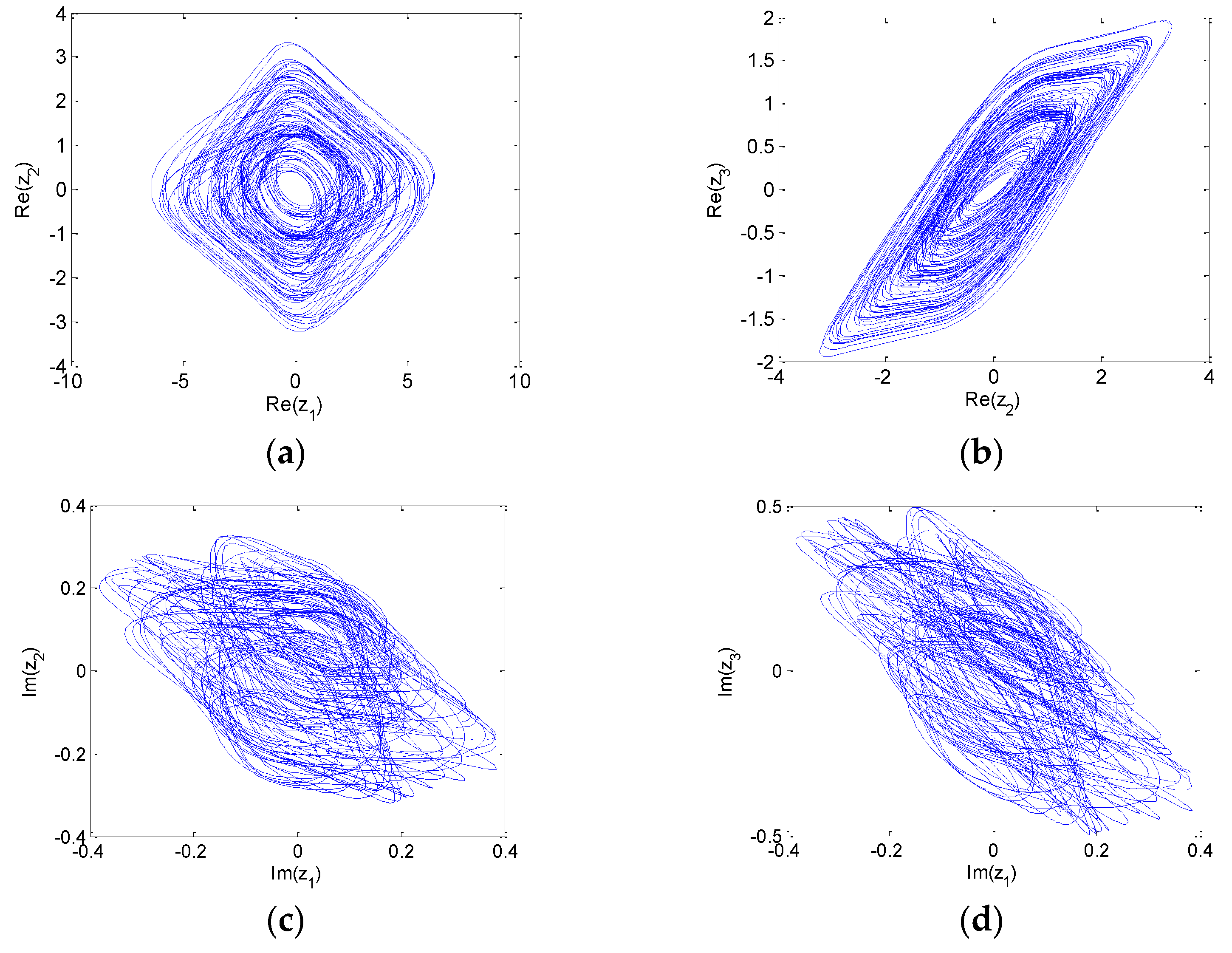
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, R.; Yang, S. Adaptive Synchronization of Fractional-Order Complex-Valued Chaotic Neural Networks with Time-Delay and Unknown Parameters. Physics 2021, 3, 924-939. https://doi.org/10.3390/physics3040058
Li M, Zhang R, Yang S. Adaptive Synchronization of Fractional-Order Complex-Valued Chaotic Neural Networks with Time-Delay and Unknown Parameters. Physics. 2021; 3(4):924-939. https://doi.org/10.3390/physics3040058
Chicago/Turabian StyleLi, Mei, Ruoxun Zhang, and Shiping Yang. 2021. "Adaptive Synchronization of Fractional-Order Complex-Valued Chaotic Neural Networks with Time-Delay and Unknown Parameters" Physics 3, no. 4: 924-939. https://doi.org/10.3390/physics3040058
APA StyleLi, M., Zhang, R., & Yang, S. (2021). Adaptive Synchronization of Fractional-Order Complex-Valued Chaotic Neural Networks with Time-Delay and Unknown Parameters. Physics, 3(4), 924-939. https://doi.org/10.3390/physics3040058



