A Novel Feature of Valence Quark Distributions in Hadrons
Abstract
:1. Introduction
2. “Height-Position” Correlation of the Peak of the Functions
3. New Relations for Valence PDFs
4. Origin of the Exponential Form of the Height-Position Correlation
5. The -Dependence of at the Vicinity of the Peak
6. Other PDFs and Hadrons
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hen, O.; Weinstein, L.B.; Piasetzky, E.; Miller, G.A.; Sargsian, M.M.; Sagi, Y. Correlated fermions in nuclei and ultracold atomic gases. Phys. Rev. C 2015, 92, 045205. [Google Scholar] [CrossRef] [Green Version]
- Hou, T.J.; Gao, J.; Hobbs, T.J.; Xie, K.; Dulat, S.; Guzzi, M.; Huston, J.; Nadolsky, P.; Pumplin, J.; Schmidt, C.; et al. New CTEQ global analysis of quantum chromodynamics with high-precision data from the LHC. Phys. Rev. D 2021, 103, 014013. [Google Scholar] [CrossRef]
- Dulat, S.; Hou, T.J.; Gao, J.; Guzzi, M.; Huston, J.; Nadolsky, P.; Pumplin, J.; Schmidt, C.; Stump, D.; Yuan, C.P. New parton distribution functions from a global analysis of quantum chromodynamics. Phys. Rev. D 2016, 93, 033006. [Google Scholar] [CrossRef] [Green Version]
- Accardi, A.; Brady, L.T.; Melnitchouk, W.; Owens, J.F.; Sato, N. Constraints on large-x parton distributions from new weak boson production and deep-inelastic scattering data. Phys. Rev. D 2016, 93, 114017. [Google Scholar] [CrossRef] [Green Version]
- Buckley, A.; Ferrando, J.; Lloyd, S.; Nordström, K.; Page, B.; Rüfenacht, M.; Schönherr, M.; Watt, G. LHAPDF6: Parton density access in the LHC precision era. Eur. Phys. J. C 2015, 75, 132. [Google Scholar] [CrossRef] [Green Version]
- Ball, R.D.; Nocera, E.R.; Rojo, J. The asymptotic behaviour of parton distributions at small and large x. Eur. Phys. J. C 2016, 76, 383. [Google Scholar] [CrossRef] [Green Version]
- Lepage, G.P.; Brodsky, S.J. Exclusive processes in perturbative quantum chromodynamics. Phys. Rev. D 1980, 22, 2157. [Google Scholar] [CrossRef] [Green Version]
- Gunion, J.F.; Nason, P.; Blankenbecler, R. Power suppressed contributions to deep inelastic processes. Phys. Rev. D 1984, 29, 2491. [Google Scholar] [CrossRef]
- Leon, C.; Sargsian, M. A non-perturbative model of mean field valence quarks. PoS 2020, LC2019, 056. [Google Scholar] [CrossRef]
- Leon, C.; Sargsian, M. Residual mean field model of valence quarks in the nucleon. arXiv 2012, arXiv:2012.14030. [Google Scholar]
- Weinberg, S. Dynamics at infinite momentum. Phys. Rev. 1966, 150, 1313–1318. [Google Scholar] [CrossRef]
- Sargsian, M.M. New properties of the high-momentum distribution of nucleons in asymmetric nuclei. Phys. Rev. C 2014, 89, 034305. [Google Scholar] [CrossRef] [Green Version]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Ball, R.D.; Bertone, V.; Carrazza, S.; Deans, C.S.; Del Debbio, L.; Forte, S.; Guffanti, A.; Hartland, N.P.; Latorre, J.I.; Rojo, J.; et al. Parton distributions for the LHC Run II. JHEP 2015, 04, 040. [Google Scholar] [CrossRef] [Green Version]
- Alekhin, S.; Blumlein, J.; Moch, S. The ABM parton distributions tuned to LHC data. Phys. Rev. D 2014, 89, 054028. [Google Scholar] [CrossRef] [Green Version]
- Jimenez-Delgado, P.; Reya, E. Delineating parton distributions and the strong coupling. Phys. Rev. D 2014, 89, 074049. [Google Scholar] [CrossRef] [Green Version]
- Ball, R.D.; Bonvini, M.; Rottoli, L. Charm in Deep-Inelastic Scattering. JHEP 2015, 11, 122. [Google Scholar] [CrossRef] [Green Version]
- Accardi, A.; Alekhin, S.; Blümlein, J.; Garzelli, M.V.; Lipka, K.; Melnitchouk, W.; Moch, S.; Owens, J.F.; Plačakytė, R.; Reya, E.; et al. A critical appraisal and evaluation of modern PDFs. Eur. Phys. J. C 2016, 76, 471. [Google Scholar] [CrossRef] [Green Version]
- Altarelli, G.; Ellis, R.K.; Martinelli, G. Leptoproduction and Drell-Yan processes beyond the leading approximation in chromodynamics. Nucl. Phys. B 1978, 143, 521. [Google Scholar] [CrossRef]
- Pumplin, J.; Stump, D.R.; Huston, J.; Lai, H.L.; Nadolsky, P.M.; Tung, W.K. New generation of parton distributions with uncertainties from global QCD analysis. JHEP 2002, 07, 012. [Google Scholar] [CrossRef]
- Barry, P.C.; Sato, N.; Melnitchouk, W.; Ji, C.R. First Monte Carlo global QCD analysis of pion parton distributions. Phys. Rev. Lett. 2018, 121, 152001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dokshitzer, Y.L.; Khoze, V.A.; Mueller, A.H.; Troian, S. Basics of Perturbative QCD; Editions Frontieres: Gif-sur-Yvette, France, 1991. [Google Scholar]
- Ellis, R.K.; Stirling, W.J.; Webber, B.R. QCD and Collider Physics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]

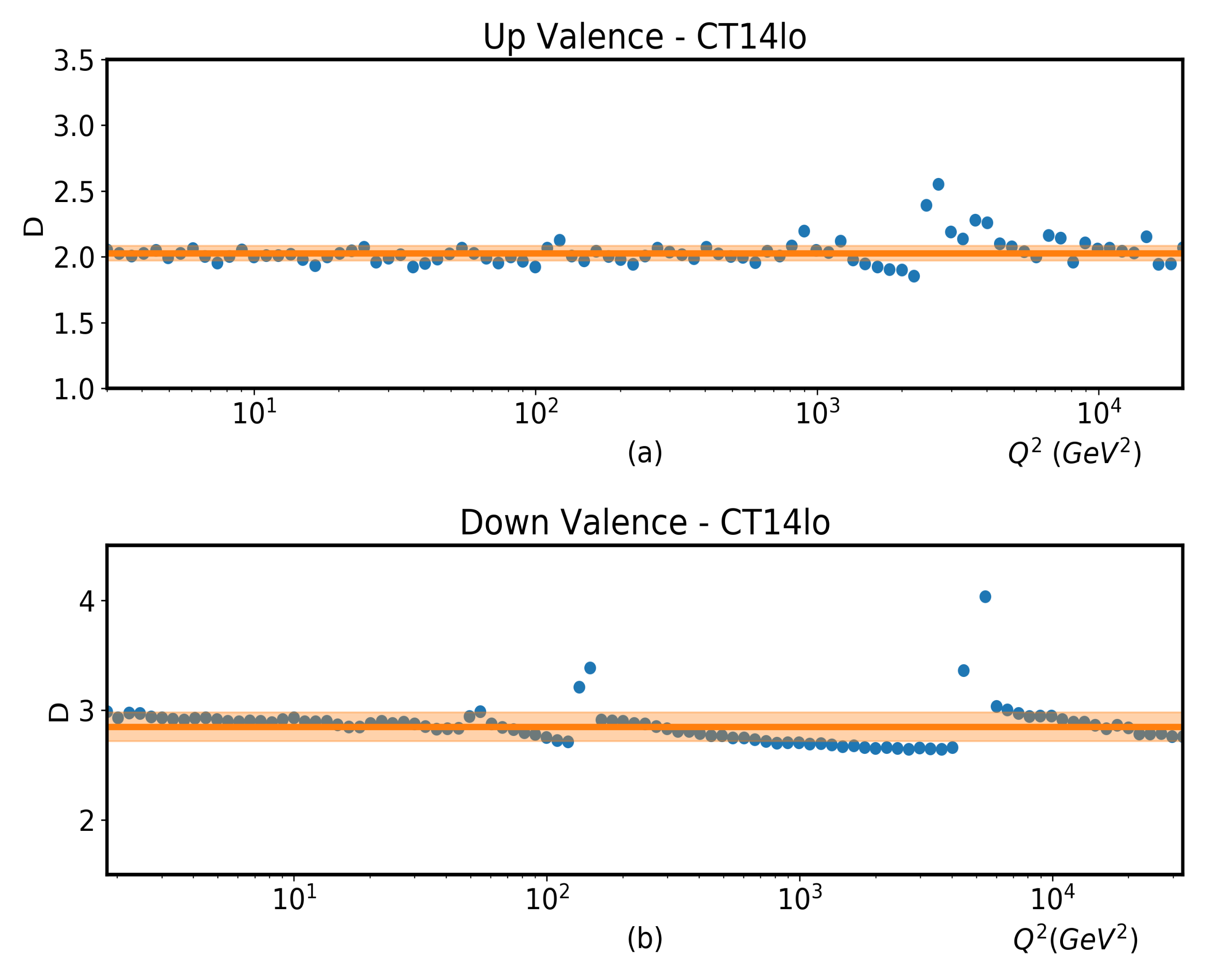

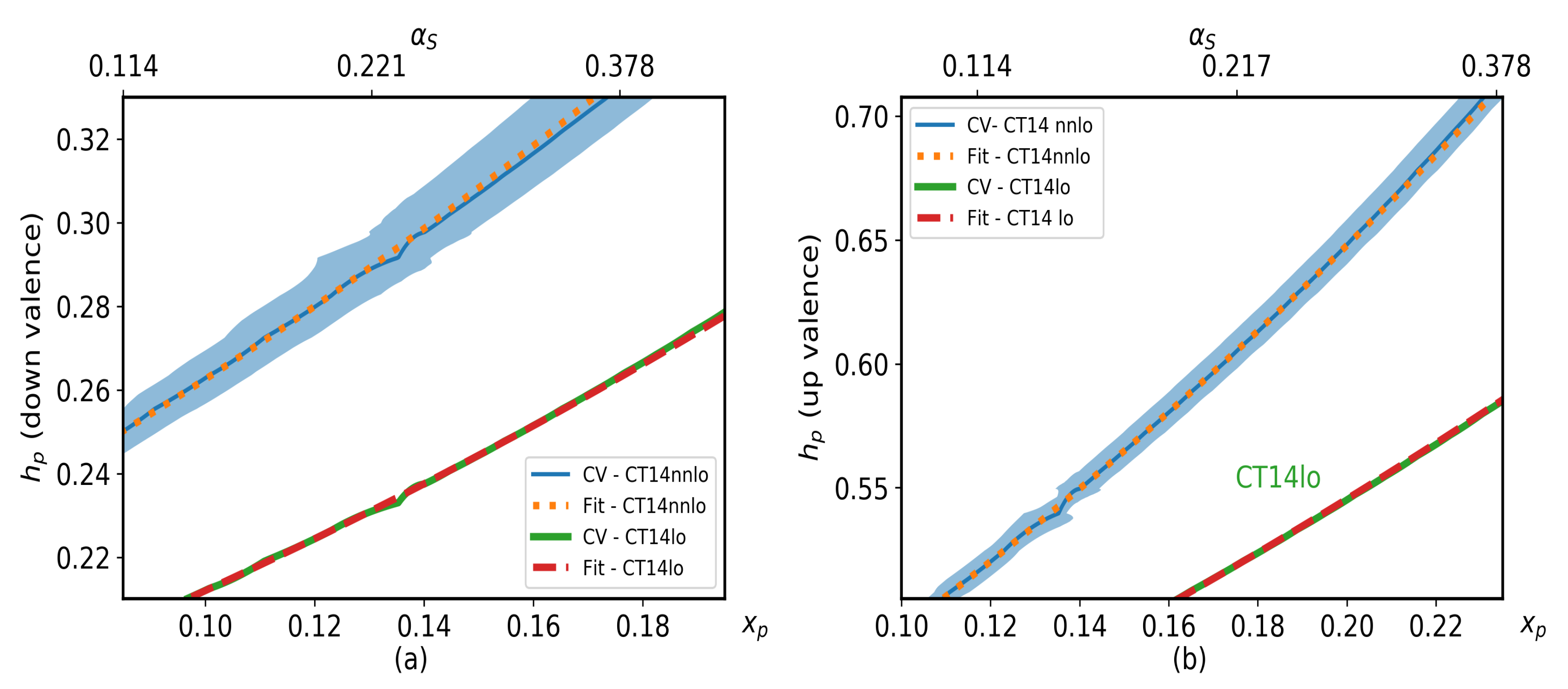
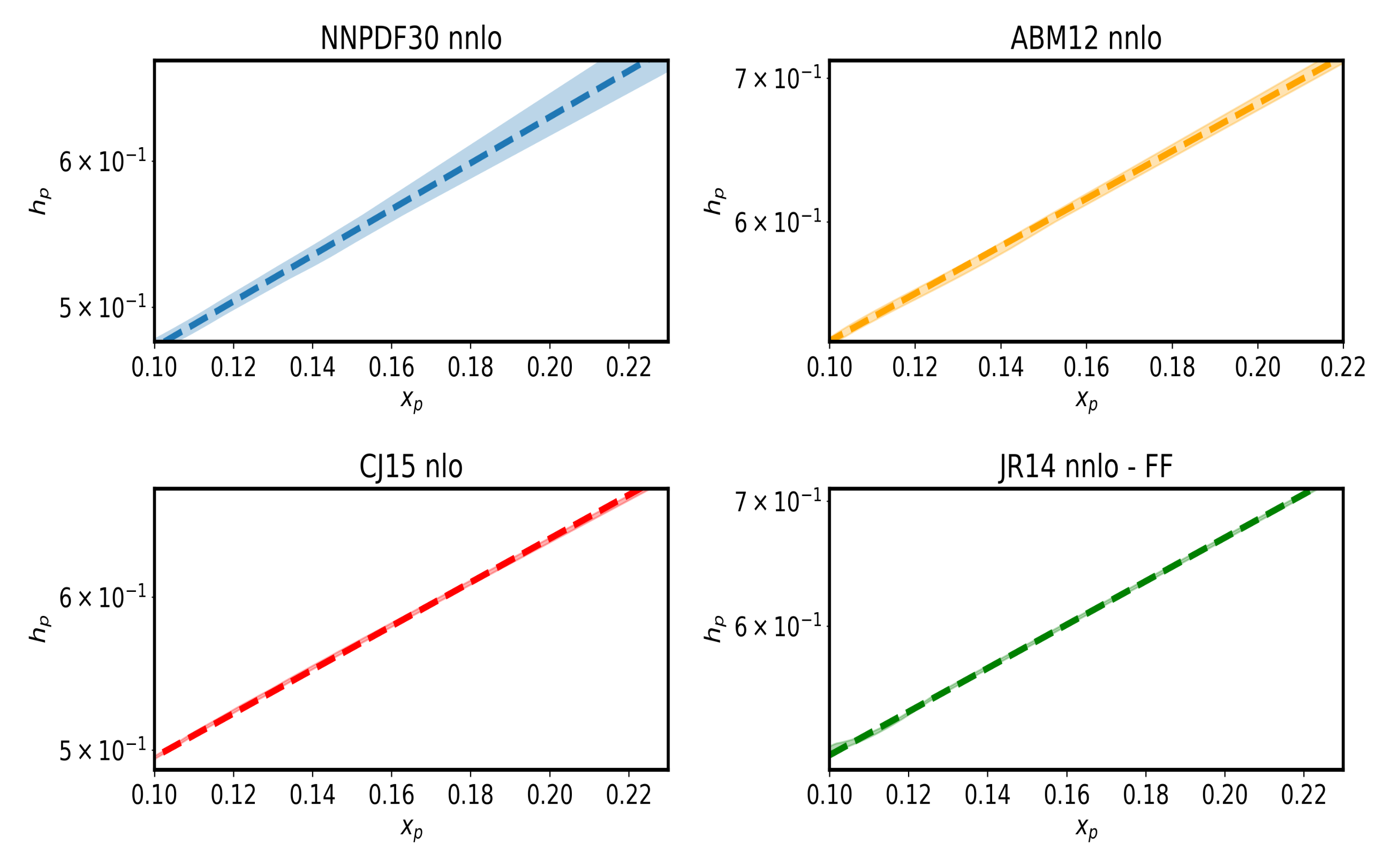


| Distribution | CT14lo | CT14nlo | CT14nnlo |
|---|---|---|---|
| 0.16, 2.8 | 0.19(1), 3.1(1) | 0.193(6), 3.1(2) | |
| 0.36, 2.02 | 0.37(1), 2.71(9) | 0.37(1), 2.7(1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon, C.; Sargsian, M.M.; Vera, F. A Novel Feature of Valence Quark Distributions in Hadrons. Physics 2021, 3, 913-923. https://doi.org/10.3390/physics3040057
Leon C, Sargsian MM, Vera F. A Novel Feature of Valence Quark Distributions in Hadrons. Physics. 2021; 3(4):913-923. https://doi.org/10.3390/physics3040057
Chicago/Turabian StyleLeon, Christopher, Misak M. Sargsian, and Frank Vera. 2021. "A Novel Feature of Valence Quark Distributions in Hadrons" Physics 3, no. 4: 913-923. https://doi.org/10.3390/physics3040057
APA StyleLeon, C., Sargsian, M. M., & Vera, F. (2021). A Novel Feature of Valence Quark Distributions in Hadrons. Physics, 3(4), 913-923. https://doi.org/10.3390/physics3040057





