Abstract
With the vaccination against Covid-19 now available, how vaccination campaigns influence the mathematical modeling of epidemics is quantitatively explored. In this paper, the standard susceptible-infectious-recovered/removed (SIR) epidemic model is extended to a fourth compartment, V, of vaccinated persons. This extension involves the time t-dependent effective vaccination rate, , that regulates the relationship between susceptible and vaccinated persons. The rate competes with the usual infection, , and recovery, , rates in determining the time evolution of epidemics. The occurrence of a pandemic outburst with rising rates of new infections requires , where and denote the initial values for the ratios of the three rates, respectively, and is the initial fraction of infected persons. Exact analytical inverse solutions for all relevant quantities of the resulting SIRV model in terms of Lambert functions are derived for the semi-time case with time-independent ratios k and b between the recovery and vaccination rates to the infection rate, respectively. These inverse solutions can be approximated with high accuracy, yielding the explicit time-dependences by inverting the Lambert functions. The values of the three parameters k, b and completely determine the reduced time evolution of the SIRV-quantities . The influence of vaccinations on the total cumulative number and the maximum rate of new infections in different countries is calculated by comparing with monitored real time Covid-19 data. The reduction in the final cumulative fraction of infected persons and in the maximum daily rate of new infections is quantitatively determined by using the actual pandemic parameters in different countries. Moreover, a new criterion is developed that decides on the occurrence of future Covid-19 waves in these countries. Apart from in Israel, this can happen in all countries considered.
1. Introduction
Statistical physics of vaccination has a rich history in physics research [1]. The model proposed here is an extension of an often employed model in epidemics research, the susceptible-infectious-recovered/removed (SIR) model. While this model can be regarded as a toy model, it has been proven to at least qualitatively capture important aspects of an epidemic and is still heavily used to determine parameters characterizing epidemics or to forecast the amount of required clinical equipment. In this study, vaccinations are taken into account and the corresponding analytic expressions are derived so that those can be used without a computer at hand. Of course, numerical models, including neural networks and artificial intelligence, are convenient frameworks that allow us to take into account many more effects and data, but the goal of the present study is not to add to this area of modeling research but to deliver some insight and analytic approximants for the solution of a well-defined problem, located in the fields of growing dynamical systems and nonlinear differential equations, which to be considered is relevant in the context of Covid-19 research.
There are several variants [2,3,4,5,6,7,8,9,10] of the SIR model, including stochastic variants [11,12,13,14,15,16,17,18,19,20,21,22,23,24] and there is a large amount of related work in the context of the SIR model in the presence of vaccination. Many works deal with vaccination strategies [13,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43], transmission among an interconnected group or population [44] and vaccination behavior by coupling the epidemic spreading with human decisions [45], or policies [46,47] using the SIR model with limited resources [48]. One of the classical variants focuses on an optimal pulse vaccination strategy [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71], others focus on thresholds and bifurcations in the dynamic epidemic model [72,73,74,75], or the analysis of the delayed SIR model [15,16,22,30,51,61,76,77,78,79]. There are several approaches that investigate the optimal control of the model with time-dependent or nonlinear functions [49,50,55,59,60,62,67,68,69,70,75,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93] and the SIR model had also been applied to networks [34,94,95,96]. While it is comparably easy to set up a network or agent-based [97,98,99] model or to solve a nonlinear problem numerically, pure analytic works are relatively scarce [100,101,102,103,104,105,106,107,108,109,110,111].
In December 2020, the effective mRNA-based Covid-19 vaccine by the companies Pfizer-BioNTech and Moderna became available. This has led to intensive vaccination campaigns in many countries over the world at different speeds. As two shots per person are needed for nearly 100 percent protection as of 10 February 2021, Israel with a t-dependent vaccination rate of day has the highest, followed by the United Arab Emirates day, United Kingdom with day, whereas Germany’s vaccination rate day is significantly smaller.
The purpose of the present paper is to analytically and quantitatively investigate, for a given ratio of the vaccination rate to infection rate , the effect on the time evolution of the ongoing epidemic waves. The analysis is based on the SIR epidemic model [112] augmented by the appropriate vaccination rates leading to the susceptible-infectious-recovered/removed-vaccinated (SIRV) epidemic model. This model is a dynamical system for the time-dependent quantities , , and denoting the relative fractions of currently susceptible, S, infectious, I, recovered/removed, R, and vaccinated, V, persons in the considered population of N persons as a function of time t (Figure 1). Since each vaccine is characterized by a certain efficiency, (effectively) vaccinated persons are defined to be no longer susceptible to being infected. In the case of negligible vaccination, assuming a constant ratio between infection and recovery rate, considerable improvements of the analytical modelling of epidemics with this compartment model have been achieved [109,110]. In what follows, these improvements are of a frequent use.
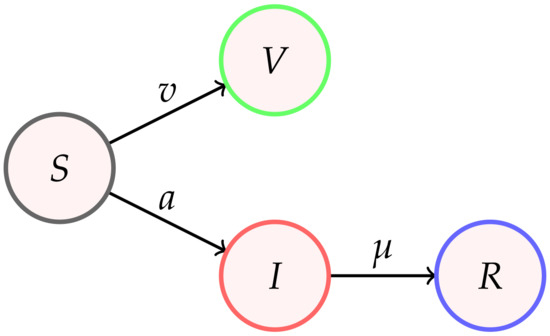
Figure 1.
Three time-dependent rates , , and entering the SIRV equations for the four compartments of susceptible, S, infectious, I, recovered, R, and vaccinated, V, population fractions. Upon introducing reduced time , the model is characterized by the assumed constant ratios and .
Application of this earlier study [113] to the monitored second waves in many countries has indicated initial () infection rates of the order of – day, considerably greater than the above vaccination rates. However, it is important to emphasize an essential difference: whereas, the initial vaccination and the recovery rate can be directly used to estimate the corresponding typical time scales, and , for vaccinations and recovery, respectively, the initial infection time scale, , additionally depends on the initial fraction of infected persons at the onset of the second wave. With this, and depending on the country, the vaccination time scale is often comparable with the infection time scale .
The inferred infection rates are slightly larger than the initial recovery rates, , so that the ratio of the two, . This is consistent with the result [110] that for a pandemic outburst with a prominent peak at a later time the ratio k has to be smaller than , where is used. For most second waves is negligibly small, so that the determined values of k less than unity are fully consistent. Then, with the above noted vaccination rates, the ratio of the vaccination to initial recovery rates is considerably smaller than the ratio k: the values are expected. Consequently, the difference is positive and only slightly smaller than k. One may refer to as the effective ratio as compared to the ratio k.
It is the purpose of this paper to quantitatively determine the influence of this small reduction of the ratio k on the time evolution of the pandemic wave. As in our earlier study [113], the present analytical calculations are based on the assumption that the ratios k and b are constants; but they hold for arbitrary time dependent infection rates , where, however, the recovery and vaccination rate follow the very same time dependence as .
Compartment models for epidemics with vaccinations have been considered before [114,115,116,117] but they were more concerned with optimizing the control of the epidemics by vaccination with limited resources. The main goal of this study is to derive analytical solutions for the dynamical SIRV. In order to keep the analysis as simple and transparent as possible, such complicating issues as age grouping, vital dynamics and/or spatial spread effects, recently investigated in the literature [118,119] with numerical solutions, are ignored here.
2. General SIRV Equations
The SIRV model is a dynamical system for time-dependent population fractions , , and , introduced above. The fractions add up to unity,
at all times (sum constraint). The SIRV differential equations accounting for vaccinations of the susceptible persons with the vaccination rate read:
where the dot denotes the t-derivative. The SIRV equations are supplemented by semi-time initial conditions (defining ),
with denoting the fraction of infected persons at time . One of the four dynamical equations can also be replaced by the sum constraint (1).
These initial conditions are sufficient to capture applications of the SIRV equations with non-vanishing and as this is identical with the present initial condition upon subtracting the nonvanishing from N. The resulting SIRV quantities are then fractions of the reduced, susceptible or currently infected population, and the fractions S and I with respect to the total population N are obtained by multiplying them both with . Similarly, the total number of recovered and vaccinated persons is plus , same for V. More formally, if denotes one of the SIRV quantities that fulfills initial condition , the time-evolution of is given by the time-evolution of X via for and for with . The initial conditions (6) are specified by , and the parameters to be introduced next have to be adjusted as well, and .
The fractions , , and are usually not measurable with high confidence, while the daily new number of infected persons, denoted by
and the fraction of vaccinated persons, , are two quantities that can be more easily measured, and are usually reported. Using Equations (2) and (5) the total cumulative number fraction J of persons, that have been infected up to the time t, is related to the SIRV quantities via
or, equivalently, upon making use of the sum constraint (1), by the sum of currently infected and currently recovered, .
Following previous investigations [109,110], as well as to make sure that the SIRV model has any predictive power, the rate is allowed to have an arbitrary time-dependency in contrast to the rates and considered to share their time-dependency with . This assumption leaves us with the two time-independent model parameters,
As it is demonstrated below, the two parameters k and b together with the initial fraction of infected persons completely determine the temporal evolution of the pandemic wave in the reduced time
2.1. Condition for Pandemic Outburst
It is instructive to calculate, with the first two SIRV equations, the initial variation of the daily number of the newly infected population fraction,
where the argument t is omitted for all functions, and Equation (9) is used. In order for a pandemic outburst with initially rising rates of new infections to occur, the bracket on the right-hand side of Equation (11) has to be positive at the starting time , so that with initially constant rate values it is required that . Making use of the first two initial conditions (6), the outburst condition reads:
- (i)
- If initially more than 50 percent () are infectious, no new pandemic outburst will occur. However, such high values of are unlikely and unrealistic.
- (ii)
- For small given values of and the ratio of recovered to infection rate k, new emerging outbreaks can be fully prevented for values of the ratio of vaccination to infection rate . The more pathogenic a virus mutation is, the smaller and closer to zero is the value of the ratio k so that the lower limit for b has to be close to unity to prevent a new outburst.
- (iii)
- For any finite value of for modeling epidemic outbreaks the relevant range of the two parameters k and b is .
- (iv)
- As an aside comment, let us note that Equation (12) demonstrates that in the SIR model with (no vaccination), a pandemic does not occur if the parameter . The SIR model correctly indicates that epidemic waves end in the case . Therefore, the recent criticism [120] about the SIR model is inappropriate and misguided.
2.2. Reduced Time
Let us consider the case when the ratios of the recovery to infection rate, , and the vaccination to infection rate, , are semipositive constants independent of time. This assumption still allows us to account for any given time-dependence of the infection rate with the caveat that the recovery and vaccination rates have exactly the same time dependence as the infection rate apart from their different initial values. In terms of the reduced time scale (10), SIRV Equations (2)–(5) reduce to:
Both equations integrate immediately to
where the integration constants have been determined with the initial conditions (6) holding now at . In terms of the reduced time the differential new number of infected persons is
while the corresponding cumulative fraction is
At , the cumulative . In reduced time, Equation (11) corresponds to
So far R, V, J, and j were expressed in terms of S and I. An additional relationship between S and I is provided by the sum constraint (1), as shown next, and this will allow us to come up with a closed equation for a single variable, to be developed in the next section.
In the present paper, analytical solutions of Equation (26) are derived for general non-zero and different values of . An implicit analytic solution is obtained that expresses the reduced in terms of a parameter , while all SIRV-functions including j are expressed in this parameter. Then, a highly accurate analytical approximation for all SIRV-functions as a function of is given. These new analytical solutions reduce in the appropriate limit to the earlier [109,110,113] solutions for the non-vaccination case . The non-recovery case and the case of are considered as special cases.
3. Dynamics of the Epidemics
3.1. Summary of Results
In light of the following rather lengthy derivation of the solution of the SIRV Equations (10)–(16) in reduced time with parameters k and b, and subject to initial condition, and , let us start with the final result. An implicit exact solution parameterized by is derived, while all SIRV quantities can be expressed in as well. Provided the reduced vaccination rate b exceeds a critical , for which the explicit expression (92) is provided, it is shown that the explicit solution of the SIRV equation can be written as follows. With the help of the following expression for a function to be defined in the next Subsection,
one obtains:
where the differential j and cumulative fractions J of infected persons are given by
If b is smaller than the critical , provided by Equation (92), the SIRV model approaches the SIR model that has been treated before, and the SIRV quantities are well captured by a simple linear superposition of the SIR result with the above SIRV solution evaluated at . Next, these expressions are derived, additional features of the solution, such as the final values at , are provided. Afterwards, special cases such as the case of are treated, and features of the SIRV equations are discussed which give rise to Equation (27). The solution (27)–(31) of the SIRV model holds for any semipositive values of k and b.
3.2. Two Useful Functions
Let us start the mathematical analysis by introducing the function,
implying
with the usually positive (for initial fractions of infected persons) initial value,
The first derivative of (32) is given by
where Equations (13) and (14) are used, and the abbreviation
is introduced. Consequently, the function
is always positive and has values as I and S are positively valued fractions at all times.
Equation (22) is identical to , and, since and with V residing in the finite interval , one finds that, after infinite time, . Similarly, Equation (21) is identical with , so that with and R residing in the finite interval , one has . Consequently, ultimately vanishes as well. At this limit, Equation (37) means that is reaching the constant , and thus is infinitely large, while its sign is given by the sign of , as long as . For , reaches a constant value.
The initial slope of evaluates to
and is thus negative for all and positive for . This implies, that the function decreases initially, undergoes a minimum at before increasing to its final value , when . For negative , monotonously decreases, while for the monotonously increases.
3.3. Mathematical Analysis
The combination of Equations (40) then provides:
or equivalently,
with the function
which is written as the derivative of B given by:
With the function (44), from Equation (37), one obtains for Equation (42) multiplied by :
with the first integral,
Here, the integration constant is fixed by the initial condition . Equation (46) then becomes
which is the first important result of this study. Along with Equation (37), this allows us, first, to identify the relation with earlier obtained solutions for special values of b and k, and, second, to derive the general solution for the epidemic time evolution for general values of b and k. As soon as, according to Equations (47) and (37), the time dependences of and are inferred, one obtains:
according to Equations (33) and (40). Since and were already expressed in terms of and in Equations (21) and (22), one obtains:
3.4. Inverse Solution for the General Case
In the general case of , the transcendental Equation (47) is solved in terms of the Lambert functions [109]. Below, it is discussed which of the two existing real-valued Lambert functions, (principal) or (non-principal), has to be applied in the corresponding parameter ranges. Until then, the W functions are used without any index representing both alternatives.
As , is set, with non-negative values of x, in order to find the so-called Lambert equation for Equation (47):
with
The transcendental Equation (52) has the solution [109]:
so that
where the identity with is employed. Using r, Equation (53), one finally finds the exact relationship between and , namely:
with
To emphasize is that E is nonnegative irrespective the sign of . At time , E evaluates to . It has been already proven above that asymptotically reaches . This implies . Since and in general, the has the sign of , and for any . Further, because the derivative of with respect to vanishes only at , and thus nowhere for positive k and b, the has no extremum with respect to . For the same reason, E has a local maximum with respect to time when exhibits a corresponding minimum in time, which is the case for . For all other values, E monotonically decreases with time from its initial value .
Inserting the solution (56) provides for Equation (37), , the nonlinear differential equation,
with the function E (57). Making use of the initial condition (34), this readily integrates to:
One thus arrives at an exact analytical solution of the SIRV equations. This to be called an inverse solution, as is expressed in terms of and not vice versa. This is a remarkably compact result, especially, since it is already known that , for the relevant case of , is not a monotonous function. However, one has to come up with a unique for each .
The solution to this at first sight apparent contradiction is provided by the two real-valued Lambert functions and that have different values over a range of negative values. For positive values of x, only is real-valued. The range of application of the two Lambert functions will be discussed in Appendix A. Here, the main outcome of these considerations is stated.
As long as exhibits a minimum, which is the case for all , Equation (59) must be interpreted as:
or, alternatively, in a more symmetric fashion, as:
where the crossover is located at , that is, where has reached its minimum, and the time, where this minimum occurs, is given by
In the absence of a minimum of , that is, for , there is no crossover, the is monotonous, and one can use Equation (59) throughout. For the argument of the Lambert function is positive, so that one has to use Equation (59) with .
For , the minimum of coincides with , hence, , so that only the second term in the second case of Equation (61) survives, again involving the principal only. The non-principal Lambert function thus only plays a role in the case .
3.5. Determination of the Minimum Value for
In order to evaluate given by Equation (61) for the case of , one needs to specify . As it was noted above, see Equation (37), the function attains its minimum, at , and a minimum exists for all . According to the solution (56), one finds the minimum value from , where , yielding . Both, the principal and the non-principal Lambert functions have the same value at , so that . Along with Equation (55) this yields the equation that determines :
Since is the value at the minimum, the inequality automatically holds. This nonlinear Equation (63) for cannot be solved analytically in general. For some special cases such as one can still write down an analytical solution. An approximant for is derived below.
4. Approximated Reduction of the Exact Solution
4.1. Approximate Inverse Solution
Here, an approximant is derived for the exact inverse solution that later is inverted exactly in order to obtain in the next Subsection. Upon introducing with given by Equation (57), the previous inverse solutions (59) and (61) for , and also defined by Equation (62), are of the form
where , and , or are treated as arbitrary coefficients for the time being, as stands for any of the two Lambert functions, so that is of the form (64) for any . Evaluating the required derivative of z with respect to x gives:
The first term can be approximated by unity when and thus , and not too close to unity, i.e., b not too small. The precise range of validity of this approximation will be worked out in Appendix B and in Section 4.4, where a critical is specified, below which the current approximation needs not be used. For and , , so that this approximation is applicable for any when . For , , so that the approximation is excellent as long as . Under such circumstances, that is, for , Equation (65) is well approximated as
with . Hence, Equation (64) is well approximated by
Then, with the substitution , corresponding to , and , one can calculate the integral (67) in closed form:
The minus sign is kept in the nominator and denominator as is typically negative. For , initially decays with time until reaches its minimum . At the minimum, . Since only for and is positive for all , Equation (68) removes the problem with the pole at at starting point, in Equation (64).
Having arrived at Equation (68), one can now identify placeholders , and in all three equations (59) (with ), (61), and (62), to write down for the various cases as well as .
Let us start with the case of and . Upon comparing the first line in Equations (61) and (64), and along with for the regime need to be used. Since is positive and, thus, z is negative, using Equation (68), this provides immediately:
Since , , the term vanishes for both . The nominator in Equation (69) can thus be replaced by unity. Exactly the same procedure, applied to the remaining cases, yields the final expression for the approximate inverse solution when :
with from Equation (57). Similarly, the time can be read off from Equation (68) by choosing , , and . Hence,
where and and the identity (see proof in Appendix C) are used to simplify the expression. Such time only exists for .
There is the remaining case of . Equation (59) implies using , , and the principal Lambert function (), as already discussed. As and, thus, have different signs for and , both the nominator and denominator in Equation (68) are multiplied by , to get rid of two different signs for positive and negative values of . At the same time, because of the identity (see proof in Appendix C), which holds for all , the logarithm of this quantity vanishes, and one arrives at the final expression for the approximate inverse solution valid for all and all ,
Notice that the argument of the logarithm is positive for both and .
It is important to realize that the value for has completely disappeared within the approximate case. Still, we can use a very similar approximation done here to obtain an explicit expression for , that might be helpful for the evaluation of the exact inverse solution and the exact as long as . If b is not too small, we can approximate the term in Equation (63) by and solve it for analytically. This yields (see Figure 2):
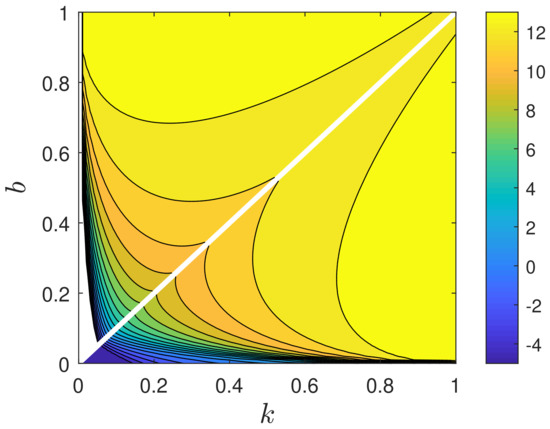
Figure 2.
Exact versus k and b in the lower right triangle, and approximate using Equation (74) above the diagonal (mirrored, to allow for a simple comparison with the exact ). All analytic results for the SIRV functions in terms of reduced time are basically exact for those k and b for which is well described by its approximant. The white space in the lower left corner is the regime of , where the SIRV model results are captured by linearly interpolating between the SIR model and the SIRV model evaluated at the critical .
Note that this value has the feature for . In practise, for , the term can be safely neglected so that
can be used, while it is possible to add this correction throughout the rest of this paper.
4.2. Approximate Direct Solution
Next, the approximate inverse solution is inverted in order to come up with an approximate direct solution of the SIRV equations. With Equations (70)–(72), the approximate expressions for , and as function of are provided for any negative or positive . Fortunately, one can proceed and invert the relationships without any further assumption to come up with the corresponding, much more convenient, explicit solution . As soon as all SIRV functions are expressed in terms of , all these quantities are then given as function of the reduced time .
Let us begin with an illustrative example. In Equation (71), is given in terms of b and . One can invert the relationship to obtain from and b, namely:
To prove the equivalence between Equations (71) and (75), one has to just insert Equation (75) into Equation (71) and to use the fact that the Lambert function is the inverse function of . More specifically, consider . Its inverse is given by because . To derive Equation (75) one thus has identified and . The same procedure can be applied to all expressions from the previous Section using different choices for y and .
One more required ingredient is however an expression for in terms of E. It can be readily deduced using the existing assumption that lead to Equation (74). To derive this Equation (74), one assumes that . Since the minimum at all times, the assumption is even more appropriate within all remaining times. With this replacement, Equation (57) reads:
and this can be solved for to arrive at
with , and where Equation (73) is used. Here, the symbol is introduced instead of E only to highlight the different argument and to avoid potential confusion. Note that this generalization of Equation (74) is compatible with the special case because . As before, it is even more convenient to drop a term of , so that coincides with the exact value. Since , the correction becomes simpler:
Having expressed in terms of and , what is left to do is to write down expressions for . With such expressions at hand, Equation (78) is the explicit solution of the SIRV equations. The depends on the range.
For , in view of Equation (70), one needs to use and to obtain the explicit , or equivalently, . Replacing y and , one thus finds:
for .
Note that there is no need to consider two regimes before and after the peak anymore. While the two Lambert functions and are very different, they share a common inverse, and Equation (79) is valid over the whole range.
To summarize, upon inserting Equation (79) into Equation (78), one ends up with a final expression for for all ,
where and were used from Equations (71) and (74) to arrive at the second line. Figure 3 compares the approximant of Equation (80) with the exact solution for three different values. For the remaining cases of , Equation (72) has to be inverted. Repeating the above procedure, one gets: for . Upon inserting this term into Equation (78), one arrives at the explicit approximate solution of the SIRV equations for :
Figure 3.
Comparison of the approximant (80) for with the exact solutions (59) and (61) (black curves) for three different values at and a relatively low . For the approximant (green), and are given by Equations (71) and (74), respectively. For larger b the performance of the approximant is even better.
Not only is this result exactly of the form we obtained for , it is moreover valid also for the special values of and , as all—at first glance problematic—divergencies have dropped out. From Equation (81), one can see that except for or , where approaches a finite value. The full expression valid for all is thus:
in full accord with the exact SIRV solution.
4.3. Time-Dependency of All Remaining SIRV Quantities
With given by Equation (81) and the corresponding
for all values of , it is now straightforward to write down all remaining SIRV quantities, as they have been expressed in terms of above. It is perhaps interesting to note that the approximant shares the most relevant features with the exact solution: , , , and (as required by Equation (38)) for all . In the limit of infinitely long times, , according to Equation (83) unless .
For , for which one can use from Equation (81) with , these expressions solve the SIRV Equations (13)–(15) exactly, as can be verified by direct insertion into Equations (13)–(16). An alternative proof is provided in Appendix G.1. Otherwise, they solve the SIRV equations to within . The version given by Equation (87) ensures that holds exactly.
It is a rather tedious exercise to insert the and functions into Equations (85)–(89). In evaluating the limiting values for , one has to carefully consider the qualitatively different regimes , , and , as well as when . This can be done but we refrain from writing down all equations for the approximate explicit solution of the SIRV equations. Instead, in Appendix G, exact solutions for special cases are provided and the approximate explicit solution are compared with the exact numerical solution for several cases. To provide an example, inserting (81) and (83) into the expressions for S (84) and I (85) yields:
Next, let us focus on the most relevant, measurable features of the SIRV model, that to be derived from the analytic approximant.
4.4. Critical Reduced Vaccination Rate
As it is demonstrated below, the approximants (81) and (83) capture the exact solution very well (or also exactly for some special cases like ) except for the regime where b stays below a critical . The limiting case of is known as SIR model and had been treated elsewhere, so that the failure of the approximant obtained does not seem to pose a problem. It is, however, possible to quantify the range of validity of Equations (81) and (83). This is done in Appendix B and leads to a critical value in terms of and k,
for the reduced vaccination rate, beyond which the approximant is very accurate; see Figure 4 for a plot of versus k and . The critical decreases with increasing k and decreasing , while it is quite sensitive to k values close to unity. At , Equation (92) evaluates to and is thus roughly proportional to in that case.
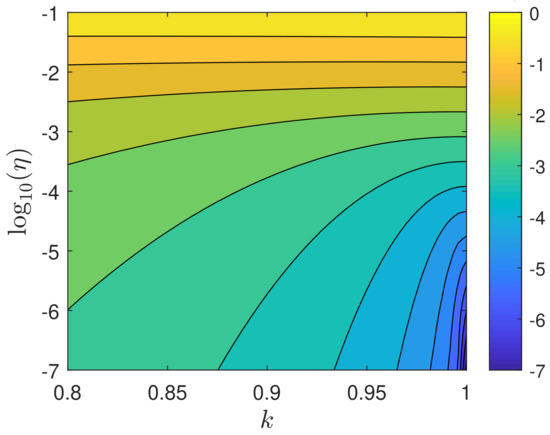
Figure 4.
The critical versus k and . The coloring scheme uses the decadic logarithm of , and the vertical axis is also logarithmic. Only a relevant range of k values is shown.
For the remaining range of the b values below one can make use of the known solution of the SIR model, that corresponds to the SIRV model with . To be specific, the characteristics of time-evolution such as peak time and height of the differential rate, or the final fraction of infected population are well captured by a simple linear interpolation between SIRV values at and the SIR values. This is worked out next to conclude with approximants that are valid for any b.
4.5. Peak Times and Peak Amplitudes
While decreases monotonically with time, both and exhibit a maximum, whose position and amplitude one can calculate from Equations (90) and (91). Whereas the general case of arbitrary is treated in Appendix E and Appendix F, here, let us limit the analysis to the relevant case of a small initially (and simultaneously) infected fraction of the population. In this limit, one obtains to leading order for all :
implying for the differential fraction of newly infected persons,
The peak time of the maximum in is thus
so that a peak in I exists only if . For the fraction of currently infected persons at peak time, one has:
Likewise, the peak time of the maximum in is at (thin colored lines in Figure 5)
where j achieves the value
or, equivalently, as the following expression is much more conveniently evaluated at small b (thin colored lines in Figure 6):
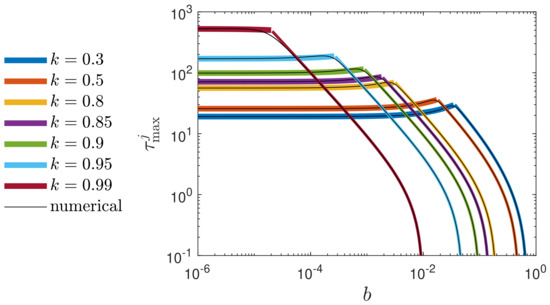
Figure 5.
Reduced peak time, , of the newly infected population fraction, , versus reduced vaccination rate, b, for various k at (double-logarithmic plot). The exact numerical solution (solid black) is compared with the approximant (98) within the regime of (thin colored), and by the corresponding linear interpolant (thick colored) for the remaining regime of very small . The limiting value exactly coincides with the of the SIR model (see Appendix G.2).
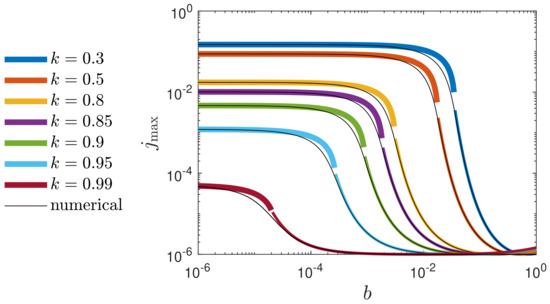
Figure 6.
Peak value of the newly infected population fraction versus reduced vaccination rate, b, for various k at (double-logarithmic plot). The exact numerical solution (solid black) is compared with the approximant (99) within the regime of (thin colored), and by the interpolant (101) (thick colored) for the remaining regime of very small . The limiting value exactly coincides with the of the SIR model (Appendix G.2).
Thus, a peak in j occurs only for , in agreement with the consideration above (see Equation (12)), as small , , is assumed here. While the peak time increases with increasing b in the regime of , it decays with b for .
The maximum rate (99) is not applicable for below a critical, very small , given by Equation (92). For small , one can make use of the known [110] exact result of the SIR model, reproduced in Equation (A63), and linearly interpolate as (thick colored lines in Figure 6)
where and are given by Equations (99) (evaluated at ) and (A63), respectively. The analytical expressions for time and amplitude of the daily number of infected persons are two of the more important results of this study. They can be immediately used to rate the effect of vaccination rate for all b, using Equation (99) for and Equation (101) for , where the critical rate is given by Equation (92).
One should keep in mind that the maximum of the is not located at , which marks the time of the minimum in . There is also a remaining apparent contradiction. While the initial slope of is positive for and thus going through a peak at a future time in that case, and taking identical values at different times, the exhibits a minimum for all . Under such latter conditions, there are at least two times that exhibit the same value. The apparent contradiction finds its explanation in the fact that cannot be expressed in terms of alone, but also involves the derivative of with respect to , which is contained in . In other words, both Lambert functions are sometimes (when and ) required to describe that is monotonically decreasing, and a single Lambert function is sometimes (when and ) sufficient to describe that exhibits a maximum. Another way to understand this feature is the fact that the expressions for the SIRV quantities have the same form irrespective the value for , that is, irrespective the occurrence of a minimum in .
4.6. Total Fraction of Infected Persons
The differential given by Equation (95) can be integrated to obtain the cumulative fraction , as shown in Appendix D. For , one, thus, obtains (thin colored lines in Figure 7):
in terms of the lower incomplete gamma function [121]. For the special case of (), Equation (102) agrees with the exact result (A54) up to order . As for , one has to distinguish two regimes: (i) the regime of , where this expression (102) is useful, (ii) the regime of small , for which one needs, on one hand, the known exact result of the SIR model, , and on the other, the value for given by Equation (102), evaluated at . Since is so very small, the direct insertion into (102) is numerically impossible. Therefore, a limiting expression is derived in Equation (A16) of Appendix D, valid for small values of b such as , that enters Equation (103) just below. Using exactly the same interpolation approach as before for , the within the regime of small is approximated with the help of Equation (102) by (thick colored lines in Figure 7):
where is the known analytical expression [110] for the SIR model, reproduced in Equation (A62), and is given by Equation (92).
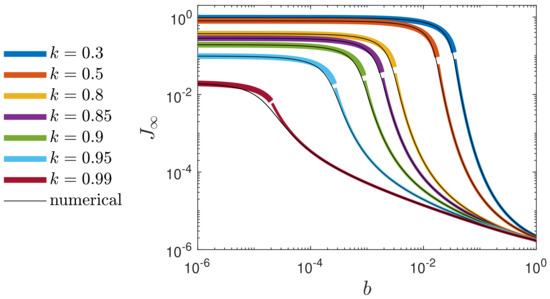
Figure 7.
Final (infinite time) fraction of infected persons, , versus reduced vaccination rate, b, for various k at (double-logarithmic plot). The exact numerical solution (solid black) is compared with the approximant (102) within the regime of (thin colored), and by the interpolant (103) (thick colored) for the remaining regime of very small . The limiting value exactly coincides with the of the SIR model (see Appendix G.2).
4.7. Differential Rate
Next, an analytical approximant for the time-dependent differential rate is provided, valid for any b, and small , . For b exceeding the critical , one can just use the expression (95). The comparison with the analytic result is excellent, see Figure 8a–c. For , on the other hand, it was already shown above that the peak time and peak amplitude are well approximated analytically by a linear superposition between the SIRV approximant evaluated at the critical , and the analytical SIR expression. The analytical expression for the full time-dependency of in this subcritical regime of is therefore not just a linear superposition of the for SIRV and SIR model, because such superposition would not recover the already determined peak time and height. Instead, as it is demonstrated in Figure 8d–f and inspired by the earlier observation that the Gauss model [99,122] captures the differential rate very well, the is well described for by the Gaussian,
with the width w, determined by [99]
where and are given by Equations (101) and (103), respectively.
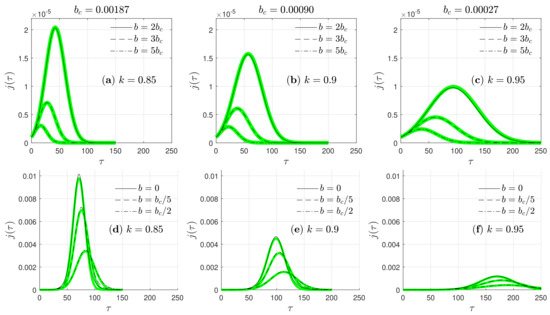
Figure 8.
Differential rate, , of infected population fraction versus reduced time, , for three different and various reduced vaccination rates, . Here, is used. The panels (a–c) show the regime , while (d–f) show results for including (SIR model). To rate the effect of the parameters, all three plots of each row are shown on identical scales. While the peak time increases with increasing k and decreasing b, the peak height dramatically decreases with increasing b. The critical depends on k and , see Equation (92) and Figure 4. The area under the curves is the total cumulative fraction of infected persons. The black lines are the exact numerical results, the green lines are the analytical approximant, given in Section 4.7.
4.8. Time Scales
Summarizing the above-made analysis, let us emphasize that SIRV-pandemic waves in the case exhibit a clear asymmetry with respect to the peak time in reduced and real time. The fraction of infected, I, and recovered, R, persons as well as the daily rate of new infections, j, vary rapidly on the order of the recovery reduced time scale , corresponding to recovery real time scale . Alternatively, the fraction of susceptible (S) and vaccinated (V) persons as well as the sum, , vary slowly on the order of the much greater vaccination reduced time scale , corresponding to the vaccination real time scale . Third, the cumulative fraction of newly infected persons, , exhibits an asymmetric time structure determined both by and . These behaviors are clearly visible in Figure 9b–d or, alternatively, in Figure 9f–h, where the time distribution of all SIRV quantities is shown in one plot for different values of b at . The behavior is qualitatively similar but quantitatively different for other values of k. Comparing the asymmetric time distribution of with empirical data then should allow the determination of both the parameters b and k.
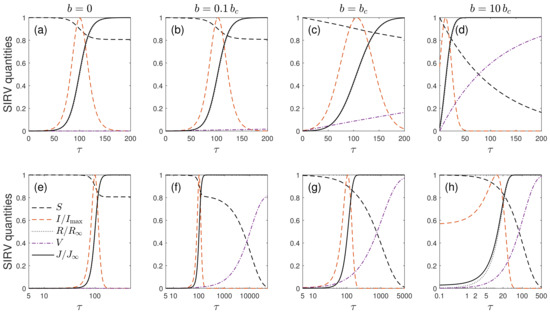
Figure 9.
Suitable normalized SIRV quantities S, , , V, and versus for the four different reduced vaccination rates at and : (a,e) (SIR model), (b,f) , (c,g) , and (d,h) . While the upper row presents the data in a linear scale, the bottom row shows the same but in a semilogarithmic fashion to appreciate the two well separated time scales.
For comparison, Figure 9a,d shows the SIR-time distributions. Here, definitely, no enhanced asymmetry occurs. Apart from the absent , all SIR quantities vary on the same recovery reduced time scale . Moreover, the SIR saturates at the finite value given by , whereas the SIRV approaches zero after infinite time as a consequence of vaccinations.
5. Comparison of Approximate with Exact Solutions
All model parameters, such as , k, and b, were determined using currently available public data [123,124] for the population amount, vaccination rate, daily number of newly deceased persons. The parameters as well as the SIRV prediction are collected in Table 1 for various countries. It should be noted here that there is some significant variation of the experimental data depending on the data source used, and that the determined model parameters are quoted here without error bars for the reason that the differences in the data bases have not yet been fully resolved. On the other hand, a statistical error can be estimated from the variation of the model parameters with time. For this reason, the daily updated model parameters are determined and reported as part of our Supplementary Material.

Table 1.
Analysis using data from 18 March 2021. For , k and a the current values for the second wave, that started at are used, all from the online resource [124]. The starting time, , of the vaccination program and the mean daily fraction v of vaccinated population since then are retrieved from Ref. [123] assuming that each person has to be vaccinated twice and that the vaccination is effective two weeks after the second shot. The remaining quantities are derived from Equations (9) and (36), i.e., via , , , and is positive if the outburst condition (12) is fulfilled. is calculated via Equation (92). Furthermore, included are the infected population fraction at various times: (i) at the end of the first wave, at the onset of vaccinations, (iii) assuming no vaccinations, (iv) assuming ongoing vaccination at the present rate, (v) assuming the vaccination rate had been twice as large. The denotes the date at which 99% of the final has been reached, and is the number of newly infected persons per 100,000 inhabitants within a single day, at peak time. The difference between and is the population fraction that profits from the current vaccination program. For all countries, , , , hold. A daily updated and extended table containing more numbers such as , v is part of our Supplementary Material.
The exact numerical solution of the SIRV model is compared with the approximant for various typical choices of k and b in Figure 8. To highlight the effect of reduced vaccination rate b, six cases for each k are shown: , , , vanishing b (SIR model), , and . These six values capture the qualitative behavior for all b. For , vaccination is basically ineffective in reducing the number of infections. For , the vaccination program is highly effective. The crossover is at , where the reduction becomes significant and where it depends roughly linearly on b. The critical as function of k and is shown in Figure 4. While basically coincides with for , at smaller k, the critical behaves nonlinear with k and , as it is shown.
In Figure 7, the exact result (solid black lines) for versus b for various k is compared with the approximant (colored lines). The gap in the colored curves marks the crossover regime, . For any b, the exact solution is captured by the SIRV approximant. The same is true for remaining quantities such as peak height and peak time , as it is demonstrated by Figure 5 and Figure 6.
6. Application to Real Data
To make predictions and to draw conclusions from the SIRV model about the ongoing pandemic and the vaccination efforts, current values of infection, vaccination and recovery rates are collected, as well as population sizes, by making use of existing online resources [123,124]. Then, the SIRV model is applied to calculate the time evolution of all the SIRV quantities, including final number of infected persons, or maximum daily number of newly infected persons. Examples are shown in Table 1, while a corresponding, daily updated table that includes even more characteristics of the second pandemic wave is part of the Supplementary Material.
Besides the input parameters of the SIRV model, such as the rates, Table 1 offers the dimensionless values for k, b, and , the criterion , the date marking the beginning of the vaccination program, and various values for the final population fraction that is getting infected before all population has been either recovered or vaccinated. As long as has positive values, new pandemic waves can occur. Table 1 indicates that apart from Israel (ISR) this can happen in all countries considered. Only Israel has applied a high enough vaccination rate so that no further Covid-19 waves can occur. Table 1 lists the population fraction that had been infected up to the end of the first pandemic wave, the cumulative fraction at the time the first person got vaccinated, the hypothetical cumulative fraction assuming there was no vaccination program, the using the current value for the mean number of vaccinated persons that gave rise to b, and the hypothetical assuming vaccinations could have been performed at twice the actual speed. In addition, Table 1 shows the maximum number of newly infected persons per day and per 100,000 inhabitants, , and the date for which 99% of the ultimately infected population fraction has been reached. Note that is not always much smaller than because the vaccination program eventually started after the peak time and because the first wave cumulative fraction sets already a lower limit.
Adding the data for all countries of Table 1 to Figure 4, one ends up with with Figure 10, where another colormap is used for the specific purpose of this figure. The brightness represents , shown as function of k and . Circles for countries have been placed at positions k and according to Table 1, and the brightness of a filled circle corresponds to the reduced vaccination rate b, also taken from Table 1. If the brightness of a circle exceeds the one of the background, the vaccination rate resides above the critical for that country. This is the case, e.g., for Israel (ISR), Great Britain (GBR), and Finland (FIN). Circles darker than background, such as for Belgium (BEL), Mexico (MEX) and Argentina (ARG) highlight the case when .
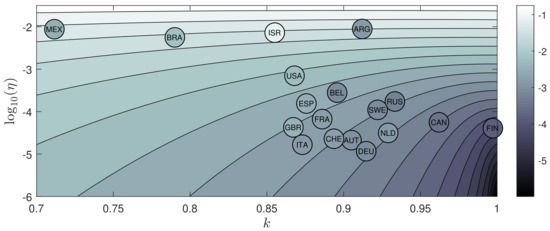
Figure 10.
Same as Figure 4 but using another colormap, where countries have been added. The brightness represents , shown as function of k and . Circles for countries have been placed at positions k and according to Table 1, and the brightness of a filled circle corresponds to the reduced vaccination rate b, also taken from Table 1.
7. Summary and Conclusions
With the now available vaccination against COVID-19 it is quantitatively explored how vaccination campaigns influence the mathematical modeling of epidemics. For this purpose, the well-known susceptible-infectious-recovered/removed (SIR) epidemic model is extended to the fourth compartment, V, of vaccinated persons and the time t-dependent vaccination rate, , that regulates the relation between susceptible and vaccinated persons. The vaccination rate competes with the infection, , and recovery, , rates in determining the time evolution of epidemics. In order for a pandemic outburst with rising rates of new infections to occur, it is required that , where and denote the initial ratios of the three rates, and is the initial fraction of infected persons.
Apparently for the first time, analytical solutions for the time-dependence of all relevant quantities of the SIRV model are derived, where j and J are the daily and cumulative fraction of new infections, respectively. Similar to the earlier analyses [109,110] of the SIR model, one of the time-dependent rates is eliminated by using the new reduced time-variable defined with the infection rate by . Moreover, the semi-time case is adopted with assumed-to-be-constant ratios and between the infection, recovery and vaccination rates. This assumption still allows us to account for any given time-dependence of the infection rate with the caveat that the recovery and vaccination rate have exactly the same time-dependence as the infection rate apart from their different initial values. Exact analytical inverse solutions for all relevant quantities Q of the resulting SIRV model in terms of Lambert functions are derived. The values of the three parameters k, b and completely determine the reduced time evolution the SIRV-quantities .
These inverse solutions can be approximated with high accuracy yielding the explicit reduced time-dependences by inverting the Lambert functions. For a given time-dependence of the infection rate , the real time-dependence can be inferred. The inversion of the Lambert functions operates well for all ratios b exceeding a small but finite critical value . In the range of the solution is interpolated using the exact SIR solution derived before at and the inverted SIRV solution at . This approach is remarkably accurate as the comparison with the exact numerical solutions of the SIRV equations indicates. The analytical solutions show that SIRV-pandemic waves in the relevant case exhibit a clear asymmetric distribution in reduced and real time. The fractions of infected, I, and recovered, R, persons as well as the daily rate of new infections, j, vary rapidly on the order of the recovery reduced time-scale, . Alternatively, the fractions of susceptible, S, and vaccinated, V, persons as well as the sum, , vary slowly on the order of the much greater vaccination reduced time-scale . This asymmetric SIRV-time behavior is significantly different from the SIR-time behavior, where no time asymmetry occurs, and, apart from the absent , all SIR quantities vary on the same recovery reduced time scale .
Clearly, the analytical solutions obtained here are superior to all numerical ones in the literature as they allow us to identify the main determining parameters of the epidemic waves and to understand the correlations between various monitored observables. The use of these exact analytical solutions is also valuable as a benchmark for solutions obtained by solving the SIRV-equations numerically.
The influence of vaccinations on the total cumulative number and the maximum rate of new infections in different countries is calculated by comparing the results obtained here with monitored real time Covid-19 data. The reduction in the final cumulative fraction of infected persons and in the maximum daily rate of new infections is quantitatively determined by using the actual pandemic parameters , k and b in different countries. The corresponding numbers for a hypothetical adopted doubled (as compared to the actual one) vaccination rate are also given, which allows us to quantitatively assess the total and maximum casualties caused by the delayed and low-level vaccination coverage in many countries. Moreover, a new criterion is developed that decides on the occurrence of future Covid-19 waves in these countries. Apart from in Israel, this can happen in all countries considered. Only Israel has applied an high enough vaccination rate so that no further Covid-19 waves can occur.
Supplementary Materials
A real-time analysis of Covid-19 data along the lines described in this work is available at https://www.complexfluids.ethz.ch/SIRV.
Author Contributions
Both authors contributed equally to this work. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in [123,124].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Range of Application for the Two Lambert Functions
As discussed before in Appendix G of Ref. [109], there is a single real-valued solution of Lambert’s equation for arguments , referred to as the principal. There are two real-valued solutions for : the principal one and the non-principal solution . For arguments below , only complex-valued solutions exist, which are of no interest here because the function is real-valued.
As the function , for the general solution (56), it is required that
with always. While for the only real-valued Lambert function is , for the values being of a particular interest here, the argument of the Lambert function is always negative. For those values, real-valued solutions exist only if
Figure A1 shows the two functions, and , entering the constraint (A1). The black line represents the upper limit (A2) and the red line represents the initial . For , the initial value provides a more restrictive upper limit for E, as E is monotonically decreasing in those cases, as already proven above.
The lower bound of the constraint (A1) is automatically fulfilled for all negative arguments of the Lambert function. The principal Lambert function applies for , corresponding to the range
which automatically fulfils the upper bound of the constraint (A1) when . The coloured area in Figure A1b represents the constraint (52). When or , the constraint (A1) is still fulfilled as long as , as this value for E, inserted into Equation (A1), gives unity. As already shown above, monotonically increases (decreases) with time for (), varies monotonically with , and . The , therefore, monotonically decreases with time for both and , and thus stays below at all times, since . The constraint (A1) is, therefore, not only fulfilled automatically for , but for all . The only exception from this statement are and , but these special cases are not discussed here.
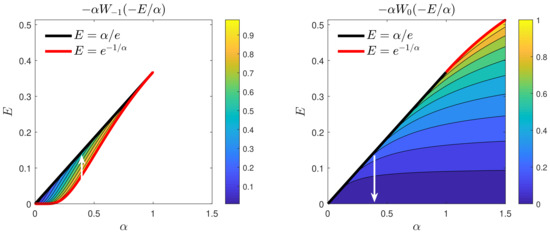
Figure A1.
Values of the (left) non-principal and (right) principal Lambert functions determining in Equation (56). The solid black line represents the upper limit, (for all ), where . Only for the coloured region below this line real-valued solutions of Equation (56) exist. The red line represents the initial , which serves as a more restrictive upper limit for . In their coloured areas, the corresponding Lambert functions apply, while the white regions cannot be reached. Points residing in ()-space that are shared by both Lambert functions are visited at different times, as exemplarily shown by the white arrows for . At earlier times the non-principal Lambert function describes , while overtakes at later times. The crossover occurs at . At this moment, both Lambert function exhibit exactly the same value. For negative , the accessible E span the huge range and are therefore not shown. For such , the colored region exists only for .
Likewise, the non-principal Lambert function potentially applies for , corresponding to the range . Together with the right-hand side of the constraint (A1), one finds that the non-principal solution potentially applies as solution in the range
The coloured area in Figure A1a represents the constraint (A4). It is not obvious at first glance why there are regions in the –E-space that fulfill both inequalities (A3) and (A4). In those regions, only one of the two Lambert functions can lead to the true . The transition between the two Lambert functions is where they meet, i.e., when . When , at early times involves . This continues until a point in time where is reached. From then on, is determined by the principal solution .
Appendix B. The Critical Vaccination Rate b c
It is straightforward to estimate the value of the parameter b, below which the approximations (81) and (83) break down. This occurs when the approximation in Equation (66), based on the assumption of values of , is no longer valid, i.e., when the minimum of Equation (74) exceeds a certain value of order unity. Consequently, the approximation tends to break down if the following equation is fulfilled for ,
This Equation (A5) can be cast into the form of the Lambert Equation (52) with the solution
in terms of the principal Lambert function . The solution is denoted here by , as the to be used is slightly different, as it is shown below. The non-principal Lambert function would produce large values for which the approximants do not require any special treatment. Using , the expression (A6) may be rewritten further. It is important to note that the approximants for the regime cannot be evaluated anymore for values well below , especially for k very close to unity. In Table A1, therefore, the best values for , that were obtained upon fitting the exact solution with the obtained approximant, are collected and compared with those of expression (A6) as well as with another formula to be derived next, that will actually be used as it captures the best with much higher accuracy than from Equation (A6).

Table A1.
Critical value of the reduced vaccination rate b to be used in the interpolants (101) and (103). Mentioned for comparison are: the best fitted value , the analytic expression (92) for that is used throughout this paper and the rough estimate according to Equation (A6). The value is used for this table; the analytic expression (92) works equally well for any .
Table A1.
Critical value of the reduced vaccination rate b to be used in the interpolants (101) and (103). Mentioned for comparison are: the best fitted value , the analytic expression (92) for that is used throughout this paper and the rough estimate according to Equation (A6). The value is used for this table; the analytic expression (92) works equally well for any .
| k | |||
|---|---|---|---|
Upon inspecting the fitted , , values for various k and , one finds that , , and there is a constant proportionality between and . In light of Equation (A16), this translates into the following equation for :
with some coefficient , which is determined empirically (Figure 2) upon comparing the exact solution with the approximant. Equation (A7) is solved for as follows:
Appendix C. Proof of Equation (72)
Here, it is proved that for all , where to recall is that . This identity was used in the derivation of Equation (72). Making use of the inverse Lambert function , one can take the inverse on both sides:
which completes the proof, but one has to be careful here. The identity holds only for those for which resides on its real-valued regime, i.e., for . Because the argument of the inverse Lambert function is only for and , the identity does not hold for . If is replaced by , the identity holds for the opposite case of .
Appendix D. Proofs of Equations (102) and (103)
With the approximate expression (95), that is useful up to order , one obtains for corresponding cumulative number fraction, with the substitution :
where is inserted and the lower incomplete gamma function [121] defined by
is used. After infinite time, from (A10), one readily obtains:
where, in the last step, the recurrence formula [121] for and is used. For the special case of , the obtained expression (A12) indeed reproduces Equation (A54) of Appendix G.1 (where we treat this special case of in detail) up to order , i.e.,
where is used. For the special case of , Equation (A12) simplifies to
As already discussed, Equation (A12) is useful when b does not exceed . This avoids that the latter expression (A14) exceeds unity and, thus, fails when b is too small.
With the asymptotic behavior of the gamma function,
from Equation (A12), one obtains for small values of :
where the Stirling’s formula is used in the last step.
Appendix E. Cumulative Fraction of Infected Persons J(τ) for Arbitrary η
Starting from the found approximants for and given by Equation (28), with from Equation (27), i.e.,
the differential rate (30) is written as
Here, we are interested in an expression for the integrated for arbitrary initial conditions , contained in , while a result valid for small was already provided with Equation (A10). To this end, using Equations (31) and (A18) one gets:
Substituting then yields:
To be able to calculate this integral, let us introduce yet another but simpler integral , parameterized by c:
Because the derivative of with respect to c evaluates to
the cumulative fraction (A20) can be expressed in terms of as
What is left to do is to calculate the integral (A21). Using the identity
applied to Equation (A21), provides:
where is substituted in the last step. Equation (A25) readily yields, upon replacing , and, using the binomials ,
with the coefficients,
that all vanish for . The exponential weight containing in front of the coefficient in Equation (A26) is kept, as this allowed us to see that one needs to take into account the first m terms of the sum, and the first m coefficients to come up with up to order . The integral in the coefficient can be expressed in terms of the lower incomplete gamma function, , so that, finally, is obtained as an infinite sum, with summands given by
To confirm that the obtained general expression reduces to (A10) already derived for small , let us evaluate Equation (A26) to first order in . With , Equation (A26) implies:
where is taken from Equation (A28), and is replaced by . The obtained Equation (A29) is indeed identical to Equation (A10).
One can rewrite further in a way that helps calculating using the recurrence formula for the lower incomplete gamma function,
Using this recurrence in Equation (A29), one ends up with
where the abbreviation,
is used only to shorten the expression. Note that . To derive expression (A31), the following identities,
as well as
are used. After infinite time the first term of Equation (A31) vanishes, and can be used. Hence,
While this appears as a tractable expression, it cannot be directly evaluated numerically for small b such as , because poses a problem. To circumvent this problem, Stirling’s formula and is used. For small values of b, one then obtains:
where, eventually, from Equation (A32) is re-inserted. For small values of , , one takes only the first term in this sum providing with :
which agrees exactly with Equation (A16). It is worthwhile noticing that for very small b: the higher order terms in the sum must be taken into account, even at small , as this ensures that stays below unity. One needs to calculate only down to , while the form (92) for ensures that .
Appendix F. Peak Time and Amplitude for b ≥ bc and Arbitrary η
The approximant , valid for and given by Equation (A18), can be written as:
with , , and , so that contains the dependency on time via x. Note that x is positive at all times, because b is positive. As soon as x varies monotonically with , to find the peak time and peak height , one needs to determine the position and value of at its maximum, provided such maximum exists. For the derivative of with respect to x, one has:
Hence, the derivative vanishes at , where solves the highly nonlinear equation,
or equivalently and more suitable for any numerical implementation,
This is an expression valid for arbitrary and in terms of the solution of Equation (A41), that can only be obtained numerically. For the special case of small , one can proceed analytically that would provide an approximate solution for .
Special Case of bc ≤ b ≪ k
For this case of small , the above p-variable (see (A38)) becomes large and is well approximated by . At the same time, the right hand side of Equation (A41) vanishes. The resulting equation for ,
is solved with the help of Lambert’s principal function as:
where p is replaced and properties of the Lambert function are used. The corresponding is still given by Equation (A42). Because is of order unity, and if holds as well, the argument of simplifies for to . This latter argument equals to within 2.5% for all , so that , and equivalently, can be used under such circumstances.
Appendix G. Exact Solutions for Special Cases
Appendix G.1. The Equal Value Case b = k Corresponding to α = 0
The general analysis above can also be used for a number of special cases to be investigated in this and the next Appendices. Let us start with the special case , so that the general Equations (37) and (47) simplify to
This proves that, for special case of , Equation (80) is actually exact and not an approximant. With Equations (A46) and (A47), one readily obtains for Equations (48) and (49):
Consequently, the rate of new infections is then given by
With the help of the sum constraint (1), the remaining is given by
With , there is no need to integrate in order to come up with a final expression for using and from Equations (A48) and (A52).
At infinite time , from Equations (A46), (A48), and (A49), one finds:
as well as , and . The only nontrivial quantity is, thus, , which one obtains from Equation (A53), inserted into Equation (A52):
For small values of k, which for correctly provides . All other expressions can also be readily evaluated in this limit with the help of . For , one, thus, gets: and , and all above expressions simplify considerably. For example,
This completes the analysis of the special case of equal values of , or equivalently, . The most noteworthy result is the significant reduction in the final cumulative number of new infections with increasing values of as compared to the SI-case with , cf. Equation (A62).
Appendix G.2. SIR-Case b = 0, k > 0
For no-vaccination campaigns (), the SIRV model reduces to the SIR model analyzed before [110,113]. For , implying , Equation (47) simplifies to:
or, with and Equation (48), to:
In terms of the positively-valued function , Equation (A58) reads:
which agrees exactly with the integrable Equation (24) in Ref. [110] yielding:
and for the rate of new infections j and the corresponding cumulative number J:
To summarize, one finds [110] for the SIR model, the special case of the SIRV model with ,
Alternative Inverse Solution
For , one obtains , so that Equation (37) reads:
Inserting the solution (A65) then provides for Equation (A64):
which, with the initial condition (34), readily integrates to the inverse exact solution:
Hence, practically all previous general results obtained in Section 3 and Section 4 also hold here with replaced by k. For values of , Equation (A68) yields:
where the time where the minimum occurs, is given by
The minimum value for the case of is determined by the condition along with Equation (A66):
The substitution then yields:
as the exact solution of the SIR model considered in the current Appendix G.2. With the substitution the solution (A76) can be further rewritten. Integrals of this form have been approximated in Ref. [109].
Appendix G.3. SIV-Case b > 0, k = 0
In the case of a negligible recovery rate , implying , Equation (47) simplifies to:
or with (the index 0 indicates that the limit is considered here) and Equation (49):
Appendix G.3.1. Symmetry Argument
By a simple symmetry argument, the solution of Equation (A78) can be expressed in terms of the SIR-function [109] G obeying Equation (A59). Setting
Equation (A78) reads:
which is identical to Equation (A57). Therefore, one can use the SIR-function , obeying Equation (A59), but now with negative values of k, to obtain for the SIV solutions,
If to follow this approach, one needs to calculate the function G for negative values of k.
Appendix G.3.2. Alternative Inverse Solution
For , one obtains , so that Equation (37) reads:
As its argument is positive, it has to be the principal Lambert function in Equation (A83). Inserting the solution (A83) then provides for Equation (A82):
which, along with the initial condition (34), readily integrates to the inverse exact solution:
Here also, nearly all previous general results obtained in Section 3 and Section 4 hold with replaced by . With
implying
one finds for Equation (A86):
The substitution then yields:
which is an exact expression for the reduced time of the SIV model considered in the current Appendix G.3.
References
- Wang, Z.; Bausch, C.T.; Bhattacharyya, S.; d’Onofrio, A.; Manfredi, P.; Perc, M.; Perra, N.; Salathe, M.; Zhao, D.W. Statistical physics of vaccination. Phys. Rep. 2016, 664, 1–113. [Google Scholar] [CrossRef]
- Cadoni, M.; Gaeta, G. Size and timescale of epidemics in the SIR framework. Phys. D 2020, 411, 132626. [Google Scholar] [CrossRef] [PubMed]
- Chekroun, A.; Kuniya, T. Global threshold dynamics of aninfection age-structured SIR epidemic model with diffusion under the Dirichlet boundary condition. J. Differ. Equ. 2020, 269, 117–148. [Google Scholar] [CrossRef]
- Imron, C.; Hariyanto; Yunus, M.; Surjanto, S.D.; Dewi, N.A.C. Stability and persistence analysis on the epidemic model multi-region multi-patches. J. Phys. Conf. Ser. 2019, 1218, 012035. [Google Scholar] [CrossRef]
- Karaji, P.T.; Nyamoradi, N. Analysis of a fractional SIR model with general incidence function. Appl. Math. Lett. 2020, 108, 106499. [Google Scholar] [CrossRef]
- Mohamadou, Y.; Halidou, A.; Kapen, P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl. Intell. 2020. [Google Scholar] [CrossRef]
- Samanta, S.; Sahoo, B.; Das, B. Dynamics of an epidemic system with prey herd behavior and alternative resource to predator. J. Phys. A 2019, 52, 425601. [Google Scholar] [CrossRef]
- Sene, N. SIR epidemic model with Mittag-Leffler fractional derivative. Chaos Solitons Fractals 2020, 137, 109833. [Google Scholar] [CrossRef]
- Simon, M. SIR epidemics with stochastic infectious periods. Stoch. Proc. Appl. 2020, 130, 4252–4274. [Google Scholar] [CrossRef]
- Tian, C.R.; Zhang, Q.Y.; Zhang, L. Global stability in a networked SIR epidemic model. Appl. Math. Lett. 2020, 107, 106444. [Google Scholar] [CrossRef]
- El Koufi, A.; Adnani, J.; Bennar, A.; Yousfi, N. Analysis of a stochastic SIR model with vaccination and nonlinear incidence rate. Int. J. Diff. Equ. 2019, 2019, 9275051. [Google Scholar] [CrossRef]
- Houy, N. Are better vaccines really better? The case of a simple stochastic epidemic SIR model. Econ. Bull. 2013, 33, 207–216. [Google Scholar]
- Jornet-Sanz, M.; Corberan-Vallet, A.; Santonja, F.J.; Villanueva, R.J. A bayesian stochastic SIRS model with a vaccination strategy for the analysis of respiratory syncytial virus. Stat. Oper. Res. Trans. 2017, 41, 159–175. [Google Scholar]
- Li, X.N.; Zhang, Q.M. Time to extinction and stationary distribution of a stochastic susceptible-infected-recovered-susceptible model with vaccination under markov switching. Math. Popul. Stud. 2020, 27, 259–274. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.Q. The threshold of a stochastic delayed SIR epidemic model with vaccination. Phys. A 2016, 461, 140–147. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.Q.; Shi, N.Z.; Hayat, T. Dynamics of a stochastic delayed SIR epidemic model with vaccination and double diseases driven by levy jumps. Phys. A 2018, 492, 2010–2018. [Google Scholar] [CrossRef]
- Miao, A.Q.; Zhang, J.; Zhang, T.Q.; Pradeep, B. Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination. Comput. Math. Meth. Med. 2017, 2017, 4820183. [Google Scholar] [CrossRef]
- Nguyen, C.; Carlson, J.M. Optimizing real-time vaccine allocation in a stochastic SIR model. PLoS ONE 2016, 11, 0152950. [Google Scholar] [CrossRef]
- Wang, F.Y.; Wang, X.Y.; Zhang, S.W.; Ding, C.M. On pulse vaccine strategy in a periodic stochastic SIR epidemic model. Chaos Solitons Fractals 2014, 66, 127–135. [Google Scholar] [CrossRef]
- Wang, L.; Teng, Z.D.; Tang, T.T.; Li, Z.M. Threshold dynamics in stochastic SIRS epidemic models with nonlinear incidence and vaccination. Comput. Math. Meth. Med. 2017, 2017, 7294761. [Google Scholar] [CrossRef]
- Witbooi, P.J. Stability of a stochastic model of an SIR epidemic with vaccination. Acta Biotheor. 2017, 65, 151–165. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.Y.; Li, X.Y. The threshold of a stochastic delayed SIRS epidemic model with temporary immunity and vaccination. Chaos Solitons Fractals 2018, 111, 227–234. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, Q.L.; Li, A.H. Behavior of a stochastic SIR epidemic model with saturated incidence and vaccination rules. Phys. A 2018, 501, 178–187. [Google Scholar] [CrossRef]
- Zhao, X.; He, X.; Feng, T.; Qiu, Z.P. A stochastic switched SIRS epidemic model with nonlinear incidence and vaccination: Stationary distribution and extinction. Int. J. Biomath. 2020, 13, 2050020. [Google Scholar] [CrossRef]
- Colombo, R.M.; Garavello, M. Optimizing vaccination strategies in an age structured SIR model. Math. Biosci. Eng. 2020, 17, 1074–1089. [Google Scholar] [CrossRef]
- Cui, Q.Q.; Xu, J.B.; Zhang, Q.; Wang, K. An nsfd scheme for sir epidemic models of childhood diseases with constant vaccination strategy. Adv. Differ. Equ. 2014, 2014, 172. [Google Scholar] [CrossRef]
- D’Onofrio, A. Pulse vaccination strategy in the SIR epidemic model: Global asymptotic stable eradication in presence of vaccine failures. Math. Comput. Model. 2002, 36, 473–489. [Google Scholar] [CrossRef]
- d’Onofrio, A. On pulse vaccination strategy in the SIR epidemic model with vertical transmission. Appl. Math. Lett. 2005, 18, 729–732. [Google Scholar] [CrossRef]
- Gao, S.J.; Ouyang, H.S.; Nieto, J.J. Mixed vaccination strategy in SIRS epidemic model with seasonal variability on infection. Int. J. Biomath. 2011, 4, 473–491. [Google Scholar] [CrossRef]
- Gao, S.J.; Xie, D.H.; Chen, L.S. Pulse vaccination strategy in a delayed SIR epidemic model with vertical transmission. Discr. Contin. Dyn. Syst. B 2007, 7, 77–86. [Google Scholar] [CrossRef]
- Kabir, K.M.A.; Tanimoto, J. Vaccination strategies in a two-layer sir/v-ua epidemic model with costly information and buzz effect. Commun. Nonlin. Sci. Numer. Simul. 2019, 76, 92–108. [Google Scholar] [CrossRef]
- Li, J.Q.; Yang, Y.L. SIR-SVS epidemic models with continuous and impulsive vaccination strategies. J. Theor. Biol. 2011, 280, 108–116. [Google Scholar] [CrossRef]
- Liu, H.L.; Yu, J.Y.; Zhu, G.T. Global stability of an age-structured SIR epidemic model with pulse vaccination strategy. J. Syst. Sci. Complex. 2012, 25, 417–429. [Google Scholar] [CrossRef]
- Liu, L.; Luo, X.F.; Chang, L.L. Vaccination strategies of an SIR pair approximation model with demographics on complex networks. Chaos Solitons Fractals 2017, 104, 282–290. [Google Scholar] [CrossRef]
- Makinde, O.D. Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 2007, 184, 842–848. [Google Scholar] [CrossRef]
- Meng, X.Z.; Chen, L.S. The dynamics of a new SIR epidemic model concerning pulse vaccination strategy. Appl. Math. Comput. 2008, 197, 582–597. [Google Scholar] [CrossRef]
- Moneim, I.A.; Greenhalgh, D. Threshold and stability results for an SIRS epidemic model with a general periodic vaccination strategy. J. Biol. Syst. 2005, 13, 131–150. [Google Scholar] [CrossRef]
- Mu, X.J.; Zhang, Q.M.; Rong, L.B. Optimal vaccination strategy for an SIRS model with imprecise parameters and levy noise. J. Franklin Inst. Eng. Appl. Math. 2019, 356, 11385–11413. [Google Scholar] [CrossRef]
- Mungkasi, S. Variational iteration and successive approximation methods for a SIR epidemic model with constant vaccination strategy. Appl. Math. Model. 2021, 90, 1–10. [Google Scholar] [CrossRef]
- Pei, Y.Z.; Liu, S.Y.; Chen, L.S.; Wang, C.H. Two different vaccination strategies in an SIR epidemic model with saturated infectious force. Int. J. Biomath. 2008, 1, 147–160. [Google Scholar] [CrossRef]
- Rashidinia, J.; Sajjadian, M.; Duarte, J.; Januario, C.; Martins, N. On the dynamical complexity of a seasonally forced discrete SIR epidemic model with a constant vaccination strategy. Complexity 2018, 2018, 7191487. [Google Scholar] [CrossRef]
- Terry, A.J. PULSE vaccination strategies in a metapopulation SIR model. Math. Biosci. Eng. 2010, 7, 455–477. [Google Scholar] [PubMed]
- Zhou, L.H.; Wang, Y.; Xiao, Y.Y.; Li, M.Y. Global dynamics of a discrete age-structured SIR epidemic model with applications to measles vaccination strategies. Math. Biosci. 2019, 308, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Karatayev, V.A.; Anand, M.; Bauch, C.T. Local lockdowns outperform global lockdown on the far side of the COVID-19 epidemic curve. Proc. Natl. Acad. Sci. USA 2020, 117, 24575–24580. [Google Scholar] [CrossRef]
- Wang, X.; Jia, D.; Gao, S.; Xia, C.; Li, X.; Wang, Z. Vaccination behavior by coupling the epidemic spreading with the human decision under the game theory. Appl. Math. Comput. 2020, 380, 125232. [Google Scholar] [CrossRef]
- Priesemann, V.; Balling, R.; Brinkmann, M.M.; Ciesek, S.; Czypionka, T.; Eckerle, I.; Giordano, G.; Hanson, C.; Hel, Z.; Hotulainen, P.; et al. An action plan for pan-European defence against new SARS-CoV-2 variants. Lancet 2021, 397, 469–470. [Google Scholar] [CrossRef]
- Priesemann, V.; Brinkmann, M.M.; Ciesek, S.; Cuschieri, S.; Czypionka, T.; Giordano, G.; Gurdasani, D.; Hanson, C.; Hens, N.; Iftekhar, E.; et al. Calling for pan-European commitment for rapid and sustained reduction in SARS-CoV-2 infections. Lancet 2021, 397, 92–93. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Yang, K.; Zhou, K.; Liang, Y.T. Optimal vaccination policies for an SIR model with limited resources. Acta Biotheor. 2014, 62, 171–181. [Google Scholar] [CrossRef]
- Abouelkheir, I.; El Kihal, F.; Rachik, M.; Elmouki, I. Optimal impulse vaccination approach for an SIR control model with short-term immunity. Mathematics 2019, 7, 420. [Google Scholar] [CrossRef]
- Church, K.E.M.; Liu, X.Z. Analysis of a SIR model with pulse vaccination and temporary immunity: Stability, bifurcation and a cylindrical attractor. Nonlinear Anal. Real World Appl. 2019, 50, 240–266. [Google Scholar] [CrossRef]
- Gao, S.J.; Teng, Z.D.; Xie, D.H. Analysis of a delayed SIR epidemic model with pulse vaccination. Chaos Solitons Fractals 2009, 40, 1004–1011. [Google Scholar] [CrossRef]
- Gao, S.J.; Zhidong, Z.D.; Nieto, J.J.; Torres, A. Analysis of an SIR epidemic model with pulse vaccination and distributed time delay. J. Biomed. Biotechn. 2007, 2007, 64870. [Google Scholar] [CrossRef]
- He, Z.L.; Nie, L.F. The effect of pulse vaccination and treatment on SIR epidemic model with media impact. Discr. Dyn. Nat. Soc. 2015, 2015, 532494. [Google Scholar] [CrossRef]
- Jiang, G.R.; Yang, Q.G. Bifurcation analysis in an SIR epidemic model with birth pulse and pulse vaccination. Appl. Math. Comput. 2009, 215, 1035–1046. [Google Scholar] [CrossRef]
- Liu, X.S.; Dai, B.X. Qualitative and bifurcation analysis of an SIR epidemic model with saturated treatment function and nonlinear pulse vaccination. Discr. Dyn. Nat. Soc. 2016, 2016, 9146481. [Google Scholar] [CrossRef]
- Liu, X.S.; Dai, B.X. Flip bifurcations of an SIR epidemic model with birth pulse and pulse vaccination. Appl. Math. Model. 2017, 43, 579–591. [Google Scholar] [CrossRef]
- Lu, Z.H.; Chi, X.B.; Chen, L.S. The effect of constant and pulse vaccination on SIR epidemic model with horizontal and vertical transmission. Math. Comput. Model. 2002, 36, 1039–1057. [Google Scholar] [CrossRef]
- Meng, X.Z.; Chen, L.S. Global dynamical behaviors for an SIR epidemic model with time delay and pulse vaccination. Taiwan. J. Math. 2008, 12, 1107–1122. [Google Scholar] [CrossRef]
- Meng, X.Z.; Chen, L.S.; Wu, B. A delay SIR epidemic model with pulse vaccination and incubation times. Nonlin. Anal. Real World Appl. 2010, 11, 88–98. [Google Scholar] [CrossRef]
- Nie, L.F.; Teng, Z.D.; Torres, A. Dynamic analysis of an SIR epidemic model with state dependent pulse vaccination. Nonlin. Anal. Real World Appl. 2012, 13, 1621–1629. [Google Scholar] [CrossRef]
- Pang, G.P.; Chen, L.S. A delayed SIRS epidemic model with pulse vaccination. Chaos Solitons Fractals 2007, 34, 1629–1635. [Google Scholar] [CrossRef]
- Qin, W.J.; Tang, S.Y.; Cheke, R.A. Nonlinear pulse vaccination in an SIR epidemic model with resource limitation. Abstr. Appl. Anal. 2013, 2013, 670263. [Google Scholar] [CrossRef]
- Sekiguchi, M.; Ishiwata, E. Dynamics of a discretized SIR epidemic model with pulse vaccination and time delay. J. Comput. Appl. Math. 2011, 236, 997–1008. [Google Scholar] [CrossRef]
- Stone, L.; Shulgin, B.; Agur, Z. Theoretical examination of the pulse vaccination policy in the SIR epidemic model. Math. Comput. Model. 2000, 31, 207–215. [Google Scholar] [CrossRef]
- Wang, L. Existence of periodic solutions of seasonally forced SIR models with impulse vaccination. Taiwan. J. Math. 2015, 19, 1713–1729. [Google Scholar] [CrossRef]
- Zhang, X.B.; Huo, H.F.; Sun, X.K.; Fu, Q. The differential susceptibility SIR epidemic model with time delay and pulse vaccination. J. Appl. Math. Comput. 2010, 34, 287–298. [Google Scholar] [CrossRef]
- Zhang, X.B.; Huo, H.F.; Sun, X.K.; Fu, Q.A. The differential susceptibility SIR epidemic model with stage structure and pulse vaccination. Nonlin. Anal. Real World Appl. 2010, 11, 2634–2646. [Google Scholar] [CrossRef]
- Zhang, X.B.; Huo, H.F.; Xiang, H.; Meng, X.Y. An SIRS epidemic model with pulse vaccination and non-monotonic incidence rate. Nonlin. Anal. Hybrid Syst. 2013, 8, 13–21. [Google Scholar] [CrossRef]
- Zhao, W.C.; Li, J.; Meng, X.Z. Dynamical analysis of SIR epidemic model with nonlinear pulse vaccination and lifelong immunity. Discret. Dyn. Nat. Soc. 2015, 2015, 848623. [Google Scholar] [CrossRef]
- Zhao, Z.; Pang, L.Y.; Chen, Y. Nonsynchronous bifurcation of SIRS epidemic model with birth pulse and pulse vaccination. Nonlin. Dyn. 2015, 79, 2371–2383. [Google Scholar] [CrossRef]
- Zhou, A.R.; Sattayatham, P.; Jiao, J.J. Dynamics of an SIR epidemic model with stage structure and pulse vaccination. Adv. Diff. Equ. 2016, 2016, 140. [Google Scholar] [CrossRef]
- d’Onofrio, A.; Manfredi, P.; Salinelli, E. Bifurcation thresholds in an SIR model with information-dependent vaccination. Math. Model. Nat. Phenom. 2007, 2, 26–43. [Google Scholar] [CrossRef]
- Gumus, O.A.K.; Selvam, A.G.M.; Vianny, D.A. Bifucaction and stability analysis of a discrete time SIR epidemic model with vaccination. Int. J. Anal. Appl. 2019, 17, 809–820. [Google Scholar]
- Rostamy, D.; Mottaghi, E. Forward and backward bifurcation in a fractional-order SIR epidemic model with vaccination. Iran. J. Sci. Technol. Trans. A 2018, 42, 663–671. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Tang, B.; Tang, S.Y. Vaccination threshold size and backward bifurcation of SIR model with state-dependent pulse control. J. Theor. Biol. 2018, 455, 75–85. [Google Scholar] [CrossRef]
- Elazzouzi, A.; Alaoui, A.L.; Tilioua, M.; Tridane, A. Global stability analysis for a generalized delayed SIR model with vaccination and treatment. Adv. Diff. Equ. 2019, 2019, 532. [Google Scholar] [CrossRef]
- Laarabi, H.; Abta, A.; Hattaf, K. Optimal control of a delayed SIRS epidemic model with vaccination and treatment. Acta Biotheor. 2015, 63, 87–97. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.Q.; Hayat, T.; Ahmad, B. Analysis of a delayed vaccinated SIR epidemic model with temporary immunity and levy jumps. Nonlin. Anal. Hybrid Syst. 2018, 27, 29–43. [Google Scholar] [CrossRef]
- Tian, X.H. Stability analysis of a delayed SIRS epidemic model with vaccination and nonlinear incidence. Int. J. Biomath. 2012, 5, 1250050. [Google Scholar] [CrossRef]
- Bakare, E.A. On the optimal control of vaccination and treatments for an SIR-epidemic model with infected immigrants. Int. J. Ecol. Econ. Statist. 2016, 37, 82–104. [Google Scholar]
- Chapman, J.D.; Evans, N.D. The structural identifiability of susceptible-infective-recovered type epidemic models with incomplete immunity and birth targeted vaccination. Biomed. Signal Proc. Control 2009, 4, 278–284. [Google Scholar] [CrossRef]
- Guo, H.J.; Chen, L.S.; Song, X.Y. Dynamical properties of a kind of SIR model with constant vaccination rate and impulsive state feedback control. Int. J. Biomath. 2017, 10, 17500930. [Google Scholar] [CrossRef]
- Kar, T.K.; Batabyal, A. Stability analysis and optimal control of an SIR epidemic model with vaccination. Biosystems 2011, 104, 127–135. [Google Scholar] [CrossRef]
- Ledzewicz, U.; Schattler, H. ON optimal singular controls for a general sir-model with vaccination and treatment. Discr. Contin. Dyn. Syst. 2011, 31, 981–990. [Google Scholar]
- Rao, F.; Mandal, P.S.; Kang, Y. Complicated endemics of an SIRS model with a generalized incidence under preventive vaccination and treatment controls. Appl. Math. Model. 2019, 67, 38–61. [Google Scholar] [CrossRef]
- Rao, X.B.; Zhao, X.P.; Chu, Y.D.; Zhang, J.G.; Gao, J.S. The analysis of mode-locking topology in an SIR epidemic dynamics model with impulsive vaccination control: Infinite cascade of stern-brocot sum trees. Chaos Solitons Fractals 2020, 139, 110031. [Google Scholar] [CrossRef]
- Zeng, G.Z.; Chen, L.S.; Sun, L.H. Complexity of an SIR epidemic dynamics model with impulsive vaccination control. Chaos Solitons Fractals 2005, 26, 495–505. [Google Scholar] [CrossRef]
- Elbasha, E.H.; Podder, C.N.; Gumel, A.B. Analyzing the dynamics of an SIRS vaccination model with waning natural and vaccine-induced immunity. Nonlin. Anal. Real World Appl. 2011, 12, 2692–2705. [Google Scholar] [CrossRef]
- Hui, J.; Chen, L.S. Impulsive vaccination of SIR epidemic models with nonlinear incidence rates. Discr. Contin. Dyn. Syst. B 2004, 4, 595–605. [Google Scholar] [CrossRef]
- Khader, M.M.; Adel, M. Numerical treatment of the fractional modeling on susceptible-infected-recovered equations with a constant vaccination rate by using gem. Int. J. Nonlin. Sci. Numer. Simul. 2019, 20, 69–75. [Google Scholar] [CrossRef]
- Li, B.L.; Qin, C.Y.; Wang, X. Analysis of an SIRS epidemic model with nonlinear incidence and vaccination. Commun. Math. Biol. Neurosci. 2020, 2020, 4262. [Google Scholar]
- Sun, C.J.; Yang, W. Global results for an SIRS model with vaccination and isolation. Nonlin. Anal. Real World Appl. 2010, 11, 4223–4237. [Google Scholar] [CrossRef]
- Lahrouz, A.; Omari, L.; Kiouach, D.; Belmaati, A. Complete global stability for an SIRS epidemic model with generalized non-linear incidence and vaccination. Appl. Math. Comput. 2012, 218, 6519–6525. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S.; Zhu, P.; Wang, J. Roles of different update strategies in the vaccination behavior on two-layered networks. Phys. Lett. A 2020, 384, 126224. [Google Scholar] [CrossRef]
- Assadouq, A.; El Mahjour, H.; Settati, A. Qualitative behavior of a SIRS epidemic model with vaccination on heterogeneous networks. Ital. J. Pure Appl. Math. 2020, 43, 958–974. [Google Scholar]
- Le Chang, S.; Piraveenan, M.; Prokopenko, M. The effects of imitation dynamics on vaccination behaviours in sir-network model. Int. J. Environ. Res. Public Health 2019, 16, 16142477. [Google Scholar] [CrossRef]
- Auchincloss, A.H.; Roux, A.V.D. A new tool for epidemiology: The usefulness of dynamic-agent models in understanding place effects on health. Am. J. Epidemiol. 2008, 168, 1–8. [Google Scholar] [CrossRef]
- Ajelli, M.; Goncalves, B.; Balcan, D.; Colizza, V.; Hu, H.; Ramasco, J.J.; Merler, S.; Vespignani, A. Comparing large-scale computational approaches to epidemic modeling: Agent-based versus structured metapopulation models. BMC Infect. Dis. 2010, 10, 190. [Google Scholar] [CrossRef]
- Schüttler, J.; Schlickeiser, R.; Schlickeiser, F.; Kröger, M. Covid-19 predictions using a Gauss model, based on data from April 2. Physics 2020, 2, 197–212. [Google Scholar] [CrossRef]
- Yildirim, A.; Cherruault, Y. Analytical approximate solution of a SIR epidemic model with constant vaccination strategy by homotopy perturbation method. Kybernetes 2009, 38, 1566–1575. [Google Scholar] [CrossRef]
- Heng, K.; Althaus, C.L. The approximately universal shapes of epidemic curves in the susceptible-exposed-infectious-recovered (SEIR) model. Sci. Rep. 2020, 10, 19365. [Google Scholar] [CrossRef]
- Barlow, N.S.; Weinstein, S.J. Accurate closed-form solution of the SIR epidemic model. Phys. D 2020, 408, 132540. [Google Scholar] [CrossRef]
- Bidari, S.; Chen, X.Y.; Peters, D.; Pittman, D.; Simon, P.L. Solvability of implicit final size equations for SIR epidemic models. Math. Biosci. 2016, 282, 181–190. [Google Scholar] [CrossRef]
- Carvalho, A.M.; Goncalves, S. An analytical solution for the Kermack-McKendrick model. Phys. A 2021, 566, 125659. [Google Scholar] [CrossRef]
- Guerrero, F.; Santonja, F.J.; Villanueva, R.J. Solving a model for the evolution of smoking habit in Spain with homotopy analysis method. Nonlinear Anal. Real World Appl. 2013, 14, 549–558. [Google Scholar] [CrossRef]
- Khan, H.; Mohapatra, R.N.; Vajravelu, K.; Liao, S.J. The explicit series solution of SIR and SIS epidemic models. Appl. Math. Comput. 2009, 215, 653–669. [Google Scholar] [CrossRef]
- Liu, J.L.; Peng, B.Y.; Zhang, T.L. Effect of discretization on dynamical behavior of SEIR and SIR models with nonlinear incidence. Appl. Math. Lett. 2015, 39, 60–66. [Google Scholar] [CrossRef]
- Van Mieghem, P. Approximate formula and bounds for the time-varying susceptible-infected-susceptible prevalence in networks. Phys. Rev. E 2016, 93, 052312. [Google Scholar] [CrossRef]
- Kröger, M.; Schlickeiser, R. Analytical solution of the SIR-model for the temporal evolution of epidemics. Part A: Time-independent reproduction factor. J. Phys. A Math. Theor. 2020, 53, 505601. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the temporal evolution of epidemics. Part B: Semi-time case. J. Phys. A Math. Theor. 2021, 54, 175601. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Explicit formulae for the peak time of an epidemic from the SIR model. Phys. D 2021, 422, 132902. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. Covid-19 and Sars-Cov-2. Modeling the present, looking at the future. Phys. Rep. 2020, 869, 1. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Schlickeiser, R. Forecast for the second Covid-19 wave based on the improved SIR-model with a constant ratio of recovery to infection rate. Preprints 2021, 2021010449. [Google Scholar] [CrossRef]
- Morton, R.; Wickwire, K.H. On the optimal control of a deterministic epidemic. Adv. Appl. Probab. 1974, 6, 622–635. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford Science Publications: Oxford, UK, 1991. [Google Scholar]
- Behncke, H. Optimal control of deterministic epidemics. Optim. Control Appl. Methods 2000, 21, 269–285. [Google Scholar] [CrossRef]
- Hansen, E.; Day, T. Optimal control of epidemics with limited resources. J. Math. Biol. 2011, 62, 423–451. [Google Scholar] [CrossRef]
- Grauer, J.; Löwen, H.; Liebchen, B. Strategic spatiotemporal vaccine distribution increases the survival rate in an infectious disease like Covid-19. Sci. Rep. 2021, 10, 21594. [Google Scholar] [CrossRef]
- Grundel, S.; Heyder, S.; Hotz, T.; Ritschel, T.K.S.; Sauerteig, P.; Worthmann, K. How to coordinate vaccination and social distancing to mitigate SARS-CoV-2 outbreaks. medRxiv 2020, 2020, 20248707. [Google Scholar] [CrossRef]
- Duclos, T.; Reichert, T. The missing Link: A closed form solution to the Kermack and McKendrick epidemic model equations. medRxiv 2021, 2021, 21252781. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; National Bureau of Standards: Washington, DC, USA, 1972.
- Kröger, M.; Schlickeiser, R. Gaussian doubling times and reproduction factors of the COVID-19 pandemic disease. Front. Phys. 2020, 8, 276. [Google Scholar] [CrossRef]
- Data Repository. 2021. Available online: https://github.com/owid/covid-19-data/blob/master/public/data/vaccinations/vaccinations.csv (accessed on 20 May 2021).
- Data Repository. 2021. Available online: https://www.complexfluids.ethz.ch/cgi-bin/covid19-waveII (accessed on 20 May 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).