The Dynamical Casimir Effect in a Dissipative Optomechanical Cavity Interacting with Photonic Crystal
Abstract
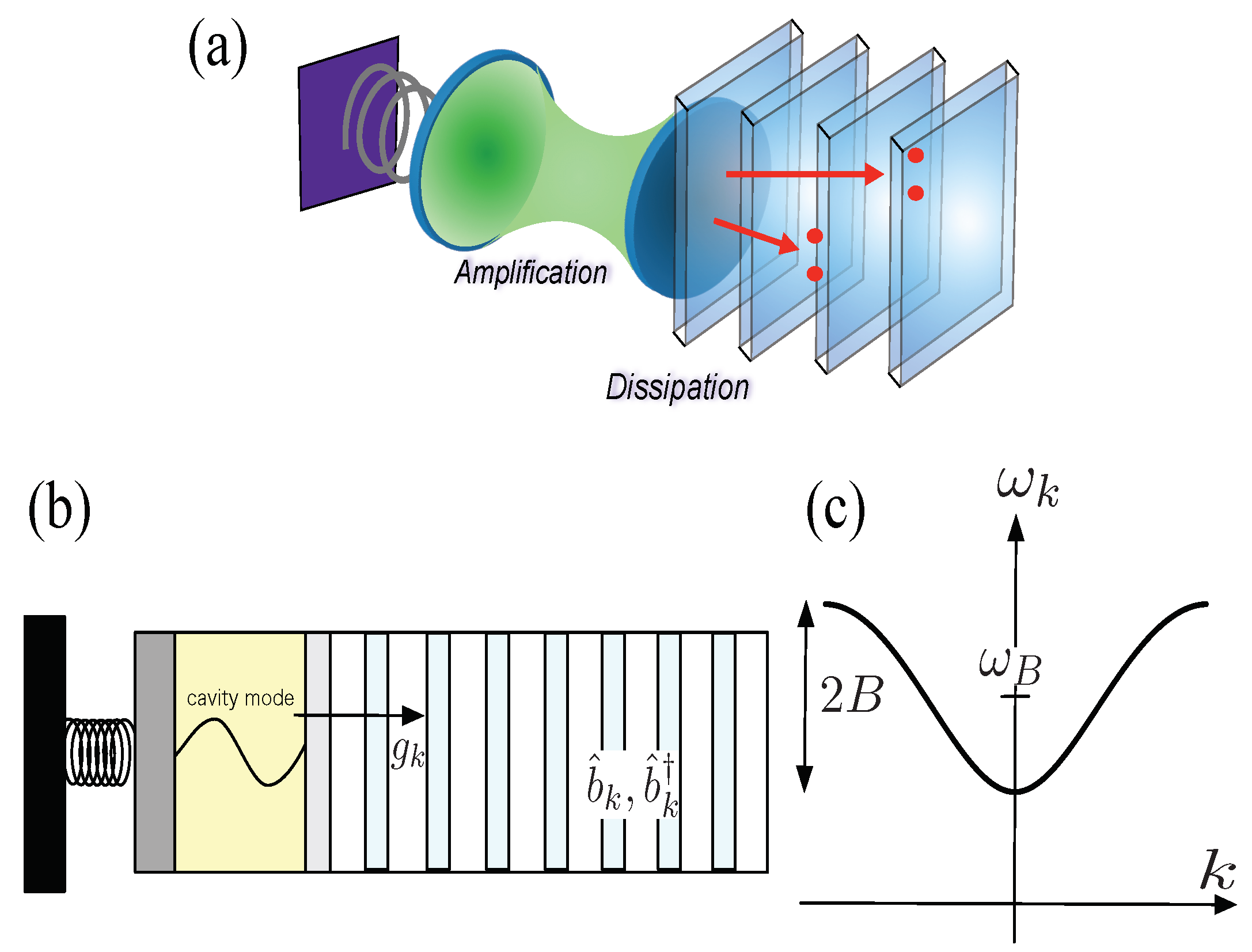
1. Introduction
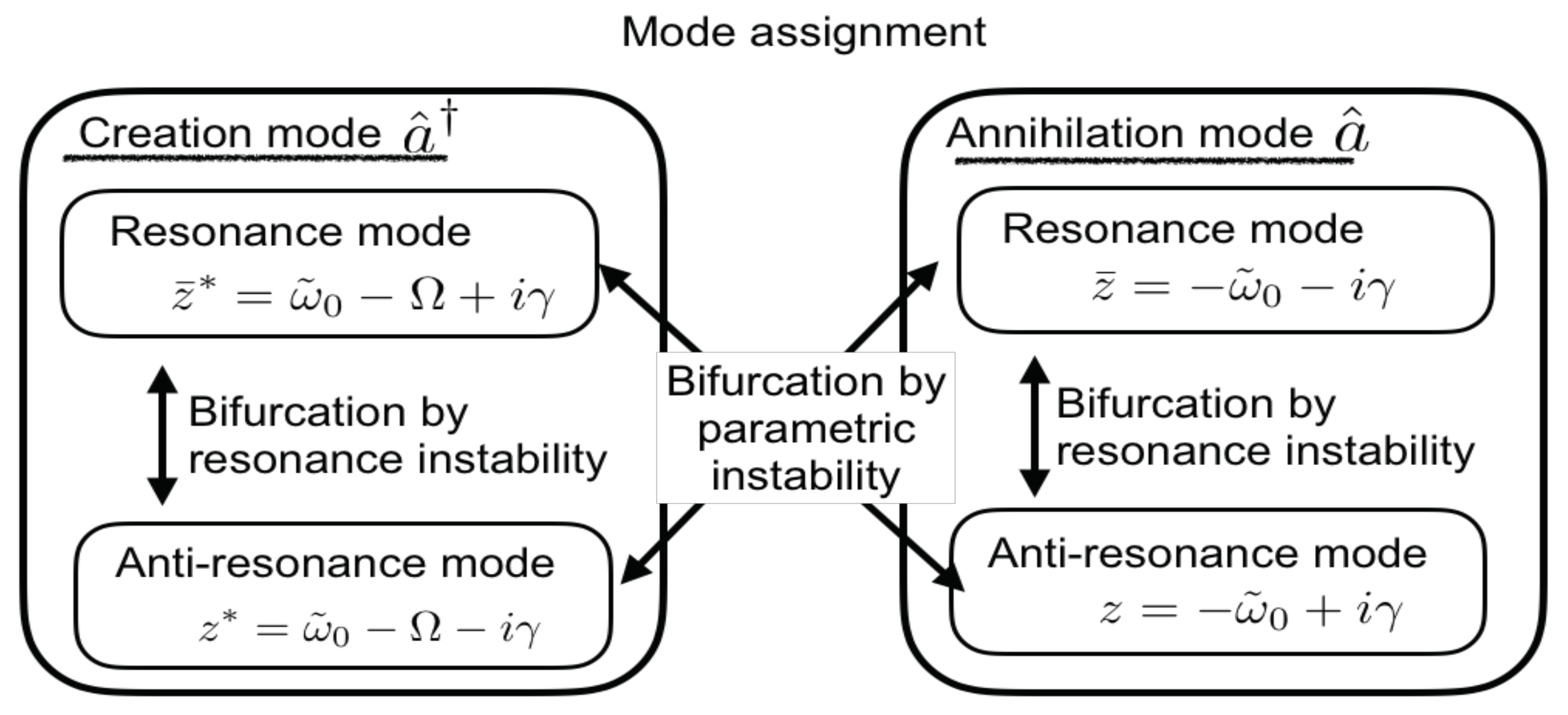
2. Model and Floquet–Liouvillian
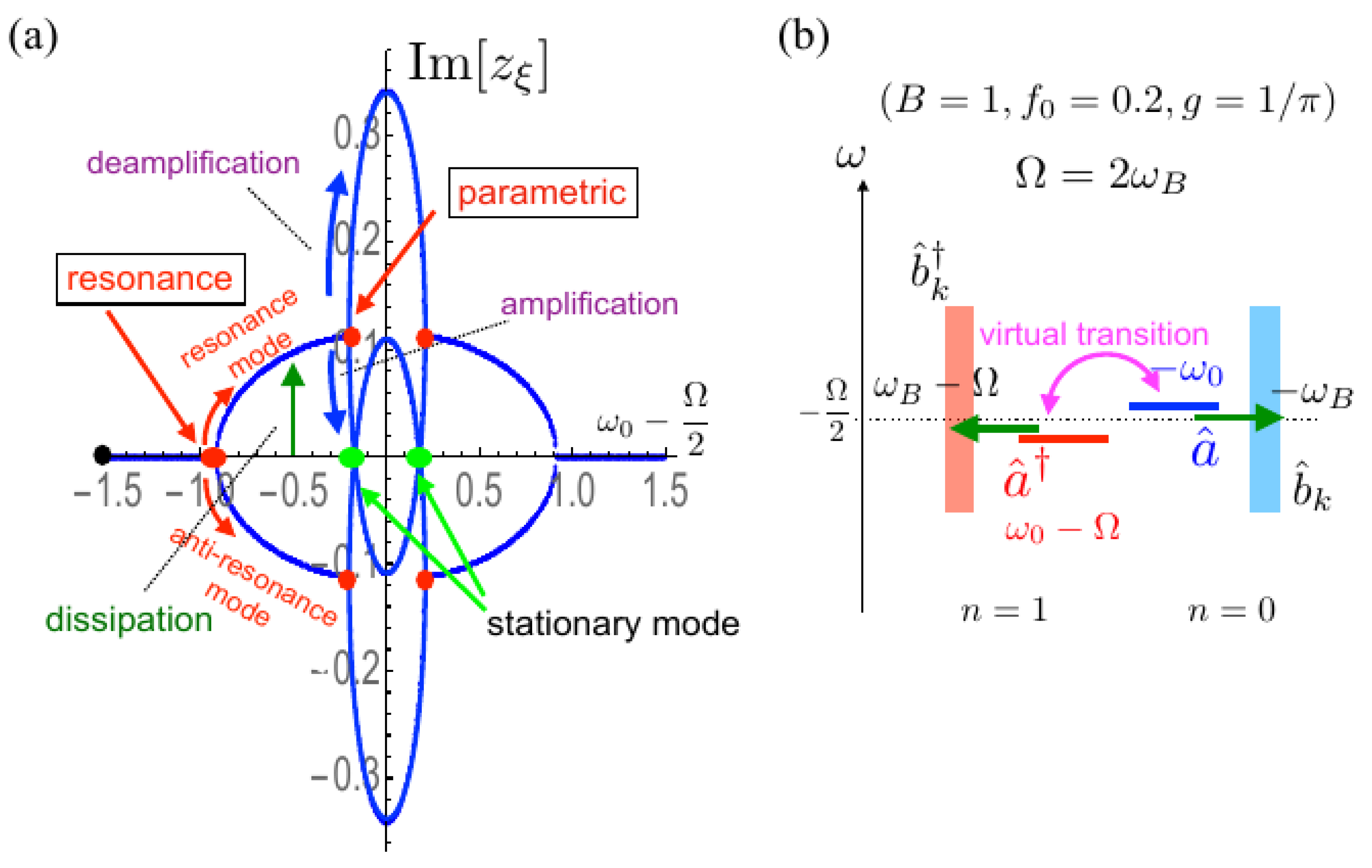
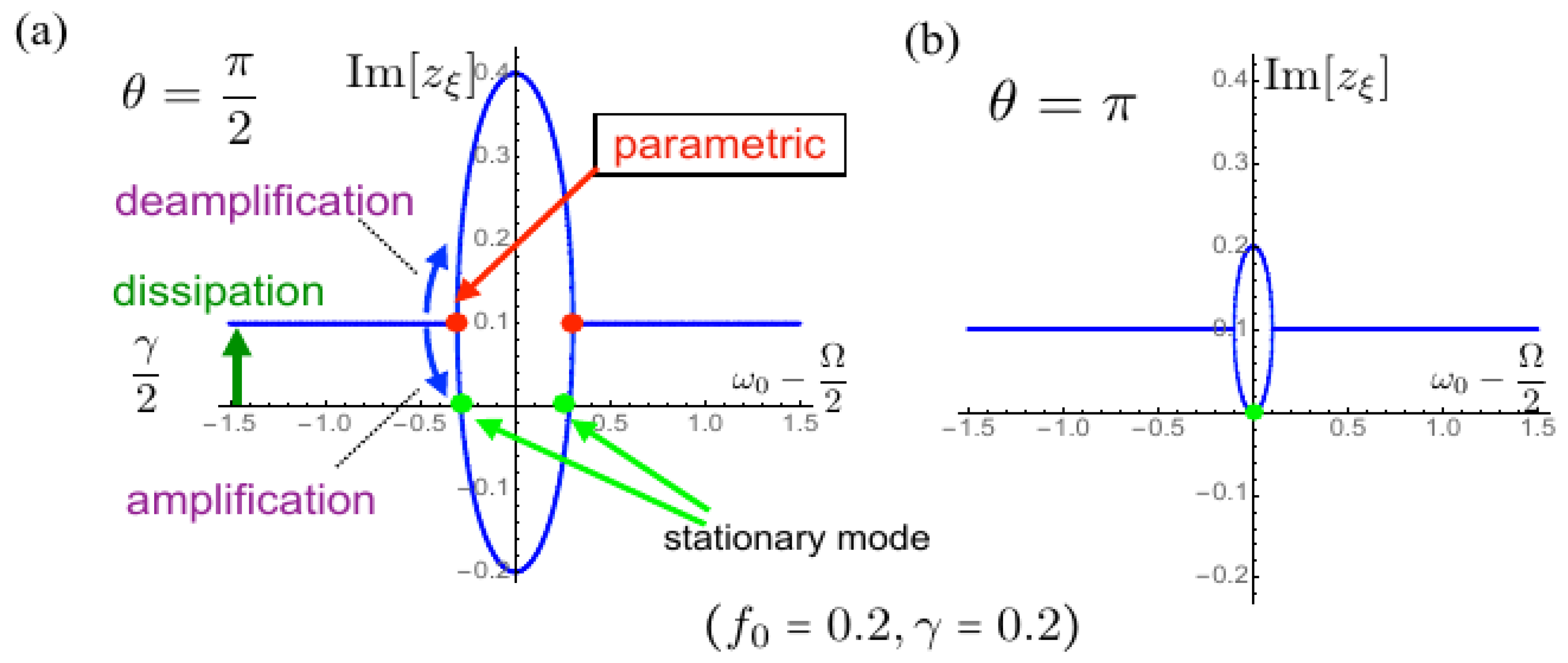
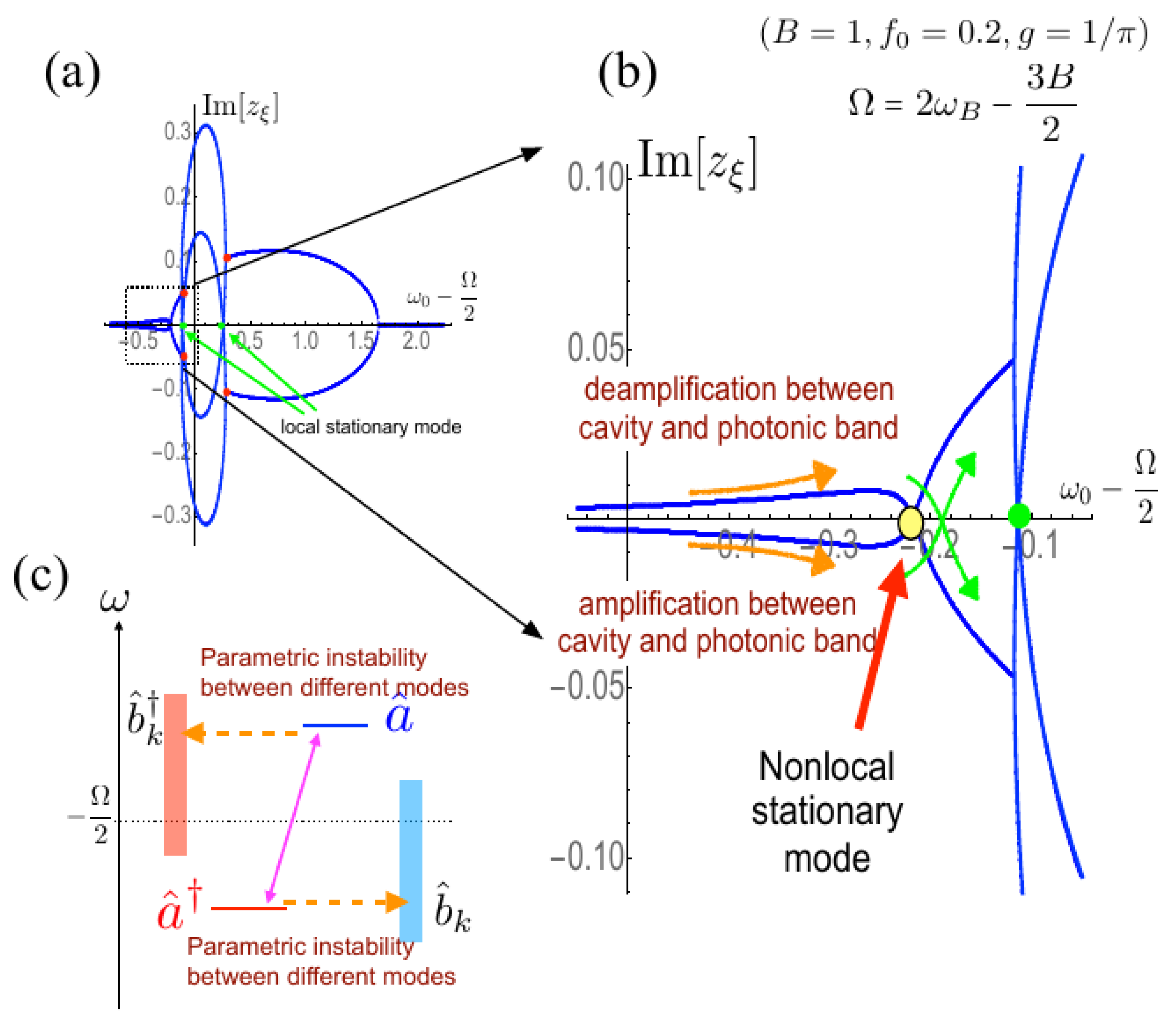
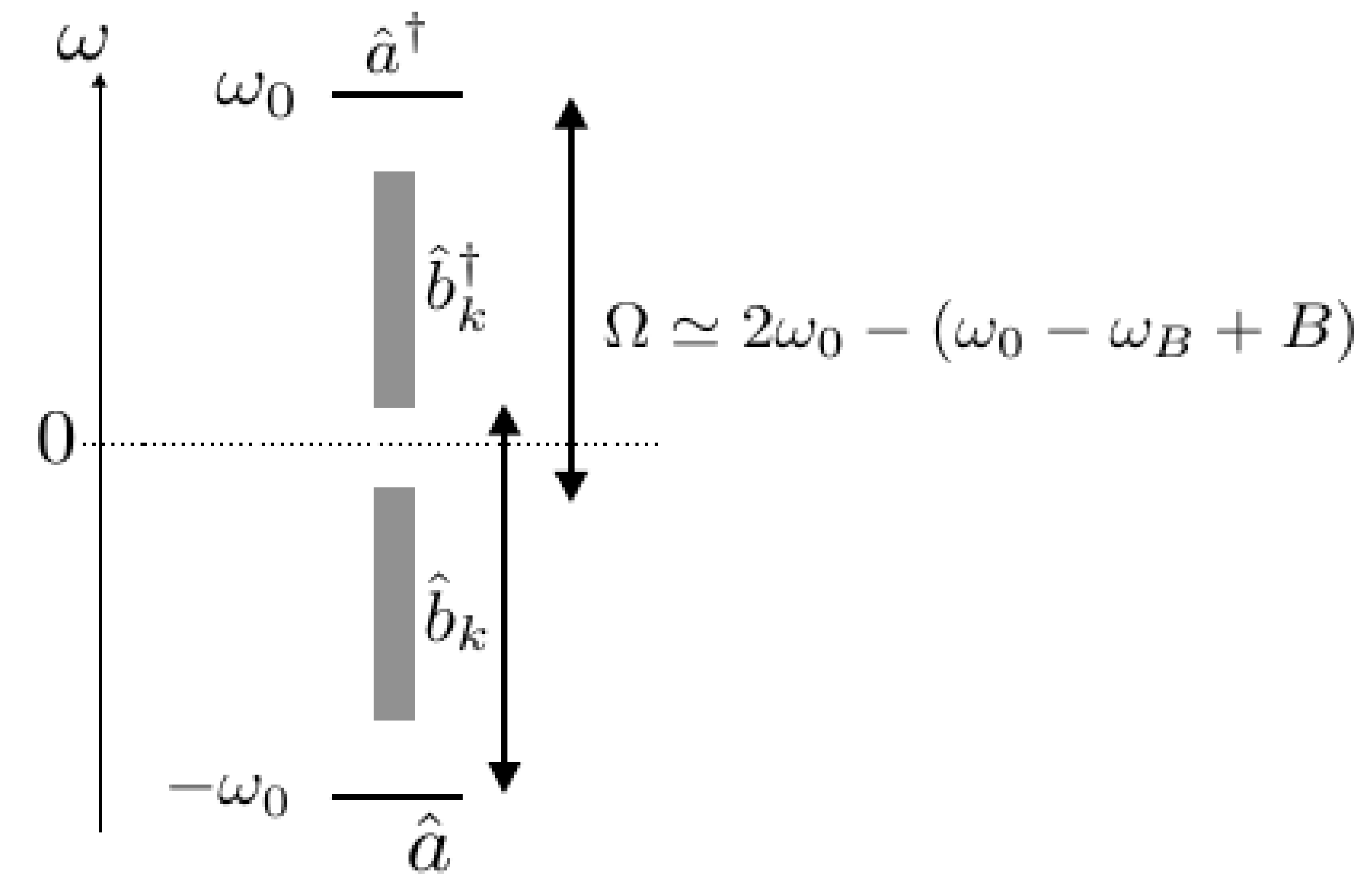
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Floquet–Liouvillian Complex Eigenvalue Problem and Effective Operator


References
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Lamb, W.E.; Retherford, R.C. Fine Structure of the Hydrogen Atom by a Microwave Method. Phys. Rev. 1947, 72, 241–243. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Quantum Theory of the Emission and Absorption of Radiation. Proc. R. Soc. Ser. A 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Weisskopf, V.; Wigner, E. Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie. Z. Phys. 1930, 63, 54–73. [Google Scholar] [CrossRef]
- Casimir, H.B.G.; Polder, D. The influence of retardation on the London-van der Waals forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Demonstration of the casimir force in the 0.6 to 6 µm range. Phys. Rev. Lett. 1997, 78, 5–8. [Google Scholar] [CrossRef]
- Moore, G.T. Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity. J. Math. Phys. 1970, 11, 2679–2691. [Google Scholar] [CrossRef]
- Fulling, S.A.; Davies, P.C.W.; Penrose, R. Radiation from a moving mirror in two-dimensional space-time: Conformal anomaly. Proc. R. Soc. Lond. Ser. A 1976, 348, 393–414. [Google Scholar] [CrossRef]
- Dodonov, V.V. Current status of the dynamical Casimir effect. Phys. Scr. 2010, 82. [Google Scholar] [CrossRef]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1–24. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376–379. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 2013, 110, 4234–4238. [Google Scholar] [CrossRef]
- Carmichael, H.J. Statistical Methods in Quantum Optics 2: Non-Classical Fields; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Mollow, B.; Glauber, R. Quantum Theory of Parametric Amplification. I. Phys. Rev. 1986, 160, 1076–1096. [Google Scholar] [CrossRef]
- Wu, L.A.; Xiao, M.; Kimble, H.J. Squeezed states of light from an optical parametric oscillator. J. Opt. Soc. Am. B 1987, 4, 1465. [Google Scholar] [CrossRef]
- Kohler, S.; Dittrich, T.; Hänggi, P. Floquet-Markovian description of the parametrically driven, dissipative harmonic quantum oscillator. Phys. Rev. E 1997, 55, 300–313. [Google Scholar] [CrossRef]
- Bender, C.M.; Dorey, P.E.; Dunning, C.; Fring, A.; Hook, D.W.; Jones, H.F.; Kuzhel, S.; Lévai, G.; Tateo, R. PT Symmetry; World Scientific: London, UK, 2019. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Prigogine, I. Time, structure, and fluctuations (Nobel Lecture, December 8, 1977). In Nobel Lectures in Chemistry 1971–1980; World Scientific Publishing Co.: Singapore, 1993. [Google Scholar]
- Petrosky, T.; Prigogine, I.; Tasaki, S. Quantum theory of non-integrable systems. Physica A 1991, 173, 175–242. [Google Scholar] [CrossRef]
- Prigogine, I. Dissipative processes in quantum theory. Phys. Rep. 1992, 219, 93–108. [Google Scholar] [CrossRef]
- Prigogine, I. Laws of nature, probability and time symmetry breaking. Physica A 1999, 263, 528–539. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Atom-Photon Interactions: Basic Processes and Applications; Wiley Interscience: New York, NY, USA, 1998. [Google Scholar]
- Collett, M.J.; Gardiner, C.W. Squeezing of intracavity and traveling-wave light fields produced in parametric amplification. Phys. Rev. A 1984, 30, 1386–1391. [Google Scholar] [CrossRef]
- Ciuti, C.; Carusotto, I. Input-output theory of cavities in the ultrastrong coupling regime: The case of time-independent cavity parameters. Phys. Rev. A 2006, 74, 033811. [Google Scholar] [CrossRef]
- Carmichael, H.J. Spectrum of squeezing and photocurrent shot noise: A normally ordered treatment. J. Opt. Soc. Am. B 1987, 4, 1588–1603. [Google Scholar] [CrossRef]
- De Liberato, S.; Gerace, D.; Carusotto, I.; Ciuti, C. Extracavity quantum vacuum radiation from a single qubit. Phys. Rev. A 2009, 80, 053810. [Google Scholar] [CrossRef]
- John, S.; Wang, J. Quantum electrodynamics near a photonic band gap: Photon bound states and dressed atoms. Phys. Rev. Lett. 1990, 64, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- John, S.; Quang, T. Spontaneous emission near the edge of a photonic band gap, 1994. Phys. Rev. A 1994, 50, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- De Liberato, S. Light-matter decoupling in the deep strong coupling regime: The breakdown of the purcell effect. Phys. Rev. Lett. 2014, 112, 016401. [Google Scholar] [CrossRef] [PubMed]
- Calajò, G.; Rizzuto, L.; Passante, R. Control of spontaneous emission of a single quantum emitter through a time-modulated photonic-band-gap environment. Phys. Rev. A 2017, 96, 023802. [Google Scholar] [CrossRef]
- Rybin, M.V.; Zherzdev, A.V.; Feoktistov, N.A.; Pevtsov, A.B. Effect of photonic crystal stop-band on photoluminescence of a-Si1-x Cx: H. Phys. Rev. B 2017, 95, 165118. [Google Scholar] [CrossRef]
- Xiang, Z.L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623–653. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Settineri, A.; Macrì, V.; Garziano, L.; Di Stefano, O.; Nori, F.; Savasta, S. Conversion of mechanical noise into correlated photon pairs: Dynamical Casimir effect from an incoherent mechanical drive. Phys. Rev. A 2019, 100, 022501. [Google Scholar] [CrossRef]
- Macrì, V.; Ridolfo, A.; Di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Nonperturbative Dynamical Casimir Effect in Optomechanical Systems: Vacuum Casimir-Rabi Splittings. Phys. Rev. X 2018, 8, 11031. [Google Scholar] [CrossRef]
- de M. e Souza, R.; Impens, F.; Neto, P.A.M. Microscopic dynamical Casimir effect. Phys. Rev. A 2018, 97, 032513. [Google Scholar] [CrossRef]
- Farías, M.B.; Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Motion induced radiation and quantum friction for a moving atom. Phys. Rev. D 2019, 100, 036013. [Google Scholar] [CrossRef]
- Petrosky, T.; Ordonez, G.; Prigogine, I. Quantum transitions and nonlocality. Phys. Rev. A 2000, 62, 042106. [Google Scholar] [CrossRef]
- Karpov, E.; Prigogine, I.; Petrosky, T.; Pronko, G. Friedrichs model with virtual transitions. Exact solution and indirect spectroscopy. J Math. Phys. 2000, 41, 118–131. [Google Scholar] [CrossRef]
- Petrosky, T.; Ordonez, G.; Prigogine, I. Space-time formulation of quantum transitions. Phys. Rev. A 2001, 64, 062101. [Google Scholar] [CrossRef]
- Ordóez, G.; Petrosky, T.; Karpov, E.; Prigogine, I. Explicit construction of a time superoperator for quantum unstable systems. Chaos Solitons Fractals 2001, 12, 2591–2601. [Google Scholar] [CrossRef]
- Hatano, N.; Nelson, D.R. Vortex pinning and non-Hermitian quantum mechanics. Phys. Rev. B 1997, 56, 8651–8673. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Petrosky, T. Nonanalytic enhancement of the charge transfer from adatom to one-dimensional semiconductor superlattice and optical absorption spectrum. Phys. Rev. B 2006, 73, 115340. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Ordonez, G.; Petrosky, T. Electron trapping in a one-dimensional semiconductor quantum wire with multiple impurities. Phys. Rev. B 2007, 76, 153308. [Google Scholar] [CrossRef]
- Tanaka, S.; Passante, R.; Fukuta, T.; Petrosky, T. Nonperturbative approach for the electronic Casimir-Polder effect in a one-dimensional semiconductor. Phys. Rev. A 2013, 88, 022518. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Kanki, K.; Petrosky, T. Higher-order time-symmetry-breaking phase transition due to meeting of an exceptional point and a Fano resonance. Phys. Rev. A 2016, 94, 022105. [Google Scholar] [CrossRef]
- Sambe, H. Steady states and quasienergies of a quantum-mechanical system in an oscillating field. Phys. Rev. A 1973, 7, 2203–2213. [Google Scholar] [CrossRef]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions. II. Ann. Phys. 1962, 19, 287–313. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A 2009, 42, 153001. [Google Scholar] [CrossRef]
- Hatano, N. Equivalence of the effective Hamiltonian approach and the Siegert boundary condition for resonant states. Fortschr. Phys. 2013, 61, 238–249. [Google Scholar] [CrossRef]
- Kanki, K.; Garmon, S.; Tanaka, S.; Petrosky, T. Exact description of coalescing eigenstates in open quantum systems in terms of microscopic Hamiltonian dynamics. J. Math. Phys. 2017, 58, 092101. [Google Scholar] [CrossRef]
- Yamane, H.; Tanaka, S. Ultrafast Dynamics of High-Harmonic Generation in Terms of Complex Floquet Spectral Analysis. Symmetry 2018, 10, 313. [Google Scholar] [CrossRef]
- Law, C.K. Effective Hamiltonian for the radiation in a cavity with a moving mirror and a time-varying dielectric medium. Phys. Rev. A 1994, 49, 433–437. [Google Scholar] [CrossRef]
- Law, C.K. Interaction between a moving mirror and radiation pressure: A Hamiltonian formulation. Phys. Rev. A 1995, 51, 2537–2541. [Google Scholar] [CrossRef] [PubMed]
- Loudon, R. The Quantum Theory of Light; OUP Oxford: Oxford, UK, 2000. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Photons and Atoms: Introduction to Quantum Electrodynamics; Wiley-VCH: Hoboken, NJ, USA, 1989. [Google Scholar]
- Fukuta, T.; Garmon, S.; Kanki, K.; Noba, K.I.; Tanaka, S. Fano absorption spectrum with the complex spectral analysis. Phys. Rev. A 2017, 96, 052511. [Google Scholar] [CrossRef]
- Tanaka, S.; Fukuta, T.; Petrosky, T. Study of Fano Resonance in the Core-Level Absorption Spectrum in Terms of Complex Spectral Analysis. In Fano Resonances in Optics and Microwaves: Physics and Applications; Kamenetskii, E., Sadreev, A., Miroshnichenko, A., Eds.; Springer: Cham, Switzerland, 2018; pp. 261–281. [Google Scholar] [CrossRef]
- Shirley, J.H. Solution of the Schrodinger Equation with a Hamiltonian Periodic in Time. Phys. Rev. 1965, 138, B979. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, S.; Kanki, K. The Dynamical Casimir Effect in a Dissipative Optomechanical Cavity Interacting with Photonic Crystal. Physics 2020, 2, 34-48. https://doi.org/10.3390/physics2010005
Tanaka S, Kanki K. The Dynamical Casimir Effect in a Dissipative Optomechanical Cavity Interacting with Photonic Crystal. Physics. 2020; 2(1):34-48. https://doi.org/10.3390/physics2010005
Chicago/Turabian StyleTanaka, Satoshi, and Kazuki Kanki. 2020. "The Dynamical Casimir Effect in a Dissipative Optomechanical Cavity Interacting with Photonic Crystal" Physics 2, no. 1: 34-48. https://doi.org/10.3390/physics2010005
APA StyleTanaka, S., & Kanki, K. (2020). The Dynamical Casimir Effect in a Dissipative Optomechanical Cavity Interacting with Photonic Crystal. Physics, 2(1), 34-48. https://doi.org/10.3390/physics2010005




