Design of a Compact Microreactor/Heat-Exchanger for a Distributed Production of Liquid Hydrocarbons from Methanol
Abstract
:1. Introduction
1.1. Methanol-to-Hydrocarbon Process
1.2. Application of Structured Catalysts and Reactors
2. Reactor Design and Reaction Kinetics
Heat Transfer Modelling
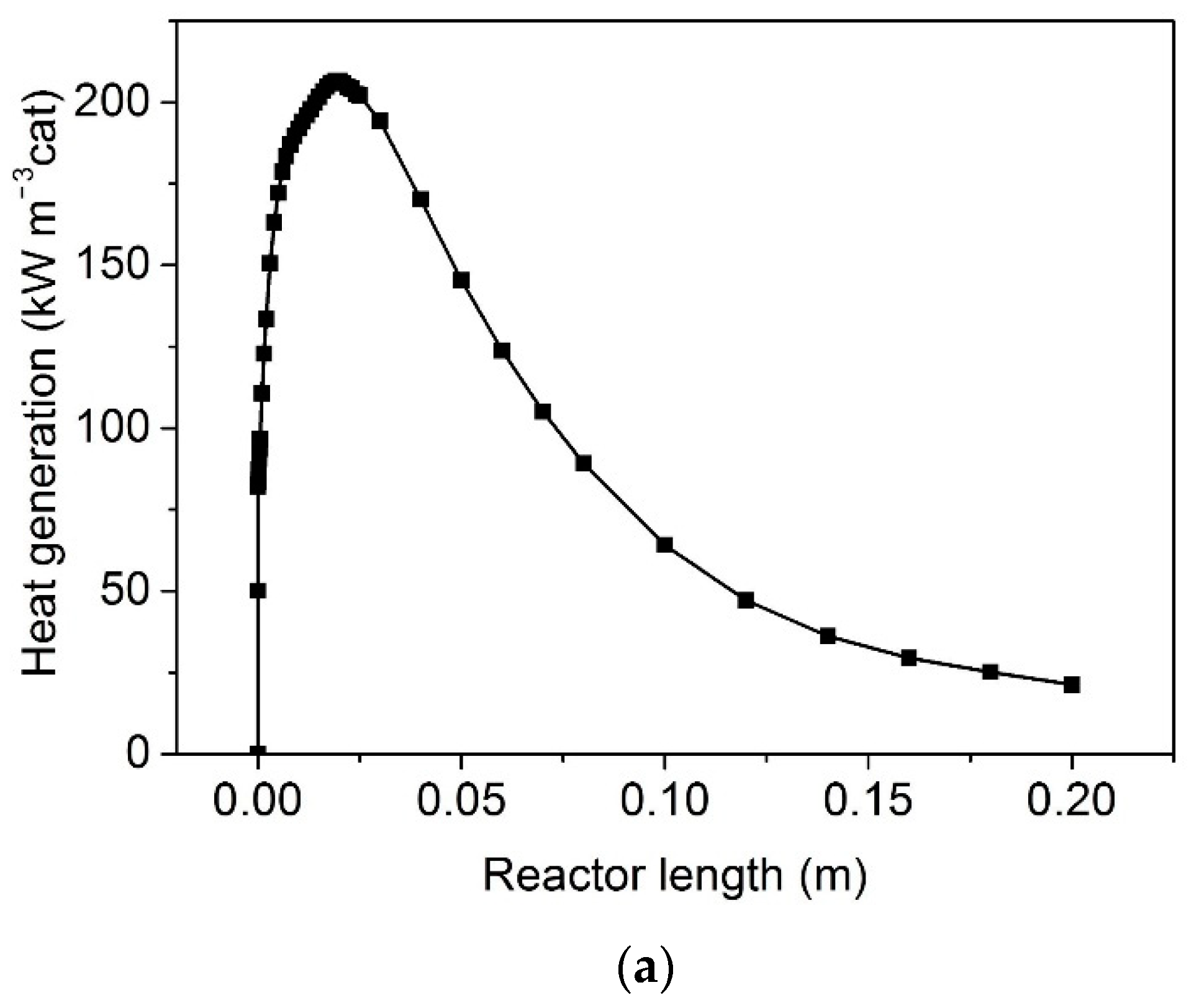
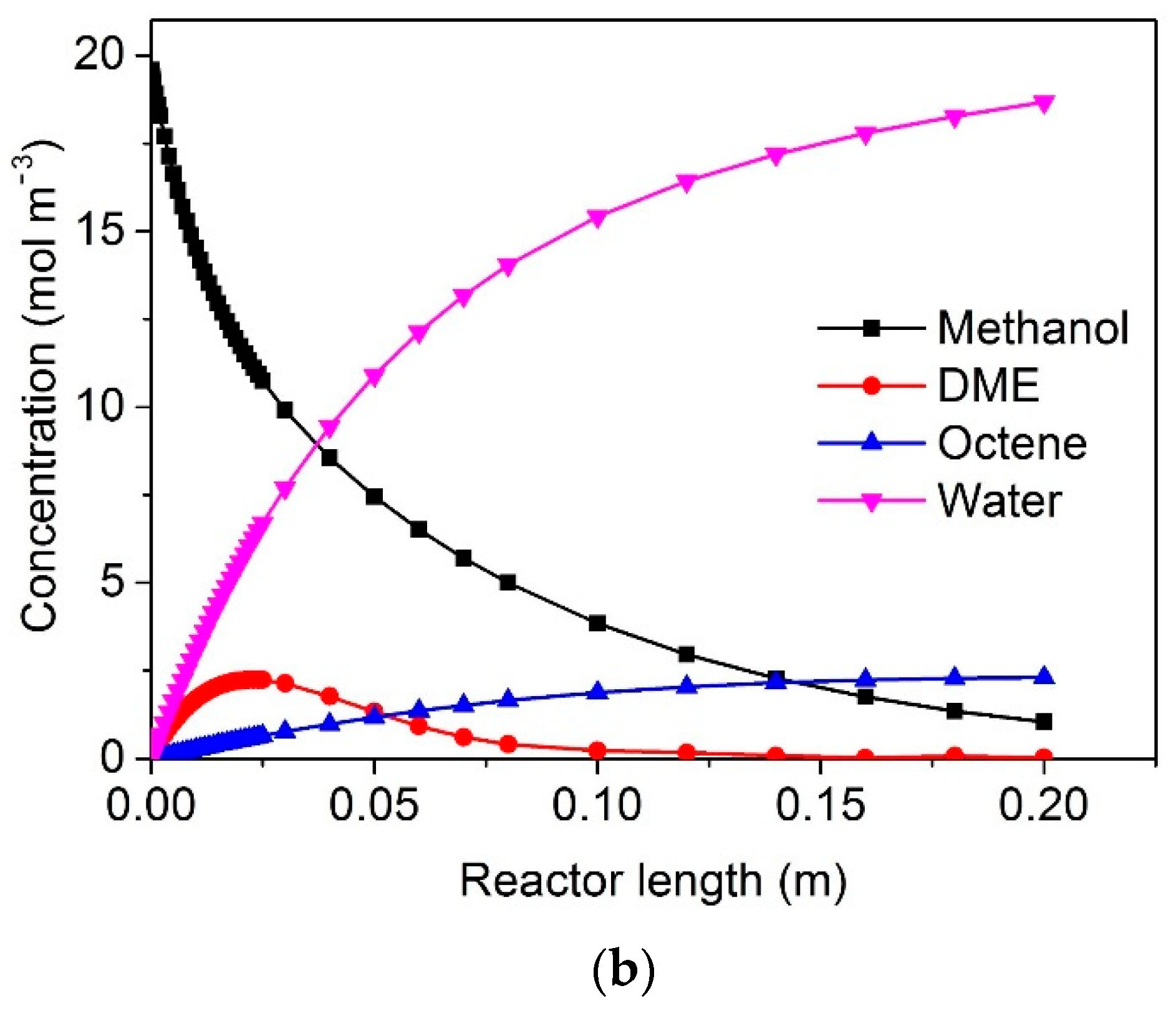
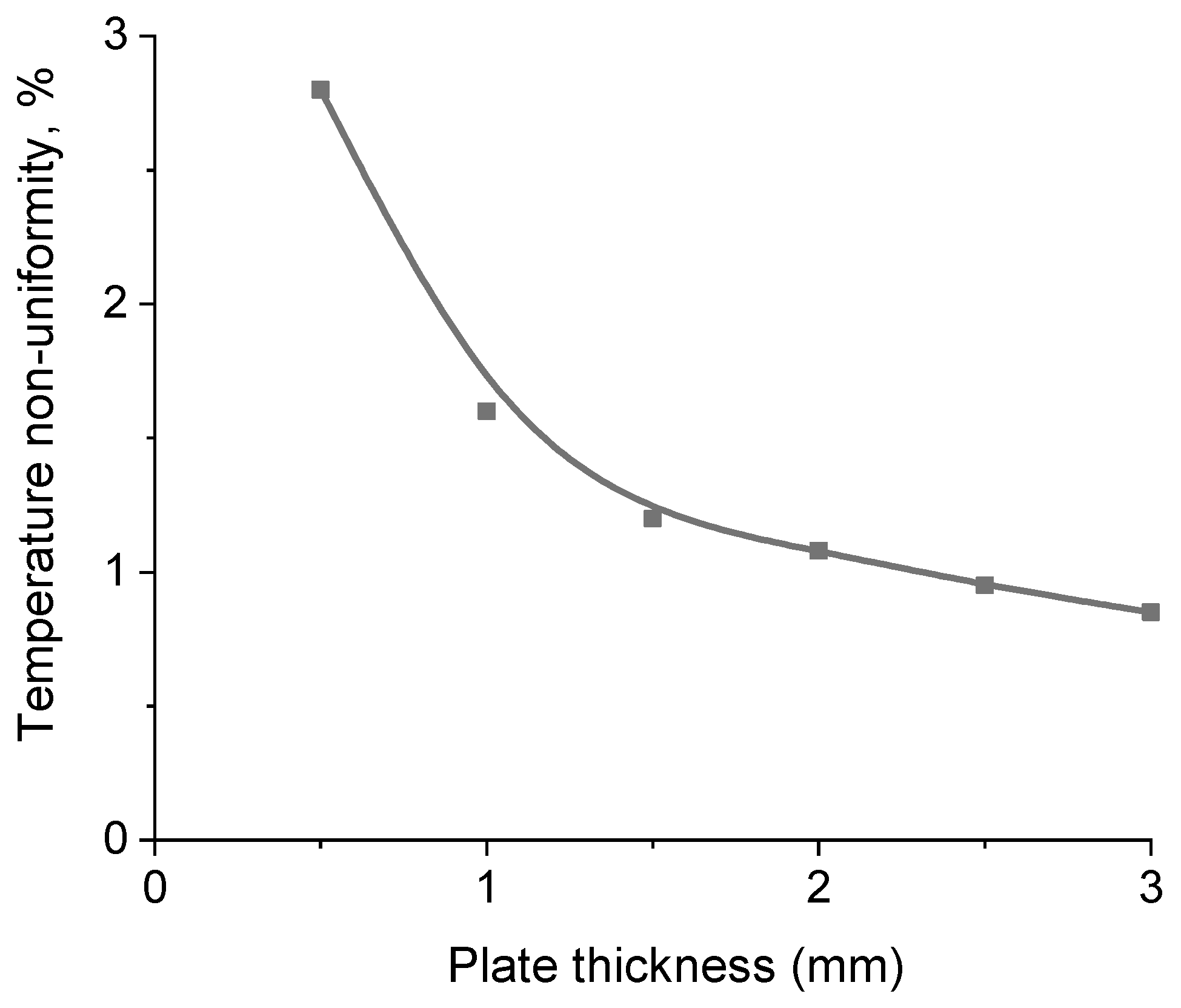
3. Results and Discussion
Effect of Flow Mode
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barnoon, P.; Toghraie, D.; Mehmandoust, B.; Fazilati, M.A.; Eftekhari, S.A. Comprehensive study on hydrogen production via propane steam reforming inside a reactor. Energy Rep. 2021, 7, 929–941. [Google Scholar] [CrossRef]
- Sundaram, S.; Kolb, G.; Hessel, V.; Wang, Q. Energy-efficient routes for the production of gasoline from biogas and pyrolysis oil—Process design and life-cycle assessment. Ind. Eng. Chem. Res. 2017, 56, 3373–3387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jadhav, S.G.; Vaidya, P.D.; Bhanage, B.M.; Joshi, J.B. Catalytic carbon dioxide hydrogenation to methanol: A review of recent studies. Chem. Eng. Res. Des. 2014, 92, 2557–2567. [Google Scholar] [CrossRef]
- Chang, C.D.; Silvestri, A.J. The conversion of methanol and other O-compounds to hydrocarbons over zeolite catalysts. J. Catal. 1977, 47, 249–259. [Google Scholar] [CrossRef]
- Yurchak, S. Development of mobil’s fixed-bed Methanul-To-Gasoline (MTG) process. In Studies in Surface Science and Catalysis; Bibby, D.M., Chang, C.D., Howe, R.F., Yurchak, S., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; Volume 36, pp. 251–272. ISBN 0167-2991. [Google Scholar]
- Chang, C.D. The New Zealand Gas- to-Gasoline plant: An engineering tour de force. Catal. Today 1992, 13, 103–111. [Google Scholar] [CrossRef]
- Khodakov, A.Y.; Chu, W.; Fongarland, P. Advances in the development of novel cobalt Fischer-Tropsch catalysts for synthesis of long-chain hydrocarbons and clean fuels. Chem. Rev. 2007, 107, 1692–1744. [Google Scholar] [CrossRef]
- De Kok, P.J.; Overtoom, R.R.M. Pearl GTL; Elsevier B.V.: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Stöcker, M. Methanol-to-hydrocarbons: Catalytic materials and their behavior. Microporous Mesoporous Mater. 1999, 29, 3–48. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, Q.; Ma, Z.; Bian, S.; Song, W. Direct observation of olefin homologations on zeolite ZSM-22 and its implications to methanol to olefin conversion. J. Catal. 2008, 258, 83–86. [Google Scholar] [CrossRef]
- Qi, L.; Wei, Y.; Xu, L.; Liu, Z. Reaction behaviors and kinetics during induction period of methanol conversion on HZSM-5 zeolite. ACS Catal. 2015, 5, 3973–3982. [Google Scholar] [CrossRef]
- Schmidt, F.; Hoffmann, C.; Giordanino, F.; Bordiga, S.; Simon, P.; Carrillo-Cabrera, W.; Kaskel, S. Coke location in microporous and hierarchical ZSM-5 and the impact on the MTH reaction. J. Catal. 2013, 307, 238–245. [Google Scholar] [CrossRef]
- Blauwhoff, P.M.M.; Gosselink, J.W.; Kieffer, E.P.; Sie, S.T.; Stork, W.H.J. Zeolites as catalysts in industrial processes. In Catalysis and Zeolites: Fundamentals and Applications; Weitkamp, J., Puppe, L., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 437–538. ISBN 978-3-662-03764-5. [Google Scholar]
- Menges, M.; Kraushaar-Czarnetzki, B. Kinetics of methanol to olefins over AlPO 4-bound ZSM-5 extrudates in a two-stage unit with dimethyl ether pre-reactor. Microporous Mesoporous Mater. 2012, 164, 172–181. [Google Scholar] [CrossRef]
- Tavan, Y.; Hosseini, S.H. From laboratory experiments to simulation studies of methanol dehydration to produce dimethyl ether—Part I: Reaction kinetic study. Chem. Eng. Process. 2013, 73, 144–150. [Google Scholar] [CrossRef]
- Mollavali, M.; Yaripour, F.; Atashi, H.; Sahebdelfar, S. Intrinsic kinetics study of dimethyl ether synthesis from methanol on γ-Al2O3 catalysts. Ind. Eng. Chem. Res. 2008, 47, 3265–3273. [Google Scholar] [CrossRef]
- Heriyanto, H.; Muraza, O.; Nasser, G.A.; Sanhoob, M.A.; Bakare, I.A.; Rochmadi, B.; Budiman, A. Development of New Kinetic models for methanol to hydrocarbons over a Ca-ZSM-5 Catalyst. Energy Fuels 2020, 34, 6245–6260. [Google Scholar] [CrossRef]
- Ma, Q.; Fu, T.; Li, H.; Cui, L.; Li, Z. Insight into the selection of the post-treatment strategy for ZSM-5 zeolites for the improvement of catalytic stability in the conversion of methanol to hydrocarbons. Ind. Eng. Chem. Res. 2020, 59, 11125–11138. [Google Scholar] [CrossRef]
- Fu, T.; Chang, J.; Shao, J.; Li, Z. Fabrication of a nano-sized ZSM-5 zeolite with intercrystalline mesopores for conversion of methanol to gasoline. J. Energy Chem. 2017, 26, 139–146. [Google Scholar] [CrossRef] [Green Version]
- Masuda, T.; Asanuma, T.; Shouji, M.; Mukai, S.R.; Kawase, M.; Hashimoto, K. Methanol to olefins using ZSM-5 zeolite catalyst membrane reactor. Chem. Eng. Sci. 2003, 58, 649–656. [Google Scholar] [CrossRef]
- Omojola, T.; Cherkasov, N.; Rebrov, E.V.; Lukyanov, D.B.; Perera, S.P. Zeolite minilith: A unique structured catalyst for the methanol to gasoline process. Chem. Eng. Process.-Process. Intensif. 2018, 131, 137–143. [Google Scholar] [CrossRef] [Green Version]
- Rebrov, E.V. Sol-gel synthesis of zeolite coatings and their application in catalytic microstructured reactors. Catal. Ind. 2009, 1, 322–347. [Google Scholar] [CrossRef]
- Rebrov, E.; Hu, G. Novel Zeolite Catalysts for Methanol to Hydrocarbon Transformation; Elsevier Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780128148082. [Google Scholar]
- Doluda, V.Y.; Stepacheva, A.A.; Lakina, N.V.; Oleg, V.; Molchanov, V.P.; Demidenko, G.N.; Valentina, G.; Panfilov, V.I.; Sulman, M.G.; Sulman, E.M. Comparison of methanol to gasoline conversion in one-step, two-step, and cascade mode in the presence of H-ZSM-5 zeolite. Int. J. Sustain. Energy 2017, 37, 970–977. [Google Scholar] [CrossRef]
- Rebrov, E.; de Croon, M.H.J.; Schouten, J. Design of a microstructured reactor with integrated heat-exchanger for optimum performance of a highly exothermic reaction. Catal. Today 2001, 69, 183–192. [Google Scholar] [CrossRef]
- Rebrov, E.V.; Duinkerke, S.A.; de Croon, M.H.J.M.; Schouten, J.C. Optimization of heat transfer characteristics, flow distribution, and reaction processing for a microstructured reactor/heat-exchanger for optimal performance in platinum catalyzed ammonia oxidation. Chem. Eng. J. 2003, 93, 201–216. [Google Scholar] [CrossRef]
- Schouten, J.C.; Rebrov, E.V.; de Croon, M.H.J.M. Miniaturization of heterogeneous catalytic reactors: Prospects for new developments in catalysis and process engineering. Chimia 2002, 56, 627–635. [Google Scholar] [CrossRef]
- Cybulski, A.; Moulijn, J.A. Monoliths in heterogeneous catalysis. Catal. Rev. 1994, 36, 179–270. [Google Scholar] [CrossRef]
- Chen, G.; Li, S.; Jiao, F.; Yuan, Q. Catalytic dehydration of bioethanol to ethylene over TiO2/γ-Al2O3 catalysts in microchannel reactors. Catal. Today 2007, 125, 111–119. [Google Scholar] [CrossRef]
- Karim, A.M.; Federici, J.A.; Vlachos, D.G. Portable power production from methanol in an integrated thermoeletric/microreactor system. J. Power Sources 2008, 179, 113–120. [Google Scholar] [CrossRef]
- Tonkovich, A.L.Y.; Yang, B.; Perry, S.T.; Fitzgerald, S.P.; Wang, Y. From seconds to milliseconds to microseconds through tailored microchannel reactor design of a steam methane reformer. Catal. Today 2007, 120, 21–29. [Google Scholar] [CrossRef]
- Kolb, G. Review: Microstructured reactors for distributed and renewable production of fuels and electrical energy. Chem. Eng. Process. Process. Intensif. 2013, 65, 1–44. [Google Scholar] [CrossRef]
- Khaodee, W.; Jiwanuruk, T.; Ountaksinkul, K.; Charojrochkul, S.; Charoensuk, J.; Wongsakulphasatch, S.; Assabumrungrat, S. Compact heat integrated reactor system of steam reformer, shift reactor and combustor for hydrogen production from ethanol. Processes 2020, 8, 708. [Google Scholar] [CrossRef]
- Shah, K.; Besser, R.S. Key issues in the microchemical systems-based methanol fuel processor: Energy density, thermal integration, and heat loss mechanisms. J. Power Sources 2007, 166, 177–193. [Google Scholar] [CrossRef]
- Shah, K.; Besser, R.S. Understanding thermal integration issues and heat loss pathways in a planar microscale fuel processor: Demonstration of an integrated silicon microreactor-based methanol steam reformer. Chem. Eng. J. 2008, 135, 46–56. [Google Scholar] [CrossRef]
- Delsman, E.R.; de Croon, M.H.J.M.; Kramer, G.J.; Cobden, P.D.; Hofmann, C.; Cominos, V.; Schouten, J.C. Experiments and modelling of an integrated preferential oxidation-heat exchanger microdevice. Chem. Eng. J. 2004, 101, 123–131. [Google Scholar] [CrossRef]
- Ryi, S.K.; Park, J.S.; Choi, S.H.; Cho, S.H.; Kim, S.H. Novel micro fuel processor for PEMFCs with heat generation by catalytic combustion. Chem. Eng. J. 2005, 113, 47–53. [Google Scholar] [CrossRef]
- Ryi, S.K.; Park, J.S.; Cho, S.H.; Kim, S.H. Fast start-up of microchannel fuel processor integrated with an igniter for hydrogen combustion. J. Power Sources 2006, 161, 1234–1240. [Google Scholar] [CrossRef]
- Grote, M.; Maximini, M.; Yang, Z.; Engelhardt, P.; Köhne, H.; Lucka, K.; Brenner, M. Experimental and computational investigations of a compact steam reformer for fuel oil and diesel fuel. J. Power Sources 2011, 196, 9027–9035. [Google Scholar] [CrossRef]
- Andisheh Tadbir, M.; Akbari, M.H. Integrated methanol reforming and oxidation in wash-coated microreactors: A three-dimensional simulation. Int. J. Hydrogen Energy 2012, 37, 2287–2297. [Google Scholar] [CrossRef]
- Anzola, A.M.; Bruschi, Y.M.; López, E.; Schbib, N.S.; Pedernera, M.N.; Borio, D.O. Heat supply and hydrogen yield in an ethanol microreformer. Ind. Eng. Chem. Res. 2011, 50, 2698–2705. [Google Scholar] [CrossRef]
- Rave, A.; Kuwertz, R.; Fieg, G.; Heck, J. Modeling and experimental investigation of the spatial heat transfer in a plate reactor with meandering millichannels. Chem. Eng. Process.-Process. Intensif. 2020, 150, 107860. [Google Scholar] [CrossRef]
- Belzunce, P.S.; Cadús, L.E.; Rodríguez, M.L. Cross-flow plate reactor for ethanol steam reforming: A theoretical study. Chem. Eng. Process.-Process. Intensif. 2021, 164, 108383. [Google Scholar] [CrossRef]
- Dubrovskiy, A.R.; Rebrov, E.V.; Kuznetsov, S.A.; Schouten, J.C. A microstructured reactor/heat-exchanger for the water-gas shift reaction operated in the 533-673 K range. Catal. Today 2009, 147, 198–203. [Google Scholar] [CrossRef]
- Roberge, D.M.; Bieler, N.; Mathier, M.; Eyholzer, M.; Zimmermann, B.; Barthe, P.; Guermeur, C.; Lobet, O.; Moreno, M.; Woehl, P. Development of an industrial multi-injection microreactor for fast and exothermic reactions—Part II. Chem. Eng. Technol. 2008, 31, 1155–1161. [Google Scholar] [CrossRef]
- Board, N.; Format, E.; Isbn, H.; Pacific, A.; Press, B. The Complete Book on Biomass Based Products (Biochemicals, Biofuels, Activated Carbon), 2015th ed.; NIIR: Delhi, India, 2008; ISBN 9788178331584. [Google Scholar]
- Keil, F.J. Methanol-to-hydrocarbons: Process technology. Microporous Mesoporous Mater. 1999, 29, 49–66. [Google Scholar] [CrossRef]
- Tavan, Y.; Hasanvandian, R. Two practical equations for methanol dehydration reaction over HZSM-5 catalyst—Part I: Second order rate equation. Fuel 2015, 142, 208–214. [Google Scholar] [CrossRef]
- Rebrov, E.V.; Schouten, J.C.; de Croon, M.H.J.M. Single-phase fluid flow distribution and heat transfer in microstructured reactors. Chem. Eng. Sci. 2011, 66, 1374–1393. [Google Scholar] [CrossRef] [Green Version]
- Rebrov, E.V.; Ismagilov, I.Z.; Ekatpure, R.P.; De Croon, M.H.J.M.; Schouten, J.C. Header design for flow equalization in microstructured reactors. AIChE J. 2007, 53. [Google Scholar] [CrossRef]
- Kockmann, N. Heat transfer and micro heat exchangers. In Transport Phenomena in Micro Process Engineering; Springer: Berlin/Heidelberg, Germany, 2007; pp. 129–162. [Google Scholar]
- Newton, H.; Wang, Q.; Sundaram, S.; Van Veen, A.; Kiesewalter, S.; Kolb, G. BIOGO: Contributing to the transformation of the petrochemical industry through advances in nanocatalysts and reactor design. Green Process. Synth. 2015, 4, 433–435. [Google Scholar] [CrossRef]
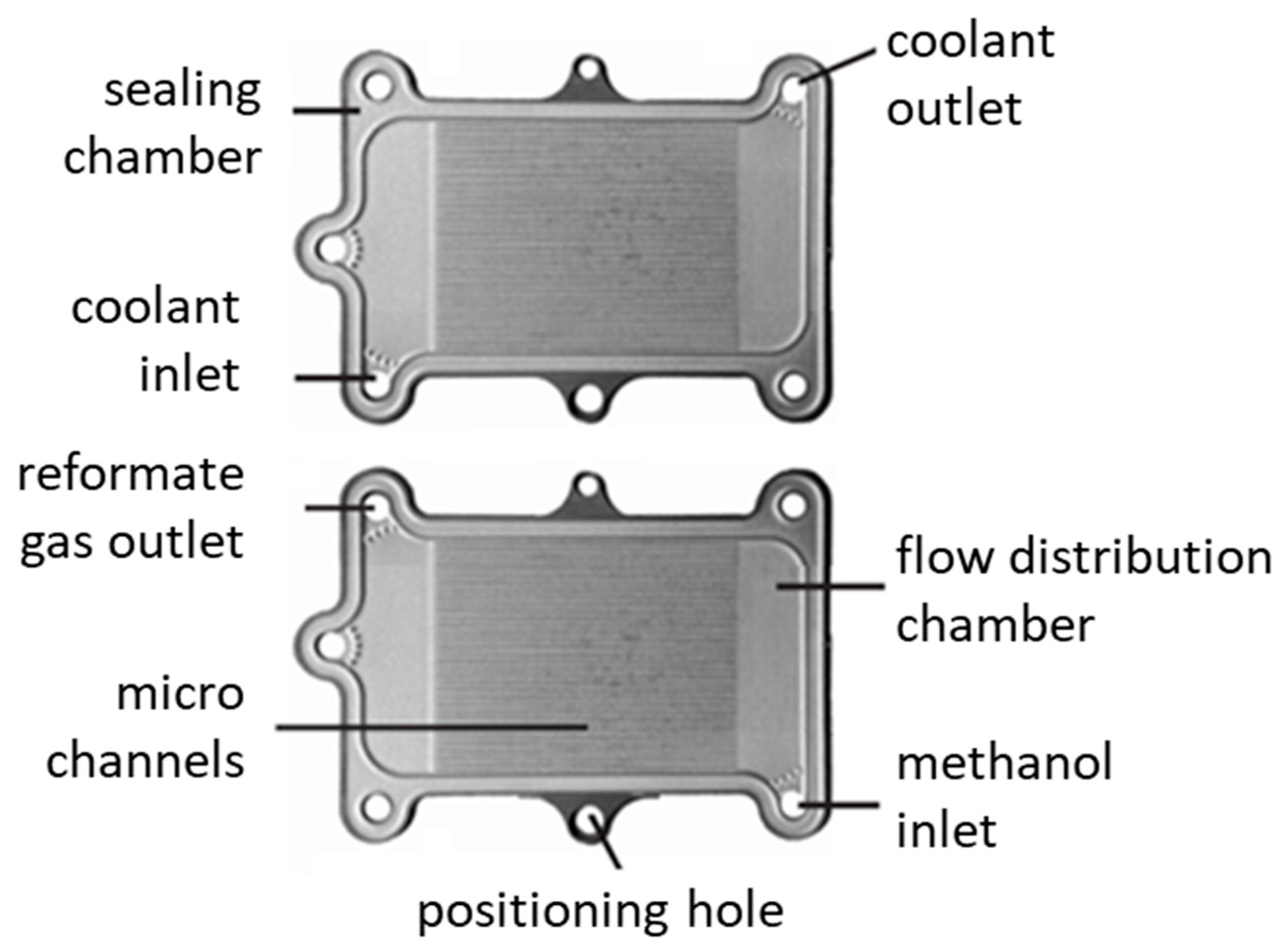
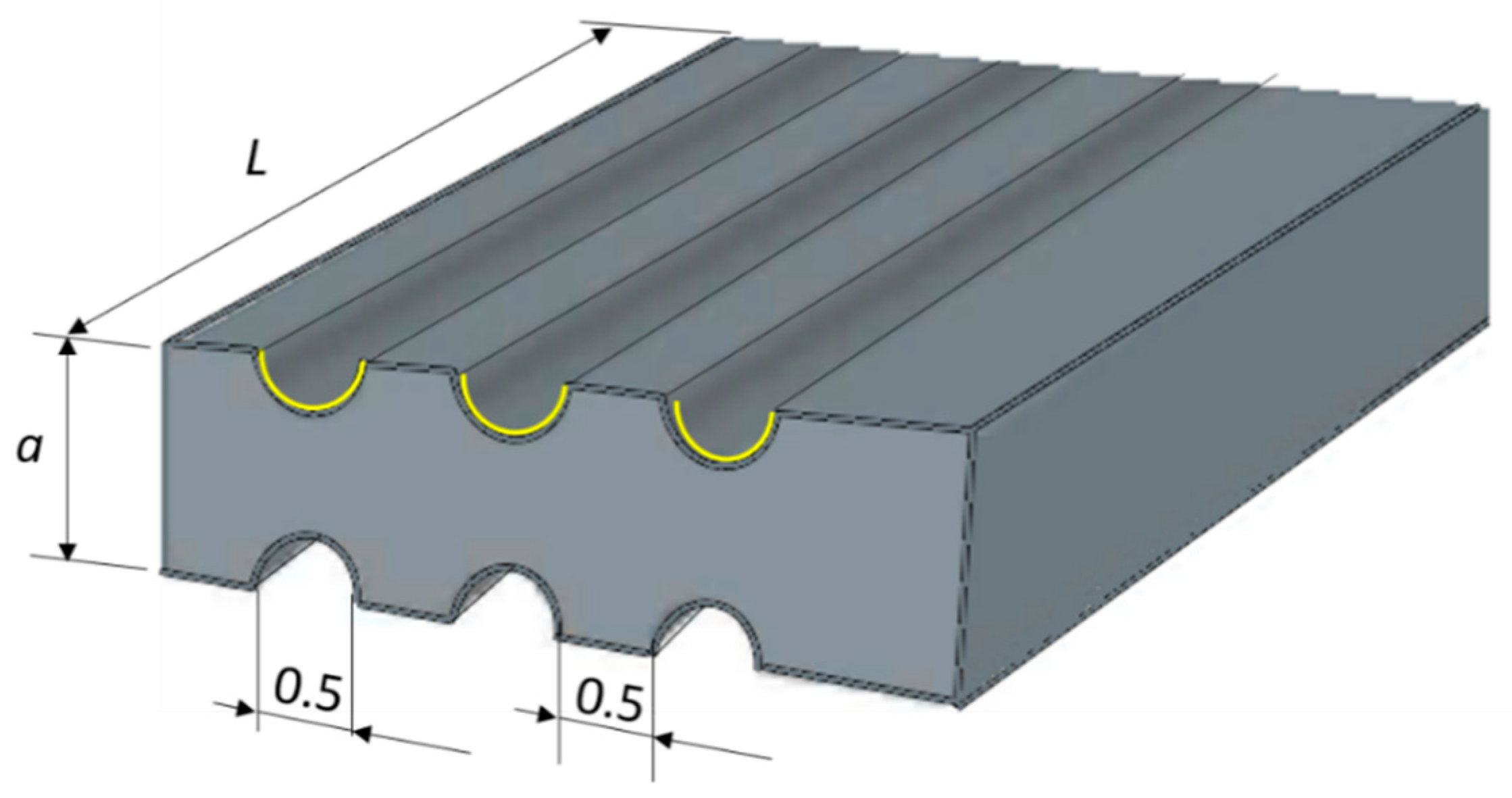

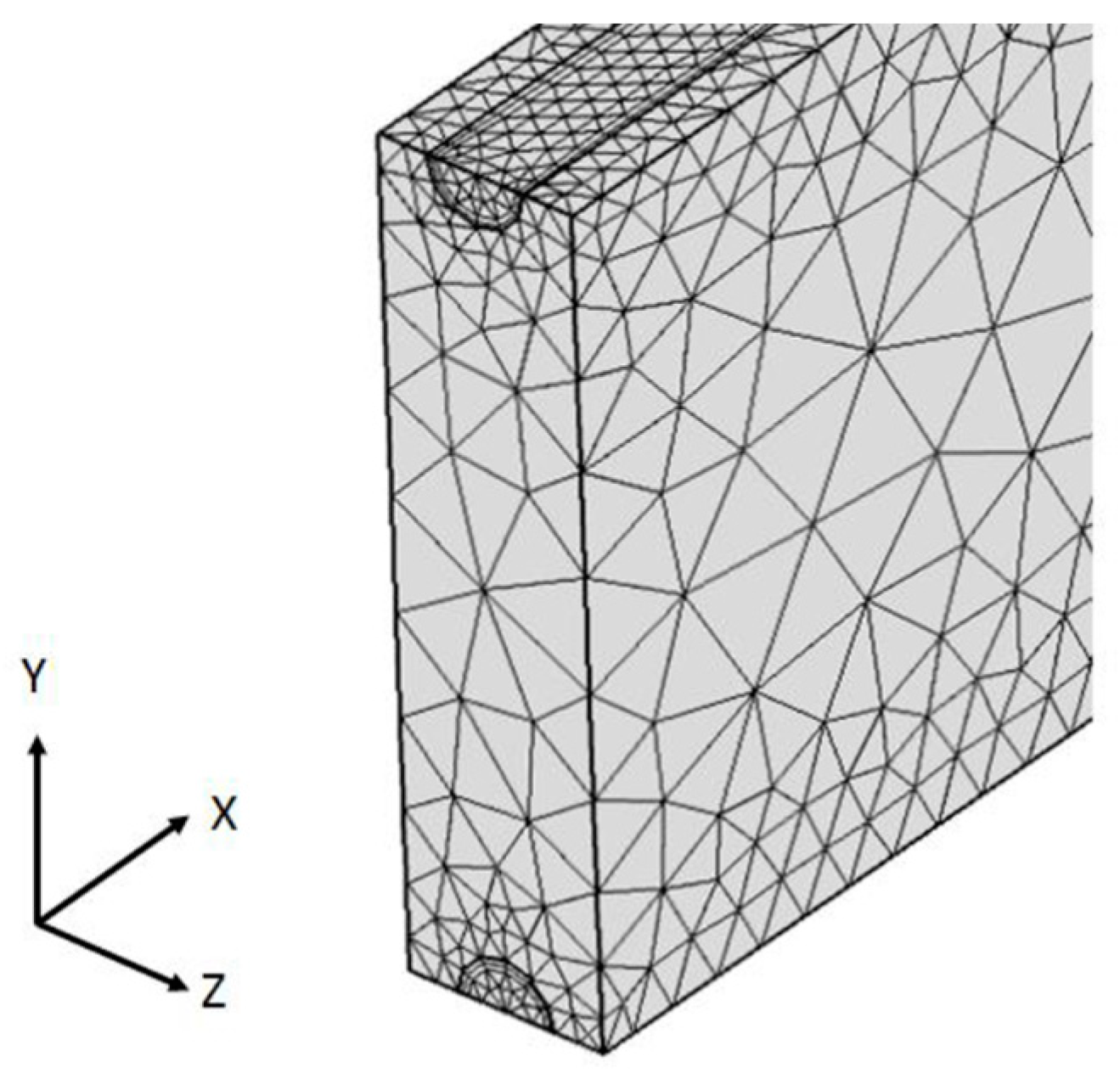
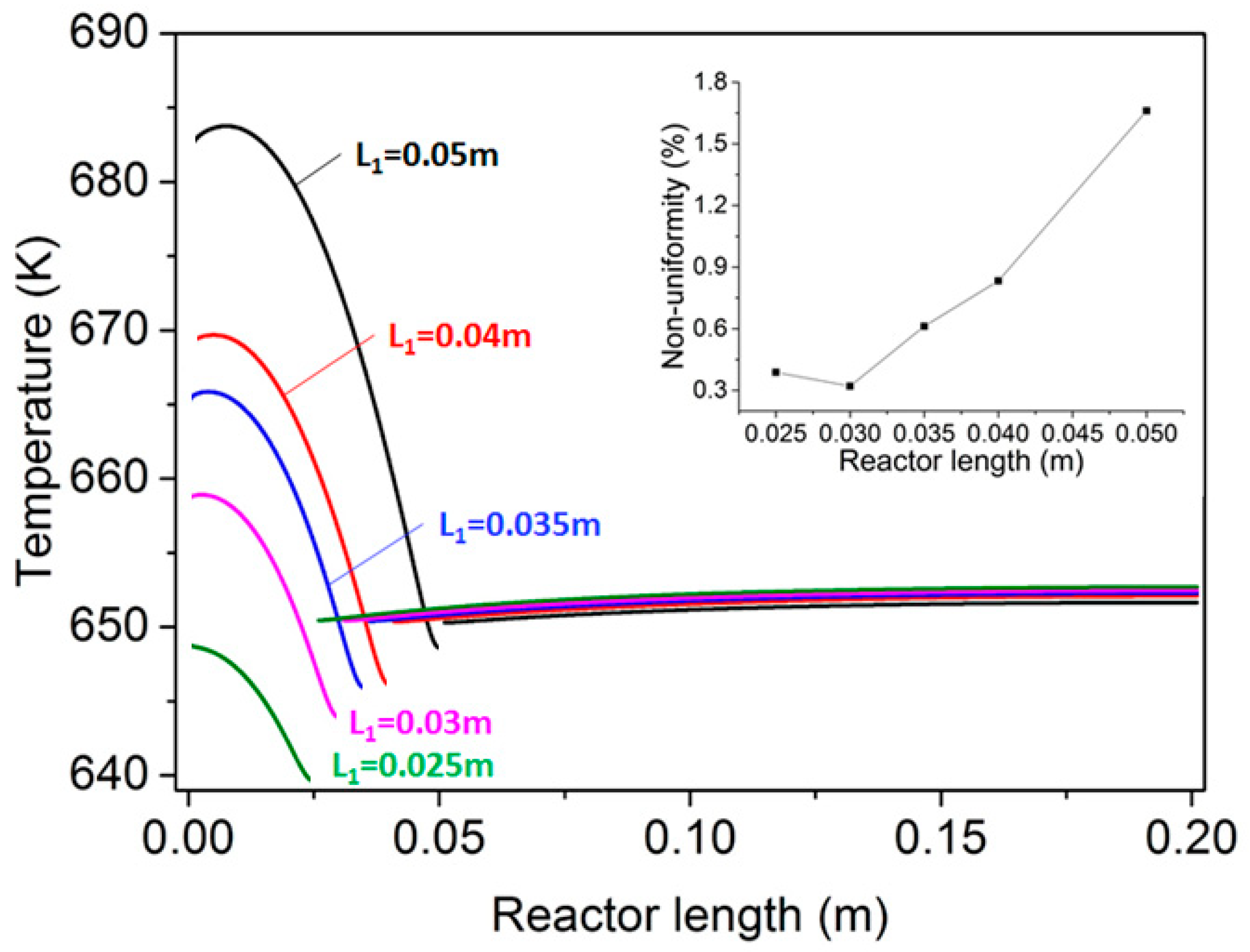
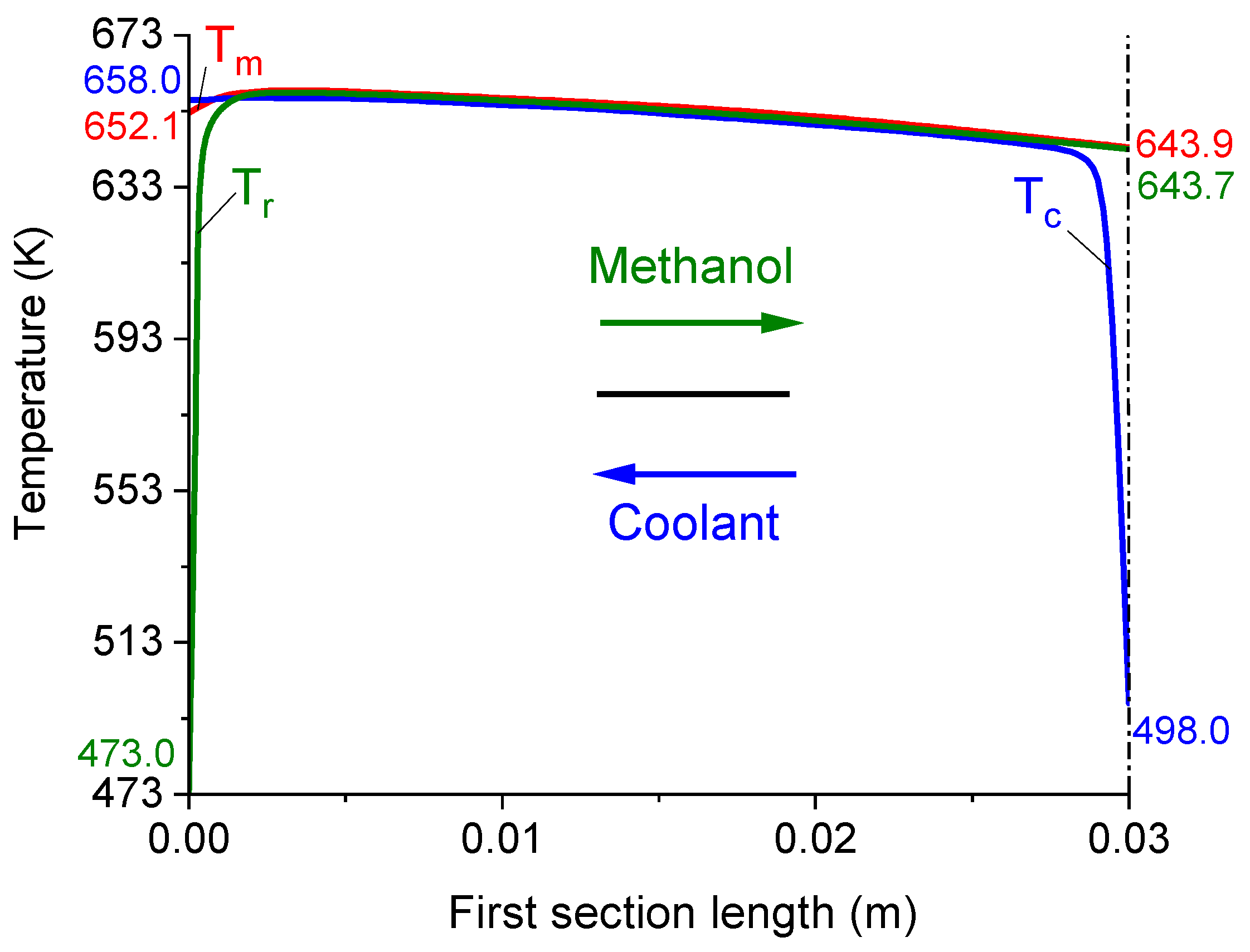
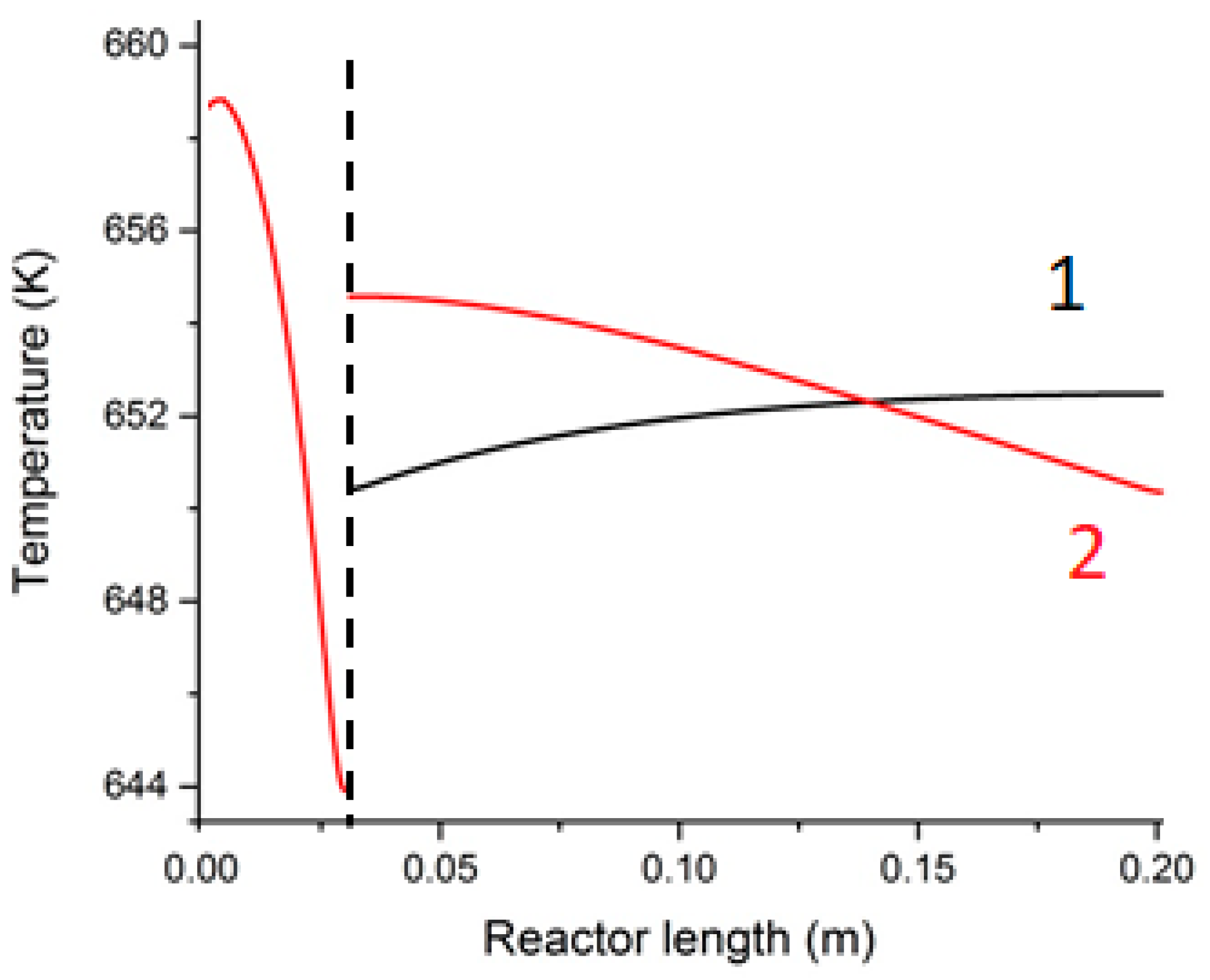
| Parameter | Value |
|---|---|
| Channel length | 0.20 m |
| Channel diameter | 0.50 mm |
| Channels per plate | 14 |
| Fin width | 0.50 mm |
| Plate thickness | 0.50–3.00 mm |
| Number of plates | 176 (+2 cover plates) |
| Total number of channels (reactant size) | 1232 |
| Thickness of the ZSM-5 coating | 0.010 mm |
| Microreactor/Heat-Exchanger Parameters | |||
|---|---|---|---|
| Reactor length (mm) | 200 (+4 mm for additional inlet chamber) | ||
| Reactor width (mm) | 16 | ||
| Reactor height (mm) | 264 | ||
| Reactor volume (cm3) | 1.01 | ||
| Methanol throughput (g h−1) | 14.1 | ||
| Parameters of a single plate a | Reaction channels | Cooling channels | |
| Section 1 | Section 2 | ||
| Channel diameter (mm) | 0.50 | 0.50 | 0.50 |
| Thickness of ZSM-5 coating (μm) | 10 | ‒ | ‒ |
| Inlet gas velocity (m s−1) | 2.71 × 10−2 | 9.0 × 10−2 | 9.0 × 10−2 |
| Re number (-) | 410 | 700 | 700 |
| Flow heat quality (W K−1) | 3.48 × 10−6 | 7.1 × 10−5 | 7.1 × 10−5 |
| Inlet gas temperature (K) | 473 | 498 | 498 |
| Outlet gas temperature (K) | 652 | 658 | 652 |
| Flow mode | Counter-current | Co-current | |
| Inlet gas flow rate (cm3 min−1 STP) b | 390 | 1310 | 1310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Cherkasov, N.; Rebrov, E.V. Design of a Compact Microreactor/Heat-Exchanger for a Distributed Production of Liquid Hydrocarbons from Methanol. Reactions 2021, 2, 427-441. https://doi.org/10.3390/reactions2040027
Hu G, Cherkasov N, Rebrov EV. Design of a Compact Microreactor/Heat-Exchanger for a Distributed Production of Liquid Hydrocarbons from Methanol. Reactions. 2021; 2(4):427-441. https://doi.org/10.3390/reactions2040027
Chicago/Turabian StyleHu, Guannan, Nikolay Cherkasov, and Evgeny V. Rebrov. 2021. "Design of a Compact Microreactor/Heat-Exchanger for a Distributed Production of Liquid Hydrocarbons from Methanol" Reactions 2, no. 4: 427-441. https://doi.org/10.3390/reactions2040027
APA StyleHu, G., Cherkasov, N., & Rebrov, E. V. (2021). Design of a Compact Microreactor/Heat-Exchanger for a Distributed Production of Liquid Hydrocarbons from Methanol. Reactions, 2(4), 427-441. https://doi.org/10.3390/reactions2040027







