Interfacial Mass Transfer in Trichloroethylene/Surfactants/ Water Systems: Implications for Remediation Strategies
Abstract
1. Introduction
2. Theoretical Approach
3. Materials and Methods
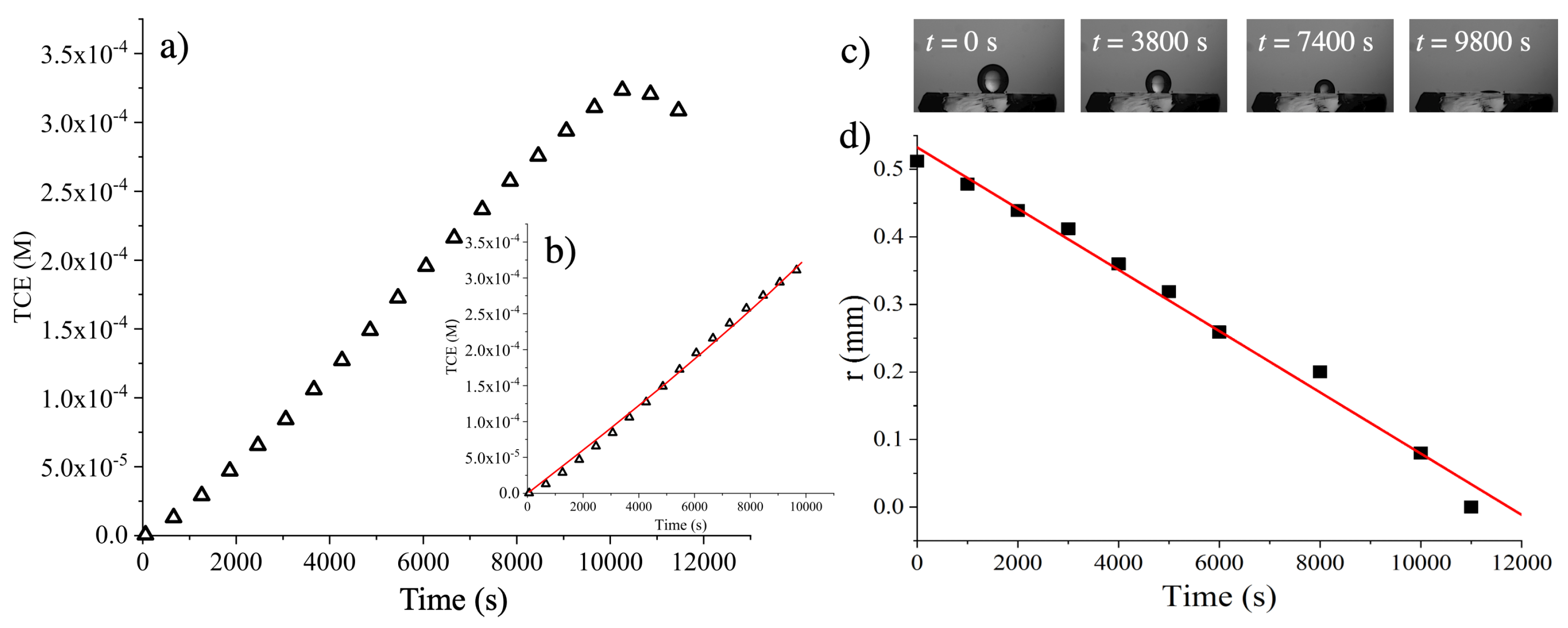
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tables
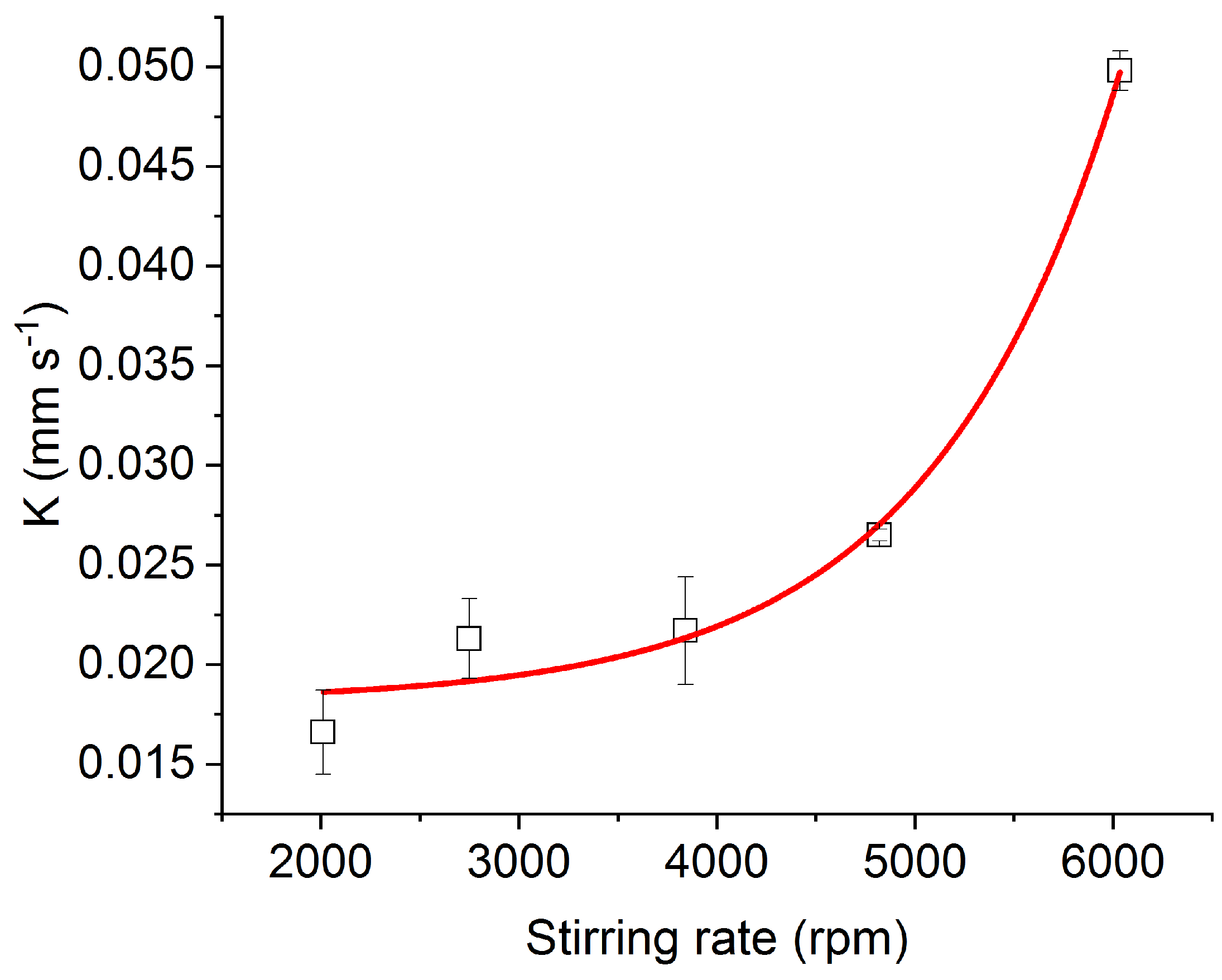
| Stirring | K | 95% | 95% | ||
|---|---|---|---|---|---|
| (rpm) | (mm s) | CI | (s) | CI | CC |
| 2010 | (1.7 ± 0.2) × 10−2 | 2.06 × 10−3 | (6.0 ± 0.2) × 10−5 | 2.12 × 10−5 | 0.956 |
| 2750 | (2.1 ± 0.2) × 10−2 | 1.96 × 10−3 | (6.0 ± 0.1) × 10−5 | 1.56 × 10−5 | 0.767 |
| 3840 | (2.1 ± 0.2) × 10−2 | 2.68 × 10−3 | (9.3 ± 0.1) × 10−5 | 1.02 × 10−6 | 0.888 |
| 4820 | (2.65 ± 0.03) × 10−2 | 2.94 × 10−4 | (9.7 ± 0.1) × 10−5 | 1.42 × 10−6 | 0.922 |
| 6034 | (4.9 ± 0.1) × 10−2 | 9.26 × 10−4 | (1.1 ± 0.1) × 10−4 | 1.48 × 10−5 | 0.899 |
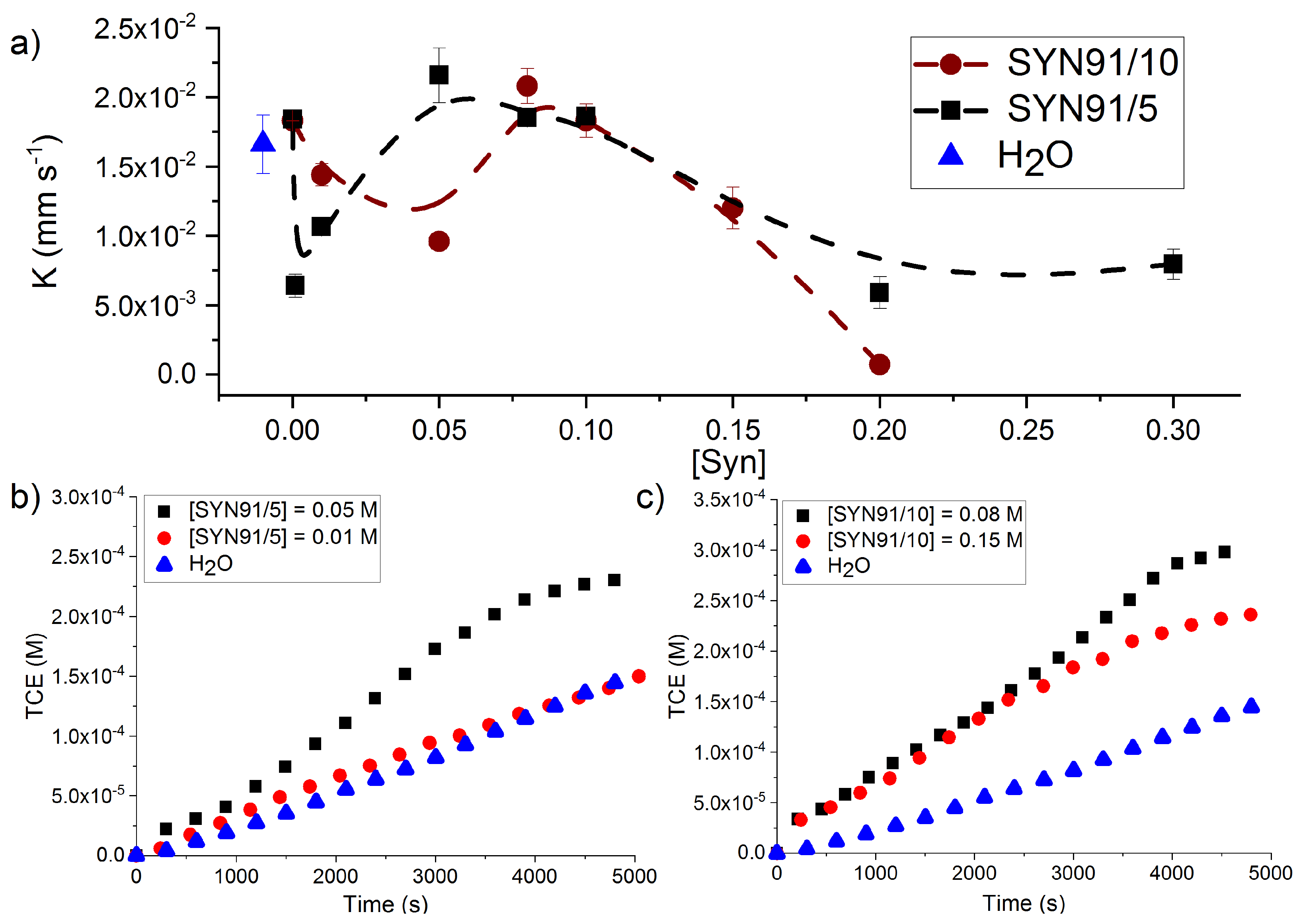
| System | SYN | K | ||||
|---|---|---|---|---|---|---|
| (M) | (mm s) | CI | (s) | CI | CC | |
| H2O | - | (1.7 ± 0.2) × 10−2 | 2.06 × 10−3 | (6.0 ± 0.2) × 10−5 | 2.12 × 10−5 | 0.956 |
| SYN91/5 | 1 × 10−4 | (1.84 ± 0.03) × 10−2 | 2.99 × 10−4 | - | - | - |
| 1 × 10−3 | (6.4 ± 0.8) × 10−3 | 8.42 × 10−4 | (2.3 ± 0.1) × 10−4 | 9.8 × 10−5 | 0.886 | |
| 0.01 | (1.06 ± 0.01) × 10−2 | 8.83 × 10−5 | (2.9 ± 0.2) × 10−5 | 2.02 × 10−6 | 0.802 | |
| 0.05 | (2.1 ± 0.1) × 10−2 | 1.98 × 10−3 | (7.1 ± 0.8) × 10−5 | 1.37 × 10−5 | 0.758 | |
| 0.08 | (1.85 ± 0.02) × 10−2 | 2 × 10−4 | (3.4 ± 0.5) × 10−5 | 8.54 × 10−6 | 0.952 | |
| 0.10 | (1.86 ± 0.01) × 10−2 | 1.01 × 10−4 | (2.8 ± 0.2) × 10−4 | 1.96 × 10−5 | 0.793 | |
| 0.20 | (5.9 ± 0.1) × 10−3 | 1.15 × 10−3 | (4.2 ± 0.1) × 10−5 | 1.26 × 10−5 | 0.897 | |
| 0.30 | (7.9 ± 0.6) × 10−3 | 1.09 × 10−3 | (2.4 ± 0.2) × 10−4 | 1.96 × 10−4 | 0.945 | |
| SYN91/10 | 1 × 10−4 | (1.83 ± 0.01) × 10−2 | 1.15 × 10−5 | (4.2 ± 0.1) × 10−5 | 1.25 × 10−6 | 0.930 |
| 0.01 | (1.44 ± 0.08) × 10−2 | 8.00 × 10−4 | - | - | - | |
| 0.05 | (9.59 ± 0.02) × 10−3 | 2.00 × 10−5 | - | - | - | |
| 0.08 | (2.0 ± 0.1) × 10−2 | 1.25 × 10−3 | (5.0 ± 0.5) × 10−5 | 5.59 × 10−6 | 0.717 | |
| 0.10 | (1.8 ± 0.1) × 10−2 | 1.21 × 10−3 | - | - | - | |
| 0.15 | (1.20 ± 0.01) × 10−2 | 1.15 × 10−3 | (2.5 ± 0.1) × 10−5 | 1.68 × 10−6 | 0.861 | |
| 0.20 | (7.1 ± 0.2) × 10−4 | 1.75 × 10−5 | (9.5 ± 0.5) × 10−5 | 3.48 × 10−6 | 0.916 |
Appendix B. Ferroin Dissolution
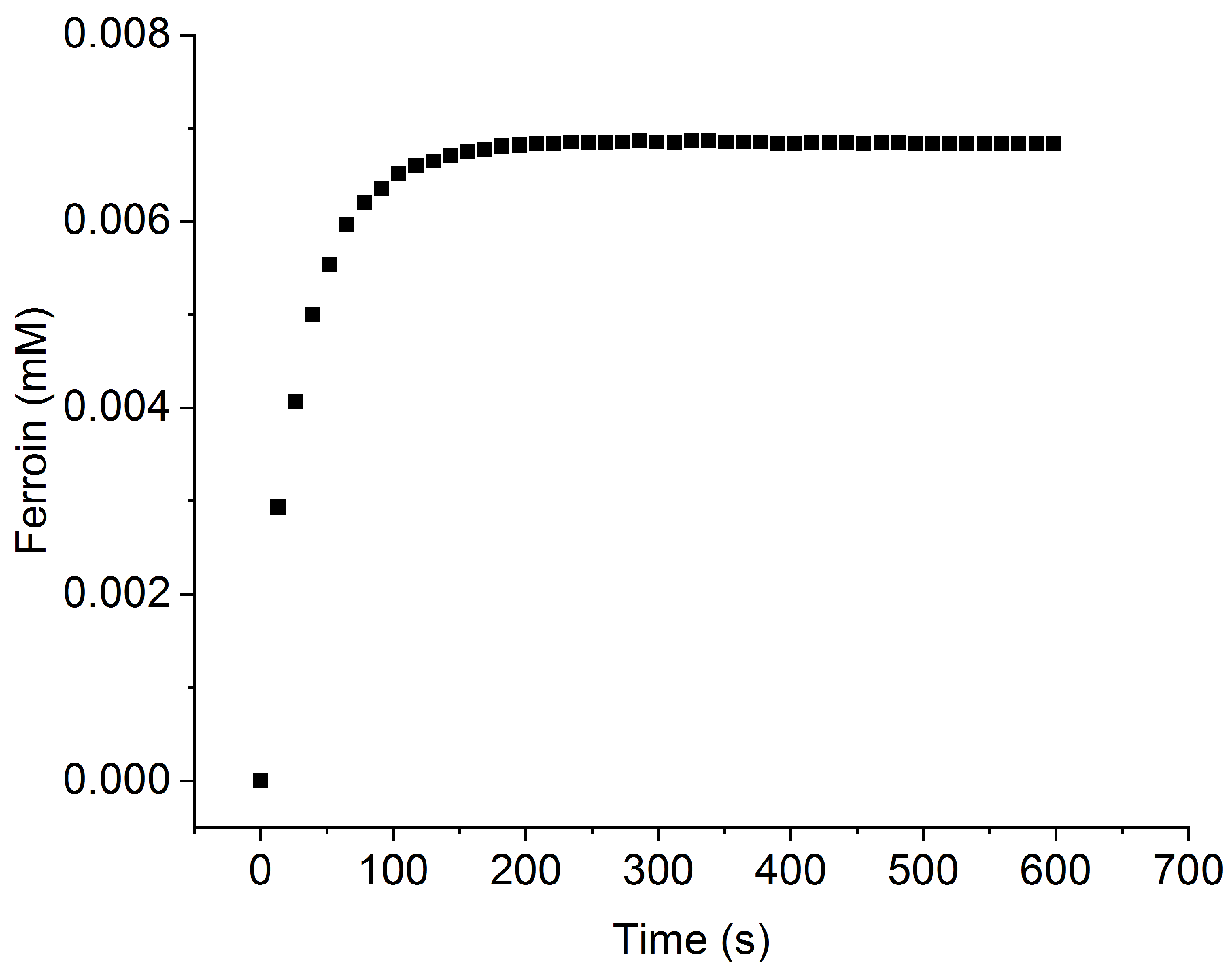
References
- Cichocki, J.A.; Guyton, K.Z.; Guha, N.; Chiu, W.A.; Rusyn, I.; Lash, L.H. Target Organ Metabolism, Toxicity, and Mechanisms of Trichloroethylene and Perchloroethylene: Key Similarities, Differences, and Data Gaps. J. Pharmacol. Exp. Ther. 2016, 359, 110–123. [Google Scholar] [CrossRef]
- Schaerlaekens, J.; Vanderborght, J.; Merckx, R.; Feyen, J. Surfactant enhanced solubilization of residual trichloroethene: An experimental and numerical analysis. J. Contam. Hydrol. 2000, 46, 1–16. [Google Scholar] [CrossRef]
- Schwille, F. Dense Chlorinated Solvents in Porous and Fractured Media: Model Experiments; Lewis Publishers: Chelsea, MI, USA, 1988. [Google Scholar]
- Pennell, K.D.; Adinolfi, A.M.; Abriola, L.M.; Diallo, M.S. Solubilization of dodecane, tetrachloroethylene, and 1, 2-dichlorobenzene in micellar solutions of ethoxylated nonionic surfactants. Environ. Sci. Technol. 1997, 31, 1382–1389. [Google Scholar] [CrossRef]
- Rossi, F.; Cucciniello, R.; Intiso, A.; Proto, A.; Motta, O.; Marchettini, N. Determination of the trichloroethylene diffusion coefficient in water. AIChE J. 2015, 61, 3511–3515. [Google Scholar] [CrossRef]
- Mulligan, C.; Yong, R.; Gibbs, B. Surfactant-enhanced remediation of contaminated soil: A review. Eng. Geol. 2001, 60, 371–380. [Google Scholar] [CrossRef]
- Intiso, A.; Miele, Y.; Marchettini, N.; Proto, A.; Sánchez-Domínguez, M.; Rossi, F. Enhanced solubility of trichloroethylene (TCE) by a poly-oxyethylene alcohol as green surfactant. Environ. Technol. Innov. 2018, 12, 72–79. [Google Scholar] [CrossRef]
- Garza-Arévalo, J.I.; Intiso, A.; Proto, A.; Rossi, F.; Sanchez-Dominguez, M. Trichloroethylene solubilization using a series of commercial biodegradable ethoxylated fatty alcohol surfactants. J. Chem. Technol. Biotechnol. 2019, 94, 3523–3529. [Google Scholar] [CrossRef]
- EPA Development Office of Research. In-Situ Chemical Oxidation–Engineering Issue. 2011. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?Lab=NRMRL&dirEntryId=156513 (accessed on 7 July 2021).
- Farrell, J.; Kason, M.; Melitas, N.; Li, T. Investigation of the Long-Term Performance of Zero-Valent Iron for Reductive Dechlorination of Trichloroethylene. Environ. Sci. Technol. 2000, 34, 514–521. [Google Scholar] [CrossRef]
- Cucciniello, R.; Intiso, A.; Castiglione, S.; Genga, A.; Proto, A.; Rossi, F. Total oxidation of trichloroethylene over mayenite (Ca12Al14O33) catalyst. Appl. Catal. B Environ. 2017, 204, 167–172. [Google Scholar] [CrossRef]
- Intiso, A.; Martinez-Triguero, J.; Cucciniello, R.; Rossi, F.; Palomares, A.E. Influence of the synthesis method on the catalytic activity of mayenite for the oxidation of gas-phase trichloroethylene. Sci. Rep. 2019, 9, 425. [Google Scholar] [CrossRef] [PubMed]
- Intiso, A.; Martinez-Triguero, J.; Cucciniello, R.; Proto, A.; Palomares, A.E.; Rossi, F. A Novel Synthetic Route to Prepare High Surface Area Mayenite Catalyst for TCE Oxidation. Catalysts 2019, 9, 27. [Google Scholar] [CrossRef]
- Cucciniello, R.; Intiso, A.; Siciliano, T.; Palomares, A.E.; Martínez-Triguero, J.; Cerrillo, J.L.; Proto, A.; Rossi, F. Oxidative Degradation of Trichloroethylene over Fe2O3-doped Mayenite: Chlorine Poisoning Mitigation and Improved Catalytic Performance. Catalysts 2019, 9, 747. [Google Scholar] [CrossRef]
- Paria, S. Surfactant-enhanced remediation of organic contaminated soil and water. Adv. Colloid Interface Sci. 2008, 138, 24–58. [Google Scholar] [CrossRef] [PubMed]
- Lominchar, M.A.; Lorenzo, D.; Romero, A.; Santos, A. Remediation of soil contaminated by PAHs and TPH using alkaline activated persulfate enhanced by surfactant addition at flow conditions. J. Chem. Technol. Biotechnol. 2018, 93, 1270–1278. [Google Scholar] [CrossRef]
- Besha, A.T.; Bekele, D.N.; Naidu, R.; Chadalavada, S. Recent advances in surfactant-enhanced In-Situ Chemical Oxidation for the remediation of non-aqueous phase liquid contaminated soils and aquifers. Environ. Technol. Innov. 2018, 9, 303–322. [Google Scholar] [CrossRef]
- Huo, L.; Liu, G.; Yang, X.; Ahmad, Z.; Zhong, H. Surfactant-enhanced aquifer remediation: Mechanisms, influences, limitations and the countermeasures. Chemosphere 2020, 252, 126620. [Google Scholar] [CrossRef]
- Sun, Y.; Li, M.; Gu, X.; Danish, M.; Shan, A.; Ali, M.; Qiu, Z.; Sui, Q.; Lyu, S. Mechanism of surfactant in trichloroethene degradation in aqueous solution by sodium persulfate activated with chelated-Fe(II). J. Hazard. Mater. 2021, 407, 124814. [Google Scholar] [CrossRef]
- Rossi, F.; Liveri, M.L.T. Chemical self-organization in self-assembling biomimetic systems. Ecol. Model. 2009, 220, 1857–1864. [Google Scholar] [CrossRef]
- Budroni, M.A.; Riolfo, L.A.; Lemaigre, L.; Rossi, F.; Rustici, M.; De Wit, A. Chemical Control of Hydrodynamic Instabilities in Partially Miscible Two-Layer Systems. J. Phys. Chem. Lett. 2014, 5, 875–881. [Google Scholar] [CrossRef]
- Griffiths, R.W. Layered double-diffusive convection in porous media. J. Fluid Mech. 1981, 102, 221–248. [Google Scholar] [CrossRef]
- Budroni, M.; Carballido-Landeira, J.; Intiso, A.; De Wit, A.; Rossi, F. Interfacial hydrodynamic instabilities driven by cross-diffusion in reverse microemulsions. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 064502. [Google Scholar] [CrossRef] [PubMed]
- Budroni, M.A.; Lemaigre, L.; De Wit, A.; Rossi, F. Cross-diffusion-induced convective patterns in microemulsion systems. Phys. Chem. Chem. Phys. 2015, 17, 1593–1600. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Budroni, M.A. Cross-diffusion-driven hydrodynamic instabilities in a double-layer system: General classification and nonlinear simulations. Phys. Rev. E 2015, 92, 063007. [Google Scholar] [CrossRef] [PubMed]
- D’Hernoncourt, J.; Zebib, A.; De Wit, A. On the classification of buoyancy-driven chemo-hydrodynamic instabilities of chemical fronts. Chaos 2007, 17, 013109. [Google Scholar] [CrossRef] [PubMed]
- Budroni, M.A.; De Wit, A. Dissipative structures: From reaction-diffusion to chemo-hydrodynamic patterns. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 104617. [Google Scholar] [CrossRef] [PubMed]
- Epstein, P.S.; Plesset, M.S. On the stability of gas bubbles in liquid-gas solutions. J. Chem. Phys. 1950, 18, 1505–1509. [Google Scholar] [CrossRef]
- Duncan, P.B.; Needham, D. Microdroplet Dissolution into a Second-Phase Solvent Using a Micropipet Technique: Test of the Epstein-Plesset Model for an Aniline-Water System. Langmuir 2006, 22, 4190–4197. [Google Scholar] [CrossRef] [PubMed]
- Su, J.T.; Needham, D. Mass Transfer in the Dissolution of a Multicomponent Liquid Droplet in an Immiscible Liquid Environment. Langmuir 2013, 29, 13339–13345. [Google Scholar] [CrossRef]
- Lohse, D.; Zhang, X. Surface nanobubbles and nanodroplets. Rev. Mod. Phys. 2015, 87, 981–1035. [Google Scholar] [CrossRef]
- Zhang, J.M.; Chen, Y.; Lohse, D.; Marin, A. Dissolution of microdroplets in a sparsely miscible liquid confined by leaky walls. J. Fluid Mech. 2021, 912. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Pant, P.; Allen, M.; Cai, Y.; Jayachandran, K.; Chen, Y. Influence of physical factors on trichloroethylene evaporation from surface water. Water Air Soil Pollut. 2007, 183, 153–163. [Google Scholar] [CrossRef]
- Teng, H.; Yamasaki, A. Dissolution of CO2 droplets in the ocean. Energy 1997, 22, 751–761. [Google Scholar] [CrossRef]
- Collins, T.J. ImageJ for microscopy. Biotechniques 2007, 43, S25–S30. [Google Scholar] [CrossRef] [PubMed]
- Levenberg, K. A method for the solution of certain nonlinear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef]
- Tomasi, R.; Noel, J.M.; Zenati, A.; Ristori, S.; Rossi, F.; Cabuil, V.; Kanoufi, F.; Abou-Hassan, A. Chemical communication between liposomes encapsulating a chemical oscillatory reaction. Chem. Sci. 2014, 5, 1854–1859. [Google Scholar] [CrossRef]
- Pennell, K.D.; Abriola, L.M.; Weber, W.J., Jr. Surfactant-enhanced solubilization of residual dodecane in soil columns. 1. Experimental investigation. Environ. Sci. Technol. 1993, 27, 2332–2340. [Google Scholar] [CrossRef]
- Grimberg, S.J.; Nagel, J.; Aitken, M.D. Kinetics of phenanthrene dissolution into water in the presence of nonionic surfactants. Environ. Sci. Technol. 1995, 29, 1480–1487. [Google Scholar] [CrossRef]
- Johnson, J.C. Mass Transfer in Porous Media: The Effect of Surfactants on the Mass Transfer Rate Coefficient. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1998. [Google Scholar]
- Bolsman, T.; Veltmaat, F.; Van Os, N. The effect of surfactant structure on the rate of oil solubilization into aqueous surfactant solutions. J. Am. Oil Chem. Soc. 1988, 65, 280–283. [Google Scholar] [CrossRef]
- Falsini, S.; Intiso, A.; Spinozzi, F.; Ristori, S.; Marchettini, N.; Garza-Arévalo, J.I.; Sanchez-Dominguez, M.; Rossi, F. Poly-Oxyethylene Alcohol as Green Surfactant for VOCs Remediation: Physico-Chemical Characterization. 2020; submitted. [Google Scholar]
- Urynowicz, M.A.; Siegrist, R.L. Interphase mass transfer during chemical oxidation of TCE DNAPL in an aqueous system. J. Contam. Hydrol. 2005, 80, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Cohen, Y.; Ryan, P.A. Multimedia modeling of environmental transport: Trichloroethylene test case. Environ. Sci. Technol. 1985, 19, 412–417. [Google Scholar] [CrossRef] [PubMed]


| System | SYN (M) | (M) |
|---|---|---|
| H2O | - | (9.74 ± 0.03) × 10−3 |
| SYN91/5 [7,8] | 1 × 10−4 | (9.74 ± 0.05) × 10−3 |
| 1 × 10−3 | 0.020 ± 0.001 | |
| 0.01 | 0.022 ± 0.002 | |
| 0.05 | 0.022 ± 0.001 | |
| 0.08 | 0.022 ± 0.003 | |
| 0.10 | 0.022 ± 0.003 | |
| 0.20 | 0.047 ± 0.002 | |
| 0.30 | 0.067 ± 0.002 | |
| SYN91/10 [8] | 1 × 10−4 | (9.74 ± 0.04) × 10−3 |
| 0.01 | 0.04 ± 0.03 | |
| 0.05 | 0.15 ± 0.01 | |
| 0.08 | 0.26 ± 0.01 | |
| 0.10 | 0.33 ± 0.02 | |
| 0.15 | 0.45 ± 0.01 | |
| 0.20 | 0.64 ± 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valletti, N.; Budroni, M.A.; Lagzi, I.; Marchettini, N.; Sanchez-Dominguez, M.; Rossi, F. Interfacial Mass Transfer in Trichloroethylene/Surfactants/ Water Systems: Implications for Remediation Strategies. Reactions 2021, 2, 312-322. https://doi.org/10.3390/reactions2030020
Valletti N, Budroni MA, Lagzi I, Marchettini N, Sanchez-Dominguez M, Rossi F. Interfacial Mass Transfer in Trichloroethylene/Surfactants/ Water Systems: Implications for Remediation Strategies. Reactions. 2021; 2(3):312-322. https://doi.org/10.3390/reactions2030020
Chicago/Turabian StyleValletti, Nadia, Marcello A. Budroni, Istvan Lagzi, Nadia Marchettini, Margarita Sanchez-Dominguez, and Federico Rossi. 2021. "Interfacial Mass Transfer in Trichloroethylene/Surfactants/ Water Systems: Implications for Remediation Strategies" Reactions 2, no. 3: 312-322. https://doi.org/10.3390/reactions2030020
APA StyleValletti, N., Budroni, M. A., Lagzi, I., Marchettini, N., Sanchez-Dominguez, M., & Rossi, F. (2021). Interfacial Mass Transfer in Trichloroethylene/Surfactants/ Water Systems: Implications for Remediation Strategies. Reactions, 2(3), 312-322. https://doi.org/10.3390/reactions2030020








