Reinforcement Learning-Based Agricultural Fertilization and Irrigation Considering N₂O Emissions and Uncertain Climate Variability

Abstract

Nitrous oxide (${\mathrm{N}}_2\mathrm{O}$) emissions from agriculture are rising due to increased fertilizer use and intensive farming, posing a major challenge for climate mitigation. This study introduces a novel reinforcement learning (RL) framework to optimize farm management strategies that balance crop productivity with environmental impact, particularly ${\mathrm{N}}_2\mathrm{O}$ emissions. By modeling agricultural decision-making as a partially observable Markov decision process (POMDP), the framework accounts for uncertainties in environmental conditions and observational data. The approach integrates deep Q-learning with recurrent neural networks (RNNs) to train adaptive agents within a simulated farming environment. A Probabilistic Deep Learning (PDL) model was developed to estimate ${\mathrm{N}}_2\mathrm{O}$ emissions, achieving a high Prediction Interval Coverage Probability (PICP) of 0.937 within a 95% confidence interval on the available dataset. While the PDL model’s generalizability is currently constrained by the limited observational data, the RL framework itself is designed for broad applicability, capable of extending to diverse agricultural practices and environmental conditions. Results demonstrate that RL agents reduce ${\mathrm{N}}_2\mathrm{O}$ emissions without compromising yields, even under climatic variability. The framework’s flexibility allows for future integration of expanded datasets or alternative emission models, ensuring scalability as more field data becomes available. This work highlights the potential of artificial intelligence to advance climate-smart agriculture by simultaneously addressing productivity and sustainability goals in dynamic real-world settings.

1. Introduction

The escalating challenge of climate change, profoundly impacting global ecosystems, requires immediate and innovative solutions. Greenhouse Gases (GHGs) play a crucial role in climate change by trapping heat in the atmosphere. Nitrous Oxide (${\mathrm{N}}_2\mathrm{O}$), a primary GHG, is produced by both natural and human-induced processes, particularly through nitrogen-based fertilizer use and other farming practices. Simultaneously, climate variability poses a formidable threat to agricultural productivity, jeopardizing food security worldwide. According to the Food and Agriculture Organization (FAO) data, approximately 828 million people still experienced hunger in 2022. Agriculture, a vital component of the global economy, faces a dual challenge—navigating the impacts of GHGs on climate change and addressing the threats posed by climate variability. This intricate interplay underscores the need for a paradigm shift in agricultural management.

Across the globe, the upward trend in ${\mathrm{N}}_2\mathrm{O}$ emissions, both historically and in projections, is primarily attributed to the expanding use of fertilizers and the growth in livestock production. Approximately 60% of the contemporary increase in ${\mathrm{N}}_2\mathrm{O}$ comes from cultivated soils receiving Nitrogen (N) fertilizers [1]. Notably, from 1990 to 2020, there has been a 34.9% increase in ${\mathrm{N}}_2\mathrm{O}$ emissions from agricultural soils [2]. Various factors can influence ${\mathrm{N}}_2\mathrm{O}$ emissions, including crop types, tillage methods, crop residue management strategies, soil moisture levels, soil temperature conditions, and aspects of fertilizer usage. These aspects encompass the quantity, type, application timing, and method of placement [3]. In addition to anthropogenic factors, climate variability also plays a pivotal role in agricultural management, considering fluctuations in temperature, rainfall, wind patterns, and other weather elements across different time and space scales [4].

In past research on agricultural management, scholars typically gathered and examined historical data to uncover crop growth patterns. These findings were then used to guide future agricultural policies and practices [5]. With the continuous advancement of computer hardware and simulation software, there has been a notable shift in research methodologies. Specialized software tools, such as Decision Support System for Agrotechnology Transfer (DSSAT) [6], Agricultural Production Systems Simulator (APSIM) [7], and AquaCrop [8], have been developed and widely adopted in the agricultural research community. These simulation tools encompass various aspects of crop development, yield, water, and nutrient needs, enabling the optimization of management practices to adapt to evolving weather and environmental conditions.

However, in the above-mentioned classical crop simulators such as DSSAT, only nitrate leaching is typically observable as an indicator of nitrogen loss, whereas direct simulation of ${\mathrm{N}}_2\mathrm{O}$ emissions is not supported. While both nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions are related to nitrogen cycling in soils, they represent distinct environmental processes and impacts. Nitrate leaching measures the loss of nitrate to groundwater, contributing to water quality concerns, but does not capture the gaseous losses of nitrogen, especially as ${\mathrm{N}}_2\mathrm{O}$, a potent greenhouse gas with major climate implications. Sole reliance on nitrate leaching as an environmental criterion is therefore insufficient for assessing the full climate impact of agricultural management, since farming practices only to reduce nitrate leaching may not effectively mitigate ${\mathrm{N}}_2\mathrm{O}$ emissions, and in some cases may even exacerbate them due to trade-offs in soil nitrogen dynamics. Consequently, both nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions need to be considered when optimizing the agricultural management.

With the rising interest in Artificial Intelligence (AI) for smart or precision agriculture [9], researchers are increasingly integrating AI techniques, including Reinforcement Learning (RL), with the established software mentioned above to simulate and formulate improved agricultural management strategies. As a subset of Machine Learning (ML), RL empowers computer programs, functioning as agents, to navigate unfamiliar and dynamic systems for specific tasks [10,11]. Romain et al. [12] transformed DSSAT into a realistic simulation environment suitable for RL, known as Gym-DSSAT, which has gained popularity in agricultural research. Wu et al. [13] demonstrated that RL-trained policies could outperform traditional empirical methods, achieving higher or similar crop yields while using fewer fertilizers, a significant advancement in sustainable agricultural practices. Complementing this, Sun et al. [14] explored RL-driven irrigation control, optimizing water usage while maintaining crop health and showcasing the potential of Gym-DSSAT in effective resource management. Furthermore, Wang et al. [15] verified the robustness of learning-based fertilization management under challenging conditions. Even in extreme weather scenarios, the RL agent demonstrated the ability to learn optimal policies, resulting in highly satisfactory outcomes. This underscores the reliability and adaptability of RL in varying environmental conditions.

Most existing studies [12,13,14] have predominantly assumed a completely observable agricultural environment, formulating the related RL problems as Markov Decision Processes (MDPs). In MDP frameworks, it is assumed that each state of the environment contains all the necessary information for the agent to identify the optimal action for achieving the objective function. However, a significant issue arises when mirroring real-world scenarios, where agents lack complete knowledge to accurately determine the state of the environment due to the often uncertain or partial nature of their observations [16]. Notably, certain state variables in Gym-DSSAT, such as the index of plant water stress, daily nitrogen denitrification, and daily nitrogen plant population uptake, may pose challenges in terms of measurements and accessibility. Wang et al. [15] delved into this issue and discovered that it can be effectively addressed through the application of Partially Observable Markov Decision Processes (POMDPs). Subsequently, they adopted Recurrent Neural Networks (RNNs) to handle the history of observations for decision-making in fertilization management. Their findings indicated that modeling the agricultural environment as a POMDP resulted in superior policies compared to the existing assumption of an MDP.

According to the above-mentioned literature review, significant knowledge gaps exist in the current scientific research. Firstly, the crop simulator is limited to evaluating environmental impacts through nitrate leaching alone, overlooking the modeling of ${\mathrm{N}}_2\mathrm{O}$ emissions from soils. This gap significantly impedes considering greenhouse gas emissions when optimizing agricultural management strategies. Second, a notable lack of comprehensive studies exists on climate variability and its uncertainties within agricultural management. Current research has predominantly simulated static weather conditions, failing to account for the model’s capacity to adapt to climate changes and extreme weather scenarios. This leads to a scientific question: “How can we achieve optimal fertilization and irrigation management strategies to maximize crop yields and minimize ${\mathrm{N}}_2\mathrm{O}$ emissions, considering uncertain climate variability?”.

According to the literature reviewed above, significant knowledge gaps persist in current scientific research regarding crop simulation models and agricultural management strategies. Firstly, existing crop simulators predominantly assess environmental impacts solely through nitrate leaching, neglecting the crucial role of ${\mathrm{N}}_2\mathrm{O}$ emissions from agricultural soils. Given that ${\mathrm{N}}_2\mathrm{O}$ is a potent greenhouse gas exhibiting nonlinear responses to fertilizer applications and varying soil conditions, omitting its emissions significantly impedes accurate assessments of agriculture’s climate impact. Consequently, current optimization frameworks risk recommending management practices misaligned with broader sustainability and climate mitigation objectives.

Secondly, there is a notable deficiency in comprehensive studies addressing climate variability and associated uncertainties within agricultural management. Most existing research assumes static or minimally varying climatic conditions, thus inadequately representing the potential for climate fluctuations and extreme weather events exacerbated by climate change. Such limitations compromise the resilience and robustness of simulation-based optimization and RL-driven agricultural policies. Policies optimized under static conditions may thus fail significantly in real-world scenarios marked by environmental uncertainty, adversely affecting both food security and environmental protection. These identified gaps highlight an essential scientific question: How can optimal fertilization and irrigation management strategies be developed to maximize crop yields and minimize ${\mathrm{N}}_2\mathrm{O}$ emissions, explicitly accounting for uncertainties and variability associated with climate change?

In this study, we present the inaugural effort to make a significant contribution to bridge the gap in understanding the mutual effects between agricultural management strategies, specifically fertilization and irrigation plans, and challenges posed by climate change. By incorporating predicted soil ${\mathrm{N}}_2\mathrm{O}$ emissions into the reward function, the developed RL method can successfully guide agents in learning farming practices to mitigate GHG emissions, with a particular focus on ${\mathrm{N}}_2\mathrm{O}$ emissions. This approach, coupled with other considerations, provides valuable insights into fostering more sustainable agricultural practices.

Another significant contribution is the enhanced uncertainty quantification of the performance of the learned optimal management policies, representing a progression from our prior study [15]. By integrating a probability ML model for ${\mathrm{N}}_2\mathrm{O}$ emission prediction and a stochastic weather generator into the crop simulator, our agents exhibit the capability to learn adaptive optimal policies for fertilization and irrigation, particularly responding to climate variability, including rising temperature and reducing rainfall. This adaptation extends to address severe climate events like droughts.

This paper is organized as follows: Section 2 introduces the formulations of POMDP and discusses Deep Q-learning, a model-free RL technique. In Section 3, we establish the ML models for ${\mathrm{N}}_2\mathrm{O}$ emissions and outline the simulation model settings. Section 4 explores the integration of ${\mathrm{N}}_2\mathrm{O}$ emissions into the management of nitrogen fertilization and irrigation while also examining the implications of weather variability, such as elevated temperatures and reduced precipitation. The paper concludes with Section 5, where we briefly summarize our findings, engage in discussion, and propose alternative solutions for future research.

2. Methodologies

In this study, we conceptualize the agricultural environment as a POMDP and employ a model-free RL method for the agent to acquire optimal policies. This section begins by establishing the mathematical framework of POMDP. Following that, we introduce Q-learning and its variations, emphasizing their relevance in addressing POMDP-related challenges. A comprehensive description of the crop simulator settings used as the RL environment, including Gym-DSSAT configuration, action space discretization, and reward function weightings, is provided in Section 3.2. The RL hyperparameters employed during training, such as the random seed value, discount factor, and other key settings, are detailed in the table at the beginning of Section 4.

2.1. POMDP

A POMDP is usually represented by a tuple $\mathcal{P}=\left(S,A,T,s_0,R,O,\mathrm{\Omega }\right)$, including a finite set of states $S=\{s_1,\dots ,s_n\}$, a finite set of actions $A=\{a_1,\dots ,a_m\}$, the initial state $s_0\in S$, and a finite set of observations $O=\{o_1,\dots ,o_q\}$. Particularly, $A\left(s\right)$ is a set of available actions at state s for the agent to take. When the agent takes an action $a\in A\left(s\right)$, a transition occurs from the current state s to the next state $s^{\prime }$ with a probability $T(s,a,s^{\prime })$. Such transition probability is denoted by a function $T:S\times A\times S\to \left[0,1\right]$ and satisfy ${\sum }_{s^{\prime }\in S}T(s,a,s^{\prime })=1$.

After each transition, the agent may receive feedback based on the reward function $R:S\times A\times S\to \mathbb{R}$, where $\mathbb{R}$ denotes the codomain (the set of real numbers). In addition to $R(s,a,s^{\prime })$, the reward function has various formulations like $R\left(s^{\prime }\right)$ and $R(s,a)$. Since the environment is partially observable, a set of possible observations the agent can perceive is defined as $O\left(s^{\prime }\right)$. There exists an observation probability function $\mathrm{\Omega }:S\times A\times O\to \left[0,1\right]$ to quantify the perception uncertainty after the agent takes action a and reaches the next state $s^{\prime }$. This function must satisfy ${\sum }_{o\in O}\mathrm{\Omega }(s^{\prime },a,o)=1$.

The primary goal of the agent in an RL problem is to learn an optimal policy that can maximize the expected return, also known as the utility. Beginning from the current state s and adhering to a policy $\xi$, the expected return is the accumulated rewards the agent can collect. It is defined below as the sum of discounted rewards over a sequence of interactions with the environment.

$$U^{\xi }\left(s\right)={\mathbb{E}}^{\xi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t,s_{t+1})|s_{t=0}=s\right]$$

(1)

where $s_t$ represents the state of the environment at time t, and $a_t$ is the action to be taken, potentially leading to the transition of the agent to the state $s_{t+1}$ at the next time, $t+1$. The discount factor, $\gamma \in [0,1]$, is commonly employed to weigh the importance of future rewards in the agent’s decision-making process. The utility in Equation (1) assesses the expected total reward an agent can accrue in the long run and is also referred to as the state value, denoted as $V\left(s\right)$.

It should be noted that model-based RL for POMDP problems requires estimating the transition function and observation probability distribution, which can be challenging and data-intensive. However, we employ model-free RL methods like Q-learning with Recurrent Neural Networks (RNNs) introduced in the next subsection to avoid such computational and data barriers while still capturing partial observability and temporal dependencies. Such approaches have been successfully applied to robotics motion planning, where agents must act under sensor limitations and environmental uncertainty [17,18].

2.2. Q-Learning

Q-learning [19] is a widely used model-free RL method, and it utilizes Q values (action values or state-action values) to evaluate and select actions during the learning process. Similar to state values, the Q value, denoted as $Q^{\xi }(s,a)$, represents the total reward an agent is expected to accumulate after taking action a at the state s while following a policy $\xi$. Q values and state values are related through $V\left(s\right)={\max }_{a}Q(s,a)$. In contrast to policy-based RL methods [20], value-based methods like Q-learning directly seek the optimal value functions. These functions are subsequently used to select actions through the greedy technique. The $\epsilon$-greedy is usually adopted during the learning process to balance exploration and exploitation.

Given that the agricultural management problems under study involve an infinite state space, traditional tabular Q-learning is not suitable. Therefore, we adopt deep Q-learning, also known as deep Q networks or DQN [21], where Q values are approximated by Deep Neural Networks (DNNs). DQN employs two DNNs with identical network architectures. However, only one DNN, referred to as the evaluation Q-network, is trained and updated with collected experiences at every step. The other DNN, known as the target Q-network, periodically copies the weights of the evaluation Q-network.

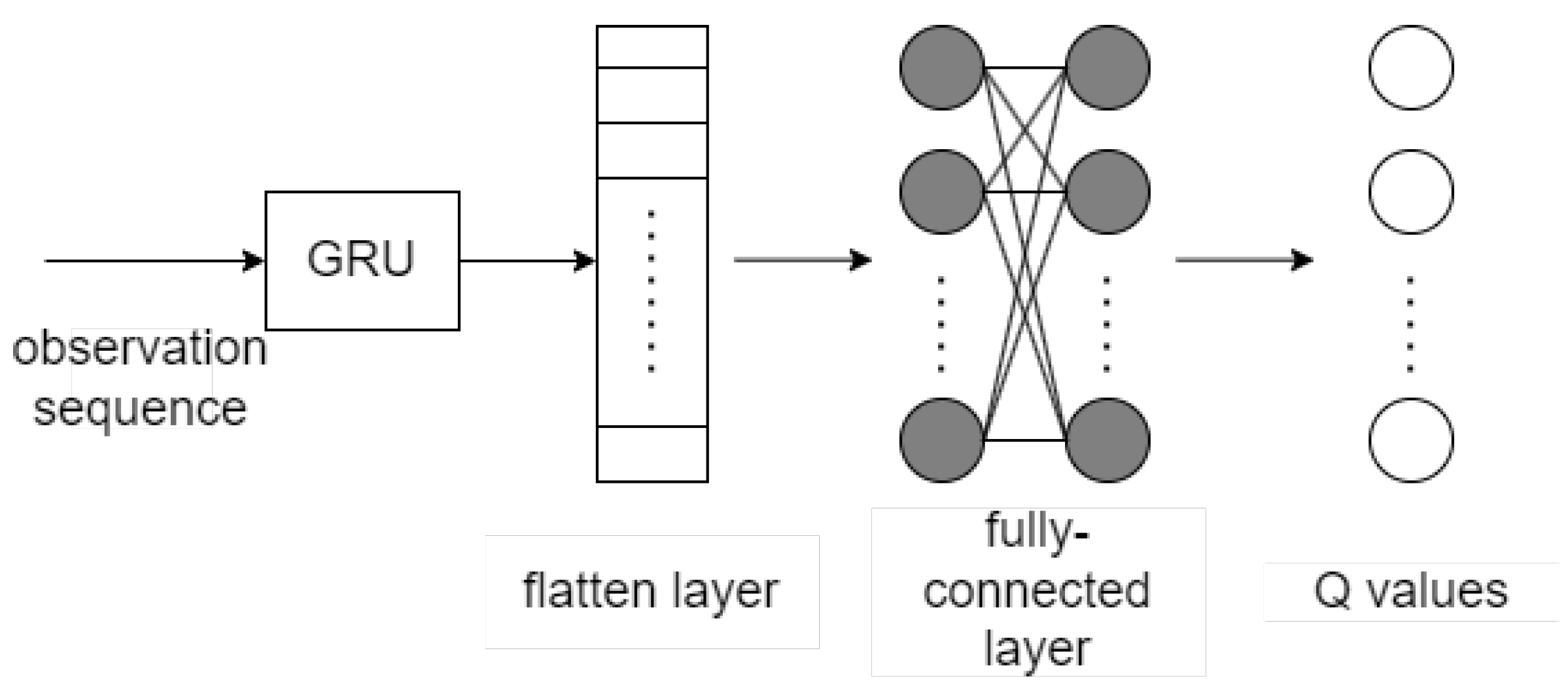
In POMDPs, decision-making relies on the history of observations instead of the current one. To address this challenge, we incorporated an RNN like Gated Recurrent Unit (GRU) [22] into the Q network architecture, as shown in Figure 1. In our prior work [15], we empirically showed that GRU-based Q-networks achieve better performance than conventional DQNs in handling temporal dependencies under POMDP settings, especially in agricultural environments. This architecture is designed to process sequences of observations. These sequential inputs are fed into a GRU layer, which maintains a hidden state to capture temporal dependencies and trends in the data. The GRU enables the network to remember relevant past information while filtering out noise, allowing it to model time-dependent changes in the environment. The GRU’s output is then passed through fully connected layers to estimate Q-values as $Q({\mathbf{o}}_t,a_t)$ where ${\mathbf{o}}_t$ represents the history of observations up to time t for each action, supporting RL-based decisions that account for both current and historical context.

It is worth noting that other sequence-modeling architectures can also be substituted for the GRU in a DQN under POMDPs. For example, Long Short-Term Memory (LSTM) [23] networks provide a deeper gating structure that can capture longer temporal dependencies, while Transformer-based [24] self-attention layers offer the ability to model global context without recurrence and have recently shown promise in RL settings. Incorporating these alternatives could further enhance representation capacity and sample efficiency, but evaluating them is left to future work; in this study we focus on the GRU variant for its favorable trade-off between performance and computational cost and to maintain consistency with our earlier experiments.

As a result, the two Q-networks in our DQN are denoted as $Q_E({\mathbf{o}}_t,a_t;{\theta }_E)$ and $Q_T({\mathbf{o}}_t,a_t;{\theta }_T)$ where ${\theta }_E$ and ${\theta }_T$ are network weights for the evaluation and target Q-networks, respectively. In each step of the learning process, the agent selects an action $a_t$ at the current state $s_t$ based on the Q values predicted from the evaluation Q-network, with the observation history ${\mathbf{o}}_t$ as the input. The $\epsilon$-greedy technique is employed for action selection.

Following the execution of the action and the transition to the next state $s_{t+1}$, the agent receives a reward $r_t=R(s_t,a_t,s_{t+1})$, observes an observation $o_{t+1}$, and generates a new observation sequence ${\mathbf{o}}_{t+1}=(o_{t-l+2},o_{t-l+3},\dots ,o_{t+1})$ with a length of l. Simultaneously, the experience, represented as $({\mathbf{o}}_t,a_t,r_t,{\mathbf{o}}_{t+1}))$, is stored in the experience replay memory [25]. Each experience contributes to one data sample, updating the Q value associated with the observation sequence and the action taken through the Bellman equation [26].

$$Q_{new}({\mathbf{o}}_t,a_t)=Q_E({\mathbf{o}}_t,a_t;{\theta }_E)+\alpha \left[r_t+\gamma \underset{a_{t+1}}{max}{Q}_T({\mathbf{o}}_{t+1},a_{t+1};{\theta }_T)-Q_E({\mathbf{o}}_t,a_t;{\theta }_E)\right]$$

(2)

where $\alpha$ is the learning rate.

At each time step, a batch of data samples is randomly selected to train and update the evaluation Q-network. Meanwhile, the target Q-network maintains constant weights until it copies from the evaluation Q-network, i.e., ${\theta }_T={\theta }_E$, after a certain number of time steps. It is important to note that standard DQN algorithms are known to sometimes overestimate Q-values, which can affect learning stability. In this work, we used the original DQN formulation and did not incorporate explicit overestimation mitigation strategies such as Double DQN, which could be considered in future research.

3. Model Setup

The simulation model generated in this study aligns with the Long-Term Ecological Research (LTER) site at the W.K. Kellogg Biological Station (KBS-LTER; 42°24^′ N, 85°24^′ W, 288 m elevation), as established in 1989 [27]. The testing field follows a no-till corn-soybean-winter wheat rotation and contains 1.6% solid organic carbon. The climate at this site is classified as humid continental, characterized by a mean annual precipitation of 1151 mm and an average temperature of 7.6 °C. For more information on agronomic management details, please refer to the KBS-LTER data tables available in [28].

3.1. ${\mathrm{N}}_2\mathrm{O}$ Emission Forecasting

Given that the Gym-DSSAT platform lacks ${\mathrm{N}}_2\mathrm{O}$ emission forecasting capabilities, this study endeavors to fill the gap by developing ML models, deterministic or probabilistic. These models aim to predict ${\mathrm{N}}_2\mathrm{O}$ emissions based on a combination of weather conditions and agricultural management practices. The dataset we used is from Saha’s study [29], spanning the years 2012 to 2017 (excluding 2015 due to instrument failure). The dataset contains numerous features. However, to align with the state variables available in Gym-DSSAT, we select four specific features, as outlined in

Table 1. Features for ${\mathrm{N}}_2\mathrm{O}$ emission forecasting models.

Variable	Description
pp2	the total precipitation in the 2 days leading up to gas sampling (mm)
pp7	the total precipitation in the 7 days leading up to gas sampling (mm)
airT	the mean daily air temperature (°C)
daysAF	the number of days that have elapsed following the application of top-dressed nitrogen fertilizer

. The model’s output is expressed in grams of nitrogen emitted per hectare each day (g ${\mathrm{N}}_2\mathrm{O}$-N/ha/d). The dataset comprises a total of 919 samples. For training and testing purposes, 80% of these samples are allocated to training and 20% to testing. To ensure robust validation, we employ a 5-fold cross-validation method.

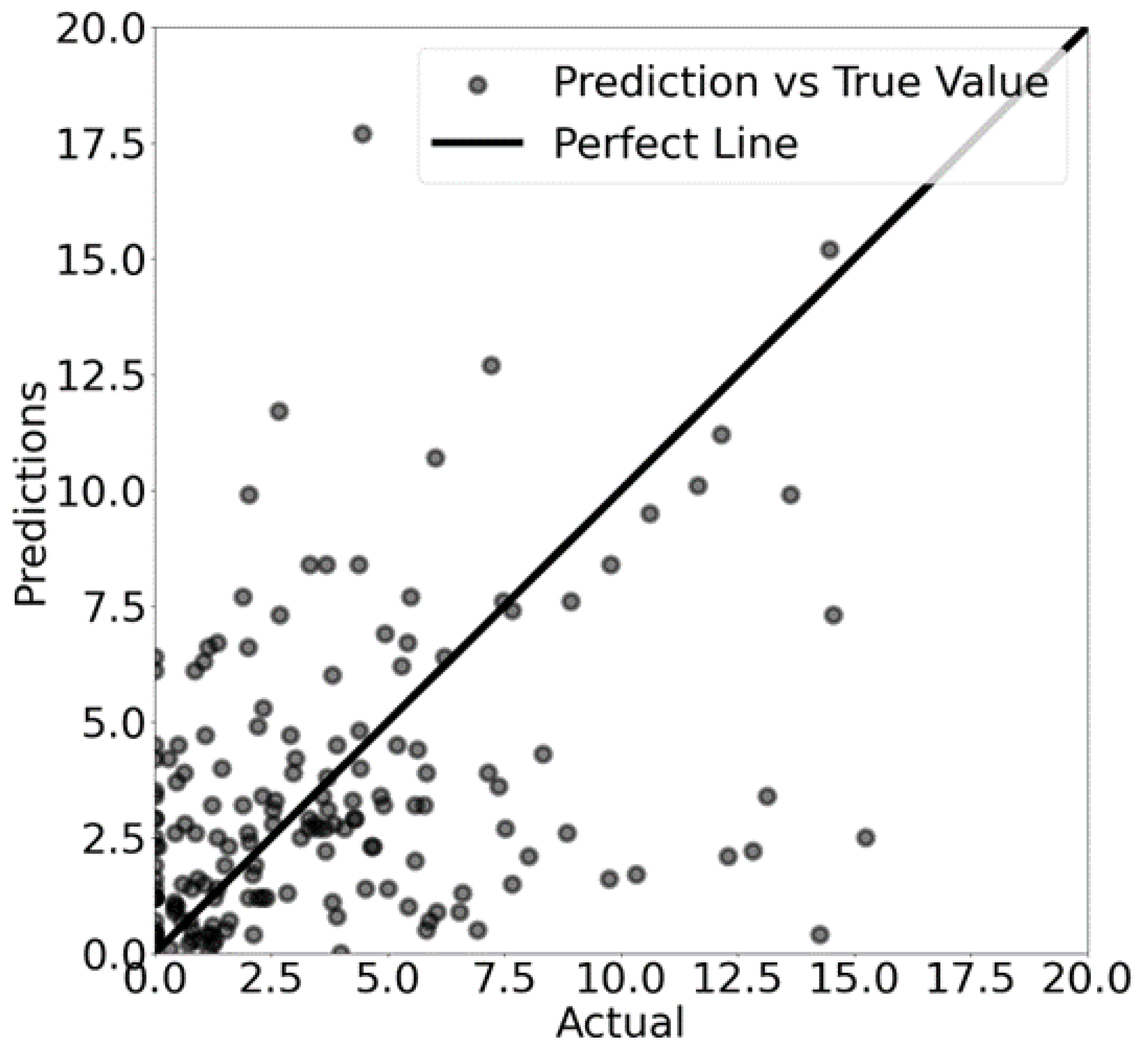
The first ML model employed for ${\mathrm{N}}_2\mathrm{O}$ prediction is a deterministic ML model with an artificial neural network (ANN). The neural network architecture comprises four layers, each consisting of 512 neurons with Rectified Linear Unit (ReLU) activation functions. Training involves a batch size of 128, a learning rate set at 0.0001, and a total of 6000 epochs. This architecture was selected to balance model complexity and computational efficiency while keeping the focus on the effect of input feature selection.The performance of the model on the testing set is visually presented in Figure 2, showcasing a comparison between predictive and true values.

Despite an extensive training regimen, the final coefficient of determination ($R^2$) for our ANN model, using only five features, stands at 0.65, indicating moderate predictive accuracy, as shown in Figure 2. It is noteworthy that various neural network architectures and activation functions were tested, and the configuration presented here yielded the best performance, balancing model complexity and computational efficiency. Although our achieved $R^2$ did not reach anticipated highs, it closely aligns with the outcomes observed in Saha’s study, where a Standard Random Forest model using 10 features also reported an $R^2$ of approximately 0.65 [29]. However, their Coupled Random Forest model, utilizing all 12 available features, achieved a higher performance with an $R^2$ of 0.78.

The deterministic ML model described earlier provides a singular optimal prediction for ${\mathrm{N}}_2\mathrm{O}$ emissions. Utilizing the sum of squared residuals as the loss function, a common practice in least square regressions, this model aims to minimize the difference between predicted and observed values. However, recognizing the inherent data uncertainty arising from measurements in the testing field, we take a different approach for training a PDL model–utilizing the maximum likelihood (MaxLike) method [30]. Unlike its deterministic counterpart, this model does not offer a single-point prediction but rather predicts a probability distribution, encompassing all potential ${\mathrm{N}}_2\mathrm{O}$ emissions.

MaxLike estimation is commonly employed to identify a suitable probability distribution with parameters that best explain data samples. Consequently, training a PDL model becomes a probability density estimation problem. This involves searching for optimal model parameters, denoted as $\theta$, with the objective of maximizing the joint probability of a given dataset $(X,y)$ where $X=(x_1,\dots ,x_n)$ and $y=(y_1,\dots ,y_n)$. The joint probability is often expressed as a likelihood function, denoted as

$$L\left(y\right|X;\theta )=P(y_1,\dots ,y_n|x_1,\dots ,x_n;\theta )=\prod _{i=1}^{n}P\left(y_i\right|x_i;\theta )$$

(3)

where the data samples are assumed to be independent and identically distributed, so the likelihood function can be reformulated as the multiplication of conditional probabilities.

As multiplying numerous small probabilities together can be numerically unstable in practice, using the sum of log conditional probabilities is common. Consequently, the Negative Log-Likelihood (NLL) function is typically employed as the cost function, as shown below. This function is minimized during the training of a PDL model.

$$min\left(\mathrm{NLL}\right)=min\left(-\sum _{i=1}^{n}logP\left(y_i\right|x_i;\theta )\right)$$

(4)

On the other hand, given that the ${\mathrm{N}}_2\mathrm{O}$ emission cannot be negative, we chose the log-normal distribution over the normal distribution, expressed as $ln\left(X\right)\sim \mathcal{N}(\mu ,{\sigma }^2)$. The probability density function is defined as

$$P\left(y_i\right|x_i;{\mu }_{x_i},{\sigma }_{x_i})={\displaystyle \frac{1}{y_i{\sigma }_{x_i}\sqrt{\pi }}}\exp \left(-{\displaystyle \frac{{(ln\left(y_i\right)-{\mu }_{x_i})}^2}{2{\sigma }_{x_i}^2}}\right)$$

(5)

where ${\mu }_{x_i}$ is the location parameter, and ${\sigma }_{x_i}$ is the scale parameter.

For the PDL model, the parameters were adjusted to prevent overfitting and improve convergence due to the probabilistic nature of the output and the smaller effective data size when modeling distributions rather than point estimates. Therefore, we employ another ANN, featuring a four-hidden-layer architecture with 16, 32, 64, and 16 neurons, respectively. Diverging from the deterministic model, the output layer of this model consists of two neurons: one for ${\mu }_x$ and the other for ${\sigma }_x$, representing the parameters of the Log-normal distribution in Equation (5). The training process spans 5000 epochs, with a batch size of 16. For configuration and training, we leverage the Tensorflow-probability package [31]. The deterministic ANN model utilized a larger batch size and more epochs to achieve stable training and effectively exploit computational resources for point prediction tasks. Conversely, the PDL model required a smaller batch size and fewer epochs, reflecting the greater complexity associated with modeling probability distributions, the necessity of avoiding overfitting, and differences in convergence behavior. Parameter selection was performed empirically through extensive experimentation to optimize validation performance for each model.

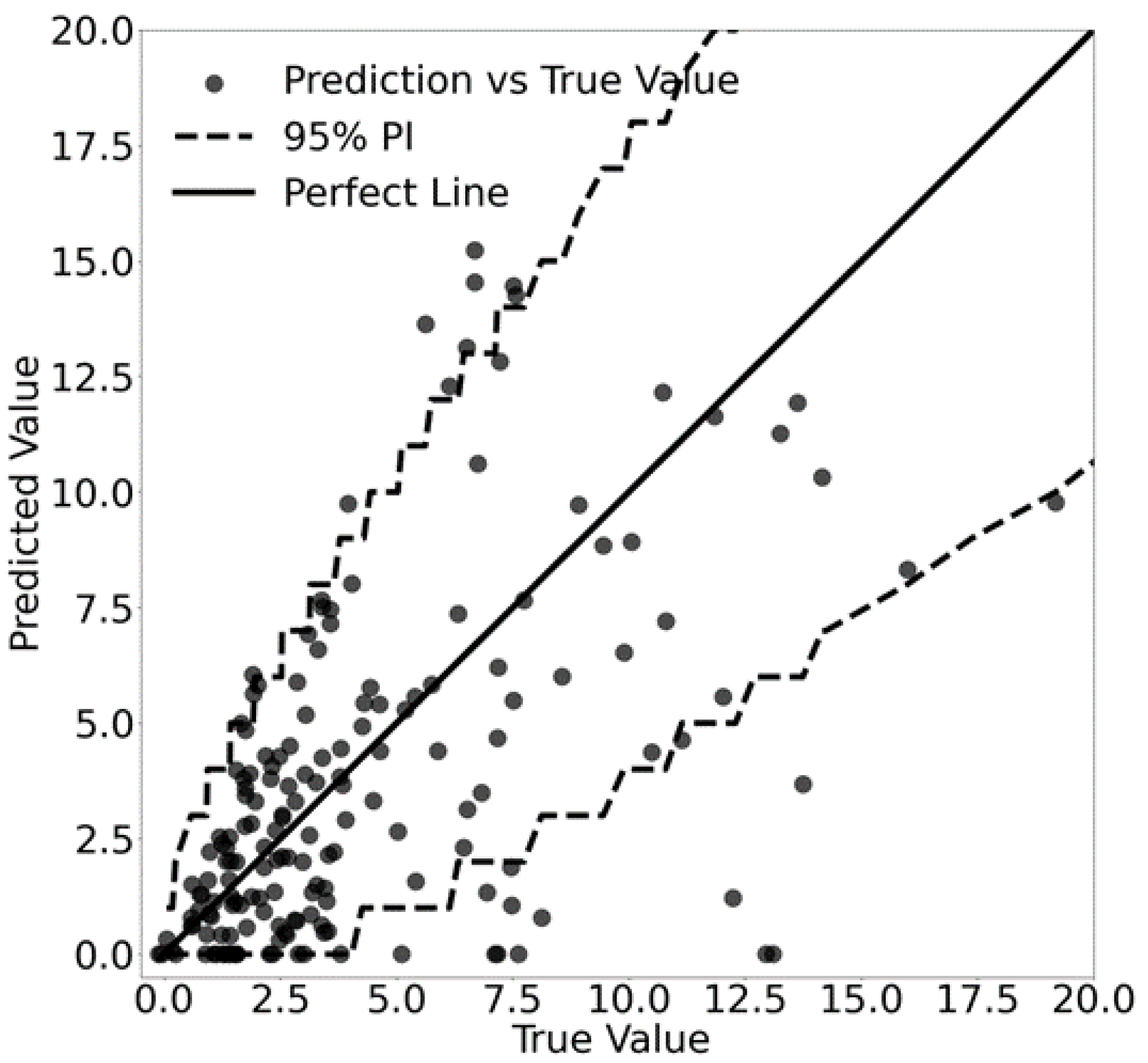
Figure 3 visually illustrates the model’s performance using the testing data. Each prediction, sampled from the predictive probability distribution, is compared to the corresponding true value or observation. The figure also includes a 95% prediction interval (PI), providing a comprehensive assessment of the model’s performance by considering not only its central tendency but also its variability.

To assess the PDL model, we calculate the Prediction Interval Coverage Probability (PICP) as below.

$$PICP={\displaystyle \frac{1}{N}}\sum _{i=1}^N\mathbf{1}(L_i\le y_i\le U_i)$$

(6)

where $L_i$ and $U_i$ denote the lower and upper bounds, respectively, of the prediction interval for the i-th data sample, $y_i$ represents the observed (or actual) values, and N is the total number of data samples. $\mathbf{1}(·)$ is the indicator function, which is 1 if the condition inside the parentheses is true and 0 otherwise. PICP quantifies the percentage of observed data points that are contained within the predicted intervals. The PICP values can vary between 0 and 1, with a value of 1 signifying that all observed values are encompassed within their respective prediction intervals and a value of 0 means that no observed values fall within their respective prediction intervals.

The PICP score for our model is 0.937 for the test set, indicating that it generally captures the data well within the 95% prediction intervals. This PDL model excels in quantifying the uncertainty of soil ${\mathrm{N}}_2\mathrm{O}$ emissions, particularly under climate variability conditions. Compared to traditional deterministic ML models, the PDL framework not only manages uncertainty more effectively but also achieves superior results using limited datasets. It also enhances model performance, particularly valuable in environmental contexts where data may be sparse or incomplete.

It is worth noting that the relatively wide prediction intervals observed in Figure 3, especially at peak emissions, likely reflect both the limited availability of data and the inherently high uncertainty associated with field measurements. On the other hand, relying solely on PICP is insufficient, as high coverage can result from overly broad intervals that are practically uninformative. Therefore, future studies will incorporate Mean Prediction Interval Width (MPIW) as an additional metric [32]. MPIW penalizes excessively wide intervals and quantifies the trade-off between interval coverage and sharpness, enhancing model informativeness and reliability.

It is important to note that the collected data [29] includes an extra input feature: the amount of N fertilization. However, the dataset only provides a single recorded value for this input feature, specifically 170 kg/ha. To estimate ${\mathrm{N}}_2\mathrm{O}$ emission across varying N input amounts, we employ regression analysis derived from Hoben’s exponential model, which has been empirically validated in prior studies for on-farm corn systems [33]. This combined approach allows us to approximate the nonlinear response of ${\mathrm{N}}_2\mathrm{O}$ emissions to varying N inputs despite the dataset’s limitations. The resulting approximation is expressed as $y\left(x\right)=y\left(170\right)·e^{0.0073·(x-170)}$ where x represents the actual N input, and $y\left(170\right)$ denotes the average daily ${\mathrm{N}}_2\mathrm{O}$ flux predicted from the ML models under the assumption of an N input of 170 kg/ha. Additionally, the sum of rainfall and irrigation is considered to calculate the precipitation-related input features (refer to Table 1) for predicting ${\mathrm{N}}_2\mathrm{O}$ emission.

3.2. Crop Simulator

This study employs Gym-DSSAT as a crop simulator, facilitating the approximation of interactions between the agent and the agricultural environment. Through RL methods, the agent learns optimal agricultural management, also called optimal policies. The Gym-DSSAT encompasses 28 internal variables. Previous studies [13,14] commonly used all these variables as state variables, assuming completely observable agriculture environments. Consequently, the learned policies in those studies mapped current observations directly to the management plan. In other words, the agent made decisions regarding fertilization and irrigation based on current observations of state variables.

However, it is important to note that there is no conclusive evidence demonstrating that these 28 internal variables can fully determine the state of the agricultural environment. Furthermore, not all of them are easily observable or accessible. Unlike the studies mentioned above, our work explicitly acknowledges the practical challenges in measuring certain variables. As established in our prior research, we model the agricultural environment as partially observable [15]. Our intelligent agents make decisions based on a history of observations from ten carefully selected state variables (listed in

Table 2. State variables of the agricultural environment used in this study.

Variable	Description
cumsumfert	cumulative nitrogen fertilizer applications (kg/ha)
dap	days after planting
istage	DSSAT maize growing stage
pltpop	plant population density (plant/m2)
rain	rainfall for the current day (mm/d)
sw	volumetric soil water content in soil layers (cm3 [water]/cm3 [soil])
tmax	maximum temperature for the current day (°C)
tmin	minimum temperature for the current day (°C)
vstage	vegetative growth stage (number of leaves)
xlai	plant population leaf area index

), chosen for their reliability in real-world agricultural settings. The selection of observation variables was guided by their practical observability in real-world agricultural settings; we prioritized variables that can be easily measured or estimated routinely in the field, or accessed online. These variables, including weather conditions, soil moisture, and basic crop traits, are prioritized due to their accessibility via common monitoring tools and internet-based data sources. Our prior studies show that modeling the agricultural environment as a POMDP with 10 selected observation variables yields policies that perform similarly to (or better than) those derived from POMDPs or MDPs using all 28 variables [15]. This approach ensures a realistic representation of the agent’s decision-making environment, aligning with real-world constraints.

In contrast to conventional approaches, we recognize the practical challenges associated with measuring certain variables. As highlighted in our previous study [15], we consider the agricultural environment to be partially observable. In our model, intelligent agents base decisions on the historical observations of a carefully selected set of ten state variables, outlined in Table 2. Our selection was based on practical considerations discussed in our previous work [15], where we systematically evaluated which state variables could be reliably observed or measured in real-world agricultural settings. The chosen variables represent those most directly accessible through the internet and common monitoring tools, such as weather, soil moisture, and basic crop characteristics. This nuanced perspective aims to offer a more realistic representation of the agent’s decision-making environment, ensuring alignment with the complexities found in real-world scenarios.

In this study, both the state and observation spaces are infinite. Gym-DSSAT, the utilized crop simulator, outputs 28 state variables representing a daily state in the agricultural environment. Ten of those state variables are selectively chosen as observations, assuming the agricultural environment is partially observable. Our selection was based on practical considerations discussed in our previous work [15], where we systematically evaluated which state variables could be reliably observed or measured in real-world agricultural settings. The chosen variables represent those most directly accessible through the internet and common monitoring tools, such as weather, soil moisture, and basic crop characteristics.

The action space encompasses different combinations of N and water quantities that can be applied in a single day. Mathematically, the action space is discretized as $(N_p,I_q)$ where $N_p=20p$ (kg/ha) represents the N input, and $I_q=10q$ (L/m²) represents the water input. Both p and q vary within the range of 0 to 4. Consequently, there are a total of 25 available actions for the agent to choose from each day. This discretization of nitrogen and water inputs was selected to reflect typical application rates encountered in field management, balancing the need for realistic simulation with computational resource considerations. While finer discretization or a continuous action space could potentially allow more precise management strategies, it would also significantly increase the computational demands during training of RL agents.

On a given day $d_t$, after the execution of a selected action involving the application of N input $N_t$ and water input $I_t$, Gym-DSSAT conducts computation for nitrate leaching $L_t$ (kg/ha) and crop yield Y (kg/ha) if harvested. Additionally, our ML models estimate ${\mathrm{N}}_2\mathrm{O}$ emissions $O_t$ (kg/ha). Following these calculations, the agent is rewarded according to the formula specified in Equation (7).

$$R_t=\left\{\begin{array}{cc}{w}_{1}Y-w_2{N}_t-w_3{I}_t-w_4{L}_t-w_5{O}_t& \mathrm{at\; harvest}\\ -w_2{N}_t-w_3{I}_t-w_4{L}_t-w_5{O}_t& \mathrm{otherwise}\end{array}\right.$$

(7)

where $w_1=0.2$, $w_2=2$, $w_3=2$, $w_4=30$, and $w_5=100$ represent the weight coefficients. It is important to highlight that $w_1$ through $w_3$ align with those utilized in previous research studies [34]. We explored alternative values for the weight assigned to nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions in the reward function and assessed the resulting outcomes. The comparative analysis for the year 2012 indicated that a weight combination of 30 and 100 yields superior results, ensuring optimal output levels while maximizing the reward.

Our research focuses on the growth and yield of corn for the year 2012, requiring the extraction of climate and soil conditions specific to that timeframe. The relevant meteorological data was obtained from the KBS-LTER website [28], offering detailed daily records of maximum and minimum temperatures, precipitation, and solar radiation. To address the variability in climatic conditions, we utilized the stochastic Weather Generator (WGEN) [35], a random weather generator integrated into DSSAT. This tool enables the generation of weather scenarios for each episode under investigation.

The WGEN categorizes its output variables into two distinct groups. The first group exclusively encompasses precipitation, while the second group comprises maximum temperature, minimum temperature, and solar radiation. This categorization is based on the understanding that the occurrence of rain on a given day significantly influences that day’s temperature and solar radiation. As a result, precipitation is generated as an independent variable each day, separate from the other variables in the second group. Then, calculations for maximum and minimum temperatures and solar radiation are executed depending on whether the day is characterized as wet or dry.

More specifically, the WGEN incorporates a precipitation element based on a Markov chain-gamma distribution model. It employs a first-order Markov chain model to predict the likelihood of rain, considering whether the previous day was wet or dry. In the case of a predicted wet day, a two-parameter gamma distribution is utilized to calculate the precipitation amount. Subsequently, the residuals for the other three variables–maximum temperature, minimum temperature, and solar radiation–are generated through a multivariate normal generation process. This process maintains the serial and cross-correlation coefficients of the variables. The final values for these three variables are determined by adding the calculated residuals to the seasonal means and standard deviations, following the methodology outlined in [36].

It is important to note that while WGEN effectively generates synthetic daily weather sequences based on historical patterns, it has inherent limitations in capturing the full climate spectrum, particularly extreme weather events, when trained on normal climate data, as in our study. Consequently, policies optimized using WGEN-generated scenarios may demonstrate limited generalizability to future climates characterized by increased frequency or severity of extreme events. We emphasize that these limitations regarding extreme events have been specifically addressed in our related study [37].

The soil properties used in this study are selected from the soil file provided by DSSAT, which contains data specifically collected at the KBS. This ensures that the simulation environment accurately reflects the real-world soil characteristics at the study site. During a crop simulation in the Gym-DSSAT environment, the planting and harvest dates, alongside the initial and terminal states of the simulated RL problems, are dynamically determined. Initially, the simulator identifies the optimal planting date by analyzing prevailing weather conditions. Then, throughout each episode, it monitors the growth stages of maize using a variable called ‘istage’ to gauge crop maturity. When ‘istage’ reaches a threshold value indicating that the crops are mature and ready for harvest, the simulation concludes, and a new episode begins. This dynamic approach ensures that the planting and harvesting dates adapt to fluctuating weather conditions, resulting in more accurate and realistic agricultural modeling.

3.3. Reinforcement Learning Based Agricultural Fertilization and Irrigation

In this research, the crop simulator and the developed ${\mathrm{N}}_2\mathrm{O}$ emission predictive model form a virtual agriculture environment, incorporating weather data. This setup allows an RL agent to interact with the environment, as depicted in Figure 4, under the assumption of partial observability. Specifically, the RL framework presented offers a clear overview of how the agent interacts sequentially with the agricultural environment under given weather conditions. The agent observes state variables (e.g., air temperature, crop growth stage) and selects actions, such as whether and how much to irrigate or fertilize. Upon execution, the crop simulator generates rewards as feedback, enabling the agent to quantitatively evaluate its actions and gradually improve decision-making.

We utilize an RNN-based DQN, enabling the agent to learn optimal policies. The sequence of observations from the past five days, including weather data, is updated daily during the learning process. No additional frame stacking or explicit state augmentation is used in this study. This sequence serves as the input to the Q networks, which output Q values (or action values) to guide the agent’s decisions on fertilizer and water usage. Notably, at the beginning of each episode, random actions are selected for the first five days to initiate the observation sequence.

Following the agent’s decision on action, the simulator and ${\mathrm{N}}_2\mathrm{O}$ emission predictive model provide the reward and state variables for the next day, based on the current state and available weather data. Historical weather data from the W.K. Kellogg Biological Station is used for scenarios with fixed weather conditions. Conversely, weather data is randomly generated using the WGEN, a stochastic weather generator, when assessing weather uncertainty. Simultaneously, the developed machine learning model predicts ${\mathrm{N}}_2\mathrm{O}$ emissions, contributing to the reward calculation. The current and next sequences of observations, alongside the reward, are compiled as an experience and stored in a memory pool. This pool is then leveraged to frequently update the Q networks by generating training batches.

4. Simulation Results and Discussions

In this study, we employ an RNN-based DQN, as detailed in Section 2.2, to facilitate the agent in learning optimal policies. The Q-networks, integrated into this approach, take a sequence of observations as input and generate Q values, guiding the agent in its action selection. The RNN layer within the Q-networks (refer to Figure 1) consists of a single hidden layer with 64 units. Its output is subsequently fed into a fully connected network. Our study utilizes a sequence comprising observations from five consecutive days to make decisions.

Throughout the learning process, we apply the $\epsilon$-greedy selection technique to strike a balance between exploration and exploitation. The discount factor, crucial for future reward, is set at 0.99. To design and update the neural networks, we employ PyTorch v2.5.0 and Adam optimizer [38], using an initial learning rate of 1 × 10⁻⁵ and a batch size of 640. The choice of parameters is based on considerations of model performance and efficiency. Simulations are conducted on two distinct machines. The first machine is equipped with an Intel Core i7-12700K processor, an NVIDIA GeForce RTX 3070 Ti graphics card, and 64 GB RAM. The second machine features an AMD 5800h processor, an NVIDIA GeForce RTX 3070 graphics card, and 32 GB of RAM. The selection of these configurations is informed by their computational capabilities and relevance to the scope of our study, as summarized in

Table 3. RL Hyperparameters used in this study.

Hyperparameters	Values
Random seed values	123
Discount factor	0.99
Initial learning rate	1 × 10−5
Batch size	640
Exploration ($ϵ$)	$0.{9991}^{n-1}$ (n is the number of episodes)
Target network update frequency	2500 steps

.

The average training time in this study is around 22 h. It is worth noting that, as RL with neural networks can exhibit non-trivial variability due to hardware differences, we took care to ensure that both machines have comparable computational power and similar GPU architectures. In our experiments, we did not observe significant performance differences attributable to hardware variation. Nevertheless, we acknowledge that hardware can be a potential source of variability, and we report our configurations here for transparency and reproducibility.

We conduct multiple simulations to explore the implications of ${\mathrm{N}}_2\mathrm{O}$ emission and climate variability on agricultural management and outcomes, particularly corn yield. First, we select the year 2012 as our baseline, utilizing authentic weather data and soil properties. By incorporating ${\mathrm{N}}_2\mathrm{O}$ emission into our reward function, we simulate the effects of ${\mathrm{N}}_2\mathrm{O}$ emission in the context of agricultural practices. Following this, we introduce variations in temperature and rainfall to assess the influence of climate variability. To enhance the model’s resilience against unpredictable weather conditions, we choose to generate randomized weather scenarios based on actual data using the WGEN, as described in Section 3.2. These scenarios are then utilized to train our models, significantly enhancing their accuracy in coping with uncertain environmental conditions.

4.1. Considering N₂O Emission

In this research, we aim to investigate the impact of ${\mathrm{N}}_2\mathrm{O}$ emissions on management practices and agricultural outcomes. Through simulations, we analyze three distinct scenarios to elucidate the relationship between nitrate leaching, soil ${\mathrm{N}}_2\mathrm{O}$ emissions, and agricultural productivity.

The first scenario focuses exclusively on the effects of nitrate leaching while deliberately omitting soil ${\mathrm{N}}_2\mathrm{O}$ emissions. This helps us isolate the direct consequences of nitrate leaching on soil and water quality without the confounding effects of ${\mathrm{N}}_2\mathrm{O}$ emissions. The second scenario centers specifically on soil ${\mathrm{N}}_2\mathrm{O}$ emissions, excluding the impacts of nitrate leaching. This approach allows agents to learn effective fertilization and irrigation strategies to control and reduce ${\mathrm{N}}_2\mathrm{O}$ emissions. The third scenario combines both nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions. By analyzing these factors concurrently, we can explore their interplay and cumulative impact on agricultural outcomes. This holistic approach enables us to develop more comprehensive and effective management strategies.

Upon comparing the actual data received from KBS [28], we gather all available information, encompassing diverse fertilization and irrigation practices across various testing fields from 2011 to 2014. The N inputs exhibit significant variation, ranging from 0 kg/ha to a maximum of 291 kg/ha, with an average input of 138 kg/ha. Yield outcomes also display variability, with the highest recorded yield at 14,023 kg/ha, the lowest at 3084 kg/ha, and an average yield of 9740 kg/ha. Additionally, the measured ${\mathrm{N}}_2\mathrm{O}$ daily fluxes reach up to 0.6 (kg/ha/d) with a median value of 0.002. Unfortunately, detailed irrigation data are not available.

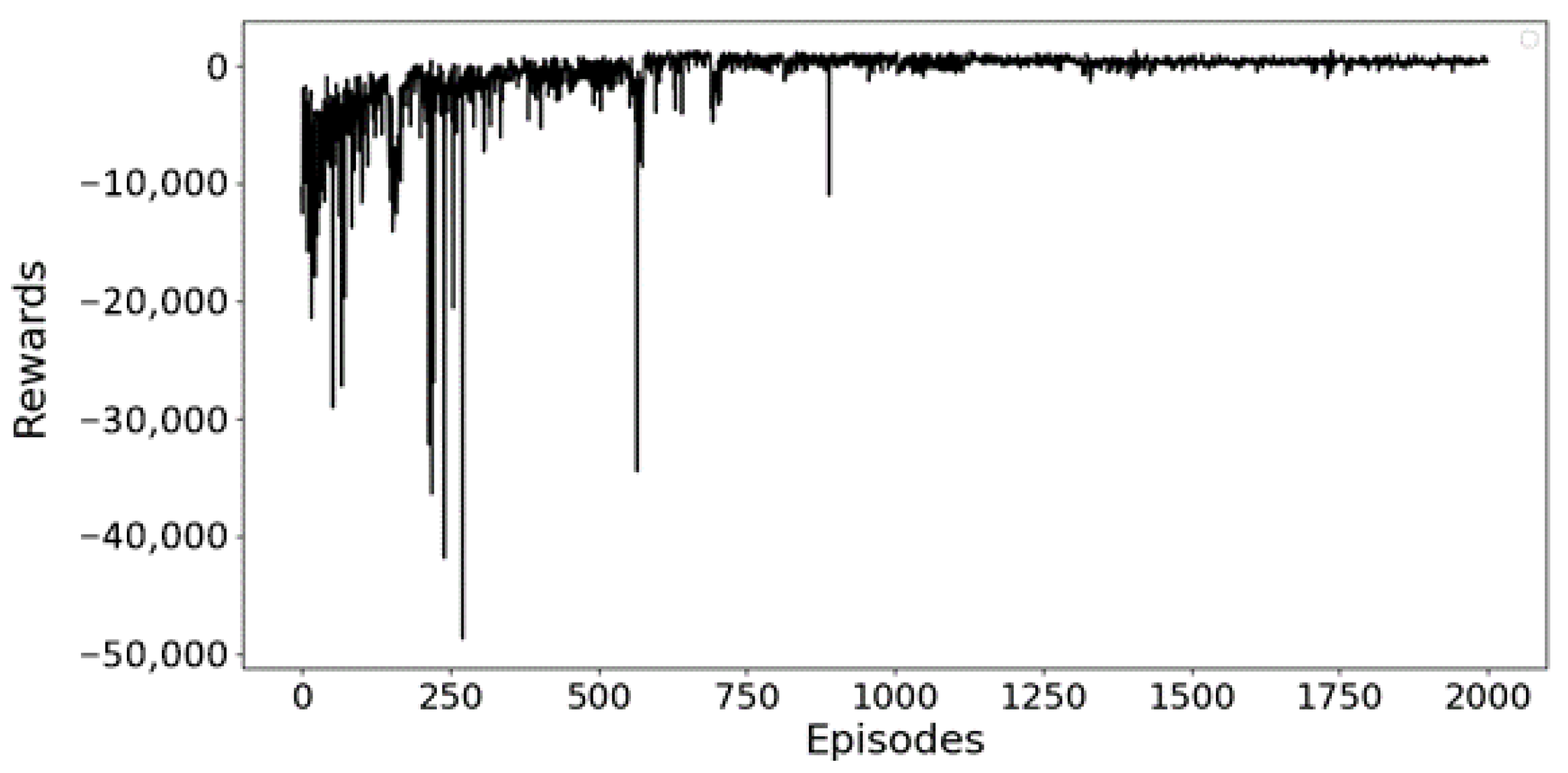
We utilize the deterministic ML model to predict daily ${\mathrm{N}}_2\mathrm{O}$ emissions for all scenarios above. Figure 5 illustrates the RL training process from episodes 2000 to 6000 for the third case, indicating the convergence to learn the optimal policy. In our simulations, following the acquisition of the optimal policy via RL in each case, we apply it to perform one realization in the year 2012. The comparative results across the three cases are presented in

Table 4. Agricultural outcomes for three different cases (Case 1: Nitrate leaching only, Case 2: ${\mathrm{N}}_2\mathrm{O}$ emission only, and Case 3: Nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emission.)

	Case 1	Case 2	Case 3
Reward	1338	1267	1272
Yield (kg/ha)	11,190	10,549	11,305
N input (kg/ha)	140	140	180
Water input (L/m2)	310	270	300
Nitrate leaching (kg/ha)	0.0009	0.21	0.175
${\mathrm{N}}_2\mathrm{O}$ emission (kg/ha)	0.314	0.223	0.251

.

Compared to the average reported corn yield in Michigan in 2012 (approximately 8290 kg/ha) [39], the yields derived from our RL-based management policy demonstrate a substantial improvement, highlighting the practical advantages of our approach. Additionally, our previous studies indicated that RL-based optimal policies outperform the expert policy recommended by DSSAT [15,37].

Data from The Mosaic Company [40] indicates that a corn crop yielding 200 bushels per acre (equivalent to 12,553 kilograms/hectare) can absorb up to 297 kg of N per hectare. When N inputs align with the crop’s requirements, there is no noticeable increase in ${\mathrm{N}}_2\mathrm{O}$ emissions. As N inputs exceed the crop’s needs, ${\mathrm{N}}_2\mathrm{O}$ emissions begin to rise dramatically [3]. The total ${\mathrm{N}}_2\mathrm{O}$ emission data during the growing season from our 2012 dataset was 0.586 kg/ha. It is important to note that there remain several days unaccounted for within the growing season, leading us to believe that the actual emissions are likely higher than this reported value. In all three examined cases, nitrogen inputs remained below the indicated threshold, resulting in lower ${\mathrm{N}}_2\mathrm{O}$ emissions than those previously reported. ${\mathrm{N}}_2\mathrm{O}$ emission is less than the record data. Furthermore, by considering ${\mathrm{N}}_2\mathrm{O}$ emission in the reward function, the resultant policies have the potential to mitigate ${\mathrm{N}}_2\mathrm{O}$ emissions in Case 2 and reduce both nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emission in Case 3, all while maintaining production levels.

Although total fertilizer and water usage quantities remained similar across cases, application strategies varied significantly. This difference arises as the RL agent strategically weighs the benefits, such as corn yield, against costs, including resource consumption and penalties for nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions, aiming to maximize overall rewards.

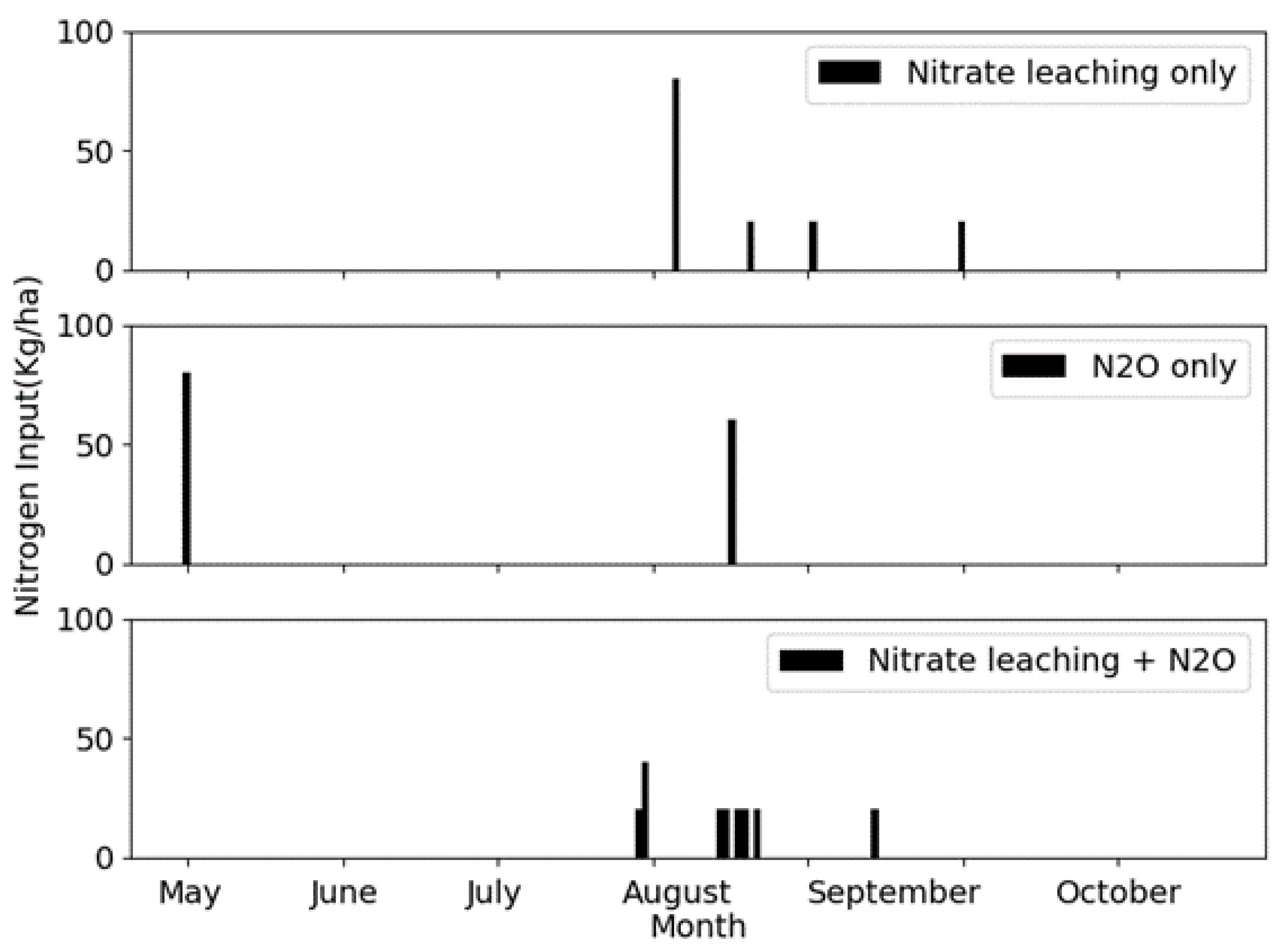
Figure 6 and Figure 7 provide detailed insights into fertilization and irrigation strategies based on optimal policies from the three scenarios. Notably, fertilizer and water applications were predominantly concentrated in August and September, critical growth months for corn. Analysis of weather data from 2012 indicates approximately 25% less precipitation during these months compared to preceding years, accompanied by higher-than-average temperatures [41], emphasizing an urgent need for effective irrigation.

In Case 1, this strategy involves high water inputs that support relatively high yields, collectively contributing to an increased total reward. However, the greater water application, combined with fertilizer use, creates conditions conducive to elevated microbial activity and denitrification in wetter soils, thereby significantly enhancing ${\mathrm{N}}_2\mathrm{O}$ emissions. Consequently, despite the high yield and reward, this approach leads to substantially increased ${\mathrm{N}}_2\mathrm{O}$ emissions. In Case 2, the agent strategically manages water and fertilizer applications to minimize ${\mathrm{N}}_2\mathrm{O}$ emissions. This optimization involves carefully adjusting the timing and frequency of these inputs to avoid creating favorable conditions for emissions. However, this emission-mitigation strategy leads to reduced nitrogen availability, subsequently lowering the crop yield compared to Case 1. In Case 3, fertilizer inputs are increased relative to Cases 1 and 2 but are carefully timed and synchronized with crop demand and soil conditions. This approach effectively balances yield improvement with environmental concerns, achieving higher yields while maintaining moderate levels of both ${\mathrm{N}}_2\mathrm{O}$ emissions and nitrate leaching.

Those align with findings by Weitz et al. [42], which emphasize that soil moisture significantly influences ${\mathrm{N}}_2\mathrm{O}$ emissions, noting the highest post-fertilization emissions occur in moist soils, with drier soils only experiencing increased emissions following rainfall. The observed dynamics between ${\mathrm{N}}_2\mathrm{O}$ emissions and nitrate leaching reflect their different underlying mechanisms: while ${\mathrm{N}}_2\mathrm{O}$ emissions are strongly influenced by soil moisture, fertilizer timing, and availability of labile nitrogen, nitrate leaching is mainly driven by excess nitrogen and water movement through the soil profile. Thus, jointly considering both environmental impacts encourages the agent to find a balanced management strategy that does not simply minimize one at the expense of the other. Instead, the RL agent learns to apply inputs at times that maximize crop uptake and minimize losses to the environment, enhancing input-use efficiency.

4.2. Temperature Rising

Significant shifts in global climate patterns have been marked by a rise in air temperature [43], primarily attributed to GHG emissions resulting from human activities. According to historical data from NASA, there has been a consistent increase in average temperatures since 1880. This trend of global warming has become more pronounced in recent years, with temperatures rising by 0.94 degrees Celsius in the past 60 years [44].

In this study, we use the year 2012 as the baseline and augment monthly maximum and minimum temperatures by up to 3 degrees Celsius using WGEN to generate random weather. In contrast to our previous investigation [15], where the temperature pattern was preserved, the randomly generated weather in this study does not replicate the identical patterns observed in 2012, introducing weather uncertainty through temperature variations. Notably, while rainfall is also randomly generated via WGEN, correspondingly, the monthly total precipitation remains the same as observed in 2012. Furthermore, we integrate the PDL model developed in Section 3.1 to assess ${\mathrm{N}}_2\mathrm{O}$ emissions, considering data uncertainty from measurements in the testing fields.

We examine temperature increases of 0.5, 1, 1.5, 2, 2.5, and 3 degrees Celsius. Additionally, we include a scenario with no temperature increase but random weather. Two types of policies are implemented: the “fixed policy,” derived from actual weather data of 2012, which considers both nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emission as discussed in Case 3 in the previous subsection, and the “optimal policies,” specifically learned at each temperature increase. Following policy learning, 300 realizations are conducted to assess the uncertainties associated with agriculture outputs and management. This approach also allows for an exploration of policy adaptability to climate variability.

To enhance the training efficiency of the agent in learning optimal policies, we leverage a transfer learning technique–fine-tuning. The evaluation Q network associated with the fixed policy serves as a pre-trained model, acting as the starting point for training optimal policies or updating the evaluation Q network at each specific temperature increase. The adoption of fine-tuning yields a significant reduction in training time compared to conventional methods that start with a random policy. 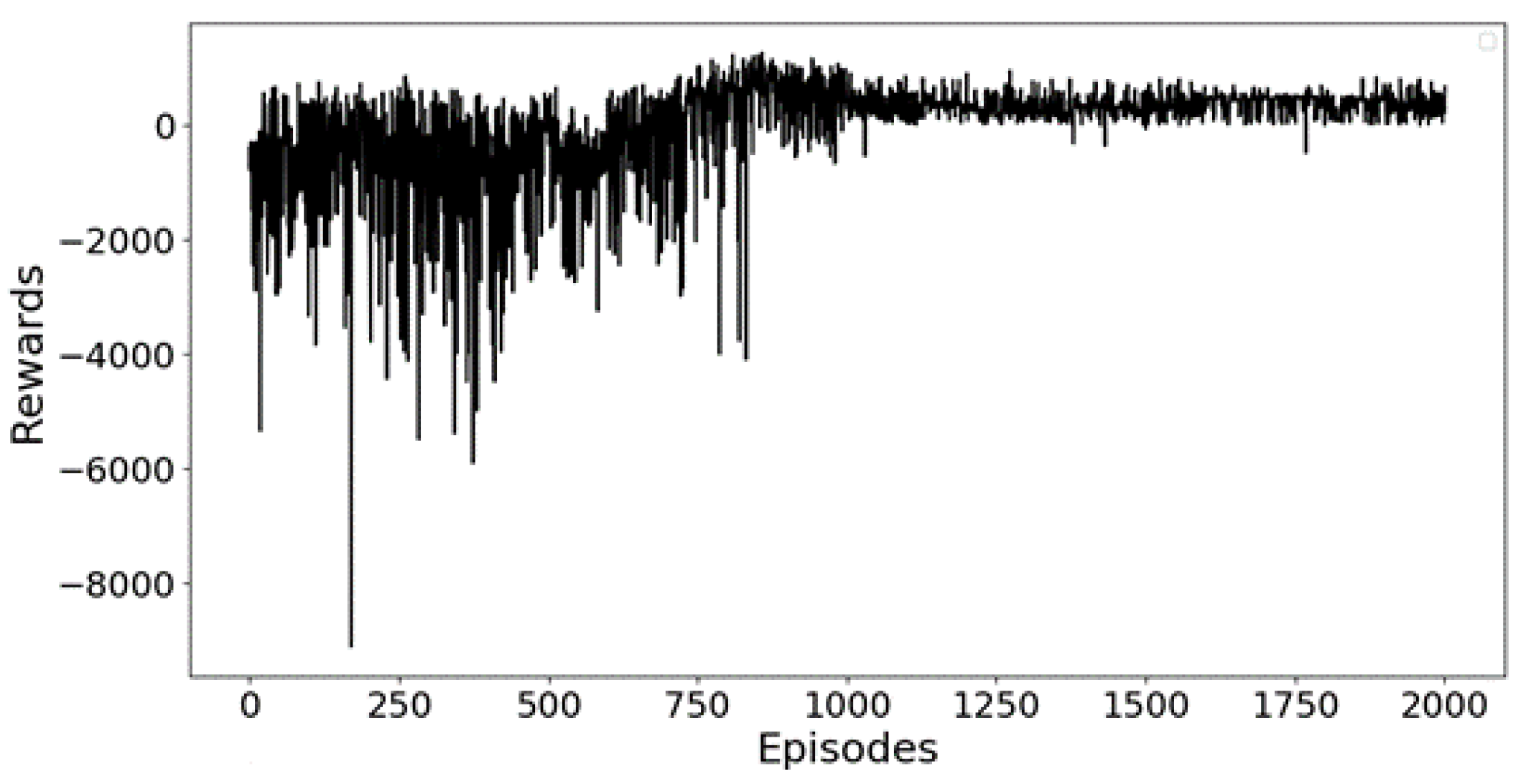Figure 8 represents the training process when the average temperature increases by 3 degrees Celsius amid weather uncertainty.

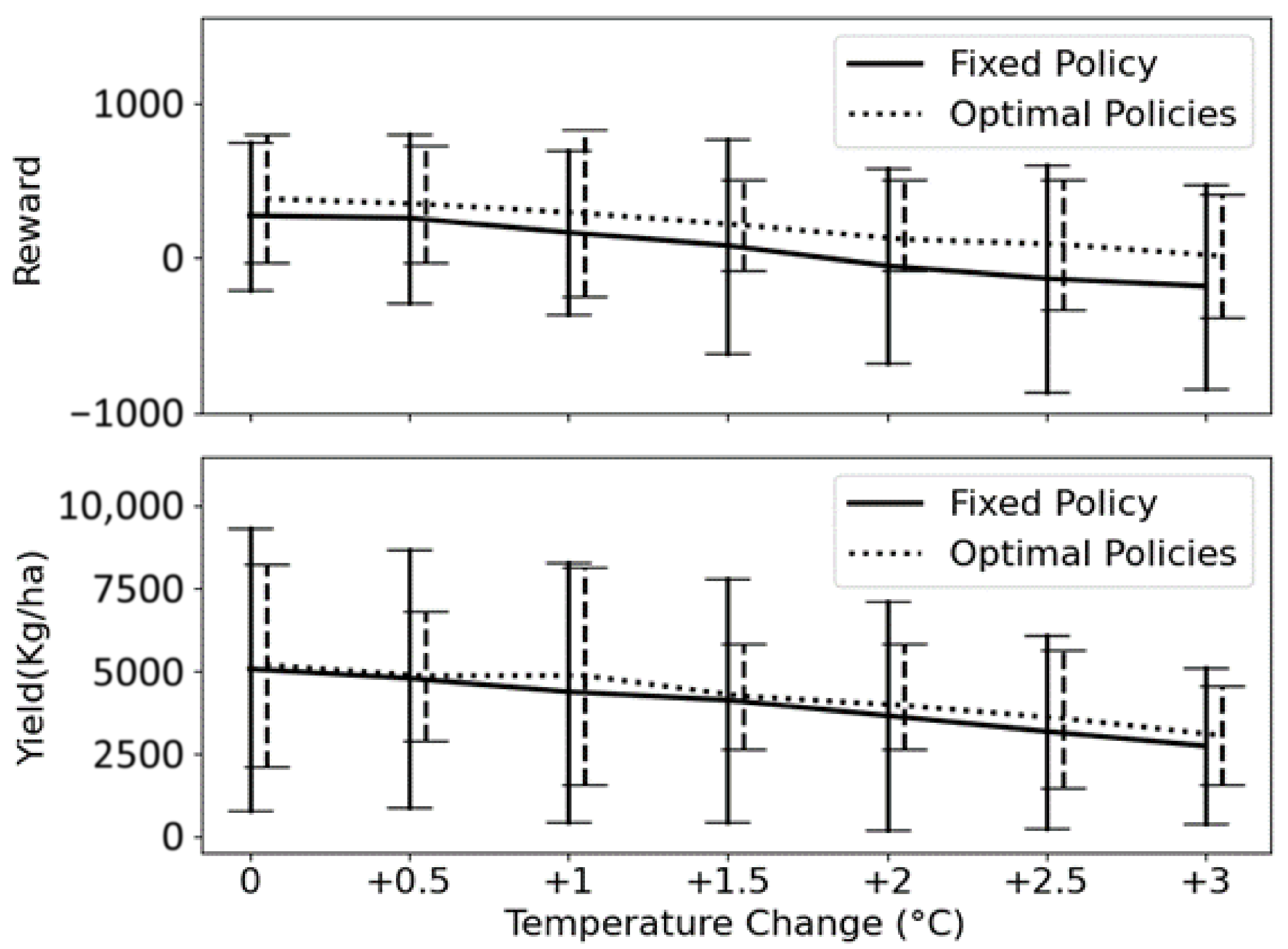
Figure 9 depicts agricultural outcomes, including corn yields and total rewards, along with 95% PIs for the fixed and optimal policies. The data shows a consistent decline in average rewards and yields with increasing temperature, underscoring the adverse effects of rising temperatures on agricultural production. Nevertheless, both fixed and optimal policies exhibit adaptive efforts to sustain the production level, with optimal policies demonstrating less uncertainties. Moreover, optimal policies consistently outperform the fixed policy, notably demonstrating higher average total rewards. This suggests the superior effectiveness of optimal policies in adapting to temperature variations.

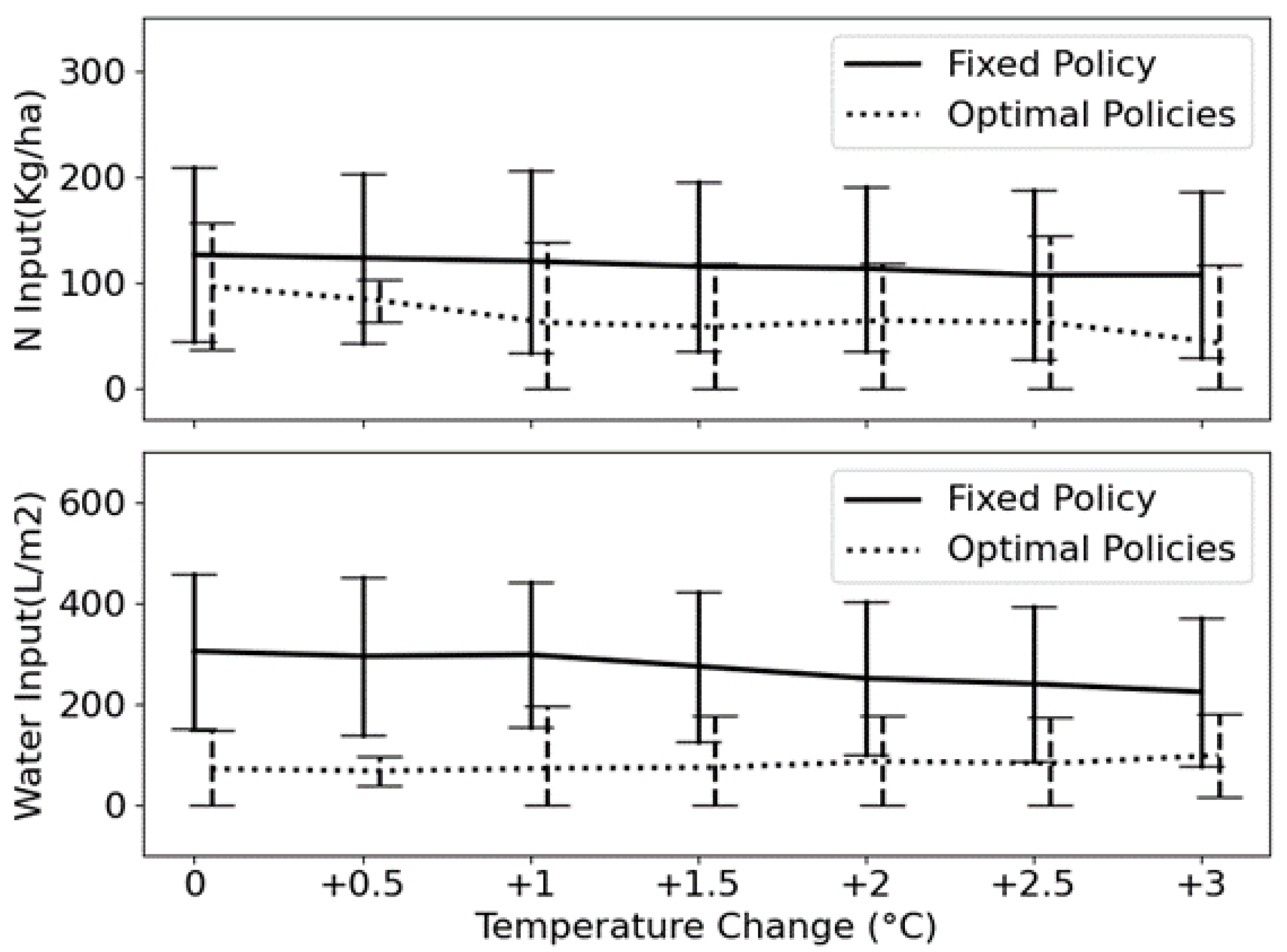
In Figure 10, it is evident that different agricultural policies lead to varying management practices, affecting N fertilization and irrigation strategies. Comparatively, the fixed policy results in generally higher N and water inputs than optimal policies. On average, the fixed policy entails 149% higher N usage and 341% higher water usage than optimal policies. Consequently, optimal policies achieve significantly higher rewards, although the resulting yields are slightly higher than the fixed policy. These large differences are because the optimal policies are learned under scenarios of climate variability, including temperature and precipitation changes, while the fixed policy is based on normal weather conditions. The RL agent, trained with climate variability and stochastic weather using WGEN, learns to apply resources more selectively, optimizing input timing and quantity in response to more challenging and uncertain conditions. In contrast, the fixed policy is tuned to a single, average climate scenario, which can result in less efficient resource allocation when applied under variable weather.

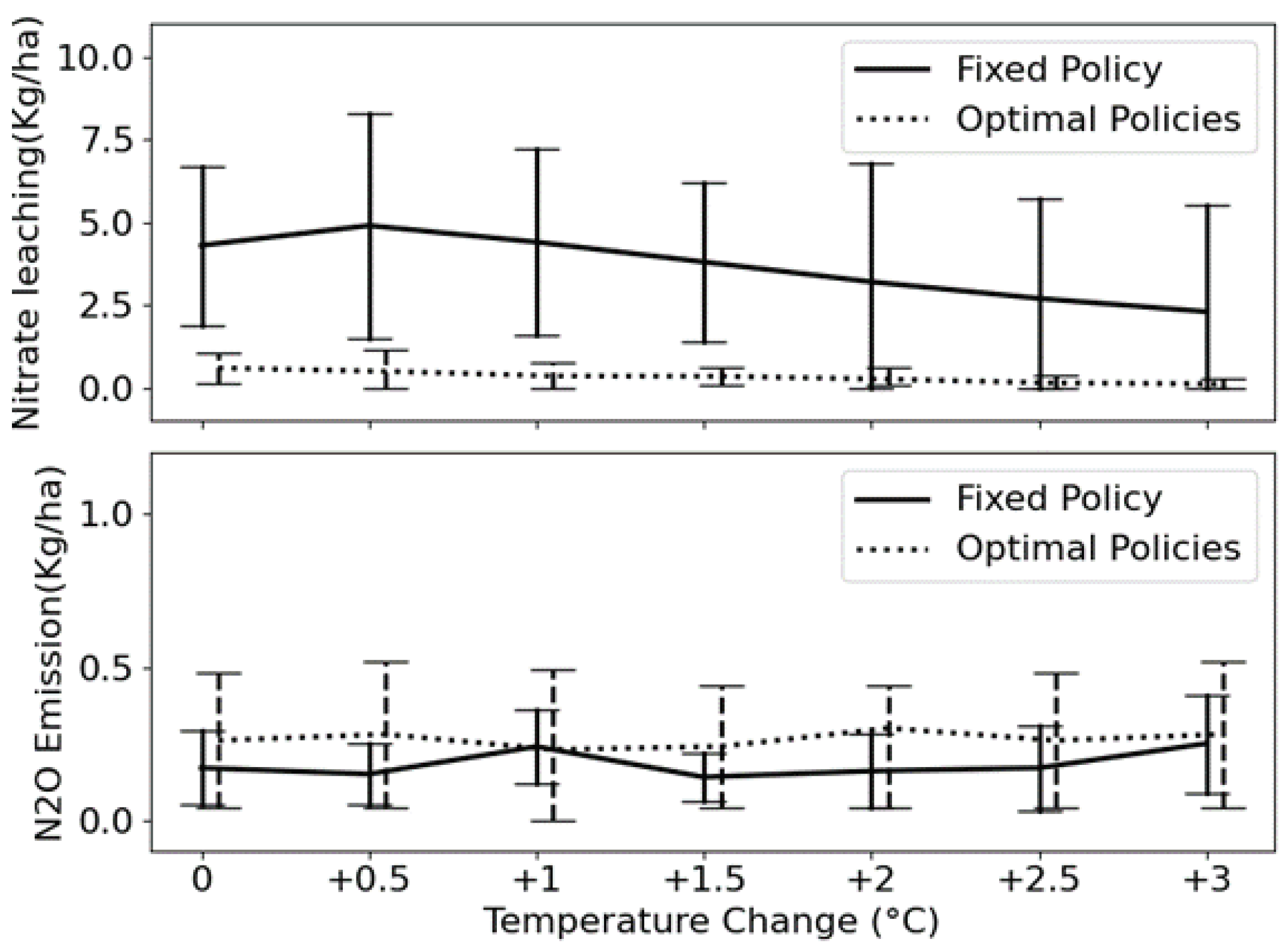
Interestingly, optimal policies exhibit a substantial reduction in nitrate leaching compared to the fixed policy, but they result in higher ${\mathrm{N}}_2\mathrm{O}$ emissions, as illustrated in Figure 11. This unexpected outcome contradicts our initial expectations and can be partially explained by the reward function defined in Equation (7). In the pursuit of maximizing the total reward, the agent seeks a delicate balance between gains, such as corn yield, and penalties, encompassing fertilizer and water usage, nitrate leaching, and ${\mathrm{N}}_2\mathrm{O}$ emission.

The optimization of fertilization and irrigation management strategies using the DQN method focuses on maximizing the total reward, which serves as the objective function. This reward function, defined in Equation (7), is crafted to strike a balance between enhancing crop yields and reducing operational costs and environmental impacts, including water usage, fertilizer application, nitrate leaching, and ${\mathrm{N}}_2\mathrm{O}$ emissions. A blending approach is employed, involving a linear combination of multiple objectives with assigned weights.

It is evident that both optimal and fixed policies demonstrate commendable performance in controlling ${\mathrm{N}}_2\mathrm{O}$ emissions, although optimal policies result in slightly higher average ${\mathrm{N}}_2\mathrm{O}$ emissions (approximately 0.1 kg/ha) than the fixed policy. Notably, optimal policies are tailored to specific climate variations and outperform the fixed policy in maximizing the total reward. However, they do so without prioritizing emission minimization; instead, they focus more on optimizing nitrogen and water usage and minimizing nitrate leaching. This approach yields a higher reward according to the defined objective function despite potentially allowing for slightly increased ${\mathrm{N}}_2\mathrm{O}$ emissions. Further discussions and potential alternative approaches are considered in the conclusions section.

4.3. Precipitation Reducing

We also investigate the impact of reduced rainfall on fertilization and irrigation management, as well as agricultural outcomes. After analyzing historical rainfall data dating back to 1950, we identified no consistent trend in annual rainfall. In our study, we base our simulations on the actual weather conditions from 2012 but make adjustments by decreasing the monthly average rainfall by 20%, 40%, 60%, and 80%, respectively, throughout the year while keeping the monthly maximum and minimum temperatures consistent, mirroring those of 2012. It is important to note that scenarios involving increased precipitation levels that may result in flood-related crop damage are not considered, as such situations fall beyond the forecasting capabilities of DSSAT. Figure 12 depicts the training process when average precipitation decreases by 80% under similar conditions of weather uncertainty.

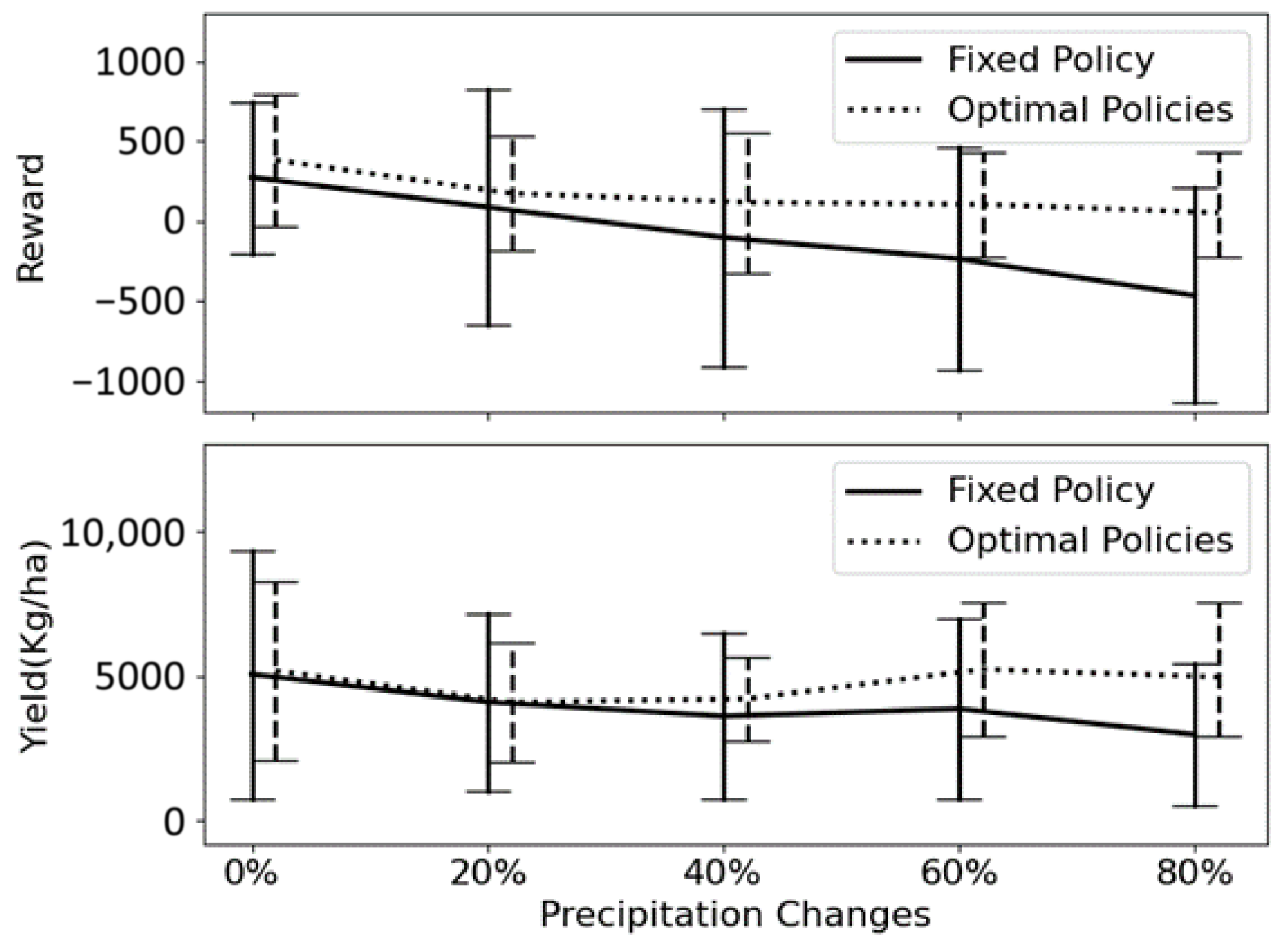
Aligned with our findings in the study of temperature variability, Figure 13 illustrates that optimal policies also exhibit superior performance compared to the fixed policy in scenarios of reduced precipitation. Optimal policies result in larger harvests and rewards, particularly under more severe conditions, such as an 80% reduction in precipitation, representing drought events. In these instances, optimal policies achieve an average yield increase of 120% and demonstrate enhanced efficiency.

Figure 14 provides insights into the factors contributing to this outcome by comparing N and water usage between the fixed and optimal policies. The fixed policy exhibits limited responsiveness to precipitation reduction, maintaining constant N and water usage. Although N inputs remain relatively stable, optimal policies display sensitivity to reduced rainfall by adjusting water input accordingly. In the case of a severe drought event with an 80% short of rainfall, the average water input increases by 300% to sustain the same corn yield. In response to precipitation reduction, optimal policies demonstrate greater adaptability to climate variability.

Figure 15 presents a comparison of nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions resulting from different management policies under scenarios of reduced monthly precipitation. Under fixed policy management, both nitrate leaching and ${\mathrm{N}}_2\mathrm{O}$ emissions remain relatively stable, displaying limited sensitivity to decreasing rainfall. Conversely, optimal policies exhibit notable adaptability to precipitation reduction. The nitrate leaching under optimal policies remains consistently low, effectively minimized even when rainfall significantly decreases. However, similar to the scenario of rising temperatures, optimal policies are associated with a slight increase in ${\mathrm{N}}_2\mathrm{O}$ emissions compared to the fixed policy. Notably, when precipitation is reduced by up to 60%, optimal policies produce ${\mathrm{N}}_2\mathrm{O}$ emissions comparable to those under fixed management, and outperform the fixed policy when precipitation is reduced by up to 80%. Although emissions rise moderately in most scenarios, this increase is relatively small compared to the advantages gained in crop yield and resource efficiency, indicating a balanced management strategy that prioritizes maintaining high productivity without excessively compromising environmental sustainability.

It should be noted that the RL agent’s decisions are strictly driven by the reward function, which does not explicitly include variables for soil or crop health. Therefore, unless such factors are incorporated into the reward structure or observation set, the agent does not directly consider them in its management strategies.

4.4. Toward Real-World Deployment

The practical implications of our RL-based agricultural management strategies are significant for policymakers and farmers adapting to increasing climate variability and environmental constraints. While our RL framework demonstrates clear advantages in simulation, particularly in optimizing trade-offs between yield, resource efficiency, and environmental impact, real-world implementation requires addressing additional challenges. Beyond weather-related uncertainties, practical deployment must account for soil heterogeneity, economic constraints, and technological barriers. To bridge this gap, user-friendly decision support systems integrating RL-generated recommendations will be essential. Coupled with local sensor networks and real-time weather data, such systems could provide adaptive guidance, enabling farmers to dynamically adjust fertilization and irrigation in response to changing conditions. Moreover, although the proposed RL framework integrating RNN and POMDP can be computationally intensive, training the RL agent and fitting the probabilistic ${\mathrm{N}}_2\mathrm{O}$ emission models may be performed offline, using high-performance computing resources in a research or institutional setting. Once optimal or robust management policies are learned, deploying them in the field requires minimal computational power, except for occasional policy updates based on incoming sensor data.

Furthermore, our study has direct relevance to the United Nations Sustainable Development Goals (SDG), particularly SDG 2 (Zero Hunger) [45] and SDG 13 (Climate Action) [46]. By explicitly optimizing for crop yield while minimizing fertilizer use and greenhouse gas emissions, our work supports the goal of ensuring food security and promoting sustainable agriculture. The explicit inclusion of ${\mathrm{N}}_2\mathrm{O}$ emissions in the reward function addresses the urgent need for climate mitigation in agriculture, advancing efforts toward SDG 13. More broadly, integrating AI into agricultural management enables the development of resilient, adaptive strategies that can help farming communities cope with climate-related risks while safeguarding both productivity and the environment.

5. Conclusions, Limitations, and Future Works

Addressing global hunger and lessening environmental consequences requires a careful balance between maximizing crop yield and limiting GHG emissions from agricultural activities. This study marks the first attempt to integrate considerations of ${\mathrm{N}}_2\mathrm{O}$ emissions into the optimization of agricultural management, with a particular focus on adapting to climate variability. Using a model-free RL method, specifically DQN with RNN-based Q networks, our research aims to train intelligent agents that learn optimal management strategies or policies to efficiently handle N fertilization and irrigation, ultimately reducing ${\mathrm{N}}_2\mathrm{O}$ emissions, minimizing nitrate leaching, and maximizing crop yields.

In this study, we account for two significant sources of uncertainty. First, a PDL model is developed to estimate ${\mathrm{N}}_2\mathrm{O}$ emissions throughout the crop growth phase. This model, which adopts the MaxLike approach to address data uncertainty, enhances the capabilities of the deterministic model. The incorporation of this probabilistic element contributes to a more comprehensive and insightful prediction framework. Secondly, to introduce variability in weather conditions, a stochastic weather generator, WGEN, is integrated into the crop simulator (Gym-DSSAT). WGEN generates random weather scenarios based on actual weather data, further enriching the study’s exploration of the agent’s resilience to climate change.

The results indicate that, by penalizing ${\mathrm{N}}_2\mathrm{O}$ emissions in the reward function, the agent can successfully balance crop yield, N and water usage, nitrate leaching, and ${\mathrm{N}}_2\mathrm{O}$ emissions, providing optimal policies. Our research extends the application of the developed framework to assess the impact of climate variability on agricultural results and practices. Specifically, we focus on scenarios involving elevated temperatures and limited rainfall. The findings reveal that the previously established policy is resilient to variations in temperature and mild changes in precipitation, but it faces challenges under severe conditions, such as extremely substantial reductions in rainfall or droughts. In contrast, the optimal policies learned based on specific weather conditions are more adaptive, particularly in light of extreme climatic events.

The simulations in this study use exclusively daily ${\mathrm{N}}_2\mathrm{O}$ emission data from 2012–2017 (excluding 2015) collected at the KBS-LTER site. Feature selection for the predictive models estimating ${\mathrm{N}}_2\mathrm{O}$ emissions was based on observable state variables in the simulator (i.e., gym-DSSAT), which may have omitted important predictors, potentially limiting model performance and generalization. Notably, the testing field received a single high-N fertilization event (170 kg N/ha), contrasting with the agent’s learned strategy of multiple, smaller applications. To improve future simulations, we plan to compile a more extensive historical dataset of daily GHG emissions (if available) under diverse N input scenarios, tailored to relevant agricultural regions. The incorporation of this broader dataset, encompassing soil-derived GHGs like ${\mathrm{N}}_2\mathrm{O}$, NOx, and others, will enhance the representativeness, accuracy, and applicability of our results.

In this research, we tackle ${\mathrm{N}}_2\mathrm{O}$ emission by introducing an additional term in the reward function. The results depict that the agent may prioritize maximizing crop yield at the potential expense of minimizing the ${\mathrm{N}}_2\mathrm{O}$ emission in order to achieve the highest total reward. As we look ahead, we plan to explore Multi-Objective Reinforcement Learning (MORL) as a potential solution that can potentially enable the simultaneous optimization of multiple conflicting objectives [47], such as maximizing crop yield while minimizing ${\mathrm{N}}_2\mathrm{O}$ emissions. By employing MORL, we will create a more nuanced reward structure that better reflects the complexity of agricultural decision-making, ensuring that environmental considerations are weighed alongside economic ones.

The RL framework developed in this study is designed for broad generalization across agricultural environments, without being constrained by specific locations, soil types, or weather patterns. By leveraging the configurable Gym-DSSAT simulator and incorporating a stochastic weather generator, the RL agent is exposed to a diverse range of soil properties, crop types, and randomized climate scenarios during training. This approach promotes robust and adaptable policies that perform well under novel conditions, avoiding overfitting to a single dataset. Furthermore, the framework explicitly accounts for real-world uncertainties, such as weather variability and ${\mathrm{N}}_2\mathrm{O}$ emission prediction errors, by integrating probabilistic deep learning models. These models provide reliable uncertainty quantification, further enhancing the framework’s generalization capability to unseen environments.

Beyond the RL-based approach used in this work, alternative methods such as expected utility maximization [48] and robust optimization [49] could also be explored for agricultural decision-making under climate variability. These methods offer different ways to handle risk and uncertainty, and may be valuable for designing resilient management strategies. Expected-utility models assume known probabilities and build risk attitudes into the utility function, making them easy to solve but unable to adapt on the fly [48]. Robust optimization drops probabilities, guarding against the worst case within a set uncertainty region—safe but often overly conservative [50]. RL instead learns through interaction, handling nonlinear dynamics without rigid distributional assumptions, yet it needs lots of data and careful reward design [26]. While not applied in this study, future research could compare these approaches with RL to further strengthen robust agricultural policy development.

Another alternative under consideration involves leveraging formal logic language to express the ${\mathrm{N}}_2\mathrm{O}$ budget as a specification. This specification can then be transformed into a finite state automaton and seamlessly integrated into the RL framework [18]. By adopting this approach, the ${\mathrm{N}}_2\mathrm{O}$ budget can be enforced through model-checking techniques. These potential approaches aim to enhance the agent’s decision-making capabilities regarding crop yield and ${\mathrm{N}}_2\mathrm{O}$ emission in a more nuanced and optimized manner.

Furthermore, our future endeavors include gathering comprehensive cost data for the relevant year, encompassing expenses such as fertilizer, water, machinery, labor, and other operational costs. Additionally, we plan to integrate economic elements such as agricultural subsidies offered by the government and possible inflation in the upcoming years. Incorporating these financial factors into our model will enable it to more accurately reflect farmers’ net income. This enhancement will significantly elevate the contribution and impact of our model, offering a more holistic understanding of the economic implications of the optimized agricultural strategies proposed.