Evaluation of Ultrasonic Sensor for Precision Liquid Volume Measurement in Narrow Tubes and Pipes
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Set-Up and Instrumentation
2.2. Data Collection Procedures
2.2.1. Calibration Data
2.2.2. Operational Performance
2.3. Data Processing and Analysis
- = calibrated height difference in tube (mm)
- = voltage measurement pre-volume (VDC)
- = voltage measurement post-volume (VDC)
- b = slope coefficient
- a = intercept coefficient
- V = Calculated volume (mL)
2.4. Uncertainty Analysis
- = combined standard uncertainty in cross-sectional area (CSA) tube or pipe.
| Source | Value | Probability Distribution | Divisor | Standard Uncertainty |
|---|---|---|---|---|
| Accuracy [a] | 0.1 V (11 mm) | Rectangular | √3 | 0.058 |
| Repeatability | 1.53 × 10−2 V (0.18 mm) | Rectangular | √3 | 8.8 × 10−3 |
| Quantization Error [b] | 0.06 V | Rectangular | √3 | 3.46 × 10−2 |
| Combined Standard sensor uncertainty, Δvpre, Δvpost | 6.79 × 10−2 | |||
| Tube/Pipe | Standard Uncertainty of the Width/Diameter (Δdi, mm) | Standard Uncertainty of the Cross-Sectional Area (ΔAi, mm2) |
|---|---|---|
| T-A | 0.127 | 0.254 |
| T-B | 0.191 | 0.381 |
| T-C | 0.254 | 0.508 |
| P-B | 0.05 | 0.314 |
| P-C | 0.127 | 0.798 |
- ΔV2 = combined standard uncertainty volume
- RMSE = root mean square error of the calibration (Equation (1))
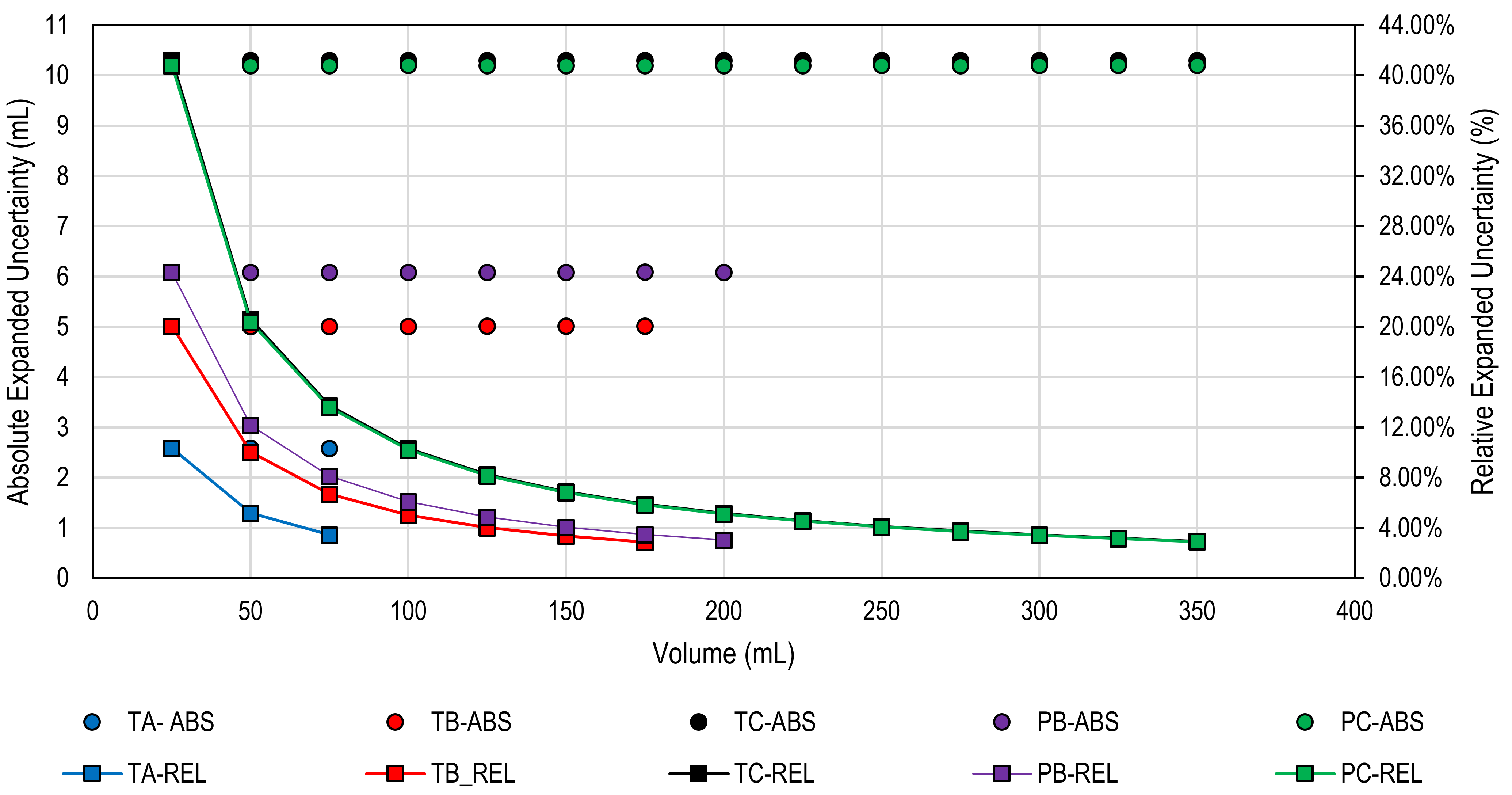
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gil, E.; Badiola, J. Design and Verification of a Portable Vertical Patternator for Vineyard Sprayer Calibration. Appl. Eng. Agric. 2007, 23, 35–42. [Google Scholar] [CrossRef]
- Oliveira, J.L.D. Behavior, Welfare, Production and Bioenergetics of Laying Hens in Alternative Housing Systems. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2019. [Google Scholar]
- Azimi, A.H.; Carpenter, T.G.; Reichard, D.L. Nozzle Spray Distribution for Pesticide Application. Trans. ASAE 1985, 28, 1410–1414. [Google Scholar] [CrossRef]
- Fisher, D.K.; Sui, R. An Inexpensive Open-Source Ultrasonic Sensing System for Monitoring Liquid Levels. Agric. Eng. Int. CIGR J. 2013, 15, 328–334. [Google Scholar]
- Krishnan, P.; Williams, T.H.; Kemble, L.J. Spray Pattern Displacement Measurement Technique for Agricultural Nozzles Using Spray Table. Trans. ASAE 1988, 31, 0386–0389. [Google Scholar] [CrossRef]
- Balasundram, S.K.; Golhani, K.; Shamshiri, R.R.; Vadamalai, G. Precision Agriculture Technologies for Management of Plant Diseases. In Plant Disease Management Strategies for Sustainable Agriculture through Traditional and Modern Approaches; Sustainability in Plant and Crop Protection; Ul Haq, I., Ijaz, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 259–278. ISBN 978-3-030-35955-3. [Google Scholar]
- ISO: 5682-1:2017; Equipment for Crop Protection Spraying—Equipment Part 1: Test Methods for Sprayer Nozzles. ISO: Geneva, Switzerland, 2017.
- Carpenter, T.G.; Reichard, D.L.; Ozkan, H.E.; Holmes, R.G.; Thornton, E. Computerized Weighing System for Analyses of Nozzle Spray Distribution. Trans. ASAE 1988, 31, 0375–0379. [Google Scholar] [CrossRef]
- Johnson, C.D. Process Control Instrumentation Technology, 7th ed.; Prentice Hall: Columbus, OH, USA, 2003; ISBN 0-13-060248-5. [Google Scholar]
- Kelemen, M.; Virgala, I.; Kelemenová, T.; Miková, Ľ.; Frankovský, P.; Lipták, T.; Lörinc, M. Distance Measurement via Using of Ultrasonic Sensor. J. Autom. Control 2015, 3, 71–74. [Google Scholar]
- Hauptmann, P.; Hoppe, N.; Püttmer, A. Application of Ultrasonic Sensors in the Process Industry. Meas. Sci. Technol. 2002, 13, R73–R83. [Google Scholar] [CrossRef]
- Paul, J.D.; Buytaert, W.; Sah, N. A Technical Evaluation of Lidar-Based Measurement of River Water Levels. Water Resour. Res. 2020, 56, e2019WR026810. [Google Scholar] [CrossRef]
- Mirzaei, F.M. Extrinsic and Intrinsic Sensor Calibration. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2013. [Google Scholar]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Beltrán, J.; Guindel, C.; de la Escalera, A.; García, F. Automatic Extrinsic Calibration Method for LiDAR and Camera Sensor Setups. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17677–17689. [Google Scholar] [CrossRef]
- Cao, M.; Si, X.; Zhang, H.; Ma, F.; Ji, P.; Yao, H. Calibration of Ultrasonic Transducer Based on Ultrasonic Logging Instrument for Shaft Sinking. Sensors 2022, 22, 6867. [Google Scholar] [CrossRef] [PubMed]
- Yatsyshyn, S.; Nazarkevych, I.; Mastylo, R. Calibration of the Ultrasonic Sensor-Range Finder by the Laser Interferometer. Meas. Equip. Metrol. 2020, 81, 10–17. [Google Scholar] [CrossRef]
- Doebelin, E.O. Measurement Systems: Application and Design, 5th ed.; McGraw-Hill: New York, NY, USA, 2004; ISBN 0-07-243886-X. [Google Scholar]
- JetBrains. PyCharm 2022.1.2 [Computer Software]; JetBrains: Prague, Czech Republic, 2022. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- SAS. JMP 2022 [Computer Software]; SAS: Cary, NC, USA, 2022. [Google Scholar]
- Gates, R.S.; Casey, K.D.; Xin, H.; Burns, R.T. Building Emissions Uncertainty Estimates. Trans. ASABE 2009, 52, 1345–1351. [Google Scholar] [CrossRef]




| Tube (T)/Pipe (P) | Inside Width/Diameter (mm) | Cross Sectional Area (CSA; mm2) | Model, Manufacturer |
|---|---|---|---|
| T-A | 15.88 | 252.02 | 8516K35, Evonik CY RO LLC, Parsippany, NJ, USA |
| T-B | 22.23 | 493.95 | 8516K37, Evonik CY RO LLC, Parsippany, NJ, USA |
| T-C | 30.96 | 957.66 | 85095K76, Westlake Compounds LLC, Houston, TX, USA |
| P-A | 25.20 | 498.76 | 48925K93, McMaster-Carr, Elmhurst, IL, USA |
| P-B | 27.00 | 581.07 | 2809N18, McMaster-Carr, Elmhurst, IL, USA |
| P-C | 35.05 | 964.97 | 48925K94, McMaster-Carr, Elmhurst, IL, USA |
| Tube/Pipe | RMSE (V) | SE of the Regression (V) | SE of the Calibration (mm) |
|---|---|---|---|
| T-A | 1.14×10−2 | 1.40×10−2 | 1.50 |
| T-B | 9.52×10−3 | 1.04×10−2 | 1.10 |
| T-C | 6.92×10−3 | 7.21×10−3 | 0.60 |
| P-A | 5.61×10−3 | 6.06×10−3 | 0.73 |
| P-B | 7.67×10−3 | 7.96×10−3 | 0.87 |
| P-C | 6.92×10−3 | 5.46×10−3 | 0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, B.C.; Bergman, R.W.; Darr, M.J. Evaluation of Ultrasonic Sensor for Precision Liquid Volume Measurement in Narrow Tubes and Pipes. AgriEngineering 2023, 5, 287-298. https://doi.org/10.3390/agriengineering5010019
Smith BC, Bergman RW, Darr MJ. Evaluation of Ultrasonic Sensor for Precision Liquid Volume Measurement in Narrow Tubes and Pipes. AgriEngineering. 2023; 5(1):287-298. https://doi.org/10.3390/agriengineering5010019
Chicago/Turabian StyleSmith, Benjamin C., Ryan W. Bergman, and Matthew J. Darr. 2023. "Evaluation of Ultrasonic Sensor for Precision Liquid Volume Measurement in Narrow Tubes and Pipes" AgriEngineering 5, no. 1: 287-298. https://doi.org/10.3390/agriengineering5010019
APA StyleSmith, B. C., Bergman, R. W., & Darr, M. J. (2023). Evaluation of Ultrasonic Sensor for Precision Liquid Volume Measurement in Narrow Tubes and Pipes. AgriEngineering, 5(1), 287-298. https://doi.org/10.3390/agriengineering5010019






