A Bunch of Gaps: Factors Behind Service Reliability in Chicago’s High-Frequency Transit Network

Highlights

What are the main findings?

• The proposed methodology expands the understanding of how the reliability of high-frequency transit is impacted by service plan, operational conditions, built environment, and human factors.
• A regression model to quantify relationships with headway regularity revealed the quality of scheduled running times, headway regularity at terminals, and driver experience as the largest determinants of route-level reliability.
• To assess impacts of local conditions, a regression model is proposed, along with a novel measure that captures how quickly bus bunching and large gaps are formed along the route segment. The model estimations showed the effectiveness of bus lanes and the deteriorating effect of left turn movements.

What are the implications of the main findings?

• The methodology can be replicated with existing datasets at other transit systems to identify the root causes of unreliability.
• The analysis supports the need for systematic improvements, such as training of junior drivers and better dispatching practices, and targeted local improvements, such as expanded bus priority infrastructure.

Abstract

Frequent transit services in urban areas have the potential to increase their accessibility to transit-dependent riders and reduce congestion by attracting new ridership through a modal shift. However, bus services operating in mixed traffic face operational challenges that reduce reliability and hinder their attractiveness. The sources of unreliability can range from local-level conditions, like the road infrastructure, to higher-level decisions, like the service plan. For the effective planning of improvement strategies, both scales of analysis must be considered. This paper uses a novel modeling framework to understand reliability by analyzing the route and segment factors separately. The Chicago Transit Authority (CTA) bus network is used as a case study for the analysis. The data reflect the operational, demand, and urban conditions of 50 high-frequency bus routes. At the route level, we use the coefficient of headway variation as the dependent variable and diverse route characteristics as explanatory variables. The results indicate that the most significant contributors to the variability of headways are variability in schedules and dispatching at terminals. It is also found that driver experience impacts reliability and that east–west routes are more unreliable than north–south routes. At the segment level, we use data from trips involved in bunching and gaps. As the dependent variable, a novel measure is formulated to capture how quickly bunching or gaps are formed. The bunching and gap events are treated as separate regression models. Findings suggest that link and dwell time variability are the most significant contributors to gap and bunching formation. In terms of infrastructure, bus lane segments reduce gap formations, and left turns increase bunching and gap formations. The insights presented can inform improvements in service and transit infrastructure planning to improve transit level of service (LOS) and support the future of sustainable, smart cities.

1. Introduction

In dense urban areas, an attractive public transit system can help reduce car dependence and, by extension, reduce congestion and increase pedestrian safety. However, for transit services running in mixed traffic, as is the case for most bus systems, operations are vulnerable to a range of challenges. On the demand side, this reduces the attractiveness of transit to riders, as studies on rider surveys identify reliability and crowding as top priorities for improvements [1]. On the supply side, it increases vehicle running times, driving up operating costs required to meet the travel needs of the system.

The literature has identified the levers within transit planning practice to address reliability issues [2], including scheduled frequency, route distance, and vehicle capacity [3]. A study based on regression models found that scheduled frequency can increase the coefficient of variation by as much as 0.2 [4]. Another study found that uneven load capacity across consecutive vehicles can increase the probability of bunching by 124% [5]. These insights have direct implications for developing robust service plans.

When service plans shift during actual operations, strategies are employed as real-time responses to emerging disturbances. Although the literature on control methods is vast, there is a limited understanding of the relationship between the upstream planning decisions and reliability performance. This paper seeks to bridge this gap by modeling impacts on reliability to elicit actionable insights for planning decisions. The designed models leverage the widespread availability of automated data collection on demand and transit operations, as well as detailed information on the built environment. This work integrates these datasets and designs models for a holistic analysis to inform strategic improvements.

The literature has produced extensive empirical analyses on the causal mechanisms of transit performance. This study addresses three main limitations in the literature. First, the literature on causal mechanisms has focused on schedule punctuality [6,7]. This study seeks to expand this to reliability-based measures, such as the coefficient of variation of headways. Second, most studies on correlations of unreliability provide exploratory analyses [8,9] but lack the inferential component. This study seeks to evaluate the impacts rigorously using regression analyses. Third, the literature related to reliability issues is centered around bunching [5]. However, gaps are an important symptom of unreliability, as boarding passengers experience severe wait times. This study bridges this gap by incorporating bunching and gaps into the same framework of headway failure formations.

Sources of unreliability can impact transit operation on multiple levels. On the one hand, broader issues like improper schedules can influence the reliability of an entire route. At a more local scale, issues like left turns and the absence of a dedicated bus lane can generate disturbances that deteriorate the headways for given trips locally. The proposed approach captures this behavior by formulating two models of varying levels of analysis granularity. The first model is formulated to estimate headway variability at the route level. Categories of factors considered include human, operational, and urban attributes. The second model uses a novel measure, the failure formation rate, as the dependent variable. The failure formation rate refers to the rate at which bunching or gaps are formed. This is extracted from trip trajectory data for trips that transition from acceptable headways to bunching or gap headways. The selected variables include operational, urban, and infrastructure factors. The attributes are measured for the segment in which the trip failure is formed. Conclusions are drawn that can inform more targeted improvement within critical segments of the network.

The main contributions of this paper are as follows:

• It studies the impacts of a comprehensive set of factors. It is the first study to examine the relationship between driver experience and reliability.
• It proposes a novel approach to extracting bunching and gap formations from trip trajectory data, enriching it with attributes pertaining to the segment in which the formation occurs. It is also the first work to extend the study of formations of trip-level reliability issues from trip bunching to include trip gaps.

The paper is structured as follows. Section 2 reviews related studies on the subject. Section 3 describes the data and methodology. Section 4 discusses the results for route and local reliability models using data for the Chicago Transit Authority (CTA). Section 5 discusses concluding remarks, implications, and future research directions.

2. Related Work

This section first describes literature related to transit reliability and subsequently describes the approaches and findings of previous exploratory and inferential studies.

2.1. Transit Reliability

Transit reliability has been the subject of extensive study. As opposed to low-frequency services, for which schedule adherence best captures quality of service, high-frequency services are assessed by how closely the observed frequency resembles the scheduled frequency. Metrics derived from observed headways are predominant in reported service quality measures in large transit agencies in the US and Europe [10]. Ref. [3] comprehensively reviews the implications of headway unreliability. First, it deteriorates the rider experience by increasing waiting times and crowding. Operationally, bunching and gaps increase vehicle running times and dwell times, requiring longer recovery times and decreasing productivity. In order to meet the need to serve travel demands, agencies must absorb these systematic inefficiencies by increasing budgets.

One symptom of headway unreliability is bus bunching. Ref. [2] reviews the literature related to bus bunching and distinguishes between systematic and non-systematic issues causing bunching. The “systematic” sources refer to recurring challenges, such as demand uncertainty, tight schedules, and driver behavior heterogeneity. Non-systematic sources relate to sudden disruptions, which may be demand-related or road incidents. An effective response to these latent issues combines operational planning decisions (longer-term), such as with better scheduling procedures, and responsive, dynamic control strategies (short-term).

2.2. Exploratory Studies

Exploratory research on transit performance has been conducted at various levels of analysis, from individual stops and street segments to entire trips and system-wide assessments. Ref. [10] assessed the system-wide reliability KPIs for 12 world-wide transit agencies, according to headway-based measures calculated from Automated Vehicle Location (AVL) data of high-frequency bus services. The KPIs included excess wait time and the standard deviation of differences between observed and scheduled headways. The results indicate that the ranking of each agency’s performance varied with the chosen indicator, as each indicator emphasizes different aspects of reliability, and performance is sensitive to traffic and dwell time conditions of the selected routes. Ref. [9] measured the spatial delays at the segment level for the King County Metro system (Seattle, USA) using General Transit Feed Specification real-time (GTFS-RT) data. The findings unveiled segments, such as highways, where trips speed up and run ahead of schedule, revealing network-wide inefficiencies from excessive time allocated in the schedule (also referred to as “padding”). The insights and methodology could help transit schedulers make schedules more efficient according to road conditions.

Further exploratory research has focused on reliability issues at the trip level, such as bus bunching events. One focus has been the spatiotemporal patterns of bus bunching occurrences. One study provided a framework for identification and data cleaning to extract bunching trip pairs from AVL data and applied it to a bus route in Nanjing, China [11]. The paper found an increased concentration of bunching closer to the end of the route. Another study applied spatial clustering to identify bus bunching hot spots in a transit system in Athens, Greece [12]. This method was extended to classify bunching events into systematic and random categories, as well as those impacting multiple overlapping bus lines [13]. The study found that bunching increases for higher scheduled frequencies and that significant bunching is observed even in a route segment with dedicated bus lanes.

Studies have also delved more deeply into the mechanics of bus bunching formations. Ref. [8] provided descriptive statistics on bunching formations for bus trips in TriMet (Portland, OR, USA), including attributes such as dwell times and the use of accessibility lifts. The analysis pointed to potential correlations between increased passenger activity and accelerated bunching formations. Ref. [14] mined bunching formation sequences in Porto, Portugal, and performed association rule analysis between delays in the bus pair and the subsequent bunching behavior. Ref. [15] extracted similar sequences in two cities in China and explored how link travel times and stop dwell times influence the headway deviations leading up to bunching events. The descriptive analysis demonstrated how link and dwell times act as independent forces that counteract or reinforce each other in the formation of bunching. The findings can inform control schemes to prevent bunching, such as by leveraging driver speed adjustments to counter delays related to dwell times.

2.3. Inferential Studies

Similarly, modeling studies explore associations with transit performance by aggregating data at various levels of analysis, ranging from the transit system to the individual trip.

Several studies assess service performance in terms of schedule punctuality. An early study formulated a multinomial logit model to evaluate impacts on the on-time status of bus trips at the next scheduled time point and tested it on observational data from TriMet (Portland, US) [6]. The model captured physical, operational, and demand features. The results indicated that the distance since the last time point significantly increased early and late arrivals, suggesting the need for more time points. Another finding was that part-time drivers were more likely to be early or late than full-time drivers, which is attributed to their lower experience. At a system level, ref. [16] conducted regression analysis to investigate associations with system-wide on-time performance (OTP) for 18 US transit agencies. The study found that hourly ridership and the congestion ranking of a city had a significant and negative effect on OTP. Finally, ref. [7] used causality-based Shapley analysis to assess the most important causes of operational delays, taking into account confounding variables. The results found that the most important contributors are the preceding stop’s delay, the delay at the terminal, and the dwell times.

More recent work has focused on factor associations with reliability-based measures, which more suitably capture service quality for high-frequency transit. Ref. [4] formulated two models to understand the impacts of operational, demand, and urban attributes on headway regularity at the route and stop segment levels. The methods were applied to data from the bus system in Santiago, Chile. The route-level model used linear regression with the dispatch headway variability as the dependent variable. The model estimation found that the operating authority of the bus route and the scheduled frequency were the biggest determinants of terminal headway variability. However, the model exhibited low explanatory power (R-squared = 0.19), suggesting the need for improved specification. For the segment-level model, the authors employed a Dynamic Panel Method to explain how headway variability propagates on stops along the route. The model used the headway variability of the three preceding stops (for the same trip) as instrument variables to account for autocorrelation effects. The results showed that the presence of off-board payment infrastructure has a significant influence in reducing headway variability.

Research has also examined the root causes behind the “life cycle” of bunching, from its formation to its persistence. Ref. [5] aimed to explain the formation of bunching in the transit system of Toronto, Canada, with two models. First, the authors formulated a binary logit model to estimate the probability of a bunching incident. The model indicated that uneven vehicle capacity in consecutive vehicles increases the odds of bunching, attributed to exacerbated dwell time differences, and that vehicle short turning increases bunching. Ref. [5] also formulated an Accelerated Failure Time (AFT) model to explain the factors associated with the time to first bunching observation for a given trip. The results showed that the AM peak exhibited quicker bunching formations and that intersections with transit signal priority are effective in extending the time until bunching events. These insights have implications for service planning and vehicle scheduling. Focusing on the duration of bunching after its first occurrence, ref. [17] applied a similar survival analysis technique. The model indicated that the number of road lanes and the proximity to points of interest, such as university campuses, significantly influenced the persistence of bunching. To the best of our knowledge, studies have not been conducted to examine the occurrences of long headways (or gaps).

3. Methodology

This section presents the study design, discusses the data sourcing and processing, and describes the proposed models for route-level and segment-level reliability.

The study focuses on high-frequency bus services for which service reliability is the critical indicator of service quality. This is not the case for low-frequency services, for which on-time arrivals are more critical to riders. At higher frequencies, however, riders tend to turn up at stops randomly, expecting the next bus to arrive within the promised headway. For this reason, only high-frequency bus routes are used for this study. High-frequency routes are generally considered to be those with scheduled headways of 10 min or less at a given period [18].

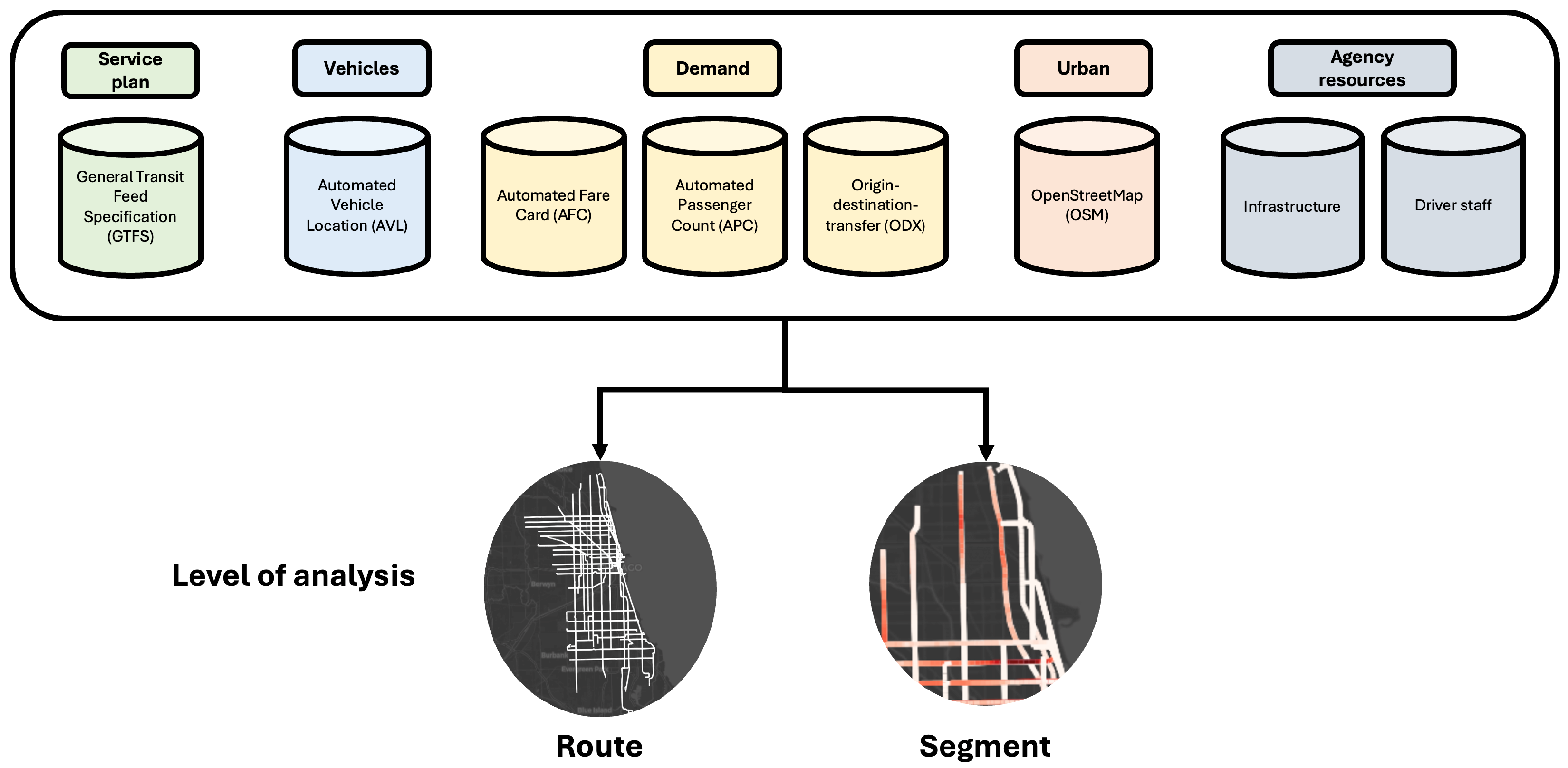
For the selected routes, a comprehensive feature set is prepared to characterize the operational and environmental conditions of the transit network. The data are sourced and aggregated at the desired level of analysis for the route and segment models, in a process broadly illustrated in Figure 1. Further details on data preparation and aggregation steps are provided throughout this section.

3.1. Route Reliability Model

For the route reliability model, a linear regression model is used. The coefficient of variation of headways is used as the dependent variable, as it is a common reliability indicator for high-frequency services. The coefficient of variation of headways for a given route is calculated as follows:

$$\begin{array}{cc}\hfill C{V}_r& ={\displaystyle \frac{{\sigma }_{h_r}}{{\mu }_{h_r}}}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill h_r& :\{h_{ij}\forall i:1,2,..N\forall j:1,2,..M\}\hfill \end{array}$$

(2)

where $C{V}_r$ is the coefficient of variation of headways for route r, and $h_r$ is the set of observed headways $h_{ij}$ for all M stops in the route and all N trips in the given period of study. $h_{ij}$ represents the observed interarrival time between trip $i-1$ and trip i at stop j.

Lower values of $C{V}_r$ represent more regular, reliable service. If the observed headways are exactly equal to the scheduled headways, $C{V}_r\approx 0$. $C{V}_r$ is directly correlated with the expected wait time of high-frequency services [19]. The interpretation of this measure is that for a route with $C{V}_r=0.50$, the riders’ expected wait time is as high as for riders of a route with 25% higher scheduled headway but with reliable service.

This measure, however, becomes less meaningful if the scheduled headways in the trips sampled vary significantly. This may be the case for many routes where the scheduled headways vary between directions and different periods according to travel patterns. For this reason, our unit of analysis for measuring $C{V}_r$ is the route–direction–period combination, and each unique combination represents a single data point in our regression analysis. This approach is similar to a related study that investigated associations at the route level [4]. This process yields 92 observations.

The independent variables considered for the model span the following categories: operational conditions, network, service plan, and human factors. The factors are listed below:

• Operational: The variation of observed headways at the terminal is considered, as it has been shown to be a major determinant of regularity [3]. A measure of how well the scheduled running times match the observed running times is also considered in order to capture system delays that may trickle down in a vehicle’s chained trips. Additionally, the level of control applied in the route can play a role in reliability and can be approximated by the number of time points, which are locations where schedule performance is enforced, e.g., drivers hold if they are running early.
• Service plan: In terms of service plan factors, the variation of scheduled headways is included. It is expected that the more irregular the scheduled headways are, the more imbalanced the demand between trips, increasing the potential for bunching and gaps. Another service plan factor considered is the degree of interlining scheduled for a route, as this introduces another layer of uncertainty to the operation.
• Network: The network-related attributes considered include the total distance covered by the route. Another aspect considered is whether the route runs on an east-west or north-south corridor. In cities with streets organized in a grid, like Chicago and New York City, most routes fit into one of the categories.
• Human factors: The impacts of bus driver behavior are analyzed. Experienced drivers may proactively regulate their speed to avoid delays [20]. Ref. [6] found experience to be a significant determinant of on-time performance. To capture the effects of experience, we use the proportion of junior and extraboard drivers serving the route. It is assumed that these categories of drivers correspond to those with the least experience.

3.2. Segment Reliability Model

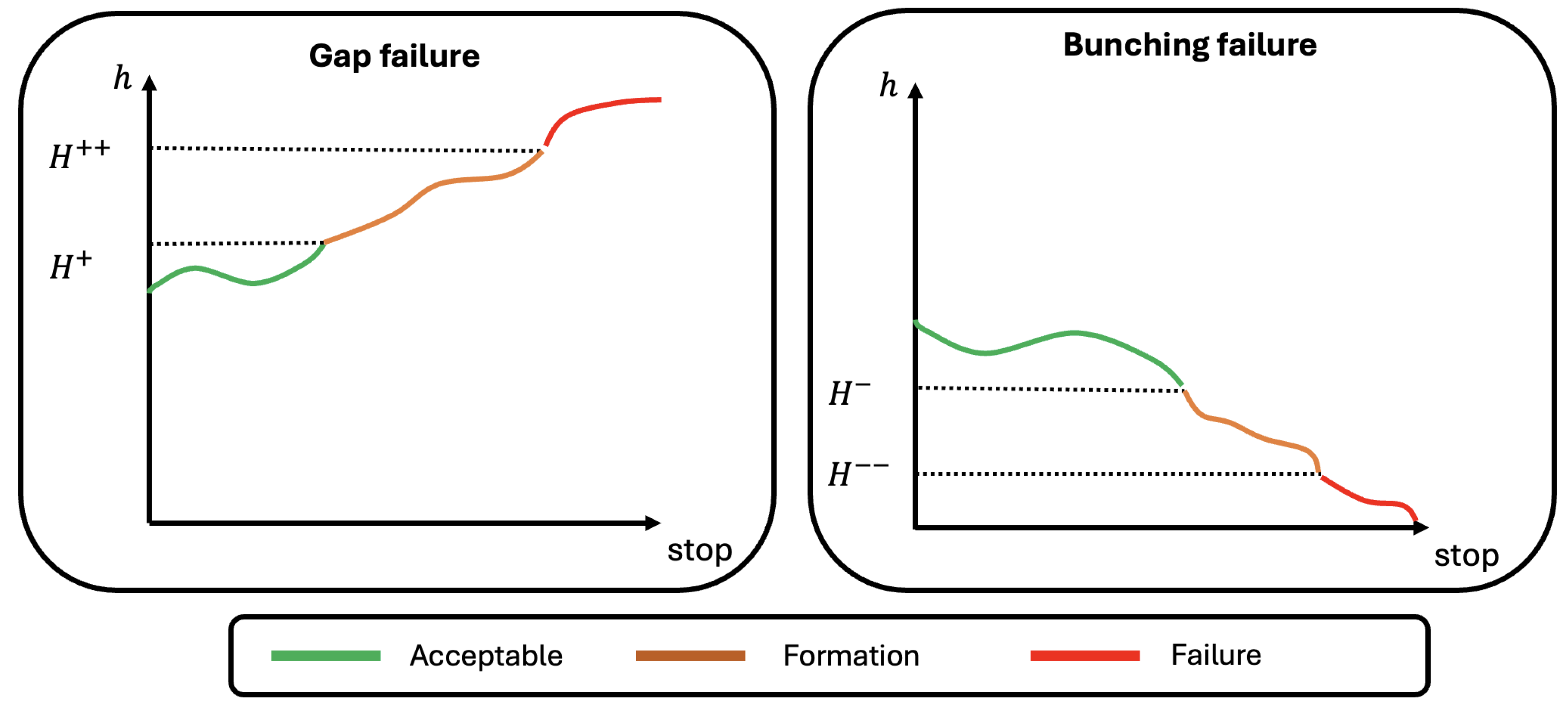
For the segment reliability model, a linear regression model is proposed. For the dependent variable, we considered a variable that measures how rapidly service headways on a given trip deteriorate from an acceptable state to a bunched or gapped state. This approach builds on the work of [14,15], which studied stop-level headway observations in which a trip’s headway gradually decays into a bunching event. The route segment with bunching or gap formations—defined in this paper as failure formations—is extracted from stop-level headway observations according to predefined headway thresholds. From this route segment, the rate of change in the stop-level headways—the failure formation rate—is used as a reliability indicator for the segments. The calculation is explained in more detail below.

A headway observation $h_{ij}$ is defined as the interarrival time between trip $i-1$ and trip i at stop j. Every $h_{ij}$ can be classified into one of five states:

• $0\le h_{ij}<H^{--}$: Bunching;
• $H^{--}\le h_{ij}<H^{-}$: Potential bunching formation;
• $H^{-}\le h_{ij}<H^{+}$: Acceptable;
• $H^{+}\le h_{ij}<H^{++}$: Potential gap formation;
• $H^{++}\le h_{ij}$: Gap.

$H^{--}$, $H^{-}$, $H^{+}$, and $H^{++}$ are predefined headway thresholds that divide the operational states. Consider a sequence of headway observations for a given trip i, i.e., $h_{i,1:M}$, where $1<j<M$ and M is the number of stops in the route served by the trip. Trip i contains a failure formation sequence (and is used for the model) if it transitions between the acceptable state, the potential failure formation state, and the failure state. Formally, the failure formation sequence of headways $h_{i,j^{\prime }:j^{″}}$ is obtained under the following conditions:

(a)

The first stop in the sequence is not the route’s first stop, i.e., $j^{\prime }>1$.

(b)

The headway in the last stop before the sequence, i.e., $h_{i,j^{\prime }-1}$, is in the acceptable state.

(c)

The number of stops ($j^{″}-j^{\prime }+1$) in the formation state sequence is between 2 and k, i.e., $2\le j^{″}-j\le k$.

(d)

The last stop in the sequence is not the final stop in the route, i.e., $j<M$.

(e)

The headway at the last stop of the sequence, i.e., $h_{i,j^{″}}$, is in either failure state (bunching or gap).

To illustrate, Figure 2 shows sample trajectories for eligible failure formation sequences in the bunching and gap cases. To avoid diluting the impact of segment attributes in the associations, we restrict the number of stops in the formation segment to k.

The magnitude of the failure formation rate is thus calculated as the average headway change between consecutive stops in the sequence, as follows:

$$F{R}_i={\displaystyle \frac{1}{j^{″}-j^{\prime }+1}}\left|h_{i{j}^{″}}-h_{i{j}^{\prime }}\right|$$

(3)

where $F{R}_i$ is the failure formation rate (in absolute) for trip i, $j^{″}-j^{\prime }+1$ is the number of stop links in the formation sequence, and $h_{i,j+1}-h_{ij}$ is the headway difference between two consecutive stops. $F{R}_i$ quantifies the average headway decrease for bunching events or the average headway increase for gap events between each pair of consecutive stops in the formation sequence. The unit of $F{R}_i$ is headway per stop (in the segment). The absolute value operator is applied for consistency between bunching (negative) and gap (positive) formation rates. Higher values of $F{R}_i$ indicate a more abrupt deterioration into failure, and lower values indicate a more gradual process. Lower values may also indicate the presence of counteracting forces—for instance, a bus lane speeding up a bus at risk of forming a gap.

As a concrete example to illustrate the effect of $F{R}_i$, consider a route with an acceptable headway of 4 min, a bunching headway threshold of 1 min, and observed bunching formation rates at two stop segments in different parts of the route as $F{R}_i=0.5$ min and $F{R}_i=1.0$ min. This indicates that a trip would bunch within six subsequent stops in the former segment and three stops in the latter segment. The latter segment gives less time for drivers or operations staff to prevent bunching before it happens. and once bunching has occurred, a longer holding time is required to separate the bunched vehicle.

Each identified formation segment is characterized by measuring its constituent attributes. The characterization process involves extracting attributes from every stop link within the segment and then combining these measurements to generate segment-level variables.

In terms of explanatory variables, a mix of operational, infrastructure, and service plan attributes was considered, as follows:

• Operational: The operational factors considered are the variability of link and dwell times, which have been identified as the main forces in the dynamics of bunching and gaps [15]. The effect of incoming transfer volumes at stops is considered, since it is hypothesized that high transfer volumes may translate to additional dwell time uncertainty at stops.
• Infrastructure: The effect of dedicated bus lanes is assessed. Other road characteristics along the route segment were considered, such as the number of lanes, signalized intersections, and turns. Right and left turns are considered separately. The effect of the conditions in the downtown area is considered by counting the number of stops at or near downtown.
• Service plan: The presence of time points, which are stops designated by agencies to enforce drivers’ adherence to the schedule, was considered. This assumes that drivers are compliant with this practice, and it is hypothesized that this improves reliability.

4. Results

This section presents the case study, model specifications, and estimations for the route and segment-level models and interprets the results.

4.1. Case Study

As a case study, the bus network of the Chicago Transit Authority (CTA) is used. The periods considered are the morning rush hour (6–9 A.M.) and afternoon rush hour (3–6 P.M.) on weekdays only. These periods allow some of Chicago’s routes that operate only during rush hours to be considered.

The data were collected on weekdays in February 2024 (excluding holidays). No major disruptions or events occurred during this period. During the AM rush hour, 31 routes are considered high-frequency, with 14 of these in both directions; in the PM rush hour, 30 routes are eligible, with 17 in both directions. These routes collectively attract more than 391 thousand daily passenger trips on weekdays. The scheduled headway ranges from 6 to 10 min (average for the period).

The data sources (summarized in Figure 1) were obtained from publicly available sources and from the CTA. Data on the service plan, schedules, and route configurations were obtained from the publicly available General Transit Feed Specification (GTFS) dataset. For vehicle data, stop arrival and departure time records are obtained from the Automated Vehicle Location (AVL) system. In terms of demand, boarding and alighting counts for every stop arrival event were made available from the Automated Passenger Count (APC) datasets. Data on transfer journeys was obtained from the Origin-Destination-Transfer (ODX) datasets. The ODX data are generated from a destination and transfer inference process applied to Automated Fare Card (AFC) data (this is further detailed in [21]). Urban attributes, such as the location of intersections and turns, were obtained from OpenStreetMap data accessible via the Python OSMnx package [22]. The level of experience of drivers was obtained from CTA’s internal datasets on the hiring date of drivers. Dedicated transit infrastructure, such as bus lane shapes and signal priority locations, was obtained directly from CTA.

4.2. Parameter Settings

For the segment reliability model, the thresholds for trip states are defined relative to the schedule headway, as is the case in most public transit agencies [10]. The final values are set according to the literature and performance standards at CTA, as follows:

$$\begin{array}{cc}\hfill H^{--}& =max(0.25S{H}_i,1)\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill H^{-}& =0.9S{H}_i\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill H^{+}& =1.1S{H}_i\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill H^{++}& =min(1.5S{H}_i,15)\hfill \end{array}$$

(7)

where the units are minutes, and $S{H}_i$ is the scheduled headway for trip i. $H^{--}$ and $H^{++}$ use a mixed rule between fixed and schedule-based values. As an example, for a scheduled headway of 8 min, the values are $H^{--}=2.0$, $H^{-}=7.2$, $H^{+}=8.8$, and $H^{++}=12.0$.

Also, trips with failure formations longer than 3 miles of route distance are excluded from the dataset for estimating segment reliability. Given Chicago’s typical stop spacing of 1/8 mile, this corresponds to $k=24$ stops. Trips with missing arrival data at any of the stops in the route are disregarded for the analysis, as well as trips that overtake another vehicle or are overtaken.

4.3. Route Reliability Model

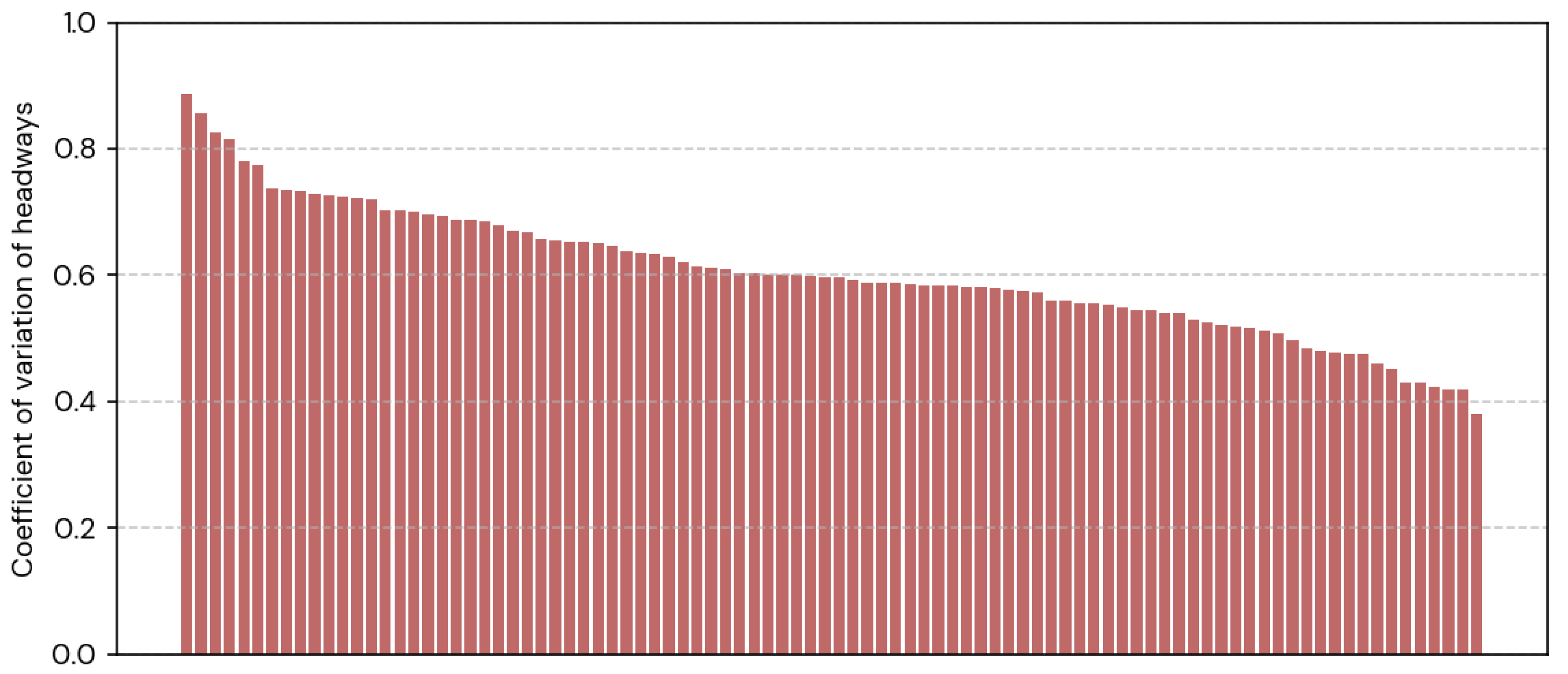
Figure 3 shows the distribution of the coefficient of variation of headways in the routes in the sample, ranked by the magnitude of $C{V}_r$. The values of $C{V}_r$ range between 0.4 and 0.8, with a median of 0.59.

The route reliability model was estimated as a linear regression model with the ordinary least squares (OLS) method. The best model was selected in terms of parameter significance and multicollinearity, resulting in the following linear function:

$$\begin{array}{c}\hfill C{V}_r={\beta }_0+{\beta }_{C{V}_{r,1}}·C{V}_{r,1}+{\beta }_{PM}·PM+{\beta }_{SchdCV}·SchdCV+{\beta }_{RunRatio}·RunRatio\\ \hfill +\beta Pint·Pint+{\beta }_{EW}·EW+{\beta }_{Dist}·Dist+{\beta }_{Pjunior}·Pjunior+{\beta }_{PXB}·PXB\end{array}$$

(8)

where

• $C{V}_{r,1}$ refers to the coefficient of variation of headways at the first stop.
• $PM$ is a dummy variable where $PM=1$ if the sample is from the afternoon period and $PM=0$ otherwise.
• $SchdCV$ is the coefficient of variation of scheduled headways.
• $RunRatio$ is the running time ratio, measured as the average actual running time divided by the average scheduled running time.
• $Pint$ refers to the fraction of trips that served a different route immediately prior to the start of the trip.
• $EW$ is a dummy variable, where $EW=1$ represents routes serving mostly east–west streets and $EW=0$ otherwise.
• $Dist$ is the total distance of the route.
• $Pjunior$ and $PXB$ quantify the proportion of trips in the route performed by junior and extraboard drivers, respectively. We define junior drivers as those hired between 2020 and 2024, which is approximately a third of the driver workforce in CTA. This metric is weighted by the number of stops that a given driver served within a trip. This helps account for cases in which a driver is substituted en route when their work shift ends.

Table 1. Estimation results for the route reliability model.

Variable	Parameter	Estimated	t-Value
Constant	${\beta }_0$	−0.107	−0.95
CV(h) at departure	${\beta }_{C{V}_{r,1}}$	0.373	4.28 *
Junior driver ratio	${\beta }_{Pjunior}$	0.304	2.75 *
CV(h) in schedule	${\beta }_{SchdCV}$	0.348	5.01 *
East-west	${\beta }_{EW}$	0.037	2.41 *
PM	${\beta }_{PM}$	0.066	3.50 *
Total distance	${\beta }_{Dist}$	0.014	2.75 *
Extraboard ratio	${\beta }_{PXB}$	0.148	1.54
Run time ratio	${\beta }_{RunRatio}$	0.206	2.10 *
Interlined ratio	${\beta }_{Pinter}$	0.059	1.51
$R^2$		70.7%
Adjusted $R^2$		67.3%
Number of samples		92

* indicates significant at the 5% level.

shows the estimated parameters for the model (the model was estimated using the Python package statsmodels [23]). The model’s adjusted $R^2$ (67.3%) shows strong predictive power in the model.

The results highlight the operational effects on headway variability. The dispatching headways at the terminal show significant and increasing effects on overall variability, which validates prior findings and emphasizes the need for terminal control [24]. The run time ratio has an increasing effect on variability, which supports the hypothesis that longer observed run times relative to the scheduled run times, reflecting a lack of sufficient recovery time, deteriorate reliability. Additionally, PM operations experience higher headway variability, pointing to the afternoon operations being more challenging than the morning operations.

For attributes related to the service plan, the scheduled headway variability showed high and significant increasing effects, which is expected given that headway disturbances can emerge more easily when the planned headways are less uniform. The association with the interlined ratio was not significant. One explanation could be that the negative effects of interlining, namely delayed trip start, are already captured in the terminal headway variability.

In terms of network attributes, it is found that route distance increases the headway variability, which validates the findings of [4]. The dummy variable for east–west routes was found to be significant and positively correlated with headway variability, indicating that east–west routes are more unreliable than north–south routes. This can be explained by the distinct urban properties between the streets of both orientations. The north–south streets were designed as major arterials with lower intersection density, requiring less stopping from buses.

As for human factors, junior drivers show a significant and increasing effect on headway variability, which validates the findings of [6,25]. The proportion of extraboard drivers increases headway variability but this relationship was not significant. The lack of significance may be explained by the diverse experience in the extraboard driver population of Chicago, unlike typical extraboard populations, which are mainly composed of early-stage drivers. Overall, these findings highlight the importance of the driver’s experience and suggest the need for increased workforce training.

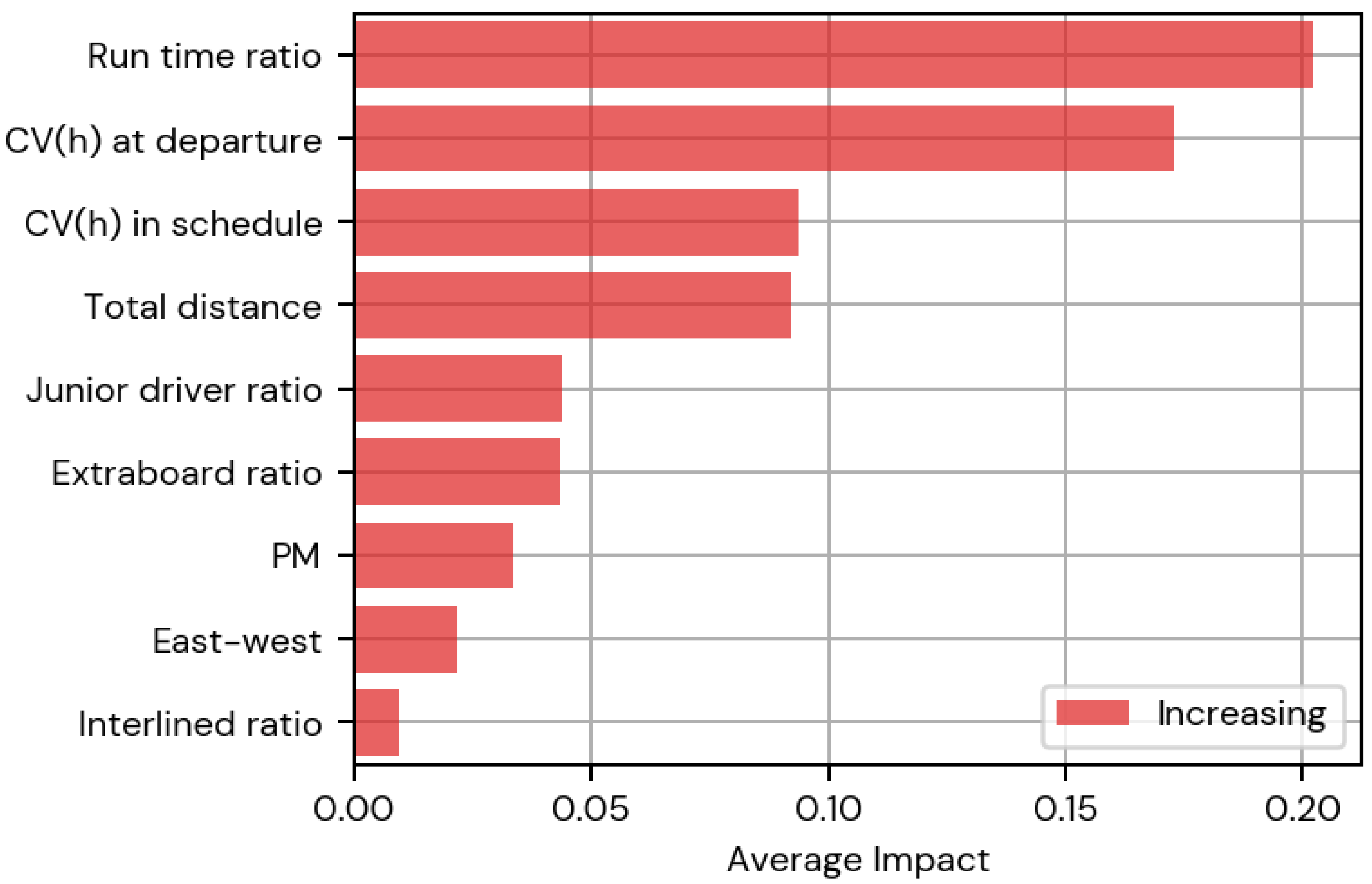
To analyze the relative importance of each independent variable in $C{V}_r$, Figure 4 shows the average impact of each variable on the estimated parameters. Based on the average impact, the run time ratio and dispatching headway variability are the biggest contributors to headway variability. To understand the implications of the average impact, consider a route with average variability $C{V}_r=0.60$. Of the total, 0.20 (33%) would be due to the run time ratio, and 0.16 (27%) would be due to the terminal headway variability. Other relevant determinants are the variability in scheduled headways, the total route distance, and the proportion of junior drivers.

4.4. Segment Reliability Model

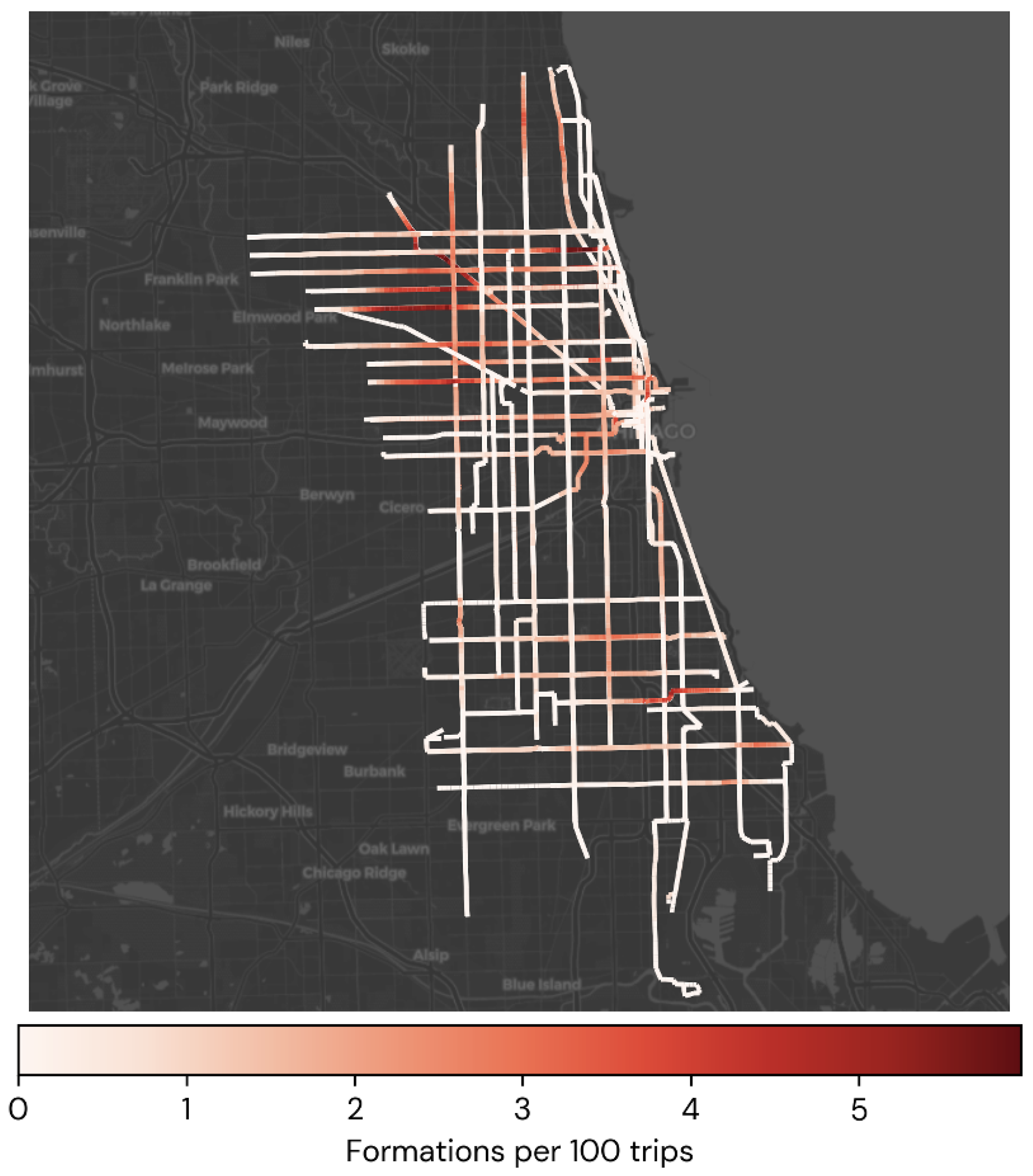
To visualize the data, Figure 5 shows the spatial distribution of failure formations for the considered routes. The plot shows increased formations along east–west routes, which validates the findings from the route-level model, which characterized them as more unreliable. There is also a significant presence of formations near the downtown area, which can be attributed to increased operational complexity, and the northwest region, which can be explained by the residential nature of its streets, which may slow down buses.

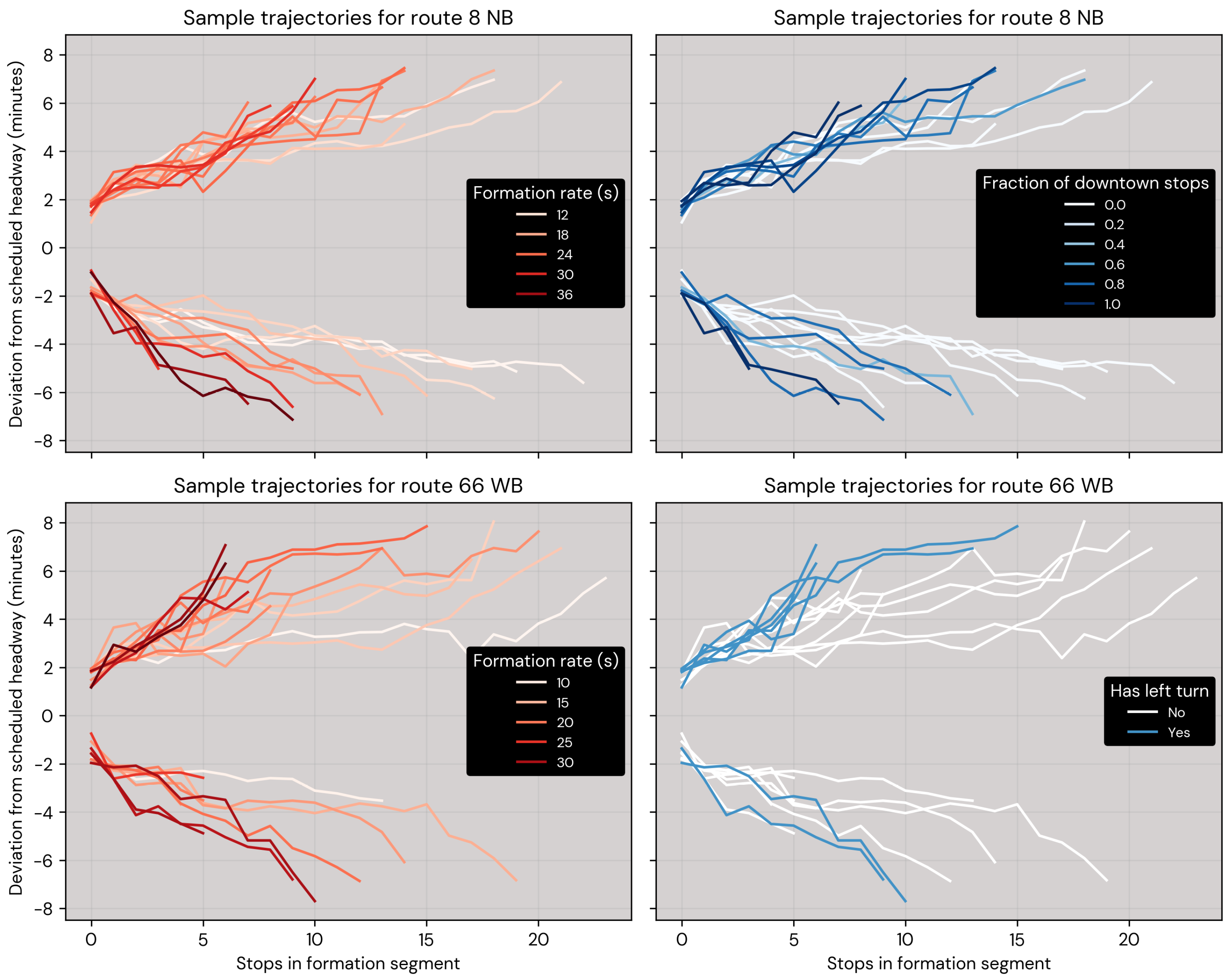
To explore patterns in the data at the trip level, Figure 6 shows selected attributes for individual trip trajectories. On the top left, trajectories for route 8 northbound are color-coded according to the magnitude of the failure formation rate ($F{R}_i$), indicating higher values for more abrupt formations. On the top right, the same trajectories are color coded based on the proportion of downtown stops. It can be observed that more abrupt formations tend to have more downtown stops, which is reasonable given the potentially increased traffic congestion and demand in downtown. The bottom plots show trip trajectories for route 66 westbound, with the bottom left visualizing the formation rates and the bottom right comparing the presence of left turns. Segments with left turns show a pattern of more abrupt formations, which may be attributed to the longer signal times for left turning.

Similar to the route-level model, a linear regression model was used to estimate the contributions of the various factors. The best model, chosen based on parameter significance, multicollinearity considerations, and interpretation of the role of the variables, is as follows:

$$\begin{array}{cc}\hfill F{R}_i=& {\beta }_0+{\beta }_{LinkVar}·LinkVar+{\beta }_{DwellVar}·DwellVar+{\beta }_{HasTP}·HasTP+{\beta }_{BusLane}·BusLane\hfill \\ \hfill & +{\beta }_{HasLTurn}·HasLTurn+{\beta }_{PTransfer}·PTransfer\hfill \end{array}$$

(9)

where

• $LinkVar$ and $DwellVar$ represent the variability of link and dwell times (in minutes), respectively. These values are calculated by first determining the standard deviation of observed dwell or link times for each stop or inter-stop segment, then averaging these standard deviations across the entire failure formation segment.
• $HasTP$ is a dummy variable, where $HasTP=1$ indicates the presence of a time point in the segment, and $HasTP=0$ otherwise.
• $HasLTurn$ is a dummy variable where $HasLTurn=1$ indicates the presence of 1 (or more) left turns in the segment, and $HasLTurn=0$ otherwise.
• $PDtwn$ refers to the fraction of bus stops in the segment that are located within the downtown area. The calculated center point of the “Loop” area, Chicago’s central business district, is used as the centroid. A stop was labeled as within downtown if it fell within a 1.5-mile radius of this centroid.
• $PTransfer$ is the average number of transfer riders (per served trip) boarding at the stops in the segment, obtained from the ODX dataset.
• $BusLane$ is the fraction of the segment distance that has a dedicated bus lane.

The model is designed in terms of the operational mechanisms affecting both bunching and gaps. However, each phenomenon may respond differently to these mechanisms. For instance, the accelerating effect of a bus lane may help resist the formation of gaps but have minimal effect on the formation of bunching. For this reason, the model parameters are estimated separately for bunching and gap events while maintaining the same model specification. Another consideration is the potential correlation of bunching and gaps for consecutive vehicles. For example, a vehicle’s bunching formation may be the result of a leading vehicle slowing down because of a gap formation. However, this phenomenon was not found to be substantial in the data, according to analysis on the headway of vehicles leading to a failure event. Only 29% of bunching events had a gap event ahead, and only 19% of gap events had a bunching event ahead.

The model parameters were estimated using the Python package statsmodels and are detailed in

Table 2. Segment reliability model regression summary.

		Bunching Model		Gap Model
Variable	Parameter	Estimated	t-Value	Estimated	t-Value
Constant effect	${\beta }_0$	7.11	6.46 *	11.63	9.20 *
Link time variation	${\beta }_{LinkVar}$	0.49	9.71 *	0.37	7.27 *
Dwell time variation	${\beta }_{DwellVar}$	0.70	6.34 *	0.63	5.41 *
Has time point	${\beta }_{HasTP}$	−3.09	−4.47 *	−6.49	−7.24 *
Bus lane proportion	${\beta }_{BusLane}$	−0.50	−0.35	−3.32	−2.35 *
Has left turn	${\beta }_{HasLTurn}$	3.29	3.05 *	−0.45	−0.48
Expected transfers per trip	${\beta }_{PTransfer}$	−3.76	−2.41 *	5.58	3.17 *
$R^2$		24.7%		24.9%
Adjusted $R^2$		24.4%		24.1%
Number of samples		828		894

* indicates significant at the 5% level.

. The adjusted $R^2$ values, consistent for both bunching and gap models, indicate reasonable predictive power.

In terms of operational features, the link and dwell time variability show a significant and increasing effect on failure formation rates. The significance of dwell times validates the prior findings in [8]. Although [15] highlights the potential of link travel times to counter dwell time delays, these results highlight how link time uncertainty can further fuel faster bunching and gap formations. Transfer volumes are found to be significant in accelerating gap formations. This is reasonable, since dwell times induced from transfer boardings can slow down buses, which makes gap formations more severe. Surprisingly, transfer volumes reduce bunching formation rates. While theory suggests that vehicle gaps (increased by transfer volumes) should promote bunching by allowing following vehicles to catch up, this finding indicates that many bunching and gap events are unrelated. Thus, for bunching events that are independent of gaps in leading vehicles, it is reasonable that transfer volumes slow down bunching formations. Left turns were found to significantly increase bunching formation rates, which validates the hypothesis that the uncertainty from challenging left-turn movements can disrupt headways. In the gap model, this relationship was not significant.

The coefficients show that the proportion of dedicated bus lanes significantly reduces the formation of gaps and shows no significant effects on bunching. This is reasonable because the speed gains from bus lanes allow vehicles to counteract longer dwell times, which occur particularly during gap formations. Also, the presence of time points in the segment has a decreasing effect on failure formations, which may indicate that the enforcement of schedule adherence indirectly improves headway adherence. Overall, these findings validate the potential benefits of agency infrastructure and operational planning.

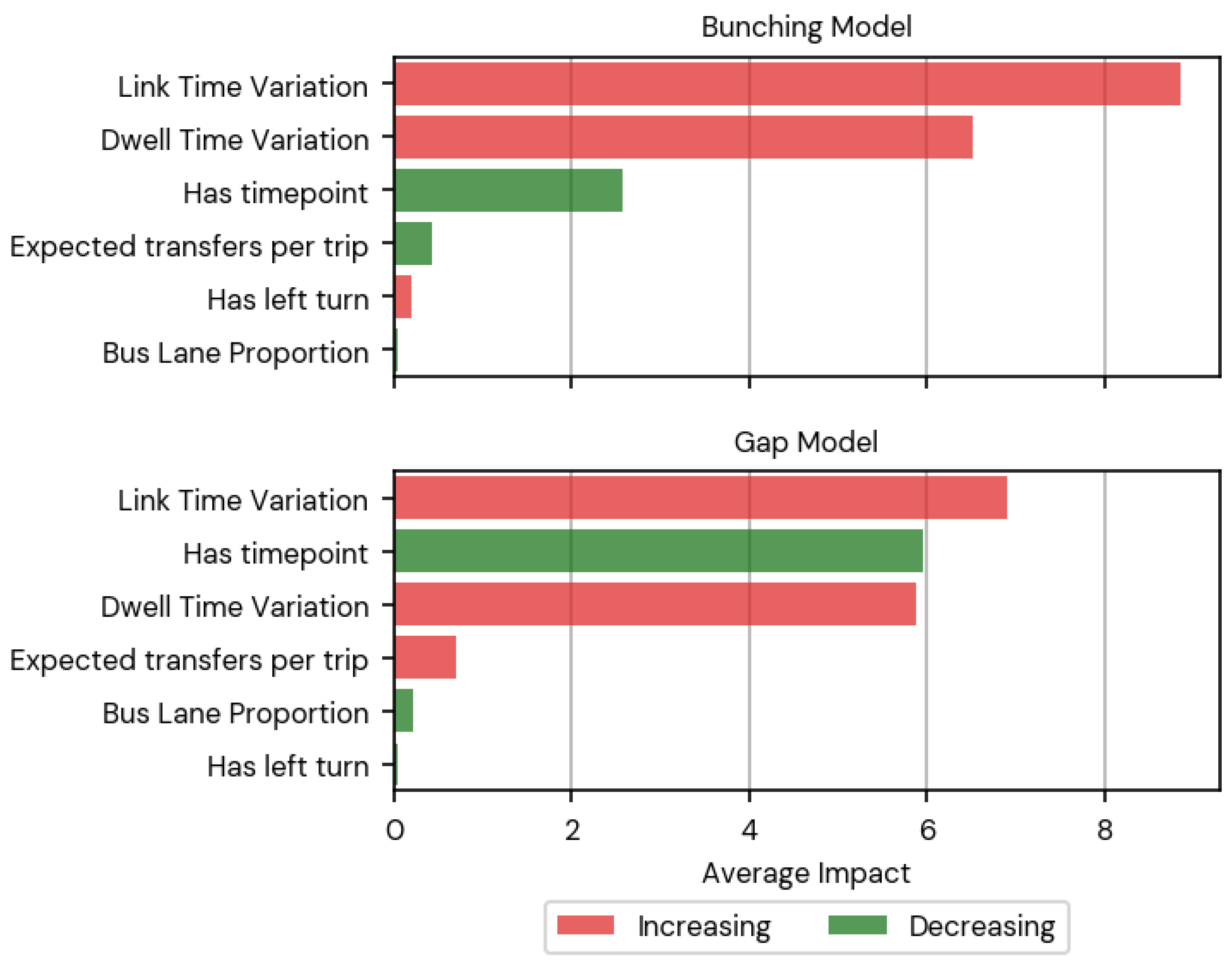
Similar to the route-level model, the average impacts were evaluated and shown in Figure 7. As observed, link time variation is the most important factor in increasing failure formation rates, followed by dwell time variation. This is surprising since bunching and gaps are often associated with dwell times. Meanwhile, the presence of a time point is observed to be the most important factor in reducing failure formations for both bunching and gaps. This finding demonstrates that bus drivers are following the guidelines of schedule adherence at time points, i.e., by holding at time points when running early. The significance of time points validates the prior findings of [6]. To evaluate the implications of average impacts, we can consider the following examples. The typical bunching event has a formation rate of 18 s per stop segment. The link time and dwell time variation collectively contribute 14 s, or 77% of the total. This is countered by the presence of time points, which reduce the formation rate by 2 s, or 11% of the total. In the case of gap events, with a typical formation rate of 19 s per stop segment, the link and dwell time variation collectively contribute 11 s, or 58%, and time points act as a stronger resisting force, with 6 s, or 32% of the total.

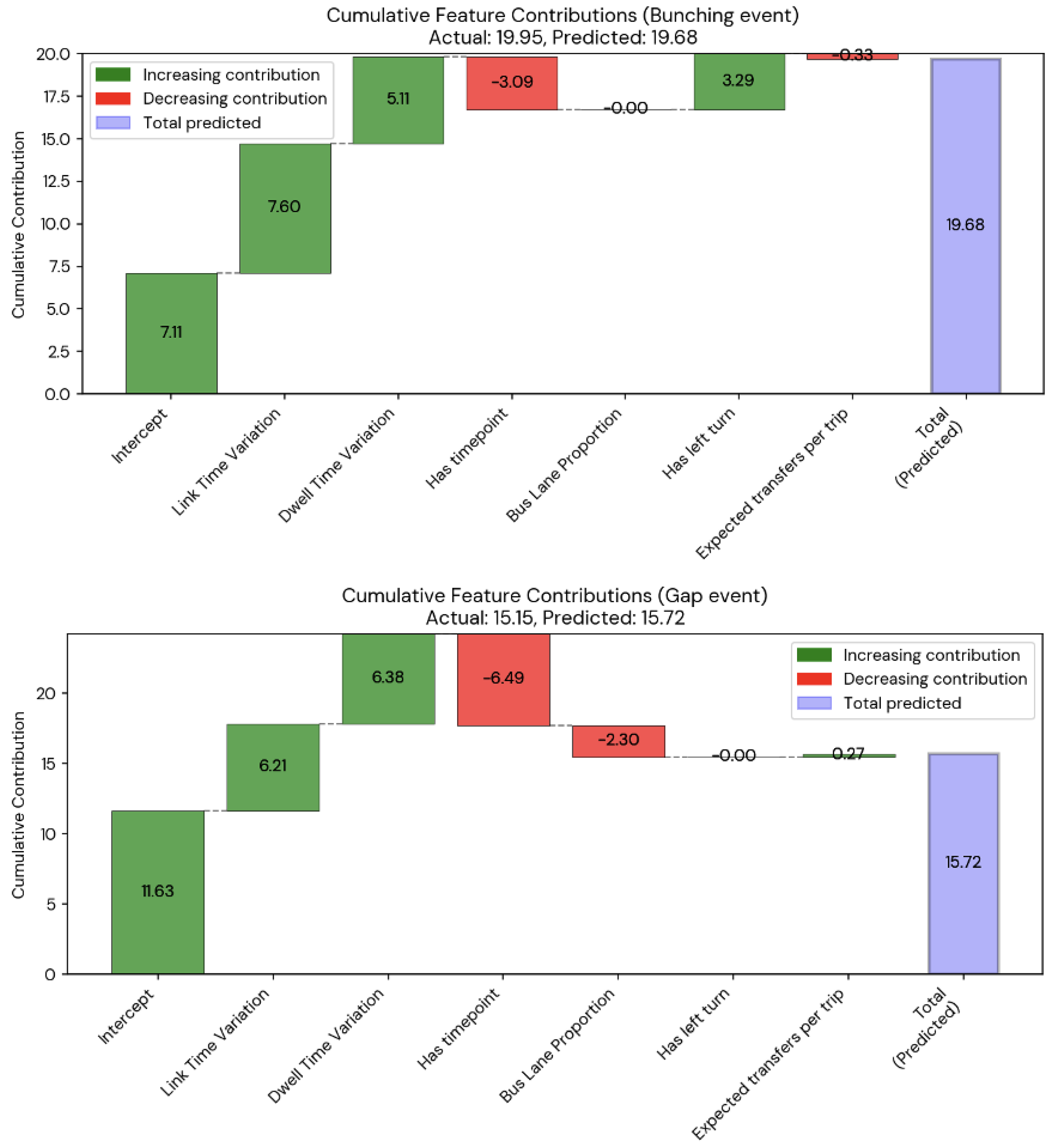
Figure 8 shows waterfall plots to visualize the relative contributions of each independent variable on the predicted variable for individual samples for the bunching and gap cases. This further illustrates how, in the gap event, the presence of time points and bus lanes reduces the formation rate. For the bunching case, time points also reduce the formation rate, but the presence of a left turn deteriorates the formation rate in nearly equal measure.

5. Implications

This section expands on the insights gathered in the results and discusses implications and recommendations.

5.1. Operations Plan

The analysis provides evidence of the potential benefits from changes in planning, scheduling, and operating procedures. These typically do not require significant additional resources or infrastructure.

Schedule-related attributes are shown to be critical to reliability, and improvements could target the various levels of schedule design. At the lowest level, i.e., the trip running time, improvements could be directed toward adequately calibrating the scheduled running times according to actual running times. In terms of intervals between trips, the variability in scheduled headways could be reduced. At the block scheduling level (trip chain for the same vehicle), the proportion of interlined trips could benefit reliability by minimizing the required deadheading travel between routes.

The route-level model results showed that headway regularity at the dispatch point significantly impacts route-level reliability. Proactive strategies can include better schedules that allow for sufficient padding at the end of the trip to reduce propagated delays. Responsive dispatching strategies can include more terminal supervision to spread departures evenly to counteract delays. This can be achieved by a supervisor on-site or a controller with remote communications with the driver.

The local model results highlighted the effect of time points in decelerating the formation of bunching and gaps. The implication is that route segments could benefit from including time points for drivers to self-correct irregularities. This strategy can be further enhanced with schedule designs that allocate sufficient schedule padding in segments between time points.

5.2. Human Factors

The proportion of junior drivers was found to be a significant factor in reduced reliability. In Chicago, drivers select work according to their seniority, which may enable the concentration of senior drivers in less challenging routes and junior drivers in more challenging routes. The findings suggest the potential for improving the allocation of drivers to routes according to their experience levels and the difficulty of routes. A previous study [26] recommended driver scheduling policies to mitigate the issues from driver heterogeneity. An alternative strategy could be to upgrade training requirements.

The proportion of the extraboard was correlated with reduced route-level reliability, albeit not significantly. Contrary to typical extraboard populations, which are mainly composed of early-stage drivers, Chicago’s extraboard includes some experienced drivers. This relationship should be studied further to understand how to strategically allocate extraboard across routes.

As mentioned earlier, time points are shown to improve reliability at the local level. A corollary of this finding is that enforcing or incentivizing schedule or regularity adherence at time points can be an improvement strategy. Incentive strategies can be financial, as is done in the Santiago transit system [27] and described in a Stockholm case study [28].

5.3. Infrastructure

The findings support a variety of infrastructure improvements. Bus lanes were shown to reduce the formation of gaps and could be extended to more critical locations. To reduce headway variability at terminals, which was shown to deteriorate route-level reliability, infrastructure upgrades at terminals could reduce layover times and improve fleet management. The models showed that dwell time variability deteriorates reliability and that stops with high transfer volumes favored the formation of gaps. To address this, station upgrades could target the reduction of dwell times, such as all-door boarding. Additionally, the results showed negative impacts of left turns on bunching, which supports upgrades to left-turn traffic signaling in order to prioritize buses.

6. Conclusions

Factors influencing service reliability can be found in high-level aspects of bus routes, such as the quality of schedules, as well as local-level attributes within bus routes, such as left-turn intersections or dedicated bus lanes. Previous research on service reliability has focused on higher-level aspects of service, with more granular analysis being limited to exploratory studies. Additionally, earlier inferential modeling approaches to understand relationships with reliability have used schedule adherence as the predicted metric.

This paper captures multilevel effects with two linear regression models. The first model is formulated to estimate headway variability at the route level. The second model estimates the rate of bunching and gaps observed at the segment level. As the dependent variable, a novel measure is presented that captures how rapidly trips transition from headways close to the scheduled headway to a bunching or gap state.

At the route level, one of the most significant contributors to unreliability was irregular terminal departures, validating previous research on the topic. The results also found that routes were less reliable if the scheduled trip time was lower compared to the observed run time, validating the hypothesized significance of schedule quality. Another interesting finding was the average level of experience of drivers, which suggests that agencies should focus on training drivers and incentivizing experienced drivers to choose more challenging routes. At the segment level, it was found that link times and dwell times are the largest contributors. In terms of road infrastructure, dedicated bus lanes reduce the formation of gaps, and left-turn intersections along the route increase bunching formations. The findings elicit various potential recommendations for practitioners. This modeling approach can serve both to identify issues and assess improvements.

While the analysis is based on Chicago, many findings are likely relevant to other large cities, given the city’s diversity of road structures, landscapes, bus route layouts, and rider demographics. Chicago’s unique features, including its grid-based street network and lakefront geography, may influence demand patterns and the role of certain variables, such as route directionality. These factors suggest that, while the general relationships may hold elsewhere, their strength could vary in cities with different street layouts, geographic constraints, or service designs.

There are several directions for future research. The proposed method assumes linear relationships, so potential nonlinear effects should be examined. For example, the impact of driver experience may exceed a simple linear trend, as the performance of one trip can influence subsequent trips. Interaction effects could also be explored, such as the combined influence of the scheduled-to-actual run time ratio and route distance. Additionally, more attributes in the model could enrich the analysis. For instance, considering how the complexity in service patterns (short turning, express service) at a detailed level impacts reliability could elicit valuable insights on route planning. At the operational level, it would be useful to investigate the effect of time points in terms of the actual schedule adherence, i.e., from observed holdings, and not just the presence of time points. In terms of urban attributes, detailed information on the road attributes could help explain the discovered discrepancies between east–west and north–south routes. However, obtaining these attributes is subject to data availability. To parse out effects at the local level, alternative time-series-based methods may allow a more detailed assessment of operational attributes preceding trip failures. Finally, the proposed approach focused on trips that result in bunching or gaps, disregarding cases in which the trip recovers back into acceptable headway ranges. Future work could target recovery cases to investigate influential factors.