Towards Trust and Reputation as a Service in Society 5.0

Highlights

What are the main findings?

• We propose a novel trust and reputation service for a decentralized blockchain-based marketplace with Smart Contract support, similar to what will be the norm in Society 5.0. Specifically, we assume that a Smart Contract is associated with each transaction. At the completion of the transaction, the Smart Contract is responsible for providing automatic feedback, replacing notoriously unreliable buyer feedback by a more objective assessment of how well the buyer and the seller have fulfilled their contractual obligations.
• We provide three applications of the proposed trust and reputation service. Specifically, we first discuss an application to a multi-segment marketplace, where a malicious seller may establish a stellar reputation by selling cheap items, only to use their excellent reputation to defraud buyers in a different market segment. Next, we demonstrate how our trust and reputation service works in the context of sellers with time-varying performance due, say, to overcoming an initial learning curve.

What are the implications of the main findings?

• More broadly, we demonstrated the feasibility of a framework for providing trust and reputation as a service in a decentralized blockchain-based marketplace that leverages smart contract support.

Abstract

Our paper was inspired by the recent Society 5.0 initiative of the Japanese Government which seeks to create a sustainable human-centric society by putting to work recent advances in technology. One of the key challenges in implementing Society 5.0 is providing trusted and secure services for everyone to use. Motivated by this challenge, this paper makes three contributions that we summarize as follows: Our first main contribution is to propose a novel blockchain and smart contract-based trust and reputation service design to reduce the uncertainty associated with buyer feedback in marketplaces that we expect to see in Society 5.0. Our second contribution is to extend Laplace’s Law of Succession in a way that provides a trust measure in a seller’s future performance in terms of their past reputation scores. Our third main contribution is to illustrate three applications of the proposed trust and reputation service. Here, we begin by discussing an application to a multi-segment marketplace, where a malicious seller may establish a stellar reputation by selling cheap items, only to use their excellent reputation score to defraud buyers in a different market segment. Next, we demonstrate how our trust and reputation service works in the context of sellers with time-varying performance due, say, to overcoming an initial learning curve. We provide a discounting scheme where older reputation scores are given less weight than more recent ones. Finally, we show how to predict trust and reputation far in the future, based on incomplete information. Extensive simulations have confirmed the accuracy of our analytical predictions.

1. Introduction and Motivation

In 2016, the Japanese Government publicized a bold initiative and a call to action for the implementation of a “Super Smart Society” announced as Society 5.0 [1,2]. The novelty of Society 5.0 is that it embodies a sustainable service-centric society enabled by the latest digital technologies. Society 5.0 was designed to meet the needs of its members by providing goods and services to the people who require them, when they are required, and in the amount required, thus enabling its citizens to live an active and comfortable life through the provision of high-quality services [1,3]. Society 5.0 provides a common societal infrastructure for prosperity based on an advanced service platform, which turns out to be its main workhorse [4].

The vision behind Society 5.0 is that the continued progress of ICT and digital technologies of all sorts will provide individuals and society tremendous opportunities for innovation, growth, and unprecedented prosperity and well-being through various forms of trusted human-to-human, human-to-machine, and machine-to-machine cooperation and collaboration. Most of these trusted forms of cooperation and collaboration between humans and machines or between autonomous machine systems have yet to be defined and understood [5,6].

Services and their effects have been studied intensely in the past two decades, and most of their dynamics are now well understood [7,8,9,10,11,12]. Recently, the emergence of Decentralized Autonomous Organizations (DAOs) has motivated the study of service provisioning in decentralized blockchain-based environments fed by open networks of contributors [13,14,15].

Our paper was inspired and motivated by some of the challenges that will have to be overcome in order to implement Society 5.0. Key among these challenges, as pointed out by several workers, is providing trusted and secure services [16,17,18]. With this in mind, we set out to explore providing trust and reputation service in Society 5.0.

Stimulated by the impetus provided by the vision of Society 5.0, decentralized markets are growing at a rapid pace, with all types of goods and services being transacted online. In such global markets, buyers and sellers engage in transactions with counterparts with whom they had little or no previous interaction. This introduces significant risks for both buyers and sellers. In order to assist buyers (sellers) with the process of choosing a trustworthy trading partner, marketplaces maintain individual reputation scores for each seller (buyer) [19,20,21,22]. These reputation scores capture, in various forms, statistical information about the past behavior of sellers (buyers) registered with the platform.

The goal of a trust and reputation service is to provide buyers with a robust framework that allows them to select future transaction partners based on a combination of objective and subjective trust measures distilled from accumulated evidence of sellers’ past behavior in the marketplace. The quality of a trust and reputation service depends, in a fundamental way, on the quality of the feedback it receives from buyers. This is even more crucial when we consider decentralized marketplaces, where there is no centralized control, unlike marketplaces such as Amazon and eBay.

Being a subjective measure, the quality of buyer feedback is notoriously hard to assess [23,24]. There are two related problems here:

• First, by soliciting feedback from “neighbors”, buyers are necessarily biased by their subjective opinions. In a truly global marketplace, like the one we expect to see in Society 5.0, it is very hard to tell, with any degree of certainty, whether or not feedback from a given buyer is an outlier and, as a result, any filtering strategy may be problematic and discriminatory to implement [23].
• Second, it is by no means clear that the feedback received from other buyers reflects reality. Indeed, as pointed out by [23] and other workers, the problem is that different buyers may rate a similar buying experience with the same seller vastly differently. In some cases, the feedback may even turn out to be more positive or more negative than the real experience with the seller would suggest. When feedback is provided by buyers from around the world who may value different aspects of the same transaction differently, it is very hard to know when a buyer provides truthful feedback [25].

Our Contributions

Our first main contribution is to propose a novel blockchain-based trust and reputation service with the goal of reducing the uncertainty associated with buyer feedback in decentralized marketplaces such as the one underlying Society 5.0. This first contribution is aligned with one of the fundamental challenges of Society 5.0, namely, providing trusted and secure services to all those who need them [16,17,18].

The novelty of our first contribution is that, in a sharp departure from common wisdom, and aligned with the work of Aljohani et al. [26], we assume that a Smart Contract (SC) is associated with each transaction. We assume that the SC in charge of the transaction is also responsible for providing feedback at the end of the transaction, replacing buyer feedback with a more objective assessment of how well the buyer and the seller have fulfilled their contractual obligations towards each other.

At the heart of any trust and reputation service must lie a trust engine, an algorithm that takes as input a seller’s reputation score and distills from it a subjective trust measure, namely, the perceived probability that on the next transaction the seller will fulfill their contractual obligations. Our second main contribution is to extend Laplace’s Law of Succession [27,28,29] in a way that provides a trust measure in a seller’s future performance in terms of their past reputation scores.

Finally, our third main contribution of the paper is to illustrate three applications of the proposed blockchain-based trust and reputation service. Specifically, in Section 6.1 and Section 6.2, we discuss two applications of our service to a multi-segment marketplace, where a malicious seller may establish an enviable reputation by selling cheap items or providing some specific service, only to use their superb reputation score to defraud buyers in a different market segment. Next, in Section 6.3, we apply the results of Section 4 in the context of sellers with time-varying performance due, for example, to overcoming initial difficulties. We provide a simple discounting scheme where older reputation scores are given less weight than more recent ones, thus focusing attention on more recent performance. Finally, in Section 6.4, we show how to predict trust and reputation scores far in the future, based on incomplete information.

The remainder of this work is organized as follows: Section 2 offers a succinct review of recently proposed blockchain-based trust and reputation systems. Section 4 introduces the proposed Laplace trust and reputation service. This is followed by Section 5, which discusses how the trust measure is updated over time. Section 6 offers three applications of the proposed Laplace trust and reputation service. Section 7 introduces our simulation model and offers simulation results. Finally, Section 8 offers concluding remarks and directions for future work.

2. Related Work

Trust and reputation models have long been of interest to economists [30,31,32,33,34,35,36,37]. The advent of e-commerce has renewed interest in online transactions, where, naturally, trust or the lack thereof is a major concern.

In recent years, a steadily increasing number of workers have investigated blockchain-based reputation systems wherein SCs may or may not play a significant role. We refer the reader to the surveys of Hendrix et al. [38], Bellini et al. [13], and Hasan et al. [14] for a comprehensive discussion. With this in mind, the main goal of this section is to review some of the recently proposed blockchain-based reputation systems.

Eltoweissy et al. [4] introduced the fundamental concept of the Marketplace of Services and showed how to implement such a concept in an environment similar to that provided by Society 5.0.

Olariu [6] provides a continuation and extension of the work of Eltoweiss et al. [4]. In [6], the author argues that the Marketplace of Services is, along with an IoT ecosystem, an integral part of a Smart Community infrastructure. Very much like Society 5.0, our Smart Community can provide a large number of diverse and evolving services offered as utilities and sold on a metered basis. We expect that most of the services offered by the Smart Community can be synthesized within the community itself, using the latest ICT and digital technologies (e.g., 3D printing, robotics, Big Data, AI, etc.), from a hierarchy of raw resources or other services.

Buechler et al. [39] developed a reputation system where SCs contribute to the task of reputation scoring by analyzing the underlying network structure. Their system allows buyers and sellers to query and record the outcomes of transactions.

Lu et al. [40] proposed a blockchain-based trust model specifically designed to improve the trustworthiness of messages in Vehicular Ad hoc Networks (VANETs). However, their system does not use SCs in any capacity. Later, Javaid et al. [41] proposed a blockchain-based and trusted Certificate Authority-based trust and reputation model for VANETs. While SCs are mentioned by the authors of [41], no specific role for SCs is mentioned in the paper, other than supporting the functionality of the blockchain. More recently, Singh et al. [42] proposed a blockchain-based trust management system in the context of the Internet of Vehicles [43,44], an extension of the VANET. In their work, the blockchain provides trust among vehicles that have no reason to trust each other. The blockchain also manages, in a reliable manner, trust and reputation across the Internet of Vehicles. However, although mentioned, there is no specific role played by SCs in their scheme.

Arshad et al. [45] presented a blockchain-based reputation system that they call REPUTABLE, which computes the reputation of sellers within a blockchain ecosystem through decentralized on-chain and off-chain implementations. REPUTABLE ensures privacy, reliability, integrity, and accuracy of reputation scores, all with minimal overhead. In order to facilitate gathering buyer feedback, REPUTABLE employs SCs. However, the SCs are not entrusted with providing feedback on their own.

Mrabet et al. [46] proposed a dynamic, decentralized reputation system for wireless sensor networks (WSNs) and mobile ad hoc networks (MANETs). Traditional reputation systems rely on central authorities, which are unsuitable for decentralized environments. The proposed system overcomes this by integrating secure multi-party computation (SMC) and blockchain technology, ensuring privacy even with dishonest parties. Nodes can participate in evaluating and being evaluated, maintaining individual ratings privately while publicizing aggregated scores. The system operates in three phases: join, rate, and update. Participants initially submit a joint transaction and are assigned to subgroups. Using the SMC protocol, subgroups compute reputation ratings without revealing individual inputs. Miners then update the final reputation score on the blockchain. While secure under the semi-honest adversarial model, the system may face challenges under a malicious adversarial model. It also features an off-chain phase to reduce storage and computation costs.

Aljohani et al. [26] proposed a prototype that overcomes the challenges of maintaining reviewer anonymity in decentralized markets by leveraging blockchain technology and SCs to create a secure and transparent environment for transactions and feedback. Their method, based on the Ethereum blockchain, mitigates the risks associated with centralized marketplaces by promoting reviewer anonymity through the use of different identities and enforcing transactions with SCs. Also, their work overcame the overhead resulting from using primitive cryptographic methods that help protect buyer anonymity. Additionally, by offering refundable review fees as a financial incentive, this approach ensures active and honest participation from reviewers, setting it apart from traditional reputation systems.

Dougan and Karacan [47] proposed a decentralized reputation system designed to enhance the reliability and confidentiality of e-commerce transactions. The system employs two authorized blockchains, Hyperledger Indy and Hyperledger Fabric, to manage sellers’ digital identities and provide feedback tokens to buyers using verified credentials and SCs. Hyperledger Indy uses zero-knowledge proofs (ZKPs) to ensure the confidentiality and authenticity of user credentials. To maintain buyer anonymity and prevent feedback from being linked to them, feedback tokens are issued as proof of transaction. Buyers use these tokens to provide feedback, ensuring they are tied to legitimate transactions.

Willems and Adams [48] developed an advanced system called GhostBuy, which ensures complete anonymity in online purchases. GhostBuy is an all-step anonymous purchase system based on data separation principles. It ensures client privacy during the purchase process by combining cryptographic methods and trusted intermediaries to oversee transactions. The architecture of GhostBuy is characterized by the separation of entities managing client information and executing orders. Encrypted data are exchanged among the parties involved in the transaction, preventing anyone from simultaneously accessing the buyer’s identity and the specifics of their purchases.

3. The Assumed Blockchain-Based Decentralized Marketplace

If a reputation system is to be successful, several conditions must be satisfied: first, the decentralized marketplace must collect, aggregate, and disseminate seller reputation scores accurately and in a timely manner; second, buyers must provide truthful feedback on their buying experience; and third, buyers must base their choice of their future transaction partners (i.e., sellers) solely on reputation scores.

The first and third conditions are relatively easy to enforce or incentivize. The second condition is far more problematic. It has been argued that if buyers consistently provide truthful feedback, isolated interactions between buyers and sellers take on attributes of long-term relationships and, as a result, the reputation scores tallied by the marketplace become a high-quality substitute of community-based reputation [49].

In this work, we assume a blockchain-based marketplace similar to that of [19,20,21,22,50,51], where the transactions between buyers and sellers are maintained as individual blocks that, once added to the blockchain, keep immutable information about the transaction. We maintain statistical information about the buyers’ and sellers’ performance as part of the blockchain.

4. The Laplace Trust and Reputation Service

The main goal of this section is to introduce our trust and reputation service.

4.1. Terminology and Definitions

Consider a decentralized marketplace and a new seller S who just joined the marketplace at time 0. We associate with the seller an urn containing an unknown number, N, of balls and an unknown composition, in terms of the number of black balls it contains. The intention is for the urn of unknown composition to represent the total number of transactions in which seller S will be involved during their career in the marketplace. Each transaction in which seller S is involved is associated with a ball extracted from the urn without replacement. If the extracted ball is black, we say that the seller has fulfilled their obligations in the corresponding transaction. The motivation for this is that every time a ball is extracted from the urn without replacement, the probability of obtaining a black ball on the next extraction changes. This is intended to capture, to some extent, the uncertainties and vagaries of seller behavior.

We define the reputation score of the seller at time t as an ordered triple whose first and second components are, respectively, the total number of transactions in which the seller was involved up to time t and the number of transactions in which the seller has fulfilled their contractual obligations up to time t. The third component is $(0,t)$ or, simply, t if no confusion can arise. Thus, initially, the seller’s reputation score is $(0,0,0)$.

Let I be the random variable denoting the initial number of black balls in the urn. Let $H_i=\{I=i\},(0\le i\le N)$, be the hypothesis that the initial composition of the urn is $(i,N-i)$, in other words, that the urn initially contains i black balls, while the remaining $N-i$ balls have other colors.

Since nothing is known à priori about the past history, skill level, and integrity profile of the seller, it makes sense to assume, as an initial prior, that all compositions of the urn are equiprobable (see [28] for a good discussion), and so

$$Pr\left[H_i\right]={\displaystyle \frac{1}{N+1}}.$$

(1)

We define ${\rho }_S(0,t)$, the trust measure in seller S at time t, to be the probability that the seller will fulfill their contractual obligations on the next transaction following t. In terms of the underlying urn, this means that the next ball extracted from the urn is black. For example, let $B_0$ be the event that on the very first transaction, the seller will fulfill their contractual obligations. Equivalently, $B_0$ is the event that on the first extraction a black ball will appear. For reasons that will become clear later, we write ${\rho }_S(0,0)$ for $Pr\left[B_0\right]$. We can write

$$\begin{array}{ccc}\hfill {\rho }_S(0,0)& =& Pr\left[B_0\right]\hfill \\ & =& \sum _{i=0}^{N}Pr\left[B_0\right|H_i]Pr\left[H_i\right]\hfill \\ & =& {\displaystyle \frac{1}{N+1}}\sum _{i=0}^N{\displaystyle \frac{i}{N}}[\mathrm{by} (1\left)\right]\hfill \\ & =& {\displaystyle \frac{1}{N(N+1)}}\sum _{i=0}^{N}i\hfill \\ & =& {\displaystyle \frac{1}{N(N+1)}}{\displaystyle \frac{N(N+1)}{2}}={\displaystyle \frac{1}{2}},\hfill \end{array}$$

(2)

which makes intuitive sense, since we have no à priori knowledge of the seller’s past behavior in the marketplace and, therefore, the trust we place in them is one-half.

4.2. Updating the Prior

Now, suppose that our seller has accumulated, in the time interval $[0,t]$, a reputation score of $(n,k,t)$. Recall that this means that out of a total of n transactions in which the seller has been involved up to time t, they have fulfilled their obligations in k of them. Equivalently, this says that from the urn mentioned above, a sample of n balls was extracted without replacement and that k of them were observed to be black.

In order to update the trust measure in our seller, we need to update our belief in the original composition of the associated urn. For this purpose, let A be the event that in a sample of n balls extracted without replacement from the urn, k black balls were observed. Once the event A is known, we update the prior in a Bayesian fashion by setting

$$\begin{array}{ccc}& & Pr\left[H_i\right|n,k]=Pr\left[H_i\right|A]={\displaystyle \frac{Pr[H_i\cap A]}{Pr\left[A\right]}}\hfill \\ & =& {\displaystyle \frac{Pr\left[A\right|H_i]Pr\left[H_i\right]}{{\sum }_{j=0}^{N}Pr\left[A\right|H_j]Pr\left[H_j\right]}}\hfill \\ & =& {\displaystyle \frac{Pr\left[A\right|H_i]}{{\sum }_{j=0}^{N}Pr\left[A\right|H_j]}}[\mathrm{by} (1\left)\right]\hfill \\ & =& {\displaystyle \frac{\frac{\left(\genfrac{}{}{0pt}{}{i}{k}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N}{n}\right)}}{{\sum }_{j=0}^N\frac{\left(\genfrac{}{}{0pt}{}{j}{k}\right)\left(\genfrac{}{}{0pt}{}{N-j}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N}{n}\right)}}}={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{{\sum }_{j=0}^N\left(\genfrac{}{}{0pt}{}{j}{k}\right)\left(\genfrac{}{}{0pt}{}{N-j}{n-k}\right)}}\hfill \\ & =& {\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N+1}{n+1}\right).}}[\mathrm{by} (\mathrm{A}3) \mathrm{in} \mathrm{Appendix}\mathrm{A}.1.]\hfill \end{array}$$

(3)

To summarize, the expression of the updated prior $Pr\left[H_i\right|n,k]$ reflects our updated belief in the initial composition of the urn as a result of seeing k black balls out of n balls extracted. In terms of our seller, upon seeing that the seller has fulfilled their obligations in k out of the first n transactions, we update the perceived intrinsic performance profile of our seller. At the risk of mild confusion, we continue to write $Pr\left[H_i\right]$ for the updated prior instead of the more cumbersome $Pr\left[H_i\right|n,k]$.

4.3. Modeling the Trust Measure

Recall that we define a seller’s (subjective) trust measure, ${\rho }_S(0,t)$, at time t as the probability of the event that on the next transaction the seller will fulfill their contractual obligations.

Theorem 1. 

Assuming that seller S has accumulated, in the interval $(0,t)$, a reputation score of $(n,k,t)$, the trust measure in S at time t is

$${\rho }_S(0,t)={\displaystyle \frac{k+1}{n+2}}.$$

Proof. 

Consider the urn associated with seller S and assume that out of the urn, a sample of n balls was extracted and k of them were observed to be black. Let B be the event that the next ball extracted from the urn is black. In terms of our marketplace, $Pr\left[B\right]$ is precisely ${\rho }_S(0,t)$. By the Law of Total Probability,

$$Pr\left[B\right]=\sum _{i=0}^{N}Pr\left[B\right|H_i]Pr\left[H_i\right].$$

(4)

Observe that $Pr\left[B\right|H_i]={\displaystyle \frac{i-k}{N-n}}$ and recall that, by (3), $Pr\left[H_i\right]={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N+1}{n+1}\right)}}.$ With this, (4) can be written as

$$\begin{array}{ccc}\hfill {\rho }_S(0,t)=Pr\left[B\right]& =& \sum _{i=0}^N{\displaystyle \frac{i-k}{N-n}}{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N+1}{n+1}\right)}}\hfill \\ & =& {\displaystyle \frac{{\sum }_{i=0}^N(i-k)·\frac{i!}{k!(i-k)!}\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{(N-n)\frac{(N+1)!}{(n+1)!(N-n)!}}}\hfill \\ & =& \sum _{i=0}^N{\displaystyle \frac{(k+1)\left(\genfrac{}{}{0pt}{}{i}{k+1}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{(N+1)\left(\genfrac{}{}{0pt}{}{N}{n+1}\right)}}\hfill \\ & =& {\displaystyle \frac{k+1}{N+1}}\sum _{i=0}^N{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k+1}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N}{n+1}\right)}}\hfill \\ & =& {\displaystyle \frac{k+1}{N+1}}{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{N+1}{n+2}\right)}{\left(\genfrac{}{}{0pt}{}{N}{n+1}\right)}}[\mathrm{by} (\mathrm{A}3]\hfill \\ & =& {\displaystyle \frac{k+1}{n+2}},\hfill \end{array}$$

and the proof of Theorem 1 is complete. □

Somewhat surprisingly, the expression of the trust measure is independent of N and depends only on n and k. This observation has interesting consequences in the context of our marketplace. Specifically, if, by time t, two sellers have accumulated the same reputation score $(n,k,t)$, then we place the same amount of trust in both of them, independent of other considerations.

To summarize this discussion, we refer the reader to Figure 1 illustrating the trust measure ${\rho }_S(0,t)$ for small values of n and k. For a better visual effect, the values of ${\rho }_S(0,t)$ for different values of k are depicted in different colors. Figure 1 also reveals that ${\rho }_S(0,0)={\displaystyle \frac{1}{2}}$, as we found in (2).

5. Updating the Trust Measure

The main goal of this section is to show how the trust measure introduced in Section 4 is updated over time.

Theorem 2. 

Assume that in the time interval $(0,t]$, seller S was involved in n transactions and that they fulfilled their contractual obligations in k of them. If in the time interval $(t,t^{\prime }]$ seller S is involved in $n^{\prime }$ additional transactions and they fulfill their contractual obligations in $k^{\prime }$ of them, then the seller’s trust measure, ${\rho }_S(0,t^{\prime })$, at time $t^{\prime }$ is

$${\rho }_S(0,t^{\prime })={\displaystyle \frac{k+k^{\prime }+1}{n+n^{\prime }+2}}.$$

(5)

Proof. 

Let $A^{\prime }$ be the event that, in a subsequent sample of size $n^{\prime }$, $k^{\prime }$ balls were observed to be black. Once the event $A^{\prime }$ is known to have occurred, it is necessary to update our prior. Proceeding in a Bayesian fashion, we write

$$\begin{array}{ccc}\hfill Pr\left[H_i\right|n,k,n^{\prime },k^{\prime }]& =& Pr\left[H_i\right|A^{\prime }]={\displaystyle \frac{Pr[H_i\cap A^{\prime }]}{Pr\left[A^{\prime }\right]}}\hfill \\ & =& {\displaystyle \frac{Pr\left[A^{\prime }\right|H_i]Pr\left[H_i\right]}{{\sum }_{j=0}^{N}Pr\left[A^{\prime }\right|H_j]Pr\left[H_j\right]}}.\hfill \end{array}$$

(6)

Notice the following:

• By (3), $Pr\left[H_i\right]={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{N+1}{n+1}\right)}}$;
• $Pr\left[A^{\prime }\right|H_i]={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i-k}{k^{\prime }}\right)\left(\genfrac{}{}{0pt}{}{N-i-(n-k)}{n^{\prime }-k^{\prime }}\right)}{\left(\genfrac{}{}{0pt}{}{N-n}{n^{\prime }}\right)}}$;
• By the Law of Total Probability, $Pr\left[A^{\prime }\right]={\sum }_{j=0}^{N}Pr\left[A^{\prime }\right|H_j]Pr\left[H_j\right]$;
• By (A7) in Appendix A.2,

  $$Pr\left[A^{\prime }\right]=\sum _{j=0}^{N}Pr\left[A^{\prime }\right|H_j]Pr\left[H_j\right]={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+k^{\prime }}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+n^{\prime }-k^{\prime }}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+n^{\prime }+1}{n+1}\right)}},$$

Consequently, Equation (6) becomes

$$Pr\left[H_i\right]=Pr\left[H_i\right|n,k,n^{\prime },k^{\prime }]={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k+k^{\prime }}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k+n^{\prime }-k^{\prime }}\right)}{\left(\genfrac{}{}{0pt}{}{N+1}{n+n^{\prime }+1}\right)}}.$$

(7)

As before, in order to simplify notation, we continue to refer to $Pr\left[H_i\right|n,k,n^{\prime },k^{\prime }]$ as $Pr\left[H_i\right]$. The expression of the prior $Pr\left[H_i\right]$ in (7) reflects our updated belief in the composition of the urn, as a result of seeing $k^{\prime }$ black balls out of $n^{\prime }$ balls in the second sample extracted.

Let $B^{\prime }$ be the event that the next ball extracted from the urn is black. In terms of our marketplace, $Pr\left[B^{\prime }\right]$ is ${\rho }_S(0,t^{\prime })$.

$$\begin{array}{ccc}\hfill Pr\left[B^{\prime }\right]& =& \sum _{i=0}^{N}Pr\left[B^{\prime }\right|H_i]Pr\left[H_i\right]\hfill \\ & =& \sum _{i=0}^N{\displaystyle \frac{i-k-k^{\prime }}{N-n-n^{\prime }}}{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{i}{k+k^{\prime }}\right)\left(\genfrac{}{}{0pt}{}{N-i}{n-k+n^{\prime }-k^{\prime }}\right)}{\left(\genfrac{}{}{0pt}{}{N+1}{n+n^{\prime }+1}\right)}}\hfill \\ & =& {\displaystyle \frac{1}{(N-n-n^{\prime })\left(\genfrac{}{}{0pt}{}{N+1}{n+n^{\prime }+1}\right)}}\sum _{i=0}^N(i-k-k^{\prime })·{\displaystyle \frac{i!}{(k+k^{\prime })!(i-k-k^{\prime })!}}\left({\displaystyle \genfrac{}{}{0pt}{}{N-i}{n-k+n^{\prime }-k^{\prime }}}\right)\hfill \\ & =& {\displaystyle \frac{k+k^{\prime }+1}{(N-n-n^{\prime })\left(\genfrac{}{}{0pt}{}{N+1}{n+n^{\prime }+1}\right)}}\sum _{i=0}^N\left({\displaystyle \genfrac{}{}{0pt}{}{i}{k+k^{\prime }+1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{N-i}{n-k+n^{\prime }-k^{\prime }}}\right)\hfill \\ & =& {\displaystyle \frac{k+k^{\prime }+1}{(N-n-n^{\prime })\left(\genfrac{}{}{0pt}{}{N+1}{n+n^{\prime }+1}\right)}}\left({\displaystyle \genfrac{}{}{0pt}{}{N+1}{n+n^{\prime }+2}}\right)\hfill \\ & =& {\displaystyle \frac{k+k^{\prime }+1}{n+n^{\prime }+2}}.\hfill \end{array}$$

(8)

□

Notice that, in spite of the laborious derivation, the final result is extremely simple and easy to compute. This is a definite advantage of our scheme.

An interesting question is to determine under which conditions the trust measure ${\rho }_S(0,t^{\prime })$ is at least as large as ${\rho }_S(0,t)$. The answer to this question is provided by the following result:

Lemma 1. 

$${\rho }_S(0,t^{\prime })\ge {\rho }_S(0,t)\iff {\displaystyle \frac{k^{\prime }}{n^{\prime }}}\ge {\displaystyle \frac{k+1}{n+2}}.$$

Proof. 

This follows from Lemma A3 in the Appendix A with $a=k+1$, $b=n+2$, $a^{\prime }=k^{\prime }$, and $b^{\prime }=n^{\prime }$. □

Refer to Figure 2 for a geometric illustration of Lemma 1. Consider a two-dimensional coordinate system where the horizontal and vertical axes capture, respectively, the total number of transactions and the number of transactions in which the seller has fulfilled their contractual obligations. Consider, further, the points $A,B,C$ of coordinates $(n+2,k+1),(n+n^{\prime }+2,k+1),(n+n^{\prime }+2,k+k^{\prime }+1)$. It is easy to see that ${\rho }_S(0,t)=tan\theta ={\displaystyle \frac{k+1}{n+2}}$ and ${\rho }_S(0,t^{\prime })=tan{\theta }^{\prime }={\displaystyle \frac{k+k^{\prime }+1}{n+n^{\prime }+2}}$. Finally, it is easy to confirm that ${\rho }_S(0,t^{\prime })\ge {\rho }_S(0,t)$ if and only if the angle $\varphi$ determined by the sides $AB$ and $AC$ of the triangle determined by the points $A,B,C$ satisfies ${\displaystyle \frac{k^{\prime }}{n^{\prime }}}=tan\varphi \ge tan\theta ={\displaystyle \frac{k+1}{n+2}}$, exactly as claimed in Lemma 1.

Theorem 2 can be readily generalized.

Theorem 3. 

For an arbitrary positive integer r, consider r successive time epochs $(t_0,t_1]$, $(t_1,t_2]$, $\cdots ,$ $(t_{i-1},t_i]$, ⋯, $(t_{r-1},t_r]$, such that in epoch $(t_{i-1},t_i],(1\le i\le r)$, our seller has been involved in $n_i$ transactions and has fulfilled their contractual obligations in $k_i$ of them. Then, the seller’s reputation score at time $t_r$ is $({\sum }_{i=1}^r{n}_i,{\sum }_{i=1}^r{k}_i,(t_0,t_r))$, and their associated trust measure is

$${\rho }_S(0,t_r)={\displaystyle \frac{{\sum }_{i=1}^r{k}_i+1}{{\sum }_{i=1}^r{n}_i+2}}.$$

(9)

Proof. 

Assume, without loss of generality, that $t_0=0$, and let t and $t^{\prime }$ denote, respectively, $t_{r-1}$ and $t_r$. In the time interval $(0,t]$, the seller has been involved in ${\sum }_{i=1}^{r-1}{n}_i$ transactions and has fulfilled their obligations in ${\sum }_{i=1}^{r-1}{k}_i$ of them. In the time interval $(t,t^{\prime }]$, our seller has been involved in $n_r$ transactions and has fulfilled their contractual obligations in $k_r$ of them.

By definition, in the interval $(0,t^{\prime }]$, the seller’s reputation score is $({\sum }_{i=1}^r{n}_i$, ${\sum }_{i=1}^r{k}_i$, $(t_0,t_r))$. Similarly, by Theorem 2, their trust measure is

$$\begin{array}{ccc}\hfill {\rho }_S(0,t_r)& =& {\displaystyle \frac{k+k^{\prime }+1}{n+n^{\prime }+2}}\hfill \\ & =& {\displaystyle \frac{\left({\sum }_{i=1}^{r-1}{k}_i\right)+k_r+1}{\left({\sum }_{i=1}^{r-1}{n}_i\right)+n_r+2}}\hfill \\ & =& {\displaystyle \frac{{\sum }_{i=1}^r{k}_i+1}{{\sum }_{i=1}^r{n}_i+2}},\hfill \end{array}$$

and the proof of Theorem 3 is complete. □

Theorem 3 has a number of consequences:

• The updated trust measure is related to the updated reputation scores, exactly as specified in Theorem 1;
• The updated trust measure does not change if the following are true:

  –

  Associativity: the seller has fulfilled their obligations in 0 of the first ${\sum }_{i=1}^{r-1}{n}_i$ transactions and in ${\sum }_{i=1}^r{k}_i$ out of the next $n_r$ transactions, provided ${\sum }_{i=1}^r{k}_i\le n_r$.

  –

  Commutativity: for any choice of subscripts $i,j$, with $(1\le i\ne j\le r)$, the $n_j$ transactions in epoch j have occurred before or after the $n_i$ transactions in epoch i;

  –

  Interchangeability: the seller has fulfilled their obligation in $k_j$ of the $n_i$ transactions in epoch i and in $k_i$ of the transactions in epoch j, provided that $k_j\le n_i$ and $k_i\le n_j$.

6. Applications of the Laplace Trust Engine

The main goal of this section is to illustrate three applications of the trust and reputation service introduced in Section 4. Specifically, in Section 6.1 and Section 6.2, we discuss two applications to a multi-segment marketplace, where a malicious seller may establish a stellar reputation by selling cheap items or by providing some specific type of service, only to use their reputation score to defraud buyers in a different market segment.

Next, in Section 6.3, we apply the results of Section 4 in the context of sellers with time-varying performance due to, say, overcoming an initial learning curve. With this in mind, we provide a discounting scheme, wherein older reputation scores are given less weight than more recent ones. Finally, in Section 6.4, we show how to predict trust and reputation scores far in the future, based on currently available information.

6.1. Price Range-Specific Trust and Reputation

We assume that the transactions in the marketplace are partitioned, by monetary value of the goods transacted, into non-overlapping price ranges $0<R_1<R_2<\cdots <R_s$ for some positive integer s. These ranges determine s market segments $M_1,M_2,\cdots ,M_s$, where market segment $M_j$ involves all the transactions within the price range $R_j$.

In all marketplaces of which we are aware [13,14,17,18,19,20,21,22,52,53], seller reputation is global, being established irrespective of their performance in different market segments.

However, this may lead to insecurities. For example, imagine a seller who has established an enviable reputation score by selling cheap items, all in the market segment corresponding to range $R_1$. Suppose that our seller decides to become involved in a different market segment, say, corresponding to price range $R_{10}$. Should their reputation score established in $R_1$ carry over to $R_{10}$? We believe that the answer should be in the negative. One reason is that, as pointed out by [54] and other workers, dishonest sellers establish stellar reputation scores by selling cheap items and use the resulting reputation score to hit-and-run in a different market segment.

To prevent this kind of attack from being mounted, we associate with each market segment a distinct reputation score and, consequently, a distinct trust measure. Also, with each market segment, we associate a different urn as discussed in the previous sections of this work. For example, if our seller has never transacted in the market segment corresponding to the price range $R_{10}$, their reputation score in that market segment is $(0,0,t)$, and, not surprisingly, their corresponding trust measure will be ${\displaystyle \frac{0+1}{0+2}}={\displaystyle \frac{1}{2}}=50\%$, capturing the idea that nothing is known about the performance of the seller in that market segment.

Consider a generic market segment $M_i,(1\le i\le s)$, and assume that up to time t, our seller has accumulated a reputation score of $(n_i,k_i,t)$ in $R_i$. Consistent with our definition, the trust measure that our seller enjoys in $M_i$ is ${\displaystyle \frac{k_i+1}{n_i+2}}$. This trust measure is local to $M_i$ and is independent of the seller’s trust measure in other market segments.

It is worth noting that, as an additional benefit, our approach provides resistance to Sybil attacks. It is well known that malicious users involve their Sybils in augmenting their reputation scores [15,55,56,57]. However, the fact that, by assumption, Smart Contracts are responsible for providing transaction feedback (including the market segment in which the transaction took place) means that this feedback will be, per force, local to one market segment, minimizing the effect of the attack. Indeed, as a result of the Sybil attack, the malicious user’s reputation may well increase in one market segment, but their reputation in other market segments will not be affected. This provides very desirable resistance to Sybil attacks.

6.2. Service-Specific Trust and Reputation

In Section 6.1, we argued that reputation scores and, therefore, the trust measure of a seller should not be global but should, instead, be specific to individual price ranges. Specifically, we made the point that reputation scores acquired by conducting business in one market segment (by dollar amount) should not carry over to a different market segment.

In this subsection, we extend the same idea to the types of services provided. The intuition is that a service provider (i.e., seller) may behave differently when providing different services. Thus, the best indicator of how the service provider will perform in the future depends on their past performance in the context of the type of services contemplated. This motivates assessing the trustworthiness of a service provider by the type of individual service of interest.

As an illustrative example, consider a plumbing contractor who may act in the marketplace as a seller of plumbing hardware but also as a provider of plumbing services such as repairs; the installation of various equipment such as gas furnaces, electric furnaces, hot water heaters, extended maintenance contracts; etc.

Our plumber may be inclined to provide higher-quality services in areas that benefit them most (e.g., installing electric water heaters) and services of lesser quality in some other areas that are less lucrative (e.g., maintenance contracts or installing gas water heaters), even though an electric water heater may cost roughly the same as a gas water heater.

The point is that the plumber’s reputation score acquired by providing one type of service should not be relevant when evaluating their trustworthiness in different service categories where they are either less competent or simply not interested in providing high-quality services.

6.3. Discounting Old Trust Measures—Leveling the Playing Field

Up to this point, we have assumed that seller behavior is constant over time. For various reasons, sellers may change their attitude and behave differently from the way they acted in the past. To accommodate this imponderable, in this subsection, we introduce a simple mechanism that allows us to discount older trust measures, giving more credence to recent reputation scores.

For an arbitrary integer r, consider r successive time epochs $(t_0,t_1],(t_1,t_2],\cdots$, $(t_{i-1},t_i],\cdots ,(t_{r-1},t_r]$ with $t_0=0$ and such that, in epoch $(t_{i-1},t_i],(1\le i\le r)$, our seller has been involved in $n_i$ transactions and has fulfilled their contractual obligations in $k_i$ of them. Recall that, given this information, the seller’s reputation score at time $t_r$ is $({\sum }_{i=1}^r{n}_i,{\sum }_{i=1}^r{k}_i,(t_0,t_r)),$ and, by Theorem 3, their associated trust measure reads

$${\rho }_S(0,t_r)={\displaystyle \frac{{\sum }_{i=1}^r{k}_i+1}{{\sum }_{i=1}^r{n}_i+2}}.$$

(10)

In order to produce a weighted version of (10), consider weights ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_r$ such that each ${\lambda }_i,(1\le i\le r),$ is either 0 or 1. Consider further the weighted trust measure ${\overline{\rho }}_S(0,t_r)$ of S defined as

$${\overline{\rho }}_S(0,t_r)={\displaystyle \frac{{\sum }_{i=1}^r{\lambda }_i{k}_i+1}{{\sum }_{i=1}^r{\lambda }_i{n}_i+2}}.$$

(11)

Suppose that our seller was facing serious problems related to a steep learning curve and their reputation scores in the first $i,(1\le i\le r-1),$ transactions $({\sum }_{j=1}^i{k}_j,{\sum }_{j=1}^i{n}_j,t_r)$ were very poor, in the sense that

$${\displaystyle \frac{{\sum }_{j=1}^i{k}_j}{{\sum }_{j=1}^i{n}_j}}<{\displaystyle \frac{{\sum }_{j=1}^r{k}_k+1}{{\sum }_{j=1}^r{n}_i+2}}$$

(12)

To accommodate the seller and to level the playing field, in the weighted version of their trust measure, we take the following weights:

$${\lambda }_1={\lambda }_2=\cdots ={\lambda }_i=0$$

and

$${\lambda }_{1+1}={\lambda }_{i+2}=\cdots ={\lambda }_r=1.$$

With these weights, the seller’s weighted trust measure at time $t_r$ is

$${\overline{\rho }}_S(0,t_r)={\displaystyle \frac{{\sum }_{j=i+1}^r{k}_j+1}{{\sum }_{j=i+1i}^r{n}_j+2}}.$$

Notice that by taking $a={\sum }_{j=1}^i{k}_j$, $b={\sum }_{j=1}^i{n}_j$, $a^{\prime }={\sum }_{j=i+1}^r{k}_j+1$, and $b^{\prime }={\sum }_{j=i+1}^r{n}_j+2$, Corollary A1 in the Appendix A guarantees that

$${\rho }_S(0,t_r)={\displaystyle \frac{{\sum }_{i=1}^r{k}_i+1}{{\sum }_{i=1}^r{n}_i+2}}<{\displaystyle \frac{{\sum }_{j=i+1}^r{k}_j+1}{{\sum }_{j=i+1}^r{n}_j+2}}={\overline{\rho }}_S(0,t_r).$$

In other words, as a result of discounting the first i transactions, the seller’s weighted trust measure has increased, focusing attention on their more recent performance.

6.4. Predicting Trust Measure and Reputation Scores over the Long Term

It is of great theoretical interest and practical relevance to be able to extrapolate the performance of a seller and predict their performance far in the future. With this in mind, consider a seller who has completed n transactions and has fulfilled their obligations in k of them. Let A be the corresponding event. We wish to predict the expected reputation score of the seller by the time their total number of transactions has reached $n+m$ for some $m\ge 0$.

Let R be the random variable that keeps track of the number of black balls among the additional m balls extracted, and assume that the event $\{R=r\}$ has occurred.

Using the expression of $H_i$ from (3), the conditional probability of the event $\{R=r\}$ given A is

$$\begin{array}{ccc}\hfill Pr[R=r|A]& =& \sum _{i=0}^{N}Pr[R=r|H_i]Pr\left[H_i\right]\hfill \\ & =& {\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}.\hfill \end{array}$$

(13)

Actually, this follows directly from (A7) in Appendix A.2 of the Appendix A by taking $r=k^{\prime }$ and $m=n^{\prime }$.

We are interested in evaluating the conditional expectation, $E\left[R\right|A]$, of R given A. For this purpose, using the Law of Total Expectation, we write

$$\begin{array}{ccc}\hfill E\left[R\right|A]& =& \sum _{r=0}^{m}rPr[R=r|A]\hfill \\ \hfill & =& \sum _{r=0}^{m}r·{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}[\mathrm{By} (13\left)\right]\hfill \\ \hfill & =& \sum _{r=0}^m\left[(k+r+1)-(k+1)\right]·{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ \hfill & =& \sum _{r=0}^m(k+r+1){\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ & -& \sum _{r=0}^m(k+1){\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ \hfill & =& \sum _{r=0}^m(k+r+1){\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& -& (k+1)\sum _{r=0}^m{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}.\hfill \end{array}$$

(15)

The two sums, (14) and (15), will be evaluated separately. We begin by evaluating the following sum:

$$\begin{array}{ccc}\hfill \sum _{r=0}^m{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}& =& {\displaystyle \frac{{\sum }_{r=0}^m\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ & =& {\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}=1[\mathrm{by} (\mathrm{A}3) \mathrm{in} \mathrm{Appendix}\mathrm{A}.1].\hfill \end{array}$$

This implies that the second sum, (15), evaluates to $k+1$.

Next, to evaluate the first sum, (14), we notice that

$$\begin{array}{ccc}\hfill (k+r+1)\left({\displaystyle \genfrac{}{}{0pt}{}{k+r}{k}}\right)& =& {\displaystyle \frac{k+1}{k+1}}(k+r+1){\displaystyle \frac{(k+r)!}{k!r!}}\hfill \\ & =& (k+1){\displaystyle \frac{(k+r+1)!}{(k+1)!r!}}\hfill \\ & =& (k+1)\left({\displaystyle \genfrac{}{}{0pt}{}{k+r+1}{k+1}}\right).\hfill \end{array}$$

(16)

Using (16), the first sum, (14), can be written as

$$\begin{array}{ccc}& & \sum _{r=0}^m(k+r+1){\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ & =& {\displaystyle \frac{k+1}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\sum _{r=0}^m\left({\displaystyle \genfrac{}{}{0pt}{}{k+r+1}{k+1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-k+m-r}{n-k}}\right)\hfill \\ & =& {\displaystyle \frac{k+1}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\left({\displaystyle \genfrac{}{}{0pt}{}{n+m+2}{n+2}}\right)\hfill \\ & =& (k+1){\displaystyle \frac{n+m+2}{n+2}}.\hfill \end{array}$$

(17)

By combining the intermediate results developed above, the expression of $E\left[R\right|A]$ becomes

$$\begin{array}{ccc}\hfill E\left[R\right|A]& =& \sum _{r=0}^m(k+r+1){\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ & -& (k+1)\sum _{r=0}^m{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{k+r}{k}\right)\left(\genfrac{}{}{0pt}{}{n-k+m-r}{n-k}\right)}{\left(\genfrac{}{}{0pt}{}{n+m+1}{n+1}\right)}}\hfill \\ & =& (k+1){\displaystyle \frac{n+m+2}{n+2}}-(k+1)\hfill \\ & =& (k+1)\left[{\displaystyle \frac{n+m+2}{n+2}}-1\right]\hfill \\ & =& m·{\displaystyle \frac{k+1}{n+2}}.\hfill \end{array}$$

(18)

The intuition behind this simple result is as follows: since nothing is known about the future, in each of the m hypothetical extractions from the urn, the success probability is the same, namely, ${\displaystyle \frac{k+1}{n+2}}$. Thus, by a well-known result, the expectation of the number of successes must be $m·{\displaystyle \frac{k+1}{n+2}}$.

Let us translate (18) into the language of trust and reputation. Consider a seller with current reputation score $(n,k,t)$. We are interested in predicting the reputation score of the seller by time T when their total number of transactions reaches $n+m$. By (18), it follows that out of a total of $n+m$ transactions, the predicted number of transactions in which our seller fulfills their obligations is $k+m{\displaystyle \frac{k+1}{n+2}}$.

To put it differently, the expected reputation score of the seller by time T, when they were involved in $n+m$ transactions, is $(n+m,k+m{\displaystyle \frac{k+1}{n+2}},T)$. Interestingly, as the following derivation shows, the seller’s predicted trust measure at time T is still ${\displaystyle \frac{k+1}{n+2}}$.

$$\begin{array}{ccc}\hfill {\rho }_S(0,T)& =& {\displaystyle \frac{k+m\frac{k+1}{n+2}+1}{n+m+2}}\hfill \\ & =& {\displaystyle \frac{k(n+2)+m(k+1)+n+2}{(n+2)(n+m+2)}}\hfill \\ & =& {\displaystyle \frac{k(n+m+2)+n+m+2}{(n+2)(n+m+2)}}\hfill \\ & =& {\displaystyle \frac{(k+1)(n+m+2)}{(n+2)(n+m+2)}}\hfill \\ & =& {\displaystyle \frac{k+1}{n+2}}.\hfill \end{array}$$

(19)

7. Simulation Results

The goal of this section is to present the results of our empirical evaluation of the trust and reputation service discussed analytically in Section 4, Section 5 and Section 6.

7.1. Simulation Model

For the purpose of empirical evaluation, we have simulated a blockchain-based decentralized marketplace with SC support, a feature of Society 5.0. The actors in the marketplace are the buyers and the sellers. We assume that an SC is associated with each transaction and, for simplicity, that each transaction involves one buyer and one seller. The SC in charge of the transaction is responsible for providing feedback at the end of the transaction, replacing notoriously unreliable buyer feedback with a more objective assessment of how well the buyer and the seller have fulfilled their contractual obligations towards each other.

The marketplace simulation model consists of a seller who is involved in transactions with multiple buyers. Each transaction can either be successful (indicating that the seller has fulfilled their contractual obligations) or fail otherwise. In the simulation, we tracked the number of successful transactions and the total transactions. The probability of a successful transaction was determined based on the goals of the experiment, as we explain in the following subsections. For each goal, we repeated the experiment a large number of times, as needed.

The remainder of this section is structured as follows: In Section 7.2, we turn our attention to a multi-segment marketplace (by dollar value of the goods transacted) and illustrate, by simulation, the reputation scores and trust measures of a generic seller in these market segments. Next, in Section 7.3, we present simulation results of seller performance in a marketplace segmented by service type, not price range. This is followed, in Section 7.4, by a simulation of the effect of a discounting strategy designed specifically to assist a seller facing a steep learning curve. Finally, in Section 7.5, we predict, by simulation, the future reputation scores and trust measure of a generic seller, using incomplete information.

7.2. Trust Measures in a Price Range-Based Multi-Segment Marketplace

The purpose of this subsection is to illustrate, by simulation, the trust measure of a seller in different market segments defined by the dollar value of the goods transacted. For the simulation, we assume that the transactions in the marketplace are divided into four non-overlapping price ranges $R_1,R_2,R_3$, and $R_4$, based on the monetary value of the items transacted. These four price ranges determine four disjoint market segments—$M_1,M_2,M_3,M_4$, where market segment $M_i$ includes all transactions falling within the price range $R_i$.

We have assumed that the seller has accumulated, over a time window of 250 units, the following performance in each of the four market segments:

• In market segment $M_1$, the seller had 85 successful transactions out of 100 total transactions;
• In market segment $M_2$, the seller had three successful transactions out of three total transactions;
• In market segment $M_3$, the seller had one successful transaction out of one total transaction;
• In market segment $M_4$, the seller had zero transactions.

Figure 3 illustrates the seller’s trust measure in each of the four market segments using (1) from Theorem 1.

Not surprisingly, even though the trust measure of the seller in market segment $M_1$ is fairly high, 86/102, their trust measure in market segment $M_3$ is a meager 2/3, while in market segment $M_4$ the seller’s performance is only 1/2, reflecting the fact that the seller has had no experience in the market segment. As a result, the seller cannot misrepresent their performance.

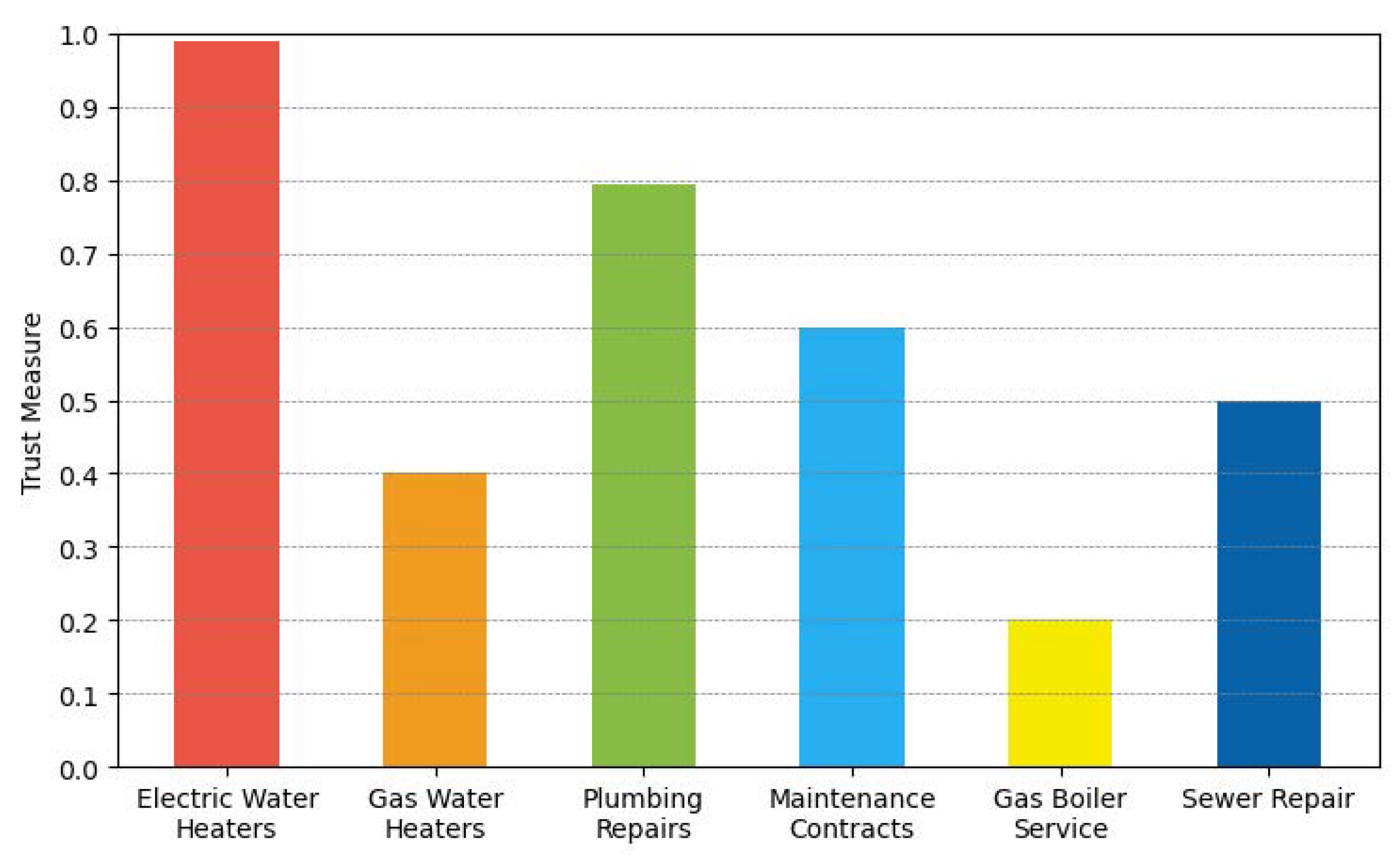
7.3. Trust Measure in a Service Type-Based Multi-Segment Marketplace

In Section 6.1, we argued that reputation scores and the trust measure of a seller should not be global but should, instead, be specific to individual price ranges. Specifically, we made the point that reputation scores acquired by conducting business in one market segment (by dollar amount) should not carry over to a different market segment. In Section 6.2, we extended the same idea to various types of services provided.

We have simulated the evolution of reputation scores and trust measures of a plumbing contractor who is offering the following services:

• General plumbing repairs;
• Electric heater installation;
• Gas heater installation;
• Long-term maintenance contracts;
• Sewer repairs;
• Gas boiler service.

Some of these services are more lucrative than others, and the plumber is more competent dealing with electric than with gas equipment. Thus, our plumber may be inclined to provide higher-quality services in areas that benefit them most (e.g., installing electric water heaters and general plumbing repairs) and those of lesser quality in some other areas that are less lucrative, e.g., installing gas water heaters or sewer repairs, even though an electric water heater may cost roughly the same as a gas water heater.

The point is that the plumber’s reputation score acquired by providing one type of service should not be relevant when evaluating their trustworthiness in different service categories where they are either less competent or simply not interested in providing high-quality services. Figure 4 illustrates the simulated plumber’s trust measure in each of the service categories above.

7.4. Illustrating the Effect of Discounting Strategies

We have simulated the reputation scores and associated trust measures of a generic seller in ten time epochs. Initially, the seller’s reputation scores are low, perhaps because of their lack of experience. We have simulated the effect of the discounting strategy presented in Section 6. The results of the simulation are summarized in Figure 5. In the figure, we plot, side by side, the seller’s aggregate trust measure without discounting as well as their weighted trust measure. In Figure 5a, which illustrates the cumulative trust measure, and Figure 5b, which illustrates the trust measure for each epoch, the effect of favoring recent performance over more remote performance becomes obvious. As it turns out, selecting the weights that focus attention on the performance of the seller in the last week presents their trust measure in the best light, as it is, conceivably, the most accurate reflection of their improvement.

7.5. Predicting Trust Measure and Reputation Scores over the Long Term

In this subsection, we present the results of simulating the convergence of the predicted and simulated long-term trust measure of a seller. For this purpose, we simulated the performance of a seller in their first 100 transactions. Our goal was to see how close the prediction of the expected number of their successful transactions was among the next 100 transactions. The results of the simulation are plotted in Figure 6. The simulation was repeated 150 times. From the figure, it is clear that the seller’s simulated long-term performance, in terms of their reputation scores (and associated trust measure), converges to the theoretically predicted performance.

8. Concluding Remarks and Open Problems

This paper was motivated by the multi-fold challenges inherent in implementing the vision of trusted and secure services in Society 5.0. The first main contribution of this paper was a novel trust and reputation service with a view to reduce the uncertainty associated with buyer feedback in decentralized marketplaces. Our trust and reputation service was inspired by a classic result in probability theory that can be traced back to Laplace.

The third main contribution was to offer three applications of the proposed trust and reputation service. Specifically, in Section 6.1 and Section 6.2, we discussed two applications to a multi-segment marketplace, where a malicious seller may establish a stellar reputation by selling cheap items or providing some specific service, only to use their excellent reputation score to defraud buyers in a different market segment. As we noted, our service can provide Sybil resistance, a much-desired attribute [56,57]. Next, in Section 6.3, we applied the results of Section 7.4 with an eye to assist a seller that tries to cope with an initial learning curve or other similar impediments. We provided a discounting scheme wherein less recent reputation scores were given less weight than more recent ones. In Section 6.4, we showed how to use our trust and reputation service to predict future reputation scores based on fragmentary information.

Last, but certainly not least, the reputation and trust service developed in this paper is expected to have applications to several domains, including banking, inventory management, vehicular networks [41], peer-to-peer networking [40], vehicular clouds and vehicular crowd sourcing in smart cities [44,58], as well as parallel and distributed processing [59]. Exploring these promising new application domains is an exciting area for future work.