Robust Peak Detection Techniques for Harmonic FMCW Radar Systems: Algorithmic Comparison and FPGA Feasibility Under Phase Noise
Abstract
1. Introduction
1.1. Challenges in Peak Detection
1.2. Review of State-of-the-Art Detection Methods
1.2.1. FFT-Based Thresholding
1.2.2. Constant False Alarm Rate (CFAR) Detectors
1.2.3. Super-Resolution and Subspace Methods
1.2.4. Time-Frequency and Denoising-Based Methods
1.2.5. Learning-Based Detection
1.2.6. Impulse Response and Waveform Design for Enhanced Peak Detection
1.3. Contribution of This Work
- A comparative study of five peak detection methods for an FMCW radar: FFT thresholding, CA-CFAR, MPM (simplified), SVD-based detection, and the proposed LTSP.
- A derivation of the mathematical models for each technique, highlighting their assumptions and operational trade-offs.
- A comprehensive Monte Carlo-based evaluation framework assessing detection performance across a wide SNR range.
- Experimental evidence that LTSP offers a favorable trade-off between computational complexity and detection robustness, particularly in noisy environments.
2. Detection Algorithms
2.1. Signal Model
2.2. FFT-Based Detection
2.3. Cell-Averaging CFAR (CA-CFAR)
2.4. Matrix Pencil Method (MPM)—Simplified
2.5. SVD-Based Subspace Detection
2.6. Learned Thresholded Subspace Projection (LTSP)
2.6.1. Motivation and Overview
2.6.2. Methodology
- (1)
- Hankel Matrix Construction:
- (2)
- Subspace Projection via Rank-1 SVD:
- (3)
- Signal Reconstruction and Spectral Analysis:
2.6.3. Adaptive Thresholding and Robustness
2.6.4. Computational Considerations
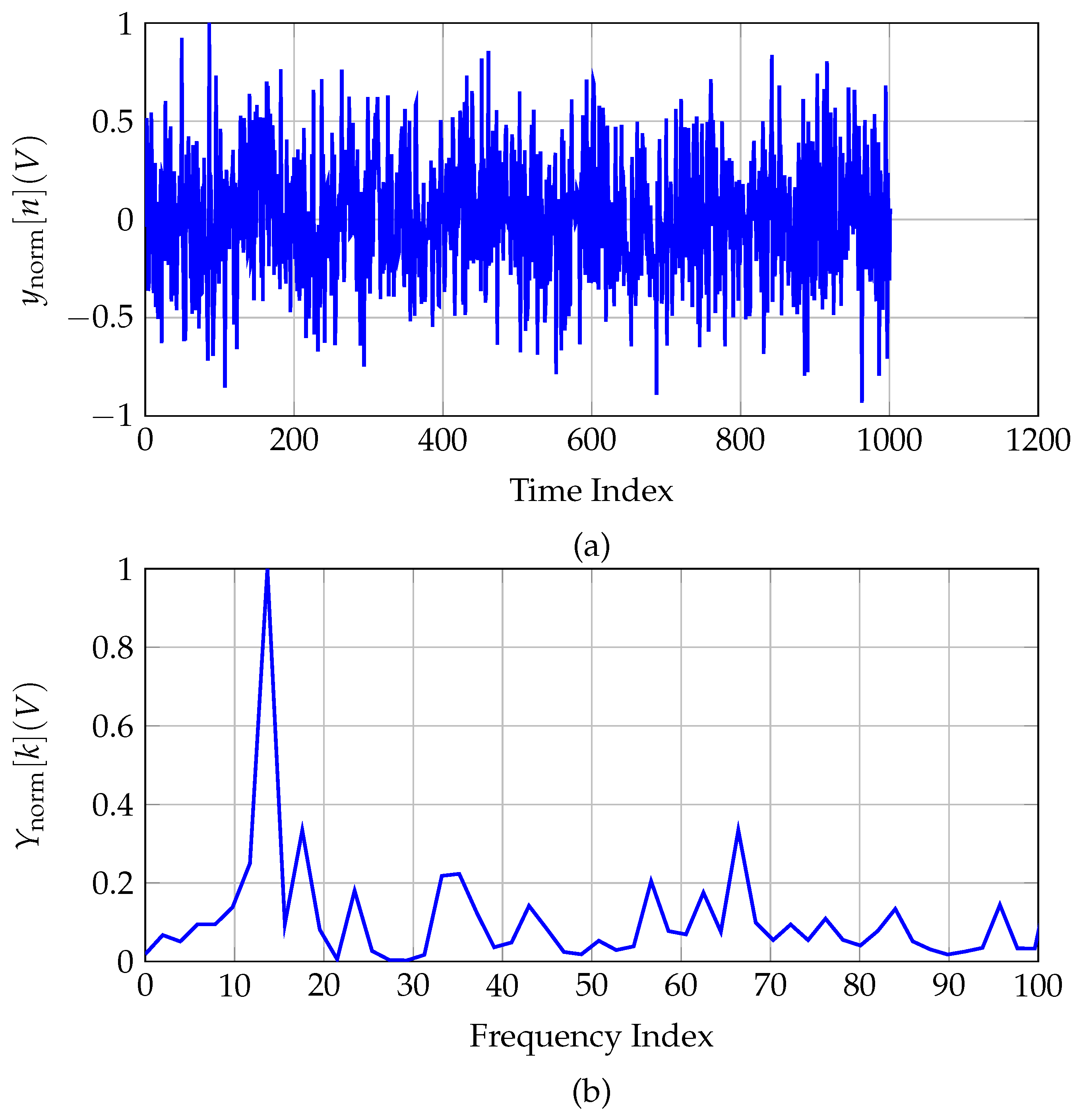
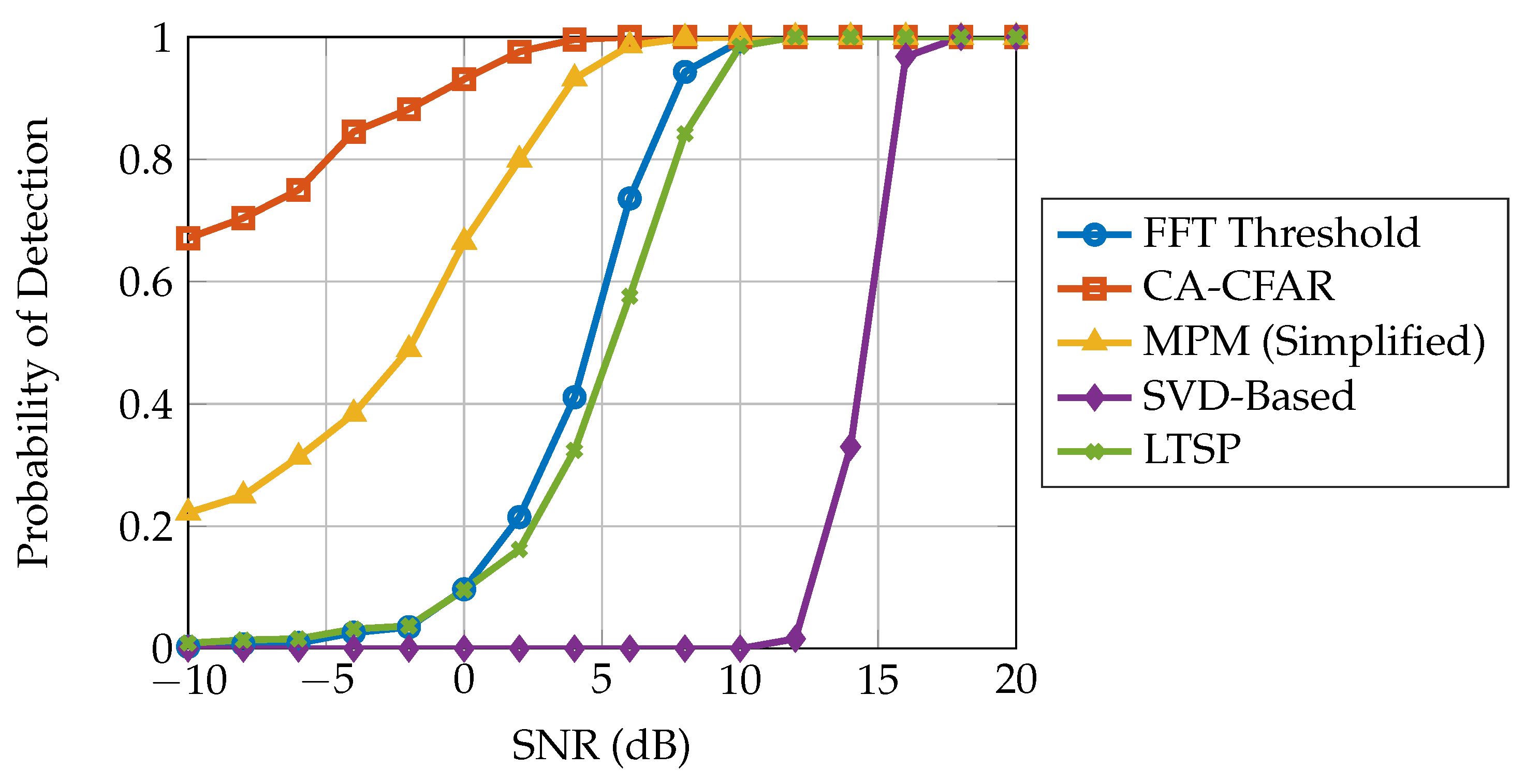
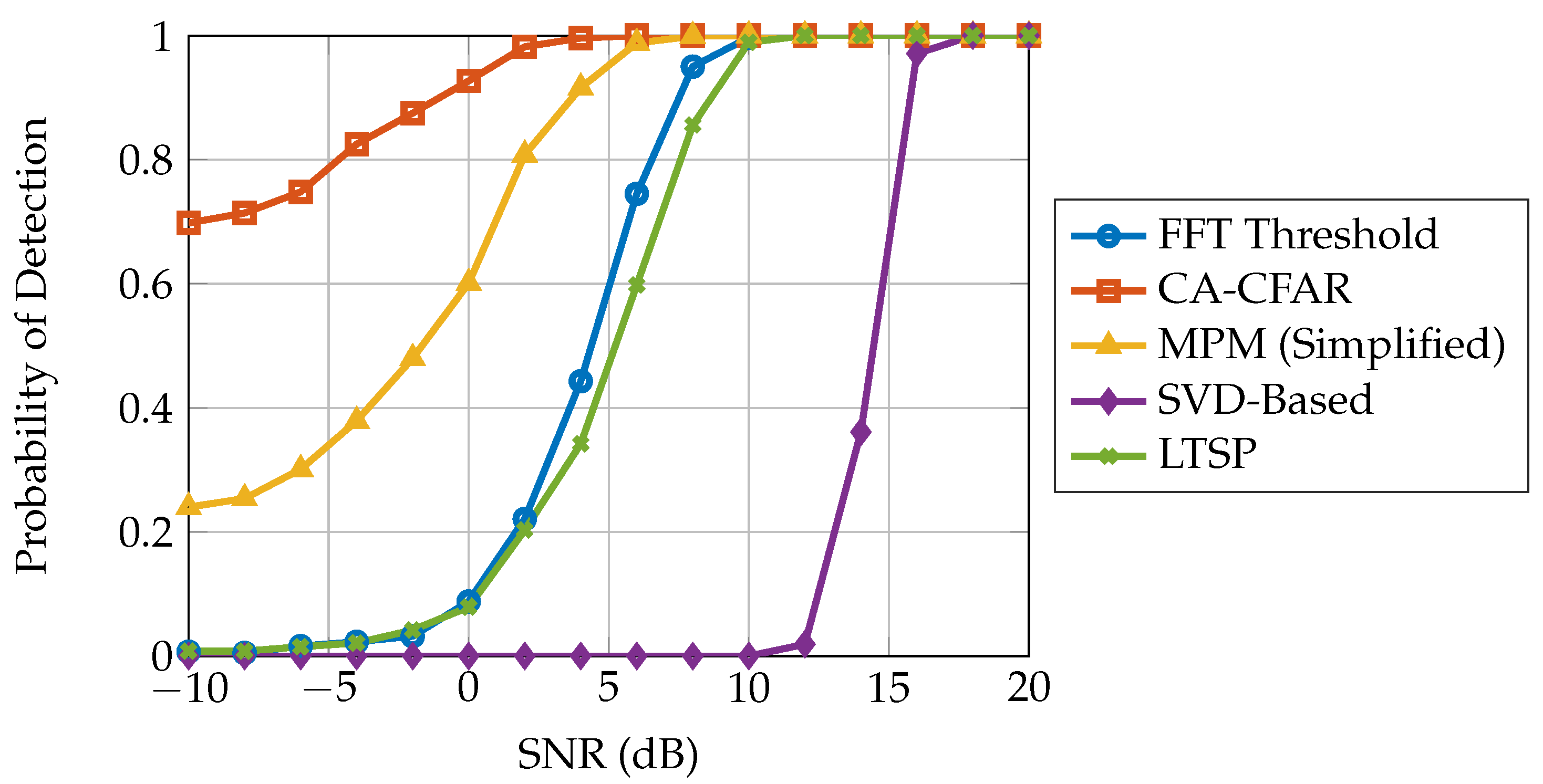
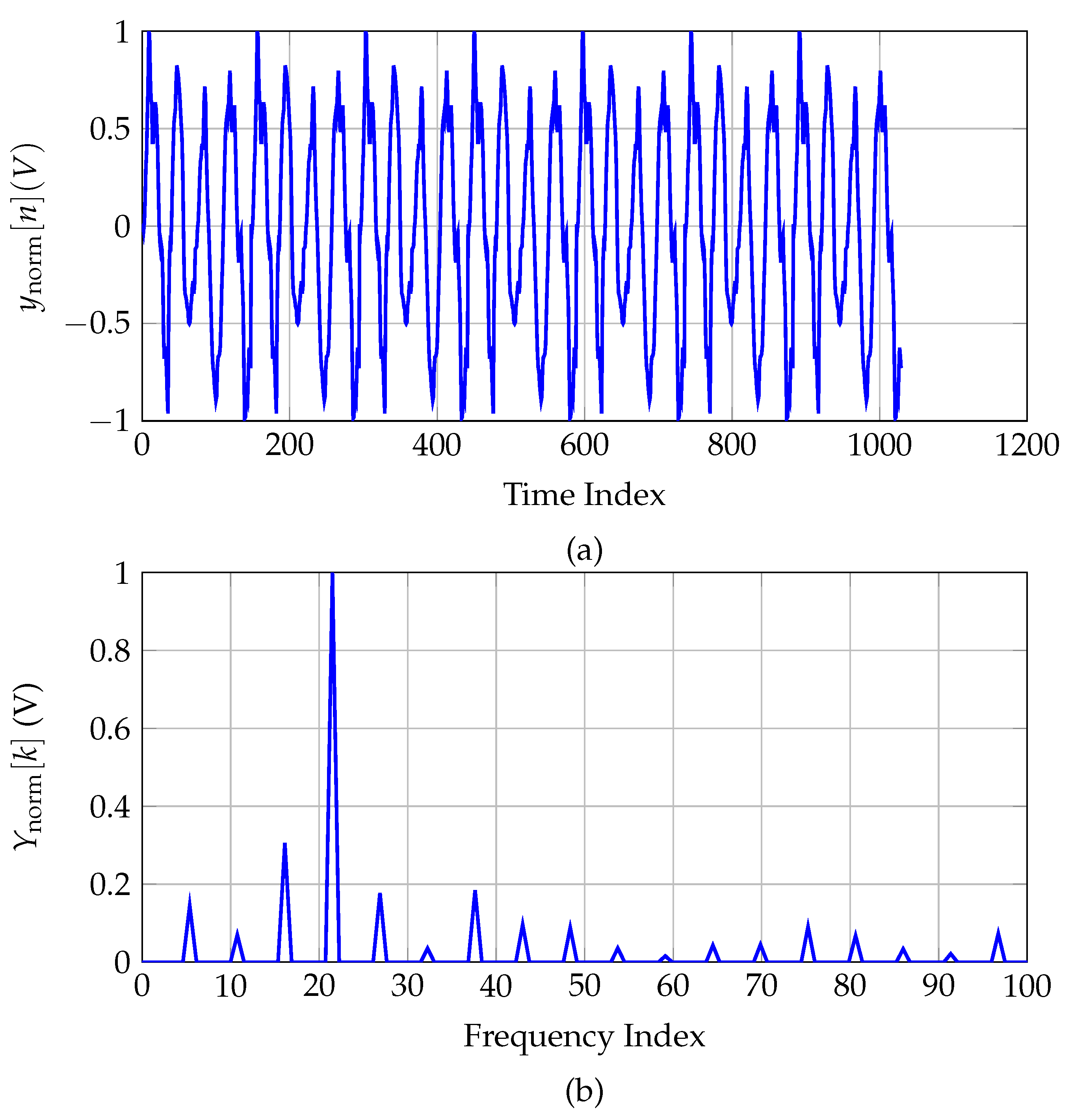
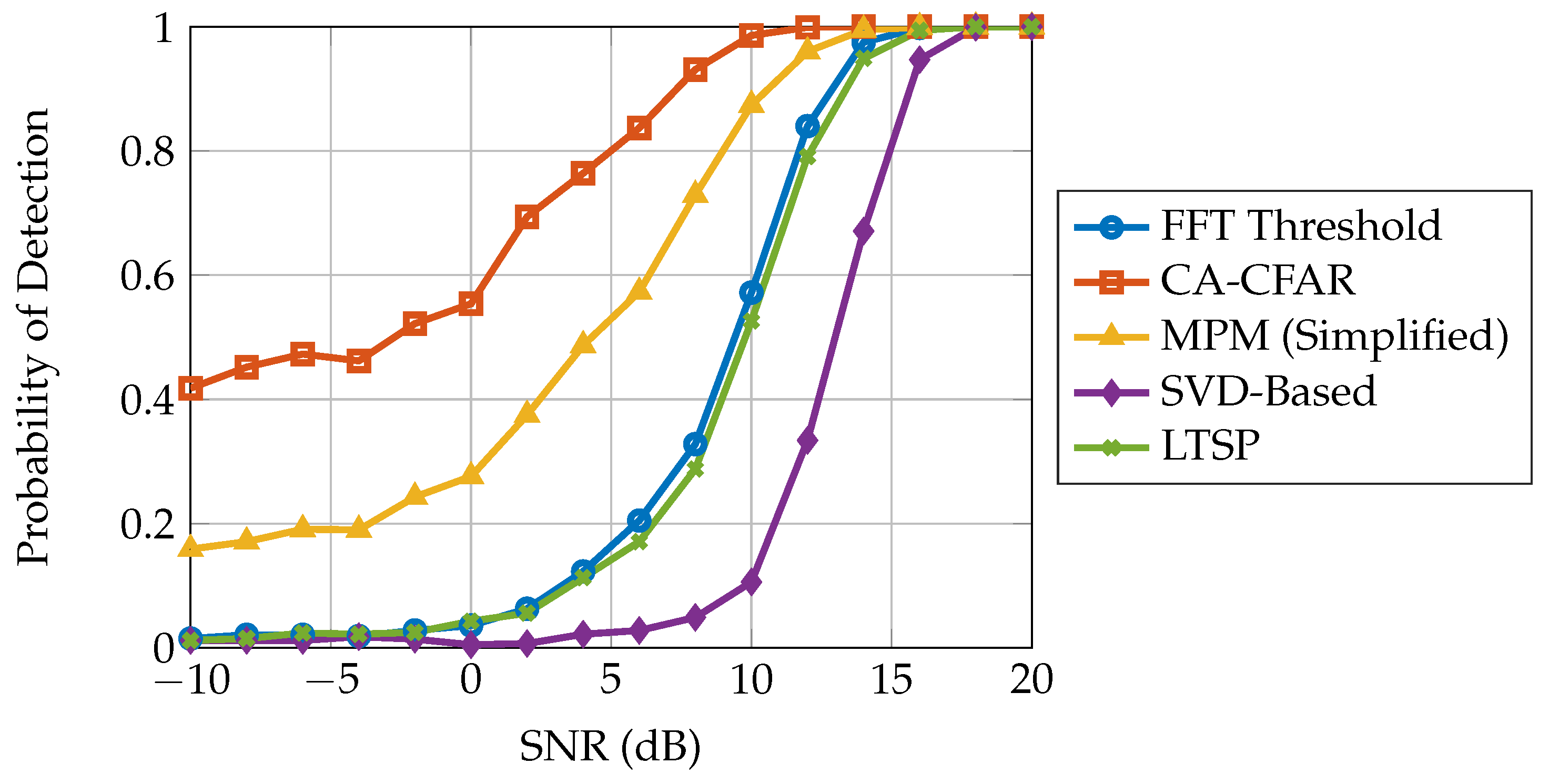
3. Simulation Results
3.1. Simulation Environment
3.2. Results
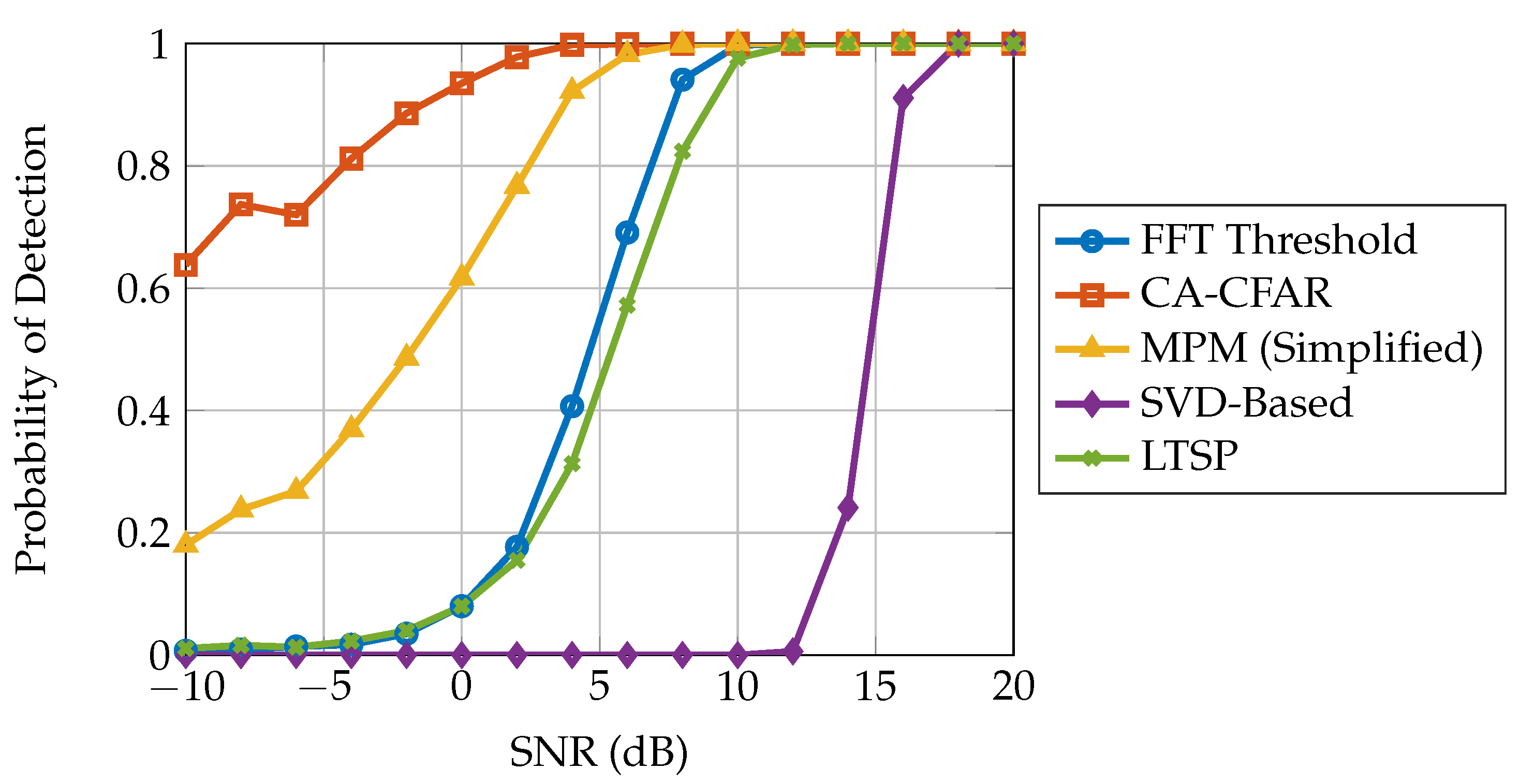
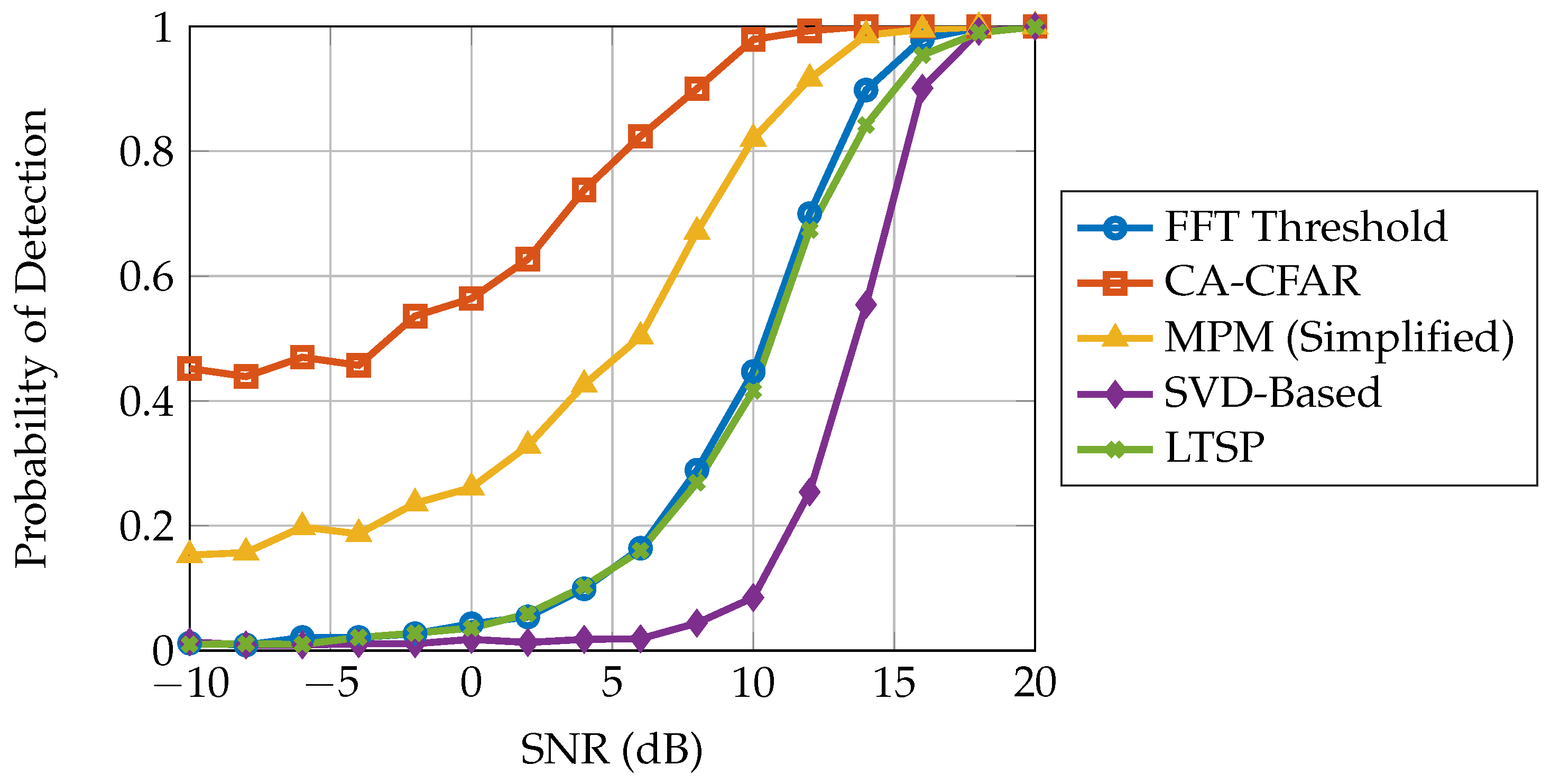
4. Measurement Setup and Results
4.1. Experimental Configuration
4.2. Measurement Procedure
4.3. Measurement Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radar: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Hasch, J.; Topak, E.; Schnabel, R.; Zwick, T.; Weigel, R.; Waldschmidt, C. Millimeter-wave technology for automotive radar sensors in the 77 GHz frequency band. IEEE Trans. Microw. Theory Tech. 2012, 60, 845–860. [Google Scholar] [CrossRef]
- Skolnik, M.I. Radar Handbook; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Rohling, H. Radar CFAR thresholding in clutter and multiple target situations. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 608–621. [Google Scholar]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T.K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 814–824. [Google Scholar] [CrossRef]
- Stanković, L. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Zoubir, A.M.; Koivunen, V.; Chakhchoukh, Y.; Muma, M. Robust Statistics for Signal Processing; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Zhao, Y.; Yarovoy, A.; Fioranelli, F. Angle-Insensitive Human Motion and Posture Recognition Based on 4D Imaging Radar and Deep Learning Classifiers. IEEE Sens. J. 2022, 22, 12173–12182. [Google Scholar] [CrossRef]
- Diskin, T.; Beer, Y.; Okun, U.; Wiesel, A. CFARnet: Deep learning for target detection with constant false alarm rate. Signal Process. 2024, 223, 109543. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, L.; Wang, J.; Chen, F. Simultaneous range ambiguity mitigation and sidelobe reduction using orthogonal non-linear frequency modulated (ONLFM) signals for satellite SAR imaging. Remote Sens. Lett. 2018, 9, 829–838. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, H.; Wang, C.; Wang, Y. A novel method of mitigating the mutual interference between multiple LFMCW radars for automotive applications. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2178–2181. [Google Scholar]
- Christian, O.; Mate, T.; Paul, M.; Franz, P. End-to-End Training of Neural Networks for Automotive Radar Interference Mitigation. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; Volume 24, pp. 1–6. [Google Scholar]
- Guo, H.; Wu, H.; Wang, Z.; He, Z.; Cheng, Z. Adaptive Target Detection in Nonhomogeneous Clutter and Multipath Environment. IEEE Trans. Aerosp. Electron. Syst. 2025, 1–15. [Google Scholar] [CrossRef]
- Sim, Y.; Heo, J.; Jung, Y.; Lee, S.; Jung, Y. FPGA Implementation of Efficient CFAR Algorithm for Radar Systems. Sensors 2023, 23, 954. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, Y.; He, D.; Guan, K.; Liao, J.; Zhong, Z. A Low-Complexity Noise Reduction Algorithm for Enhanced Target Detection in FMCW Radar. IEEE Trans. Veh. Technol. 2023, 72, 15227–15236. [Google Scholar] [CrossRef]
- Zhao, W.; Xing, S.; Ni, F.; Tian, Y.; Liu, Q. FMCW radar-based high-precision range estimation with generalized eigenvalue decomposition algorithm. Measurement 2025, 255, 117957. [Google Scholar] [CrossRef]
- Venon, A.; Dupuis, Y.; Vasseur, P.; Merriaux, P. Millimeter Wave FMCW RADARs for Perception, Recognition and Localization in Automotive Applications: A Survey. IEEE Trans. Intell. Veh. 2022, 7, 533–555. [Google Scholar] [CrossRef]
- Hao, Z.; Yan, H.; Dang, X.; Ma, Z.; Jin, P.; Ke, W. Millimeter-Wave Radar Localization Using Indoor Multipath Effect. Sensors 2022, 22, 5671. [Google Scholar] [CrossRef] [PubMed]
- Arsalan, M.; Santra, A.; Will, C. Improved Contactless Heartbeat Estimation in FMCW Radar via Kalman Filter Tracking. IEEE Sens. Lett. 2020, 4, 7001304. [Google Scholar] [CrossRef]
- Jiang, M.; Guo, S.; Luo, H.; Yao, Y.; Cui, G. A Robust Target Tracking Method for Crowded Indoor Environments Using mmWave Radar. Remote Sens. 2023, 15, 2425. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef]
- Bai, X.; Wang, G.; Liu, S.; Zhou, F. High-Resolution Radar Imaging in Low SNR Environments Based on Expectation Propagation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1275–1284. [Google Scholar] [CrossRef]
- Mohan, A.; Meena, H.K.; Wajid, M.; Srivastava, A. FPGA-Based Real-Time Multi-Class Vehicle Classification Using mmWave Radar. IEEE Embed. Syst. Lett. 2025, 1–4. [Google Scholar] [CrossRef]
- Giuffrida, L.; Masera, G.; Martina, M. A Survey of Automotive Radar and Lidar Signal Processing and Architectures. Chips 2023, 2, 243–261. [Google Scholar] [CrossRef]
- Almorin, H.; Le Gal, B.; Jego, C.; Kissel, V. Model Based Design of FMCW Radar Processing Systems on FPGA Platforms. In Proceedings of the 26th Euromicro Conference on Digital System Design (DSD), Durres, Albania, 6–8 September 2023; pp. 24–29. [Google Scholar] [CrossRef]
- Mishra, A.; Li, C. A Review: Recent Progress in the Design and Development of Nonlinear Radars. Remote Sens. 2021, 13, 4982. [Google Scholar] [CrossRef]
- Khaliel, M.; Batra, A.; Fawky, A.; Kaiser, T. Low-Profile Harmonic Transponder for IoT Applications. Electronics 2021, 10, 2053. [Google Scholar] [CrossRef]
- Tschapek, P.; Körner, G.; Carlowitz, C.; Vossiek, M. Detailed Analysis and Modeling of Phase Noise and Systematic Phase Distortions in FMCW Radar Systems. IEEE J. Microwaves 2022, 2, 648–659. [Google Scholar] [CrossRef]
- Pavlov, O.I.; Guseva, O.; Yashchyshyn, Y.; Narytnyk, T.; Saiko, V.; Avdeyenko, G.L. Mathematical Modeling of FMCW Radar: Sounding Signal Simulation. Radioelectron. Commun. Syst. 2023, 66, 648–657. [Google Scholar] [CrossRef]
- Tschapek, P.; Körner, G.; Hofmann, A.; Carlowitz, C.; Vossiek, M. Phase Noise Spectral Density Measurement of Broadband Frequency-Modulated Radar Signals. IEEE Trans. Microw. Theory Tech. 2022, 70, 2370–2379. [Google Scholar] [CrossRef]
- Dao, X.; Gao, M.; Ke, Z.; Zhou, Y. Efficient estimation of phase noise in FMCW system containing leakage signal. ISA Trans. 2020, 102, 221–229. [Google Scholar] [CrossRef] [PubMed]
- El-Awamry, A.; Zheng, F.; Kaiser, T.; Khaliel, M. Harmonic FMCW Radar System: Passive Tag Detection and Precise Ranging Estimation. Sensors 2024, 24, 2541. [Google Scholar] [CrossRef] [PubMed]
- El-Awamry, A.; Zheng, F.; Kaiser, T.; Khaliel, M. Impact of Phase Noise on Range Estimation Accuracy in Harmonic FMCW Radar Systems. IEEE Access 2025, 13, 42669–42688. [Google Scholar] [CrossRef]








| Reference | Detection Technique | Phase Noise Handling | Hardware Consideration | Validation |
|---|---|---|---|---|
| [13] | Deep CNN-based peak detection | Requires training dataset | Not addressed | Simulated only |
| [14] | Adaptive CFAR | Moderate resilience | Not addressed | Simulated |
| [22] | Subspace detection (e.g., MUSIC, MPM) | Limited to ideal noise | No | Simulation |
| [16] | Fast FFT + local peak estimation | Poor at low SNR | FPGA-targeted | Hardware tested |
| [29] | Phase noise modeling in FMCW | Yes (analytical) | No | Model-based |
| This Work | LTSP + CA-CFAR + SVD + MPM | High resilience under phase noise | FPGA (BRAM, LUT, DSP estimated) | Simulation + measurement |
| Criterion | FFT Thresholding | CA-CFAR | MPM (Simplified) | SVD-Based Detection | LTSP (Proposed) |
|---|---|---|---|---|---|
| Detection Principle | Max magnitude in FFT spectrum | Adaptive thresholding based on local noise estimate | Local peak detection with dynamic threshold | Ratio of dominant to median singular values from Hankel SVD | Reconstruct signal from rank-1 SVD mode, then detect FFT peak |
| Processing Flow | FFT → argmax | FFT → sliding window noise estimation → threshold test | FFT → find prominent local peaks | Hankel matrix → full SVD → energy ratio test | Hankel matrix → rank-1 SVD → diagonal averaging → FFT → peak detection |
| Phase Noise Resilience | Low (sensitive to spectral distortion) | High (robust against clutter and phase noise) | Moderate (better than FFT due to local peak constraint) | Poor under phase noise and SNR mismatch | Moderate to high (robust in mid-SNR and phase noise environments) |
| SNR Range of Effectiveness | High SNR only | Wide range (especially low to mid SNR) | Mid SNR | High SNR only | Mid SNR (5–15 dB) with moderate phase noise |
| Computational Complexity | (rank-1) | ||||
| Hardware Feasibility | Very high (FFT IP cores available) | High (simple arithmetic operations) | High (simple peak and threshold logic) | Low (full SVD is computationally intensive) | Moderate (rank-1 SVD with FFT, suitable for HLS or co-design) |
| Technique | Complexity | DSP Usage | BRAM | LUT/FF Usage |
|---|---|---|---|---|
| FFT Threshold | Medium * | Low–Medium | Moderate | |
| CA-CFAR | Low | Low | Low–Medium | |
| MPM (Simplified) | Low | Low | Moderate | |
| SVD-Based | High | High | Very High | |
| LTSP (SVD + FFT) | High | High | Very High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Awamry, A.; Zheng, F.; Kaiser, T.; Khaliel, M. Robust Peak Detection Techniques for Harmonic FMCW Radar Systems: Algorithmic Comparison and FPGA Feasibility Under Phase Noise. Signals 2025, 6, 36. https://doi.org/10.3390/signals6030036
El-Awamry A, Zheng F, Kaiser T, Khaliel M. Robust Peak Detection Techniques for Harmonic FMCW Radar Systems: Algorithmic Comparison and FPGA Feasibility Under Phase Noise. Signals. 2025; 6(3):36. https://doi.org/10.3390/signals6030036
Chicago/Turabian StyleEl-Awamry, Ahmed, Feng Zheng, Thomas Kaiser, and Maher Khaliel. 2025. "Robust Peak Detection Techniques for Harmonic FMCW Radar Systems: Algorithmic Comparison and FPGA Feasibility Under Phase Noise" Signals 6, no. 3: 36. https://doi.org/10.3390/signals6030036
APA StyleEl-Awamry, A., Zheng, F., Kaiser, T., & Khaliel, M. (2025). Robust Peak Detection Techniques for Harmonic FMCW Radar Systems: Algorithmic Comparison and FPGA Feasibility Under Phase Noise. Signals, 6(3), 36. https://doi.org/10.3390/signals6030036







