EEG-TCNTransformer: A Temporal Convolutional Transformer for Motor Imagery Brain–Computer Interfaces
Abstract
1. Introduction
2. Background
- First sub-project: EEG-TCNet and EEG-Conformer are trained and validated with different hyperparameters (i.e., filters, kernel sizes).
- Second sub-project: EEG signals are preprocessed with a bandpass filter, then input in training and testing EEG-TCNet and EEG-Conformer.
3. Methods
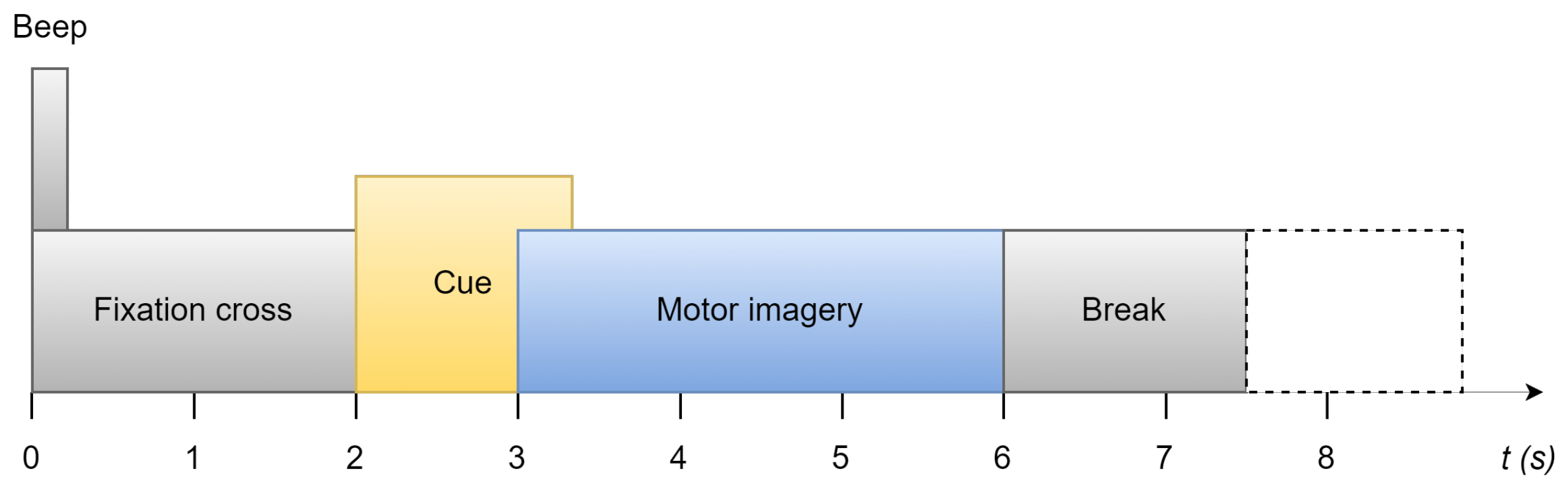
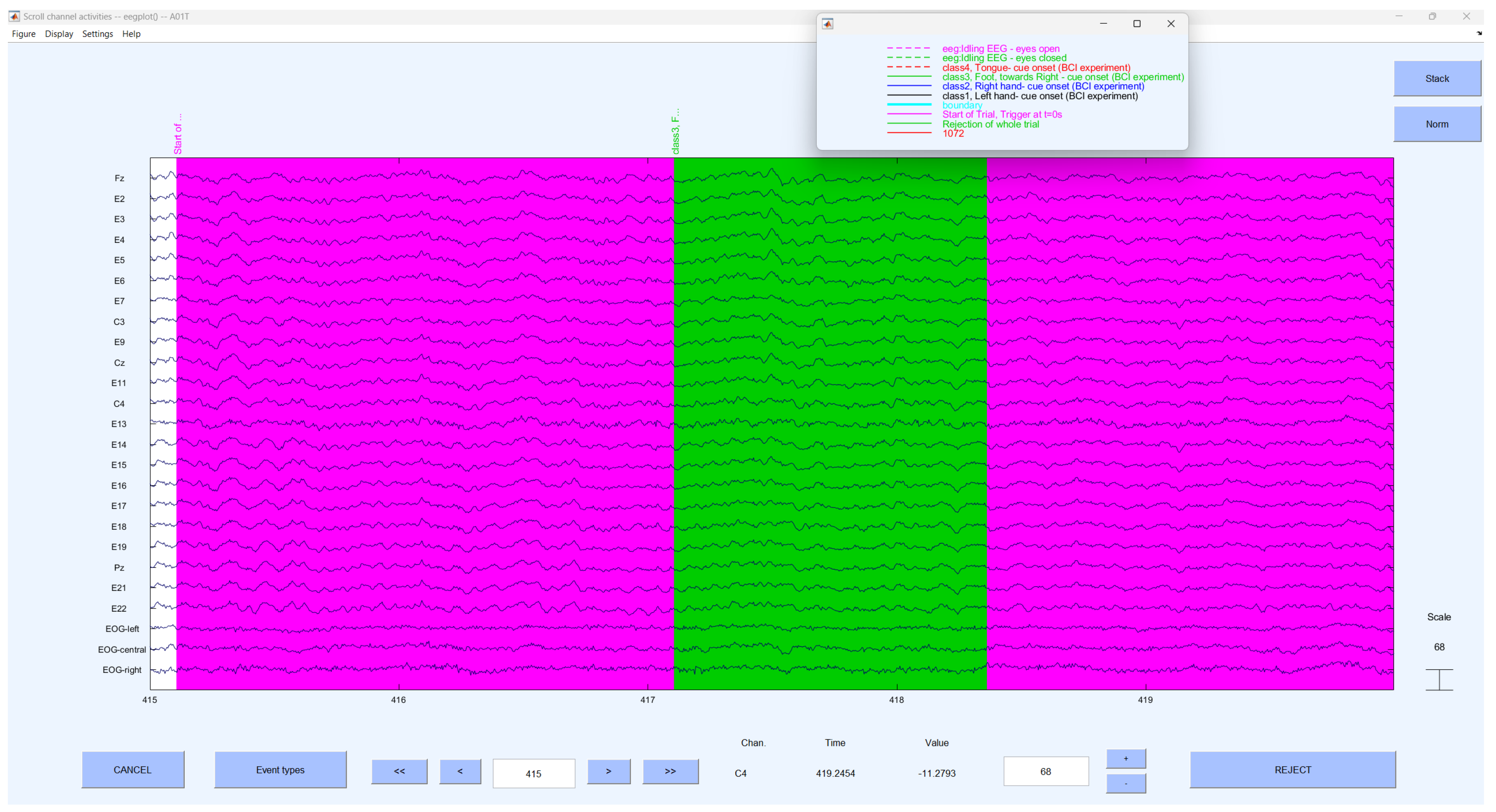
3.1. Dataset
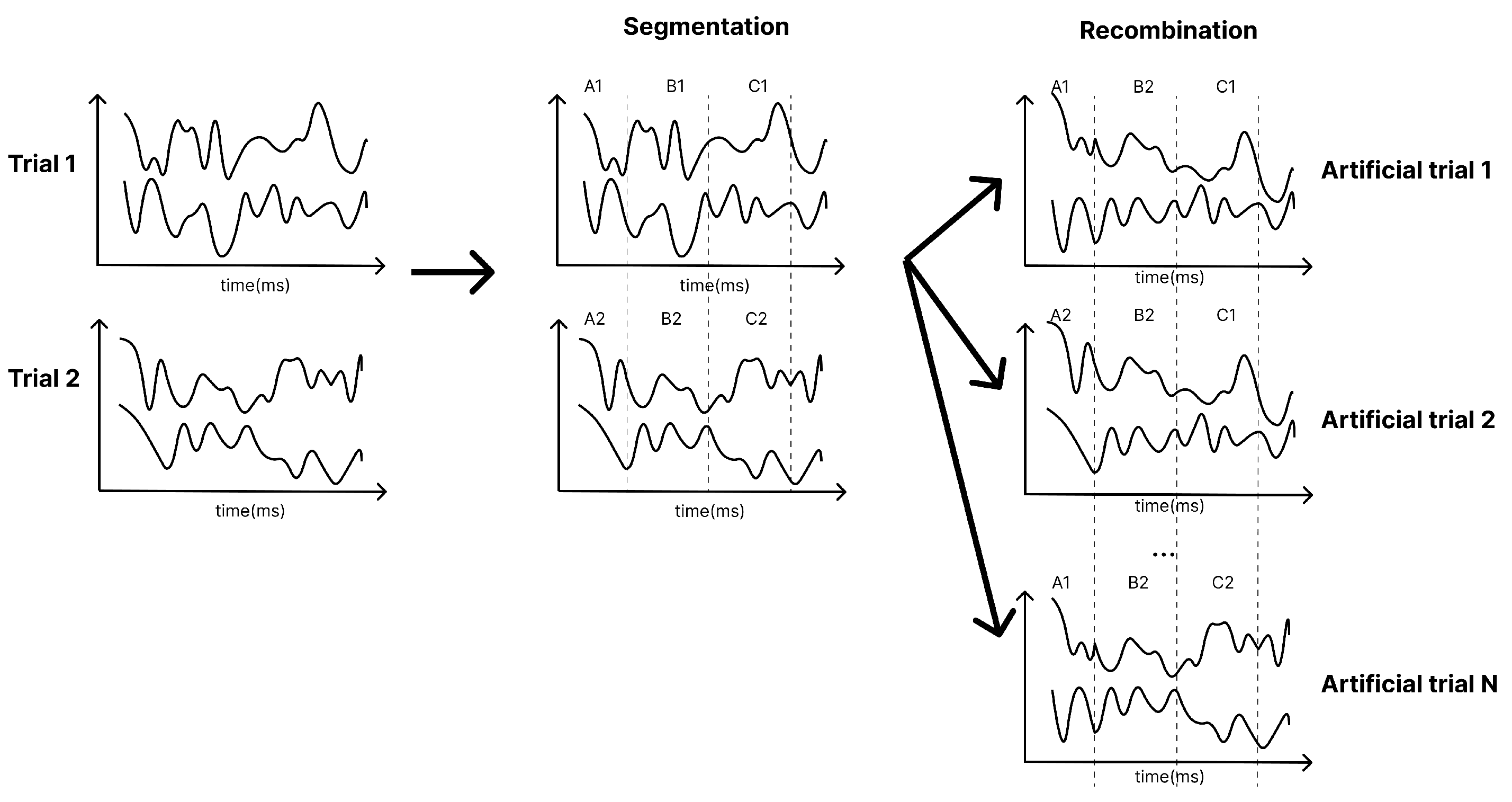
3.2. Preprocessing
| is parameter related to the ripples in the stop-band; | |
| is the nth-order Chebyshev polynomial; | |
| is the stop-band edge frequency; and | |
| f | is the frequency variable. |
| z | is the standardised value; |
| x | is the original value; |
| is the mean of the distribution; and | |
| is the standard deviation of the distribution |
3.3. EEG-TCNet
- (a)
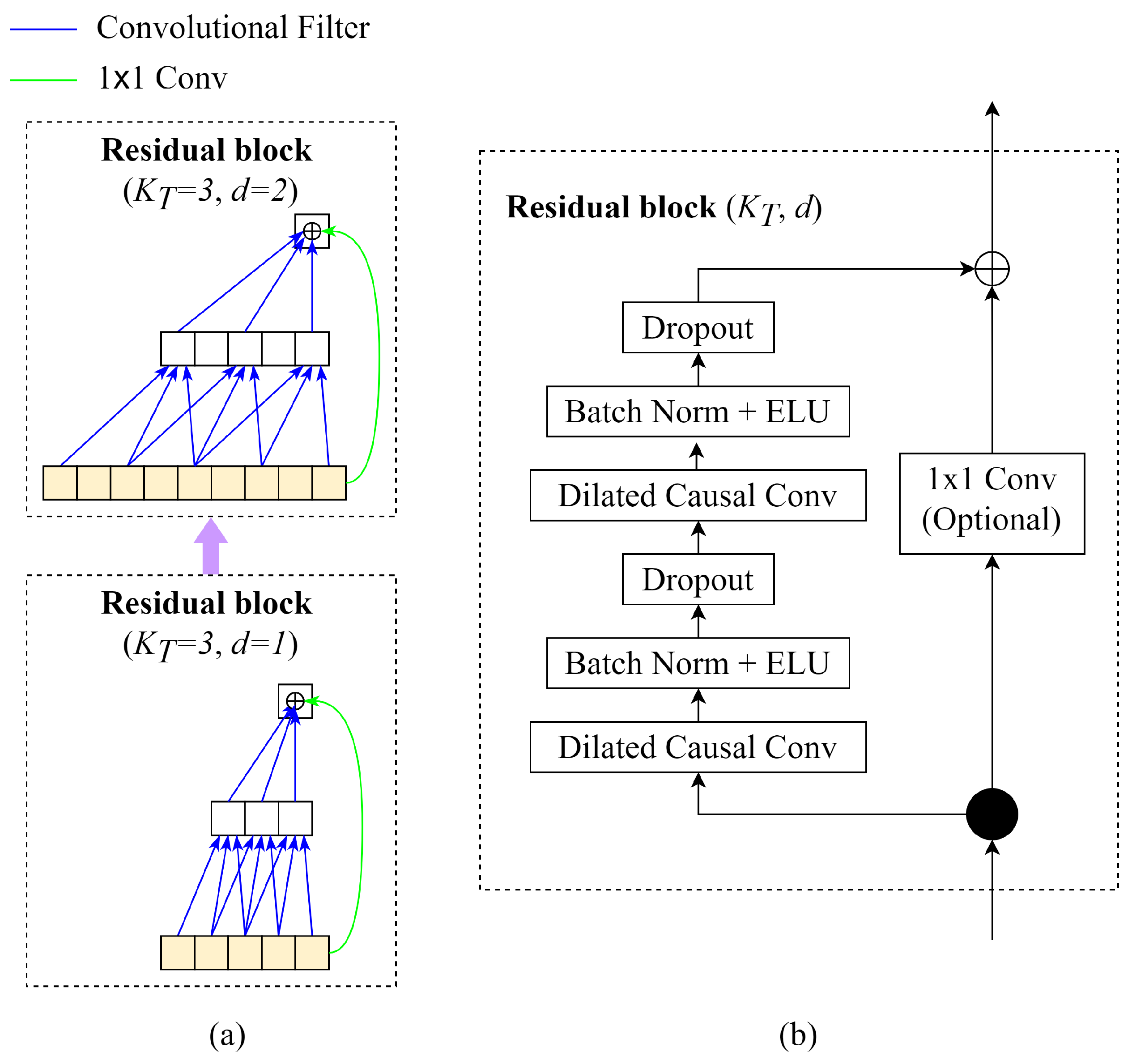
- Causal Convolutions: TCN aims to produce the output of the same size as the input, so TCN uses a 1D fully convolutional network with each hidden layer having the same size as the input layer. To keep the length of subsequent layers equal to the previous ones, zero padding of length (kernel size: 1) is applied. Moreover, to prevent information leakage from a feature to the past in training, only the inputs from time t and earlier determine the output at time t.
- (b)
- Dilated Convolutions: The major disadvantage of regular causal convolutions is that the network must be extremely deep or have large filters to obtain a large receptive field size. A sequence of dilated convolutions could increase the receptive field exponentially by increasing dilation factors d.
- (c)
- Residual Blocks: In EEG-TCNet, the weight normalisation in the original TCN is replaced by batch normalisation. The residual blocks have a stack of two layers of dilated convolution, batch normalisation with ELU, and dropout. The skip connection 1 × 1 convolution is applied from the input to the output feature map to ensure the same shape of input and output tensors.
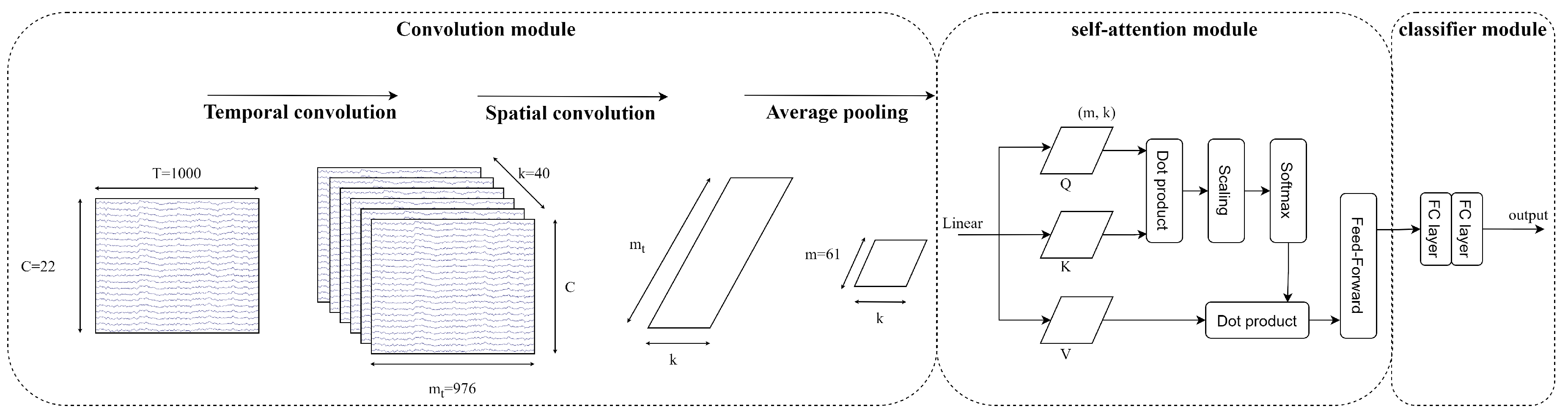
3.4. EEG-Conformer
- (a)
- Convolution module: The EEG signals after preprocessing and augmenting are learned through two 1D temporal and spatial convolution layers. The first temporal convolution layer learns the time dimension of input, and then the spatial convolution layer learns the spatial features. The spatial features are the information between the electrode channels. Then, the feature maps go through batch normalisation to avoid overfitting and the nonlinearity activation function ELU. The average pooling layer smooths the feature maps and rearranges to put all feature channels of each temporal point as a token into the self-attention module.
- (b)
- Self-attention module: The self-attention module has advantages in learning global features and long sequence data, which improve the CNN weaknesses. The self-attention module calculates as below:where Q is a matrix of stacked temporal queries, K and V are temporal matrices that denote key and value, and k is the length of tokens.Multi-head attention (MHA) is applied to strengthen representation performance. The tokens are separated into the same shape h segments, described as follows:where MHA is the multi-head attention , indicating the query, key, and value acquired by a linear transformation of a segment token in the lth head, respectively.
- (c)
- Classifier module: The features from the self-attention module go through two fully connected layers. The Softmax function is utilised to predict M labels. Cross-entropy loss is utilised as a cost function as follows:where is the batch size, M is the number of target labels (M = 4), y is the ground truth, and is the prediction.
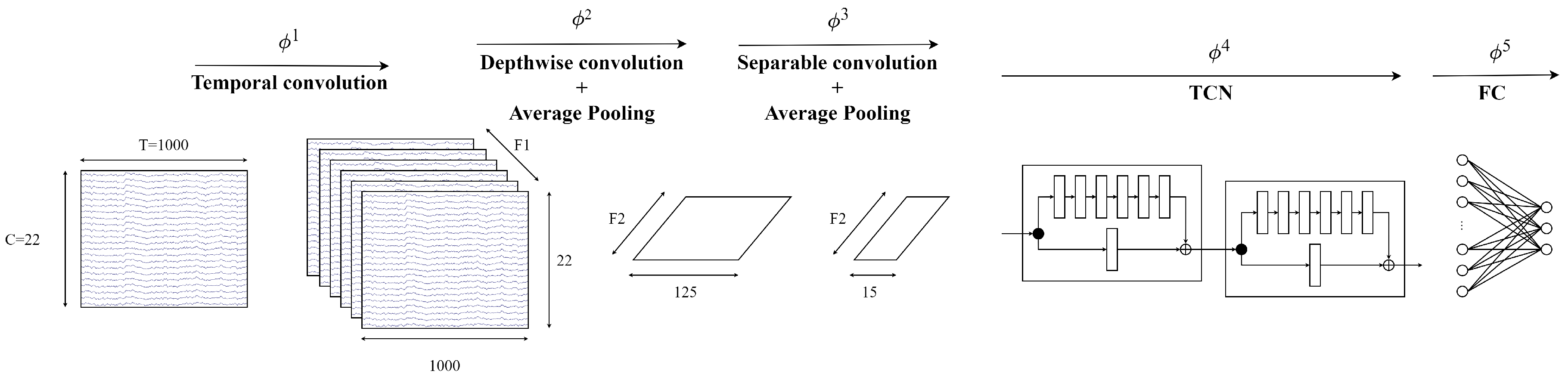
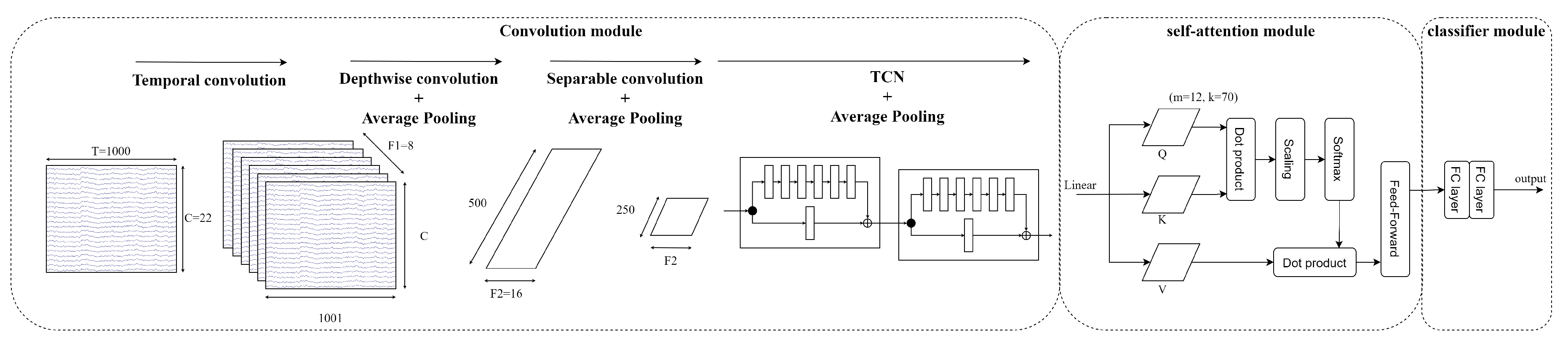
3.5. EEG-TCNTransformer
- (a)
- Convolution module: The sequence of a 2D convolution layer, depthwise convolution layer, separable convolution layer, and average pooling layer extracts the temporal and spatial information in EEG signals. After that, a sequence of TCN blocks continues to learn large receptive fields efficiently with small parameters because of dilated causal convolution and a residual block structure. In this study, the different numbers of filters k in a TCN block and the numbers of a TCN block T are validated to select the best hyperparameter for EEG-TCNTransformer. Then, the average pooling layer smooths the features and rearranges the features to the shape of channels of each temporal point.
- (b)
- Self-attention module: Six self-attention blocks with a multi-head attention architecture learn the global temporal dependencies in features from the convolution module. The self-attention module calculates as below:where Q is a matrix of stacked temporal queries, K and V are temporal matrices that denote key and value, and k is the length of tokens.Multi-head attention (MHA) is applied to strengthen representation performance. The tokens are separated into the same shape h segments, described as follows:where MHA is the multi-head attention , indicating the query, key, and value acquired by a linear transformation of a segment token in the lth head, respectively.
- (c)
- Classifier module: Two fully connected layers transform the features into M labels that calculate probability distribution by the Softmax function. The loss function is the cross-entropy loss, as follows:where is the batch size, M is the number of target labels (M = 4), y is the ground truth, and is the prediction.
4. Experiments and Results
4.1. Experimental Setup
4.2. Training and Testing Preparation
- Without a bandpass filter, data are loaded from Matlab files, and for each trial, , which is equivalent to 4 s from the cue section to the end of the motor imagery section.
- With a bandpass filter, data are exactly the same as above; then the data are processed by a bandpass filter step with the order of the filter N and the minimum attenuation required in the stop band .
- Regarding EEG-TCNet, each subject is trained with 1000 epochs with a learning rate of 0.001, the criterion is categorical cross-entropy, the optimiser is Adam, and the activation function is ELU.
- With regard to EEG-Conformer, each subject is trained with 2000 epochs with a learning rate of 0.0002, the criterion is cross-entropy, the optimiser is Adam, the activation function in the convolution module and classification module is ELU, and the activation function in self-attention blocks is GELU.
- With respect to EEG-TCNTransformer, each subject is trained 5000 epochs with a learning rate of 0.0002, the criterion is cross-entropy, the optimiser is Adam, the activation function in EEGNet module, TCN module and classification module is ELU, and the activation function in self-attention blocks is GELU.
4.3. EEG-TCNet with Different Hyperparameters
4.4. EEG-TCNet with Different Bandpass Filter Parameters
4.5. EEG-Conformer with Different Hyperparameters
4.6. EEG-Conformer with Different Bandpass Filter Parameters
4.7. EEG-TCNTransformer with Different Hyperparameters
4.8. EEG-TCNTransformer with Different Bandpass Filter Parameters
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. TCNet Training Results
Appendix A.1. Experiment EEG-TCNet with Different Hyperparameters
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average Accuracy (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 16 | 10 | 4 | 79.36 | 59.36 | 91.21 | 67.11 | 75.72 | 56.28 | 75.09 | 81.92 | 75.00 | 73.45 |
| 6 | 16 | 10 | 6 | 82.21 | 60.07 | 94.51 | 72.37 | 75.72 | 62.33 | 76.17 | 84.13 | 79.55 | 76.34 |
| 6 | 16 | 10 | 8 | 82.92 | 59.72 | 95.24 | 74.56 | 75.72 | 66.98 | 81.23 | 82.66 | 76.52 | 77.28 |
| 6 | 16 | 12 | 4 | 80.78 | 66.43 | 93.77 | 66.23 | 77.90 | 58.14 | 93.14 | 83.03 | 82.95 | 78.04 |
| 6 | 16 | 12 | 6 | 80.43 | 60.78 | 93.77 | 76.75 | 80.80 | 64.19 | 88.45 | 83.03 | 83.33 | 79.06 |
| 6 | 16 | 12 | 8 | 83.63 | 67.49 | 91.21 | 67.98 | 80.80 | 65.12 | 76.53 | 83.76 | 84.47 | 77.89 |
| 6 | 16 | 14 | 4 | 75.09 | 53.00 | 88.28 | 67.11 | 75.72 | 54.88 | 76.17 | 81.55 | 75.00 | 71.87 |
| 6 | 16 | 14 | 6 | 78.65 | 61.48 | 89.38 | 73.68 | 75.72 | 64.65 | 92.78 | 82.29 | 76.89 | 77.28 |
| 6 | 16 | 14 | 8 | 82.56 | 60.42 | 95.60 | 74.12 | 75.72 | 68.84 | 92.06 | 76.75 | 76.14 | 78.02 |
| 6 | 32 | 10 | 4 | 76.51 | 63.96 | 91.21 | 72.37 | 79.35 | 53.49 | 75.09 | 82.29 | 75.38 | 74.40 |
| 6 | 32 | 10 | 6 | 82.21 | 68.20 | 94.51 | 65.35 | 76.09 | 64.65 | 91.34 | 80.07 | 80.68 | 78.12 |
| 6 | 32 | 10 | 8 | 76.16 | 57.95 | 95.24 | 75.44 | 78.99 | 63.26 | 88.09 | 86.72 | 85.23 | 78.56 |
| 6 | 32 | 12 | 4 | 81.49 | 56.89 | 91.58 | 70.18 | 72.10 | 61.40 | 77.62 | 82.66 | 84.47 | 75.38 |
| 6 | 32 | 12 | 6 | 80.43 | 65.37 | 94.87 | 74.56 | 79.35 | 61.86 | 91.70 | 80.44 | 81.44 | 78.89 |
| 6 | 32 | 12 | 8 | 82.56 | 56.18 | 93.41 | 75.88 | 78.62 | 61.40 | 91.70 | 84.87 | 85.98 | 78.96 |
| 6 | 32 | 14 | 4 | 83.63 | 59.01 | 94.51 | 67.98 | 70.65 | 60.00 | 90.25 | 78.60 | 79.17 | 75.98 |
| 6 | 32 | 14 | 6 | 76.16 | 61.84 | 97.07 | 80.26 | 73.55 | 60.93 | 81.23 | 83.76 | 81.82 | 77.40 |
| 6 | 32 | 14 | 8 | 85.05 | 66.78 | 91.21 | 71.49 | 75.36 | 60.93 | 87.73 | 77.86 | 76.89 | 77.03 |
| 6 | 48 | 10 | 4 | 87.54 | 63.96 | 93.41 | 70.61 | 75.36 | 57.67 | 75.81 | 82.66 | 78.03 | 76.12 |
| 6 | 48 | 10 | 6 | 79.36 | 59.36 | 89.74 | 70.61 | 76.45 | 65.58 | 90.25 | 83.39 | 79.17 | 77.10 |
| 6 | 48 | 10 | 8 | 78.65 | 63.25 | 93.04 | 72.81 | 81.16 | 63.26 | 91.70 | 81.92 | 82.95 | 78.75 |
| 6 | 48 | 12 | 4 | 78.65 | 51.94 | 91.94 | 69.30 | 73.91 | 64.65 | 84.12 | 81.92 | 83.71 | 75.57 |
| 6 | 48 | 12 | 6 | 88.26 | 64.66 | 97.07 | 63.60 | 79.35 | 63.26 | 90.97 | 81.55 | 81.82 | 78.95 |
| 6 | 48 | 12 | 8 | 83.27 | 61.84 | 94.87 | 77.63 | 79.71 | 66.51 | 76.17 | 83.39 | 82.20 | 78.40 |
| 6 | 48 | 14 | 4 | 79.00 | 57.95 | 91.21 | 70.18 | 71.38 | 59.53 | 90.25 | 84.13 | 81.06 | 76.08 |
| 6 | 48 | 14 | 6 | 77.22 | 56.54 | 93.04 | 71.93 | 78.99 | 61.86 | 76.90 | 84.13 | 79.55 | 75.57 |
| 6 | 48 | 14 | 8 | 83.27 | 65.72 | 92.67 | 76.32 | 77.54 | 57.67 | 78.34 | 81.92 | 80.30 | 77.08 |
| 8 | 16 | 10 | 4 | 79.36 | 62.54 | 89.74 | 71.05 | 72.46 | 60.00 | 90.25 | 85.98 | 83.33 | 77.19 |
| 8 | 16 | 10 | 6 | 82.21 | 67.14 | 95.24 | 69.30 | 76.45 | 67.91 | 90.61 | 82.29 | 80.68 | 79.09 |
| 8 | 16 | 10 | 8 | 83.27 | 67.49 | 94.14 | 76.32 | 80.43 | 66.51 | 91.34 | 80.07 | 75.76 | 79.48 |
| 8 | 16 | 12 | 4 | 82.92 | 60.78 | 93.04 | 67.98 | 66.30 | 62.79 | 93.14 | 80.81 | 82.20 | 76.66 |
| 8 | 16 | 12 | 6 | 81.49 | 66.43 | 93.41 | 70.61 | 77.17 | 64.65 | 88.81 | 84.50 | 85.23 | 79.15 |
| 8 | 16 | 12 | 8 | 82.21 | 67.49 | 94.14 | 78.07 | 73.91 | 67.44 | 88.45 | 83.76 | 85.61 | 80.12 |
| 8 | 16 | 14 | 4 | 78.65 | 57.60 | 88.64 | 66.23 | 80.43 | 60.47 | 92.78 | 84.13 | 82.20 | 76.79 |
| 8 | 16 | 14 | 6 | 79.72 | 67.14 | 93.04 | 68.86 | 80.43 | 55.81 | 88.81 | 83.39 | 79.17 | 77.37 |
| 8 | 16 | 14 | 8 | 81.14 | 61.13 | 92.67 | 75.88 | 79.35 | 66.51 | 88.09 | 79.70 | 80.68 | 78.35 |
| 8 | 32 | 10 | 4 | 85.77 | 65.72 | 95.24 | 75.88 | 76.09 | 56.74 | 88.81 | 81.92 | 75.76 | 77.99 |
| 8 | 32 | 10 | 6 | 82.56 | 67.49 | 93.77 | 78.51 | 79.71 | 64.65 | 90.25 | 85.61 | 84.85 | 80.82 |
| 8 | 32 | 10 | 8 | 82.56 | 65.72 | 94.14 | 76.32 | 84.06 | 65.58 | 92.42 | 84.13 | 86.36 | 81.26 |
| 8 | 32 | 12 | 4 | 82.92 | 61.13 | 91.58 | 64.91 | 76.45 | 59.53 | 91.34 | 81.92 | 79.17 | 76.55 |
| 8 | 32 | 12 | 6 | 83.63 | 66.43 | 94.87 | 75.00 | 75.72 | 66.51 | 87.73 | 85.24 | 84.47 | 79.96 |
| 8 | 32 | 12 | 8 | 82.92 | 61.48 | 94.51 | 73.68 | 79.35 | 65.12 | 91.34 | 76.75 | 82.20 | 78.59 |
| 8 | 32 | 14 | 4 | 79.36 | 60.78 | 97.07 | 72.37 | 77.90 | 61.86 | 88.45 | 82.29 | 87.12 | 78.58 |
| 8 | 32 | 14 | 6 | 81.85 | 67.84 | 94.51 | 71.05 | 75.72 | 65.58 | 89.17 | 85.61 | 79.92 | 79.03 |
| 8 | 32 | 14 | 8 | 82.92 | 57.60 | 95.60 | 73.68 | 80.80 | 65.12 | 89.89 | 82.66 | 83.33 | 79.07 |
| 8 | 48 | 10 | 4 | 82.21 | 54.06 | 92.31 | 63.60 | 75.36 | 58.14 | 75.09 | 79.70 | 79.92 | 73.38 |
| 8 | 48 | 10 | 6 | 81.85 | 66.08 | 95.24 | 76.32 | 78.26 | 62.79 | 85.92 | 82.29 | 79.17 | 78.66 |
| 8 | 48 | 10 | 8 | 83.27 | 64.66 | 95.24 | 78.95 | 80.07 | 67.91 | 86.64 | 83.03 | 84.85 | 80.51 |
| 8 | 48 | 12 | 4 | 81.14 | 62.19 | 94.87 | 70.18 | 78.99 | 60.47 | 84.12 | 79.34 | 82.20 | 77.05 |
| 8 | 48 | 12 | 6 | 81.85 | 67.49 | 93.41 | 72.37 | 76.81 | 58.60 | 88.81 | 83.03 | 83.33 | 78.41 |
| 8 | 48 | 12 | 8 | 82.92 | 61.48 | 90.84 | 76.32 | 79.71 | 65.58 | 90.61 | 81.18 | 83.71 | 79.15 |
| 8 | 48 | 14 | 4 | 83.99 | 56.18 | 94.87 | 75.00 | 78.26 | 62.79 | 89.53 | 84.13 | 83.71 | 78.72 |
| 8 | 48 | 14 | 6 | 81.14 | 72.44 | 95.60 | 80.26 | 80.07 | 62.79 | 91.34 | 84.13 | 81.44 | 81.02 |
| 8 | 48 | 14 | 8 | 80.78 | 65.37 | 94.87 | 71.05 | 78.62 | 64.19 | 80.87 | 84.13 | 84.47 | 78.26 |
| 10 | 16 | 10 | 4 | 82.56 | 61.84 | 93.77 | 65.79 | 77.17 | 58.60 | 88.09 | 84.13 | 83.33 | 77.25 |
| 10 | 16 | 10 | 6 | 80.07 | 62.54 | 93.04 | 71.93 | 79.35 | 62.79 | 89.17 | 84.13 | 79.55 | 78.06 |
| 10 | 16 | 10 | 8 | 80.43 | 65.72 | 93.77 | 76.32 | 77.90 | 65.58 | 92.06 | 83.76 | 82.95 | 79.83 |
| 10 | 16 | 12 | 4 | 81.49 | 64.66 | 93.04 | 73.68 | 74.28 | 58.60 | 94.58 | 84.13 | 79.17 | 78.18 |
| 10 | 16 | 12 | 6 | 83.63 | 63.96 | 92.67 | 69.74 | 77.90 | 63.26 | 92.78 | 82.66 | 82.58 | 78.80 |
| 10 | 16 | 12 | 8 | 81.14 | 62.90 | 93.77 | 73.68 | 81.88 | 66.51 | 92.42 | 82.66 | 83.71 | 79.85 |
| 10 | 16 | 14 | 4 | 81.49 | 60.78 | 94.14 | 76.32 | 79.35 | 65.12 | 92.06 | 84.87 | 82.20 | 79.59 |
| 10 | 16 | 14 | 6 | 80.43 | 66.08 | 95.24 | 75.44 | 77.17 | 68.84 | 91.34 | 83.39 | 78.41 | 79.59 |
| 10 | 16 | 14 | 8 | 82.21 | 64.66 | 93.04 | 77.63 | 77.54 | 66.98 | 89.53 | 84.13 | 79.17 | 79.43 |
| 10 | 32 | 10 | 4 | 83.27 | 64.31 | 95.24 | 74.56 | 74.64 | 62.33 | 89.17 | 81.92 | 81.44 | 78.54 |
| 10 | 32 | 10 | 6 | 85.05 | 69.61 | 94.14 | 79.82 | 77.90 | 62.79 | 89.53 | 80.81 | 84.09 | 80.42 |
| 10 | 32 | 10 | 8 | 85.05 | 68.90 | 95.60 | 76.32 | 76.81 | 66.05 | 90.61 | 83.76 | 84.85 | 80.88 |
| 10 | 32 | 12 | 4 | 81.85 | 58.66 | 95.97 | 69.30 | 79.71 | 63.72 | 90.25 | 83.76 | 79.17 | 78.04 |
| 10 | 32 | 12 | 6 | 82.92 | 65.02 | 93.77 | 71.93 | 79.71 | 61.40 | 89.89 | 85.24 | 84.47 | 79.37 |
| 10 | 32 | 12 | 8 | 81.85 | 69.96 | 93.41 | 74.12 | 80.43 | 66.51 | 89.17 | 84.87 | 86.36 | 80.74 |
| 10 | 32 | 14 | 4 | 84.70 | 62.90 | 94.14 | 70.18 | 77.90 | 60.93 | 89.89 | 83.03 | 85.23 | 78.76 |
| 10 | 32 | 14 | 6 | 83.99 | 66.78 | 95.24 | 71.93 | 83.33 | 61.86 | 92.06 | 83.03 | 84.47 | 80.30 |
| 10 | 32 | 14 | 8 | 82.92 | 62.54 | 94.87 | 74.12 | 81.52 | 68.37 | 90.25 | 86.72 | 85.98 | 80.81 |
| 10 | 48 | 10 | 4 | 83.63 | 61.13 | 94.14 | 68.42 | 78.62 | 58.60 | 90.97 | 83.39 | 71.97 | 76.77 |
| 10 | 48 | 10 | 6 | 84.70 | 62.54 | 93.77 | 73.25 | 76.45 | 66.98 | 89.89 | 83.39 | 85.98 | 79.66 |
| 10 | 48 | 10 | 8 | 84.70 | 65.72 | 93.77 | 73.25 | 76.45 | 62.79 | 82.67 | 85.24 | 83.71 | 78.70 |
| 10 | 48 | 12 | 4 | 82.21 | 65.02 | 94.87 | 69.74 | 76.09 | 59.53 | 77.26 | 85.24 | 82.20 | 76.91 |
| 10 | 48 | 12 | 6 | 83.63 | 72.79 | 93.41 | 69.30 | 78.99 | 64.19 | 90.61 | 84.13 | 85.23 | 80.25 |
| 10 | 48 | 12 | 8 | 86.12 | 71.02 | 94.87 | 80.26 | 76.81 | 69.30 | 87.00 | 81.18 | 85.23 | 81.31 |
| 10 | 48 | 14 | 4 | 81.85 | 59.72 | 94.87 | 72.37 | 77.54 | 56.74 | 90.25 | 84.50 | 81.44 | 77.70 |
| 10 | 48 | 14 | 6 | 82.21 | 68.90 | 96.70 | 77.19 | 78.99 | 60.93 | 91.34 | 87.82 | 79.55 | 80.40 |
| 10 | 48 | 14 | 8 | 86.12 | 69.96 | 95.60 | 75.88 | 80.43 | 60.93 | 88.09 | 83.76 | 82.95 | 80.42 |
Appendix A.2. Experiment EEG-TCNet with Different Parameters of Chebyshev Type 2 Filter
| N | rs | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 20 | 76.87 | 51.24 | 92.31 | 65.35 | 37.68 | 50.70 | 75.09 | 78.97 | 79.17 | 67.49 |
| 4 | 30 | 80.43 | 52.65 | 91.58 | 58.33 | 35.87 | 45.58 | 71.84 | 83.39 | 79.17 | 66.54 |
| 4 | 40 | 77.94 | 48.41 | 89.38 | 52.63 | 34.78 | 46.98 | 73.29 | 83.39 | 82.20 | 65.44 |
| 4 | 50 | 76.87 | 47.35 | 91.94 | 56.58 | 33.33 | 47.44 | 68.59 | 78.60 | 79.17 | 64.43 |
| 4 | 60 | 77.94 | 38.52 | 91.21 | 51.75 | 35.87 | 44.65 | 61.37 | 85.24 | 84.09 | 63.40 |
| 4 | 70 | 80.78 | 33.57 | 91.58 | 50.00 | 35.87 | 46.51 | 63.54 | 81.92 | 78.03 | 62.42 |
| 4 | 80 | 81.49 | 41.34 | 92.31 | 46.49 | 35.51 | 45.58 | 54.87 | 77.12 | 76.14 | 61.21 |
| 4 | 90 | 79.72 | 34.98 | 93.77 | 45.61 | 34.06 | 43.72 | 51.62 | 59.78 | 66.29 | 56.62 |
| 4 | 100 | 77.94 | 36.04 | 91.21 | 43.42 | 37.32 | 41.86 | 48.74 | 53.87 | 48.11 | 53.17 |
| 5 | 20 | 78.65 | 54.06 | 92.31 | 66.23 | 46.74 | 43.26 | 74.73 | 84.13 | 79.55 | 68.85 |
| 5 | 30 | 81.85 | 51.24 | 89.01 | 66.67 | 35.87 | 45.12 | 74.73 | 83.39 | 81.44 | 67.70 |
| 5 | 40 | 78.65 | 50.53 | 91.94 | 58.33 | 32.61 | 48.37 | 77.98 | 83.39 | 80.30 | 66.90 |
| 5 | 50 | 76.51 | 48.76 | 91.58 | 54.39 | 35.51 | 44.19 | 71.12 | 82.29 | 82.20 | 65.17 |
| 5 | 60 | 73.67 | 49.12 | 91.21 | 57.46 | 37.68 | 49.77 | 69.31 | 82.66 | 80.68 | 65.73 |
| 5 | 70 | 76.16 | 49.82 | 89.74 | 56.14 | 35.87 | 43.26 | 63.90 | 81.55 | 81.82 | 64.25 |
| 5 | 80 | 82.21 | 34.63 | 91.94 | 54.82 | 36.96 | 51.16 | 64.98 | 80.07 | 82.58 | 64.37 |
| 5 | 90 | 72.95 | 36.04 | 91.58 | 47.37 | 34.06 | 50.23 | 58.84 | 81.55 | 80.68 | 61.48 |
| 5 | 100 | 77.58 | 35.34 | 94.51 | 42.98 | 36.59 | 45.12 | 51.99 | 74.17 | 78.03 | 59.59 |
| 6 | 20 | 81.49 | 56.18 | 90.48 | 59.21 | 35.51 | 40.00 | 84.84 | 79.34 | 82.58 | 67.74 |
| 6 | 30 | 78.65 | 52.30 | 89.01 | 56.58 | 34.42 | 48.84 | 79.78 | 84.50 | 76.89 | 66.77 |
| 6 | 40 | 78.65 | 49.82 | 89.74 | 64.47 | 37.32 | 45.12 | 73.65 | 79.70 | 83.33 | 66.87 |
| 6 | 50 | 80.43 | 47.00 | 92.67 | 60.96 | 36.59 | 46.05 | 81.95 | 79.34 | 80.30 | 67.25 |
| 6 | 60 | 76.51 | 50.88 | 89.74 | 49.56 | 34.78 | 44.65 | 72.20 | 80.44 | 74.62 | 63.71 |
| 6 | 70 | 78.29 | 53.36 | 92.31 | 57.02 | 37.68 | 47.91 | 67.87 | 81.92 | 83.33 | 66.63 |
| 6 | 80 | 78.65 | 36.75 | 91.58 | 52.19 | 31.52 | 49.77 | 68.23 | 83.39 | 81.06 | 63.68 |
| 6 | 90 | 76.16 | 40.64 | 90.48 | 57.89 | 33.70 | 54.88 | 66.06 | 80.81 | 84.47 | 65.01 |
| 6 | 100 | 79.36 | 37.46 | 92.67 | 52.63 | 34.78 | 49.77 | 66.43 | 82.29 | 82.95 | 64.26 |
| 7 | 20 | 77.94 | 54.42 | 89.74 | 69.74 | 36.23 | 46.05 | 75.09 | 81.92 | 73.86 | 67.22 |
| 7 | 30 | 81.85 | 56.18 | 91.21 | 64.91 | 44.57 | 45.12 | 78.70 | 81.55 | 81.44 | 69.50 |
| 7 | 40 | 79.00 | 51.94 | 90.48 | 72.37 | 56.88 | 51.16 | 82.67 | 82.29 | 78.79 | 71.73 |
| 7 | 50 | 73.67 | 51.59 | 88.64 | 51.32 | 32.25 | 43.26 | 74.01 | 83.03 | 78.03 | 63.98 |
| 7 | 60 | 80.07 | 48.41 | 90.84 | 58.77 | 34.78 | 49.30 | 76.17 | 81.92 | 78.03 | 66.48 |
| 7 | 70 | 79.00 | 50.18 | 90.48 | 49.56 | 38.41 | 47.91 | 70.40 | 83.03 | 81.06 | 65.56 |
| 7 | 80 | 74.73 | 49.12 | 90.48 | 54.39 | 32.97 | 40.00 | 72.92 | 82.29 | 80.68 | 64.18 |
| 7 | 90 | 80.43 | 35.34 | 91.21 | 49.56 | 38.77 | 54.88 | 66.06 | 79.70 | 81.44 | 64.15 |
| 7 | 100 | 79.72 | 35.34 | 90.48 | 53.95 | 35.51 | 48.84 | 67.87 | 83.76 | 83.33 | 64.31 |
| 8 | 20 | 75.09 | 50.18 | 87.55 | 55.26 | 36.59 | 46.98 | 76.17 | 83.39 | 75.00 | 65.13 |
| 8 | 30 | 80.07 | 55.12 | 92.31 | 63.60 | 38.77 | 44.19 | 81.95 | 80.81 | 81.82 | 68.74 |
| 8 | 40 | 76.16 | 52.30 | 91.58 | 63.60 | 38.41 | 52.09 | 83.39 | 81.55 | 79.55 | 68.73 |
| 8 | 50 | 75.80 | 50.88 | 90.48 | 59.65 | 38.77 | 47.91 | 80.51 | 80.81 | 84.09 | 67.65 |
| 8 | 60 | 81.49 | 48.06 | 93.04 | 54.82 | 37.32 | 48.84 | 80.51 | 80.44 | 81.82 | 67.37 |
| 8 | 70 | 79.00 | 54.06 | 89.74 | 51.32 | 29.35 | 40.00 | 77.62 | 81.55 | 81.44 | 64.90 |
| 8 | 80 | 79.00 | 47.00 | 90.11 | 48.68 | 35.14 | 43.72 | 71.48 | 80.44 | 84.85 | 64.49 |
| 8 | 90 | 78.29 | 45.94 | 90.11 | 45.18 | 38.77 | 52.09 | 75.81 | 81.92 | 80.68 | 65.42 |
| 8 | 100 | 76.87 | 46.64 | 91.58 | 49.56 | 37.32 | 46.51 | 67.15 | 80.81 | 80.30 | 64.08 |
Appendix B. EEG-Conformer Training Results
Appendix B.1. Experiment EEG-Conformer with Different Hyperparameters
| k | N | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 6 | 88.26 | 58.66 | 94.87 | 73.25 | 76.45 | 62.79 | 87.00 | 87.08 | 79.55 | 78.66 |
| 30 | 6 | 86.48 | 57.95 | 95.24 | 73.68 | 75.36 | 59.07 | 87.00 | 86.35 | 81.06 | 78.02 |
| 40 | 6 | 83.99 | 57.95 | 94.51 | 78.07 | 78.62 | 63.72 | 88.81 | 88.56 | 82.58 | 79.64 |
| 50 | 6 | 86.12 | 54.42 | 93.77 | 74.12 | 75.36 | 58.60 | 89.53 | 87.82 | 81.06 | 77.87 |
| 60 | 6 | 84.34 | 57.60 | 93.77 | 72.37 | 78.62 | 60.47 | 85.20 | 87.82 | 79.55 | 77.75 |
| 20 | 7 | 86.83 | 61.13 | 94.87 | 73.25 | 76.81 | 59.07 | 85.56 | 88.19 | 79.17 | 78.32 |
| 30 | 7 | 86.48 | 59.01 | 93.77 | 74.12 | 76.45 | 63.26 | 90.97 | 87.82 | 81.82 | 79.30 |
| 40 | 7 | 85.41 | 55.12 | 94.87 | 71.93 | 76.45 | 58.14 | 90.61 | 89.30 | 82.58 | 78.27 |
| 50 | 7 | 84.70 | 52.65 | 94.87 | 73.25 | 76.09 | 58.14 | 88.45 | 88.19 | 79.55 | 77.32 |
| 60 | 7 | 85.05 | 51.94 | 94.87 | 74.56 | 77.54 | 60.00 | 89.53 | 88.19 | 82.20 | 78.21 |
| 20 | 8 | 85.41 | 61.48 | 93.41 | 71.49 | 76.81 | 61.40 | 84.48 | 88.56 | 82.95 | 78.44 |
| 30 | 8 | 86.83 | 53.71 | 94.87 | 71.49 | 75.72 | 60.00 | 90.25 | 89.30 | 81.44 | 78.18 |
| 40 | 8 | 85.77 | 56.18 | 94.14 | 71.93 | 78.26 | 60.00 | 91.34 | 87.45 | 81.44 | 78.50 |
| 50 | 8 | 87.54 | 54.06 | 93.41 | 71.49 | 78.99 | 63.72 | 84.84 | 88.19 | 79.92 | 78.02 |
| 60 | 8 | 84.34 | 53.36 | 93.41 | 73.68 | 78.26 | 62.33 | 90.25 | 88.19 | 80.30 | 78.24 |
| 20 | 9 | 87.54 | 60.42 | 94.14 | 77.63 | 76.45 | 65.58 | 81.95 | 89.30 | 80.68 | 79.30 |
| 30 | 9 | 86.83 | 55.48 | 93.77 | 76.32 | 78.26 | 61.40 | 90.25 | 88.19 | 81.06 | 79.06 |
| 40 | 9 | 85.77 | 54.42 | 92.67 | 74.56 | 77.90 | 59.07 | 92.06 | 87.82 | 82.95 | 78.58 |
| 50 | 9 | 86.12 | 54.77 | 94.51 | 74.56 | 75.36 | 60.47 | 90.25 | 86.72 | 83.33 | 78.45 |
| 60 | 9 | 87.19 | 53.36 | 93.41 | 71.93 | 76.45 | 59.53 | 90.61 | 87.82 | 82.20 | 78.06 |
| 20 | 10 | 87.54 | 60.42 | 91.94 | 75.88 | 77.90 | 64.19 | 88.09 | 88.56 | 82.95 | 79.72 |
| 30 | 10 | 87.54 | 54.06 | 94.14 | 73.25 | 77.54 | 60.93 | 92.42 | 89.30 | 84.09 | 79.25 |
| 40 | 10 | 85.77 | 50.88 | 94.51 | 78.51 | 79.35 | 59.07 | 91.70 | 88.19 | 79.92 | 78.65 |
| 50 | 10 | 87.19 | 56.18 | 94.14 | 72.37 | 77.90 | 59.07 | 85.56 | 88.56 | 81.82 | 78.09 |
| 60 | 10 | 86.48 | 52.30 | 94.51 | 75.44 | 77.54 | 60.47 | 88.81 | 89.30 | 83.71 | 78.73 |
Appendix B.2. Experiment EEG-Conformer with Different Parameters of Chebyshev Type 2 Filter
| N | rs | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 20 | 90.04 | 63.96 | 92.67 | 81.58 | 79.71 | 66.98 | 94.95 | 88.56 | 88.26 | 82.97 |
| 4 | 30 | 90.75 | 60.07 | 92.31 | 81.58 | 65.94 | 65.58 | 93.86 | 88.56 | 87.12 | 80.64 |
| 4 | 40 | 91.10 | 56.89 | 92.67 | 81.58 | 57.97 | 65.58 | 92.78 | 88.56 | 87.50 | 79.40 |
| 4 | 50 | 89.68 | 59.36 | 93.04 | 78.95 | 55.07 | 65.58 | 90.61 | 87.82 | 88.26 | 78.71 |
| 4 | 60 | 87.90 | 60.07 | 93.77 | 78.07 | 49.64 | 64.65 | 84.12 | 88.56 | 87.50 | 77.14 |
| 4 | 70 | 86.48 | 49.82 | 93.77 | 71.05 | 46.01 | 63.72 | 80.87 | 87.45 | 86.36 | 73.95 |
| 4 | 80 | 87.19 | 48.76 | 93.77 | 62.28 | 45.65 | 64.65 | 77.26 | 84.50 | 85.61 | 72.19 |
| 4 | 90 | 86.48 | 47.35 | 93.41 | 59.65 | 43.12 | 57.67 | 68.23 | 78.23 | 75.00 | 67.68 |
| 4 | 100 | 81.85 | 45.94 | 91.58 | 56.58 | 39.86 | 53.95 | 59.21 | 67.53 | 66.29 | 62.53 |
| 5 | 20 | 90.39 | 59.36 | 93.77 | 86.40 | 75.36 | 71.16 | 95.31 | 87.08 | 87.50 | 82.93 |
| 5 | 30 | 91.81 | 60.42 | 93.41 | 82.89 | 67.75 | 63.26 | 94.22 | 87.08 | 86.74 | 80.84 |
| 5 | 40 | 90.39 | 62.90 | 94.14 | 85.09 | 59.42 | 64.65 | 92.42 | 86.72 | 87.12 | 80.32 |
| 5 | 50 | 90.39 | 58.30 | 92.67 | 83.33 | 56.16 | 65.58 | 93.14 | 88.19 | 87.50 | 79.48 |
| 5 | 60 | 88.97 | 59.36 | 93.04 | 79.82 | 54.71 | 64.19 | 91.34 | 88.56 | 85.98 | 78.44 |
| 5 | 70 | 87.90 | 61.48 | 93.77 | 77.19 | 50.00 | 66.51 | 84.84 | 88.19 | 87.50 | 77.49 |
| 5 | 80 | 85.41 | 55.83 | 92.67 | 73.25 | 48.91 | 65.12 | 83.75 | 88.56 | 87.88 | 75.71 |
| 5 | 90 | 87.54 | 50.18 | 93.41 | 65.35 | 43.84 | 68.84 | 78.70 | 86.35 | 88.64 | 73.65 |
| 5 | 100 | 86.12 | 49.12 | 94.14 | 61.40 | 44.57 | 66.05 | 70.76 | 84.87 | 82.95 | 71.11 |
| 6 | 20 | 88.61 | 59.01 | 92.31 | 80.70 | 78.26 | 68.84 | 96.39 | 88.56 | 87.50 | 82.24 |
| 6 | 30 | 91.46 | 57.60 | 93.77 | 82.46 | 73.55 | 63.26 | 94.58 | 87.45 | 87.12 | 81.25 |
| 6 | 40 | 91.10 | 59.72 | 93.41 | 84.21 | 64.13 | 66.51 | 93.86 | 86.72 | 87.12 | 80.75 |
| 6 | 50 | 89.68 | 61.13 | 91.94 | 83.77 | 59.42 | 66.05 | 94.22 | 88.56 | 86.74 | 80.17 |
| 6 | 60 | 89.58 | 60.76 | 93.40 | 79.17 | 52.78 | 62.85 | 91.32 | 86.81 | 87.85 | 78.28 |
| 6 | 70 | 90.04 | 60.07 | 93.04 | 79.39 | 53.99 | 66.05 | 92.42 | 87.08 | 86.36 | 78.71 |
| 6 | 80 | 87.54 | 60.78 | 93.77 | 78.07 | 51.81 | 66.51 | 87.73 | 88.56 | 88.26 | 78.11 |
| 6 | 90 | 85.77 | 58.30 | 93.41 | 76.32 | 49.64 | 65.58 | 84.84 | 89.30 | 86.36 | 76.61 |
| 6 | 100 | 85.05 | 53.36 | 93.41 | 72.81 | 47.10 | 65.12 | 81.59 | 85.98 | 87.88 | 74.70 |
| 7 | 20 | 89.32 | 61.48 | 93.04 | 85.96 | 75.00 | 70.70 | 95.31 | 86.72 | 87.12 | 82.74 |
| 7 | 30 | 89.68 | 59.72 | 93.41 | 85.09 | 69.93 | 67.91 | 94.95 | 86.72 | 87.88 | 81.70 |
| 7 | 40 | 91.10 | 59.01 | 94.14 | 84.21 | 68.48 | 64.65 | 93.86 | 87.45 | 86.74 | 81.07 |
| 7 | 50 | 91.10 | 60.07 | 93.41 | 84.21 | 64.49 | 66.05 | 91.34 | 87.45 | 86.74 | 80.54 |
| 7 | 60 | 89.68 | 60.78 | 93.04 | 84.21 | 60.14 | 66.98 | 92.78 | 88.93 | 85.98 | 80.28 |
| 7 | 70 | 89.32 | 58.66 | 93.41 | 81.14 | 54.71 | 67.44 | 93.14 | 87.45 | 85.98 | 79.03 |
| 7 | 80 | 90.04 | 59.36 | 92.67 | 80.70 | 53.62 | 69.30 | 88.09 | 87.08 | 87.88 | 78.75 |
| 7 | 90 | 87.90 | 61.84 | 92.31 | 78.07 | 50.36 | 65.12 | 90.25 | 88.93 | 87.50 | 78.03 |
| 7 | 100 | 85.41 | 60.07 | 93.41 | 77.19 | 48.55 | 63.72 | 85.56 | 88.93 | 88.26 | 76.79 |
| 8 | 20 | 90.28 | 59.72 | 93.75 | 82.29 | 69.10 | 63.54 | 95.49 | 88.54 | 87.85 | 81.17 |
| 8 | 30 | 91.10 | 61.48 | 93.41 | 85.53 | 71.38 | 65.58 | 94.58 | 86.72 | 86.74 | 81.84 |
| 8 | 40 | 90.04 | 62.90 | 93.04 | 83.33 | 69.20 | 67.91 | 94.22 | 88.19 | 88.26 | 81.90 |
| 8 | 50 | 91.81 | 60.78 | 93.77 | 82.89 | 67.75 | 65.58 | 93.14 | 87.08 | 85.61 | 80.94 |
| 8 | 60 | 91.10 | 60.78 | 93.77 | 82.46 | 62.32 | 65.58 | 93.14 | 87.82 | 86.74 | 80.41 |
| 8 | 70 | 89.68 | 59.72 | 92.31 | 82.02 | 57.97 | 66.51 | 91.70 | 88.56 | 87.50 | 79.55 |
| 8 | 80 | 90.39 | 59.01 | 93.41 | 82.02 | 56.16 | 66.51 | 91.34 | 87.45 | 85.61 | 79.10 |
| 8 | 90 | 90.04 | 58.66 | 92.67 | 80.70 | 55.80 | 68.37 | 89.17 | 86.72 | 87.50 | 78.85 |
| 8 | 100 | 88.97 | 60.78 | 92.31 | 75.44 | 51.81 | 66.05 | 91.34 | 88.56 | 87.12 | 78.04 |
Appendix C. EEG-TCNTransformer Training Results
Appendix C.1. Experiment EEG-TCNTransformer with Different Hyperparameters
| T | k | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 85.41 | 60.42 | 91.21 | 79.82 | 56.52 | 60.00 | 85.20 | 84.87 | 79.17 | 75.85 |
| 1 | 20 | 82.56 | 66.43 | 92.67 | 78.07 | 63.41 | 59.07 | 86.28 | 85.61 | 76.89 | 76.78 |
| 1 | 30 | 85.05 | 66.08 | 91.94 | 84.21 | 74.64 | 66.98 | 88.81 | 84.13 | 83.33 | 80.57 |
| 1 | 40 | 84.34 | 69.26 | 93.41 | 81.14 | 76.09 | 59.07 | 90.25 | 85.24 | 84.85 | 80.40 |
| 1 | 50 | 85.05 | 62.19 | 93.41 | 80.26 | 76.81 | 57.67 | 89.17 | 84.50 | 84.85 | 79.32 |
| 1 | 60 | 87.19 | 66.08 | 93.41 | 80.70 | 78.26 | 64.65 | 89.53 | 85.61 | 87.50 | 81.44 |
| 1 | 70 | 83.99 | 66.43 | 95.24 | 77.63 | 77.54 | 65.12 | 89.17 | 86.72 | 88.26 | 81.12 |
| 1 | 80 | 86.48 | 63.96 | 95.60 | 79.39 | 76.45 | 66.98 | 90.25 | 84.50 | 87.88 | 81.28 |
| 1 | 90 | 85.41 | 63.60 | 95.24 | 80.26 | 77.54 | 59.53 | 91.34 | 88.19 | 87.50 | 80.96 |
| 1 | 100 | 87.54 | 61.84 | 94.87 | 81.58 | 77.90 | 58.14 | 90.97 | 86.72 | 84.85 | 80.49 |
| 2 | 10 | 85.77 | 65.02 | 90.48 | 70.18 | 68.12 | 58.60 | 89.53 | 84.87 | 76.14 | 76.52 |
| 2 | 20 | 85.05 | 71.38 | 92.31 | 80.70 | 66.30 | 64.65 | 87.73 | 86.35 | 76.89 | 79.04 |
| 2 | 30 | 83.63 | 67.49 | 93.04 | 84.21 | 81.52 | 65.12 | 89.53 | 86.35 | 78.03 | 80.99 |
| 2 | 40 | 83.27 | 66.43 | 94.14 | 82.46 | 84.06 | 67.44 | 88.81 | 84.50 | 83.33 | 81.60 |
| 2 | 50 | 84.34 | 68.90 | 93.41 | 82.89 | 81.16 | 65.12 | 89.17 | 85.98 | 86.74 | 81.97 |
| 2 | 60 | 83.27 | 67.14 | 93.41 | 86.40 | 80.43 | 66.05 | 92.78 | 86.72 | 87.88 | 82.68 |
| 2 | 70 | 86.48 | 65.37 | 94.51 | 84.21 | 80.80 | 68.37 | 89.53 | 85.98 | 87.88 | 82.57 |
| 2 | 80 | 86.48 | 66.43 | 94.87 | 84.21 | 81.52 | 62.33 | 89.89 | 85.98 | 87.88 | 82.18 |
| 2 | 90 | 83.63 | 65.02 | 94.51 | 83.33 | 81.16 | 64.19 | 90.25 | 86.72 | 87.50 | 81.81 |
| 2 | 100 | 85.77 | 64.66 | 94.51 | 83.77 | 80.80 | 67.44 | 87.73 | 87.82 | 86.74 | 82.14 |
| 3 | 10 | 80.07 | 72.79 | 90.48 | 71.05 | 67.39 | 58.14 | 89.17 | 81.92 | 74.62 | 76.18 |
| 3 | 20 | 84.70 | 68.55 | 93.77 | 79.82 | 72.10 | 63.72 | 90.97 | 83.03 | 73.11 | 78.86 |
| 3 | 30 | 87.19 | 65.72 | 94.87 | 83.77 | 80.80 | 69.30 | 91.70 | 85.24 | 79.92 | 82.06 |
| 3 | 40 | 88.61 | 66.08 | 94.51 | 87.28 | 79.35 | 68.37 | 91.34 | 84.87 | 84.85 | 82.81 |
| 3 | 50 | 86.12 | 67.49 | 93.77 | 83.33 | 83.70 | 66.98 | 89.89 | 87.45 | 85.98 | 82.75 |
| 3 | 60 | 83.99 | 66.43 | 93.41 | 80.70 | 81.52 | 65.58 | 89.53 | 86.35 | 87.12 | 81.63 |
| 3 | 70 | 87.90 | 68.90 | 94.51 | 82.02 | 81.88 | 68.37 | 89.53 | 88.56 | 89.02 | 83.41 |
| 3 | 80 | 82.21 | 67.14 | 91.94 | 81.58 | 82.25 | 63.26 | 89.89 | 86.35 | 87.12 | 81.30 |
| 3 | 90 | 86.83 | 65.72 | 93.77 | 82.46 | 78.99 | 68.37 | 83.03 | 87.45 | 89.39 | 81.78 |
| 3 | 100 | 85.41 | 62.19 | 93.04 | 82.89 | 78.62 | 66.05 | 88.81 | 86.72 | 87.50 | 81.25 |
Appendix C.2. Experiment EEG-TCNTransformer with Different Parameters of Chebyshev Type 2 Filter
| T | k | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | Average Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 79.72 | 53.71 | 90.48 | 76.32 | 68.84 | 54.42 | 81.59 | 78.97 | 86.74 | 74.53 |
| 2 | 10 | 83.63 | 63.25 | 93.41 | 79.39 | 76.45 | 61.86 | 91.34 | 85.98 | 87.12 | 80.27 |
| 3 | 10 | 79.72 | 54.42 | 87.91 | 82.02 | 74.28 | 55.35 | 85.56 | 80.07 | 83.71 | 75.89 |
| 4 | 10 | 81.85 | 66.43 | 93.41 | 71.93 | 78.62 | 63.26 | 90.25 | 83.39 | 86.36 | 79.50 |
| 5 | 10 | 77.94 | 59.01 | 92.31 | 78.51 | 77.17 | 61.86 | 87.73 | 83.76 | 85.61 | 78.21 |
| 6 | 10 | 80.07 | 63.25 | 93.77 | 75.00 | 77.17 | 63.26 | 87.36 | 82.29 | 87.12 | 78.81 |
| 7 | 10 | 78.29 | 62.19 | 91.58 | 77.19 | 77.90 | 63.26 | 89.89 | 83.39 | 84.85 | 78.73 |
| 8 | 10 | 78.29 | 61.13 | 93.77 | 80.26 | 75.00 | 64.19 | 89.17 | 83.39 | 87.50 | 79.19 |
| 9 | 10 | 80.07 | 61.84 | 91.21 | 79.39 | 79.71 | 63.72 | 89.89 | 83.76 | 86.74 | 79.59 |
| 10 | 10 | 79.00 | 62.90 | 93.41 | 80.70 | 71.74 | 62.33 | 89.17 | 83.39 | 85.61 | 78.69 |
| 1 | 20 | 78.65 | 56.89 | 90.11 | 66.23 | 66.30 | 59.07 | 74.01 | 77.86 | 87.88 | 73.00 |
| 2 | 20 | 79.00 | 56.54 | 93.41 | 78.51 | 73.55 | 64.65 | 89.53 | 81.92 | 86.74 | 78.21 |
| 3 | 20 | 78.65 | 52.30 | 89.38 | 75.44 | 57.25 | 52.09 | 80.14 | 79.70 | 86.36 | 72.37 |
| 4 | 20 | 77.58 | 54.77 | 89.01 | 73.25 | 67.03 | 53.02 | 87.36 | 80.44 | 86.36 | 74.31 |
| 5 | 20 | 80.07 | 54.42 | 85.71 | 77.19 | 68.12 | 50.70 | 83.03 | 79.34 | 84.85 | 73.71 |
| 6 | 20 | 81.14 | 54.42 | 89.38 | 70.61 | 69.57 | 53.02 | 86.64 | 80.44 | 86.74 | 74.66 |
| 7 | 20 | 80.07 | 53.71 | 86.45 | 75.00 | 63.77 | 51.16 | 83.39 | 81.55 | 85.23 | 73.37 |
| 8 | 20 | 80.43 | 53.00 | 88.64 | 75.88 | 69.93 | 51.16 | 84.12 | 80.44 | 86.74 | 74.48 |
| 9 | 20 | 79.00 | 53.00 | 87.55 | 74.12 | 65.22 | 53.95 | 84.48 | 81.18 | 86.74 | 73.92 |
| 10 | 20 | 80.07 | 53.71 | 89.01 | 75.44 | 67.03 | 48.37 | 82.67 | 81.18 | 86.36 | 73.76 |
| 1 | 30 | 78.29 | 54.42 | 90.48 | 51.75 | 63.04 | 56.28 | 74.01 | 78.97 | 88.26 | 70.61 |
| 2 | 30 | 76.16 | 54.42 | 90.84 | 76.32 | 72.46 | 68.37 | 85.92 | 79.70 | 87.12 | 76.81 |
| 3 | 30 | 78.65 | 54.42 | 90.84 | 76.32 | 51.09 | 53.02 | 75.09 | 79.34 | 86.74 | 71.72 |
| 4 | 30 | 79.72 | 53.71 | 89.74 | 78.51 | 55.43 | 53.02 | 85.56 | 79.34 | 86.74 | 73.53 |
| 5 | 30 | 77.58 | 50.53 | 90.84 | 75.88 | 52.90 | 51.16 | 81.59 | 79.34 | 86.36 | 71.80 |
| 6 | 30 | 79.72 | 50.88 | 90.48 | 76.32 | 51.45 | 46.98 | 84.12 | 79.70 | 85.61 | 71.69 |
| 7 | 30 | 79.00 | 50.88 | 87.18 | 77.63 | 56.52 | 46.05 | 79.78 | 79.70 | 85.61 | 71.37 |
| 8 | 30 | 79.72 | 51.24 | 87.18 | 72.81 | 52.54 | 46.98 | 86.28 | 80.07 | 85.61 | 71.38 |
| 9 | 30 | 79.72 | 50.88 | 86.08 | 79.39 | 56.16 | 47.44 | 83.39 | 80.07 | 85.98 | 72.12 |
| 10 | 30 | 79.72 | 49.12 | 87.18 | 71.05 | 53.26 | 49.77 | 83.75 | 80.07 | 86.36 | 71.14 |
References
- Zhang, X.; Zhang, T.; Jiang, Y.; Zhang, W.; Lu, Z.; Wang, Y.; Tao, Q. A novel brain-controlled prosthetic hand method integrating AR-SSVEP augmentation, asynchronous control, and machine vision assistance. Heliyon 2024, 10, e26521. [Google Scholar] [CrossRef] [PubMed]
- Chai, R.; Ling, S.H.; Hunter, G.P.; Tran, Y.; Nguyen, H.T. Brain-Computer Interface Classifier for Wheelchair Commands Using Neural Network with Fuzzy Particle Swarm Optimization. IEEE J. Biomed. Health Inform. 2014, 18, 1614–1624. [Google Scholar] [CrossRef] [PubMed]
- Ferrero, L.; Soriano-Segura, P.; Navarro, J.; Jones, O.; Ortiz, M.; Iáñez, E.; Azorín, J.M.; Contreras-Vidal, J.L. Brain–machine interface based on deep learning to control asynchronously a lower-limb robotic exoskeleton: A case-of-study. J. Neuroeng. Rehabil. 2024, 21, 48. [Google Scholar] [CrossRef]
- Armour, B.S.; Courtney-Long, E.A.; Fox, M.H.; Fredine, H.; Cahill, A. Prevalence and causes of paralysis—United States, 2013. Am. J. Public Health 2016, 106, 1855–1857. [Google Scholar] [CrossRef] [PubMed]
- Berger, H. Über das Elektrenkephalogramm des Menschen. Arch. Psychiatr. Nervenkrankh. 1929, 87, 527–570. [Google Scholar] [CrossRef]
- Hicks, R.J. Principles and Practice of Positron Emission Tomography. J. Nucl. Med. 2004, 45, 1973–1974. [Google Scholar]
- Mellinger, J.; Schalk, G.; Braun, C.; Preissl, H.; Rosenstiel, W.; Birbaumer, N.; Kübler, A. An MEG-based brain-computer interface (BCI). NeuroImage 2007, 36, 581–593. [Google Scholar] [CrossRef]
- Naseer, N.; Hong, K.S. fNIRS-based brain-computer interfaces: A review. Front. Hum. Neurosci. 2015, 9, 3. [Google Scholar] [CrossRef]
- Sorger, B.; Reithler, J.; Dahmen, B.; Goebel, R. A Real-Time fMRI-Based Spelling Device Immediately Enabling Robust Motor-Independent Communication. Curr. Biol. 2012, 22, 1333–1338. [Google Scholar] [CrossRef]
- Ramoser, H.; Muller-Gerking, J.; Pfurtscheller, G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabil. Eng. 2000, 8, 441–446. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter Bank Common Spatial Pattern (FBCSP) in Brain-Computer Interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 2390–2397. [Google Scholar] [CrossRef]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2017, 14, 016003. [Google Scholar] [CrossRef] [PubMed]
- Ieracitano, C.; Mammone, N.; Hussain, A.; Morabito, F.C. A novel multi-modal machine learning based approach for automatic classification of EEG recordings in dementia. Neural Netw. 2020, 123, 176–190. [Google Scholar] [CrossRef] [PubMed]
- Kousarrizi, M.R.N.; Ghanbari, A.A.; Teshnehlab, M.; Shorehdeli, M.A.; Gharaviri, A. Feature Extraction and Classification of EEG Signals Using Wavelet Transform, SVM and Artificial Neural Networks for Brain Computer Interfaces. In Proceedings of the 2009 International Joint Conference on Bioinformatics, Systems Biology and Intelligent Computing, Shanghai, China, 3–5 August 2009; pp. 352–355. [Google Scholar] [CrossRef]
- Chen, C.Y.; Wu, C.W.; Lin, C.T.; Chen, S.A. A novel classification method for motor imagery based on Brain-Computer Interface. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 4099–4102. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain-computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef] [PubMed]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Ingolfsson, T.M.; Hersche, M.; Wang, X.; Kobayashi, N.; Cavigelli, L.; Benini, L. EEG-TCNet: An Accurate Temporal Convolutional Network for Embedded Motor-Imagery Brain-Machine Interfaces; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020; pp. 2958–2965. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Umirzakova, S.; Whangbo, T.K. Detailed feature extraction network-based fine-grained face segmentation. Knowl.-Based Syst. 2022, 250, 109036. [Google Scholar] [CrossRef]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M.; Amin, S.U.; Altuwaijri, G.A.; Abdul, W.; Bencherif, M.A.; Faisal, M. Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: A review. Neural Comput. Appl. 2023, 35, 14681–14722. [Google Scholar] [CrossRef]
- Pfeffer, M.A.; Ling, S.S.H.; Wong, J.K.W. Exploring the frontier: Transformer-based models in EEG signal analysis for brain-computer interfaces. Comput. Biol. Med. 2024, 178, 108705. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Wang, Y.; Liu, B.; Bao, X. EEG Classification Algorithm of Motor Imagery Based on CNN-Transformer Fusion Network; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022; pp. 1302–1309. [Google Scholar] [CrossRef]
- Ma, Y.; Song, Y.; Gao, F. A Novel Hybrid CNN-Transformer Model for EEG Motor Imagery Classification; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q.; Liu, B.; Gao, X. EEG Conformer: Convolutional Transformer for EEG Decoding and Visualization. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 710–719. [Google Scholar] [CrossRef]
- Brunner, C.; Leeb, R.; Müller-Putz, G. BCI Competition 2008–Graz Data Set A; Institute for Knowledge Discovery, Graz University of Technology: Graz, Austria, 2024. [Google Scholar] [CrossRef]
- Wriessnegger, S.C.; Brunner, C.; Müller-Putz, G.R. Frequency specific cortical dynamics during motor imagery are influenced by prior physical activity. Front. Psychol. 2018, 9, 1976. [Google Scholar] [CrossRef] [PubMed]
- Ouadfeul, S.A.; Aliouane, L. Wave-Number Filtering; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Lotte, F. Signal processing approaches to minimize or suppress calibration time in oscillatory activity-based brain-computer interfaces. Proc. IEEE 2015, 103, 871–890. [Google Scholar] [CrossRef]



| Layer | Type | Filter | Kernel | Output |
|---|---|---|---|---|
| Input | (1, C, T) | |||
| Conv2D | (1, ) | (, C, T) | ||
| BatchNorm | ||||
| DepthwiseConv2D | (C, 1) | (, 1, T) | ||
| BatchNorm | ||||
| EluAct | ||||
| AveragePool2D | (, 1, T//8) | |||
| Dropout | ||||
| SeparableConv2D | (1, 16) | (, 1, T//8) | ||
| BatchNorm | ||||
| EluAct | ||||
| AveragePool2D | (, 1, T//64) | |||
| Dropout | ||||
| TCN | ||||
| Dense | 4 | |||
| SoftMaxAct |
| EEGNet module | 6, 8, 10 | |
| 16, 32, 48 | ||
| TCN module | 10, 12, 14 | |
| 4, 6, 8 |
| Average Accuracy (%) | ||||
|---|---|---|---|---|
| 6 | 75.38 | |||
| 8 | 32 | 12 | 4 | 76.55 |
| 10 | 78.04 | |||
| 16 | 76.66 | |||
| 8 | 32 | 12 | 4 | 76.55 |
| 48 | 77.05 | |||
| 10 | 77.99 | |||
| 8 | 32 | 12 | 4 | 76.55 |
| 14 | 78.58 | |||
| 4 | 76.55 | |||
| 8 | 32 | 12 | 6 | 79.96 |
| 8 | 78.59 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | |
|---|---|---|---|---|---|---|---|---|---|
| 6 | 10 | 6 | 6 | 8 | 10 | 10 | 10 | 8 | |
| 48 | 48 | 32 | 32 | 32 | 48 | 16 | 48 | 32 | |
| 12 | 12 | 14 | 14 | 10 | 12 | 12 | 14 | 14 | |
| 6 | 6 | 6 | 6 | 8 | 8 | 4 | 6 | 4 |
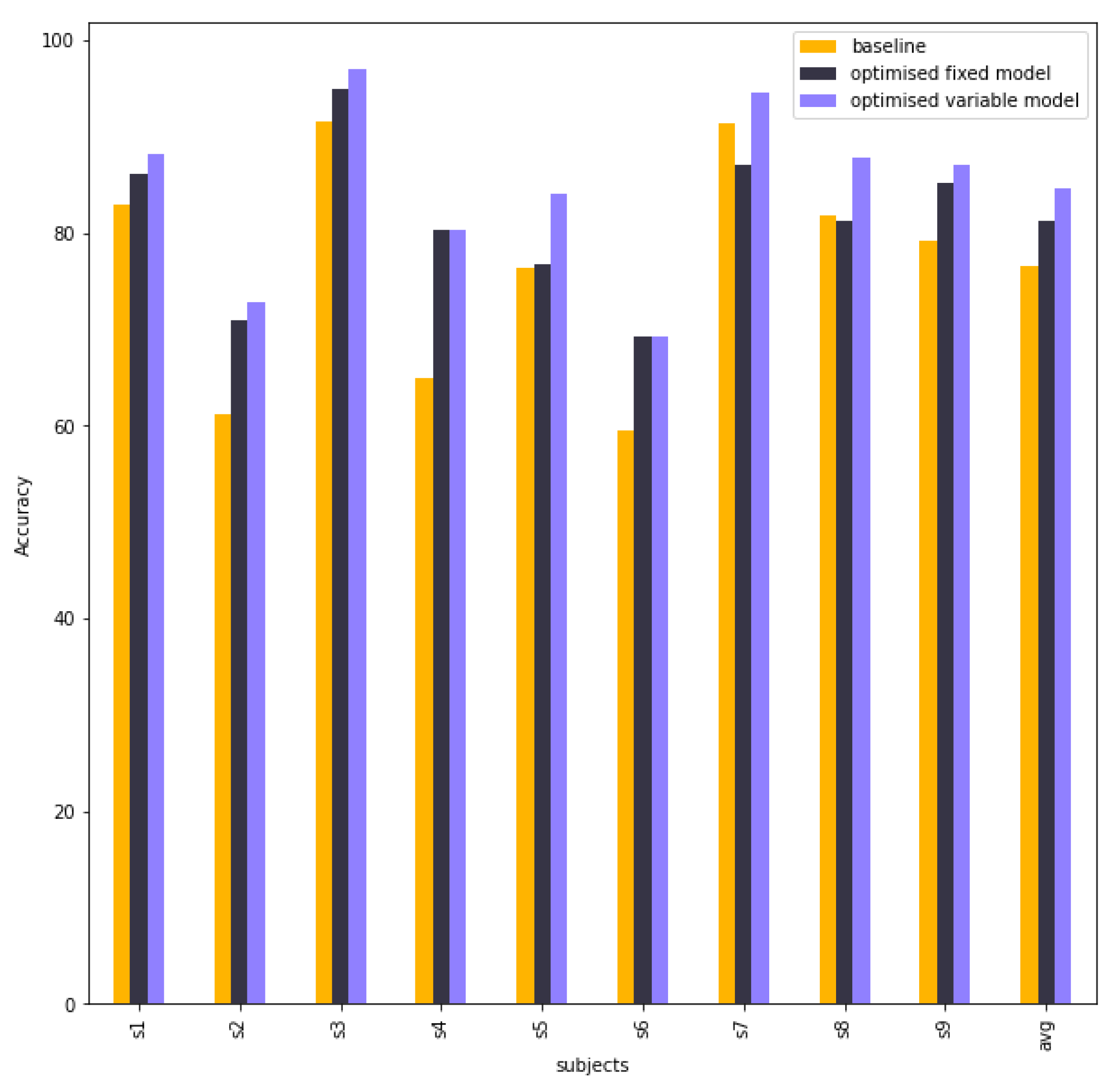
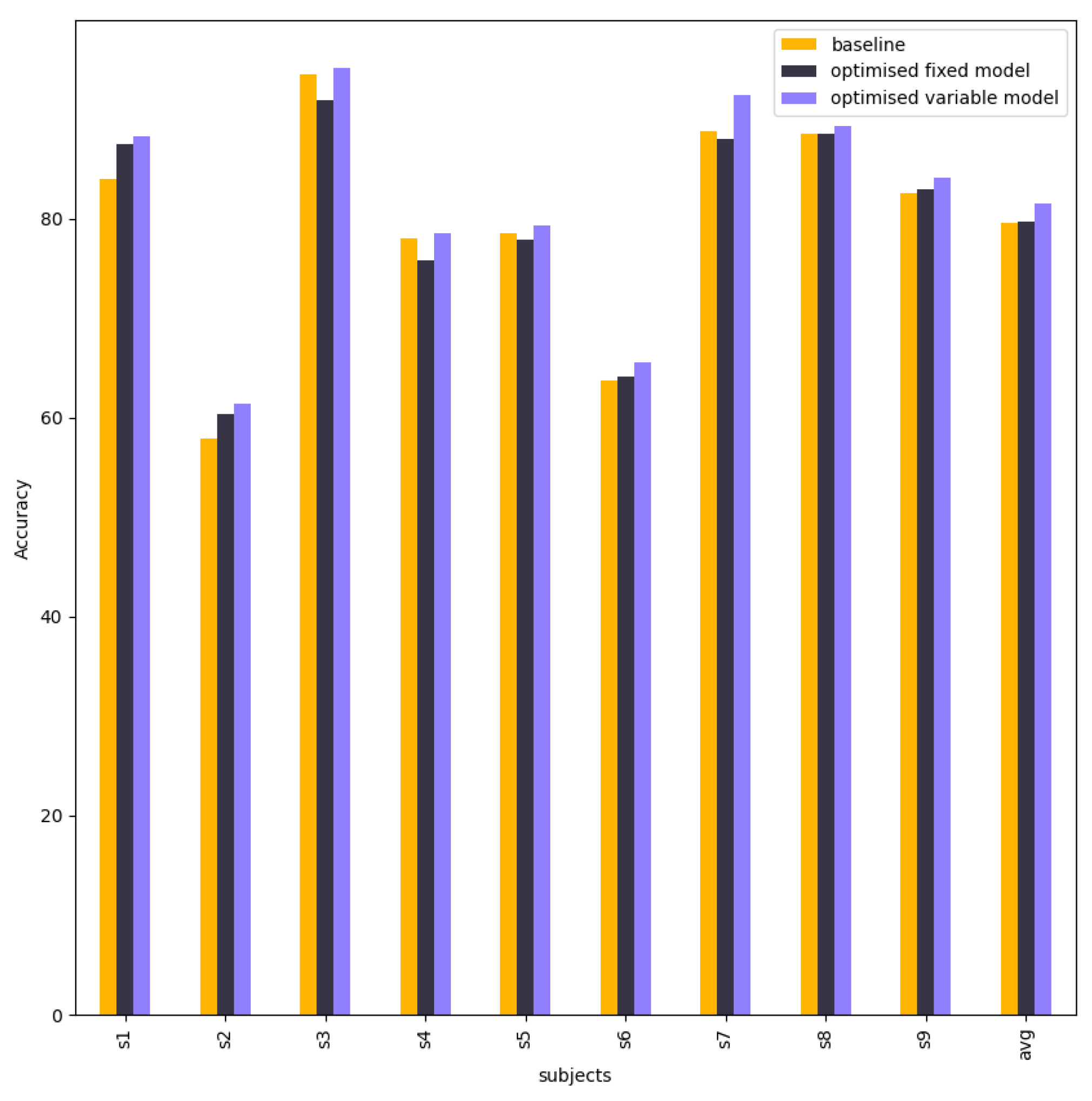
| Subject | Baseline | Fixed Model | Variable Model |
|---|---|---|---|
| S1 | 82.92 | 86.12 | 88.26 |
| S2 | 61.13 | 71.02 | 72.79 |
| S3 | 91.58 | 94.87 | 97.07 |
| S4 | 64.91 | 80.26 | 80.26 |
| S5 | 76.45 | 76.81 | 84.06 |
| S6 | 59.53 | 69.30 | 69.30 |
| S7 | 91.34 | 87.00 | 94.58 |
| S8 | 81.92 | 81.18 | 87.82 |
| S9 | 79.17 | 85.23 | 87.12 |
| Average | 76.55 | 81.31 | 84.59 |
| N | 4, 5, 6, 7, 8 |
| 20, 30, 40, 50, 60. 70, 80, 90, 100 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | |
|---|---|---|---|---|---|---|---|---|---|
| N | 5 | 6 | 5 | 7 | 7 | 6 | 6 | 4 | 8 |
| 80 | 20 | 100 | 40 | 40 | 90 | 20 | 60 | 80 |
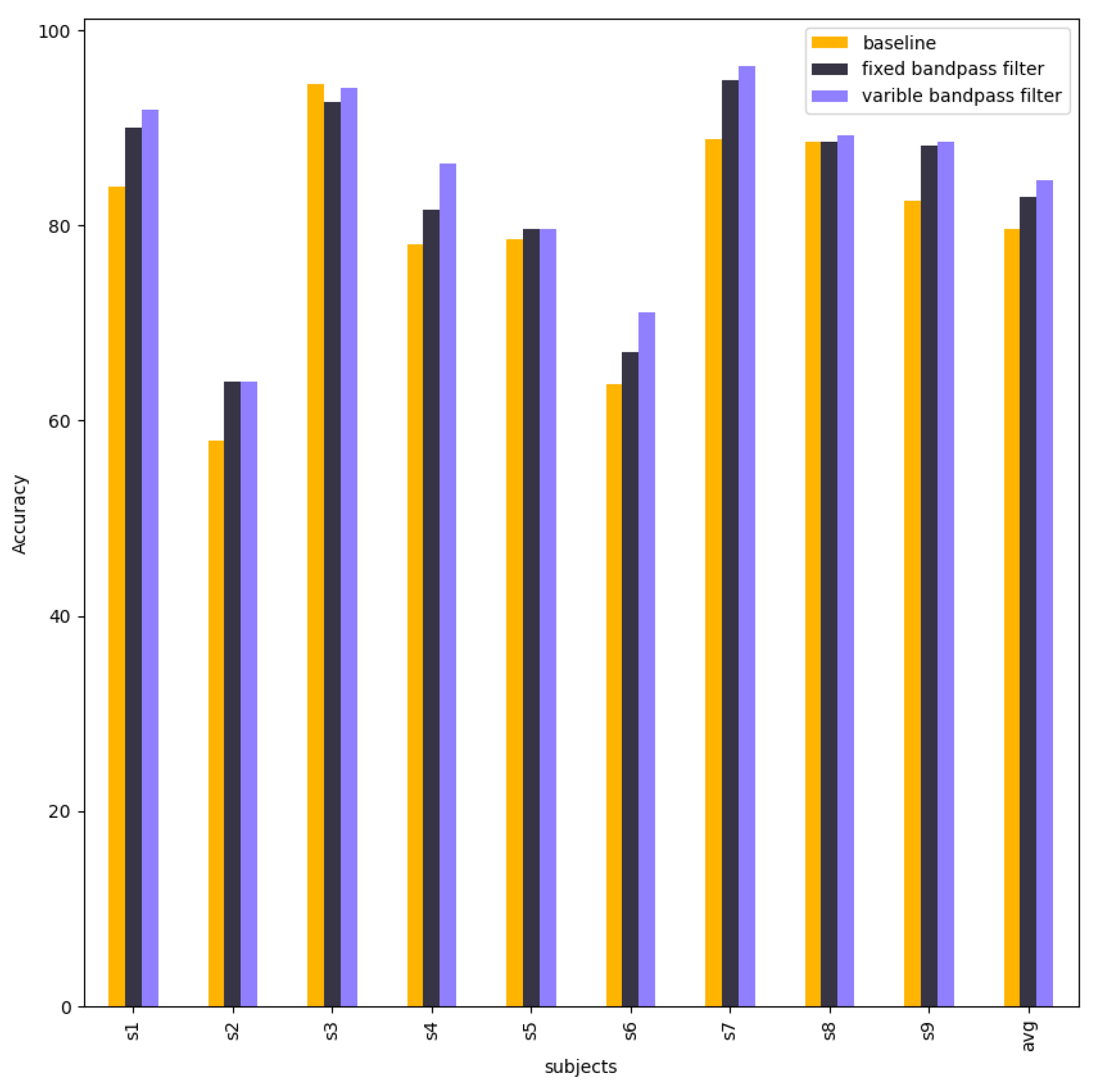
| Subject | Baseline | Fixed Bandpass Filter | Variable Bandpass Filter |
|---|---|---|---|
| S1 | 82.92 | 79.00 | 82.21 |
| S2 | 61.13 | 51.94 | 56.18 |
| S3 | 91.58 | 90.48 | 94.51 |
| S4 | 64.91 | 72.37 | 72.37 |
| S5 | 76.45 | 56.88 | 56.88 |
| S6 | 59.53 | 51.16 | 54.88 |
| S7 | 91.34 | 82.67 | 84.84 |
| S8 | 81.92 | 82.29 | 85.24 |
| S9 | 79.17 | 78.79 | 84.85 |
| Average | 76.55 | 71.73 | 74.66 |
| Layer | In | Out | Kernel | Stride |
|---|---|---|---|---|
| Temporal Conv | 1 | k | (1, 25) | (1, 1) |
| Spatial Conv | k | k | (, 1) | (1, 1) |
| Avg Pooling | k | k | (1, 75) | (1, 15) |
| Rearrange | (k, 1, m) → (m, k) | |||
| k | 20, 30, 40, 50, 60 |
| N | 6, 7, 8, 9, 10 |
| k | N | Average Accuracy (%) |
|---|---|---|
| 20 | 78.66 | |
| 30 | 78.02 | |
| 40 | 6 | 79.64 |
| 50 | 77.86 | |
| 60 | 77.74 | |
| 6 | 79.64 | |
| 7 | 78.27 | |
| 40 | 8 | 78.50 |
| 9 | 78.58 | |
| 10 | 78.65 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | |
|---|---|---|---|---|---|---|---|---|---|
| k | 20 | 20 | 30 | 40 | 40 | 20 | 30 | 40 | 30 |
| N | 6 | 8 | 6 | 10 | 10 | 9 | 10 | 7 | 10 |
| Subject | Baseline | Fixed Model | Variable Model |
|---|---|---|---|
| S1 | 83.99 | 87.54 | 88.26 |
| S2 | 57.95 | 60.42 | 61.48 |
| S3 | 94.51 | 91.94 | 95.24 |
| S4 | 78.07 | 75.88 | 78.51 |
| S5 | 78.62 | 77.90 | 79.35 |
| S6 | 63.72 | 64.19 | 65.58 |
| S7 | 88.81 | 88.09 | 92.42 |
| S8 | 88.56 | 88.56 | 89.30 |
| S9 | 82.58 | 82.95 | 84.09 |
| Average | 79.64 | 79.72 | 81.58 |
| N | 4, 5, 6, 7, 8 |
| 20, 30, 40, 50, 60, 70, 80, 90, 100 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | |
|---|---|---|---|---|---|---|---|---|---|
| N | 5 | 4 | 5 | 5 | 4 | 5 | 6 | 6 | 5 |
| 30 | 20 | 40 | 20 | 20 | 20 | 20 | 90 | 90 |
| Subject | Baseline | Fixed Bandpass Filter | Variable Bandpass Filter |
|---|---|---|---|
| S1 | 83.99 | 90.04 | 91.81 |
| S2 | 57.95 | 63.96 | 63.96 |
| S3 | 94.51 | 92.67 | 94.14 |
| S4 | 78.07 | 81.58 | 86.40 |
| S5 | 78.62 | 79.71 | 79.71 |
| S6 | 63.72 | 66.98 | 71.16 |
| S7 | 88.81 | 94.95 | 96.39 |
| S8 | 88.56 | 88.56 | 89.30 |
| S9 | 82.58 | 88.26 | 88.64 |
| Average | 79.64 | 82.97 | 84.61 |
| k | T | |||
| 1 | 2 | 3 | ||
| 10 | 75.85 | 76.52 | 76.16 | |
| 20 | 76.78 | 79.04 | 78.86 | |
| 30 | 80.57 | 80.99 | 82.06 | |
| 40 | 80.40 | 81.60 | 82.81 | |
| 50 | 79.32 | 81.96 | 82.75 | |
| 60 | 81.44 | 82.68 | 81.63 | |
| 70 | 81.12 | 82.57 | 83.41 | |
| 80 | 81.28 | 82.18 | 81.30 | |
| 90 | 80.96 | 81.81 | 81.78 | |
| 100 | 80.49 | 82.13 | 81.25 | |
| Subject | EEG-TCNet | EEG-Conformer | EEG-TCNTransformer (Confidence Interval (%)) |
|---|---|---|---|
| S1 | 82.92 | 83.99 | 87.90 (95.48) |
| S2 | 61.13 | 57.95 | 68.90 (93.59) |
| S3 | 91.58 | 94.51 | 94.51 (98.36) |
| S4 | 64.91 | 78.07 | 82.02 (94.64) |
| S5 | 76.45 | 78.62 | 81.88 (93.59) |
| S6 | 59.53 | 63.72 | 68.37 (93.04) |
| S7 | 91.34 | 88.81 | 89.53 (95.87) |
| S8 | 81.92 | 88.56 | 88.56 (96.59) |
| S9 | 79.17 | 82.58 | 89.02 (95.68) |
| Average | 76.55 | 79.64 | 83.41 (95.20) |
| EEG-TCNet | EEG-Conformer | EEG-TCNTransformer | |
|---|---|---|---|
| S1 | 84.60 | 83.92 | 87.90 |
| S2 | 66.57 | 58.00 | 69.16 |
| S3 | 91.98 | 94.47 | 94.50 |
| S4 | 69.95 | 78.03 | 81.75 |
| S5 | 79.21 | 78.67 | 81.88 |
| S6 | 64.36 | 63.74 | 68.33 |
| S7 | 91.97 | 88.90 | 89.65 |
| S8 | 82.36 | 88.57 | 88.64 |
| S9 | 80.62 | 82.60 | 89.02 |
| Average | 79.07 | 79.66 | 83.43 |
| EEG-TCNet | EEG-Conformer | EEG-TCNTransformer | |
|---|---|---|---|
| S1 | 82.94 | 84.69 | 87.84 |
| S2 | 61.31 | 58.66 | 71.28 |
| S3 | 91.55 | 94.54 | 94.78 |
| S4 | 64.30 | 78.14 | 82.46 |
| S5 | 76.53 | 78.88 | 81.95 |
| S6 | 59.74 | 63.98 | 70.47 |
| S7 | 91.44 | 88.27 | 89.90 |
| S8 | 81.98 | 89.51 | 88.64 |
| S9 | 79.23 | 83.81 | 89.09 |
| Average | 76.56 | 80.16 | 84.05 |
| EEG-TCNet | EEG-Conformer | EEG-TCNTransformer | |
|---|---|---|---|
| S1 | 82.90 | 83.96 | 87.85 |
| S2 | 61.51 | 57.95 | 68.18 |
| S3 | 91.45 | 94.48 | 94.48 |
| S4 | 61.62 | 78.06 | 81.73 |
| S5 | 75.05 | 78.60 | 81.80 |
| S6 | 58.78 | 63.75 | 68.19 |
| S7 | 91.43 | 88.80 | 89.51 |
| S8 | 82.08 | 88.84 | 88.53 |
| S9 | 79.38 | 82.14 | 89.00 |
| Average | 76.02 | 79.62 | 83.25 |
| N | ||||
| 10 | 20 | 30 | ||
| 1 | 74.53 | 73.00 | 70.61 | |
| 2 | 80.27 | 78.21 | 76.81 | |
| 3 | 75.89 | 72.37 | 71.72 | |
| 4 | 79.50 | 74.31 | 73.53 | |
| 5 | 78.21 | 73.71 | 71.80 | |
| 6 | 78.81 | 74.66 | 71.69 | |
| 7 | 78.73 | 73.37 | 71.37 | |
| 8 | 79.19 | 74.48 | 71.38 | |
| 9 | 79.59 | 73.92 | 72.12 | |
| 10 | 78.69 | 73.76 | 71.14 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, A.H.P.; Oyefisayo, O.; Pfeffer, M.A.; Ling, S.H. EEG-TCNTransformer: A Temporal Convolutional Transformer for Motor Imagery Brain–Computer Interfaces. Signals 2024, 5, 605-632. https://doi.org/10.3390/signals5030034
Nguyen AHP, Oyefisayo O, Pfeffer MA, Ling SH. EEG-TCNTransformer: A Temporal Convolutional Transformer for Motor Imagery Brain–Computer Interfaces. Signals. 2024; 5(3):605-632. https://doi.org/10.3390/signals5030034
Chicago/Turabian StyleNguyen, Anh Hoang Phuc, Oluwabunmi Oyefisayo, Maximilian Achim Pfeffer, and Sai Ho Ling. 2024. "EEG-TCNTransformer: A Temporal Convolutional Transformer for Motor Imagery Brain–Computer Interfaces" Signals 5, no. 3: 605-632. https://doi.org/10.3390/signals5030034
APA StyleNguyen, A. H. P., Oyefisayo, O., Pfeffer, M. A., & Ling, S. H. (2024). EEG-TCNTransformer: A Temporal Convolutional Transformer for Motor Imagery Brain–Computer Interfaces. Signals, 5(3), 605-632. https://doi.org/10.3390/signals5030034







