Adaptive Filtering for Multi-Track Audio Based on Time–Frequency Masking Detection
Abstract
1. Introduction
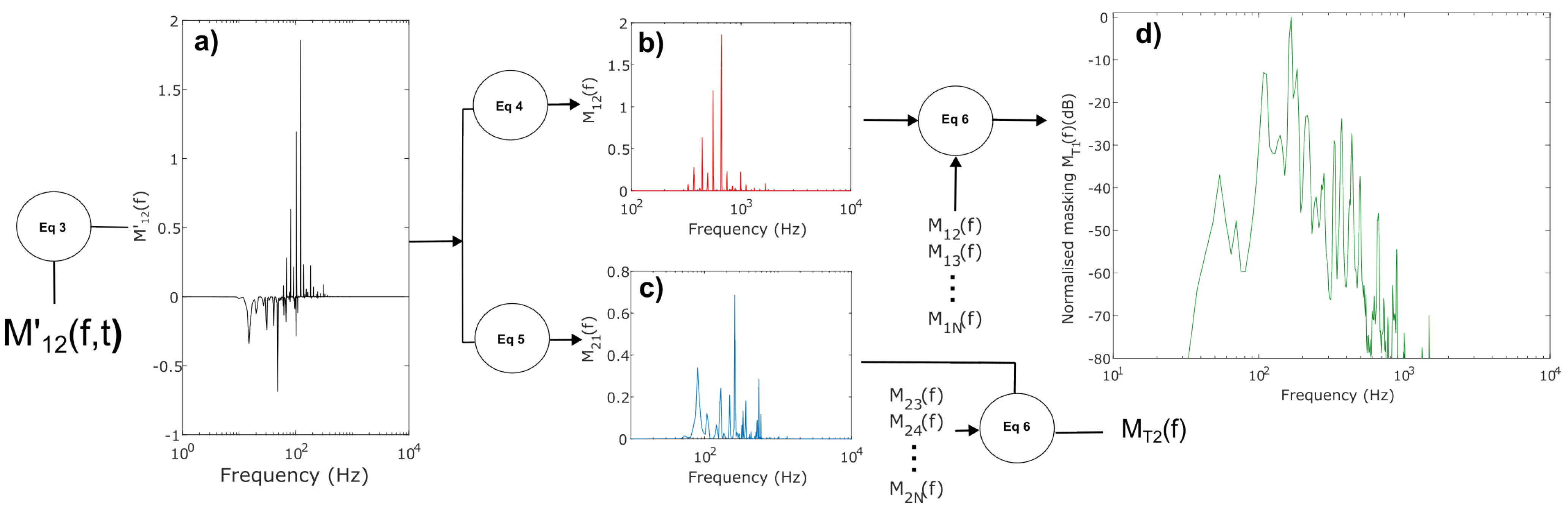
2. Evaluation of Masking and Filtering
- —this term evaluates how relevant it is to calculate masking at this specific time and frequency. For instance, if the amplitude of one track is close to zero, then masking would be small.
- —this term evaluates the relative magnitude and polarity of masking. Positive values for indicate this is the masker while negative indicates it is the maskee. This is an important term to differentiate the masker from the maskee at different times.
- —this is a normalisation term to ensure scale invariance that the same results will be provided if the same non-zero dB gain is applied to both tracks.
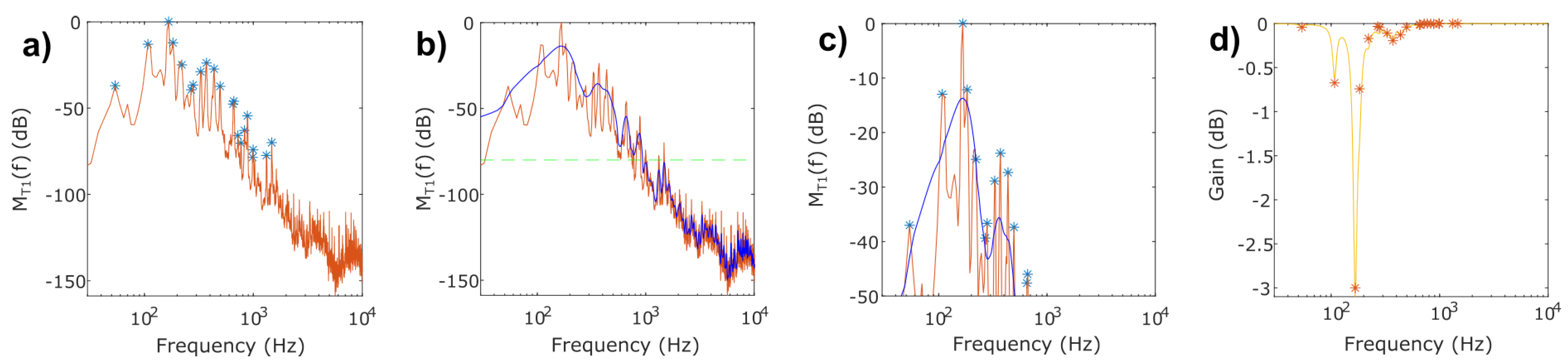
Filter Design
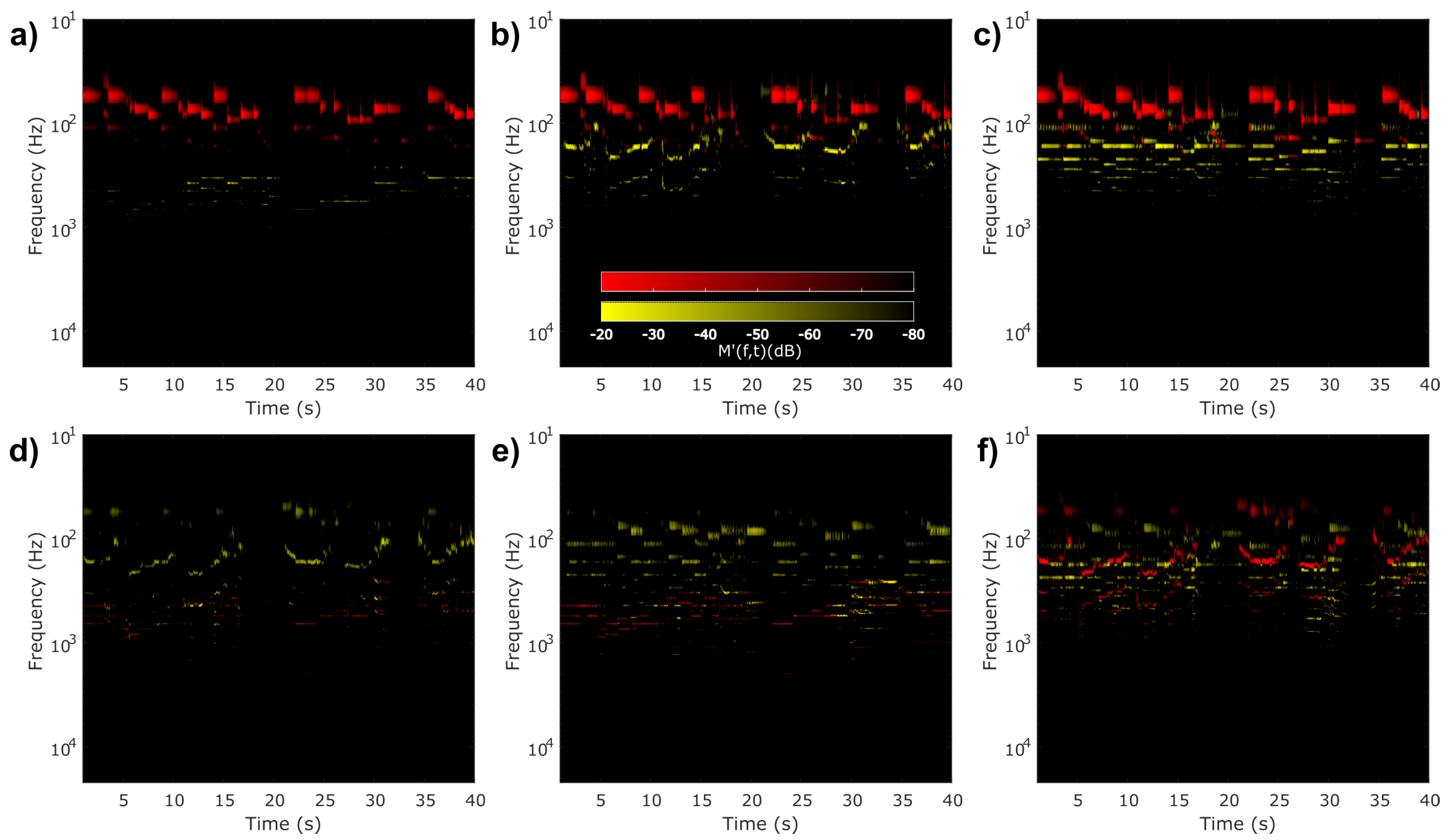
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hagen, A.N. Datafication, Literacy, and Democratization in the Music Industry. Pop. Music. Soc. 2022, 45, 184–201. [Google Scholar] [CrossRef]
- Eiriz, V.; Leite, F.P. The digital distribution of music and its impact on the business models of independent musicians. Serv. Ind. J. 2017, 37, 875–895. [Google Scholar] [CrossRef]
- Guo, X. The Evolution of the Music Industry in the Digital Age: From Records to Streaming. J. Sociol. Ethnol. 2023, 5, 7–12. [Google Scholar] [CrossRef]
- Owsinski, B. The Mixing Engineer’s Handbook; Bobby Owsinski Media Group: Burbank, CA, USA, 2022; p. 391. [Google Scholar]
- Steinmetz, C.J.; Pons, J.; Pascual, S.; Serrà, J. Automatic multitrack mixing with a differentiable mixing console of neural audio effects. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing Proceedings, Toronto, ON, Canada, 6–11 June 2021; pp. 71–75. [Google Scholar] [CrossRef]
- Zaknich, A.; Lee, G.E. An audio equalisation linear phase FIR filter design method using RBF based smoothing and interpolation. In Proceedings of the 4th International Conference on Intelligent Sensing and Information Processing, ICISIP 2006, Bangalore, India, 15 October–18 December 2006; pp. 109–114. [Google Scholar] [CrossRef]
- Välimäki, V.; Reiss, J.D. All About Audio Equalization: Solutions and Frontiers. Appl. Sci. 2016, 6, 129. [Google Scholar] [CrossRef]
- Perez-Gonzalez, E.; Reiss, J.D. Automatic Mixing. In DAFX: Digital Audio Effects: Second Edition; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 523–549. [Google Scholar] [CrossRef]
- Välimäki, V.; Parker, J.D.; Savioja, L.; Smith, J.O.; Abel, J.S. Fifty years of artificial reverberation. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1421–1448. [Google Scholar] [CrossRef]
- Tan, K.; Xu, Y.; Zhang, S.X.; Yu, M.; Yu, D. Audio-Visual Speech Separation and Dereverberation with a Two-Stage Multimodal Network. IEEE J. Sel. Top. Signal Process. 2020, 14, 542–553. [Google Scholar] [CrossRef]
- Schörkhuber, C.; Klapuri, A.; Sontacchi, A. Audio pitch shifting using the constant-q transform. J. Audio Eng. Soc. 2013, 61, 562–572. [Google Scholar]
- Wilmering, T.; Moffat, D.; Milo, A.; Sandler, M.B. A History of Audio Effects. Appl. Sci. 2020, 10, 791. [Google Scholar] [CrossRef]
- Senior, M. Mixing Secrets for the Small Studio; Routledge: New York, NY, USA, 2018; p. 432. [Google Scholar]
- Scott, J.J.; Kim, Y.E. Analysis of Acoustic Features for Automated Multi-Track Mixing. In Proceedings of the 12th International Society for Music Information Retrieval Conference (ISMIR 2011), Miami, FL, USA, 24–28 October 2011. [Google Scholar]
- Scott, J.J.; Prockup, M.; Schmidt, E.M.; Kim, Y.E. Automatic Multi-Track Mixing Using Linear Dynamical Systems. In Proceedings of the 8th Sound and Music Computing Conference, Padova, Italy, 6–9 July 2011. [Google Scholar]
- Wakefield, J.; Dewey, C. An Investigation into the Efficacy of Methods Commonly Employed by Mix Engineers to Reduce Frequency Masking in the Mixing of Multitrack Musical Recordings. In Proceedings of the Audio Engineering Society 138th European Convention, Warsaw, Poland, 7–10 May 2015. [Google Scholar]
- Reed, D. Perceptual assistant to do sound equalization. In Proceedings of the 5th International Conference on Intelligent User Interfaces, Proceedings IUI, New Orleans, LA, USA, 9–12 January 2000; pp. 212–218. [Google Scholar] [CrossRef]
- Greenwood, D.D. Auditory Masking and the Critical Band. J. Acoust. Soc. Am. 1961, 33, 484–502. [Google Scholar] [CrossRef]
- Gonzalez, E.P.; Reiss, J.D. Improved control for selective minimization of masking using inter-channel dependancy effects. In Proceedings of the 11th International Conference on Digital Audio Effects (DAFx-08), Espoo, Finland, 1–4 September 2008. [Google Scholar]
- Hafezi, S.; Reiss, J.D. Autonomous Multitrack Equalization Based on Masking Reduction. J. Audio Eng. Soc. 2015, 63, 312–323. [Google Scholar] [CrossRef]
- Wichern, G.; Robertson, H.; Wishnick, A. Quantitative analysis of masking in multitrack mixes using loudness loss. In Audio Engineering Society Convention 141; Audio Engineering Society: Cambridge, MA, USA, 2016; p. 9646. [Google Scholar]
- Tom, A.; Reiss, J.D.; Depalle, P. An Automatic Mixing System for Multitrack Spatialization for Stereo Based on Unmasking and Best Panning Practices. In Proceedings of the 146th AES Convention, Dublin, Ireland, 20–23 March 2019. [Google Scholar]
- Gullfoss DAW Plugin. Gullfoss Information Webpage. Soundtheory LTD. Available online: https://www.soundtheory.com/gullfoss (accessed on 8 May 2024).
- Soothe 2 DAW Plugin. Soothe 2 Information Webpage. Oeksound Ltd. Available online: https://oeksound.com/plugins/soothe2 (accessed on 6 May 2024).
- Reference DAW Plugin. Reference Information Webpage. Mastering the Mix LTD. Available online: https://www.masteringthemix.com/products/reference (accessed on 22 May 2024).
- Liu, W. Literature survey of multi-track music generation model based on generative confrontation network in intelligent composition. J. Supercomput. 2023, 79, 6560–6582. [Google Scholar] [CrossRef]
- Liu, X.; Mourgela, A.; Ai, H.; Reiss, J.D. An automatic mixing speech enhancement system for multi-track audio. arXiv 2024, arXiv:2404.17821. [Google Scholar] [CrossRef]
- Man, B.D.; Reiss, J.D.; Stables, R. Ten Years of Automatic Mixing. In Proceedings of the 3rd Workshop on Intelligent Music Production, Salford, UK, 15 September 2017. [Google Scholar]
- Xu, H.; Zhou, S.; Qin, W.; Litak, G. An Improved Interpolation Algorithm for the Damped Signal Based on Hann Window. In Proceedings of the 2022 14th International Conference on Signal Processing Systems, ICSPS 2022, Zhenjiang, China, 18–20 November 2022; pp. 269–277. [Google Scholar] [CrossRef]
- Huang, H.; Luo, J.; Moaveni, M.; Tutumluer, E.; Hart, J.M.; Beshears, S.; Stolba, A.J. Field Imaging and Volumetric Reconstruction of Riprap Rock and Large-Sized Aggregates: Algorithms and Application. Transp. Res. Rec. 2019, 2673, 575–589. [Google Scholar] [CrossRef]
- Orfanidis, S.J. High-Order Digital Parametric Equalizer Design. J. Audio Eng. Soc. 2015, 53, 1026–1046. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Pérez-Cota, F. Adaptive Filtering for Multi-Track Audio Based on Time–Frequency Masking Detection. Signals 2024, 5, 633-641. https://doi.org/10.3390/signals5040035
Zhao W, Pérez-Cota F. Adaptive Filtering for Multi-Track Audio Based on Time–Frequency Masking Detection. Signals. 2024; 5(4):633-641. https://doi.org/10.3390/signals5040035
Chicago/Turabian StyleZhao, Wenhan, and Fernando Pérez-Cota. 2024. "Adaptive Filtering for Multi-Track Audio Based on Time–Frequency Masking Detection" Signals 5, no. 4: 633-641. https://doi.org/10.3390/signals5040035
APA StyleZhao, W., & Pérez-Cota, F. (2024). Adaptive Filtering for Multi-Track Audio Based on Time–Frequency Masking Detection. Signals, 5(4), 633-641. https://doi.org/10.3390/signals5040035



