Next Article in Journal
Understanding How Image Quality Affects Transformer Neural Networks
Next Article in Special Issue
Daily Streamflow Forecasting Using AutoML and Remote-Sensing-Estimated Rainfall Datasets in the Amazon Biomes
Previous Article in Journal
Design of Infinite Impulse Response Filters Based on Multi-Objective Particle Swarm Optimization
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Signals
Volume 5
Issue 3
10.3390/signals5030030
signals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review of Rainfall Estimation in Indonesia: Data Sources, Techniques, and Methods

by
Maulana Putra
,
Mohammad Syamsu Rosid
and
Djati Handoko
*
Department of Physics, FMIPA Universitas Indonesia, Depok 16424, Indonesia
*
Author to whom correspondence should be addressed.
Signals 2024, 5(3), 542-561; https://doi.org/10.3390/signals5030030
Submission received: 6 June 2024 / Revised: 31 July 2024 / Accepted: 9 August 2024 / Published: 16 August 2024
(This article belongs to the Special Issue Rainfall Estimation Using Signals)
Browse Figures
Versions Notes

Abstract

:
Rainfall information with high spatial and temporal resolution are essential in various fields. Heavy rainfall in a short period can cause problems and disasters that result in loss of life and damage to property. Conversely, the absence of rain for an extended period can also have negative social and economic impacts. Data accuracy, wide spatial coverage, and high temporal resolution are challenges in obtaining rainfall information in Indonesia. This article presents information on data sources and methods for measuring rainfall and reviews the latest research regarding statistical algorithms and machine learning to estimate rainfall in Indonesia. Rainfall information in Indonesia was obtained from several sources. Firstly, the method of direct rainfall measurement conducted with both manual and automatic rain gauges was reviewed; however, this data source provided minimal results, with uneven spatial density. Secondly, the application of remote sensing estimation using both radar and weather satellites was reviewed. The estimated rainfall results obtained using remote sensing showed more comprehensive spatial coverage and higher temporal resolution. Finally, we reviewed rainfall products obtained from model calculations, using both statistical and machine learning by integrating measurement and remote sensing data. The results of the review demonstrated that rainfall estimation products applied in remote sensing using machine learning models have the potential to produce more accurate spatial and temporal data. However, the validation of rainfall data from direct measurements is required first. This research’s contribution can provide practitioners and researchers in Indonesia and the surrounding region with information on problems, challenges, and recommendations for optimizing rainfall measurement products using appropriate adaptive technology.

1. Introduction

Rainfall information with high spatial and temporal resolution is essential, especially in areas that cover a large region, such as Indonesia. Rainfall and its impacts are often associated with floods and landslides [1,2]. Prevention efforts against floods and landslides require accurate rainfall information [3]. In addition to disasters, rainfall can impact several sectors, including agriculture, transportation, and energy. Rainfall intensity influences the agricultural system, as water availability significantly affects agricultural productivity [4,5]. Rainfall can also cause land, sea, and air transportation accidents [6,7,8,9]. In the field of resources and energy, many efforts are underway to generate electricity from rainfall, both directly and indirectly. Rainfall is also strongly related to the amount of power generated by hydropower plants [10,11].
Rainfall can be measured using two methods: direct observation through rain gauges and indirect estimation through remote sensing [12,13,14]. Rain gauges can accurately measure rainfall at each observation point [11,15]; however, this method provides only limited spatial information [16,17,18,19,20], especially in remote and marine areas. Through remote sensing techniques, such as radar and satellite imagery, rainfall can also be estimated based on the presence of rain clouds. On the one hand, weather radar can estimate rainfall with high resolution (20 × 20 m2) over a large area [21] using the Z–R (reflectivity–rain rate) relationship [22,23]. However, this empirical relationship is insufficient to capture rainfall variability in space and time [24,25,26]. In addition, several factors can affect the accuracy of rainfall estimation values: errors in estimating radar reflectivity factors [27], differences in sampling between weather radar and rain gauges [28], natural variability in raindrop size and distribution [29], and instrument errors [30,31]. On the other hand, satellites have a wider coverage area than weather radar, particularly over oceans. Weather satellites estimate rainfall intensity by linking the peak cloud temperature produced through visible (VIS) or infrared (IR) light reflectivity [32]. The developed techniques cannot be universally applied because of the indirect relationship between rainfall and satellite-measured parameters [33].
In measuring rainfall, wide spatial coverage with a high level of accuracy becomes a major issue. Indonesia’s total surface area of rain gauges is only 1.29 × 10−9% of the country’s total area. In addition, the integrated national weather radar network continues to fall short of covering the entire observation area [34,35]. The distribution of automatic rain gauge equipment and weather radar throughout Indonesia is shown in Figure 1. Moreover, weather satellite images with global coverage have resolution limitations [36]. This condition explains why using only one data source cannot fulfill Indonesia’s requirement for reliable rainfall data.
This article presents the study results of various sources of rainfall information data from several instruments used in the Indonesian region. Furthermore, it reviews recent studies on utilizing statistical algorithms, machine learning, and deep learning for rainfall estimation implemented in the Indonesian region. The results can be used as a guide for future study.

2. Rainfall Data Source

2.1. Rain Gauges

Rain gauges are classified into recording and non-recording types [37]. Non-recording rain gauges commonly in operation in Indonesia are the manual observatory (OBS) and Hellman types, due to their simplicity and low maintenance costs. With non-recording rain gauges, data collection is conducted manually; hence, the result is highly dependent on the reading accuracy of operators, and the timing of rainfall occurrence is unknown because the data obtained are cumulative [38]. Furthermore, some examples of recording rain gauges include mechanical mechanisms (based on floatation or weight), electric instruments (tipping bucket and capacitance sensor), and point rainfall calculation-based sensors (vibration-based disdrometer and optical rain gauge) [39]. Although many precipitation measurement mechanisms have been developed, the tipping bucket is the world’s most widely used rain gauge [40] due to its major advantages—low cost, simplicity, and low energy consumption [41]. In addition to the tipping bucket rain gauge, several countries use optical rain gauges for precipitation measurement [42] because this instrument can observe the size and falling velocity of the precipitation particles and then classify the type of rain [43]. In Indonesia, most tipping bucket rain gauges are installed on equipment systems, such as automatic rain gauges (ARGs), automatic weather systems (AWSs), agroclimate automatic weather systems (AAWS), and marine automatic weather systems (MAWSs). Furthermore, the tipping bucket and optical rain gauge are installed simultaneously on weather observation equipment systems for aviation, namely, the automated weather observing system (AWOS). This is to meet aviation safety requirements by covering the entire rain range. Under light rainfall conditions, optical rain gauges can more accurately measure rainfall than tipping bucket rain gauges [44]. Conversely, tipping bucket rain gauges are more accurate than optical rain gauges during heavy rainfall [1]. Figure 2 illustrates the types of rain gauges in operation in Indonesia.

2.2. Weather Radar

2.2.1. Weather Radar Type

Based on their frequency bands, weather radars are divided into three types: S, C, and X bands. Each type has its characteristics, advantages, and disadvantages [45]. Currently, weather radars in Indonesia are dominated by C-band types and several X-band ones. These have been adjusted to account for diverse topographical conditions [46].
  • The S-band weather radar operates at a 2.7–2.9 GHz frequency and has an 8–15 cm wavelength. Since attenuation has little effect on this type of radar, it has a range of up to 300 km. However, due to its wide beam width, its quantitative precipitation estimation (QPE) range only approaches 200 km [45]. While the S-band weather radar has advantages, due to several factors it may not be as suitable as the C-band radar if used in Indonesia. The S-band works at low frequencies with large lambda, so the penetration is deep because the attenuation effect is negligible. However, with a large lambda, the resolution and accuracy of the measurement results are low. Therefore, while using the S-band radar has some benefits, the C-band radar remains the best option for weather monitoring and forecasting in Indonesia.
  • The C-band weather radar operates at a 5.6–5.65 GHz frequency with a 4–8 cm wavelength. It can detect rainfall up to a distance of 200 km. The signal attenuation received is significantly stronger than that of the S-band radar, limiting the QPE range to 100–150 km [45]. The C-band weather radar is widely used in Indonesia because it effectively detects and monitors the types of precipitation commonly found in the region, such as convective storms, tropical cyclones, and heavy rainfall events [47,48]. For many years, the C-band radar has also been extensively used in Indonesia, and the country has established a reliable network of C-band radar stations [34]. The data from these radar stations are used by the Indonesian Meteorology, Climatology, and Geophysics Agency (BMKG) to provide accurate weather forecasts and early warnings of severe weather events to the public [49].
  • The X-band weather radar functions at a 9.3–9.5 GHz frequency and has the smallest wavelength of 2.5–4 cm. It is more sensitive to hydrometeors than the S-band or C-band weather radars. The X-band radar measurement range can extend up to 50 km. Signal attenuation caused by rain is the strongest in the X-band radar compared with that of the S-band and C-band radars, greatly limiting QPE. Accurate QPE is usually achieved at 30 km [45]. The X-band weather radar is not commonly used for weather monitoring in Indonesia due to several factors, such as its limited range and susceptibility to attenuation. Because the X-band radar has a much shorter range than other radar frequencies, it is less practical for weather monitoring over large areas, such as the Indonesian archipelago [35]. Another limitation of the X-band radar is its susceptibility to attenuation, which occurs when the radar signal is absorbed or scattered by particles in the atmosphere. As mentioned, attenuation can result in critical data loss and erroneous forecasts, especially in high-precipitation regions, such as Indonesia [50].

2.2.2. Weather Radar Product

Weather radar has product features that can be utilized as needed. Weather radar’s standard image products include the following:
  • Plan Position Indicator (PPI)
This product is displayed as a cone-shaped sector projected onto a two-dimensional (2D) map. The weather radar antenna rotates to scan radial tracks. The distance from the radar and height above the ground is depicted as concentric circles [51]. Since the PPI requires an elevation angle, the beam height increases as the distance grows. The heights of displayed data differ depending on the distance. To obtain maximum results from PPI products in Indonesia, it is necessary to pay attention to height, angle, and distance when scanning weather radar [52]. This is important because PPI products can experience coalescence with strong echo clutter at close distances at low elevations, which results in the product having a high level of uncertainty. The PPI display has a high level of uncertainty, which can affect rainfall estimation [53].
  • Constant Altitude PPI
The constant altitude plan position indicator (CAPPI) is a slice of volume data at a constant altitude. The elevation scan data values at the lower and upper levels are linearly interpolated to estimate the data at the CAPPI altitude. The advantage of this product is that it reduces ground clutter around the radar location. The amount of ground clutter around the radar decreases substantially with increasing altitude. A distance of 3.5 km is found to be the most suitable and sufficient application of the CAPPI to avoid ground clutter [54]. The application of CAPPI products in Indonesia needs to consider the distance between the radar and the area being observed. A study in Indonesia [55] showed that a CAPPI applied at a distance of more than 50 km can produce poor-quality data, considering that long distances can reduce data accuracy [56].
  • Column Maximum
Column maximum (CMAX) is a product that shows the maximum data value in a particular location. The displayed value is the maximum value of the observed volume scanning data. A CMAX product converts a set of polar volumes to Cartesian volumes and displays the maximum value for each vertical column. Physically, CMAX represents the maximum amount of possible rainfall in an area [57]. Meteorologists can view the estimated worst-case scenario overall by using the CMAX product instead of comparing several two-dimensional images from multiple layers and three-dimensional products. This tool helps in the observation of high-intensity rainfall from convective clouds, which often occurs in Indonesia [47]. Several studies in Indonesia have shown that the use of CMAX produces a more representative product in estimating rainfall [52,55].
A comparison of the mechanisms and results of radar image products is shown in Figure 3 and Table 1.
Estimating rainfall using radar in Indonesia is a complex process influenced by factors such as topography, distance from the radar, and Z–R relationships. Topography affects the propagation of radar signals, especially in mountainous areas, which can cause radar shadows and bias rainfall estimates [61]. Distance is also important because increasing the distance from the radar can reduce the estimation accuracy due to signal attenuation and divergence [62]. The Z–R relationship, which relates radar reflectivity to rainfall intensity, is often adapted to local conditions to improve estimation accuracy [63]. Dual-polarization radar has been introduced, producing significant improvements in rainfall estimation using additional information such as differential reflectivity (ZDR) and phase differential ratio (KDP) which can increase precision and reduce errors in rainfall estimates in various topographic conditions and distances [64].
Table 1. Weather radar products and their advantages and disadvantages.
Table 1. Weather radar products and their advantages and disadvantages.
Weather Radar ProductAdvantagesDisadvantages
PPIEasy to interpret and used for fast analysis [65], suitable for regions in Indonesia with local rain patterns, such as islands with quick and dynamic rain cycles.Limited to one elevation angle.
CAPPIIt is more accurate for estimating rainfall at a certain height [66]. It is helpful for several users in Indonesia, such as those in the aviation sector.Requires more time for data processing.
CMAXIt provides information on maximum rainfall intensity [66], which is very useful for detecting extreme rainfall, which often occurs in Indonesia.Potentially overestimates.

2.3. Weather Satellite

Weather satellites are used to study and monitor the Earth’s weather and climate [32]. Weather satellites can observe cloud tops, including rain-producing clouds, far from the Earth’s surface [67,68,69]. Some weather satellites can also provide rainfall estimates. Several types of weather satellites are used in Indonesia, including Himawari, Global Satellite Mapping of Precipitation (GSMaP), Global Precipitation Measurement (GPM), and Tropical Rainfall Measuring Mission (TRMM).
The Himawari satellite is the most commonly used because it has several products directly related to weather analysis, such as the infrared-enhanced product for analyzing cloud-top temperature [70,71,72], further aiding in rainfall estimation [73]. Moreover, it produces enhanced water vapor data for displaying atmospheric humidity conditions [74,75], and several other usable channels [76]. By analyzing the IR brightness temperature (BT) at 10.4 microns and multiple IR BT differences (BTD), researchers have developed rainfall probability maps in Indonesia [77]. RGB values for cloud-color appearance [76,78], such as during monitoring of the mesoscale convective complex (MCC) around the Indonesian capital have been used, whereby the Himawari-8 satellite detected dense clouds with small ice particles and cloud top temperatures below −50 °C, which were visualized as red and yellow dots, indicating conditions of severe storm [76]. Figure 4 shows Himawari satellite imagery, satellite temperature graphs, and rainfall graphs when high rainfall intensity occurs in one region in Indonesia.
The GSMaP is also widely used for rainfall estimation mapping in Indonesia [79,80]. GSMap shows a good correlation with rain gauge observations at daily and monthly scales, although it tends to overestimate rainfall and exceptionally light rainfall events [81]. GPM satellites in Indonesia have shown varying effectiveness levels depending on the region and timescale. They generally show good correlation with rain gauge data on annual, seasonal and monthly scales, although performance is less reliable on daily and hourly scales [82]. Their performance varies with topography, showing better accuracy in flat and moderately high areas [83]. Lastly, the TRMM satellite is extensively used to analyze rainfall with tropical region characteristics [84]. Specifically in Indonesia, the effectiveness of TRMM satellite rainfall estimates has been studied extensively, revealing its potential and limitations. The linear correction model significantly improves the validity of TRMM data for daily rainfall estimation [85]. The TRMM tends to underestimate rainfall intensity, requiring correction to improve performance [86]. TRMM data require careful correction to improve accuracy.
One of the challenges of weather satellite observation is the parallax effect, which causes the observed object’s position to differ from its actual position. This can be corrected by comparing cloud data from weather satellite observations with reflectivity data from weather radar observations [87]. Figure 5 shows satellite parallax correction for the entire territory of Indonesia.

3. Estimation Methods and Techniques

3.1. Statistical Application

Rainfall measured using several rain gauges and radar or weather satellite sensing can be used to estimate average rainfall in an area at a specific time interval. Moreover, the estimation method can be classified into two categories based on whether it uses rain gauge data or radar-based or weather-satellite-based estimation. Both estimation approaches are illustrated in Figure 6.
Data from a single rain gauge cannot represent rainfall in a given area. Thus, rainfall data from several rain gauges located throughout the area are required [90,91]. Furthermore, spatial data interpolation methods are required to estimate rainfall around known points. To generate spatially distributed rainfall fields, several interpolation methods for rain gauge points have been applied, including Thiessen polygon, inverse distance weighting, linear spline, and kriging [92,93], as shown in Table 2. With their respective advantages and disadvantages, these methods have been implemented for case studies in Indonesia [94,95,96]. The results showed that spatial interpolation of rain gauge data is necessary to estimate rainfall, especially in Indonesia, in order to overcome data limitations and environmental and other physiographic conditions. Due to the complexity of the topography and geography in Indonesia, the choice of interpolation method for estimating rainfall is very important. However, selecting the optimal interpolation method must also consider the unique characteristics of each region more specifically. In addition, interpolation methods that only use rain gauges as data sources must incorporate data from other sources [97]. This is because combining multiple rainfall data sources, such as rain gauges, weather radar, and weather satellites, can provide more accurate rainfall estimates [98].
The correlation between weather radar reflectivity data and rainfall intensity data from rain gauges produces an empirical equation of the Z–R relationship [20,103]. Modifications to the empirical equation constant have been applied for rainfall estimation in several Indonesian regions [104,105,106]. As a result, each study region has a distinct Z–R equation that can produce rainfall estimates with good statistical indicators. One study demonstrated that the relationship between radar reflectivity and rainfall can be developed using three different techniques: the traditional matching method (TMM), the probability matching method (PMM), and the window probability matching method (WPMM), as shown in Figure 7. The results revealed that PMM and WPMM provided a better relationship than TMM [24].
Statistical methods can be used to validate satellite data using rain gauges [33,107,108,109,110] or weather radar measurement methods [111,112,113,114]. In the case of validation using rain gauges, it is important to consider the number and distribution of rain gauges, as these factors can significantly influence the estimation results.

3.2. Machine Learning Approaches

The machine learning approach for estimating rainfall in Indonesia has been applied to several different case studies. With backpropagation, the multi-layer perceptron (MLP) algorithm was used to estimate rainfall at locations lacking direct rainfall observation data. The input data consisted of radar data validated with automatic rainfall observation data collected around a single polarization radar observation. The results improved the rainfall detection accuracy by 79% and reduced the error value in rainfall estimation [115], as shown in Figure 8. The MLP algorithm, with its ability to handle non-linear patterns, can model the relationship between the complexity of weather data and observed rainfall. Non-linear activation functions in the MLP algorithm, such as ReLU (rectified linear unit) or sigmoid, allowing the model to learn non-linear relationships between input and output features [116,117]. However, the MLP algorithm has a risk of overfitting because the model tends to memorize training data patterns without regularization [118]. The model’s performance decreases on new data. In addition, the MLP algorithm has an architecture with many layers and many neurons [117]. Training this model requires intensive mathematical operations, including matrix multiplication, vector operations, and non-linear activation for each neuron in each layer. The requirement for large computing resources [119,120] will be a problem if implemented on a large scale in Indonesia.
Another study compared the decision tree, random forest, adaptive boosting, and gradient boosting machine learning algorithms. All four algorithms optimized rainfall estimation using rain gauge, radar, and satellite data, with the gradient boosting algorithm outperforming the other three [121]. A similar study compared tree-based algorithms for rainfall estimation in different regions using radar measurements [122,123]. Regions with local [123] and equatorial [122] rainfall patterns have high and even rainfall throughout the year. The difference between the wet and dry seasons is not very clear [124]. Rainfall estimation using the adaptive boosting algorithm shows the worst results in these regions. Heterogeneous and fluctuating data training can increase weather radar uncertainty. When adaptive boosting encounters difficult data points to estimate correctly, this algorithm gives high weight to these points with the aim of increasing model performance. Mathematically, adaptive boosting gives high weight to incorrect data, which means that its performance decreases if there is excessive noise [125]. The relationship between radar reflectivity and rainfall can be categorized as complex data due to various physical and atmospheric factors that influence each other [30]. Decision trees with complex datasets are complicated tree structures with many nodes representing specific features and patterns from the training data [126]. For example, in cases of inconsistent or irrelevant rainfall fluctuations, the decision tree separates the data based on these fluctuations. This can cause the decision tree to be too specific to the training data [127]. As a result, the model will overfit due to being unable to generalize well on new test data, which causes poor rainfall estimation results. Using random forests and gradient boosting can produce better rainfall estimates. Random forest has the ability to handle noise in data because it uses many decision trees independently [128]. By considering multiple features and random subsets of the training data, random forests tend to be more tolerant of noise [129] because they can reduce overfitting on each individual decision tree [130]. This allows the model to be more general and stable [131], including in estimating rainfall. Gradient boosting is also effective in managing missing data [130], which may be caused by weather radar and rain gauges, and can correct model weaknesses by reducing the gradient of the loss function [132,133]. In the boosting process, the model focuses on more difficult samples and then gradually improves its performance; the next model tries to correct the errors made by the previous model [134]. This makes gradient boosting suitable for use in cases of complex data estimation and can produce more accurate rainfall estimates than decision tree, random forest, and adaptive boosting algorithms [122,123].
Ensemble learning techniques have achieved state-of-the-art performance in diverse machine learning applications by combining the predictions from two or more base models [135]. Ensemble learning methods were also applied to produce better rainfall estimates. Although accurate in rainfall estimation, the limitation of ensemble learning techniques is that they require tuning hyperparameters [136,137]. This can affect the overall performance and behavior of the model [138]. Hyperparameter optimization studies for rainfall estimation in Indonesia have been discussed [139]. Tuning the hyperparameters carried out in the XGBoost algorithm can improve the accuracy of the rainfall estimation model.

4. Discussion

Estimating rainfall in Indonesia using a combination of rain gauge, radar, and weather satellite data is critical because the country comprises a large and varied geographic area with relatively high rainfall, with many regions often experiencing floods and landslides. Accurate rainfall estimation can aid in water resource management, reduce natural disaster risks, and improve the quality of life for communities [140,141]. Rain gauges directly measure rainfall in a specific area over a certain period, while a weather radar obtains information on the speed and direction of water particles in rain clouds, allowing for the estimation of rainfall location and intensity. Weather satellites are used to collect data on weather conditions in larger areas, even on a global scale. Weather satellites can also provide a broad picture of clouds and rainfall in a particular area.
Rain gauges, although simple and low in cost, have the disadvantage of collecting data that depend on the accuracy of the measurements and the inaccuracy of observation times [142,143,144]. Weather radar has several types, with their respective characteristics, advantages, and disadvantages. Although S-band-based radars offer better coverage, they are susceptible to attenuation, especially in areas with heavy rain such as Indonesia. On the other hand, C-band-based radar is more suitable for use in Indonesia because it is effective in detecting the type of rainfall that commonly occurs in the region [35]. However, the use of X-band-based radar in Indonesia is limited due to its shorter range and susceptibility to attenuation. X-band produces higher spatial–temporal resolution products [145]. This type is suitable for urban hydrology applications in Indonesia. In addition, the use of data from weather satellites such as Himawari, GSMaP, and TRMM has been widely adopted for estimating rainfall in Indonesia. Nevertheless, challenges such as parallax effects need to be taken into account to ensure the accuracy of observations [146]. In facing this challenge, integrating data from various sources and understanding the characteristics of each tool is the key to increasing the accuracy of rainfall estimates in Indonesia.
The approach to estimating rainfall in Indonesia through the use of rain gauge, weather radar, and weather satellite data shows a variety of methods and techniques that have been applied. The traditional approach of using rain gauge data faces challenges in overcoming the inability of a single rain gauge to represent rainfall in an area. Therefore, spatial interpolation methods are needed to estimate rainfall around known points, using various methods such as Thiessen polygon, inverse distance weighting, linear spline, and kriging. The choice of interpolation method must take into account the unique characteristics of each region [147,148].
The distribution of rain gauges shown in Figure 1 highlights a concerning disparity in gauge density in Indonesia. Papua Island, in the eastern region of Indonesia, has fewer rain gauges even though the region has local rain patterns with its diverse topography. In contrast, Java Island, in the southern region of Indonesia, has a monsoon pattern and non-complex topography, but the rain gauge distribution there is very dense. The rain gauge density in Indonesia needs attention, as it can impact the selection of statistical models and methods. In addition, statistical models do not always have accurate results [26,149], depending on the linear relationships between variables.
Furthermore, the relationship between reflectivity weather radar data and rainfall intensity data from rain gauges produces an empirical equation for the Z–R relationship. Constant adjustments to empirical equations have been applied to estimate rainfall in several regions of Indonesia, with each region having a different Z–R equation. However, combining these two data sources requires consideration of seasonal differences, types of rain events, topography, and the distance between the rain gauge and radar [105,106,150]. Mountain and urban areas in Indonesia should utilize X-band radar because it has a shorter wavelength, which allows precipitation detection with higher spatial resolution. It is crucial in urban areas that require detailed mapping. In addition, the X-band radar is more effective in overcoming beam blockage problems in mountainous areas because its working range allows more flexible placement and better avoidance of physical obstacles. C-band and S-band radars are suitable for placement on flatlands or coasts with wide ocean coverage. Longer ranges are critical for detecting tropical storms that develop over the ocean and move toward land. In addition, flatland and coastal areas usually do not have many physical obstacles, such as mountains or tall buildings, allowing for wider radar coverage.
Statistical method validation can be carried out using satellite data with a rain gauge or weather radar. In data validation using rain gauges, it is important to consider the number and distribution of rain gauges because these factors can significantly influence the estimation results. Meanwhile, machine learning approaches have been applied to estimate rainfall in Indonesia using algorithms such as multi-layer perceptron (MLP), decision tree, random forest, adaptive boosting, gradient boosting, and XGBoost. In the course of our research regarding rainfall estimation, especially in Indonesia, we determined that the optimality of machine learning algorithms depends on the characteristics of the data used [130].
We have reviewed the rapid development of the application of machine learning around the world, including rainfall estimation [151,152,153]. It shows great potential for application in Indonesia as a tropical country. For example, research using over-parameterized neural network methods with remote sensing data can describe the spatial patterns of each type of rain in tropical regions [154]. Another study developed a monthly rainfall estimation model using monthly rainfall data for 54 years by combining optimization algorithms, including artificial bee colony, particle swarm optimization, imperialism competitive algorithm, and artificial neural network (ANN). The research results can help the climate planning process in tropical regions [155]. Furthermore, new methods combining data from various sources such as rain gauges, radar, and satellites to estimate rainfall have been introduced for areas that are difficult to reach by traditional measuring instruments [151]. Some of these approaches would be appropriate if applied in remote and maritime areas, which are often challenges in Indonesia. The computing technology of machine learning enables the quick and efficient processing of more significant data. Machine learning models can also capture complex non-linear patterns and relationships to produce accurate and adaptive rainfall estimates. These developments and successes should be applied to several case studies in Indonesia.
Several studies show that in general, the trend of using machine learning is starting to be implemented in the rainfall estimation process in Indonesia. These studies can be supported by the availability of C-band and X-band weather radar networks, as well as information from satellites that can be accessed. As data sources increase and the resolution of rainfall estimates increases, the challenge for the future is to prepare the capacity of the processing system so that the computing process can run optimally [156,157]. This is also in line with improvements in hyperparameter tuning and feature selection in training data.
The results of research regarding rainfall estimates in Indonesia found several problems, including the uneven distribution of rain gauges even though they function as actual rain gauges and are often used as verification tools, limited coverage, and suitability of the use of radar types for different regional conditions, corrections to satellite data and inaccuracies in statistical methods in dealing with variations in rain patterns. The development of machine learning in the world has been very rapid, providing more accurate rainfall estimates, but it has yet to be widely applied in Indonesia. Optimizing data integration methods from various sources has also been widely carried out globally, but it is only sometimes optimal when applied to rain patterns in Indonesia. The current challenge for estimating rainfall in Indonesia is how to optimize the integration of data from various existing sources, namely rain gauges, weather radar, and satellites, so that they can complement one another, taking into account the differences in rainfall patterns in Indonesia, namely, seasonal, equatorial, and local patterns.
From all the reviews, we can provide several recommendations regarding rainfall estimates. Place rain gauges more evenly in an area. The use of mobile technology can be a solution to fill gaps in distribution. Next, consider using a weather radar that suits the area’s characteristics, correcting and calibrating satellite data with ground-truthing data. With limited data sources, combining rain gauge, radar, and weather satellite data must be used for better rainfall estimation results. Finally, develop and apply more adaptive statistical methods or, at the same time, adopt machine learning technology, which has proven to be more successful. Table 3 describes the summary of the review results of estimating rainfall in Indonesia.

5. Conclusions

Focusing on Indonesia, this article presents various rainfall data from instrumentation and estimation models. Rainfall is a significant meteorological parameter that has a direct impact on many aspects of life, such as agriculture, transportation, and energy. Rainfall can be directly measured with a rain gauge or indirectly estimated using weather radar and satellites. In Indonesia, the tipping bucket is the most widely used type of rainfall sensor. The tipping bucket sensor can measure rainfall per point directly near the ground’s surface, is relatively accurate, and is often used to validate remote rainfall sensors. Moreover, Indonesia has a national weather radar network that can provide data with high spatial and temporal resolution, which can improve rainfall representation. Weather satellites are also used to observe atmospheric dynamics globally. Various approaches to rainfall estimation in Indonesia tend to rely on the quality and characteristics of the data. With advancements in technology, ensemble learning-based approaches have been implemented to improve the accuracy of rainfall estimation in Indonesia. Future research challenges will of course be oriented toward more accurate and universal rainfall estimates. Further efforts are needed, including data merging and selection, the use of universal ensemble learning, hyperparameter tuning, and product resolution improvement.

Author Contributions

Conceptualization, M.P.; methodology, M.P.; validation, M.S.R. and D.H.; formal analysis, M.P., M.S.R. and D.H.; investigation, M.P., M.S.R. and D.H; resources, M.P.; data curation, M.P.; writing—original draft preparation, M.P.; writing—review and editing, M.P., M.S.R. and D.H.; visualization, M.P.; supervision, M.S.R. and D.H. All authors have read and agreed to the published version of the manuscript.

Funding

The second author is funded by the Faculty of Mathematics and Natural Sciences, Universitas Indonesia under the Publication Grant Scheme 2024.

Data Availability Statement

Data are available upon request.

Acknowledgments

The authors are grateful to the Meteorology, Climatology, and Geophysics Agency (BMKG) for providing data and facilities for this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Nystuen, J.A. Relative Performance of Automatic Rain Gauges under Different Rainfall Conditions. J. Atmos. Ocean. Technol. 1999, 16, 1025–1043. [Google Scholar] [CrossRef]
  2. Ying, L.K. Rainfall Characteristics and Its Effect on Road Infrastructure Health. Int. J. Integr. Eng. 2019, 11, 234–246. [Google Scholar]
  3. Mohamed, G.A.I.; Althobiani, F.W. Modern Technology Applications and Rainfall Flooding Disasters Prevention. Int. J. Comput. Technol. 2018, 17, 7350–7354. [Google Scholar] [CrossRef]
  4. Frisvold, G.B.; Murugesan, A. Use of Weather Information for Agricultural Decision Making. Weather Clim. Soc. 2013, 5, 55–69. [Google Scholar] [CrossRef]
  5. Torres, M.; Howitt, R.; Rodrigues, L. Analyzing Rainfall Effects on Agricultural Income: Why Timing Matters. EconomiA 2019, 20, 1–14. [Google Scholar] [CrossRef]
  6. Cao, Y.; Wu, Z.; Xu, Z. Effects of Rainfall on Aircraft Aerodynamics. Prog. Aerosp. Sci. 2014, 71, 85–127. [Google Scholar] [CrossRef]
  7. Perera, L.P.; Soares, C.G. Weather Routing and Safe Ship Handling in the Future of Shipping. Ocean Eng. 2017, 130, 684–695. [Google Scholar] [CrossRef]
  8. Sangkharat, K.; Thornes, J.E.; Wachiradilok, P.; Pope, F.D. Determination of the Impact of Rainfall on Road Accidents in Thailand. Heliyon 2021, 7, e06061. [Google Scholar] [CrossRef] [PubMed]
  9. Zhou, X.; Cheng, L.; Li, M. Assessing and Mapping Maritime Transportation Risk Based on Spatial Fuzzy Multi-Criteria Decision Making: A Case Study in the South China Sea. Ocean Eng. 2020, 208, 107403. [Google Scholar] [CrossRef]
  10. Adegbehin, A.B.; Iguisi, E.O.; Yusuf, Y.O.; Zubairu, I.; Anumonye, E.N. Effect of Weather Parameters on Hydroelectric Power Generation in Kainji Dam Niger State, Nigeria. In Proceedings of the Annual Conference of the Association of Nigerian Geographers (UNILAG ANG-2016), Lagos, Nigeria, 10–15 April 2016. [Google Scholar]
  11. Mineo, C.; Ridolfi, E.; Moccia, B.; Russo, F.; Napolitano, F. Assessment of Rainfall Kinetic-Energy–Intensity Relationships. Water 2019, 11, 1994. [Google Scholar] [CrossRef]
  12. Kidd, C.; Huffman, G. Global Precipitation Measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
  13. Pickering, B.S.; Iii, R.R.N.; Jeffery, J.; Dufton, D.; Lukach, M. Evaluation of Multiple Precipitation Sensor Designs for Precipitation Rate and Depth, Drop Size and Velocity Distribution, and Precipitation Type. J. Hydrometeorol. 2021, 22, 703–720. [Google Scholar] [CrossRef]
  14. Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
  15. Nazaripour, H.; Mansouri Daneshvar, M.R. Rain Gauge Network Evaluation and Optimal Design Using Spatial Correlation Approach in Arid and Semi-Arid Regions of Iran. Theor. Appl. Climatol. 2016, 129, 1255–1261. [Google Scholar] [CrossRef]
  16. Gyasi-Agyei, Y. Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis. Water 2020, 12, 1906. [Google Scholar] [CrossRef]
  17. Jia, Y.; Li, Z.; Xu, C.; Jin, S.; Deng, H. A Comparison of Precipitation Measurements with A PWS100 Laser Sensor and A Geonor T-200B Precipitation Gauge at A Nival Glacial Zone in Eastern Tianshan, Central Asia. Atmosphere 2020, 11, 1079. [Google Scholar] [CrossRef]
  18. Leonarduzzi, E.; Molnar, P. Data Limitations and Potential of Hourly and Daily Rainfall Thresholds for Shallow Landslides. Nat. Hazards Earth Syst. Sci. 2020, 2020, 1–25. [Google Scholar] [CrossRef]
  19. Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and Sampling Uncertainties: A Rain Gauge Perspective. J. Geophys. Res. Atmos. 2008, 113, 11102. [Google Scholar] [CrossRef]
  20. Wu, H.; Chen, Y.; Chen, X.; Liu, M.; Gao, L.; Deng, H. A New Approach for Optimizing Rain Gauge Networks: A Case Study in the Jinjiang Basin. Water 2020, 12, 2252. [Google Scholar] [CrossRef]
  21. Franch, G.; Maggio, V.; Coviello, L.; Pendesini, M.; Jurman, G.; Furlanello, C. TAASRAD19, a high-resolution weather radar reflectivity dataset for precipitation nowcasting. Sci. Data 2020, 7, 234. [Google Scholar] [CrossRef] [PubMed]
  22. Ramli, S.; Abu Bakar, S.H.; Tahir, W. Radar hydrology: New Z/R Relationships for Klang River Basin, Malaysia Based On Rainfall Classification. In Proceedings of the 2011 IEEE Colloquium on Humanities, Science and Engineering, CHUSER 2011, Penang, Malaysia, 5–6 December 2011; pp. 537–541. [Google Scholar] [CrossRef]
  23. Yeo, J.X.; Lee, Y.H.; Ong, J.T. Radar Measured Rain Attenuation with Proposed Z–R Relationship at A Tropical Location. AEU—Int. J. Electron. Commun. 2015, 69, 458–461. [Google Scholar] [CrossRef]
  24. Anjaneyulu, A.; Moharana, S.; Ray, K.; Chembolu, V.; Dutta, S. Relation Between Weather Radar Reflectivity and Rainfall Rate: A case Study in North Indian Regions. In Proceedings of the National Conference on Emerging Technology Trends in Agricultural Engineering, Nirjuli, Indian, 7–9 November 2014. [Google Scholar]
  25. Dutta, D.; Sharma, S.; Kannan, B.A.M.; Venketswarlu, S.; Gairola, R.M.; Rao, T.N.; Viswanathan, G. Sensitivity of ZR Relations and Spatial Variability of Error in A Doppler Weather Radar Measured Rain Intensity. Indian J. Radio Space Phys. 2012, 41, 448–460. [Google Scholar]
  26. Sobli, N.H.M.; Ismail, A.F.; Md Isa, F.N.; Mansor, H. Assessment of Radar Reflectivity-Rainfall Rate, Z-R Relationships for a Convective Event in Malaysia. Int. J. Electr. Energy 2013, 1, 239–243. [Google Scholar] [CrossRef]
  27. Wu, S.J.; Lien, H.C.; Hsu, C.T.; Chang, C.H.; Shen, J.C. Modeling Probabilistic Radar Rainfall Estimation at Ungauged Locations Based on Spatiotemporal Errors Which Correspond to Gauged Data. Hydrol. Res. 2013, 46, 39–59. [Google Scholar] [CrossRef]
  28. Piccolo, F.; Chirico, G.B. Sampling Errors in Rainfall Measurements by Weather Radar. Adv. Geosci. 2005, 2, 151–155. [Google Scholar] [CrossRef]
  29. Ochou, A.D.; Zahiri, E.-P.; Bamba, B.; Koffi, M. Understanding the Variability of Z-R Relationships Caused by Natural Variations in Raindrop Size Distributions (DSD): Implication of Drop Size and Number. Atmos. Clim. Sci. 2011, 1, 147–164. [Google Scholar] [CrossRef]
  30. Nikahd, A.; Hashim, M.; Nazemosadat, M.J. A Review of Uncertainty Sources on Weather Ground-Based Radar for Rainfall Estimation. Appl. Mech. Mater. 2016, 818, 254–271. [Google Scholar] [CrossRef]
  31. Van De Beek, C.Z.; Leijnse, H.; Hazenberg, P.; Uijlenhoet, R. Close-range Radar Rainfall Estimation and Error Analysis. Atmos. Meas. Tech. 2016, 9, 3837–3850. [Google Scholar] [CrossRef]
  32. Sahoo, S.; Rout, S.; Khare, N.; Patra, S.; Nayak, S. Satellite Meteorology—A review. Van Sangyan 2017, 4, 19–23. [Google Scholar]
  33. Chua, Z.W.; Kuleshov, Y.; Watkins, A. Evaluation of Satellite Precipitation Estimates Over Australia. Remote Sens. 2020, 12, 678. [Google Scholar] [CrossRef]
  34. Permana, D.S.; Hutapea, T.D.; Praja, A.S.; A I Paski, J.; Makmur, E.E.S.; Haryoko, U.; Umam, I.H.; Saepudin, M.; Adriyanto, R. The Indonesia In-House Radar Integration System (InaRAISE) of Indonesian Agency for Meteorology Climatology and Geophysics (BMKG): Development, Constraint, and Progress. IOP Conf. Ser. Earth Environ. Sci. 2019, 303, 012051. [Google Scholar] [CrossRef]
  35. Prakasa, A.; Utami, F.D. Sistem Informasi Radar Cuaca Terintegrasi BMKG. J. Telecommun. Electron. Control Eng. (JTECE) 2019, 1, 78–87. [Google Scholar] [CrossRef]
  36. Maier, M.W.; Gallagher, F.W.; Germain, K.S.; Anthes, R.; Zuffada, C.; Menzies, R.; Piepmeier, J.; Di Pietro, D.; Coakley, M.M.; Adams, E. Architecting The Future of Weather Satellites. Bull. Am. Meteorol. Soc. 2021, 102, E589–E610. [Google Scholar] [CrossRef]
  37. Subramanya, K. Engineering Hydrology; Tata McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
  38. Maftukhah, T.; Wijonarko, S.; Rustandi, D. Comparison and correlation among measurement results of observatory, hellman, and tipping bucket sensors. Instrumentasi 2016, 40, 7. [Google Scholar] [CrossRef]
  39. Strangeways, I. Precipitation: Theory, Measurement and Distribution; Cambridge University Press (CUP): Cambridge, UK, 2006; pp. 1–290. ISBN 9780521851176. [Google Scholar] [CrossRef]
  40. Muñoz, P.; Célleri, R.; Feyen, J. Effect of the Resolution of Tipping-Bucket Rain Gauge and Calculation Method on Rainfall Intensities in an Andean Mountain Gradient. Water 2016, 8, 534. [Google Scholar] [CrossRef]
  41. Segovia-Cardozo, D.A.; Bernal-Basurco, C.; Rodríguez-Sinobas, L. Tipping Bucket Rain Gauges in Hydrological Research: Summary on Measurement Uncertainties, Calibration, and Error Reduction Strategies. Sensors 2023, 23, 5385. [Google Scholar] [CrossRef] [PubMed]
  42. Nitu, R.; Wong, K. CIMO Survey on National Summaries of Methods and Instruments for Solid Precipitation Measurement at Automatic Weather Stations; WMO: Geneva, Switzerland, 2010; Volume 425. [Google Scholar]
  43. Ro, Y.; Chang, K.H.; Hwang, H.; Kim, M.; Cha, J.W.; Lee, C. Comparative study of rainfall measurement by optical disdrometer, tipping-bucket rain gauge, and weighing precipitation gauge. Nat. Hazards 2024, 120, 2829–2845. [Google Scholar] [CrossRef]
  44. Liu, X.C.; Gao, T.C.; Liu, L. A Comparison of Rainfall Measurements from Multiple Instruments. Atmos. Meas. Tech. 2013, 6, 1585–1595. [Google Scholar] [CrossRef]
  45. Sokol, Z.; Szturc, J.; Orellana-Alvear, J.; Popová, J.; Jurczyk, A.; Célleri, R. The Role of Weather Radar in Rainfall Estimation and Its Application in Meteorological and Hydrological Modelling—A Review. Remote Sens. 2021, 13, 351. [Google Scholar] [CrossRef]
  46. Rahayu, W.I.; Prianto, C.; Novia, E.A. Perbandingan Algoritma K-Means dan Naive Bayes untuk Memprediksi Prioritas Pembayaran Tagihan Rumah Sakit Berdasarkan Tingkat Kepentingan Pada PT. Pertamina (Persero). J. Tek. Inform. 2021, 13, 1–8. [Google Scholar]
  47. Prasetyo, B.; Pusparini, N.; Fitria, W. Weather Radar Application for Identification of Extreme Weather Conditions Fluctuation (Case Study: Flood in Medan City on October 5th 2018). J. Sains Teknol. Modif. Cuaca 2019, 20, 13–21. [Google Scholar] [CrossRef]
  48. Zhu, B.; Pu, Z.; Putra, A.W.; Gao, Z. Assimilating c-band radar data for high-resolution simulations of precipitation: Case studies over western sumatra. Remote Sens. 2022, 14, 42. [Google Scholar] [CrossRef]
  49. Anugrah, J.; Paski, I.; Permana, D.S. Using the c-band Doppler weather radar data to reconstruct extreme rainfall event on 11th march 2018 in Bangka island, Indonesia. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; pp. 1–6. [Google Scholar] [CrossRef]
  50. Hambali, R.; Legono, D.; Jayadi, R. Correcting Radar Rainfall Estimates Based on Ground Elevation Function. J. Civ. Eng. Forum 2019, 5, 301–310. [Google Scholar] [CrossRef]
  51. Daliakopoulos, I.N.; Tsanis, I.K. A Weather Radar Data Processing Module for Storm Analysis. J. Hydroinform. 2012, 14, 332–344. [Google Scholar] [CrossRef]
  52. Efendi, U.; Nadiansyah, R.; Afriza, P.R.; Nugraheni, I.R.; Ali, A. Uji Akurasi Estimasi Curah Hujan Produk Radar CUACA C-BAND di Wilayah Pontianak. In Proceedings of the Seminar Nasional Geografi III, Yogyakarta, Indonesia, 2 November 2019; pp. 776–785. [Google Scholar]
  53. Anagnostou, E.N.; Krajewski, W.F.; Smith, J. Uncertainty Quantification of Mean-Areal Radar-Rainfall Estimates. J. Atmos. Ocean. Technol. 1997, 16, 206–215. [Google Scholar] [CrossRef]
  54. Da Silveira, R.B.; Holt, A.R. An Automatic Identification of Clutter and Anomalous Propagation in Polarization-Diversity Weather Radar Data Using Neural Networks. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1777–1788. [Google Scholar] [CrossRef]
  55. Tondang, Y.M.; Situmorang, M.; Ikhsan, T.; Darmawan, Y. Accuracy of Weather Radar Products for Rainfall Estimation in North Sumatra Region. Prisma Sains Jurnal Pengkajian Ilmu dan Pembelajaran Matematika dan IPA IKIP Mataram 2023, 11, 351–357. [Google Scholar] [CrossRef]
  56. Uijlenhoet, R.; Van Der Wielen, S.H.; Berne, A. Uncertainties in rainfall retrievals from ground-based weather radar: Overview, case study, and simulation experiment. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 2385–2436. [Google Scholar]
  57. Yoon, S.; Jeong, C.; Lee, T. Flood Flow Simulation Using CMAX Radar Rainfall Estimates in Orographic Basins. Meteorol. Appl. 2014, 21, 596–604. [Google Scholar] [CrossRef]
  58. Satriyabawa, I.K.M.; Pratama, W.N. Analisis Kejadian Puting Beliung di Stasiun Meteorologi Juanda Surabaya Menggunakan Citra Radar Cuaca dan Model WRF-ARW (Studi Kasus Tanggal 4 Februari 2016). In Prosiding SNSA; Departemen Statistika Fmipa Universitas Padjadjaran: Bandung, Indonesia, 2016; pp. 89–97. [Google Scholar]
  59. On-Demand Constant Altitude Plan Position Indicator (CAPPI). Available online: https://iris.vaisala.com/doc/en_US/cappi_height_value.html (accessed on 3 May 2024).
  60. On-Demand Plan Position Indicator (PPI). Available online: https://iris.vaisala.com/doc/en_US/ppi_elevation_angle.html (accessed on 3 May 2024).
  61. Montopoli, M.; Roberto, N.; Adirosi, E.; Gorgucci, E.; Baldini, L. Investigation of weather radar quantitative precipitation estimation methodologies in complex orography. Atmosphere 2017, 8, 34. [Google Scholar] [CrossRef]
  62. Sebastianelli, S.; Russo, F.; Napolitano, F.; Baldini, L. On precipitation measurements collected by a weather radar and a rain gauge network. Nat. Hazards Earth Syst. Sci. 2013, 13, 605–623. [Google Scholar] [CrossRef]
  63. Auipong, N.; Trivej, P. Study of Z-R relationship among different topographies in Northern Thailand. J. Phys. Conf. Ser. 2018, 1144, 012098. [Google Scholar] [CrossRef]
  64. Kim, H.; Suk, M.; Park, H.; Lee, G.; Ko, J. Dual-polarization radar rainfall estimation in Korea according to raindrop shapes obtained by using a 2-D video disdrometer. Atmos.Meas.Tech 2016, 9, 3863–3878. [Google Scholar] [CrossRef]
  65. Rinehart, R.E. Radar for Meteorologists; Rinehart Publications: New York, NY, USA, 2010. [Google Scholar]
  66. Doviak, R.J.; Zrnic, D.S. Doppler Radar and Weather Observations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
  67. Diniyati, E.; Syofyan, D.Q.; Mulya, A. Pemanfaatan Satelit Himawari-8 dengan Metode NWP dan RGB untuk Menganalisis Kondisi Atmosfer Saat Banjir di Sidoarjo Tanggal 28 Mei 2020. JPIG J. Pendidik. Dan Ilmu Geogr. 2021, 6, 1–14. [Google Scholar] [CrossRef]
  68. Putri, R.J.A. Pemanfaatan Data Satelit Himawari-8 Untuk Analisis Kejadian Hujan Sangat Lebat di Kabupaten Nabire, Papua Tengah (Tanggal 12, 21, dan 22 Maret 2016). In Prosiding SNSA; Departemen Statistika Fmipa Universitas Padjadjaran: Bandung, Indonesia, 2016; pp. 195–204. [Google Scholar]
  69. Rizkiafama, V.A.; Dzikiro, T.K.; Safril, A. Pemanfaatan Data Satelit Himawari-8 Serta Data Curah Hujan Dan Hari Hujan Bulanan Dalam Analisis Kejadian Banjir Kota Padang, 9 September 2017 dan 26 September 2018. In Prosiding SNFA (Seminar Nasional Fisika Dan Aplikasinya); Universitas Sebelas Maret: Kota Surakarta, Indonesia, 2018; pp. 264–276. [Google Scholar]
  70. Novitasari, D.C.R.; Supatmanto, B.D.; Rozi, M.F.; Hermansah; Farida, Y.; Setyowati, R.D.N.; Ilham; Junaidi, R.; Arifin, A.Z.; Fatoni, A.R. Rainfall Prediction Based on Himawari-8 IR Enhanced Image Using Backpropagation. J. Phys. Conf. Ser. 2020, 1501, 012011. [Google Scholar] [CrossRef]
  71. Rinaldy, N.; Saragih, I.J.A.; Wandala Putra, A.; Redha Nugraheni, I.; Wijaya Yonas, B. Identification of Mesoscale Convective Complex (MCC) phenomenon with image of Himawari 8 Satellite and WRF ARW Model on Bangka Island (Case Study: 7–8 February 2016). IOP Conf. Ser. Earth Environ. Sci. 2017, 98, 012002. [Google Scholar] [CrossRef]
  72. Yudistira, R.D.; Mahubessy, R.; Krisnawan, G.D.; Wisnawa, G.G.; Tirtanegara, I.M.K.; Fadlan, A.; Wardoyo, E. Utilization of surface meteorological data, Himawari-8 satellite data, and radar data to analyze landspout in Sumenep, East Java, Indonesia (case study of 20 November 2017). IOP Conf. Ser. Earth Environ. Sci. 2019, 374, 012038. [Google Scholar] [CrossRef]
  73. Jumianti, N.; Marzuki, M.; Harjupa, W.; Risyanto; Putranto, M.F. Prediction of Extreme Rainfall of September 9, 2020 in Padang City Based on Clouds Brightness Temperature Difference from Himawari-8 Satellite Data. Springer Proc. Phys. 2022, 275, 771–787. [Google Scholar] [CrossRef]
  74. Dharma, C.S.; Trilaksono, N.J. Rain Detection using Himawari-8 Imagery; Case Study Singkawang West Kalimantan. IOP Conf. Ser. Earth Environ. Sci. 2021, 750, 012011. [Google Scholar] [CrossRef]
  75. Nur Auliya, M.; Mulya, A. Hail Identification Based on Weather Factor Analisys and Himawari 8 Satellite Imagery (Case Study of Hail on 2nd March 2021 in Malang Indonesia). Int. J. Remote Sens. Earth Sci. 2021, 18, 217–228. [Google Scholar] [CrossRef]
  76. Fatkhuroyan; Wati, T. Detection of mesoscale convective complexes using multispectral RGB technique of Himawari-8 (Case Study: Jakarta, 20 February 2017). IOP Conf. Ser. Earth Environ. Sci. 2018, 149, 012032. [Google Scholar] [CrossRef]
  77. Risyanto; Lasmono, F.; Nugroho, G.A. Identification of rainfall area in Indonesia using infrared channels of Himawari-8 Advance Himawari Imager (AHI). IOP Conf. Ser. Earth Environ. Sci. 2019, 303, 012057. [Google Scholar] [CrossRef]
  78. Fadhilah, M.J.; Mulya, A. Analisis Dinamika Atmosfer dan Identifikasi Sebaran Awan Konvektif Menggunakan Metode RGB pada Citra Satelit Himawari-8 Terkait Banjir di Kab. Jayawijaya, Wamena (Studi Kasus: Periode 9 Maret 2021). J. Tek. SILITEK 2022, 1, 121–134. [Google Scholar] [CrossRef]
  79. Asferizal, F. Analisis Perbandingan Kehandalan Data Hujan GSMaP, TRMM, GPM dan PERSIANN Terhadap Data Obsevasi Dalam Rentang Waktu Penelitian 2020–2021. Orig. Artic. J. Infrastruct. Plan. Des. 2022, 2, 33–41. [Google Scholar]
  80. Saragih, I.J.A.; Putra, A.W.; Nugraheni, I.R.; Rinaldy, N.; Yonas, B.W. Identification of the Sea-Land Breeze Event and Influence to the Convective Activities on the Coast of Deli Serdang. IOP Conf. Ser. Earth Environ. Sci. 2017, 98, 012003. [Google Scholar] [CrossRef]
  81. Ramadhan, R.; Marzuki, M.; Yusnaini, H.; Muharsyah, R.; Tangang, F.; Vonnisa, M.; Harmadi, H. A Preliminary Assessment of the GSMaP Version 08 Products over Indonesian Maritime Continent against Gauge Data. Remote Sens. 2023, 15, 1115. [Google Scholar] [CrossRef]
  82. Ramadhan, R.; Muharsyah, R.; Marzuki; Yusnaini, H.; Vonnisa, M.; Hashiguchi, H.; Suryanto, W.; Sholihun. Evaluation of GPM IMERG Products for Extreme Precipitation over Indonesia. J. Phys. Conf. Ser. 2022, 2309, 012008. [Google Scholar] [CrossRef]
  83. Tulistiawan, P.E.; Karang, I.W.G.A.; Osawa, T. Validation of Satellite Rainfall Product (GPM-IMERG) an Bali and Nusa Tenggara: A Comparison of Normal Seasons, El Nino and La Nina Events. J. Geogr. 2023, 15, 165. [Google Scholar] [CrossRef]
  84. Talakua, P.; Sediyono, E.; Joko, S.Y. Analisis Rawan Kebakaran Hutan Di Seram Maluku Berbasis Citra Landsat 8 Menggunakan MetodeInverse Distance Weighted. J. Tek. Inform. Sist. Inf. 2018, 4, 511–520. [Google Scholar]
  85. Binsar Sahat Maruli Tua Simbolon, R.; Soeryamassoeka, S. Jurnal Teknik Sipil Correction Equation of Rainfall Data Maximum a Day on Tropical Rainfall Measuring Mission (TRMM) in Sekayam sub-watershed. J. Tek. Sipil 2023, 23, 2621. [Google Scholar] [CrossRef]
  86. Sanjaya, S.; Yudianto, D. Application of TRMM in Deriving Intensity-Duration-Frequency Curve in Bandung Area. IOP Conf. Ser. Earth Environ. Sci. 2021, 832, 012046. [Google Scholar] [CrossRef]
  87. Bieliński, T. A parallax shift effect correction based on cloud height for geostationary satellites and radar observations. Remote Sens. 2020, 12, 365. [Google Scholar] [CrossRef]
  88. Septian Pandjaitan, B.; Faqih, A.; Alfahmi, F. Overshooting Top of Convective Cloud in Extreme weather Events over Java Region Based on Visual Identification of Himawari 8 Imagery. J. Meteorol. Dan Geofis. 2023, 24, 53–64. [Google Scholar] [CrossRef]
  89. Morbidelli, R. Rainfall: Modeling, Measurement and Applications; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
  90. Ningsih, D.H.U. Metode Thiessen Polygon untuk Ramalan Sebaran Curah Hujan Periode Tertentu pada Wilayah yang Tidak Memiliki Data Curah Hujan. J. Teknol. Inf. Din. 2012, 17, 154–163. [Google Scholar]
  91. Lotfy, A.; Ali, A.; Hassan, A.; Bakr, M.; Al-Handasah, D.; Elmoustafa, A. Impact of Reducing Rain Gauges Numbers on accuracy of Estimated Mean Areal Precipitation. Curr. Sci. Int. 2018, 7, 70–78. [Google Scholar]
  92. Cheng, M.; Wang, Y.; Engel, B.; Zhang, W.; Peng, H.; Chen, X.; Xia, H. Performance Assessment of Spatial Interpolation of Precipitation for Hydrological Process Simulation in the Three Gorges Basin. Water 2017, 9, 838. [Google Scholar] [CrossRef]
  93. Shope, C.L.; Maharjan, G.R. Modeling spatiotemporal precipitation: Effects of density, interpolation, and land use distribution. Adv. Meteorol. 2015, 2015, 174196. [Google Scholar] [CrossRef]
  94. Arianti, I.; Soemarno; Hasyim, A.W.; Sulistyono, R. Rainfall estimation by using Thiessen polygons, Inverse Distance Weighted, Spline, and Kriging methods: A case study in Pontianak, West Kalimantan. Int. J. Educ. Res. 2018, 6, 1–10. [Google Scholar]
  95. Giarno, G.; Didiharyono, D.; Fisu, A.A.; Mattingaragau, A. Influence Rainy and Dry Season to Daily Rainfall Interpolation in Complex Terrain of Sulawesi. IOP Conf. Ser. Earth Environ. Sci. 2020, 469, 012003. [Google Scholar] [CrossRef]
  96. Jaya, I.G.N.M.; Ruchjana, B.N.; Abdullah, A.S.; Andriyana, Y. Comparison of IDW and GP models with application to spatiotemporal interpolation of rainfall in Bali Province, Indonesia. J. Phys. Conf. Ser. 2021, 1722, 012080. [Google Scholar] [CrossRef]
  97. Yang, W.; Liu, J.; Li, M.; Guo, Z. Isophote-Constrained Autoregressive Model with Adaptive Window Extension for Image Interpolation. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 1071–1086. [Google Scholar] [CrossRef]
  98. Tauro, F.; Selker, J.; van de Giesen, N.; Abrate, T.; Uijlenhoet, R.; Porfiri, M.; Manfreda, S.; Caylor, K.; Moramarco, T.; Benveniste, J.; et al. Measurements and Observations in The XXI Century (MOXXI): Innovation and Multi-Disciplinarity to Sense The Hydrological Cycle. Hydrol. Sci. J. 2018, 63, 169–196. [Google Scholar] [CrossRef]
  99. Pasaribu, J.M.; Haryani, N.S. Perbandingan teknik interpolasi dem srtm dengan metode inverse distance weighted (idw), natural neighbor dan spline (comparison of dem srtm interpolation techniques using inverse distance weighted (idw), natural neighbor and spline method). J. Penginderaan Jauh Pengolah. Data Citra Digit. 2012, 9, 126–139. [Google Scholar]
  100. Kurniawan, A.; Makmur, E.; Supari. Menentukan Metode Interpolasi Spasial Curah Hujan Bulanan Terbaik Di Jawa Timur (Determining the Best Monthly Rainfall Spatial Interpolation Method in East Java). In Proceedings of the Seminar Nasional Geomatika 2020: Informasi Geospasial Untuk Inovasi Percepatan Pembangunan Berkelanjutan, Bogor, Indonesia, 15–16 October 2020; pp. 263–272. [Google Scholar]
  101. Paramasivam, C.R.; Venkatramanan, S. An introduction to various spatial analysis techniques. In GIS and Geostatistical Techniques for Groundwater Science; Elsevier: Amsterdam, The Netherlands, 2019; pp. 23–30. [Google Scholar] [CrossRef]
  102. Rahmawati, N. Space-time variogram for daily rainfall estimates using rain gauges and satellite data in mountainous tropical Island of Bali, Indonesia (Preliminary Study). J. Hydrol. 2020, 590, 125177. [Google Scholar] [CrossRef]
  103. Kim, T.J.; Kwon, H.H.; Kim, K.B. Calibration of the reflectivity-rainfall rate (Z-R) relationship using long-term radar reflectivity factor over the entire South Korea region in a Bayesian perspective. J. Hydrol. 2021, 593, 125790. [Google Scholar] [CrossRef]
  104. Ali, A.; Deranadyan, G.; Hairuly Umam, I. An Enhancement to The Quantitative Precipitation Estimation Using Radar-Gauge Merging. Int. J. Remote Sens. Earth Sci. (IJReSES) 2020, 17, 65. [Google Scholar] [CrossRef]
  105. Marzuki; Hashiguchi, H.; Vonnisa, M.; Harmadi; Muzirwan; Nugroho, S.; Yoseva, M. Z-R Relationships for Weather Radar in Indonesia from the Particle Size and Velocity (Parsivel) Optical Disdrometer. In Proceedings of the Progress in Electromagnetics Research Symposium, Toyama, Japan, 1–4 August 2018; pp. 37–41. [Google Scholar] [CrossRef]
  106. Hutapea, T.D.F.; Permana, D.S.; Praja, A.S.; Muzayanah, L.F. Modification of Z-R Relationship Constants in Surabaya Radar for Improving The Accuracy of Rainfall Estimates. J. Meteorol. Dan Geofis. 2021, 21, 91–97. [Google Scholar] [CrossRef]
  107. Rahmawati, N.; Rahayu, K.; Yuliasari, S.T. Performance of daily satellite-based rainfall in groundwater basin of Merapi Aquifer System, Yogyakarta. Theor. Appl. Clim. 2021, 146, 173–190. [Google Scholar] [CrossRef]
  108. Putri Misnawati, N.L.J.A.; Sagita, N. Bias Correction of Rain Estimation Using GPM-IMERG Over Java Island. Megasains 2022, 13, 26–33. [Google Scholar] [CrossRef]
  109. Serrat-Capdevila, A.; Merino, M.; Valdes, J.B.; Durcik, M. Evaluation of the performance of three satellite precipitation products over Africa. Remote Sens. 2016, 8, 836. [Google Scholar] [CrossRef]
  110. Fatkhuroyan, F.; Wati, T.; Sukmana, A.; Kurniawan, R. Validation of Satellite Daily Rainfall Estimates Over Indonesia. Forum Geogr. 2018, 32, 170–180. [Google Scholar] [CrossRef]
  111. So, D.; Shin, D. Classification of precipitating clouds using satellite infrared observations and its implications for rainfall estimation. Q. J. R. Meteorol. Soc. 2018, 144, 133–144. [Google Scholar] [CrossRef]
  112. Pejcic, V.; Garfias, P.S.; Mühlbauer, K.; Trömel, S.; Simmer, C. Comparison between precipitation estimates of ground-based weather radar composites and GPM’s DPR rainfall product over Germany. Meteorol. Z. 2020, 29, 451–466. [Google Scholar] [CrossRef]
  113. Schwaller, M.R.; Robert Morris, K. A ground validation network for the global precipitation measurement mission. J. Atmos. Ocean. Technol. 2011, 28, 301–319. [Google Scholar] [CrossRef]
  114. Kim, J.H.; Ou, M.L.; Park, J.D.; Morris, K.R.; Schwaller, M.R.; Wolff, D.B. Global precipitation measurement (GPM) ground validation (GV) prototype in the Korean Peninsula. J. Atmos. Ocean. Technol. 2014, 31, 1902–1921. [Google Scholar] [CrossRef]
  115. Pamuji Waskita, T.; Harmoko Saputro, A.; Sopaheluwakan, A.; Ryan, M. Machine Learning System for Rainfall Estimates from Single Polarization Radar. In Proceedings of the International Conferences on Information System and Technology (CONRIST 2019), Yogyakarta, Indonesia, 5–6 December 2019; pp. 41–48. [Google Scholar] [CrossRef]
  116. Balas, V.E.; Mastorakis, N.E.; Popescu, M.-C.; Balas, V.E. Multilayer Perceptron and Neural Networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
  117. Kumar Biswas, S.; Siddique, A.; Mahmudul, M.; Mia, A.; Biswas, K.; Urmi, M.C. An Algorithm for Training Multilayer Perceptron (MLP) for Image Reconstruction Using Neural Network without Overfitting. Artic. Int. J. Sci. Technol. Res. 2015, 4, 2. [Google Scholar]
  118. Kolluri, J.; Kotte, V.K.; Phridviraj, M.S.B.; Razia, S. Reducing Overfitting Problem in Machine Learning Using Novel L1/4 Regularization Method. In Proceedings of the 4th International Conference on Trends in Electronics and Informatics, ICOEI 2020, Tirunelveli, India, 15–17 June 2020; pp. 934–938. [Google Scholar] [CrossRef]
  119. Osowski, S.; Siwek, K.; Markiewicz, T. MLP and SVM Networks-a Comparative Study. In Proceedings of the 6th Nordic Signal Processing Symposium, Espoo, Finland, 11 June 2004. [Google Scholar]
  120. Çolakoğlu, N.; Akkaya, B. Comparison of Multi-class Classification Algorithms on Early Diagnosis of Heart Diseases. In Proceedings of the Recent Advance in Data Science and Business Analytics, Istanbul, Turkey, 25–28 September 2019; pp. 162–172. [Google Scholar]
  121. Putra, M.; Rosid, M.S.; Handoko, D. Rainfall Estimation Using Machine Learning Approaches with Raingauge, Radar, and Satellite Data. In Proceedings of the International Conferernce on Electrical Engineering and Informatics (ICELTICs), Banda Aceh, Indonesia, 27–28 September 2022. [Google Scholar]
  122. Darmastowo, F.R.; Rosid, M.S.; Handoko, D. Rainfall Estimation in Equatorial Region Using Weather Radar-Based Machine Learning. In Proceedings of the International Seminar on Application for Technology of Information and Communication, Semarang, Indonesia, 16–17 September 2023. [Google Scholar]
  123. Nareswari, B.N.A.; Putra, M.; Handoko, D. Convective Rainfall Estimation From Radar Measurement using Tree-Based Machine Learning. In Proceedings of the 18th IMT-GT International Conference on Mathematics, Statistics and their Applications, Agra, India, 24–26 March 2023; pp. 34–38. [Google Scholar] [CrossRef]
  124. Anggraini, N.; Jumarang, M.I. Curah Hujan bulanan di Kota Pontianak Berdasarkan Metode Quadratic-Hill Climbing. PRISMA FISIKA 2014, 2, 15–18. [Google Scholar]
  125. Modarres, Z.G.; Shabankhah, M.; Kamandi, A. Making AdaBoost Less Prone to Overfitting on Noisy Datasets. In Proceedings of the 6th International Conference on Web Research (ICWR), Tehran, Iran, 22–23 April 2020; pp. 251–259. [Google Scholar]
  126. Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2006; pp. 165–192. [Google Scholar] [CrossRef]
  127. Leiva, R.G.; Anta, A.F.; Mancuso, V.; Casari, P. A novel hyperparameter-free approach to decision tree construction that avoids overfitting by design. IEEE Access 2019, 7, 99978–99987. [Google Scholar] [CrossRef]
  128. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  129. Aziz, N.; Akhir, E.A.P.; Aziz, I.A.; Jaafar, J.; Hasan, M.H.; Abas, A.N.C. A Study on Gradient Boosting Algorithms for Development of AI Monitoring and Prediction Systems. In Proceedings of the International Conference on Computational Intelligence (ICCI), Bandar Seri Iskandar, Malaysia, 8–9 October 2020; pp. 11–16. [Google Scholar]
  130. Tufail, S.; Riggs, H.; Tariq, M.; Sarwat, A.I. Advancements and Challenges in Machine Learning: A Comprehensive Review of Models, Libraries, Applications, and Algorithms. Electronics 2023, 12, 1789. [Google Scholar] [CrossRef]
  131. Talekar, B. A Detailed Review on Decision Tree and Random Forest. Biosci. Biotechnol. Res. Commun. 2020, 13, 245–248. [Google Scholar] [CrossRef]
  132. Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
  133. Hosen, S.; Amin, R. Significant of Gradient Boosting Algorithm in Data Management System. Eng. Int. 2021, 9, 85–100. [Google Scholar] [CrossRef]
  134. Ma, L.; Zhang, G.; Lu, E. Using the gradient boosting decision tree to improve the delineation of hourly rain areas during the summer from advanced Himawari imager data. J. Hydrometeorol. 2018, 19, 761–776. [Google Scholar] [CrossRef]
  135. Mienye, I.D.; Sun, Y. A Survey of Ensemble Learning: Concepts, Algorithms, Applications, and Prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
  136. Tran, N.T.; Tran, T.T.G.; Nguyen, T.A.; Lam, M.B. A new grid search algorithm based on XGBoost model for load forecasting. Bull. Electr. Eng. Inform. 2023, 12, 1857–1866. [Google Scholar] [CrossRef]
  137. Fan, M.; Xiao, K.; Sun, L.; Zhang, S.; Xu, Y. Automated Hyperparameter Optimization of Gradient Boosting Decision Tree Approach for Gold Mineral Prospectivity Mapping in the Xiong’ershan Area. Minerals 2022, 12, 1621. [Google Scholar] [CrossRef]
  138. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
  139. Yasper, A.; Handoko, D.; Putra, M.; Aliwarga, H.K.; Rosid, M.S.R. Hyperparameters Optimization in XGBoost Model for Rainfall Estimation: A Case Study in Pontianak City. J. Penelit. Pendidik. IPA 2023, 9, 7113–7121. [Google Scholar] [CrossRef]
  140. Nikolopoulos, E.I.; Crema, S.; Marchi, L.; Marra, F.; Guzzetti, F.; Borga, M. Impact of uncertainty in rainfall estimation on the identification of rainfall thresholds for debris flow occurrence. Geomorphology 2014, 221, 286–297. [Google Scholar] [CrossRef]
  141. Fernando, K.; Wickramasuriya, S.S.; Fernando, W.C.D.K. Investigation of Probable Maximum Precipitation for Disaster Risk Reduction in Sri Lanka. 2016. Available online: https://www.researchgate.net/publication/303910137 (accessed on 31 May 2024).
  142. Lanza, L.G.; Stagi, L. Certified Accuracy of Rainfall Data as a Standard Requirement in Scientific Investigations. Adv. Geosci. 2008, 16, 43–48. [Google Scholar] [CrossRef]
  143. Habib, E.; Krajewski, W.F.; Kruger, A. Sampling errors of tipping-bucket rain gauge measurements. J. Hydrol. Eng. 2001, 6, 159–166. [Google Scholar] [CrossRef]
  144. Wang, J.; Fisher, B.L.; Wolff, D.B. Estimating rain rates from tipping-bucket rain gauge measurements. J. Atmos. Ocean. Technol. 2008, 25, 43–56. [Google Scholar] [CrossRef]
  145. Hosseini, S.H.; Hashemi, H.; Berndtsson, R.; South, N.; Aspegren, H.; Larsson, R.; Olsson, J.; Persson, A.; Olsson, L. Evaluation of a new X-band weather radar for operational use in south Sweden. Water Sci. Technol. 2020, 81, 1623–1635. [Google Scholar] [CrossRef] [PubMed]
  146. Nugraha Jonathan, H.; Fahdiran, R. Penentuan lokasi terbaik untuk estimasi curah hujan berdasarkan efek paralaks dan suhu puncak awan menggunakan data satelit himawari-8 (studi kasus di wilayah Indonesia bagian tengah). Pros. Semin. Nas. Fis. E-J. 2024, 12, FA-43. [Google Scholar] [CrossRef]
  147. Bahtiar, R.; Wijayanto, Y.; Budiman, S.A.; Saputra, T.W. Perbedaan Karakteristik Sebaran Spasial Hujan di Kabupaten Jember Menggunakan Metode Inverse Distance Weighted (IDW) dan Poligon Thiessen. Differences in the Spatial Distribution Characteristics of Rainfall in Jember Regency Using the Inverse Distance Weighted (IDW) and Thiessen Polygon Methods. Berk. Ilm. Pertan. 2022, 5, 1–5. [Google Scholar]
  148. Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall spatial estimations: A review from spatial interpolation to multi-source data merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
  149. Inlaung, K.; Nakapan, S. Study of radar rainfall estimation using geographic information systems over Chiang Mai province. J. Phys. Conf. Ser. 2018, 1144, 012089. [Google Scholar] [CrossRef]
  150. Ardiyanto, L.; Hanif, A.M.; Alfaridzi, M.; Ariwibowo, S.; Wardoyo, E.; Redha Nugraheni, I. Estimasi Curah Hujan Radar Cuaca dengan Hubungan Z-R Berbeda pada Tipe Awan Hujan Konvektif dan Stratiform di Lampung. Pros. SNFA (Semin. Nas. Fis. Apl.) 2019, 4, 51–60. [Google Scholar] [CrossRef]
  151. Guarascio, M.; Folino, G.; Chiaravalloti, F.; Gabriele, S.; Procopio, A.; Sabatino, P. A Machine Learning Approach for Rainfall Estimation Integrating Heterogeneous Data Sources. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4200111. [Google Scholar] [CrossRef]
  152. Hassan, D.; Isaac, G.A.; Taylor, P.A.; Michelson, D. Optimizing Radar-Based Rainfall Estimation Using Machine Learning Models. Remote Sens. 2022, 14, 5188. [Google Scholar] [CrossRef]
  153. Chandrasekar, V.; Tan, H.; Chen, H. A Machine Learning System for Rainfall Estimation from Spaceborne and Ground Radars. In Proceedings of the 2017 32nd General Assembly and Scientific Symposium of the International Union of Radio Science, URSI GASS 2017, Montreal, QC, Canada, 19–26 August 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2017; pp. 1–2. [Google Scholar] [CrossRef]
  154. You, H.; Wang, J.; Wong, R.K.W.; Schumacher, C.; Saravanan, R.; Jun, M. Prediction of Tropical Pacific Rain Rates with Over-parameterized Neural Networks. Artif. Intell. Earth Syst. 2024, 3. [Google Scholar] [CrossRef]
  155. Allawi, M.F.; Abdulhameed, U.H.; Adham, A.; Sayl, K.N.; Sulaiman, S.O.; Ramal, M.M.; Sherif, M.; El-Shafie, A. Monthly rainfall forecasting modelling based on advanced machine learning methods: Tropical region as case study. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2243090. [Google Scholar] [CrossRef]
  156. Xu, R.; Zhang, T. Combining Cloud and Mobile Computing for Machine Learning. arXiv 2024, arXiv:2402.04880. [Google Scholar]
  157. Grzesik, P.; Mrozek, D. Combining Machine Learning and Edge Computing: Opportunities, Challenges, Platforms, Frameworks, and Use Cases. Electronics 2024, 13, 640. [Google Scholar] [CrossRef]
Signals 05 00030 g001
Figure 1. The distribution of automatic rain gauges includes 1233 units (green triangles), and the integrated weather radar network consists of 42 units (yellow) operating in the Indonesian region.
Figure 1. The distribution of automatic rain gauges includes 1233 units (green triangles), and the integrated weather radar network consists of 42 units (yellow) operating in the Indonesian region.
Signals 05 00030 g001
Signals 05 00030 g002
Figure 2. The most commonly operated rain gauges in Indonesia.
Figure 2. The most commonly operated rain gauges in Indonesia.
Signals 05 00030 g002
Signals 05 00030 g003
Figure 3. Comparison of radar imagery products and illustrations of the PPI, CAPPI, and CMAX products: (a) radar imagery of PPI dBZ products at an elevation of 0.5°, (b) CAPPI dBZ products at 0.5 km, and (c) CMAX products (modified from [58]). (d) PPI, (e) CAPPI, and (f) CMAX measurement mechanisms (modified from [59,60]).
Figure 3. Comparison of radar imagery products and illustrations of the PPI, CAPPI, and CMAX products: (a) radar imagery of PPI dBZ products at an elevation of 0.5°, (b) CAPPI dBZ products at 0.5 km, and (c) CMAX products (modified from [58]). (d) PPI, (e) CAPPI, and (f) CMAX measurement mechanisms (modified from [59,60]).
Signals 05 00030 g003
Signals 05 00030 g004
Figure 4. Satellite imagery depicting atmospheric conditions in one region of Indonesia during high rainfall intensity: (a) rainfall during floods in Sidoarjo City, (b) time series graph of cloud peak temperature, red box shows the time of occurrence during floods and (c) cloud phase distinction RGB satellite imagery product. The yellowish color signifies a thick and high cloud containing ice particles. Red circle shows the location of Sidoarjo City (modified from [67]).
Figure 4. Satellite imagery depicting atmospheric conditions in one region of Indonesia during high rainfall intensity: (a) rainfall during floods in Sidoarjo City, (b) time series graph of cloud peak temperature, red box shows the time of occurrence during floods and (c) cloud phase distinction RGB satellite imagery product. The yellowish color signifies a thick and high cloud containing ice particles. Red circle shows the location of Sidoarjo City (modified from [67]).
Signals 05 00030 g004
Signals 05 00030 g005
Figure 5. Parallax correction (in km) of Himawari-8 satellite based on cloud-top height of 15 km for the entire Territory of Indonesia. Cloud-top height in convective clouds is an essential feature in extreme weather nowcasting performed by weather forecasters to represent the core location of the severe region of the convective cloud (modified from [88]).
Figure 5. Parallax correction (in km) of Himawari-8 satellite based on cloud-top height of 15 km for the entire Territory of Indonesia. Cloud-top height in convective clouds is an essential feature in extreme weather nowcasting performed by weather forecasters to represent the core location of the severe region of the convective cloud (modified from [88]).
Signals 05 00030 g005
Signals 05 00030 g006
Figure 6. Rainfall estimation approaches using (a) rain gauges and (b) radar or weather satellite methods (modified from [89]).
Figure 6. Rainfall estimation approaches using (a) rain gauges and (b) radar or weather satellite methods (modified from [89]).
Signals 05 00030 g006
Signals 05 00030 g007
Figure 7. An illustration of the (a) TMM, (b) PMM, and (c) WPMM techniques (modified from [24]).
Figure 7. An illustration of the (a) TMM, (b) PMM, and (c) WPMM techniques (modified from [24]).
Signals 05 00030 g007
Signals 05 00030 g008
Figure 8. Conceptual diagram of the MLP algorithm for rainfall estimation using single-polarization radar (a) and the estimation results compared with the radar equation (b) (modified from [115]).
Figure 8. Conceptual diagram of the MLP algorithm for rainfall estimation using single-polarization radar (a) and the estimation results compared with the radar equation (b) (modified from [115]).
Signals 05 00030 g008
Table 2. Several rain gauge interpolation methods, descriptions, and advantages and disadvantages, which are applied in Indonesia.
Table 2. Several rain gauge interpolation methods, descriptions, and advantages and disadvantages, which are applied in Indonesia.
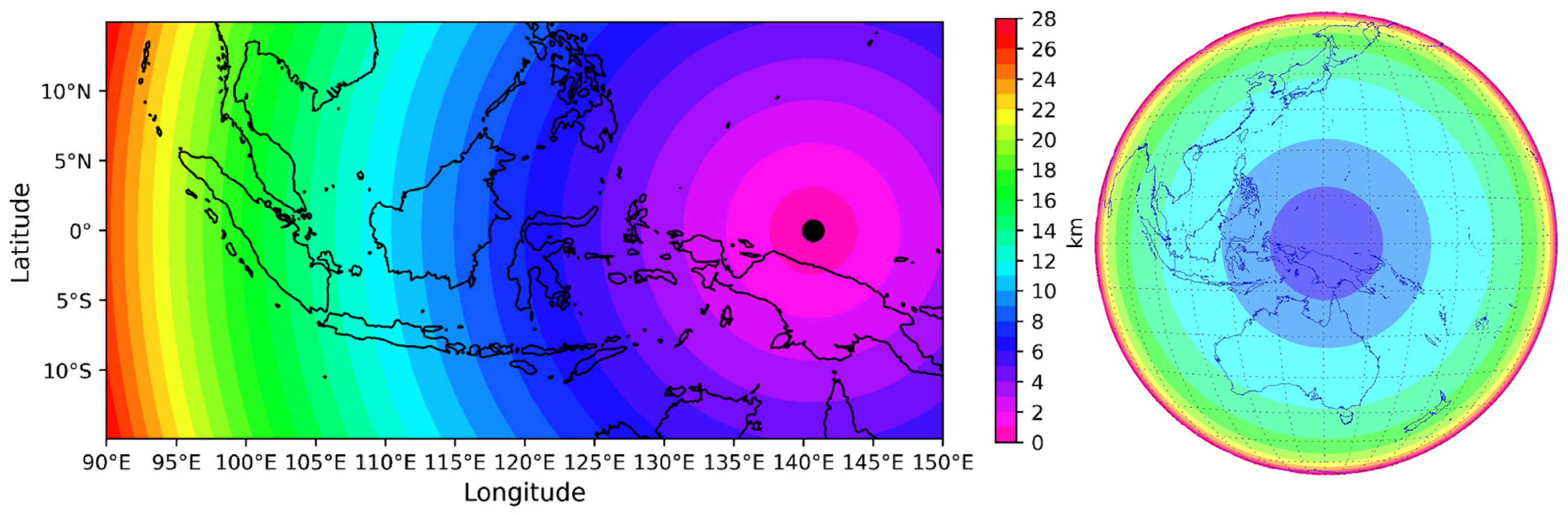
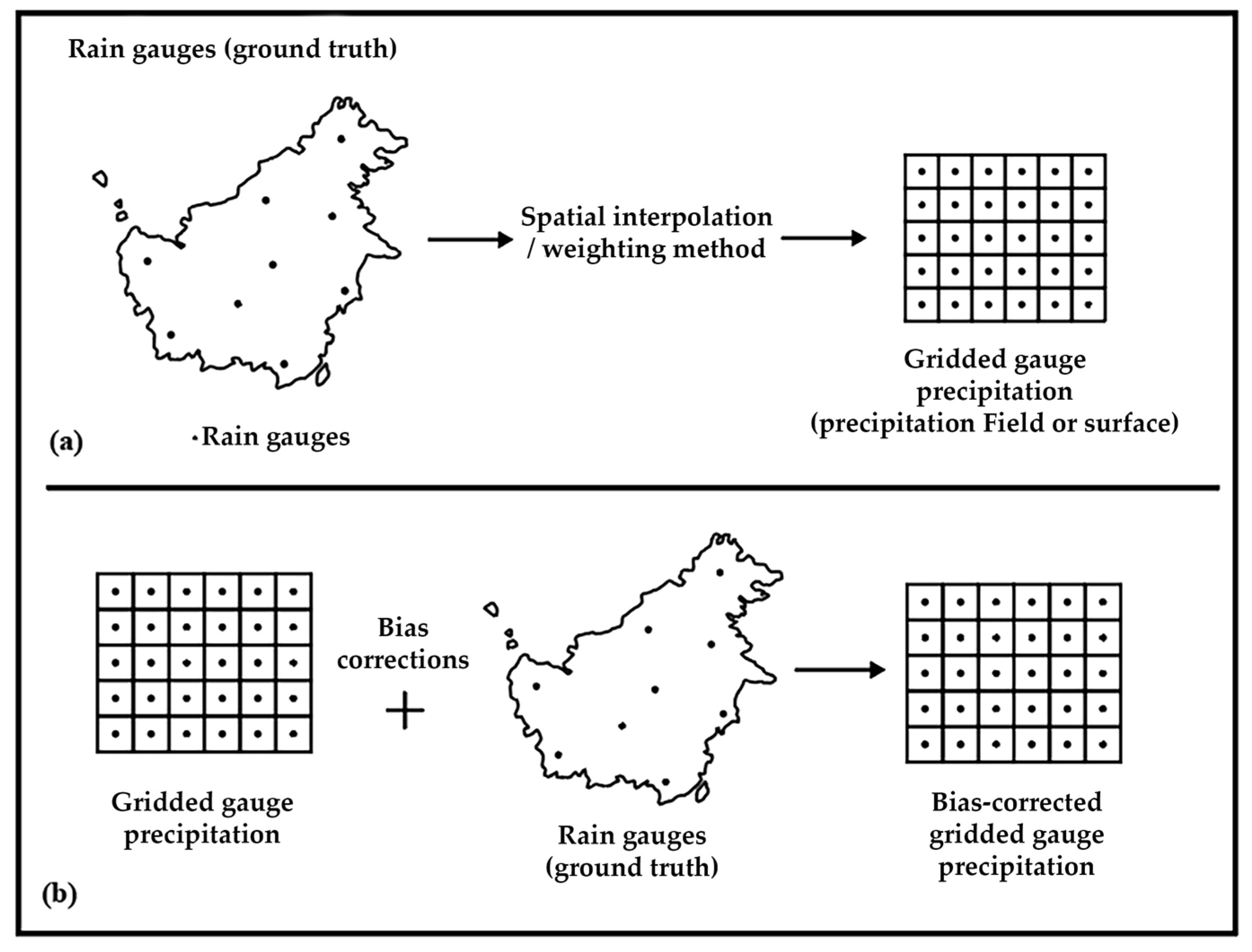
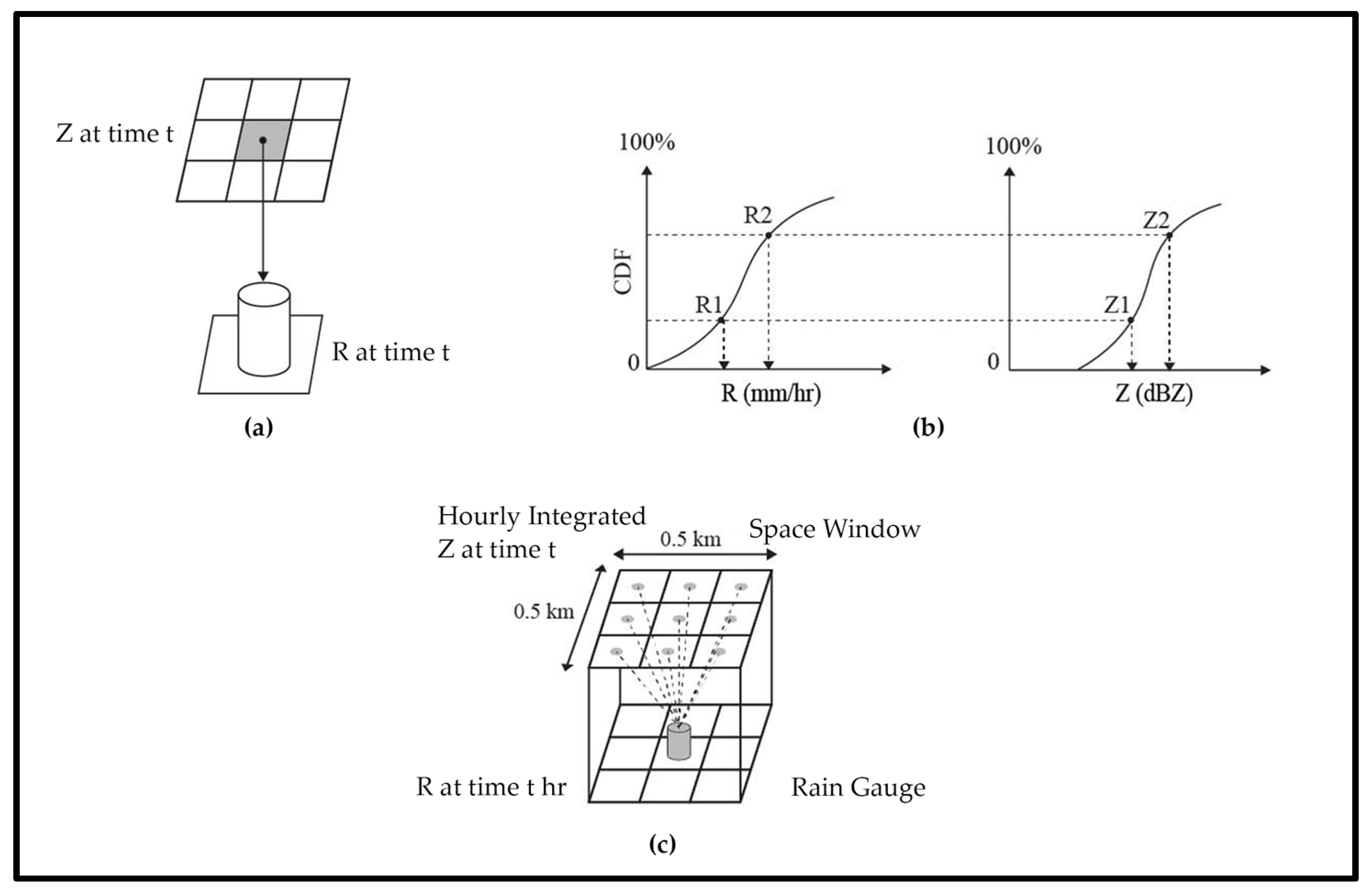
Rain Gauge Interpolation MethodDescription, Advantages, and DisadvantagesImplementation in Indonesia
Thiessen polygonThis method divides the area into polygons, each containing one rain gauge, and each point in the polygon is represented by data from the rain gauge. If the rain gauge distribution is tight, this method can provide a fairly good estimate because each polygon covers a specific area. However, this method does not consider topographic variations [92]. Relatively flat areas with a dense rain gauge distribution will be suitable for this method.Applied in Pontianak City by dividing the area into polygons based on the location of the rain stations. The rainfall classification is only divided into two classes, and this area is classified as having high rainfall [94]. Unfortunately, there is no explicit mention of statistical metrics and validation results.
Inverse Distance WeightingThis method gives greater weight to closer points [99]. Even though it produces smoother interpolations, IDW is still susceptible to bias if the rain gauge is uneven, especially in complex mountainous areas, where rainfall variations can be high. This method is more appropriate to use in locations with dense and even rain gauge points.Successfully applied in East Java Province for interpolation of monthly rainfall with dense points [100], with an RMSE value of 100.435 mm
SplineUsing mathematical functions to minimize surface curvature, it forms a spline to estimate areal rainfall. It can produce a continuous interpolation function, but is very dependent on the distribution and density of data points [94], and therefore it is not suitable for application in areas with significant topographic diversity.Produced smooth and continuous rainfall maps in Pontianak City. However, it is less effective if there is a significant value difference at a very short distance between measurement points [94]. Unfortunately, there is no explicit mention of statistical metrics or validation results.
KrigingGeostatistical interpolation considers the distance and degree of variation between known data points when estimating values in an unknown area [101]. Suitable for areas with uneven distribution of rain gauge stations.Applied in the Bali Region. With a daily time scale, the results help understand the spatial pattern of rainfall in the study area [102]. The RMSE value varies, mostly below 20 mm·day−1
Table 3. Summary of the review results of data sources, techniques, and methods for estimating rainfall in Indonesia.
Table 3. Summary of the review results of data sources, techniques, and methods for estimating rainfall in Indonesia.
Discussion AreaCurrent ConditionsRecommendations and Potential Improvements
Rainfall Data SourceRain gaugeThe distribution of rain gauge points is unevenly distributed.Manage the ideal rain gauge distribution; place weather radar according to technical and non-technical characteristics; implement bias correction according to regional conditions. And combine existing data sources in Indonesia.
Weather radarNot all weather radar placements are compatible with instrument and topographic characteristics.
Weather SatelliteBias correction has been implemented but needs to be adjusted to the conditions of each region.
Rainfall Estimation Methods and TechniquesStatistical Application It has been widely applied but is less adaptive to regional conditions.Developing the application of machine learning for rainfall estimation in Indonesia
Machine Learning ApproachesIts implementation still needs to be more common.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Putra, M.; Rosid, M.S.; Handoko, D. A Review of Rainfall Estimation in Indonesia: Data Sources, Techniques, and Methods. Signals 2024, 5, 542-561. https://doi.org/10.3390/signals5030030

AMA Style

Putra M, Rosid MS, Handoko D. A Review of Rainfall Estimation in Indonesia: Data Sources, Techniques, and Methods. Signals. 2024; 5(3):542-561. https://doi.org/10.3390/signals5030030

Chicago/Turabian Style

Putra, Maulana, Mohammad Syamsu Rosid, and Djati Handoko. 2024. "A Review of Rainfall Estimation in Indonesia: Data Sources, Techniques, and Methods" Signals 5, no. 3: 542-561. https://doi.org/10.3390/signals5030030

APA Style

Putra, M., Rosid, M. S., & Handoko, D. (2024). A Review of Rainfall Estimation in Indonesia: Data Sources, Techniques, and Methods. Signals, 5(3), 542-561. https://doi.org/10.3390/signals5030030

Article Metrics

Back to TopTop