Daily Streamflow Forecasting Using AutoML and Remote-Sensing-Estimated Rainfall Datasets in the Amazon Biomes

Abstract

Reliable streamflow forecasting is crucial for several tasks related to water-resource management, including planning reservoir operations, power generation via Hydroelectric Power Plants (HPPs), and flood mitigation, thus resulting in relevant social implications. The present study is focused on the application of Automated Machine-Learning (AutoML) models to forecast daily streamflow in the area of the upper Teles Pires River basin, located in the region of the Amazon biomes. The latter area is characterized by extensive water-resource utilization, mostly for power generation through HPPs, and it has a limited hydrological data-monitoring network. Five different AutoML models were employed to forecast the streamflow daily, i.e., auto-sklearn, Tree-based Pipeline Optimization Tool (TPOT), H2O AutoML, AutoKeras, and MLBox. The AutoML input features were set as the time-lagged streamflow and average rainfall data sourced from four rain gauge stations and one streamflow gauge station. To overcome the lack of training data, in addition to the previous features, products estimated via remote sensing were leveraged as training data, including PERSIANN, PERSIANN-CCS, PERSIANN-CDR, and PDIR-Now. The selected AutoML models proved their effectiveness in forecasting the streamflow in the considered basin. In particular, the reliability of streamflow predictions was high both in the case when training data came from rain and streamflow gauge stations and when training data were collected by the four previously mentioned estimated remote-sensing products. Moreover, the selected AutoML models showed promising results in forecasting the streamflow up to a three-day horizon, relying on the two available kinds of input features. As a final result, the present research underscores the potential of employing AutoML models for reliable streamflow forecasting, which can significantly advance water-resource planning and management within the studied geographical area.

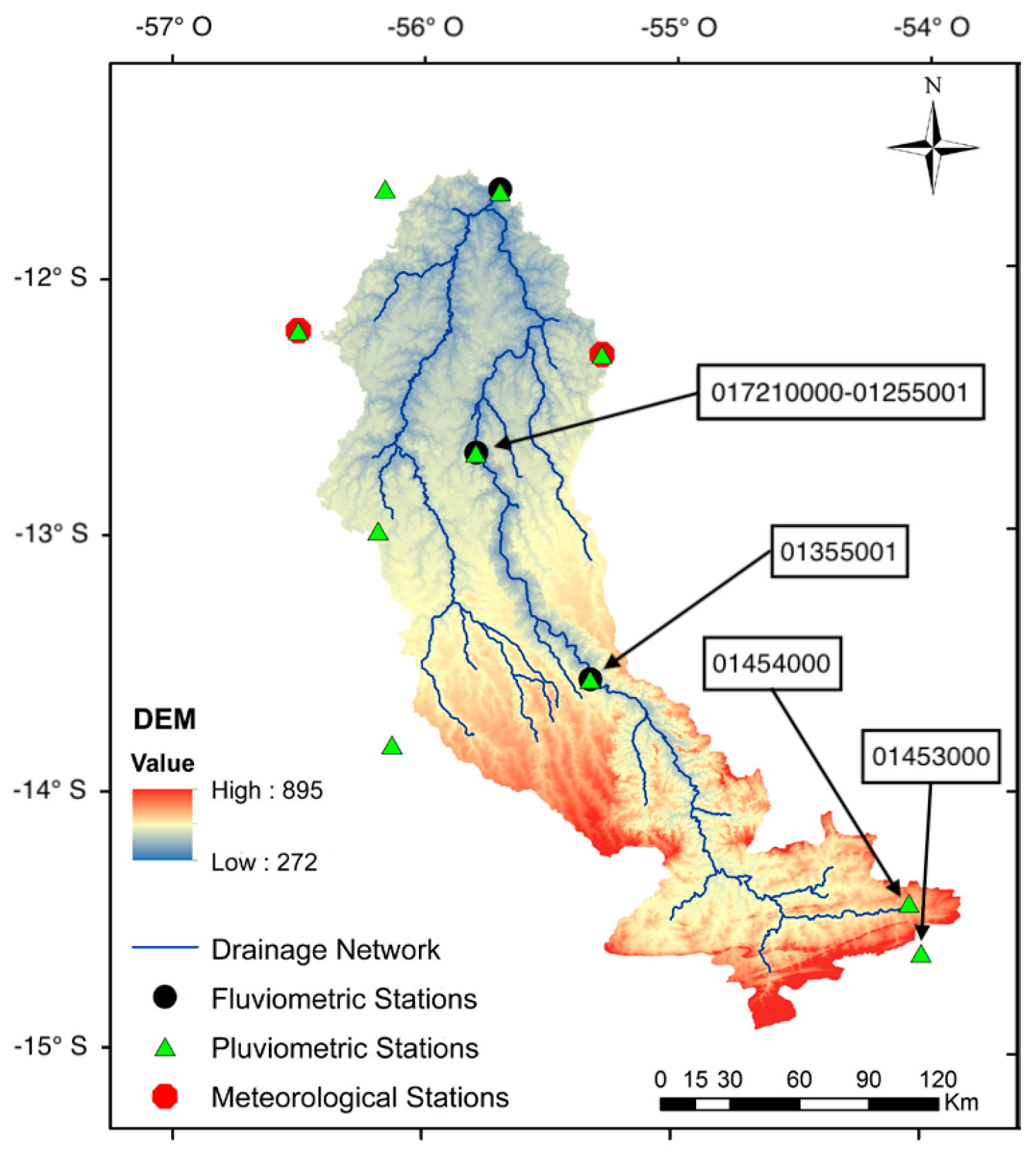
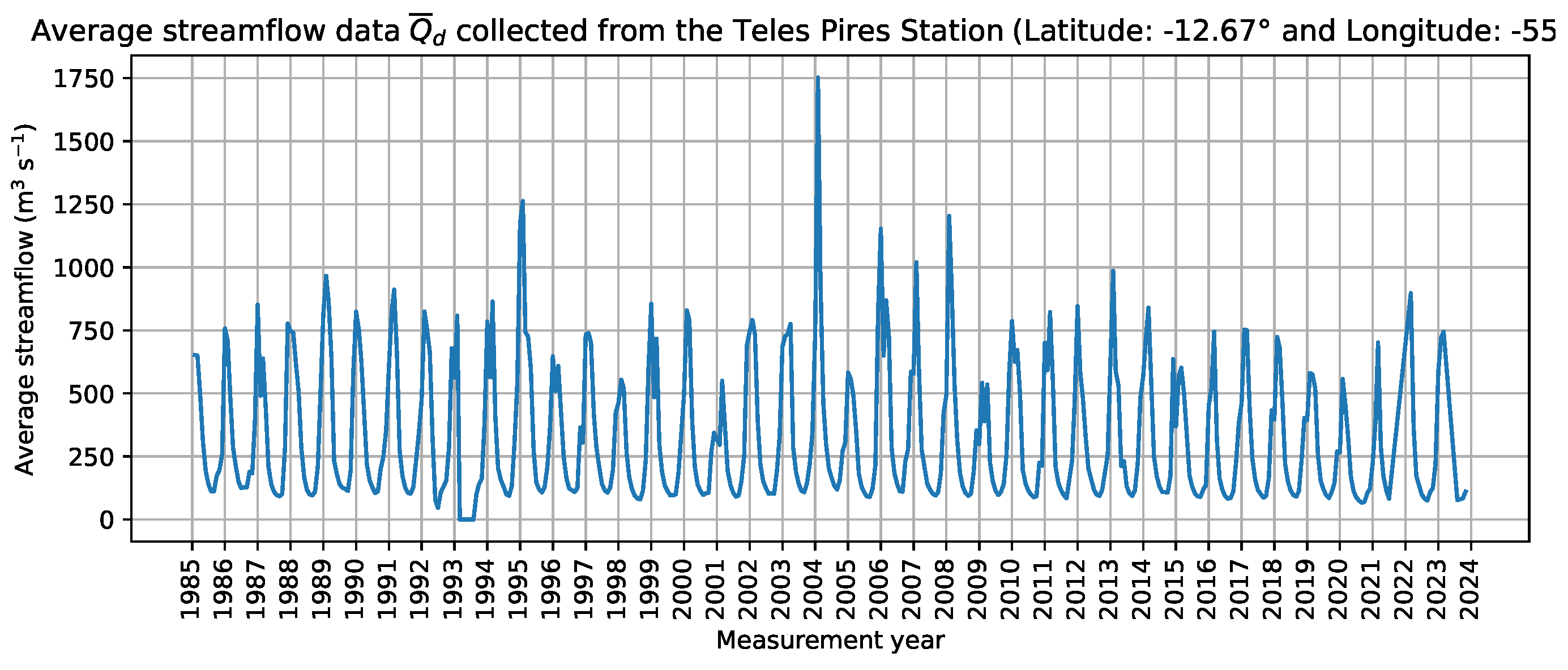
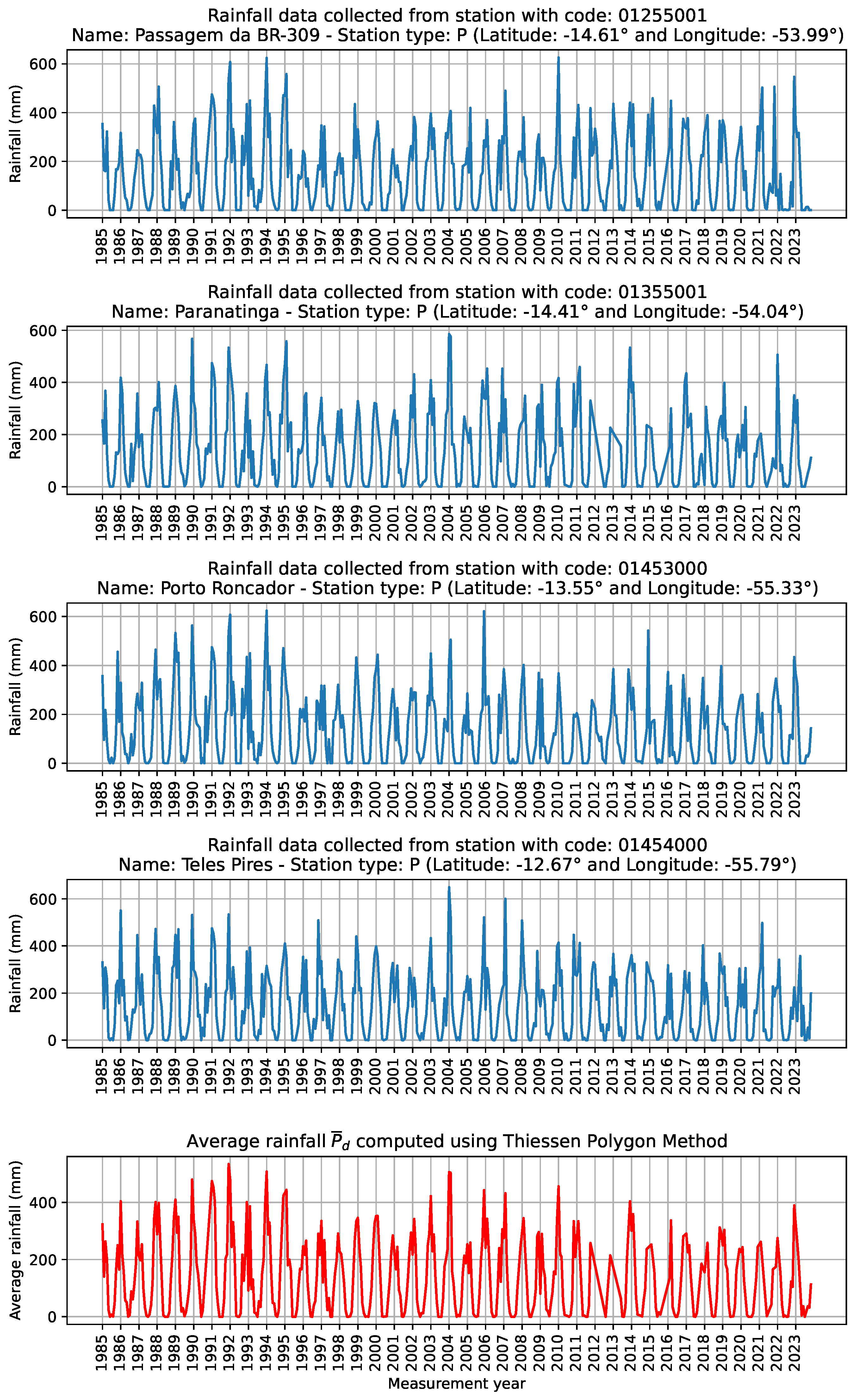
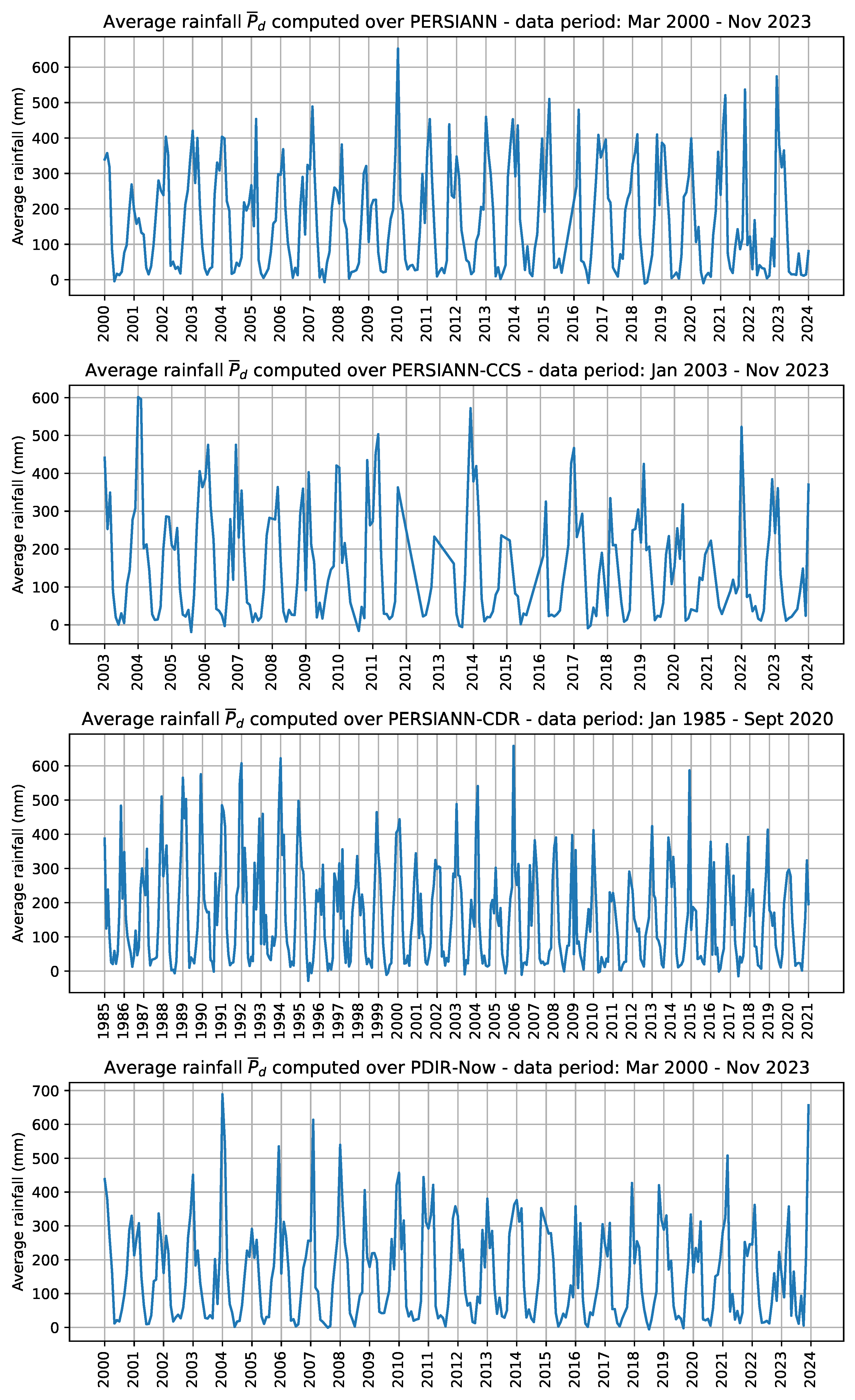
1. Introduction

Reliable streamflow forecasting is crucial for several applications, such as reservoir management [1], predicting energy generation in hydroelectric installations [2], flood mitigation [3], designing hydraulic schemes [4], assessing the impact of human-induced changes on water accessibility [5], and estimating the occurrence of extreme climate phenomena [6]. The wide spectrum of the mentioned applications highlights the essential need for accurate streamflow predictions [7]. Consequently, there is an increasing demand for improved short-term and long-term streamflow predictions to enhance water-resource management practices [7,8]. However, reliability in streamflow forecasts remains a significant challenge within the field of water-resource management. Indeed, the difficulty in accurate hydrological forecasting is primarily due to the dynamic relations and considerable spatial and temporal variability of the elements that regulate the hydrological cycle that convert rainfall into river flows [9]. Moreover, the transformation of rainfall into runoff is generally nonlinear [10], thus leading to additional complexities in its proper modeling.

Precipitation is the primary source of water input into a river basin, directly influencing river flow through several hydrological processes [7,9,11]: when precipitation occurs, it can either infiltrate the soil, contributing to groundwater recharge or become surface runoff, which flows over the land and into rivers and streams. The amount and intensity of precipitation, along with the characteristics of the watershed, such as soil type, vegetation cover, and topography, determine the proportion of water that becomes runoff versus infiltration [7,8]. During periods of heavy rainfall, the soil’s infiltration capacity can be exceeded, leading to increased surface runoff and higher river flows. Conversely, during dry periods, reduced precipitation results in lower river flow as groundwater contributions diminish [5,6]. Additionally, the temporal distribution of precipitation events, such as the occurrence of prolonged rainfall versus short, intense storms, plays a crucial role in shaping the river flow patterns [9]. Understanding the reported dynamics is essential for accurate streamflow forecasting and effective water-resource management, particularly in regions with limited hydrological data like the Amazon basin [7,8,9].

The transformation of rainfall into runoff has been modeled in multiple ways through physical [12], conceptual [13], and empirical approaches [14]. Physical and conceptual models provide a comprehensive mathematical formulation of the hydrological elements that govern the transformation of rainfall into streamflow [12,13]. However, the application of the latter models requires comprehensive data about the considered basin, including climatic conditions, soil features, and characteristics of drainage channels. As a consequence, the need for such extensive hydrometeorological data can render physical and conceptual models impractical or result in subpar performance in predicting rainfall-runoff in watersheds with limited available data [7]. On the other hand, empirical models, often based on Machine Learning (ML), can identify correlations between input and output data of hydrological systems without taking into account the involved physical processes [15,16,17]. Indeed, ML models can forecast the hydrological components of interest by employing mathematical equations that only fit the available training data. Traditional ML-based hydrological models, for instance, based on k-Nearest Neighbors (k-NN), Support Vector Machine (SVM), Random Forest (RF), Artificial Neural Networks (ANNs), and Deep Learning (DL) have proven to be effective in predicting the streamflow in basins with limited hydrometeorological data [16,17].

Regarding ML models, according to Islam et al. [18], it must be noted that within the field of hydrology, the latter models are particularly relevant when the focus is put on the model’s reliability and/or simplicity rather than the ability to effectively represent the underlying hydrological, physical processes. For instance, high reliability in predictions is crucial for operational uses both in reservoirs and flood alert systems [1,3]. Indeed, several recent research works, including the ones of De Sousa et al. [19] and Filho et al. [20], focused on the applicability of ML models to daily streamflow forecasting in the Amazon biomes and such authors underscored the remarkable performances of several traditional ML models in the context of Amazon basin, where limited hydrometeorological data were available. Incidentally, similar findings resulting in the successful application of ML-based forecasting models were obtained in other regions of Brazil with comparable hydrometeorological characteristics, e.g., in the Brazilian state of Pernambuco by Da Silva et al. [21]. Furthermore, it was noted that the effectiveness of ML models in streamflow forecasting is not only due to their resilience in handling the scarcity of available hydrometeorological information but also in dealing with the frequent non-stationary nature of the considered data [19,22]. Finally, De Sousa et al. [19] showed that historical rainfall and streamflow data alone are mostly sufficient to exploit ML for streamflow forecasting.

Even if the traditional ML models demonstrated their effectiveness in the context of streamflow forecasting, they often present several drawbacks to their effective applicability. In particular, traditional ML models typically require a deep understanding of each of the employed underlying ML algorithms and their adjustable parameters and hyperparameters for effective model selection and tuning [23,24,25]. Furthermore, the process of manually training, selecting the proper model, and tuning the respective hyperparameters is often time-consuming, in particular when dealing with ML algorithms allowing the possibility of adjusting a wide set of parameters and hyperparameters, each with multiple or even continuous degrees of freedom [24,25,26]. Last but not least, every step of the traditional ML pipeline required to obtain a fully working forecasting ML model, i.e., data preprocessing, feature extraction, repeated model training and testing, hyperparameter tuning, and final model selection must be done manually [23,24,25].

Automated Machine-Learning (AutoML) models were introduced to mitigate the above-mentioned issues, and they offer several advantages over the traditional ML pipeline [23,24,25]. First, AutoML models reduce the need for deep expertise in each of the employed ML algorithms, as they completely automate data preprocessing, feature extraction, repeated model training and testing, hyperparameter tuning, and final model selection by significantly simplifying the entire ML design process for researchers [23,24,25]. Furthermore, the provided automation does not only reduce design complexity but also drastically cuts down the time required for developing reliable ML models, as it can efficiently test a vast space of candidate optimal models and respective hyperparameters, something that would often be impractical to do manually [23,24,25,26]. Finally, AutoML models streamline the entire ML pipeline—from data preprocessing to final model selection—ensuring that each step is optimally performed without or with minimal manual intervention [23,24,25]. As a final result, the design of ML forecasting models becomes a completely end-to-end design process, which, in the context of hydrology, could accelerate the development of reliable ML-based models for streamflow prediction, even in environments with limited hydrometeorological data. Indeed, recently, AutoML was applied in a few related studies that focused on streamflow forecasting with remarkable forecasting performance [27,28,29].

Designing streamflow ML forecasting models that both require minimal training data and can automate training, testing, tuning, and final model selection is crucial for hydrological studies in world regions with limited data available, such as the Amazon [19,20,30]. Indeed, the Amazon basin has a lower density of hydrometeorological stations compared to other regions in Brazil and worldwide [19,20]. Moreover, the existing network of stations suffers from issues related to limited historical data, uneven distribution, data series inconsistencies, and limited measurement periods [19,20]. Such data gaps are partly due to the region’s vast size and the inaccessibility of areas where monitoring stations are located, such as national parks and indigenous lands where the Amazon rainforest is constantly preserved. In the presented scenario, ML models have highly proven effectiveness in accurately representing the hydrological behavior of the considered Amazon region even with limited data, as demonstrated by previous studies [19,20], and AutoML models could further enhance such forecasting performance.

Water resources in the Amazon basin hold significant value, primarily for the production of hydroelectric energy through the construction of dams [31]. Unfortunately, the latter process leads to several environmental issues, including biodiversity loss [32], local social impacts [33], flooding of rainforest areas [34], and disruptions of the region hydrological cycle [35]. Currently, three Hydroelectric Power Plants (HPPs)—Sinop, Colíder Pesqueiro do Gil, and Teles Pires—are operational in the upper Teles Pires River basin [36]. Furthermore, the construction of two additional HPPs in the Amazon region—the Jirau and Santo Antônio dams (on the Madeira River, Rondônia) and the Belo Monte dam (on the Xingu River, Pará)—recently indicated a growing demand for hydroelectric production in the considered region [37]. As a consequence, the Brazilian National Electric System Operator (Operador Nacional do Sistema Elétrico—ONS) started to manage water accumulation reservoirs and to compute streamflow predictions relying on stochastic models [19,38]. As well as stochastic models, the ONS also employed conceptual models like SMAP [39,40], but such models reported limited precision [38,40]. Thus, the potential of other ML-based forecasting models, such as the ones represented by AutoML warrants exploration for improving the performance of the critical streamflow prediction task in the Amazon region.

The importance of computing accurate streamflow forecasts cannot be understated for effective water-resource planning and management in the Amazon basin region. Thus, given the constraints of the existing hydrometeorological data and the requirement for reliable streamflow predictions, the objective of the present study is to exploit AutoML methods to effectively forecast the daily streamflow in the selected geographical area. Furthermore, the objective is even to improve the forecasting performances of the already existing ML-based forecasting methods previously applied in the same context. Towards the latter aims the present research relied both on data sourced from several rain and streamflow gauge stations and rainfall products estimated through remote sensing, in line with previously investigated approaches [19,20,21,30]. The employed estimates included Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN), PERSIANN—Cloud Classification System (PERSIANN-CCS), PERSIANN—Climate Data Record (PERSIANN-CDR), and PERSIANN—Dynamic Infrared Rain rate near real-time (PDIR-Now), where the latter one represents a recently introduced product just recently tested in the context of streamflow forecasting [41,42].

The forthcoming part of the article is organized as follows: Section 2 reports the latest ML-based approaches which addressed the problem of streamflow forecasting, even with particular focus on the Amazon biomes; Section 3 describes the geographical area of interest on which it is focused the present study, the employed datasets, the selected AutoML models along with their experimental settings, and the analyzed metrics for final evaluation of the AutoML models; Section 4 reports the obtained results of the present study; Section 5 discusses the reported findings, even with respect to the previous research works which addressed the same objectives; and Section 6 draws the conclusions of the carried research and suggests potential future directions.

2. Related Works

In recent years, researchers have employed several ML-based models to forecast the streamflow due to their high accuracy and flexibility [16,17]. For instance, ANNs/DL-based models [43,44], RF-based models [18,19,45], SVM-based models [46,47,48], and AutoML-based models [27,28,29] have been used to provide reliable streamflow forecasts.

Adnan et al. [46] evaluated several ML models for predicting monthly streamflows using precipitation and temperature inputs, including the Optimally Pruned Extreme Learning Machine (OP-ELM), Least Square Support Vector Machine (LSSVM), Multivariate Adaptive Regression Splines (MARS), and M5 Model Tree (M5Tree). The results obtained by the authors revealed that LSSVM and MARS-based models outperformed OP-ELM and M5Tree models in streamflow prediction, even without the necessity for local input data.

Meshram et al. [44] compared three ML-based techniques, i.e., Adaptive Neuro-Fuzzy Inference System (ANFIS), Genetic Programming (GP), and ANNs, to forecast the streamflow in the Shakkar watershed (Narmada Basin, India). The latter models incorporated past streamflow data and cyclic terms in the input vector to create suitable time-series models for streamflow forecasting. To evaluate the models’ performances, standard time-series forecasting metrics were used. Results indicated that the ANFIS model achieved the best performance in time-series streamflow forecasting, with the GP model and the ANN model ranking second and third, respectively. The study highlighted that models incorporating cyclic terms significantly outperformed those relying solely on previous streamflow data.

Kumar et al. [27] employed ML models to predict daily streamflow using hydrometeorological data related to rainfall, temperature, relative humidity, solar radiation, wind speed, and the one-day lag value of the streamflow. Among the employed ML models, i.e., bagging ensemble learning, boosting ensemble learning, Gaussian Process Regression (GPR), and the AutoML-GWL model [49], the bagging ensemble-learning model resulted as the most effective with a correlation coefficient $R=0.80$ and Root Mean Square Error $RMSE=218$. The authors even tested the Soil and Water Assessment Tool (SWAT) physical-based model; however, even the bagging ensemble-learning ML model demonstrated superior predictive strength (SWAT: $R=0.82$; $RMSE=281$).

Lee et al. [28] developed a Multi-inflow Prediction Ensemble (MPE) model for dam inflow prediction using the auto-sklearn AutoML model [50]. The MPE model combined ensemble models for high and low inflow prediction to enhance the prediction accuracy. The study compared the MPE model performance with a conventional auto-sklearn-based ensemble model, finding that the MPE model significantly improved predictions during both flood and non-flood periods. The MPE model reduced RMSE and Mean Absolute Error (MAE) by $22.1\%$ and $24.9\%$, respectively, and the designed model increased the coefficient of determination ($R^2$) and Nash–Sutcliffe efficiency coefficient by $21.9\%$ and $35.8\%$, respectively. The results indicated that the MPE model could enhance water-resource management and dam operation, benefiting the environment and society.

Tu et al. [29] reconstructed long-term natural flow time-series for inflows into the Pearl River Delta (within the state of China) using global reanalysis datasets, observation data, and ensemble ML models. The study found that the quality of reconstruction provided by the employed AutoGluon AutoML model was superior with respect to the other employed ML models on large-scale datasets. Furthermore, the computed Indicator of Hydrologic Alteration and Range of Variability Analysis (IHA-RVA) revealed that climate variability, reservoir regulation, and human activities significantly altered the natural flow regime, typically smoothing the natural flow variability. As a final result, the research provided an efficient and reliable method for reconstructing natural river flows.

De Oliveira et al. [30] evaluated the performance of the Large-Scale Distributed Hydrological Model (MGB-IPH) in forecasting water availability in the upper Teles Pires River basin. Despite the lack of climatic and hydrologic data in the region, the MGB-IPH model, calibrated and validated using data from three fluviometric stations, proved to be effective. The model performance was verified using the Nash–Sutcliffe Efficiency Index and the Bias metric. The results demonstrated that the MGB-IPH model could forecast the flow regimes in the upper Teles Pires basin with high reliability in terms of the employed metrics. Overall, the study indicated that the MGB-IPH model is applicable for water management in the basin, thus in areas with limited hydrometeorological data.

De Sousa et al. [19] assessed the performance of k-NN, SVM, RF, and ANNs ML-based models for daily streamflow prediction in a transitional region between the Savanna and Amazon biomes in the state of Brazil. The results reported by the authors indicated that the employed ML models provided reliable streamflow predictions for up to three days, even in the Amazon basin, where limited hydrometeorological data are available.

Filho et al. [20] developed ANNs ML-based models to predict floods in the Branco River within the Amazon basin. The ML models leveraged river levels and average rainfall data estimated from the remotely sensed rainfall PDIR-Now product. Hourly water level data were recorded by fluviometric telemetric stations of the Brazilian National Water Agency (Agência Nacional de Águas—ANA). The multilayer perceptron served as the framework for the ANNs, with the number of neurons in each layer determined through proper hyperparameter tuning methods.

Da Silva et al. [21] investigated ML models to predict streamflows for proper management of the Jucazinho Dam in the state of Pernambuco, Brazil. Relying on SVR, RF, and ANNs models, the study aimed to forecast the streamflow at the considered dam. Data normalization and Spearman’s correlation were used to enhance the final ML model’s accuracy. Evaluated using metrics such as the Nash–Sutcliffe efficiency coefficient and the coefficient of determination ($R^2$), the SVM model showed the best forecasting performance but was prone to underestimate long-term streamflow values, while RF and ANN models overestimated them likely due to overfitting. The study highlighted the effectiveness of ML in improving dam management in water-scarce regions such as Pernambuco, Brazil.

As reported in the previous paragraphs, recent research works have significantly enhanced the application of ML models for streamflow forecasting, offering various advantages and limitations depending on the specific model and context. ANNs and DL models [43,44] have gained attention due to their ability to model complex nonlinear relationships between inputs and outputs, making them particularly effective when ample data are available. However, such models often suffer from overfitting, particularly when applied to small datasets or regions with limited hydrometeorological data, as observed by Meshram et al. [44]. In contrast, RF-based models [18,19,45] offer robustness and interpretability, making them a preferred choice in scenarios where the dataset includes noise or missing values. However, their computational cost and the potential for overfitting in high-dimensional datasets remain challenges. SVM models [46,47,48] have shown remarkable accuracy in streamflow prediction, particularly for small-to-moderate datasets, thanks to their ability to manage nonlinear patterns. Yet, SVMs are computationally intensive and require careful tuning of hyperparameters, which can be a disadvantage in practical applications. AutoML approaches [27,28,29] have recently emerged as powerful tools that automate the model selection and tuning process, offering a balanced trade-off between performance and ease of use. The AutoML-based models have demonstrated superior performance in various hydrological contexts by optimizing the selection of algorithms and hyperparameters, though their black-box nature may limit interpretability and user trust in certain applications. Overall, while the choice of model depends on the specific requirements of the study, the latest research suggests that a combination of ensemble methods and automated model optimization techniques, such as those provided by AutoML frameworks, can significantly enhance the accuracy and reliability of streamflow forecasts, particularly in data-scarce or highly variable climatic regions.

3. Materials and Methods

3.1. Geographical Area of Interest

The geographical area of interest on which the present study was focused is the upper reaches of the Teles Pires River within the Amazon basin, located in the state of Brazil (refer to Figure 1). The upper Teles Pires River basin encompasses a drainage region of 14,030.98 km², with average elevation of 455.6 m, average slope of 0.03 mm⁻¹, maximum altitude of 895 m, and minimum altitude of 272 m (refer both to Figure 1 and Figure 2) [30,51].

The confluence of the Teles Pires and the Juruena Rivers gives rise to the Tapajós River, a significant tributary of the Amazon River. Moreover, the upper Teles Pires River traverses the Amazon biomes, regions where the primary economic activities are represented by agriculture and livestock farming, producing commodities such as soybeans, corn, and cotton [52]. The considered basin is even a significant source of electrical power due to the presence of three sequentially built HPPs [31,36]: moving downstream, the first HPP is Sinop, followed by the Colíder Pesqueiro do Gil HPP, and finally, the Teles Pires HPP [36].

The upper Teles Pires River basin region primarily experiences a tropical hot and humid climate. The mean annual precipitations in the latter region range between 1706.7 mm and 2036.2 mm, and the peak rainfall occurs from October to April (rainy season), while the lowest precipitation period occurs from May to September (dry season). The monthly rainfall in June, July, and August is typically less than 20 mm, with 0 mm being the most common registered value. Furthermore, the average monthly air temperature in the considered region varies from 23.0 °C to 25.8 °C, with an annual mean of 24.7 °C [19,53].

3.2. Employed Datasets

Table 1. The table reports both the rain and streamflow gauge stations employed in the present research. The “Code” column refers to the station identifiers used in the Brazilian national hydrometeorological network. Within the column “Station Type”, the letter “F” denotes a streamflow (Fluviometric) gauge station, while the letter “P” denotes a rain (Pluviometric) gauge station. The “Latitude” and “Longitude” columns report the coordinates for each of the considered stations.

Name	Code	Station Type	Latitude (°)	Longitude (°)
Teles Pires	017210000	F	−12.67°	−55.79°
Passagem da BR-309	01453000	P	−14.61°	−53.99°
Paranatinga	01454000	P	−14.41°	−54.04°
Porto Roncador	01355001	P	−13.55°	−55.33°
Teles Pires	01255001	P	−12.67°	−55.79°

reports the rain and streamflow measurement stations leveraged in the present research. Such stations are under the control of ANA, and their location is noted in Figure 2. The employed historical data series collected from the reported stations can be accessed on the online platform “Hidroweb”, which is provided by the Brazilian National Water Resources Information System (Sistema Nacional de Informações sobre Recursos Hídricos—SNIRH, https://www.snirh.gov.br/hidroweb/serieshistoricas accessed on 1 September 2024).

The selected AutoML models were trained and tested relying on daily surface rainfall and streamflow data within the time-span from January 1985 to November 2023. Any time interval lacking collected data was omitted from the study.

The streamflow data ${\overline{Q}}_d$ collected on the day d from the streamflow gauge station noted with code 017210000 in Table 1, are shown in Figure 3. The latter streamflow time-series was composed of 14,212 samples.

The well-known Thiessen polygon method [54] was employed to compute the average daily rainfall within the basin:

$${\overline{P}}_d={\displaystyle \frac{{\sum }_{i=1}^n{P}_i{A}_i}{A_t}},$$

(1)

in which $A_i$ represents the area of influence (in squared kilometers) for the i-th rain gauge station, which recorded rainfall of $P_i$ (in millimeters) on the day d, the number n, set to 4, represents the number of the employed stations, and $A_t$ denotes the total area (in squared kilometers) of the considered basin. The rainfall data collected from the four rain gauge stations, reported in Table 1, and the computed average daily rainfall ${\overline{P}}_d$ in the basin were shown in Figure 4. The four time-series collected from the four rain gauge stations on which the average daily rainfall ${\overline{P}}_d$ was computed were composed of 14,212 samples.

Alongside surface rainfall data, the present study also relied on rainfall data derived from remote sensing. In particular, the latter data included precipitation estimates from remotely sensed products using ANNs, i.e., PERSIANN, PERSIANN-CCS, PERSIANN-CDR, and PDIR-Now products (refer to

Table 2. The table reports the exploited rainfall datasets estimated through remote sensing [41,42]. The spatial resolution, selected data period, update frequency, and number of computed samples for each considered product are reported.

Product	Spatial Resolution (°)	Selected Data Period	Update Frequency	Number of Computed Samples
PERSIANN	${0.25}^{\circ }\times {0.25}^{\circ }$	March 2000–November 2023	Every 2 days	8640 samples
PERSIANN-CCS	${0.04}^{\circ }\times {0.04}^{\circ }$	January 2003–November 2023	Real-time	7980 samples
PERSIANN-CDR	${0.25}^{\circ }\times {0.25}^{\circ }$	January 1985–September 2020	No longer updated	13,023 samples
PDIR-Now	${0.04}^{\circ }\times {0.04}^{\circ }$	March 2000–November 2023	Every 15–60 min	8640 samples

) [41,42]. The latter products were provided by the Center for Hydrometeorology and Remote Sensing (CHRS), located at the University of California (UC), Irvine, CA, USA. The average daily precipitation for the latter products was computed using a standard arithmetic approach: for each day, all the available precipitation measurements were averaged to produce a single daily average precipitation value. The daily average precipitation on the day d, namely ${\overline{P}}_d$, was calculated for each remote-sensing product using the following formula:

$${\overline{P}}_d={\displaystyle \frac{1}{n_d}}\sum _{i=1}^{n_d}{P}_i$$

(2)

where $n_d$ represents the number of precipitation measurements recorded in the day d, and $P_i$ denotes the individual precipitation measurement. The computed average daily rainfall ${\overline{P}}_d$ derived from remote-sensing products was shown in Figure 5. The original datasets containing raw estimates are available on https://chrsdata.eng.uci.edu accessed on 1 September 2024.

As a final remark, in the present study, outlier detection was not performed, as the raw data were already validated by the dataset providers, i.e., SNIRH [19,20] and CHRS [41,42], to ensure the accuracy and reliability of the provided datasets.

3.3. AutoML Models Description and Experimental Settings

With the aim of carrying out a comprehensive study, we selected five AutoML models based on different conceptual design choices, including auto-sklearn [50], Tree-based Pipeline Optimization Tool (TPOT) [55], H2O AutoML [56], AutoKeras [57], and MLBox [58]. All the listed AutoML models will be introduced in the next paragraphs of the present subsection. Despite the differences in their design principles, all the employed AutoML models automated the process of training and testing a large selection of optimal candidate ML models, along with the tuning of their respective hyperparameters. All the selected AutoML models were tested relying on the Python programming language (release 3.12.0), executed on Microsoft^® Windows^® 11 Enterprise operating system. The code to execute the employed AutoML models was not developed from scratch, but the already available Python libraries provided by the developers of the models were leveraged for each of them. The references to each of the latter Python libraries are, respectively, provided within each reported publication [50,55,56,57,58]. The workstation used for running the experiments was equipped with a 12th generation Intel^® Core™i9-12900 processor (with 5.10 GHz maximum clock frequency, 16 cores, and 24 threads) and 64 GB of RAM (of type DDR5—4400 MHz).

The auto-sklearn AutoML model is built over the scikit-learn library [59], developed in the Python programming language [50]. It employs 15 ML models, 4 data preprocessing techniques, and 14 feature preprocessing methods, thus resulting in a vast hypothesis space. Within such space, auto-sklearn formulates a Combined Algorithm Selection and Hyperparameter (CASH) optimization problem and employs Bayesian optimization to solve such a problem, aiming to find the optimal performing ML pipeline.

The TPOT AutoML model is designed to automatically build and optimize ML pipelines using the well-established evolutionary computation method known as Genetic Programming (GP) [55]: at the start of each TPOT run, a fixed number of pipelines is created to form what is commonly referred to in GP as a “population”. Then, GP is employed to evolve the latter set of pipelines that have been applied to the data, i.e., the population, and a subset of these is preserved based on their predictive performance. Finally, the highest-performing pipeline is kept either when TPOT achieves convergence or after a specified number of TPOT runs, as defined in advance by the researcher.

H2O AutoML is designed to simplify the process of automatically training and testing a wide ensemble of ML models [56]. First, the H2O model applies data preprocessing steps, such as imputation, one-hot encoding, and standardization. Then, the H2O AutoML trains a random grid of several ML algorithms, for instance including Gradient Boosting Machines (GBMs), Deep Neural Networks (DNNs), and Generalized Linear Models (GLMs), relying on a carefully selected hyperparameter space. The individual models are then optimized through cross-validation to ensure the highest predictive performance. Additionally, the H2O model trains two stacked ensembles of models: the first one incorporates all the employed ML models (optimized for model performance), and the second one includes just the best-performing ML model for each algorithm class (optimized for production use). The output of H2O AutoML is finally an object containing a “leaderboard” that ranks all the trained ML models based on a custom user-defined performance metric, making it straightforward to identify the optimal performing ML models.

AutoKeras is an AutoML model specifically designed for DL architectures, built over the Keras Python library [57]. AutoKeras relies on the principle of network morphism, which allows the functionality of a DL network to be preserved while its underlying architecture is altered. In particular, AutoKeras leverages Bayesian optimization to steer network morphism in the search for the optimal DL architecture for the given problem and dataset. To effectively surf the wide resulting search space, the developers of AutoKeras devised a specific neural network kernel and a tree-structured optimization algorithm.

MLBox is an AutoML Python library that provides a suite of features aimed at streamlining the ML pipeline [58]. The latter ones include fast data reading and distributed data preprocessing, cleaning, and formatting which simplifies the often complex and time-consuming task of preparing the data to be provided as input to ML models. Furthermore, MLBox is also capable of highly robust feature selection, with the aim of ensuring data quality and reliability of training data. Another key feature is the MLBox capability of performing accurate hyperparameter optimization processes in high-dimensional spaces, thus allowing the fine-tuning of ML models to achieve optimal predicting performance. Furthermore, MLBox includes the latest state-of-the-art predictive ML models for both classification and regression tasks, such as RF, Bagging, and Light GBM. Finally, MLBox provides predictions even endowed with ML model interpretations, thus aiding both in the understanding and transparency of the trained ML models.

The five AutoML models employed in this study exhibit distinct structural characteristics and operational methodologies. Indeed, auto-sklearn leverages Bayesian optimization to surf a vast hypothesis space, integrating multiple preprocessing and feature selection techniques. TPOT utilizes genetic programming to evolve machine-learning pipelines, optimizing them through evolutionary algorithms. H2O AutoML combines various machine-learning algorithms, including Gradient Boosting Machines, Deep Neural Networks, and Generalized Linear Models, and employs ensemble learning to enhance predictive performance. AutoKeras focuses on deep learning, utilizing network morphism and Bayesian optimization to identify optimal neural network architectures. MLBox emphasizes ease of use with robust feature selection and hyperparameter optimization, primarily leveraging tree-based models like LightGBM and Random Forest. Such structural differences influence the adaptability, computational efficiency, and suitability of the selected AutoML models for different types of datasets and prediction tasks.

Table 3. Covariates related to streamflow (denoted as Q) and rainfall (denoted as P) were employed as input features to train the AutoML models. In particular, the mean time-lagged streamflow (${\overline{Q}}_t$) and rainfall (${\overline{P}}_t$) for the considered basin were leveraged relying on five different methods: Thiessen, PERSIANN, PERSIANN-CCS, PERSIANN-CDR, and PDIR-Now. The time-lag l for which the streamflow predictions were computed was set as $1\le l\le 3$ days in the present research. The last two columns report the development and test data intervals employed for all the selected feature sets.

Time-Lag (Days)	Models Input Features (${\overline{\mathit{Q}}}_{\mathit{t}}$ and ${\overline{\mathit{P}}}_{\mathit{t}}$)	Predicted Outputs	Development Data Interval	Test Data Interval
1	Thiessen	${\overline{Q}}_{t+1}$	1985–2012	2013–2023
1	PERSIANN	${\overline{Q}}_{t+1}$	2000–2016	2017–2023
1	PERSIANN-CCS	${\overline{Q}}_{t+1}$	2003–2017	2018–2023
1	PERSIANN-CDR	${\overline{Q}}_{t+1}$	1985–2010	2011–2020
1	PDIR-Now	${\overline{Q}}_{t+1}$	2000–2016	2017–2023
2	Thiessen	${\overline{Q}}_{t+2}$	1985–2012	2013–2023
2	PERSIANN	${\overline{Q}}_{t+2}$	2000–2016	2017–2023
2	PERSIANN-CCS	${\overline{Q}}_{t+2}$	2003–2017	2018–2023
2	PERSIANN-CDR	${\overline{Q}}_{t+2}$	1985–2010	2011–2020
2	PDIR-Now	${\overline{Q}}_{t+2}$	2000–2016	2017–2023
3	Thiessen	${\overline{Q}}_{t+3}$	1985–2012	2013–2023
3	PERSIANN	${\overline{Q}}_{t+3}$	2000–2016	2017–2023
3	PERSIANN-CCS	${\overline{Q}}_{t+3}$	2003–2017	2018–2023
3	PERSIANN-CDR	${\overline{Q}}_{t+3}$	1985–2010	2011–2020
3	PDIR-Now	${\overline{Q}}_{t+3}$	2000–2016	2017–2023

reports the features employed to train the selected AutoML models and the resulting predicted outputs. Identical datasets were set across all the AutoML models, and the unique induced variation was in the time-lag of the predicted streamflow, extending it up to 3 days, to assess the forecasting performance of the models. For each feature set, the AutoML models were trained, validated, and tested using daily surface rainfall and streamflow data collected from the time periods specified in Table 3. In particular, average streamflow and rainfall data were used jointly as input features where the data were available for both the employed features. The available data for each feature was split to include the last $30\%$ of the data in the final test set, ensuring a final assessment of AutoML models on unseen data. The remaining $70\%$ of the dataset was used for models’ development. On the latter data, a 10-fold cross-validation approach was applied to train and validate the AutoML models, where for each step, a different fold served as a validation set while the other ones were used for training. For each kind of input feature, identical folds with the same data were used for training and validating the models, and AutoML models were finally tested on the same test set. Table 3 reports the development and test data leveraged intervals for all the employed feature sets. The specific settings of the employed Python libraries for training each AutoML model are reported in Appendix A.

3.4. Metrics for AutoML Models Evaluation

The daily streamflow forecasting capabilities of AutoML models were assessed using the following performance metrics: Mean Absolute Error (MAE—Equation (3)), Root Mean Square Error (RMSE—Equation (4)), Bias (BIAS—Equation (5)), Nash–Sutcliffe Efficiency Index (NSEI—Equation (6)), and Kling–Gupta Efficiency Index (KGEI—Equation (7)):

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|O_i-P_i\right|,$$

(3)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(O_i-P_i)}^2},$$

(4)

$$\mathrm{BIAS}={\displaystyle \frac{1}{N}}\sum _{i=1}^N(O_i-P_i),$$

(5)

$$\mathrm{NSEI}=1-{\displaystyle \frac{{\sum }_{i=1}^N{(O_i-P_i)}^2}{{\sum }_{i=1}^N{(O_i-\overline{O})}^2}},$$

(6)

$$\mathrm{KGEI}=1-\sqrt{{(r-1)}^2+{\left({\displaystyle \frac{{\sigma }_e}{{\sigma }_o}}-1\right)}^2+{(\mathrm{BIAS}-1)}^2},$$

(7)

where $P_i$ represents the predicted streamflow (in m³ s⁻¹), $O_i$ is the observed streamflow (in m³ s⁻¹), $\overline{O}$ stands as the average of the observed streamflow (in m³ s⁻¹), N is the number of values contained in the sample, r represents the correlation coefficient between the observed and predicted data, ${\sigma }_e$ is the standard deviation of the data predicted by the model, and ${\sigma }_o$ is the standard deviation of the observed data.

Regarding the NSEI and KGEI metrics, assessment of the models was carried out relying on the performance categorization proposed in past research works related to the present one [19,60]: an NSEI value equal to 1 reported an equal match between the model predicted data and the actual data; a value greater than $0.75$ implied model predictions of high quality; an NSEI value between $0.36$ and $0.75$ reported that the model performance was sufficient; finally, a NSEI value less than $0.36$ denoted unsatisfactory predictions. The latter categorization was equally used to assess the model’s performance with KGEI.

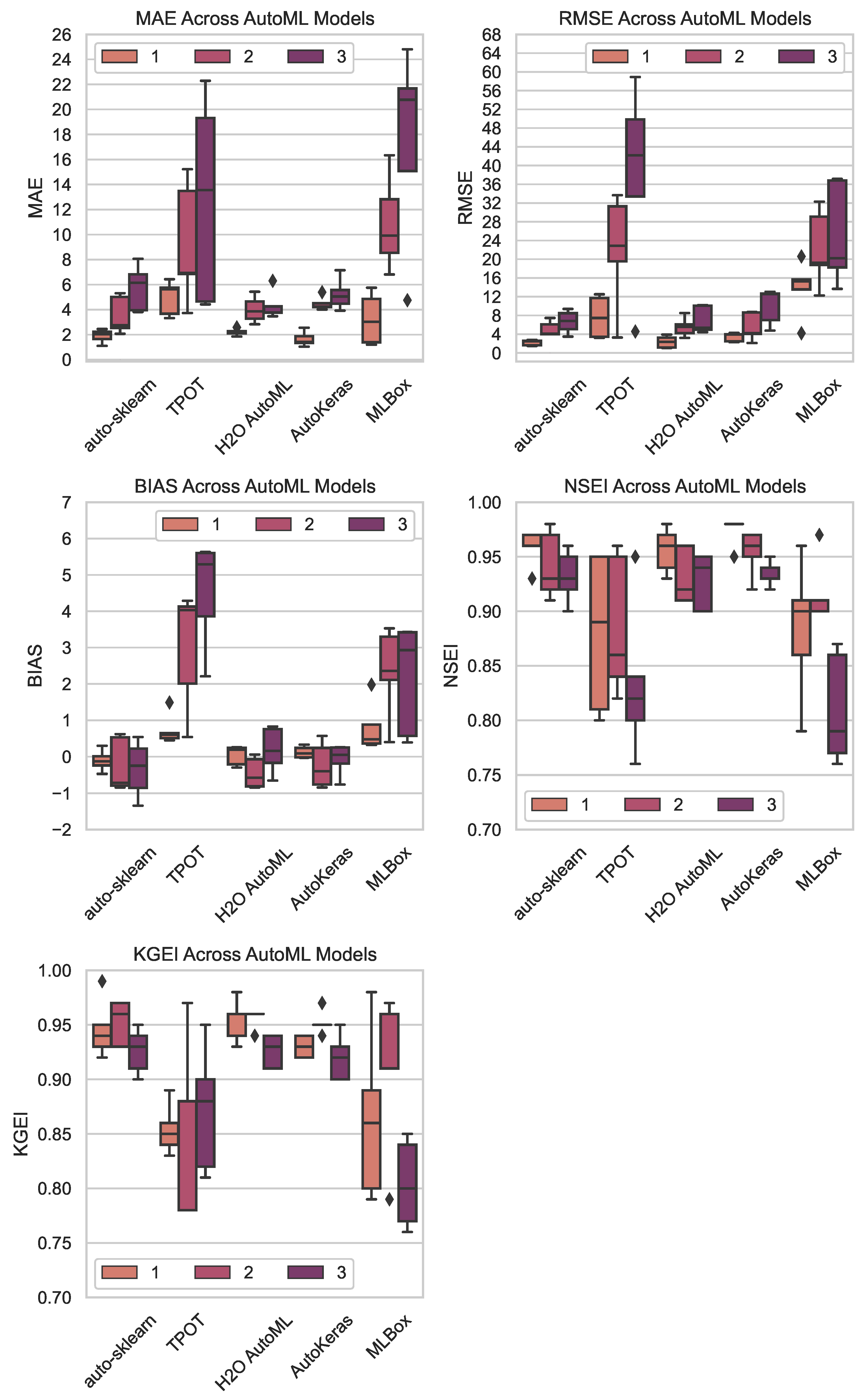
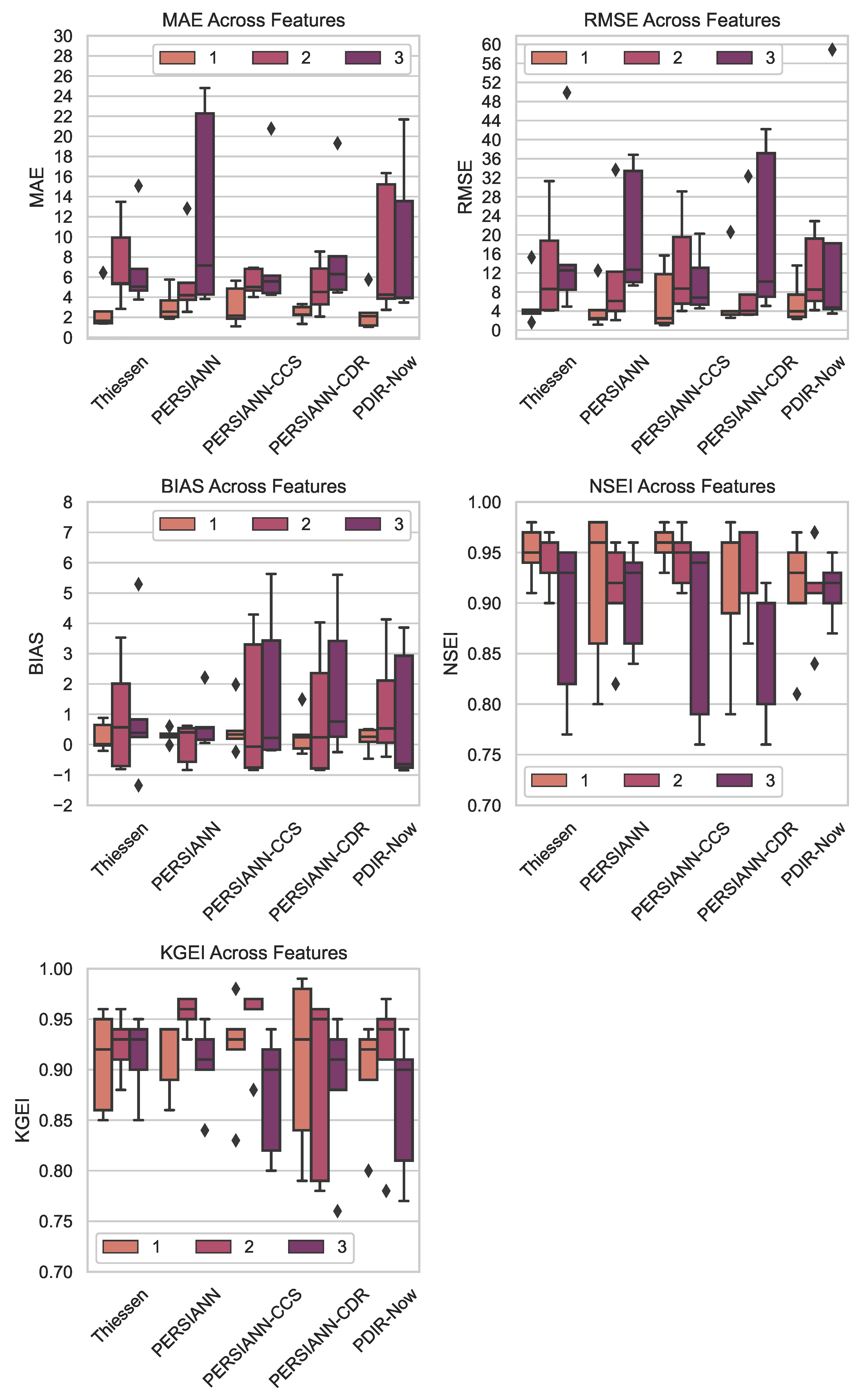
4. Results

The Figure 6 and Figure 7 present the daily streamflow forecasting performance on the test set for the five employed AutoML models, five feature sets, and three different forecasting time-lags. Both the figures report the test set forecasting performance through five separate subplots, each corresponding to a different performance metric, previously described in Section 3.4. Specifically, Figure 6 shows the forecasting performance gained by AutoML models for each selected metric over all the employed features. On the other hand, Figure 7 displays the forecasting performance gained for each metric when each selected feature was used as input over all the employed AutoML models. Both Figure 6 and Figure 7 display results by providing summary statistics in each subplot through box plots, color-coded with three different colors, each representing a different time-lag.

Regarding the results shown in Figure 6, proper statistical tests were applied to understand: (1) if there were any statistically significant differences among the employed AutoML models regarding the test set performance; (2) If the answer to the first point was positive, which specific AutoML models showed statistically significantly different performance with respect to other ones. Among the most common statistical tests to assess the first point, we may find the Analysis of Variance (ANOVA) [61]. However, the application of ANOVA requires that several assumptions be met to obtain reliable findings, such as normality (groups should be approximately normally distributed), homogeneity of variances (variances among groups should be approximately equal), and independence (observations must be independent of each other). Even if independence may be reasonably assumed in the present study, normality and homogeneity of variances were not guaranteed by the analyzed results. Indeed, the Shapiro–Wilk test [62] and the Fligner–Killeen test [63] were computed over results to check the latter two properties, with test groups defined by grouping the obtained model results by AutoML model and performance metric.

First, the Shapiro–Wilk test was applied. The null hypothesis of the Shapiro–Wilk test assumes that the data follow a Normal distribution, and if the p-value obtained from the test is less than the chosen significance level $\alpha$ (commonly set to $\alpha =0.05$), the null hypothesis is rejected and there is sufficient evidence to conclude that the data do not follow a Normal distribution. The tested AutoML models showed a p-value greater than $\alpha =0.05$, except for TPOT in MAE ($p=0.008$), AutoKeras in RMSE ($p=0.015$), MLBox ($p=0.009$) and TPOT ($p=0.029$) in BIAS, and finally TPOT in NSEI ($p=0.04$). As a result, normality was not guaranteed within five out of twenty-five (the 20%) of the defined groups.

Next, the Fligner–Killeen test was applied to check the homogeneity of variances among groups. The null hypothesis of the latter test set all the group variances to be equal, and with a p-value less than the chosen significance level $\alpha$ (typically $\alpha =0.05$), the null hypothesis is rejected. In particular, a different Fligner–Killeen test was performed for each performance metric to compare the AutoML model’s performance variances on the same metric scale. As a result, the performed tests showed statistically significant differences in variances for all the metrics, as all the computed p-values were less than $\alpha =0.05$. In particular, the p-values found by the executed Fligner–Killeen tests ranged within $0.000\le p\le 0.009$.

As a consequence of the found non-normality and non-homogeneity of variances, the ANOVA test could not be leveraged and, as an alternative, the Kruskal–Wallis test [64] was applied to understand if it existed any statistically significant difference among the employed AutoML models regarding the test set performance. The Kruskal–Wallis test allows the complete dropping of the normality and homogeneity of variances assumptions while requiring only the independence one. The null hypothesis of the latter test states that the medians of all the selected groups are equal, and the alternative hypothesis states that at least one group has a different median from the other ones. In the case the computed p-value is under a chosen significance level $\alpha$ (typically $\alpha =0.05$), the null hypothesis is rejected, and at least one group median is statistically significantly different from the other group medians. As with the previously applied statistical tests, the Kruskal–Wallis test was applied with test groups defined by grouping the obtained model results by AutoML model and performance metric. In particular, a different Kruskal–Wallis test was performed for each metric to compare the AutoML model median performances on the same metric scale. As a result, the Kruskal–Wallis test indicated statistically significant differences in the AutoML model median performances for all the employed metrics, as all the computed p-values were inferior to the chosen significance level $\alpha =0.05$. In particular, the p-values found by the executed Kruskal–Wallis were equal to $p=0.00$ for all the analyzed performance metrics.

Since the Kruskal–Wallis test indicated that the selected AutoML models showed statistically significantly different median performances, the Dunn post hoc test [65] was then executed to understand which specific AutoML models showed different median performances above other ones. As with the Kruskal–Wallis test, the Dunn test does not require the normality and homogeneity of variances assumptions, but only the independence one. The Dunn test is leveraged to perform multiple pairwise comparisons, and for each pair of groups being compared, the null hypothesis states that there is no difference in the central tendency, typically the median, between the two groups. On the other hand, the alternative hypothesis states that there is a statistically significant difference in the central tendency between the two groups being compared. The null hypothesis in the Dunn test is rejected when the p-value is less than a chosen significance level $\alpha$ (usually $\alpha =0.05$).

As with the previously applied statistical tests, the Dunn test was applied with test groups defined by grouping the obtained model results by AutoML model and performance metric. In particular, different pairwise Dunn tests were performed for each metric to compare the AutoML models’ median performances on the same metric scale. The Dunn test computed p-values, reported in

Table 4. The computed p-values with the Dunn test. Pairwise computed p-values are reported for each couple of AutoML models and performance metrics. For the sake of readability, the p-values less than the chosen significance level $\alpha =0.05$ are reported as bold and underlined text.

Model	AutoKeras	H2O	MLBox	TPOT	Auto-Sklearn
MAE
AutoKeras	1.000	1.000	0.038	0.038	1.000
H2O	1.000	1.000	0.020	0.019	1.000
MLBox	0.038	0.020	1.000	1.000	0.022
TPOT	0.038	0.019	1.000	1.000	0.022
auto-sklearn	1.000	1.000	0.022	0.022	1.000
RMSE
AutoKeras	1.000	1.000	0.002	0.040	1.000
H2O	1.000	1.000	0.000	0.008	1.000
MLBox	0.002	0.000	1.000	1.000	0.000
TPOT	0.040	0.008	1.000	1.000	0.004
auto-sklearn	1.000	1.000	0.000	0.004	1.000
BIAS
AutoKeras	1.000	1.000	0.001	0.000	1.000
H2O	1.000	1.000	0.001	0.000	1.000
MLBox	0.001	0.001	1.000	1.000	0.000
TPOT	0.000	0.000	1.000	1.000	0.000
auto-sklearn	1.000	1.000	0.000	0.000	1.000
NSEI
AutoKeras	1.000	0.835	0.000	0.001	1.000
H2O	0.835	1.000	0.030	0.046	1.000
MLBox	0.000	0.030	1.000	1.000	0.007
TPOT	0.001	0.046	1.000	1.000	0.013
auto-sklearn	1.000	1.000	0.007	0.013	1.000
KGEI
AutoKeras	1.000	1.000	0.043	0.014	1.000
H2O	1.000	1.000	0.004	0.001	1.000
MLBox	0.043	0.004	1.000	1.000	0.011
TPOT	0.014	0.001	1.000	1.000	0.003
auto-sklearn	1.000	1.000	0.011	0.003	1.000

, indicated two distinct groups of AutoML models in terms of median performance: Indeed, the first one consisting of AutoKeras, H2O AutoML, and auto-sklearn, generally showed no statistically significant difference in median performance among themselves across all the employed metrics, as indicated by their respective p-values close to $p=1.00$; The second one, including MLBox and TPOT, also showed no significant difference in median performance between them. However, the two latter models showed significant differences when compared to the ones included in the first group across all the metrics. The last point is due to the p-values less than $\alpha =0.05$ when comparing MLBox and TPOT with the models in the first group.

Upon analyzing the AutoML models performance results displayed in Figure 6, the above-noted statistically significant differences in the computed p-values are reflected in the reported performance metrics. Indeed, auto-sklearn consistently achieves lower median MAE, RMSE, and BIAS across different features compared to MLBox and TPOT for each of the considered time-lags. Moreover, auto-sklearn gained NSEI and KGEI median values closer to $1.00$ with respect to MLBox and TPOT. Similarly, H2O AutoML and AutoKeras also tended to perform better in terms of all the employed performance metrics with respect to MLBox and TPOT. On the other hand, the two latter AutoML models still showed competitive performance, particularly in terms of the NSEI and KGEI metrics, where they all reached median performance above the value of $0.75$, which still suggests high-quality model predictions, according to the categorization reported in the Section 3.4.

Regarding the results shown in Figure 7, part of the statistical tests previously applied was used to understand: (1) if there were any statistically significant differences among the employed input features regarding the test set performance; (2) If the answer to the first point was positive, which specific feature sets allowed to gain statistically significantly different forecasting performance with respect to other ones. Tests were performed with test groups defined by grouping the obtained model results by feature kind and performance metric. The Shapiro–Wilk test and Fligner–Killeen test were computed over results to check the normality and homogeneity of variance assumptions.

First, the Shapiro–Wilk test results indicated that the null hypothesis of normality was rejected for most of the employed features at a significance level of $\alpha =0.05$. In particular, for MAE and Bias, the null hypothesis was rejected for all the employed features. For RMSE, all the features rejected the null hypothesis except PERSIANN-CCS ($p=0.088$). For NSEI, PDIR-Now (with $p=0.224$), PERSIANN ($p=0.094$), and PERSIANN-CDR ($p=0.082$) did not reject the null hypothesis. Lastly, for KGEI, PERSIANN ($p=0.103$) and Thiessen ($p=0.062$) did not reject the null hypothesis. As a result, the normality assumption was not guaranteed within 19 out of 25 (the $76\%$) of the analyzed groups.

Next, the Fligner–Killeen test was applied to check the homogeneity of variances among groups. In particular, a different Fligner–Killeen test was performed for each performance metric to compare performance variances on the same metric scale gained when leveraging each input feature. As a result, the performed tests showed no statistically significant differences in-group variances for all the employed metrics, as all the computed p-values were greater than the significance level $\alpha =0.05$. In particular, the p-values found by the executed Fligner–Killeen tests ranged within $0.146\le p\le 0.884$.

The Kruskal–Wallis was finally executed, with test groups defined by grouping the obtained model results by feature kind and performance metric. In particular, a different Kruskal–Wallis test was performed for each performance metric to compare performance medians on the same metric scale, gained when leveraging each employed feature. As a final result, the Kruskal–Wallis test indicated no statistically significant differences in the AutoML model median performances with respect to the employed features, as all the computed p-values were greater than the chosen significance level $\alpha =0.05$. In particular, the p-values found by the executed Kruskal–Wallis tests ranged between $0.448\le p\le 0.996$ for all the analyzed metrics. Therefore, post hoc pairwise Dunn tests were not executed.

Furthermore, the forecasting performances of all the possible combinations of AutoML models and input features were ranked by providing them a performance score: The score ${\mathrm{AutoML}}_{\mathrm{score}}(m,f,l)$ was calculated for each combination of AutoML model m, input feature f, and time-lag l, by taking the sum of the absolute differences between the test set performance of the AutoML model m and the optimum value for each employed performance metric (value 0 for MAE, RMSE, and BIAS; value 1 for NSEI and KGEI). The obtained scores were then summed over the time-lag values l to obtain the total score ${\mathrm{AutoML}}_{\mathrm{score}}^{\mathrm{T}}(m,f)$ for each combination of AutoML model m and feature f. The lower the total score, the better the considered combination of model and feature. In

Table 5. The AutoML models and respective input features ranked by the ${\mathrm{AutoML}}_{\mathrm{score}}^{\mathrm{T}}$ score. For the sake of readability, the table is sorted in ascending order according to the computed score. The ranking of the combinations, from 1 to 25, is reported in the first column. Furthermore, a horizontal line divides the table relying on the two groups of models found with the Dunn post hoc tests: Group 1 includes auto-sklearn, AutoKeras, and H2O AutoML; Group 2 includes TPOT and MLBox.

Ranking	AutoML Model	Input Features	${\mathbf{AutoML}}_{\mathbf{score}}^{\mathbf{T}}$
1	auto-sklearn	PDIR-Now	23.79
2	AutoKeras	PDIR-Now	23.81
3	H2O AutoML	PERSIANN-CCS	23.83
4	H2O AutoML	Thiessen	24.40
5	auto-sklearn	PERSIANN	26.13
6	H2O AutoML	PDIR-Now	26.15
7	auto-sklearn	PERSIANN-CCS	26.19
8	AutoKeras	PERSIANN-CDR	26.40
9	auto-sklearn	PERSIANN-CDR	28.97
10	H2O AutoML	PERSIANN	30.14
11	auto-sklearn	Thiessen	30.42
12	H2O AutoML	PERSIANN-CDR	30.78
13	AutoKeras	PERSIANN	32.25
14	AutoKeras	PERSIANN-CCS	37.32
15	AutoKeras	Thiessen	38.48
16	TPOT	PERSIANN-CCS	64.02
17	MLBox	Thiessen	79.74
18	TPOT	PERSIANN-CDR	90.26
19	MLBox	PDIR-Now	96.56
20	MLBox	PERSIANN	98.70
21	MLBox	PERSIANN-CCS	106.76
22	TPOT	PERSIANN	113.39
23	MLBox	PERSIANN-CDR	113.65
24	TPOT	Thiessen	117.77
25	TPOT	PDIR-Now	133.17

, the ${\mathrm{AutoML}}_{\mathrm{score}}^{\mathrm{T}}$ is reported for each combination of AutoML model and feature.

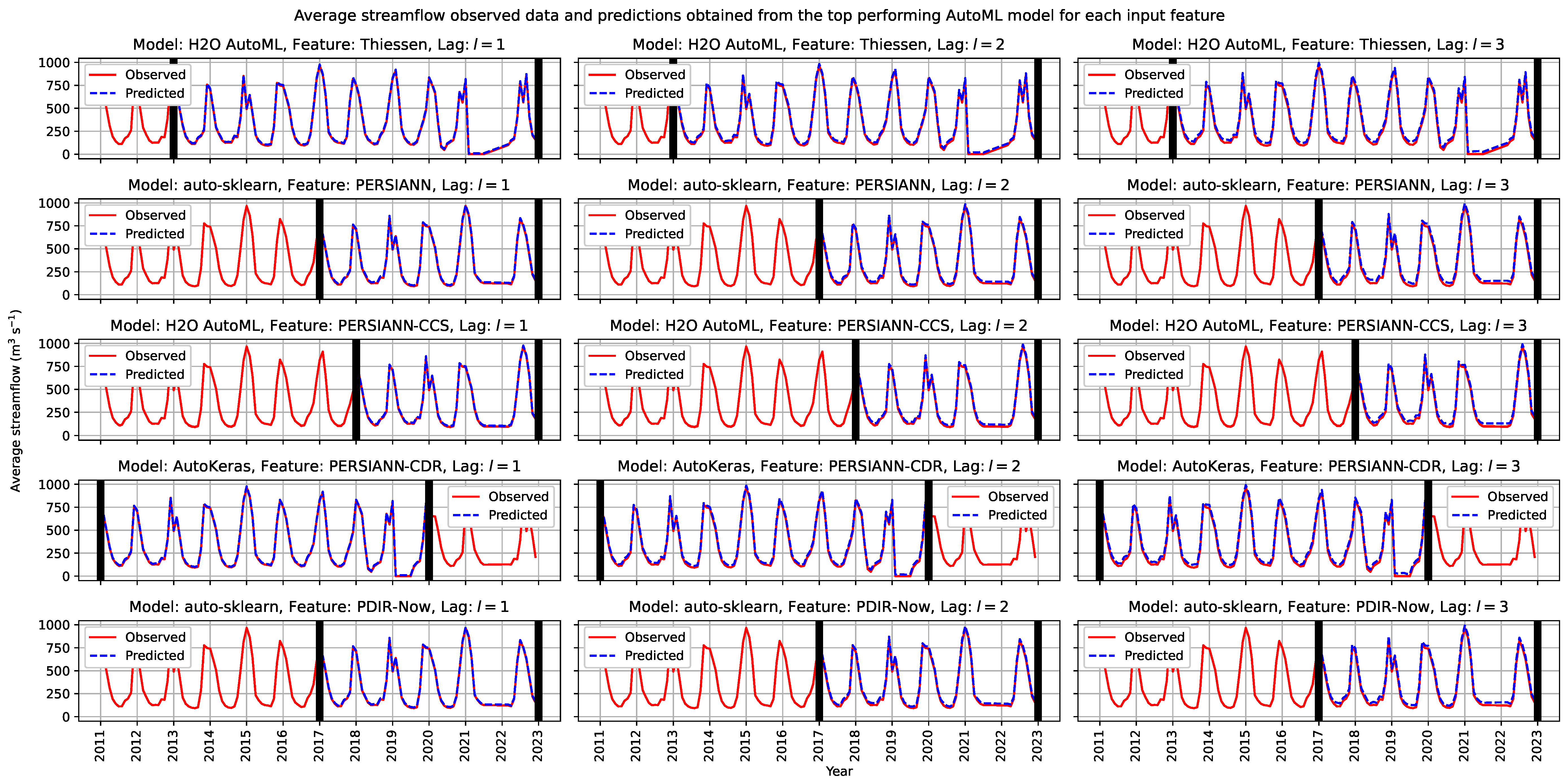
Finally, the top performing AutoML model for each input feature was additionally run on the test data for each of the selected time-lag, $1\le l\le 3$. The latter data were unseen by the trained AutoML models for all the selected input features. According to Table 5, the top performing AutoML models for each input feature set according to the ${\mathrm{AutoML}}_{\mathrm{score}}^{\mathrm{T}}$ metric were, respectively, H2O AutoML for Thiessen, auto-sklearn for PERSIANN, H2O AutoML for PERSIANN-CCS, AutoKeras for PERSIANN-CDR, and auto-sklearn for PDIR-Now. The average streamflow observed data and predictions obtained from the AutoML models were reported in Figure 8.

Regarding Figure 8, the performance of the AutoML models was evaluated across different seasons to understand their robustness and reliability under varying climatic conditions. The Amazon basin experiences distinct wet and dry seasons, which significantly influence streamflow patterns. During the wet season (October to April), the models demonstrated higher prediction accuracy due to the increased availability of rainfall data, which is a primary driver of streamflow. Conversely, during the dry season (May to September), the prediction accuracy slightly decreased, reflecting the reduced rainfall input and the increased reliance on historical streamflow data. This seasonal variation highlights the models’ dependency on accurate and timely rainfall data for optimal performance.

5. Discussion

The experimental results confirmed that the usage of time-delayed rainfall and streamflow data provided reliable input features to train AutoML models designed to forecast future streamflow. Indeed, rainfall data plays a crucial role within hydrological forecasting models, being the primary way of water influx into a hydrographic basin [19,66]. Moreover, the time-delayed streamflow provides a representation of the moisture condition in watersheds, given that runoff happens post-soil saturation [19,67]. As previously noted by De Sousa et al. [19] and Filho et al. [20], the application of ML for predicting the daily streamflow in the Amazon basin offers significant benefits, particularly due to the lack of available hydrometeorological data. Indeed, even the findings described in the present study indicate that ML-based models are a viable solution in the context of basins with inadequate hydrological monitoring and a lack of fundamental information required for the proper implementation of physical and/or conceptual rainfall-runoff models.

According to the results shown in Figure 6, the executed Dunn post hoc tests revealed two groups of AutoML models with similar in-group median forecasting performances: Group 1 includes auto-sklearn, AutoKeras, and H2O AutoML, while Group 2 includes TPOT and MLBox. In addition to the results of the executed Dunn tests, even the computed AutoML model score ${\mathrm{AutoML}}_{\mathrm{score}}^{\mathrm{T}}$ highlighted the difference in forecasting performance between the two found groups of AutoML models: Regarding the scored combinations of employed models and features reported in Table 5, over the $15\mathrm{th}$ ranked position (included) only combinations with AutoML models within Group 1 do appear. On the other hand, under the $16\mathrm{th}$ ranked position (included), only combinations with models within Group 2 are listed. Indeed, it must be noted that if pairwise score differences are computed between the sorted scored combinations, the highest score difference found is between the $15\mathrm{th}$ and $16\mathrm{th}$ combination, with a score difference of $25.54$. As already described in Section 4, not only did the AutoML models within Group 1 show median forecasting performances superior with respect to the models contained in Group 2, but they even achieved a minimal loss of median forecasting performance when increasing the time-lag prediction l up to $l=3$. Indeed, for the models contained in the first group, median test forecasting performances were contained in the same order of magnitude for MAE and RMSE for each set lag. On the other hand, for the AutoML models contained in the second group the order of magnitude of the latter two metrics tended to increase by one unit when increasing the prediction time-lag up to $l=3$. Minimal variations were observed with respect to the Bias metric. Regarding NSEI and KGEI, the median performances of AutoML models within Group 1 were greater than the value of $0.90$ for each employed time-lag, while for models of Group 2, they tended to reach inferior values, even below $0.80$.

The structural differences between the AutoML models led to varying performances in streamflow forecasting. Indeed, auto-sklearn, AutoKeras, and H2O AutoML consistently outperformed TPOT and MLBox across most of the employed metrics. The superior performance of auto-sklearn, AutoKeras, and H2O AutoML can be attributed to their advanced optimization techniques and the ability to integrate a broader range of ML algorithms and hyperparameters. In contrast, TPOT’s reliance on genetic programming and MLBox’s limited model selection and feature processing capabilities resulted in less optimal predictions. Such differences underscore the importance of selecting appropriate AutoML models based on their structural characteristics to achieve reliable and accurate streamflow forecasts.

Regarding the above-reported findings, as already noted by previous literature, it was found that TPOT could underperform if compared to other AutoML models due to several reasons: (1) The TPOT training phase is highly computationally expensive [68]. Indeed, the TPOT GP search process involves evolving a potentially huge population of ML models and respective configurations over several generations, which can be significantly more time-consuming with respect to the techniques leveraged by other AutoML models. The latter point is particularly relevant in the case when large datasets or complex ML models are employed; (2) The TPOT performance can be highly sensitive to the difficult setting of its GP-related parameters, such as population size and mutation rate, which can lead to sub-optimal results [69]; (3) Last, but not least, TPOT may not perform optimally in situations where the optimal ML pipeline requires advanced ML models that are not included in the TPOT available configuration, such as advanced DL models. Indeed, the pipeline elements leveraged by TPOT only include algorithms and ML models borrowed from the well-known Python scikit-learn library [55].

As with TPOT, MLBox may underperform if compared to other AutoML models for several reasons: (1) One of the primary reasons is represented by the lack of available ML models to be leveraged, with respect to the other employed AutoML models in the present study [58]. Indeed, MLBox only includes LightGBM, RF, Extra Trees, Trees, Bagging, AdaBoost, and Linear ML models. The limited availability of usable ML models could limit the MLBox capability of capturing complex patterns in the training data that more advanced ML models are capable of, such as Stacking, SVM, ANNs, and DL models; (2) Additionally, the MLBox feature selection process is limited to standard feature processing techniques, which could lead to sub-optimal feature sets being used for ML models training; (3) Finally, while the MLBox limited amount of adjustable parameters could be seen as an advantage towards the fast developing of ML models, it could also represent a drawback in scenarios where a careful selection of the ML pipeline settings is required. As a result, the high MLBox emphasis on ease of usage may result in a trade-off with the resulting ML model performance, particularly when complex or large-scale datasets are leveraged.

The AutoML models employed in the present research were selected based on their proven effectiveness in handling limited training data and their previous remarkable performances reported in the previous literature [23,24,25]. Moreover, the employed dataset and forecasting performance metrics were selected according to the previous work of De Sousa et al. [19], which focused on streamflow forecasting with ML models in the same Amazon sub-region analyzed in the present study. Furthermore, the same forecasting metrics were even leveraged by Filho et al. [20], which even focused on the Amazon basin. In particular, the first group of AutoML models showed, for each employed time-lag, median forecasting performances better of an order of magnitude with respect to the ones reported in De Sousa et al. [19], in terms of MAE and RMSE. Comparable performances were reached in terms of BIAS, NSEI, and KGEI. It must be noted that even regarding the second group of AutoML models, TPOT and MLBox reached superior median forecasting performances regarding MAE and RMSE with respect to De Sousa et al. [19] for each employed time-lag. Superior median test performances were even obtained with respect to De Oliveira et al. [30], which focused on the same sub-region of the present study in terms of the computed NSEI and Bias metrics. Comparable forecasting performances were obtained with respect to Filho et al. [20], which computed predictions within another sub-region of the Amazon basin relying on the PDIR-Now product and ANNs. However, in the latter case, it must be noted that in contrast with De Sousa et al. [19] and De Oliveira et al. [30], the employed dataset was based on an Amazon sub-region different with respect to the one analyzed by the present study, since the authors focused on data related to the Branco River basin. As a result, it is difficult to compare the ML model performances reported by Filho et al. [20] with the ones of the present research. Last, but not least, it must be noted that the authors developed an ANN-based forecasting model with a forecast horizon only limited to a 1 day time-lag.

According to the results shown in Figure 7, the Kruskal–Wallis test performed in Section 4 indicated no statistically significant differences in the AutoML model’s median performances with respect to all the employed features. In particular, the performance related to the remotely sensed estimated products (PERSIANN, PERSIAN-CSS, PERSIANN-CDR, and PDIR-Now) showed considerable promising results as input factors for predicting the streamflow with AutoML models. Indeed, such features based on remote sensing can augment the data used for training and testing ML models, particularly in wide areas like the Amazon basin, therefore enhancing the reliability of streamflow forecasts for the management of HPPs. The latter features could serve as a viable alternative to mitigate the uncertainties arising from the sparse distribution of rainfall gauge stations, thus leading to limited data available. Moreover, it must be noted that remotely sensed estimated products could have a superior representation of average rainfall in the considered basin. Indeed, it must be noted that the rainfall in the Amazon basin is primarily convective, characterized by high intensity, brief duration, and limited spatial distribution [70]. As a result, the average rainfall recorded by surface pluviometric stations could be skewed, especially in the considered area where hydrological data-monitoring networks are sparse. It must be finally noted that new fluviometric and pluviometric stations were installed in the upper Teles Pires River basin, but they registered only a few years of data for training and testing of ML models. Hence, we decided not to employ the available data related to the latter stations, as done by the previous recent study of De Sousa et al. [19].

Satellite rainfall products have been successfully employed in the past literature as input data for hydrological models to forecast the streamflow [19,20,66,71]. In addition to the products employed in the present study, other products were leveraged in the past literature, such as the Tropical Rainfall Measuring Mission (TRMM) products [72]. However, within the present research, we opted not to employ the TRMM product since it has been no longer in operation since 2015. Furthermore, it must be noted that sometimes, the process of updating remotely sensed databases is time-consuming, and it is carried out with several days of delay, rendering it impractical for short-term streamflow predictions. Indeed, the products selected for the present study (refer to Table 2) are mostly promptly updated, facilitating reliable predictions for HPPs, except for the PERSIANN-CDR, which was last updated in September 2020. Thus, the latter product may represent a secondary option when deciding to employ one of the AutoML models and feature sets developed in the present study. To facilitate the selection of which AutoML models and input feature sets researchers could employ, it must be noted that recent studies compared the hydrological application and reliability of the employed satellite rainfall products: Eini et al. [73] reported that PERSIANN-CDR and PDIR-Now tend to show better estimates if compared to other products, while the PERSIANN product tends to be less reliable in daily precipitation and runoff modeling. Similarly, Baig et al. [74] found that PERSIANN-CDR and PDIR-Now tend to provide better rainfall estimates with respect to other products, particularly in terms of capturing extreme rainfall events and the spatial distribution of rainfall. Hence, even though the results found by the present study indicated no statistically significant differences in the AutoML models median performance with respect to all the employed input features, we suggest relying on AutoML models where input features are represented by the PDIR-Now product. In particular, not only the last product is currently updated constantly every 15–60 min (refer to Table 2), but with respect to the PERSIANN-CDR product, it is still currently updated and maintained. Moreover, according to the ${\mathrm{AutoML}}_{\mathrm{score}}^{\mathrm{T}}$ performance evaluation reported in Table 5, both the two highest ranked combinations of employed AutoML models and features leveraged PDIR-Now as input feature, respectively, with the auto-sklearn and AutoKeras AutoML models.

It must finally mentioned that the current study on daily streamflow forecasting using AutoML presents a few limitations: (1) the study relies heavily on the availability and accuracy of remote-sensing data, which, even if data are usually validated, can be subject to errors and inconsistencies, particularly in regions with dense forest cover like the Amazon. The sparse distribution of ground-based hydrometeorological stations in the Amazon basin further exacerbates this issue, as it limits the ability to validate and calibrate remote-sensing data effectively. Additionally, the study’s focus on a specific sub-region of the Amazon basin means that the findings may not be generalizable to other areas with different hydrological and climatic conditions. The use of historical data for model training also poses a limitation, as it may not fully capture the impacts of recent land use changes and climate variability on streamflow patterns. Moreover, while the AutoML models employed in the study automate many aspects of the machine-learning pipeline, they still require significant computational resources and a certain, even if limited, level of expertise to set up and interpret the results. The present study also acknowledges that the transformation of rainfall into runoff is a complex, nonlinear process influenced by numerous factors, which may not be fully captured by the models used. Finally, the reliance on daily average rainfall and streamflow data may overlook important sub-daily variations and extreme events that could significantly impact streamflow forecasting accuracy. The reported limitations highlight the need for ongoing improvements in data collection, model development, and computational techniques to enhance the reliability and applicability of streamflow forecasts in the Amazon basin and similar regions.

6. Conclusions and Future Directions

The objective of the present research was to assess the effectiveness of AutoML models and remote-sensing-estimated rainfall datasets in forecasting the daily streamflow in the upper reaches of the Teles Pires River in the Amazon basin. Moreover, the aim was to improve the existing forecasting results obtained by the previous research works which addressed the same task in the context of the considered Amazon sub-region. A final review of the above-reported findings underscores the following main points:

• The employed AutoML models have proven to be effective in forecasting the daily streamflow of the upper Teles Pires River up to 3 days. A specific group of AutoML models, including auto-sklearn, AutoKeras, and H2O AutoML, showed superior median performance in streamflow forecasting. Thus, the latter AutoML models represented a practical solution for predicting the daily streamflow in basins that lack extensive hydrometeorological data, like the Amazon one.
• The streamflow of the upper Teles Pires River can be predicted using precipitation data estimated through remote sensing. Indeed, all the employed products showed comparable forecasting performances when they were used as input features for the AutoML models, even if PDIR-Now represented a preferable input feature due to its highest obtained performance score, fast refresh rate, and current active maintenance.

In addition to the above-mentioned findings, in the present study, we introduced several novel approaches to enhance the application of AutoML for daily streamflow forecasting in the Amazon biomes. Such innovations include:

• Customized feature engineering: we developed a novel feature engineering pipeline that integrates both time-lagged streamflow and the latest remote-sensing-estimated rainfall data. Such a pipeline was specifically tailored to address the challenges posed by the limited hydrological data available in the Amazon basin.
• Hybrid data integration: unlike traditional approaches that rely solely on ground-based measurements, we incorporated multiple remote-sensing products, i.e., PERSIANN, PERSIANN-CCS, PERSIANN-CDR, and PDIR-Now, to enrich the training dataset. This hybrid integration significantly improved the AutoML models’ ability to generalize and predict streamflow accurately.
• Advanced model selection and hyperparameter tuning: a multi-stage AutoML process was employed. Such an approach not only automated the model selection and hyperparameter tuning but also ensured that the most optimal models were selected based on a comprehensive evaluation of multiple performance metrics.
• Performance metrics customization: the standard performance metrics built in the AutoML models were customized to include MAE, RMSE, Bias, NSEI, and KGEI. Such a comprehensive set of metrics provided a holistic evaluation of the model’s predictive capabilities.
• Strong statistical analysis: an extensive statistical analysis was performed, including the Kruskal–Wallis test and Dunn post hoc test, to rigorously compare the performance of different AutoML models and feature sets. Such level of statistical scrutiny, to the best of our knowledge not done in previous studies, ensured the robustness and reliability of the presented findings.

These innovative approaches underscore the significant contributions of our research in advancing the application of AutoML for hydrological forecasting in data-scarce regions like the Amazon basin.

The developed AutoML models demonstrated reliable streamflow forecasts up to 3 days, serving as potential tools for decision-makers, particularly in relation to the appropriate planning and management of water resources within the Amazon basin. The ultimate goal of the latter is to improve the efficiency of reservoir operations for various purposes, including the hydroelectric production of electricity, flood control, providing water for human consumption, and proper irrigation.

Despite the promising reported results, future developments could still arise from the present study. In particular, future works could take into account remote sensing and reanalysis data as input for ML models aimed at streamflow predictions. For instance, Lian et al. [75] employed Evapotranspiration (ET) data to limit the uncertainty of ET and enhance streamflow predictions, showing that incorporating additional variables could enhance the outcome of the forecasts. Furthermore, Touseef et al. [76] also reported that the usage of ET data obtained through remote sensing could improve streamflow forecasting.

Furthermore, in the present research, time-lagged streamflow and daily average rainfall data were leveraged as input features. However, for future works, it might be interesting to include the surface runoff as an additional input feature. To achieve the latter point, the underground flow component could be eliminated using numerical filters, as done in previous research works which employed daily precipitation and runoff with a 2 day lag to forecast the streamflow in mountainous regions [77,78,79]. The latter method could potentially enhance the prediction of peak streamflows in the basin. Finally, despite the obtained satisfactory results in predicting the streamflow using rainfall data derived from remote sensing, the employed data were not calibrated with respect to surface data. Lack of calibration could lead to estimation errors caused by the global scale of the employed products. Therefore, calibrating data could enhance the effectiveness of the used products.