Abstract
We present an algorithm for extracting basis functions from the chaotic Lorenz system along with timing and bit-sequence statistics. Previous work focused on modifying Lorenz waveforms and extracting the basis function of a single state variable. Importantly, these efforts initiated the development of solvable chaotic systems with simple matched filters, which are suitable for many spread spectrum applications. However, few solvable chaotic systems are known, and they are highly dependent upon an engineered basis function. Non-solvable, Lorenz signals are often used to test time-series prediction schemes and are also central to efforts to maximize spectral efficiency by joining radar and communication waveforms. Here, we provide extracted basis functions for all three Lorenz state variables, their timing statistics, and their bit-sequence statistics. Further, we outline a detailed algorithm suitable for the extraction of basis functions from many chaotic systems such as the Lorenz system. These results promote the search for engineered basis functions in solvable chaotic systems, provide tools for joining radar and communication waveforms, and give an algorithmic process for modifying chaotic Lorenz waveforms to quantify the performance of chaotic time-series forecasting methods. The results presented here provide engineered test signals compatible with quantitative analysis of predicted amplitudes and regular timing.
1. Introduction
Chaotic waveforms play a significant role in the development of spread spectrum communication [1,2,3,4], radar [5,6,7], sonar [8,9] and emerging dual-purpose [10,11] systems. Additionally, these waveforms are often used to test time series prediction algorithms [12,13] due to their essentially unpredictable nature [14,15]. This quality leads to seemingly contradictory qualities in chaotic systems: they are inherently deterministic, yet capable of producing practically random (given finite memory and finite resolution of a system’s initial condition) behavior, making them unique and valuable for complex engineering applications. Despite their potential, accurately quantifying the effects of chaotic waveforms on engineering metrics is challenging due to the lack of closed-form analytic solutions. Nonetheless, these waveforms have enabled exciting new engineering directions and hold promise for the development of better predictive algorithms and more secure, robust, and precise communication and sensing systems. Specifically, waveforms generated by the well-known chaotic Lorenz system [15], are commonly used as test signals for time series prediction algorithms involving neural networks [16], support vector machines [17], echo state networks [18], neuro-fuzzy systems [19], and reservoir computers [20]. Further, chaotic Lorenz waveforms have served as candidates for joint radar-communication systems that aim to prioritize spectral efficiency [10,11].
In this paper, we build upon the existing work of Hayes [21] to further solidify the relationship between chaotic dynamics and random processes, particularly in the context of measurable dynamics [22] and ergodic theory [23] through the lens of information theory [24,25]. Hayes identified oscillatory basis functions that decay in different directions (both causally and acausally), which can be linearly combined with random weighting factors to produce deterministic chaotic waveforms that approximate solutions to chaotic systems. This insight suggests that straight-forward signal processing techniques [26] that rely on linear analysis and synthesis methods (i.e., convolution sums) can be used to guide the application of chaos in engineered systems in a quantifiable and meaningful way. However, previous work [21] lacked details regarding the specific implementation of algorithms, the statistics of the bit sequences used, and the timing information that is discarded by the resulting algorithms. In this paper, we provide these essential details to enhance the accessibility and applicability of these techniques with the intent of quantifying advances in machine learning algorithms and waveform design for communication and sensing applications. Here, we report three new contributions: (1) a presentation of a detailed realization of Hayes’s algorithm, (2) the statistics of the bitstreams produced by the chaotic Lorenz system as associated with extracted basis functions, and (3) the statistics of the timing information that is removed from non-uniform chaotic Lorenz systems.
This manuscript is structured as follows. In the introduction section, we describe the use and impact of chaotic Lorenz waveforms on various applications, including time series prediction algorithms, communication systems, and ranging sensors. In Section 2, we present the materials and methods used. We define the chaotic Lorenz system, evaluate the entropic content of its waveforms, and describe partitions to the phase space used to define symbol sequences. In Section 2.2 and Section 2.3, we discuss the process of extracting approximate basis functions from time-regularized Lorenz waveforms. In this section, we provide timing and algorithmic details. In Section 2.4 and Section 2.5, we detail the algorithm used for basis function extraction. The results of these algorithms for all three state variables of the Lorenz system are presented. Section 3 provides a discussion of these results. Finally, we conclude with our remarks in Section 4.
1.1. Lorenz Waveforms for Time Series Prediction
Time series prediction algorithms predict future values of a given signal based on past observations. The ability of these algorithms to accurately predict the behavior of chaotic systems is a key test of their effectiveness. Importantly, the seemingly conflicting attributes of deterministic but entropic waveforms enable their use as a benchmark for testing time series prediction algorithms because they exhibit complex and unpredictable behavior. Solutions to the chaotic systems such as the Lorenz equations are well-known for their sensitivity to initial conditions. As a result, small perturbations of that constitute similar observations between two chaotic waveforms at an early portion of a time series will impose deviations between the initially similar waveforms observed later in time. This chaotic nature makes Lorenz waveforms ideal candidates for testing time series prediction algorithms. Lorenz waveforms are scientifically reproducible but their long-term predictions provides a challenging problem that requires sophisticated techniques that fit the scope of many machine learning efforts.
There are two primary advantages to using chaotic Lorenz waveforms in time series predictions. First, the determinism of chaotic Lorenz waveforms offers repeatable, rigorous, and standardized benchmarks that pair easily with clearly described dynamical structures such as the location of the system’s fixed points. Second, the Lorenz system is well-defined and widely studied. The ubiquity of the Lorenz system allows research comparisons that can clearly illustrate relative performance of different algorithms by means of the same, standardized test data. Thus, strengths and weaknesses of these algorithms can be evenly considered, compared, and discussed. Within these evaluations, these waveforms enable researchers to study various factors on the algorithm performance in relation to algorithmic parameters, training data length, and even the presence of noise. The systematic study of these types of factors results in two important capabilities: (1) the analysis of parameter impact on algorithm performance, and (2) new insight into both limitations and strengths of various approaches to time series predictions problems.
However, one significant issue with chaotic waveforms involves the quantification of time-series prediction beyond the short, initial predictable regions of the time series. Determinism does allow for computationally taxing numerical methods to provide quantitative (albeit approximate) evaluation for piece-wise sections of data. This approach is sub-optimal when compared to many standard signal construction techniques [26] but is necessary due to the lack of closed-form solutions for trajectories produced by the Lorenz system [14].
1.2. Lorenz Waveforms for Communication Systems
Chaotic Lorenz waveforms have been proposed for use in communication systems for a variety of applications. One application is to provide a secure and robust means of transmitting information [27,28]. The chaotic nature of the waveform can make it difficult to intercept or decode by unwanted parties, For some cases, this quality enhances the security and privacy of communication schemes. Another use of chaotic Lorenz waveforms in communication systems is to provide signals for spread spectrum techniques [27] that lead to efficient spectral usage that supports multi-user applications [4]. These schemes are often achieved by modulating signals with a chaotic waveform such that the resulting transmitted waveform’s spectrum is spread over a wide bandwidth. These schemes have further been suggest to improve the resistance of the communication system to interference and jamming.
In a landmark finding, chaotic waveforms were shown to synchronize [29]. This property enables various receiver schemes in communication systems [10,27]. By transmitting reference waveforms that synchronize a receiver to the waveform, accurate timing and phase alignment of transmitted signals can be achieved. This technique can be used in a variety of communication systems, including radar [11,30] and sonar [30], as well as wireless networks [31,32]. These attributes provide several benefits to communication systems including the aforementioned security, resistance to interference and jamming enhancements.
Although, these systems have the ability to synchronize signals with high accuracy. The use of chaotic waveforms often requires sophisticated signal processing techniques and can be more computationally intensive than traditional waveforms. This drawback must be taken into account in the design and implementation of potential communication systems. We note that the reduction of these computational taxes is largely solved by employing solvable chaotic systems [2] that are important extensions of the simplifications of the chaotic Lorenz system put forth by Hayes [21].
1.3. Lorenz Waveforms for Ranging Sensors
Chaotic Lorenz waveforms have been used in ranging sensors [5]. Some detection, ranging and doppler applications require signals that are difficult to detect or intercept. The chaotic nature of the waveform can make it difficult to distinguish from noise, which in turn can enhance the security and reliability of a given sensor. Other sensor applications benefit in terms of range measurements, velocity measurements and ambiguity properties. Traditional sensor techniques tend to utilize repeating waveforms that lack entropy (non-entropic). The non-repeating and spread spectrum characteristics of chaotic waveforms provide entropy to these sensor schemes. As a result, they benefit ranging and detection schemes by creating near-thumbtack ambiguity functions [5,10,11]. The resulting waveforms can give low correlation sidelobe levels, flat power spectral density and reduced ambiguity in range and Doppler measurement.
Chaotic radar and sonar schemes also support applications that require tracking moving targets, detecting the presence of stationary objects and imaging applications. These techniques have historically constituted chaotic imaging which lead to new opportunities in areas such as remote sensing [10], medical imaging [33], and non-destructive testing [34]. The benefits related to these sensor advances parallel those found in chaotic communication systems including enhanced security, improved range and velocity measurements, and the ability to perform high resolution imaging. Similarly, drawbacks to these techniques also parallel chaotic communication systems as these schemes require sophisticated signal processing techniques and can be computationally intensive.
1.4. Impact on Engineering Landscapes
Important engineering prblems demand entropic waveforms such as those produced by the chaotic Lorenz system. These problems include the evaluation of machine learning algorithms as well as the growing density of co-located communication systems and ranging sensors. First, consider early sensors and communication systems that were not densely located. For example, early warning radar systems from the 1940s generally detected targets that initially did not contain electronics competing with signal processing goals. Now, frequency modulated continuous wave (FMCW) radars comprise one of the many sensors in consumer automobiles [4]. A modern issue is that these FMCW waveforms are naturally incompatible in dense sensor networks due to the signal processing errors that arise as these waveforms interfere and cause ‘ghost’ targets or ‘jam’ one another [35].
Similarly, a growing number of devices communicate. Modern communication systems must carefully share resources via channel allocation and clever spread spectrum techniques. Many emerging applications and technologies demand communication and sensing with high data rates. Worse, trends such as the Internet of Things (IoT) exacerbate resource-sharing issues as smart devices become prevalent [36]. Personal devices that monitor health and perform real-time sensing, learning and communication see an increasing need for security, authentication and waveform diversity [4,37]. Chaotic systems naturally solve some of these issues, but often require analysis beyond traditional engineering methods.
Unfortunately, chaotic systems almost always lack equations that guide engineering design or quantitative measure. This fact is not surprising as nonlinear, coupled, ordinary differential equations (ODEs) almost always preclude closed-form analytic solutions [38]. Some chaotic behavior may be analyzed using traditional (albeit sometimes advanced) techniques for ODEs [22,39,40]. However, many standard signal processing techniques rely on assumptions of linear time-invariant (LTI) systems [26] (such as superposition, convolution, etc.) and are not helpful when nonlinearity is introduced [14]. This restriction complicates the inclusion of chaotic systems in engineering practice. Despite the need for advanced analysis, chaos is a notably mature topic with vast contributions of depth and importance. One especially effective tool set, called symbolic dynamics, takes an information-theoretic approach to understanding chaos by abstracting continuous variables as symbols in discrete partitions [41].
The intersection of symbolic dynamics, communication and ergodic theory gave rise to innovations by Hayes who translated chaotic dynamics into engineered waveforms with expressions compatible with standard engineering practice [21]. This previous work paired concepts from symbolic dynamics with conventional communication techniques to extract basis functions from chaotic signals. Surprisingly, these basis functions may be recombined through linear superposition via a convolution sum to produce engineered waveforms that approximate those generated by chaotic systems. This result implied that these waveforms can keep their desirable chaotic properties while allowing optimal detection via a matched filter receiver. These results are not only surprising, but important as traditional signal processing methods for LTI systems [26] are generally considered to be ill-suited and discouraged for use with nonlinear differential equations [14,38].
Unfortunately, the novelty and multidisciplinary nature of Hayes work [21] may tend to impede engineers and dynamicists from adopting methods developed under these previous efforts despite their direct applications to current machine learning and waveform design issues. We note that the cross-pollination of topics that involve chaos, information theory, communication and signal processing still grows in importance today and is compounded by trends in machine learning and IoT as previously discussed.
The primary goal of this manuscript is to illuminate specific practices at the intersection of methods in nonlinear dynamics, information theory and signal processing such that appropriate background and techniques are clearly imparted to those seeking benefit from entropic waveforms via chaotic dynamics paired with traditional engineering representations. The impact of these efforts are expected to include topics related to machine learning, time series prediction, waveform design for communication and sensing systems, the study of solvable chaotic systems and likely other areas that call for inherently entropic designs such as hardware security. Specifically, we provide vital algorithmic details for the extraction of basis functions from chaotic systems. Further, we show bit statistics and basis functions for all three variables of the chaotic Lorenz system for the first time.
2. Materials and Methods
In this section, the materials and methodology to extract basis functions from the chaotic Lorenz system are provided. First in Section 2.1, the chaotic Lorenz system is defined and discussed. The chaotic Lorenz system has long served as a standard tool to aid the study of nonlinear dynamics as well as signal processing. This system of nonlinear differential equations will serve as the model test-bed for processing entropic waveforms. Next in Section 2.2, we motivate the extraction of basis functions as analog ‘information primitives’ from chaotic Lorenz waveforms. It is well-known that the timing of waveform peaks in the solutions of the chaotic Lorenz system is irregular. Next in Section 2.3, an algorithm is described that enforces regularized timing for the peaks of the waveforms produces by the chaotic Lorenz system. The statistics of the these timings are also provided. Time-regularized chaotic Lorenz waveforms may be temporally aligned in order to extract ‘information primitive’ waveforms where bits of information content are selected to correspond to desired symbol sequences. For example, discrepancies in information content between two waveforms by partitioning schemes. In this work, we seek an averaged basis function that represents an analog information primitive that corresponds to a single bit of information difference found in antipodal, chaotic Lorenz waveforms. Next in Section 2.4, a detailed example that extracts a single basis function from the chaotic Lorenz system is provided. Finally in Section 2.5, a detailed algorithm for the extraction of a library of continuous-time basis functions from the chaotic Lorenz system (as well as their average) is provided with progressive details of the algorithm’s intermediate results.
2.1. The Chaotic Lorenz System: Sensitivity, Information Creation & Symbolic Dynamics
Famously, Edward Lorenz abstracted models for atmospheric convection rolls into a system of ordinary differential equations [15]. Although the simplified system is somewhat detached from atmospheric science, it is a staple in for the study of complex systems and chaos [14]. For certain parameter ranges, the system (1) is sensitive to its initial conditions, (2) produces irregular oscillations that are aperiodic, (3) has a behavior that is unpredictable in the long-term, and (4) is bounded to a strange attractor with fractal dimension despite the system’s deterministic nature [14]. Analysis in these regimes has shown that the system has no stable fixed points or limit cycles, however trajectories remain confined to a bounded region and are eventually attracted to a set of zero volume [14,15].
The Lorenz system is defined as
where and quadratic nonlinearities are presented by terms and . Here, we have selected traditionally studied values , , and which produce robustly chaotic waveforms. We note that where indicates a subcritical Hopf bifurcation value for parameter . Values of past this bifurcation indicate the potential for growing complexity in waveforms produced by the system. These equations and parameter values have long served communities in nonlinear dynamics and signal processing by allowing the study of entropic waveforms. We note that simulations on finite state machines can lead to misleading periodicities for some studies. We subsequently describe simulation details that largely avoids these behaviors. In addition to bifucation, traditional analysis shows this dissipative system’s fixed points as well as its local/global stability. Importantly for this work, symmetry in these equations allows the selection of a partition that can produce antipodal bits at properly selected Poincarè sections. Namely, the symmetry indicates that a planar partition that intersects yields antipodal symbols for as shown in Figure 1. Similarly, a planar partition that intersects yields antipodal symbols for .
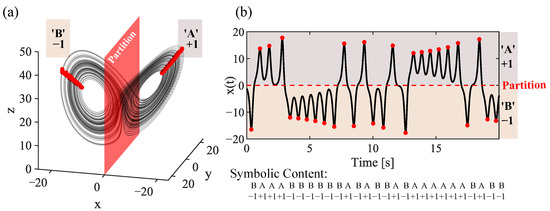
Figure 1.
Runge-Kutta (MATLAB ODE45) integration of the Lorenz equations showing (a) a partitioned phase space defining symbols from a Poincarè section (red dots) of the chaotic attractor (black) and (b) the time series of the variable (black) with peaks (red) defining symbols from a Poincarè section.
Computer-based experiments can characterize the Lorenz system’s chaotic behavior through observation. For example, Wolf’s algorithm numerically finds Lyaponuv exponents which define the system’s sensitivity to initial conditions [42]. For a d-dimensional chaotic dynamical system, nearby trajectories are expected to diverge exponentially in the long-term. This divergence is defined using neighboring initial conditions in an infinitesimal d-sphere and occurs in a relatively local portion of the trajectory within an orbit. As the system evolves in time, the flow deforms the sphere of initial conditions into an ellipsoid of time-evolved points. The deformation in each dimension is defined by the resulting ellipsoid’s principal axis to give i one-dimensional Lyaponuv exponents defined as
Although this limit approaches ∞, relatively few data points are needed in practice as the divergence is exponential. The number of data points n needed for Wolf’s algorithm is given by a rule-of-thumb maximum between the point density requirement: ≈ and the number of points per orbit multiplied by the number of orbits: ≈ where d is the dimensionality of the attractor which gives a conservative worst case length of ≈30,000 data points. Fortunately, these types of algorithms often converge more quickly than the rule-of-thumb indicates (≈10,000 points for Lorenz) and usually requires ≈100 orbits of the attractor. It has been noted that the Lorenz system poses significant challenge due to the ill-defined orbit period [42]. These irregular timings can be observed in the peaks and valleys indicated in the time-series data in Figure 1.
The magnitude of the exponents indicate a bit-rate for which the system creates or destroys information by translating its dynamics into a quantitative measure using the lens information theory [42,43]. The units of the exponents for continuous-time flows (differential equations) are or and for discrete-time iterated maps (difference equations). The aforementioned local orbit divergence gives an important distinction regarding information content produced by the system. A Lyaponuv exponent, in spirit, characterizes the stretching mechanisms of a chaotic system that generates new information from the the micro-scale (precision of initial conditions beyond our measurement/memory capacity or small noise perturbations in a heat bath) and not the folding mechanisms that keep the chaotic system bounded. Wolf et. al. reported positive Lyaponuv exponents of the Lorenz system to have a magnitude of with parameter values , , and . Initial conditions were specified using 20-bit precision (one part per million) and the prediction of the resulting time-series could not be extended beyond 9 s on average yielding . This result indicates the Lorenz system will tend to uncover ≈20 bits of new information from a spherical neighborhood of initial conditions with a radius corresponding to 20-bit precision in ≈20 orbits.
Methods related to the traditional analysis of ODEs and numerical analysis through observing time-series provide invaluable tools for understanding the dynamics of the Lorenz system as well as developing signal processing algorithms for engineering applications. However, abstraction of the system into symbols and the study of the resulting symbolic dynamics provides deep insight that pairs directly with information and communication theory. In practice, these techniques sample a trajectory’s state at discrete intervals and study the symbolic sequences obtained through partitioning (or thresholding) rules that coarse-grain the system’s time-series. Though, these techniques are not new, they are notably powerful and continue to strengthen an underlying connection between nonlinear dynamics and information theory [2,21,24,44].
The symmetry of the Lorenz attractor has been used to construct partitions that aid in symbolic analysis. A partitioned state space that corresponds to abstracted symbols A or B may be studied as symbolic dynamics that represent various underlying behaviors too burdensome to uncover through the traditional analysis of ODEs. Importantly, symbolic dynamics serves as the appropriate tool to study the Lorenz system’s periodic orbits. Historically, symbolic dynamics naturally permitted the study of the stable but elusive ‘period-5’ orbit which traditional methods tend to overlook [45]. In fact, symbolic dynamics has illuminated an encompassing view of the Lorenz system through dissection of the system’s periodic orbits [46]. These orbits form the skeleton of the the system’s attractor. Through this symbolic analysis, algorithms were developed to find the density of periodic orbits close to a desired point in phase space [46].
2.2. Extracting Approximate Basis Functions from Time-Series Simulations
Combining concepts of information creation in continuous, chaotic flows with symbolic dynamics allows for the extraction of basis function waveforms that constitute one bit of information difference between segments of a measured time-series. This notion further articulated and refined perceptions of the Lorenz system through the lens of communication signals [21] and surprisingly implied optimal signal processing related to Lorenz waveforms despite their unpredictability [44]. Starting with a symbolic description of Lorenz waveforms as depicted in Figure 1, k-bit symbol sequences may be selected that correspond to natural trajectories (i.e., ) of the Lorenz system. Arbitrarily symbol definitions may allow ‘A’ to represent a ‘+1’ bit and symbol ‘B’ to represent a ‘0’ bit. Here, we note that some schemes prefer antipodal bit definitions where the ‘0’ bit is defined as ‘−1’ and opt for this antipodal arrangement as shown in [21]. A comparison (mathematical difference) of trajectories for which their symbolic content varies by one bit of information (a Hamming distance of 1) produces a library of ‘information primitive’ waveforms that may be used in signal processing applications. Each of these waveforms constitutes a continuous-time information theoretic signature related to a single bit of information generated by the Lorenz system.
2.3. Regularizing Timing for the Lorenz Waveforms
Regarding Figure 1, the aforementioned ‘ill-defined orbit periods’ cause irregular timings in the peaks and valleys that define the Poincarè section and (in part) establish the symbolic content in these waveforms. These non-uniform intervals create issues for engineering applications as well as extracting basis functions from the Lorenz system. First, the irregular timing is incompatible with engineered systems that rely on regular clocks. Second, the information content embeded in continuous state variables needs to be extracted with a common time origin and time scale.
An important pre-processing step is to provide a means to regularize the timing intervals such that the Poincarè returns are uniform. Original waveforms with irregular timing are shown alongside waveforms that have been processed to achieve regular timing in Figure 2. This figure displays both time-series and statistical, histogram data of the time spacing between peaks for an waveform with ≈1000 peaks.
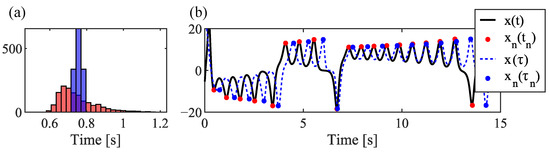
Figure 2.
(a) Histograms of timing intervals for the unmodified, irregular Lorenz waveform (red) showing a broad distribution and for the timing-regularized Lorenz waveform (blue) showing a narrow distribution. (b) Time-series waveform for the unmodified, irregular Lorenz waveform (black) with Poincarè sections indicated at irregular time intervals (red dots) and waveform for the timing-regularized Lorenz waveform (dashed-blue) with Poincarè sections indicated at regular time intervals (blue dots).
The algorithm used here was adapted through an example noted by Hayes [21] for the case of sampled systems and is valid for simulations with a known time-step. If the time-series for the signal is sampled from peak to peak (including both peaks and valleys) with uniform timing, then the number of samples between the peaks will tend to be non-uniform as some orbits tend to return to the Poincarè section slower or faster than others. Slow trajectories will tend to contain more samples between peaks, and fast trajectories will tend to contain less samples between peaks.
Regular timing may be imposed on the irregular Lorenz waveform by reproducing the sampled with a variable clock rate (i.e., using a digital-to-analog converter). The reproduced should be time compressed (sped up) proportional to the number of samples between peaks. This method effectively spaces the peak returns in uniformly and results in regular sample rate for the symbolic content of the Lorenz waveform. Loosely, one proposed method to accomplish this algorithmically uses the following steps:
- (i)
- measure and store the number of samples & indices between two peaks
- (ii)
- extend each data segment to convenient a sample interval (i.e., 50 samples or 100 samples)
- (iii)
- pad new x(t) values and increment new indices
- (iv)
- define a regeneration sample rate & corresponding period
- (v)
- time stretch/compress segment proportionally by original number of samples
- (vi)
- repeat for each pair of peaks
and pseudo-code for this algorithm is given by Algorithm 1. We note that this algorithm has not optimized towards any specific performance metric and is intended to serve as an operational guide to illuminate approaches to implement techniques suggested by Hayes [21].
| Algorithm 1 Algorithm that regularizes timing between Poincarè returns |
| for each k in peaks do |
▹ Regularize timing between two peaks |
for i=1:numSamples-length(iROrig) do |
▹ Pad x(t) to a convenient length i.e., 6023 samples would map to 6050 |
end for |
▹ Define regeneration sample rate & period |
▹ Regenerate x(t) with sample-proportionate time compression |
while do |
▹ Populate samples using regeneration period |
end while |
end for |
2.4. Extracting a Single Basis Function as an Information Primitive
This subsection illustrates the extraction of a basis function as an information primitive by comparing continuous-time trajectory amplitudes that differ by only one symbolic bit of information. This concept is successful because it exploits the determinism of the chaotic Lorenz system. Consider two waveform segments as time series data from the x variable of the Lorenz system with equal length in time and . If these waveforms represent 8 bits of symbolic content (coarse-grained) and differ only in the 7th bit, then a continuous-time (fine-grained) representation of an information primitive may be established relating to state variable x.
Concisely, this arrangement consists of two waveforms with a Hamming distance of 1 and will share an exponentially similar initial condition as governed by Lyaponuv exponents inherent to the Lorenz equations. To extract a single instance of this information primitive (called a basis function from here on), one simply takes the difference aligned with some desired bit mask defining the time location where the Hamming distance between the two waveforms is non-zero. We note that this possibility is enabled by the regularized timing of the two waveforms where t represents the original time vector related to the Lorenz system and represents a time vector that has been regularized for even time spacing of the waveform’s symbolic content. A graphical depiction of this arrangement is provided by Figure 3. In practice, the algorithms described in this work hold a time-regularized template waveform and its symbolic content in memory while various waveform segments produced by the Lorenz oscillator are ‘scanned.’ These scanned, time-regularized waveforms are first compared symbolically to check if a non-zero Hamming distance has the correct bit index (time location). If this Hamming distance criterion is met, the difference of the two waveforms constitutes a single instance of a basis function as shown in Figure 3.
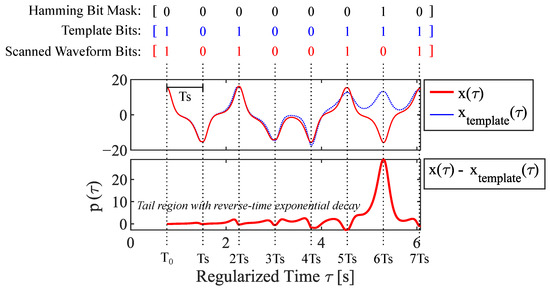
Figure 3.
Graphical representation of two time-regularized waveforms with symbolic content that meets the Hamming distance criterion. (Top) Sample waveforms from state variable x after being time-regularized. (Bottom) Resulting basis function .
Cataloging sequences with small Hamming distances from Lorenz waveforms to produce libraries containing various signatures can be computationally taxing if not impossible in practice for large k. Fortunately, chaotic systems’ exponential sensitivity to small differences combined with their determinism forces a convenient shape for each resulting basis waveforms. If a bit vector representing the bit-wise Hamming distance between two waveforms serves as the bit mask , the resulting basis waveforms exhibit an exponentially decaying tail as . The acausal property of these resulting waveforms indicates determinism. As each tail decays, the difference between any two compared waveforms segments from state variable x (i.e., ) exponentially decreases as well as the spherical radius of the neighborhood containing the initial conditions of each waveform ( and ). This favorable behavior implies that an accurate representation of an instance may be obtained even with small bit lengths k.
Heuristically, bit lengths of ≈8 [bits] work well, but result in bit combinations to process and catalog. Previous analyses processed bit lengths from 8 [bits] to 10 [bits] and averaged resulting libraries of ≈1000 basis function waveforms. A straight-forward approach to obtain these averages involves generating significantly long (1000–5000 [s] with timestep [s]), aperiodic time-series simulations. These types of computer experiments integrated on finite state machines may tend toward periodicity that is unfaithful to real-world implementations of the Lorenz system. This is partly due to finite memory and precision on representing initial conditions and . Further, the presence of microscopic noise in physical systems is always present.
One important numerical ‘trick’ that avoids these periodicity issues without using high precision data types is to intentionally introduce a small amount of numerical noise by integrating the equations with parameter values , , etc. This small modification is commonly employed and has been discussed at conferences and post-doc appointments, but to the author’s knowledge has not been described in popular texts. This method is generally sufficient for the time-series in this work where an adjustment of was chosen for time-series on the order of to time steps, though other methods may be needed to simulate notably larger, aperiodic time-series. One such approach may involve the control of chaotic systems to produce desired bit sequences that differ in accordance with the aforementioned Hamming distance bit mask. Efficient control schemes involve small perturbations [47] and have been proposed of the Lorenz system in order to observe rare events such as a trajectory entering a spherical neighborhood with radius of 0.1 near the origin. The probability of such a trajectory is reported to 1 in orbits. Rare events such as these are more probable as desired bit lengths increase and may become impractical with the brute force generation of aperiodic, long time-series data.
2.5. Extracting Multiple Basis Functions to Form an Average Basis Function
As examples of waveform segments and their information content vary in the time evolution of x trajectories, resulting basis functions also vary. These variations are illustrated in Figure 4 which shows a long waveform sample (≈50 s with ≈160 bits of symbolic content) where smaller 8-bit segments of symbolic content are captured to generate waveform templates. These templates are held in memory and compared against all other consecutive 8-bit segments that exist in the waveform sample . This comparison ‘scans’ and captures instances of the Hamming distance criterion being met between the stored template and the sliding comparison segments .
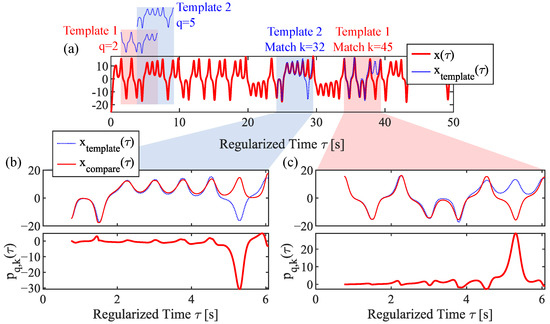
Figure 4.
(a) Two long waveform segments from state variable x after being time-regularized. (b) Two examples of waveform segments with symbolic content that meets the Hamming distance criterion and their resulting instances of basis function . (c) Two examples of waveform segments similar to Figure 4b with the exception that the summed peak is not inverted. Cases for Figure 4b,c must be accounted for when designing basis function extraction algorithms.
Algorithmically, this scanning first consists of creating templates with the following steps:
- (i)
- set a global scanning index q to iterate template storage over the long waveform sample ,
- (ii)
- store the template segment of to form the instance of ,
- (iii)
- extract the symbolic content of the instance of .
Next for a single iteration of q, the template is compared throughout the waveform by the following nested scan with the steps:
- (i)
- set a scanning index k to iterate over the long waveform sample
- (ii)
- store the template segment of to form the instance of
- (iii)
- extract the symbolic content of the instance of
- (iv)
- perform a test of the Hamming distance criterion between the symbolic content of the instance of and the symbolic content of the instance of .
For cases where the Hamming distance criterion is met, an instance of the basis function is stored. Note, as shown in Figure 4, that some instances of may have an inverted peak and should be corrected to have a positive peak. This process is continued until the k index is exhausted throughout the long waveform sample . Upon completion of the final k index, the global index q is incremented, and the nested scan is repeated. As the global index q is exhausted, the long waveform sample has served to populate many instances of the basis function which can be averaged.
This process is highlighted with an example waveform in Figure 4. Two specific instances of the Hamming distance criterion being met for global index q and scanning index k and lead to two specific examples of a basis function . The first basis function instance is illustrated by Figure 4a, and obtained from the global index (highlighted in red and labeled as Template 1). The Hamming distance criterion is met in this instance for a scanning index (highlighted in red and labeled Template 1 Match). Note that results in a negative peak, as illustrated in the left plots of Figure 4b, so it first inverted before being stored as an instance of . Similarly, another instance of is illustrated by Figure 4a, but this time is obtained from the global index (highlighted in blue and labeled as Template 2). The Hamming distance criterion is met in this instance for a scanning index (highlighted in blue and labeled Template 2 Match).
This complete algorithm is outlined in a detailed flowchart in Appendix A with Figure A1. It should be noted that the symbolic content that constitutes the bits used in the evaluation of the Hamming distance criterion is not evenly distributed. The statistics of these bits influence the shape of the average basis function. In the next section of this work we report the results of this algorithm, the statistics of these bit sequences and the impact of those statistics on the shape of the extracted and averaged basis function .
3. Results
The algorithm described in the Materials and Methods section and illustrated in Appendix A by Figure A1 was applied and results are provided in Figure 5 for the state variable x. Long (≈5,000,000 samples) waveforms produced via Runga-Kutta (MATLAB ODE45) integration of the chaotic Lorenz system with the parameters , and with , resulted in a total waveform length of . These parameters were selected to avoid prominent periodicities that may not accurately represent the natural density of trajectories. The resulting time series was first regularized with respect to the timing of symbolic content to form . The results of processing the basis function extraction of long waveform sample are given by Figure 5.
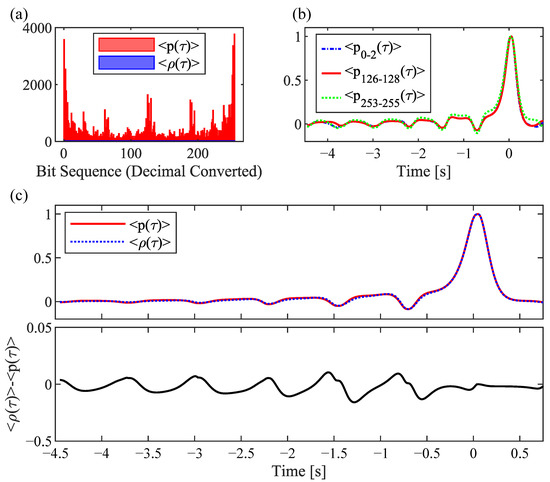
Figure 5.
Results of processing a 5000 [s], ≈5,000,000 timestep chaotic Lorenz waveform via Runga-Kutta (MATLAB ODE45) integration with the parameters , and with , and length 5000 [s]. (a) Bit statistics for each 8-bit long segment used to establish that the Hamming distance criterion was met. The red histogram shows the natural density of symbolic content provided by the x state variable. This red histogram constitutes the symbol sequences that are used to average the basis function . The blue histogram shows uniformly distributed bit sequences (all bit sequences are represented evenly with ≈200 examples of each) and constitutes the average basis function . (b) Averaged basis functions in various regions of the red histogram from (a). (c) The resulting averaged basis functions for both natural bit density (solid red) and uniformly distributed bit density (dashed blue). Below each of these averaged basis functions show their small difference.
These results are presented in three parts: (i) natural vs. uniform bit statistics (shown in Figure 5a), (ii) extracted and averaged basis functions for three primary regions of natural bit statistics (shown in Figure 5b), and (iii) the extracted and averaged basis functions with natural bit statistics , uniform bit statistics , and the small difference between the two (shown in Figure 5c). In Figure 5a, bit statistics for each 8-bit long segment are shown. These statistics are used to establish that the Hamming distance criterion has been met and thus constitute the symbolic content involved with constructing basis function averages. The red histogram in the figure shows the natural density of symbolic content provided by the x state variable and indicates the proportion of each symbol sequence used to average the basis function . The blue histogram shows uniformly distributed bit sequences, where all bit sequences are represented evenly with approximately 200 examples of each. This histogram constitutes the average basis function .
In Figure 5b, averaged basis functions in three regions of the red histogram that demonstrate prominently occurring bit sequences from Figure 5a are shown. The first prominent statistical peak (second most likely region) was identified heuristically as the bit sequences 0–2 (decimal) that correspond to the bit sequences [00000000], [00000001], and [00000010] (binary). Similarly, the next region (third most likely) was identified as bit sequences 126–128 and the final region was identified as bit sequences 253–255. Averaged basis function for each region is computed and showed a small, but non-zero difference. In Figure 5c, the resulting averaged basis functions for both natural bit density (solid red) and uniformly distributed bit density (dashed blue) are shown. The difference between these two results is provided below the time series. Finally, Figure 6 shows the results for bit statistics and extracted, averaged basis functions of all three state variables of the chaotic Lorenz system.
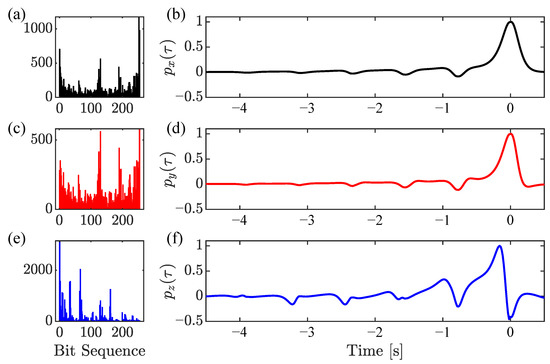
Figure 6.
(a) Bit statistics for instances where the Hamming distance criterion was met resulting in a recorded instance of a basis function for the state variable x. (b) Extracted, averaged basis function for state variable x. (c) Bit statistics for state variable y. (d) Extracted, averaged basis function for state variable y. (e) Bit statistics for state variable z. (f) Extracted, averaged basis function for state variable z.
Discussion
These results validate the effectiveness of extracting basis functions using the proposed algorithm. In previous sections, three independent, non-averaged basis functions were given by Figure 3 and Figure 4. The bit statistics and averaged waveforms for the x variable in respect to the natural dynamics of the chaotic Lorenz oscillator and uniformly distributed representations of bit sequences in Figure 5 along with difference between the average basis function for natural Lorenz bit statistics and uniform bit statistics (which is small). Finally, we report extracted waveforms from all three state variables x, y, and z in Figure 6 with natural Lorenz bit statistics.
The extracted and averaged basis function for the state variable x is in high agreement with Hayes’s work [21]. The underlying statistics of the bit sequences chosen to construct have a quantifiable impact on the shape of the resulting basis function as shown by the data in Figure 5b. If the contributions of these bit sequences are not statistically balanced, the resulting, average basis function may be distorted. Interestingly, the difference between averaged basis function with natural bit sequences and the averaged basis function with uniform bit sequences was small. This is likely due to the fact that the natural bit statistics are dominated by sequences with histogram peaks that are ‘statistically balanced.’ To the author’s knowledge, these bit statistics have not been previously reported in regard to constructing basis functions for chaotic Lorenz waveforms. Similarly, novel data are given by Figure 2 that shows the natural timing statistics of chaotic Lorenz peaks for the time evolution of state variable x.
Finally, the bit statistics and extracted average basis functions for all three state variables given in Figure 6 indicate a well-known correlation between state variables x and y as their extracted basis functions are qualitatively similar with similar bit sequence statistics. Interestingly, the details of state variable z do not clearly lend themselves to waveform synthesis as readily as the results from state variables x and y. First, we note the non-uniformity and imbalance of bit sequence statistics involved with constructing the average basis function . Second, we note that the forward-time tail of does not tend to cleanly resolve to zero amplitude. In fact, for some collections of bit sequences, becomes ill-behaved in amplitude and would inject unwanted inter-symbol interference if used to reconstruct a chaotic time series of state variable z. This may imply that the symbolic timing for the information content inherent to state variable z is different and possibly more complicated (non-trivial) when compared to the symbolic timing of the other two state variables. The primary observations from these results is that (1) state variable x and waveforms with similar properties from other chaotic systems can make a straight-forward candidate for test signals and waveform design, and (2) state variable z merits further investigation as its statistics and timing complexity subvert its candidacy as a test signal or two inspire further waveform design.
4. Conclusions
This study aimed to enhance the accessibility and applicability of chaotic dynamics and random processes through the lens of information theory, measurable dynamics, and ergodic theory. Previously, Hayes’ [21] work provided insights into the relationship between chaotic dynamics and random processes, particularly in the context of linearly combining oscillatory basis functions as information primitive structures. Random weighting factors may be used to produce deterministic chaotic waveforms that approximate solutions to chaotic systems through simple convolutional sums that include these information primitives. Here we have provided essential details regarding the specific implementation of algorithms, the statistics of the bit sequences used, and the timing information that is discarded in the resulting algorithms. We have evaluated all three of the Lorenz state variables and provided information primitives and bit sequence statistics for each. These results may be used for quantiative measurement of chaotic waveforms in applications such as machine learning algorithms for time series prediction and waveform design for communication and sensing. The findings presented here validate the extraction of basis functions from chaotic systems for two of the three state variables of the chaotic Lorenz system and identify future directions for understanding more complex behavior in relation to the state variable z.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
A.N. Beal would like to acknowledge Scott T. Hayes for his creative and seemingly prescience insight towards expressing chaotic waveforms via information primitive functions.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
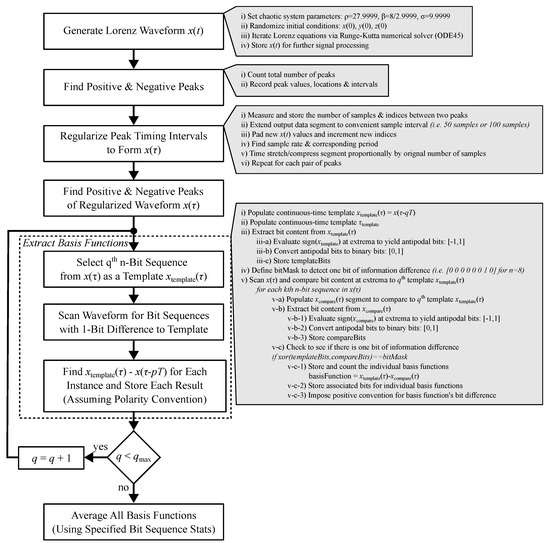
Figure A1.
Detailed flowchart for algorithm used to extract basis functions from the chaotic Lorenz system.
References
- Kaddoum, G. Wireless chaos-based communication systems: A comprehensive survey. IEEE Access 2016, 4, 2621–2648. [Google Scholar] [CrossRef]
- Corron, N.J.; Blakely, J.N.; Stahl, M.T. A matched filter for chaos. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 023123. [Google Scholar] [CrossRef]
- Ren, H.P.; Baptista, M.S.; Grebogi, C. Wireless communication with chaos. Phys. Rev. Lett. 2013, 110, 184101. [Google Scholar] [CrossRef]
- Beal, A.N.; Cohen, S.D.; Syed, T.M. Generating and detecting solvable chaos at radio frequencies with consideration to multi-user ranging. Sensors 2020, 20, 774. [Google Scholar] [CrossRef]
- Pappu, C.S.; Flores, B.C.; Debroux, P.S.; Boehm, J.E. An Electronic Implementation of Lorenz Chaotic Oscillator Synchronization for Bistatic Radar Applications. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2001–2013. [Google Scholar] [CrossRef]
- Wang, B.; Xu, H.; Yang, P.; Liu, L.; Li, J. Target detection and ranging through lossy media using chaotic radar. Entropy 2015, 17, 2082–2093. [Google Scholar] [CrossRef]
- Beal, A.; Blakely, J.; Corron, N.; Dean, R., Jr. High frequency oscillators for chaotic radar. In Proceedings of the Radar Sensor Technology XX, Baltimore, MD, USA, 17–21 April 2016; Volume 9829, pp. 142–152. [Google Scholar]
- Corron, N.J.; Stahl, M.T.; Chase Harrison, R.; Blakely, J.N. Acoustic detection and ranging using solvable chaos. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 023119. [Google Scholar] [CrossRef]
- Syed, T.M.; Pappu, C.S.; Beal, A.N. Drastically reduced sensor hardware for solvable chaos-based sonar. Electron. Lett. 2022, 58, 810–812. [Google Scholar] [CrossRef]
- Pappu, C.S.; Beal, A.N.; Flores, B.C. Chaos Based Frequency Modulation for Joint Monostatic and Bistatic Radar-Communication Systems. Remote Sens. 2021, 13, 4113. [Google Scholar] [CrossRef]
- Pappu, C.S.; Carroll, T.L.; Flores, B.C. Simultaneous radar-communication systems using controlled chaos-based frequency modulated waveforms. IEEE Access 2020, 8, 48361–48375. [Google Scholar] [CrossRef]
- Carroll, T.L.; Pecora, L.M. Network structure effects in reservoir computers. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083130. [Google Scholar] [CrossRef]
- Carroll, T.L. Optimizing memory in reservoir computers. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 023123. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Dudul, S.V. Prediction of a Lorenz chaotic attractor using two-layer perceptron neural network. Appl. Soft Comput. 2005, 5, 333–355. [Google Scholar] [CrossRef]
- Mukherjee, S.; Osuna, E.; Girosi, F. Nonlinear prediction of chaotic time series using support vector machines. In Proceedings of the Neural Networks for Signal Processing VII, 1997 IEEE Signal Processing Society Workshop, Amelia Island, FL, USA, 24–26 September 1997; pp. 511–520. [Google Scholar]
- Li, D.; Han, M.; Wang, J. Chaotic time series prediction based on a novel robust echo state network. IEEE Trans. Neural Networks Learn. Syst. 2012, 23, 787–799. [Google Scholar] [CrossRef] [PubMed]
- Miranian, A.; Abdollahzade, M. Developing a local least-squares support vector machines-based neuro-fuzzy model for nonlinear and chaotic time series prediction. IEEE Trans. Neural Networks Learn. Syst. 2012, 24, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, D.J.; Bollt, E.; Griffith, A.; Barbosa, W.A. Next generation reservoir computing. Nat. Commun. 2021, 12, 5564. [Google Scholar] [CrossRef]
- Hayes, S.T. Chaos from linear systems: Implications for communicating with chaos, and the nature of determinism and randomness. J. Phys. Conf. Ser. 2005, 23, 215. [Google Scholar] [CrossRef]
- Bollt, E.M.; Santitissadeekorn, N. Applied and Computational Measurable Dynamics; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Shimada, I.; Nagashima, T. A numerical approach to ergodic problem of dissipative dynamical systems. Prog. Theor. Phys. 1979, 61, 1605–1616. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Weaver, W. Recent contributions to the mathematical theory of communication. ETC Rev. Gen. Semant. 1953, 10, 261–281. [Google Scholar]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H.; Ding, J.J. Signals and Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1997; Volume 2. [Google Scholar]
- Cuomo, K.M.; Oppenheim, A.V.; Strogatz, S.H. Synchronization of Lorenz-based chaotic circuits with applications to communications. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 626–633. [Google Scholar] [CrossRef]
- Pan, J.; Ding, Q.; Du, B. A new improved scheme of chaotic masking secure communication based on Lorenz system. Int. J. Bifurc. Chaos 2012, 22, 1250125. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Fenwick, A.; Williams, C.; Harman, S. Chaotic signals in radar and sonar. In 2006 International Waveform Diversity & Design Conference; IEEE: Manhattan, NY, USA, 2006; pp. 1–6. [Google Scholar]
- Ge, Y.; Zhang, W.; Gao, F.; Li, G.Y. Frequency synchronization for uplink massive MIMO with adaptive MUI suppression in angle domain. IEEE Trans. Signal Process. 2019, 67, 2143–2158. [Google Scholar] [CrossRef]
- Wang, C.; Pang, M.; Xu, L.; Zhao, L.; Yao, Y.; Wang, W. Time Synchronization and Signal Detection in Non-Orthogonal Unicast and Broadcast Networks. In IEEE Transactions on Broadcasting; IEEE: Manhattan, NY, USA, 2023. [Google Scholar]
- DeCocco, B.; LaVenture, R.; Pappu, C.S.; Yi-Lin, F. Chaotic waveforms for medical imaging. Multiscale Imaging Spectrosc. 2023, 12363, 36–46. [Google Scholar]
- Fasel, T.R.; Todd, M.D.; Park, G. Piezoelectric active sensing using chaotic excitations and state space reconstruction. In Proceedings of the Health Monitoring and Smart Nondestructive Evaluation of Structural and Biological Systems IV, San Diego, CA, USA, 5 May 2005; Volume 5768, pp. 253–263. [Google Scholar]
- Tanis, S. Automotive radar and congested spectrum: Potential urban electronic battlefield. Microw. J. 2019, 62, 48. [Google Scholar]
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Hassan, W.H. Current research on Internet of Things (IoT) security: A survey. Comput. Netw. 2019, 148, 283–294. [Google Scholar]
- Jordan, D.; Smith, P. Nonlinear Ordinary Differential Equations: An Introduction for Scientists and Engineers; OUP Oxford: Oxford, UK, 2007. [Google Scholar]
- Wiggins, S.; Wiggins, S.; Golubitsky, M. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2. [Google Scholar]
- Cvitanovic, P.; Artuso, R.; Mainieri, R.; Tanner, G.; Vattay, G.; Whelan, N.; Wirzba, A. Chaos: Classical and Quantum; Niels Bohr. Institute: Copenhagen, Denmark, 2005; Volume 69, p. 25. [Google Scholar]
- Barrio, R.; Shilnikov, A.; Shilnikov, L. Kneadings, Symbolic Dynamics and Painting Lorenz Chaos. Int. J. Bifurc. Chaos 2012, 22, 1230016. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Shaw, R. Strange Attractors, Chaotic Behavior, and Information Flow. Z. Naturforschung A 1981, 36, 80–112. [Google Scholar] [CrossRef]
- Corron, N.J.; Blakely, J.N. Chaos in optimal communication waveforms. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150222. [Google Scholar] [CrossRef]
- Fang, H.P.; Hao, B.L. Symbolic dynamics of the Lorenz equations. Chaos Solitons Fractals 1996, 7, 217–246. [Google Scholar] [CrossRef]
- Viswanath, D. Symbolic dynamics and periodic orbits of the Lorenz attractor. Nonlinearity 2003, 16, 1035. [Google Scholar] [CrossRef]
- Shinbrot, T.; Grebogi, C.; Yorke, J.A.; Ott, E. Using small perturbations to control chaos. Nature 1993, 363, 411–417. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).