Transient Vibro-Acoustic Characteristics of Double-Layered Stiffened Cylindrical Shells
Abstract
1. Introduction
2. Prediction Method for Noise Under Transient Impact Loads
2.1. Transient Structural Dynamics Theory
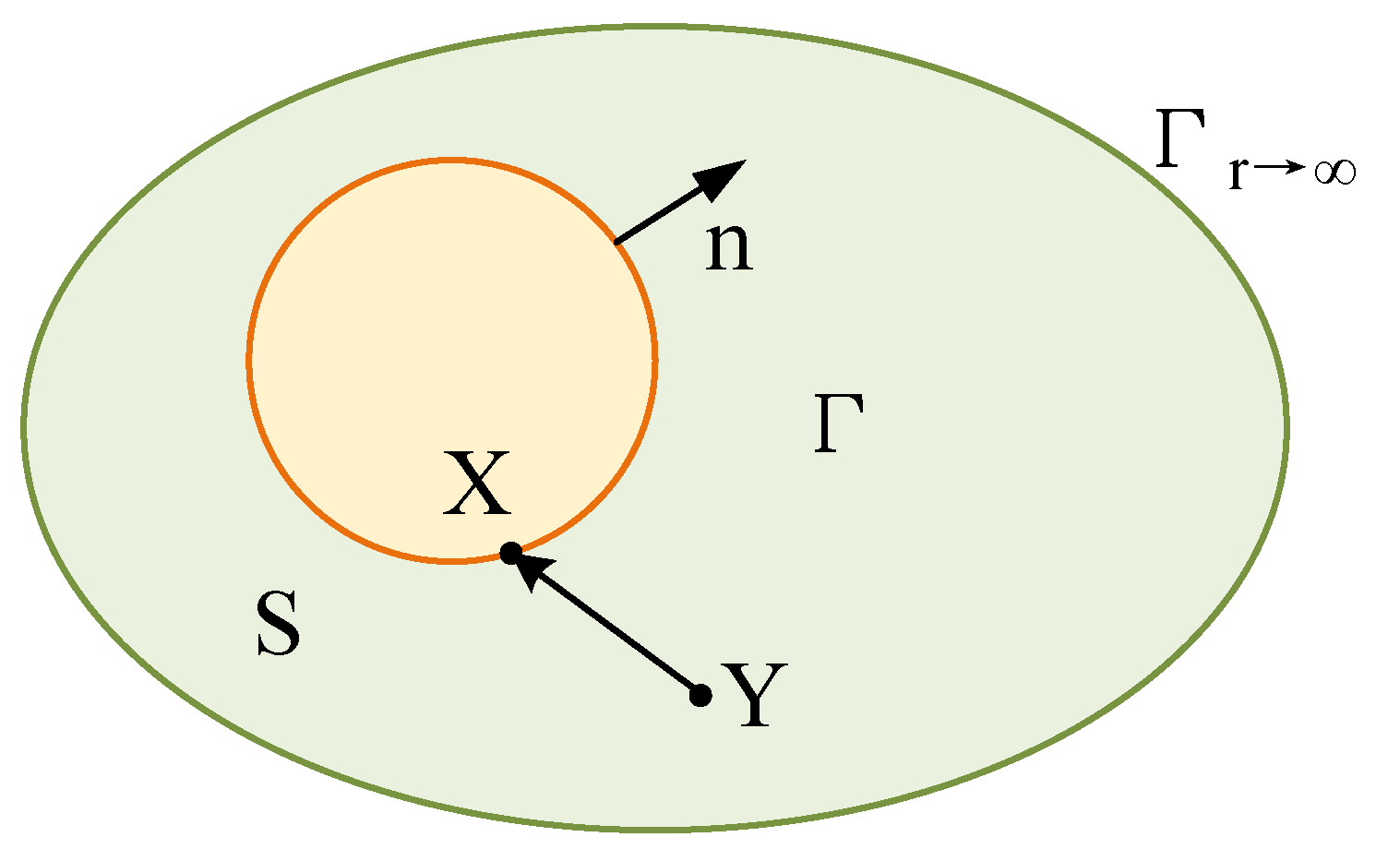
2.2. Boundary Element Theory Based on Wave Equation
2.3. Transient Signal Analysis Method
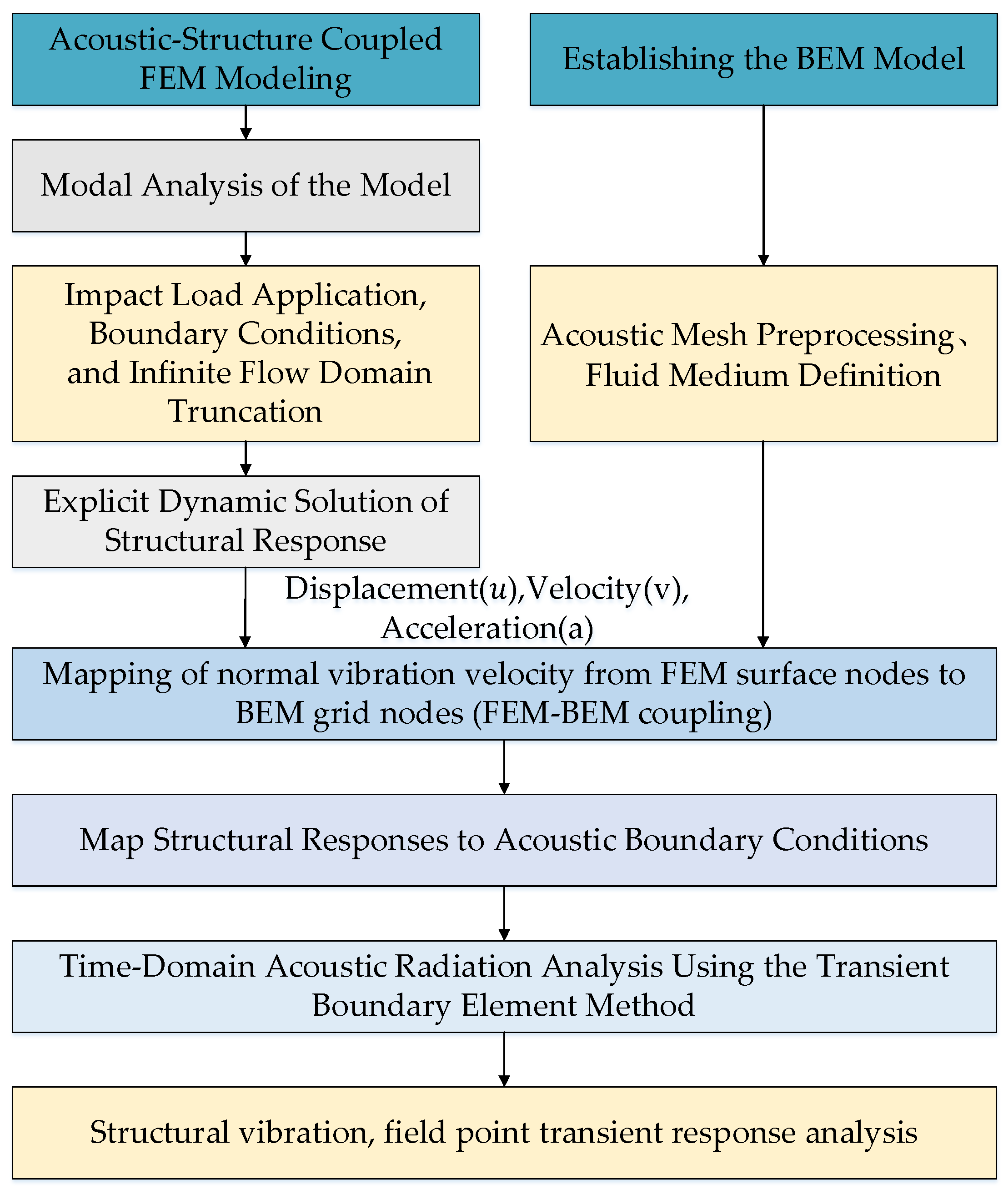
2.4. Prediction Process of Underwater Transient Radiated Noise of Ship Structure
- (1)
- Divide the prediction solution for transient radiated noise into structural vibration response solution and radiated noise solution. Develop separate structural finite element (FEM) and acoustic boundary element (BEM) models. Subsequently, perform modal analysis on the FEM model to characterize its vibration behavior, and conduct preprocessing of the structural-acoustic mesh and fluid medium definition for the BEM model.
- (2)
- Define the boundary conditions and external fluid domain for the FEM model to approximate realistic operational conditions. Then, based on explicit dynamics, solve the transient vibration response of the structure under various impact loads.
- (3)
- Input the structural vibration response obtained in the previous step as boundary conditions for the acoustic field. Solve the acoustic boundary integral equation using the time-domain boundary element method (BEM) to obtain the time-varying acoustic pressure distribution within the fluid field.
- (4)
- Perform time-frequency characteristic analysis on the structural transient vibration response and acoustic radiation using wavelet transform.
3. Validation of Transient Impact Noise Calculation Method
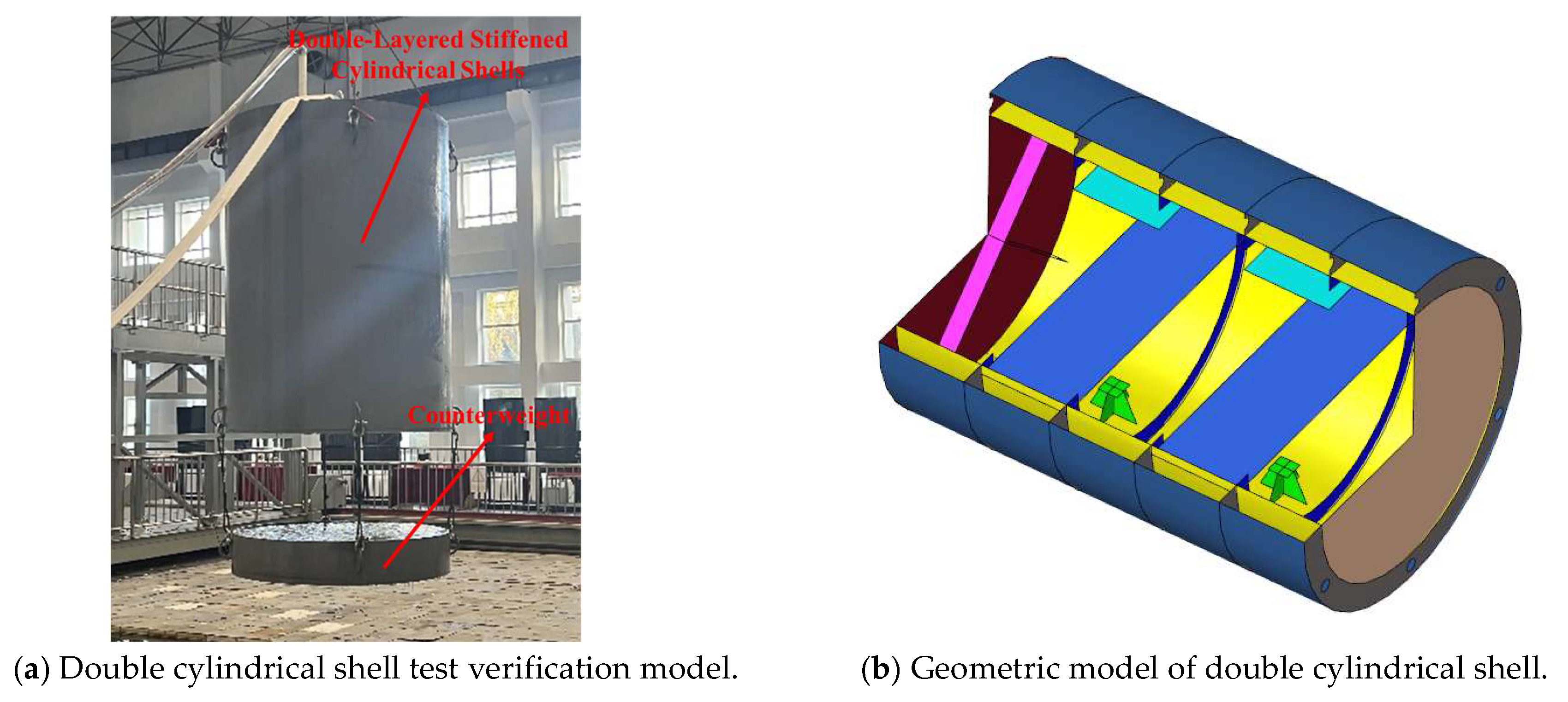
3.1. Introduction of Double Stiffened Cylindrical Shell Model
3.2. Experiment Content
3.3. Numerical Model of Double Stiffened Cylindrical Shell
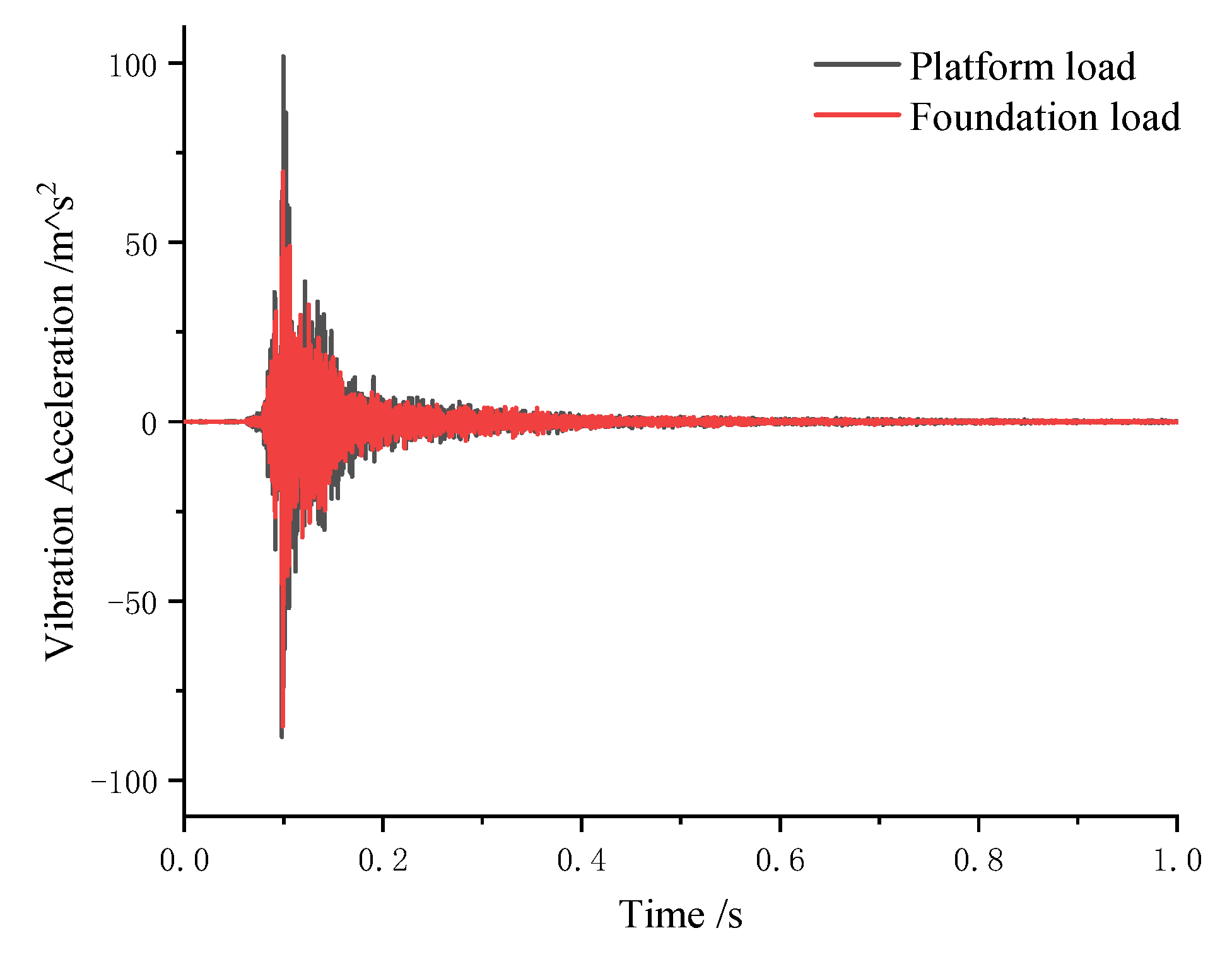
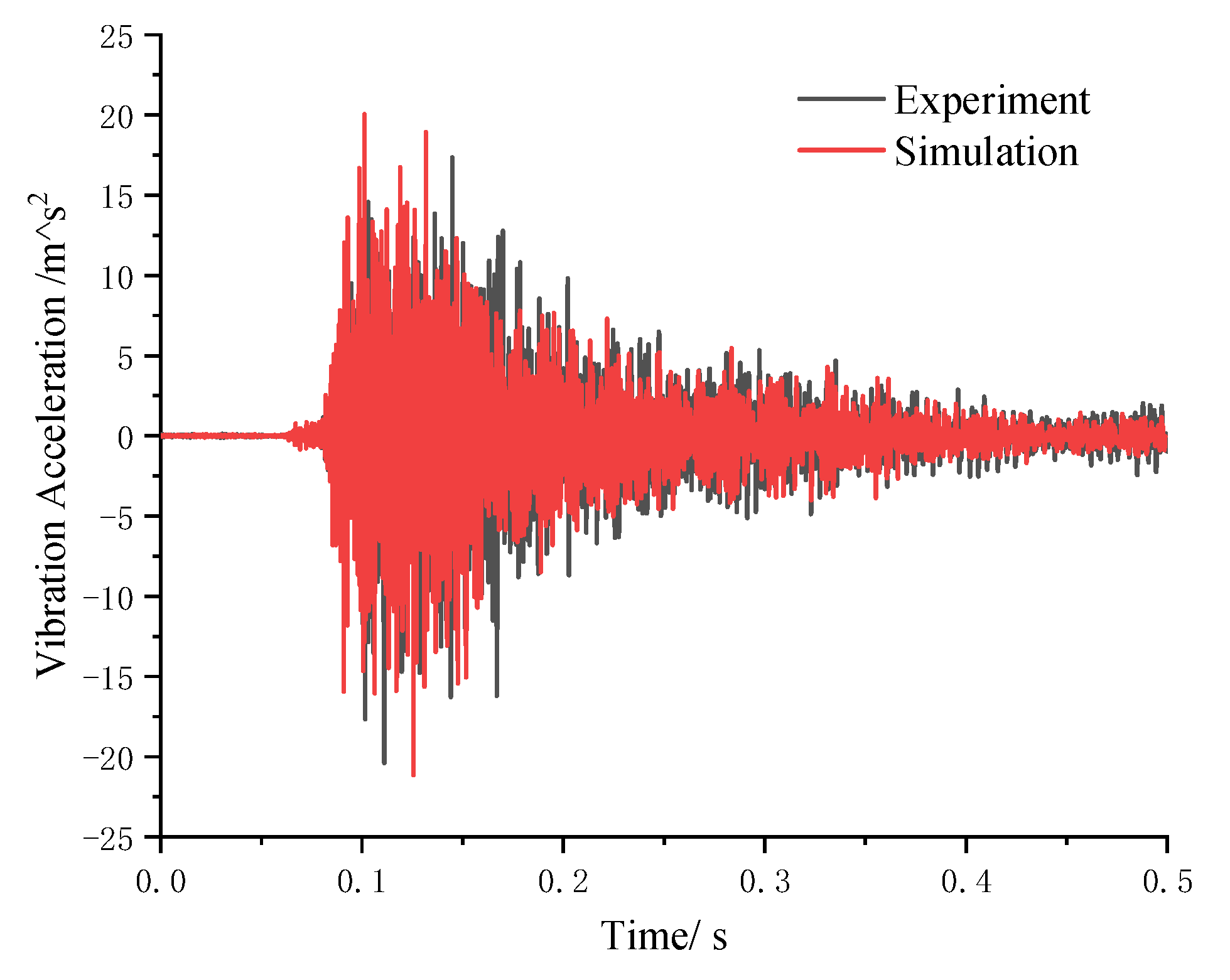
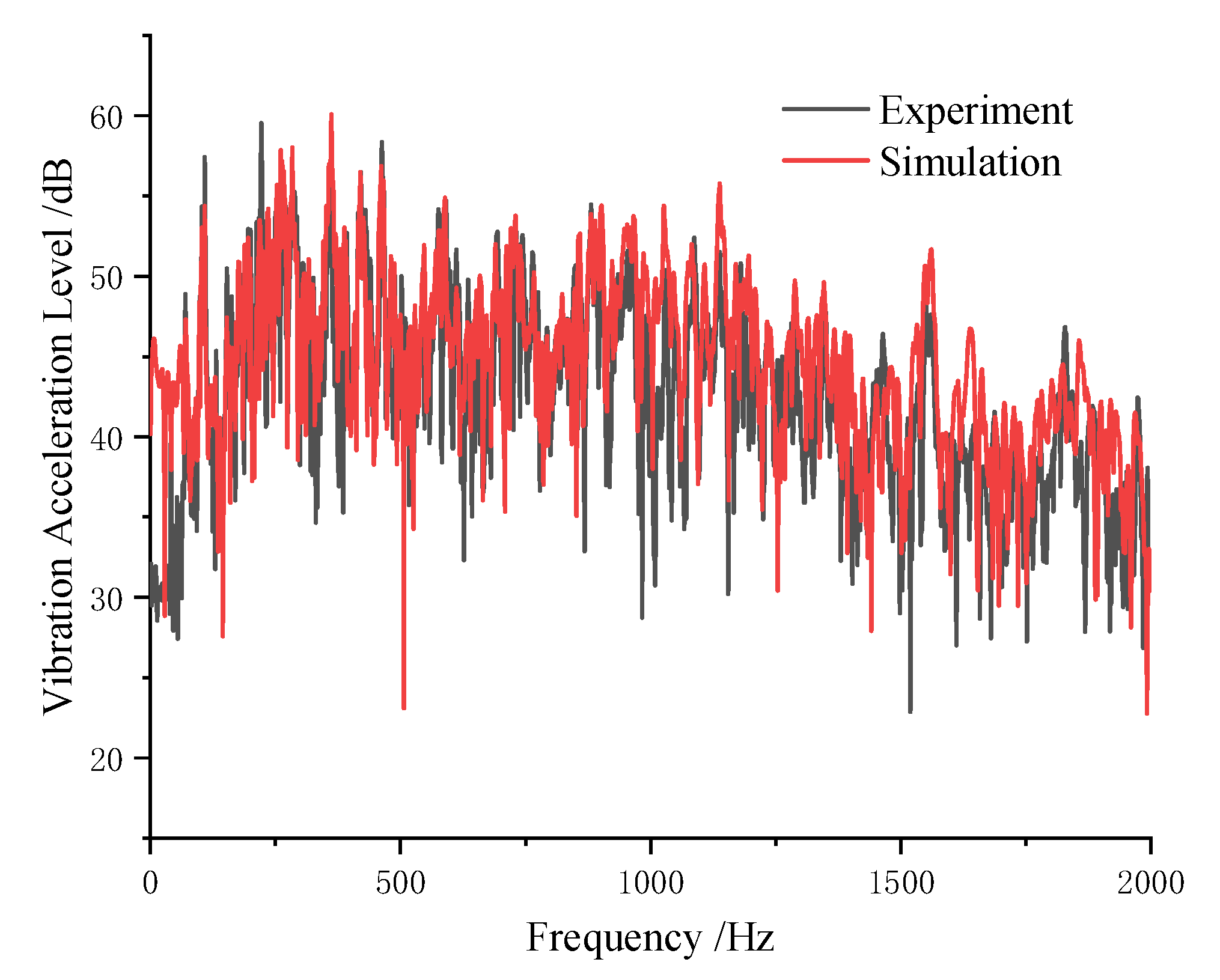
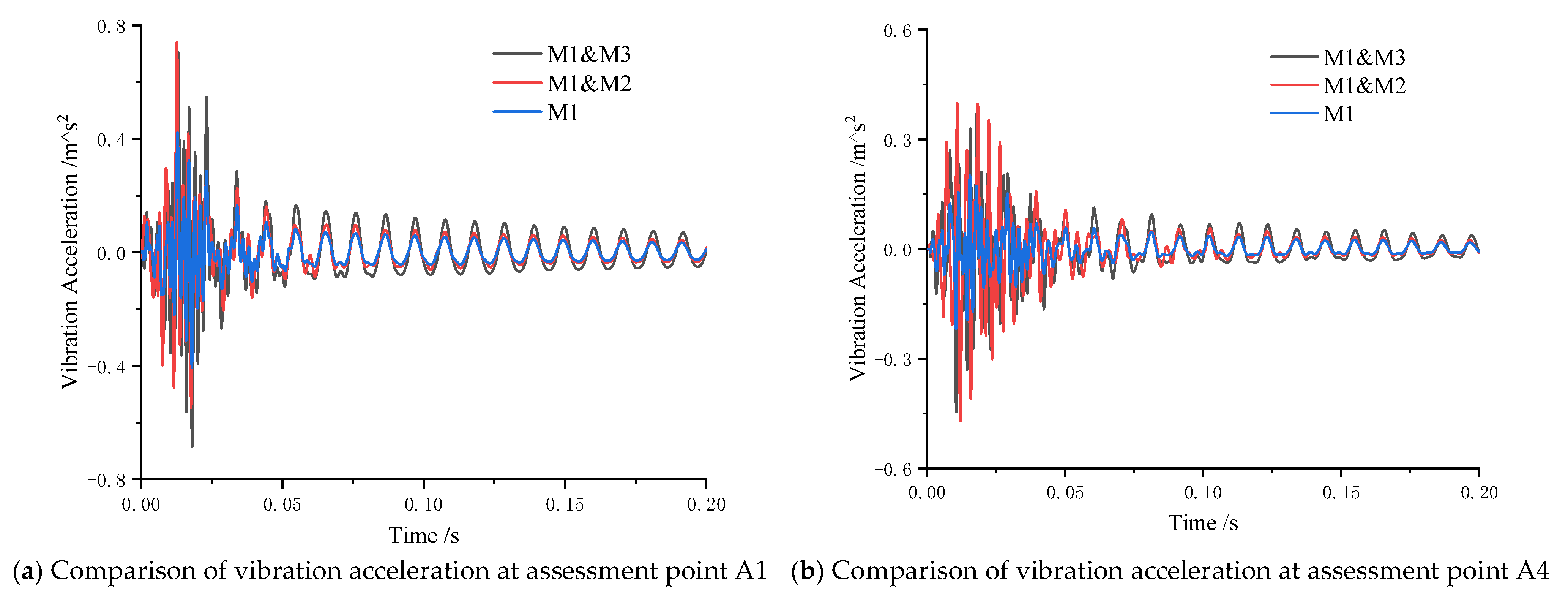
3.4. Comparative Analysis of Transient Vibration Response
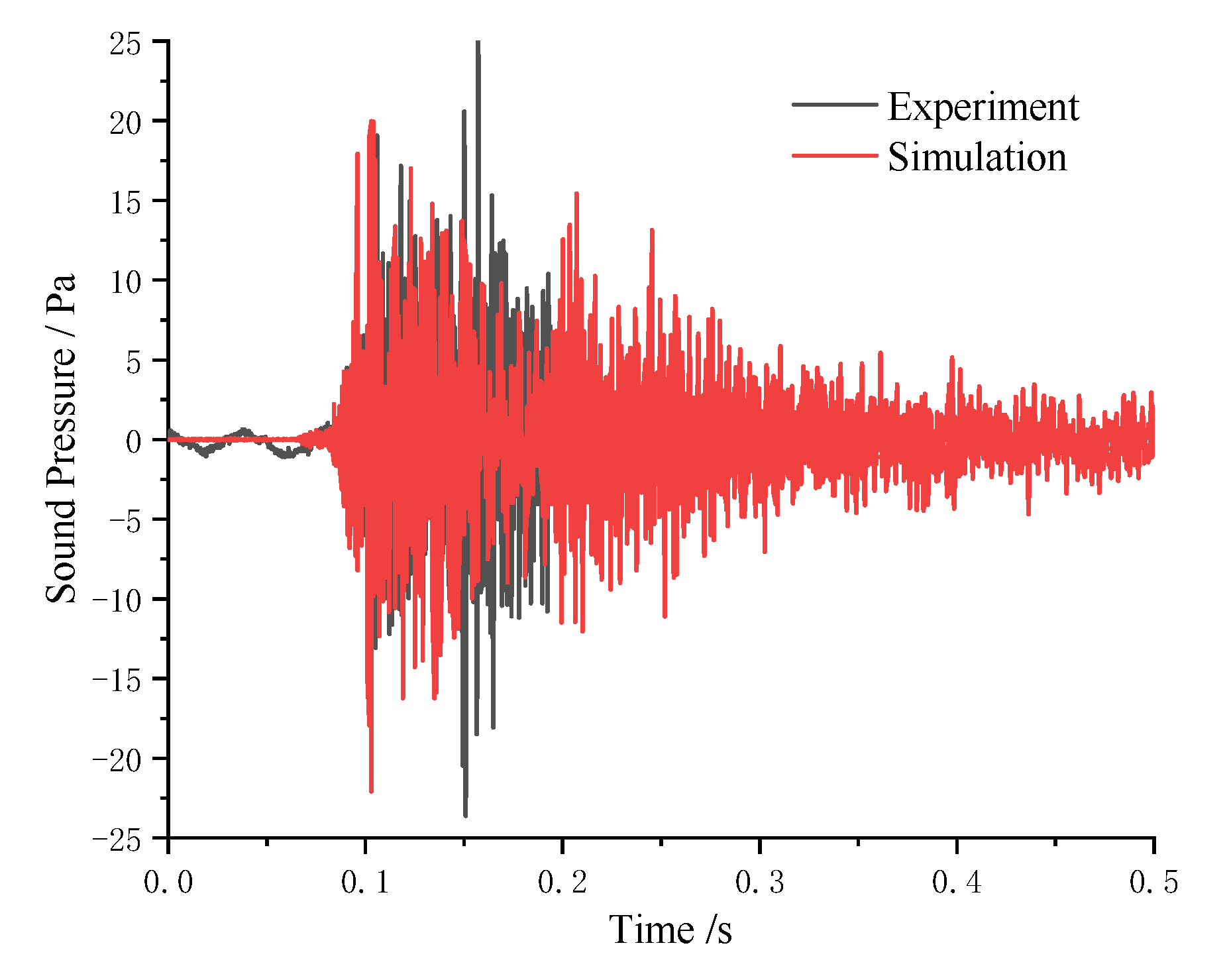
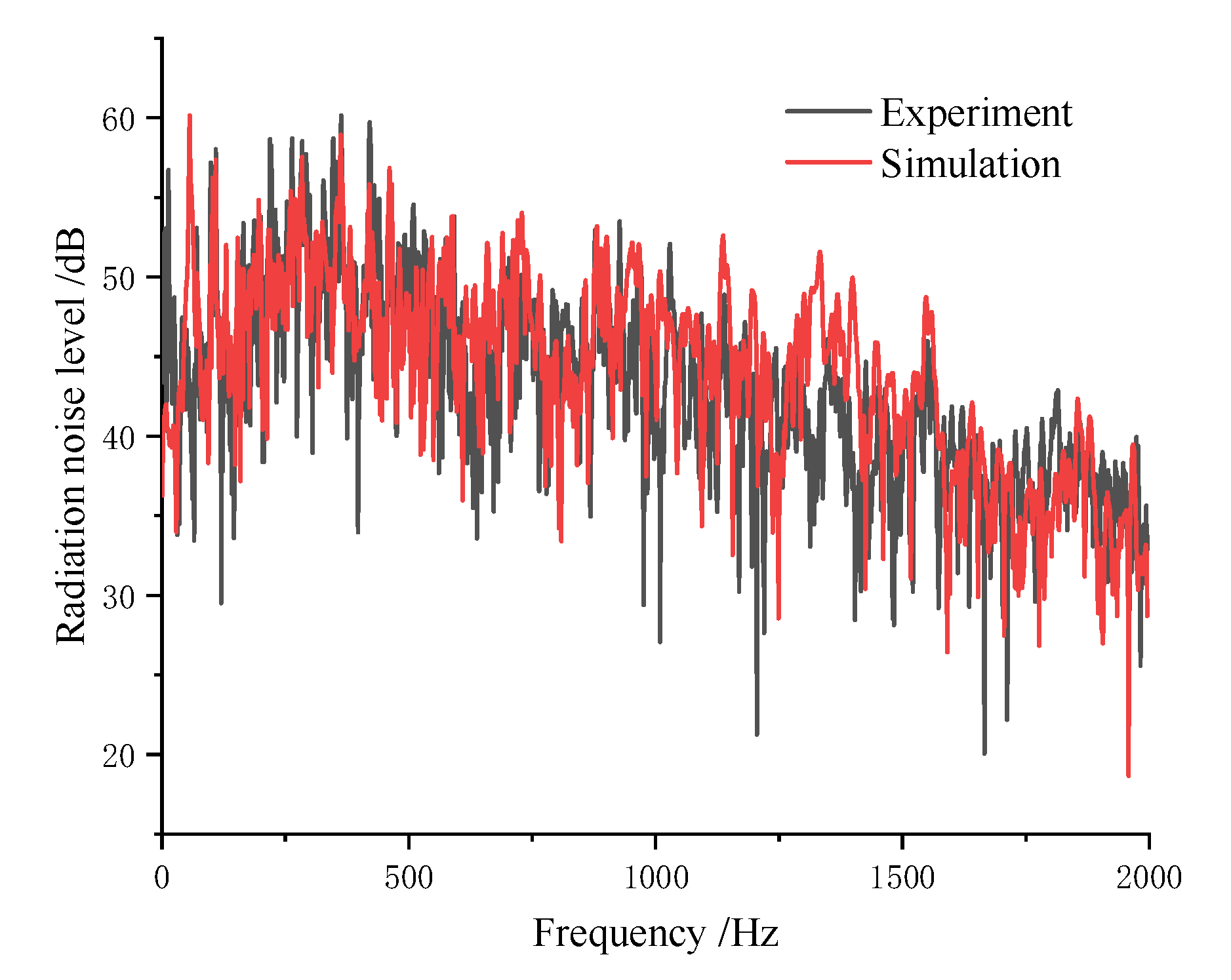
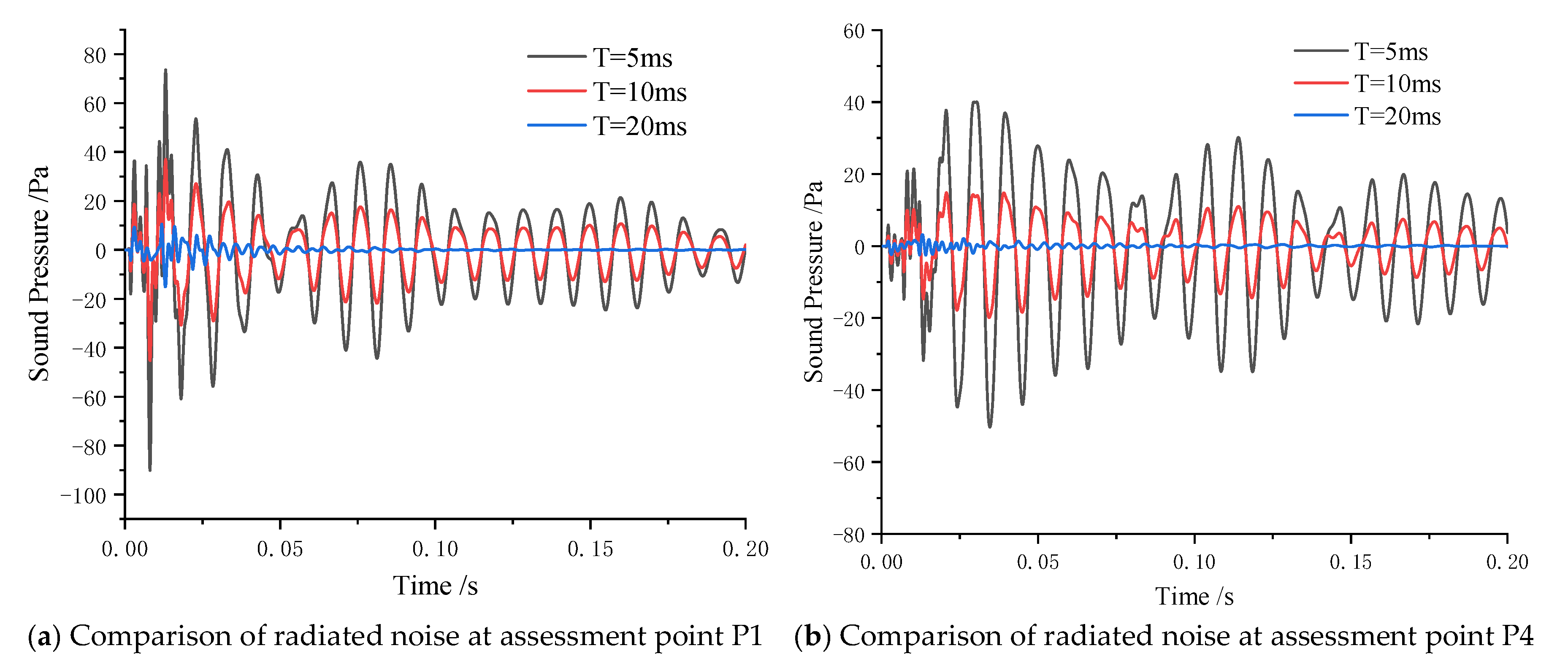
3.5. Comparative Analysis of Transient Vibration Noise
4. Analysis of Transient Vibro-Acoustic Characteristics of Double Stiffened Cylindrical Shell
4.1. Transient Impact Load and Working Condition Setting
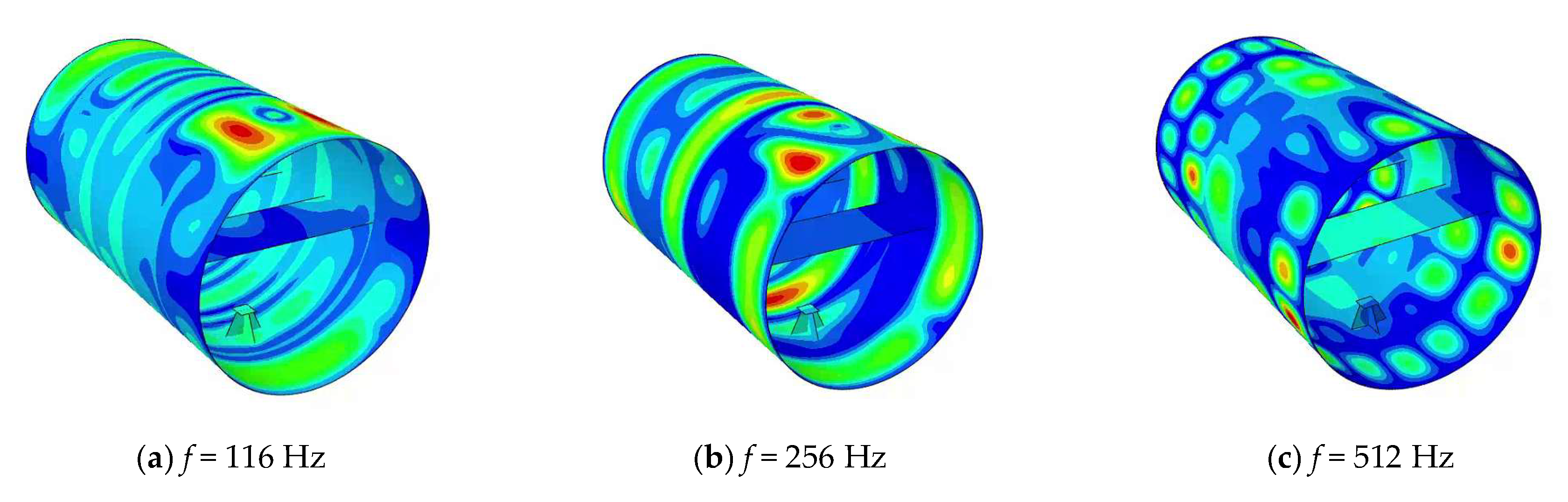
4.2. Modal Analysis of Double Stiffened Cylindrical Shell
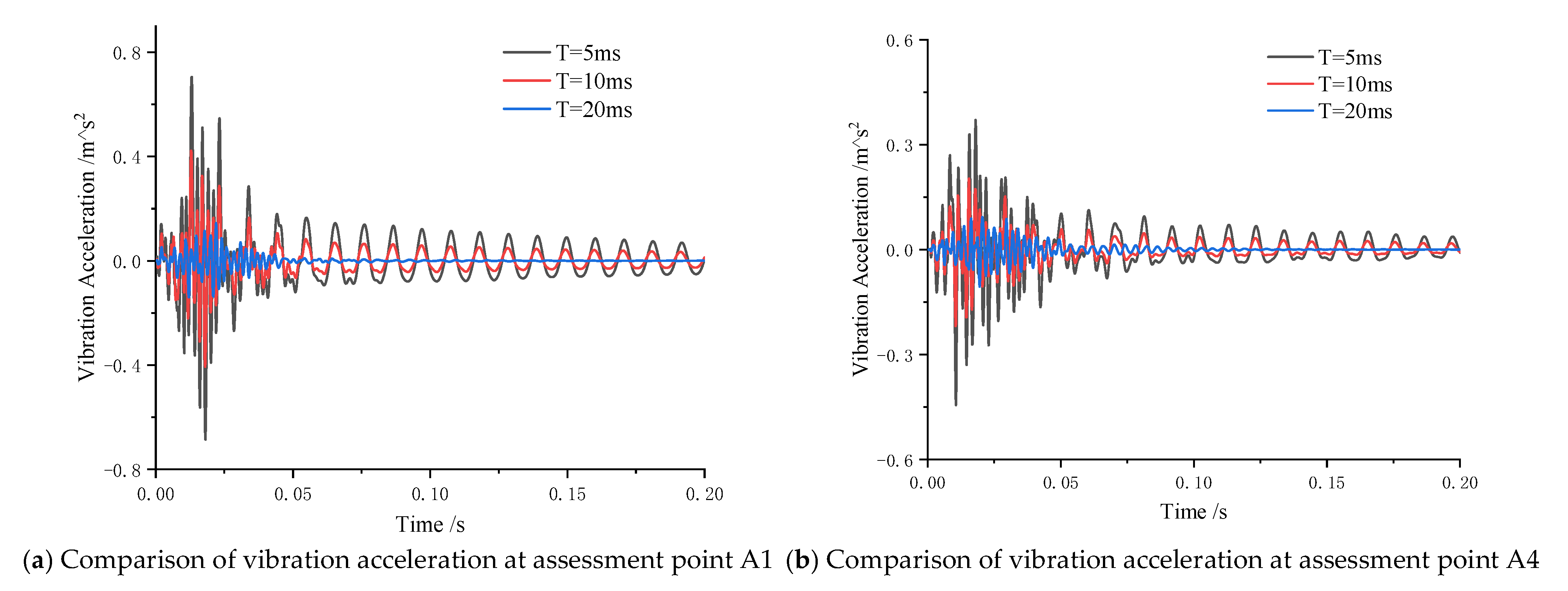
4.3. Transient Vibration Response Analysis of Double Stiffened Cylindrical Shell
- (1)
- Effect of Transient Load Pulse Width on Vibration Response of Stiffened Cylindrical Shell
- (2)
- Influence of Transient Load Location on the Vibration Response of Stiffened Cylindrical Shells
4.4. Transient Radiated Noise Analysis of Double-Layered Stiffened Cylindrical Shells
- (1)
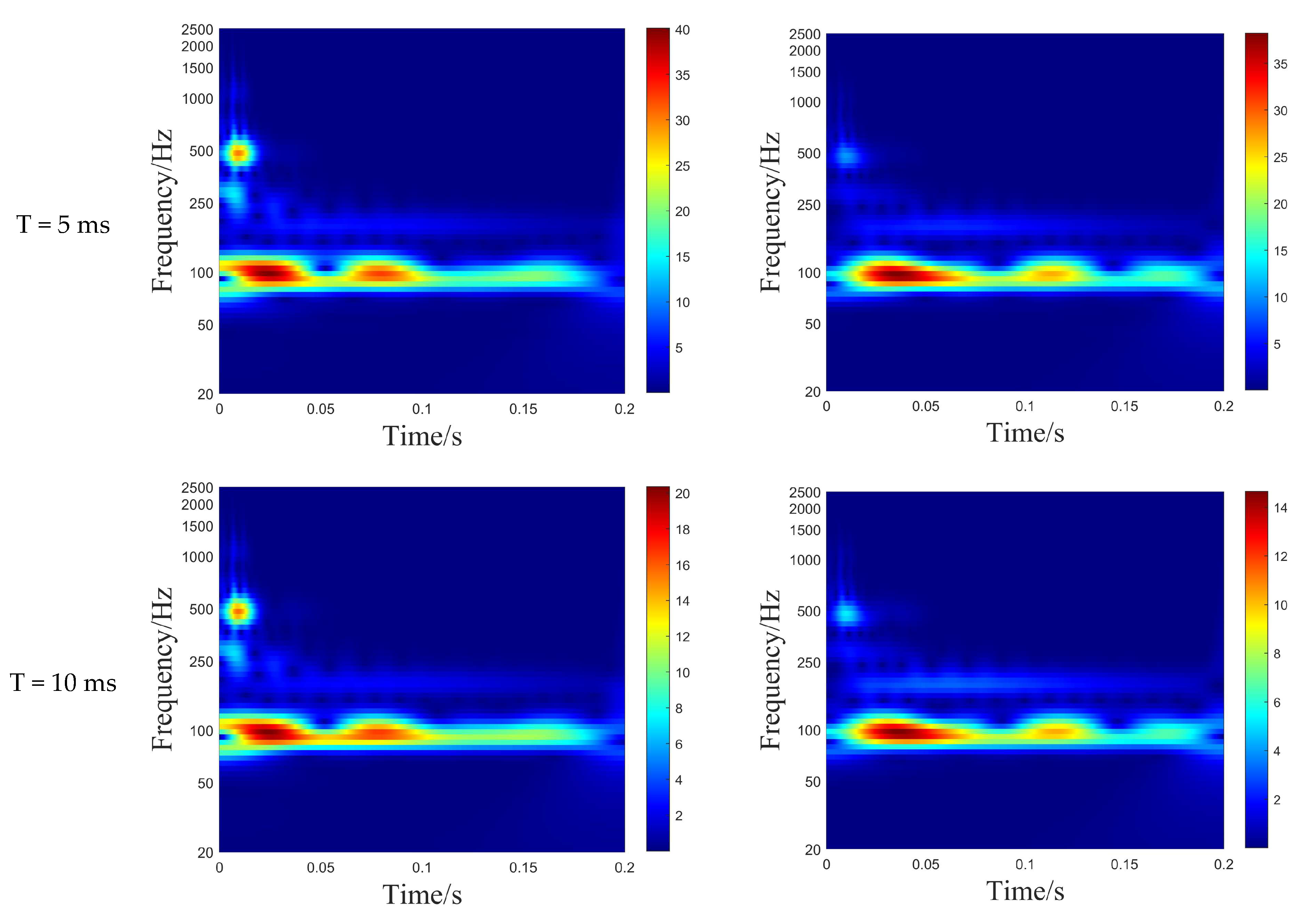
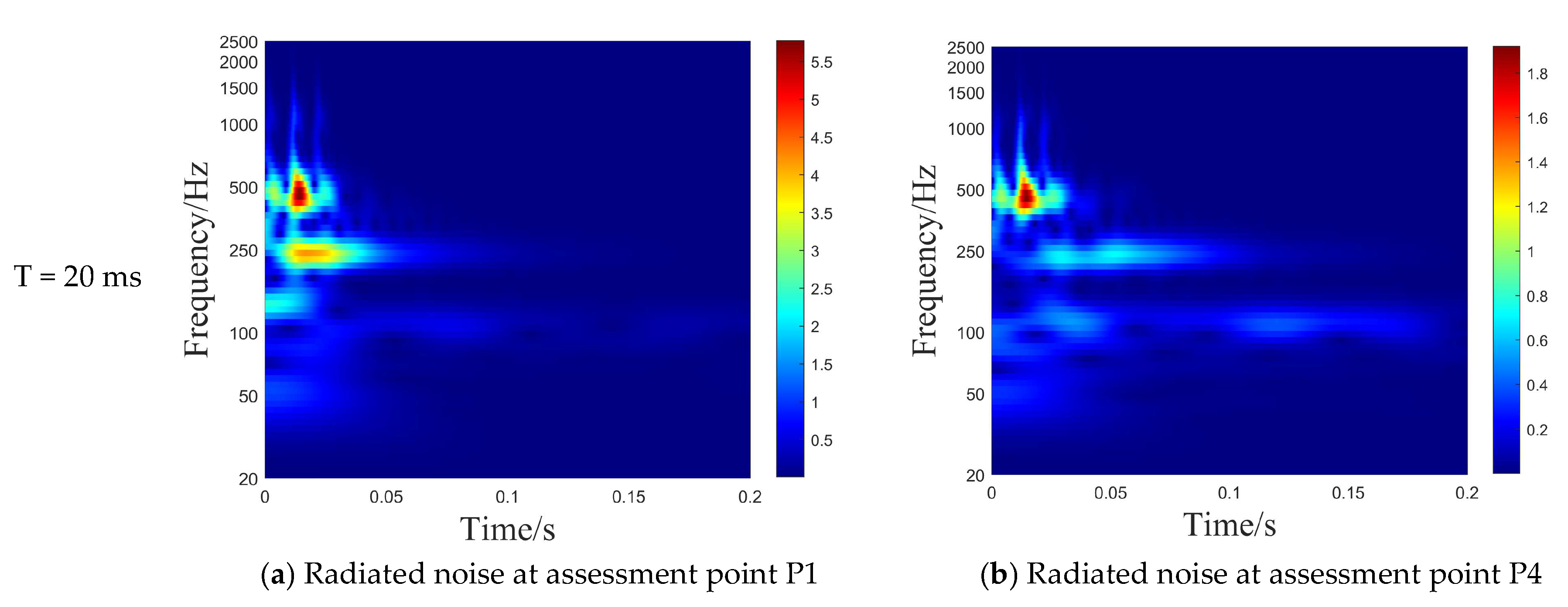
- Influence of Transient Load Pulse Width on Radiated Noise of Stiffened Cylindrical Shell
- (2)
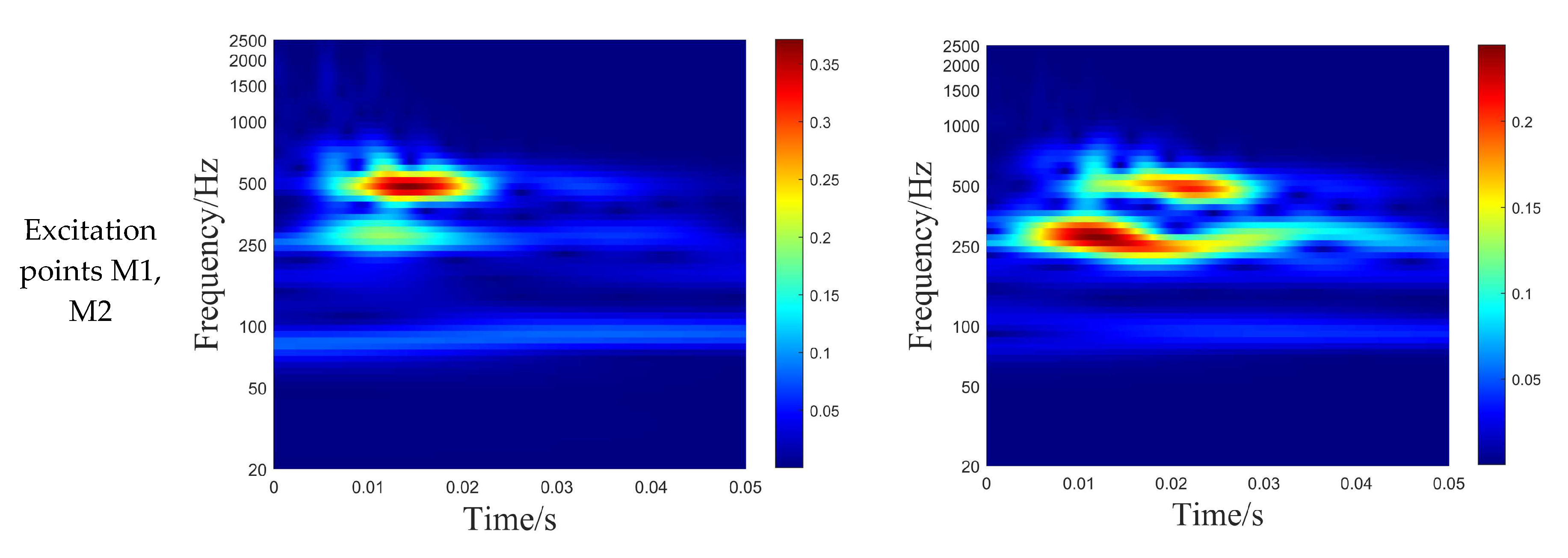
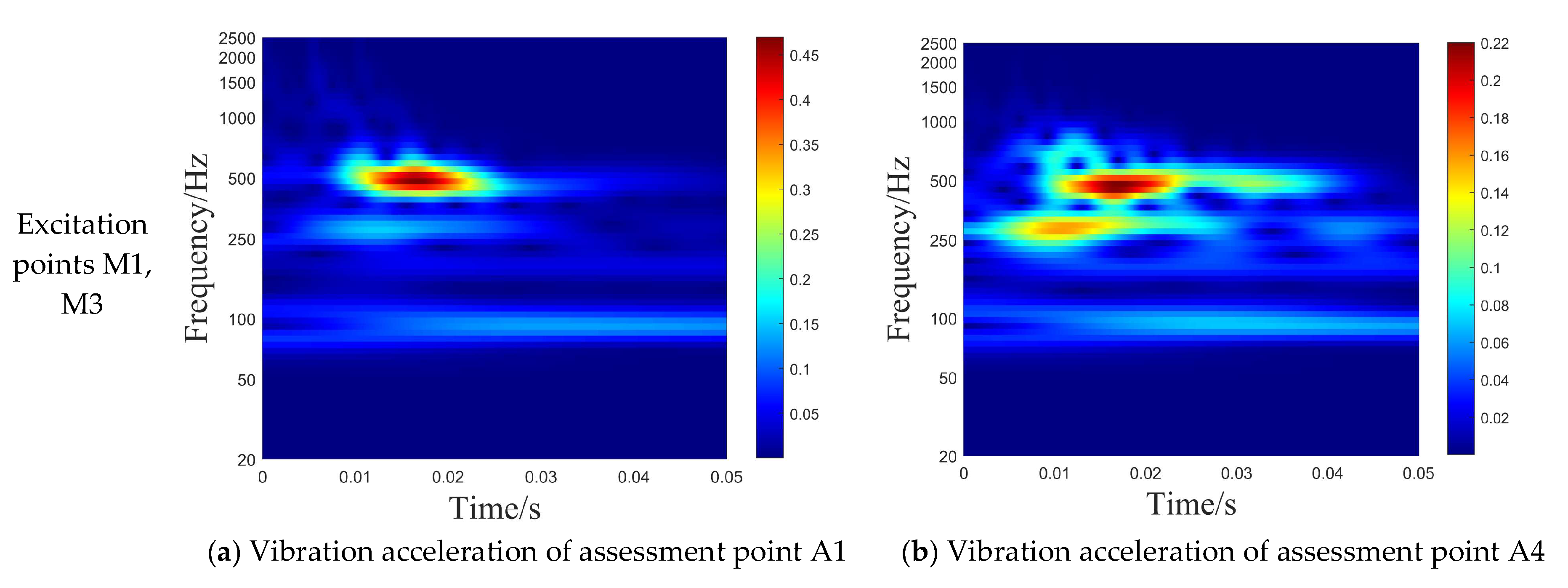
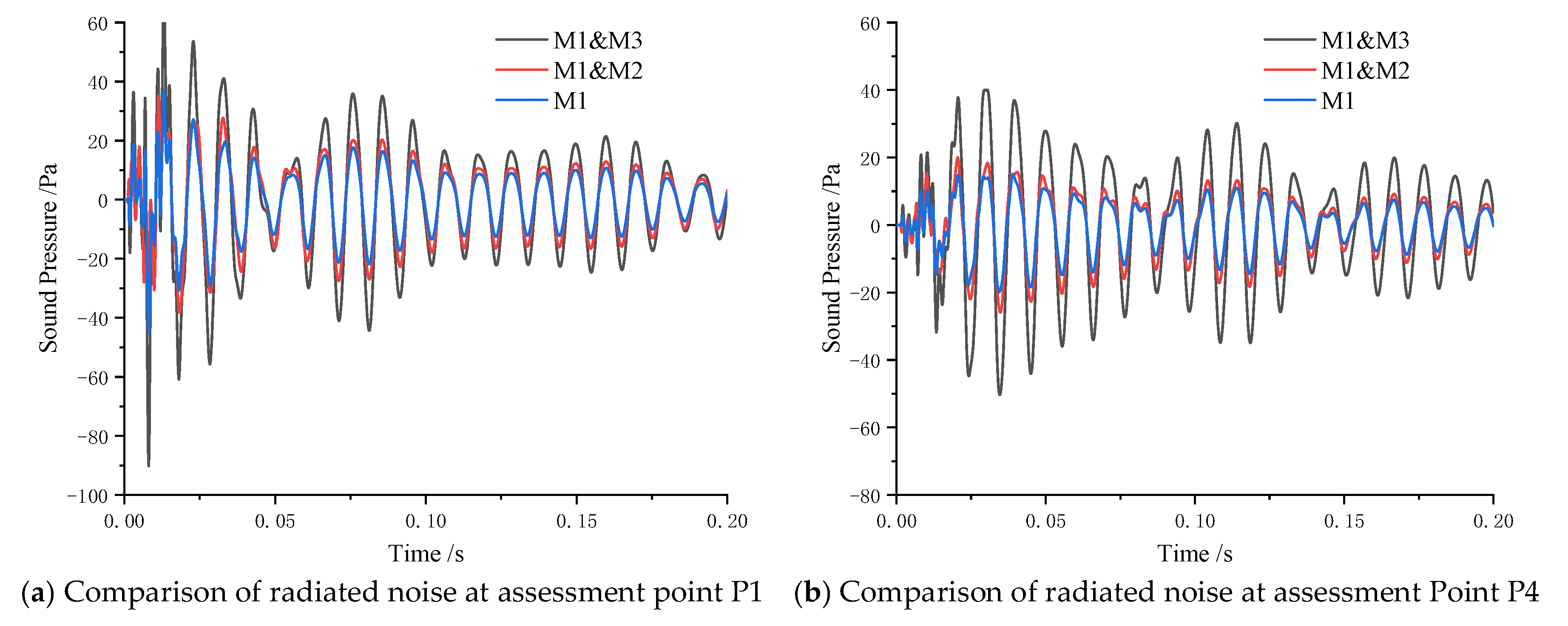
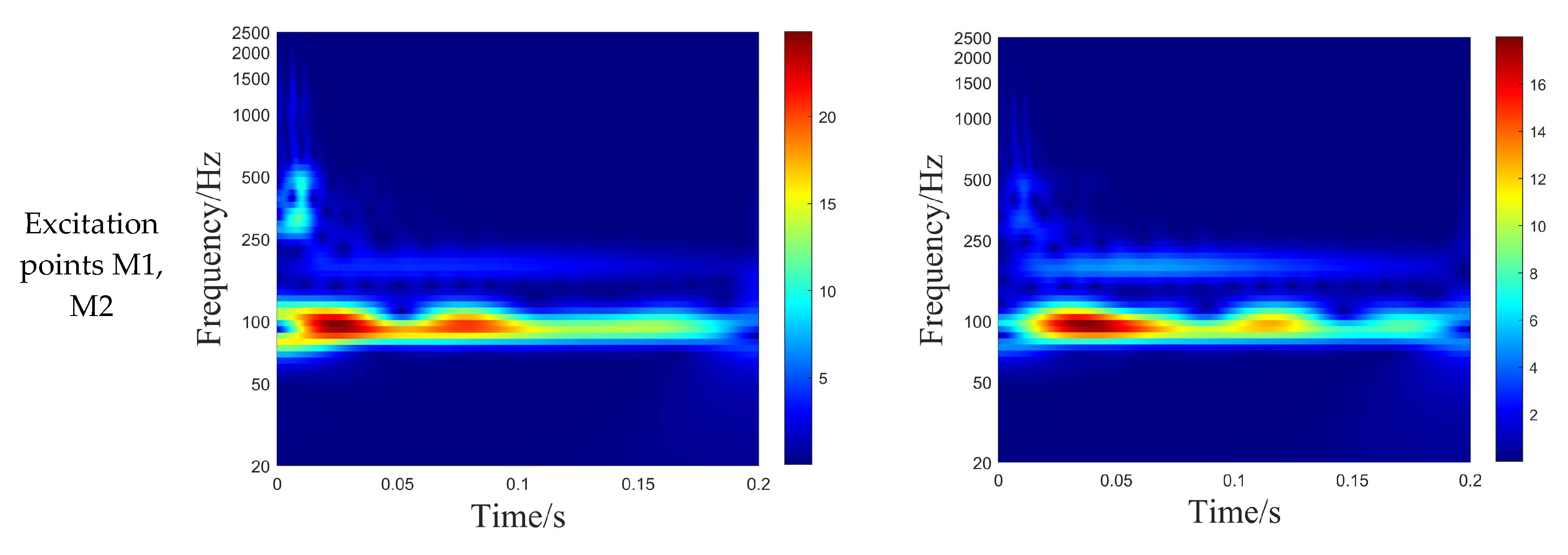
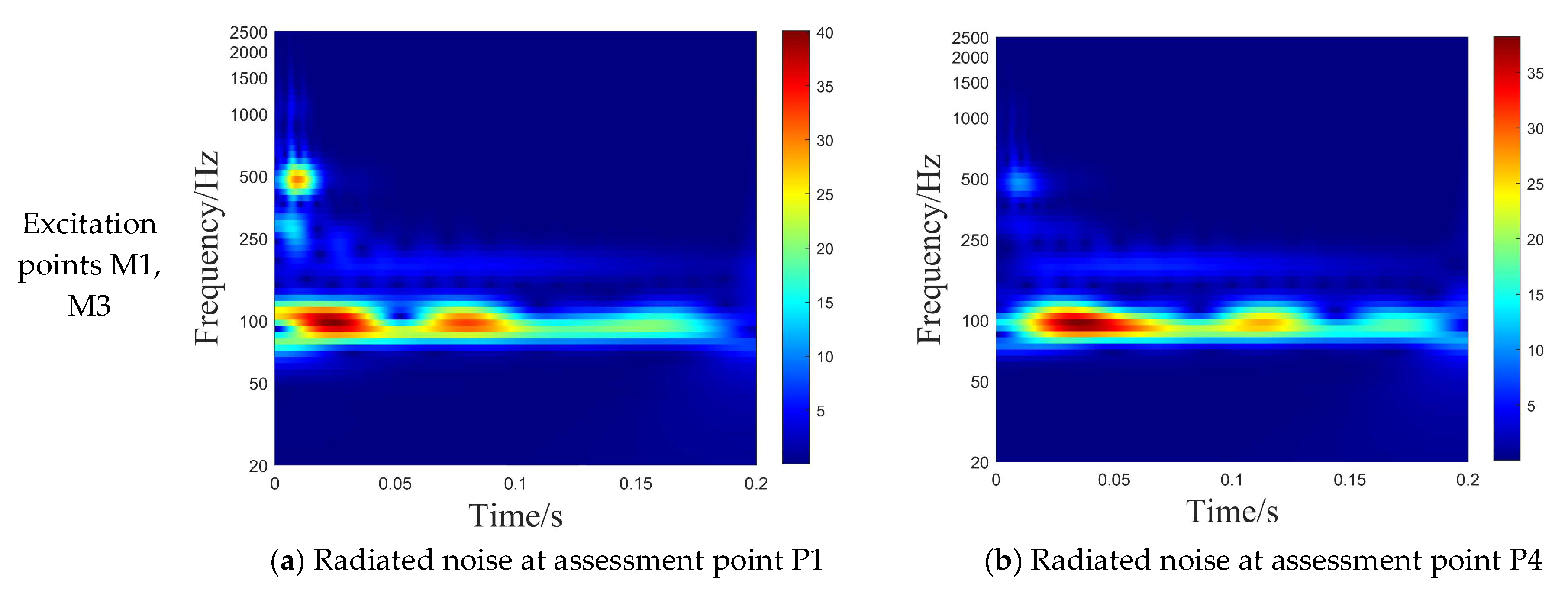
- Effect of Transient Load Position on Radiated Noise from Double-Layered Stiffened Cylindrical Shells
4.5. Transient Vibro-Acoustic Characteristic Analysis of Double-Layered Stiffened Cylindrical Shells
- (1)
- When impact loads share identical peak magnitudes, a shorter pulse width reduces the time available for the vibration system to dissipate energy and attenuate the response, resulting in larger vibration amplitudes.
- (2)
- The energy distribution of structural vibration responses correlates with the modality of the structure. The smaller the pulse width of the excitation load is, the more natural modes of the structure can be excited, and the local modes of the structure will also affect the vibration of the structure at the assessment point.
- (3)
- When excitation positions are bilaterally configured, the structure exhibits the maximum vibration response amplitude. Additionally, the vibration system requires a longer duration to dissipate energy and attenuate the response, while also more readily exciting low-frequency vibration modes.
- (4)
- Compared with the structural vibration response, the attenuation time of radiation noise is longer than that of structural vibration, and the duration of low-frequency radiation noise is longer than that of high-frequency radiation noise.
5. Conclusions
- (1)
- The vibration acceleration and sound pressure levels obtained from experimental measurements and numerical simulations show excellent agreement, thereby validating the accuracy and effectiveness of the time-domain finite element/boundary element (FEM/BEM) method employed in this study.
- (2)
- The vibro-acoustic radiation generated by double-layered stiffened cylindrical shells under transient impact loads exhibits distinct oscillatory characteristics, which are closely related to the structure’s inherent damping and natural modes.
- (3)
- Both the pulse width and loading position of transient impact loads influence structural vibro-acoustic radiation. The smaller the pulse width of the transient impact load, the more effectively it excites the natural modes of the structure, thereby affecting the resulting vibro-acoustic radiation. Similarly, when the spatial distribution of the excitation positions resembles the structure’s low-order mode shapes, it also more readily excites the low-order natural modes of the structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pang, F.; Li, H.; Wang, X.; Miao, X.; Li, S. A semi analytical method for the free vibration of doubly-curved shells of revolution. Comput. Math. Appl. 2018, 75, 3249–3268. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Xiong, Y.; Wu, W. Simulation and investigations on the vibro-acoustic behavior of cylindrical shells in ice-covered water. Results Phys. 2019, 15, 102764. [Google Scholar] [CrossRef]
- Bonhage, M.; Adler, J.T.; Kolhoff, C.; Hentschel, O.; Schlesier, K.-D.; Panning-von Scheidt, L.; Wallaschek, J. Transient amplitude amplification of mistuned structures: An experimental validation. J. Sound Vib. 2018, 436, 236–252. [Google Scholar] [CrossRef]
- Lin, C.; Zou, M.; Jiao, H.; Liu, P. Identification of non-stationary excitation and analysis of transient radiation noise on steering engine. J. Ship Mech. 2016, 20, 758–767. [Google Scholar]
- Kingan, M.J.; Yang, Y.; Mace, B.R. Sound transmission through cylindrical structures using a wave and finite element method. Wave Motion 2019, 87, 58–74. [Google Scholar] [CrossRef]
- Manconi, E.; Mace, B.R.; Garziera, R. Wave propagation in laminated cylinders with internal fluid and residual stress. Appl. Sci. 2023, 13, 5227. [Google Scholar] [CrossRef]
- Ross, A.; Ostiguy, G. Propagation of the initial transient noise from an impacted plate. J. Sound Vib. 2007, 301, 28–42. [Google Scholar] [CrossRef]
- Li, J.; Shi, Z.; Liu, L.; Song, C. An efficient scaled boundary finite element method for transient vibro-acoustic analysis of plates and shells. Comput. Struct. 2020, 231, 106211. [Google Scholar] [CrossRef]
- Aimi, A.; Desiderio, L.; Di Credico, G. Partially pivoted ACA based acceleration of the energetic BEM for time-domain acoustic and elastic waves exterior problems. Comput. Math. Appl. 2022, 119, 351–370. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Z.; Liu, Y. A time-domain boundary element method using a kernel-function library for 3D acoustic problems. Eng. Anal. Bound. Elem. 2024, 161, 103–112. [Google Scholar] [CrossRef]
- Takahashi, T.; Tanigawa, M.; Miyazawa, N. An enhancement of the fast time-domain boundary element method for the three-dimensional wave equation. Comput. Phys. Commun. 2022, 271, 108229. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, A.; Qin, B.; Wang, Q.; Zhong, R. Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation. Eur. Phys. J. Plus 2020, 135, 582. [Google Scholar] [CrossRef]
- Liu, C.-C.; Li, F.-M.; Chen, Z.-B.; Yue, H.-H. Transient wave propagation in the ring stiffened laminated composite cylindrical shells using the method of reverberation ray matrix. J. Acoust. Soc. Am. 2013, 133, 770–780. [Google Scholar] [CrossRef] [PubMed]
- Dalton, E.; Burton Chambers, N.S.I.; Chambers, N.S.I. Analysis and validation testing of impulsive load response in complex, multi-compartmented structures. In Proceedings of the 36th Structures, Structural Dynamics and Materials Conference, New Orleans, LA, USA, 10–13 April 1995; p. 1243. [Google Scholar]
- Zou, M.-S.; Peng, S.-L.; Yang, Y.-N.; Liu, Y. Time-domain calculation method for sound radiation of underwater vehicles strictly coupled with nonlinear floating raft isolation system. Thin-Walled Struct. 2025, 216, 113662. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, D.; Li, Q. Underwater radiated noise numerical analysis of polar transport vessels under ship-ice-water-air coupling continuous icebreaking based on the S-ALE algorithm. Ocean Eng. 2024, 309, 118511. [Google Scholar] [CrossRef]
- Menton, R.T.; Magrab, E.B. Farfield radiation of internally generated transient acoustic pulses transmitted through a spherical shell. J. Acoust. Soc. Am. 1974, 55, 237–246. [Google Scholar] [CrossRef]
- Chappell, D.; Harris, P.; Henwood, D.; Chakrabarti, R. Transient acoustic radiation from a thin spherical elastic shell. In Integral Methods in Science and Engineering: Techniques and Applications; Birkhäuser: Boston, MA, USA, 2008; pp. 47–54. [Google Scholar]
- Christoforou, A.P.; Swanson, S. Analysis of simply-supported orthotropic cylindrical shells subject to lateral impact loads. J. Appl. Mech. 1990, 57, 376–382. [Google Scholar] [CrossRef]
- Hoai, L.; Tu, P.H.; Tran, V.K.; Hue, N.T. An isogeometric approach for vibration characteristics analysis of functionally graded triply periodic minimal sandwich curved-doubly shell integrated with magneto-electro surface layers subjected to low-velocity impact load. Def. Technol. 2025, 50, 101–125. [Google Scholar] [CrossRef]
- Pandey, A.M.; Gopal, K.N. Transient vibration and sound radiation analysis of simply supported functionally graded sandwich plates. Compos. Struct. 2022, 290, 115520. [Google Scholar] [CrossRef]
- Liu, J.; Hao, C.; Ye, W.; Yang, F.; Lin, G. Free vibration and transient dynamic response of functionally graded sandwich plates with power-law nonhomogeneity by the scaled boundary finite element method. Comput. Methods Appl. Mech. Eng. 2021, 376, 113665. [Google Scholar] [CrossRef]
- Chappell, D.; Harris, P.; Henwood, D.; Chakrabarti, R. A stable boundary element method for modeling transient acoustic radiation. J. Acoust. Soc. Am. 2006, 120, 74–80. [Google Scholar] [CrossRef]
- Geng, L.; Chen, X.-G.; He, S.-P.; He, C.-D. Reconstruction of transient acoustic field using sparse real-time near-field acoustic holography. J. Sound Vib. 2024, 568, 117973. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.; Wu, S.; Li, Y. Transient energy response analysis of vibro-acoustic systems with fuzzy uncertainty. J. Aircr. 2021, 58, 210–215. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Li, L.; Hao, H.; Chen, W.; Shao, Y. Machine learning prediction of structural dynamic responses using graph neural networks. Comput. Struct. 2023, 289, 107188. [Google Scholar] [CrossRef]
- Hu, Y. Underwater transient signal detection under two noise reduction methods. In Proceedings of the 2024 IEEE 4th International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 24–26 May 2024; pp. 929–932. [Google Scholar]
- Yu, T.-k.; Liu, W.-s.; Shi, S.-g.; Long, J. Measurement and assessment method for ship radiating transient noise. In Proceedings of the 2017 2nd International Conference on Automation, Mechanical Control and Computational Engineering (AMCCE 2017), Beijing, China, 25–26 March 2017; pp. 215–225. [Google Scholar]
- Yu, T.; Xiong, C.; Wang, X.; Dai, X.; Xuefeng, T. Rapid acquisition method of sea vessel radiating transient noise effective time based on the power-law. In Proceedings of the 2nd International Conference on Mechatronics Engineering and Information Technology (ICMEIT 2017), Dalian, China, 13–14 May 2017; pp. 507–514. [Google Scholar]
- Leissing, T.; Audoly, C.; Lachambre, H.; Stempfel, G. Advanced signal processing methods for the analysis of transient radiated noise from submarines. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Melbourne, Australia, 16–19 November 2014; pp. 852–861. [Google Scholar]
- Gao, C.; Zhang, H.; Li, H.; Pang, F.; Wang, H. Numerical and experimental investigation of vibro-acoustic characteristics of a submerged stiffened cylindrical shell excited by a mechanical force. Ocean Eng. 2022, 249, 110913. [Google Scholar] [CrossRef]
- Tonazzi, D.; Meziane, A.; Culla, A.; Biateau, C.; Pepe, G.; Massi, F. Material Damping Estimation within Low-, Medium-and High-Frequency Ranges. Int. J. Appl. Mech. 2024, 16, 2450056. [Google Scholar] [CrossRef]

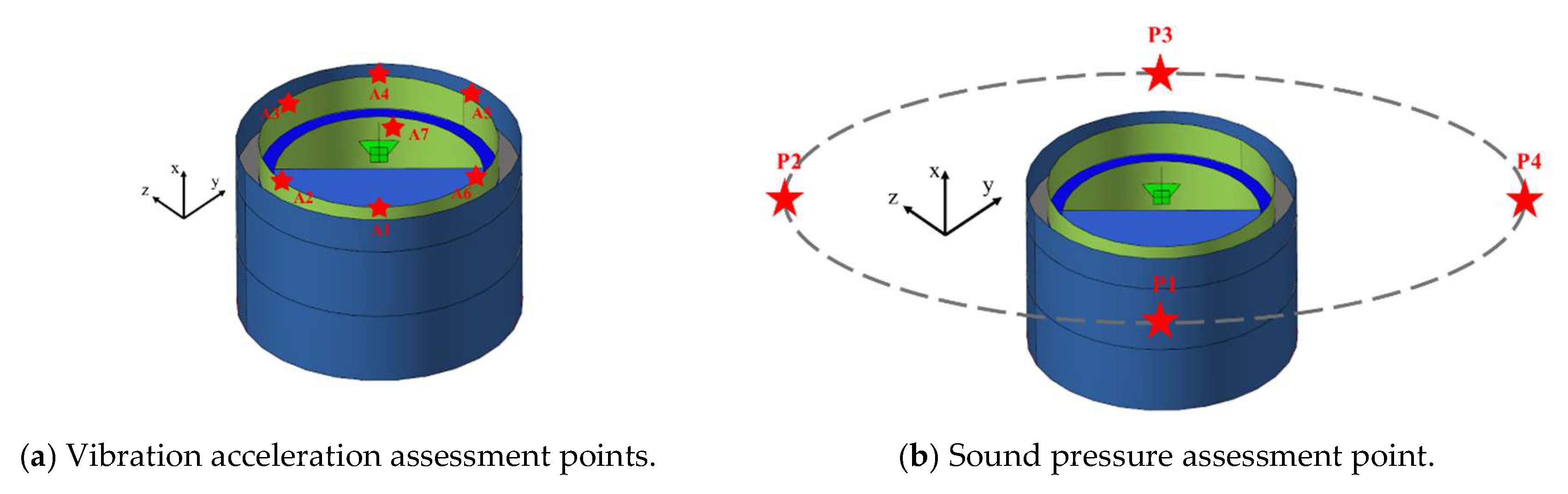

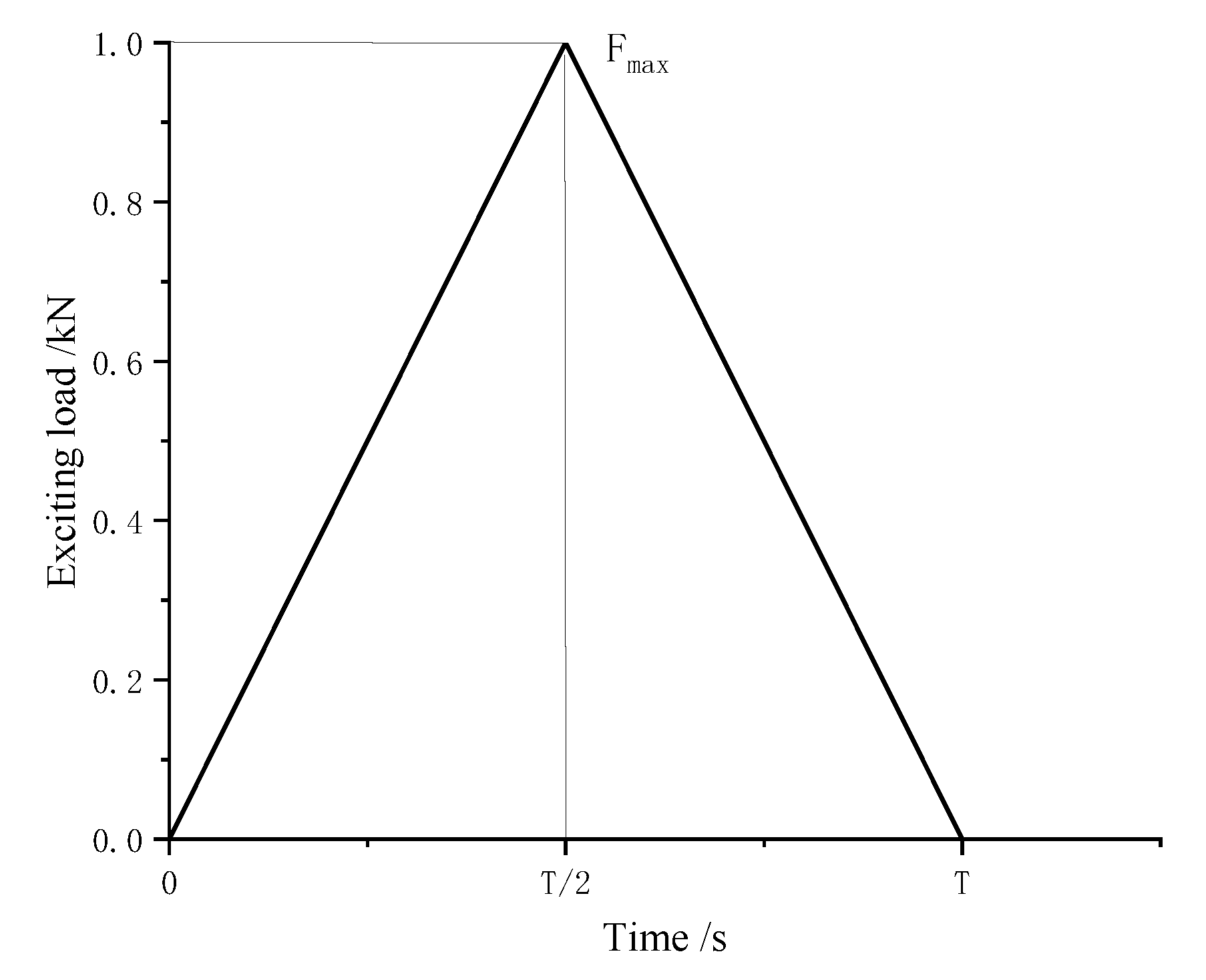

| Parameter | Numerical Value (m) |
|---|---|
| Shell radius | 0.75 |
| Inner shell radius | 0.63 |
| Model length | 2.0 |
| Shell thickness | 0.01 |
| Inner shell thickness | 0.01 |
| Ring rib section a × b | 0.01 × 0.008 |
| Ring rib spacing | 0.4 |
| Condition Number | Load Amplitude (N) | Load Pulse Length(ms) | Loading Position | Inner Shell Thickness (m) | Vibration Acceleration Measuring Point Position | Sound Field Assessment Point Position |
|---|---|---|---|---|---|---|
| mode 1 | 1000 | 5 | M1 | 0.01 | A1, A4 | P1, P4 |
| mode 2 | 1000 | 10 | M1 | 0.01 | A1, A4 | P1, P4 |
| mode 3 | 1000 | 20 | M1 | 0.01 | A1, A4 | P1, P4 |
| mode 4 | 1000 | 10 | M1, M2 | 0.01 | A1, A4 | P1, P4 |
| mode 5 | 1000 | 10 | M1, M3 | 0.01 | A1, A4 | P1, P4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Miao, W.; Zhao, Z.; Gao, C.; Pang, F. Transient Vibro-Acoustic Characteristics of Double-Layered Stiffened Cylindrical Shells. Acoustics 2025, 7, 50. https://doi.org/10.3390/acoustics7030050
Luo Q, Miao W, Zhao Z, Gao C, Pang F. Transient Vibro-Acoustic Characteristics of Double-Layered Stiffened Cylindrical Shells. Acoustics. 2025; 7(3):50. https://doi.org/10.3390/acoustics7030050
Chicago/Turabian StyleLuo, Qirui, Wang Miao, Zhe Zhao, Cong Gao, and Fuzhen Pang. 2025. "Transient Vibro-Acoustic Characteristics of Double-Layered Stiffened Cylindrical Shells" Acoustics 7, no. 3: 50. https://doi.org/10.3390/acoustics7030050
APA StyleLuo, Q., Miao, W., Zhao, Z., Gao, C., & Pang, F. (2025). Transient Vibro-Acoustic Characteristics of Double-Layered Stiffened Cylindrical Shells. Acoustics, 7(3), 50. https://doi.org/10.3390/acoustics7030050








