Numerical Investigation of Influence of Entropy Wave on the Acoustic and Wall Heat Transfer Characteristics of a High-Pressure Turbine Guide Vane
Abstract
1. Introduction
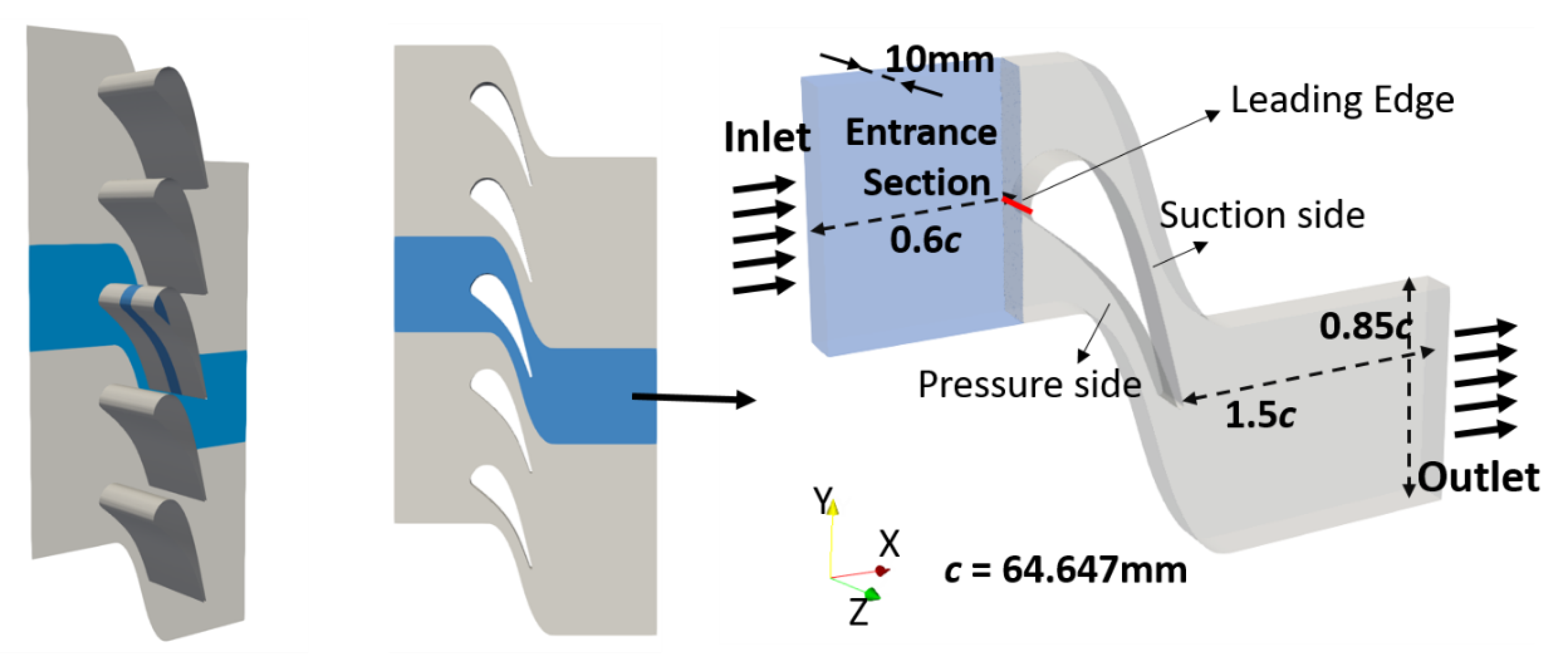
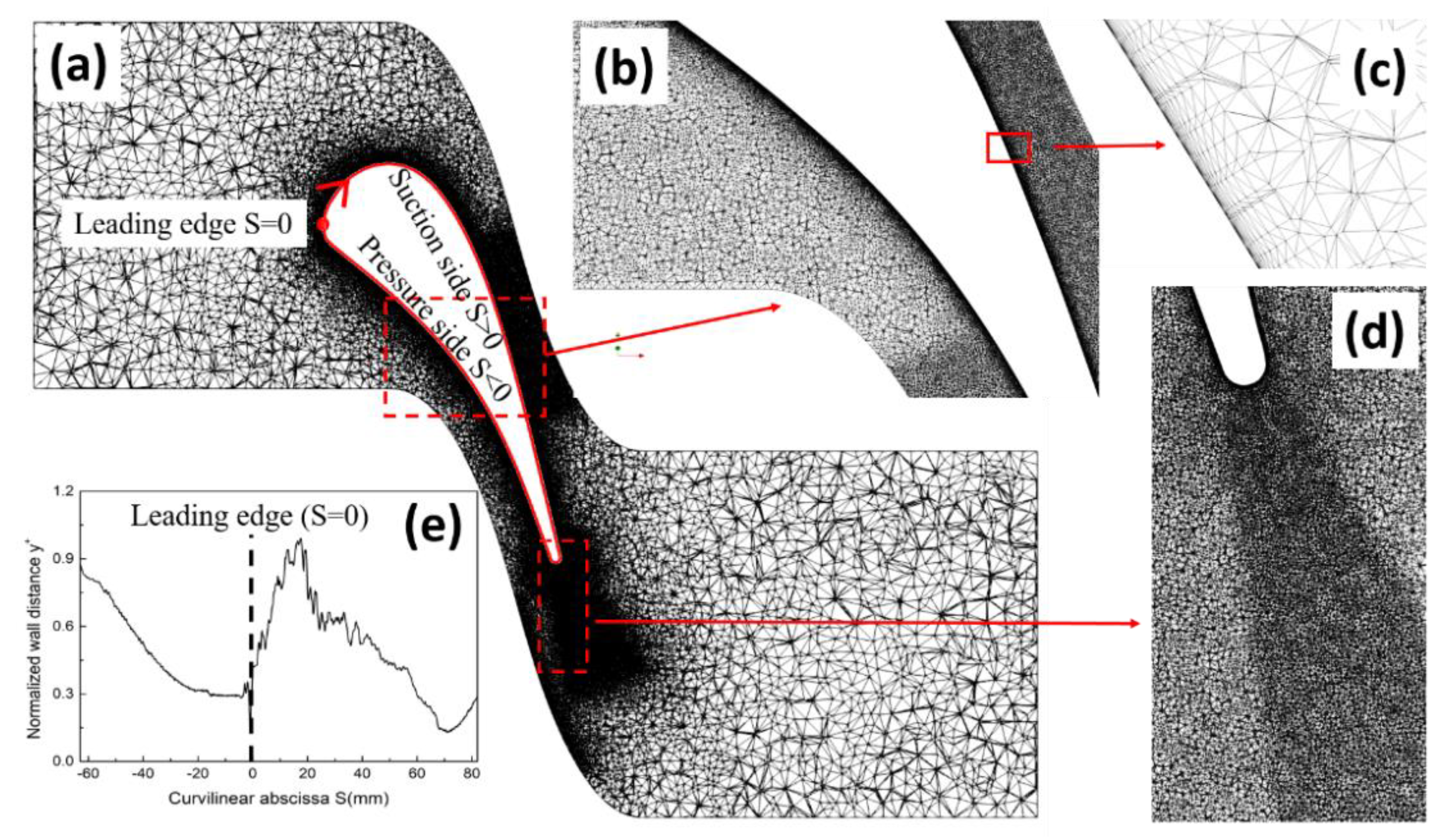
2. Numerical Setup
3. Results and Discussions
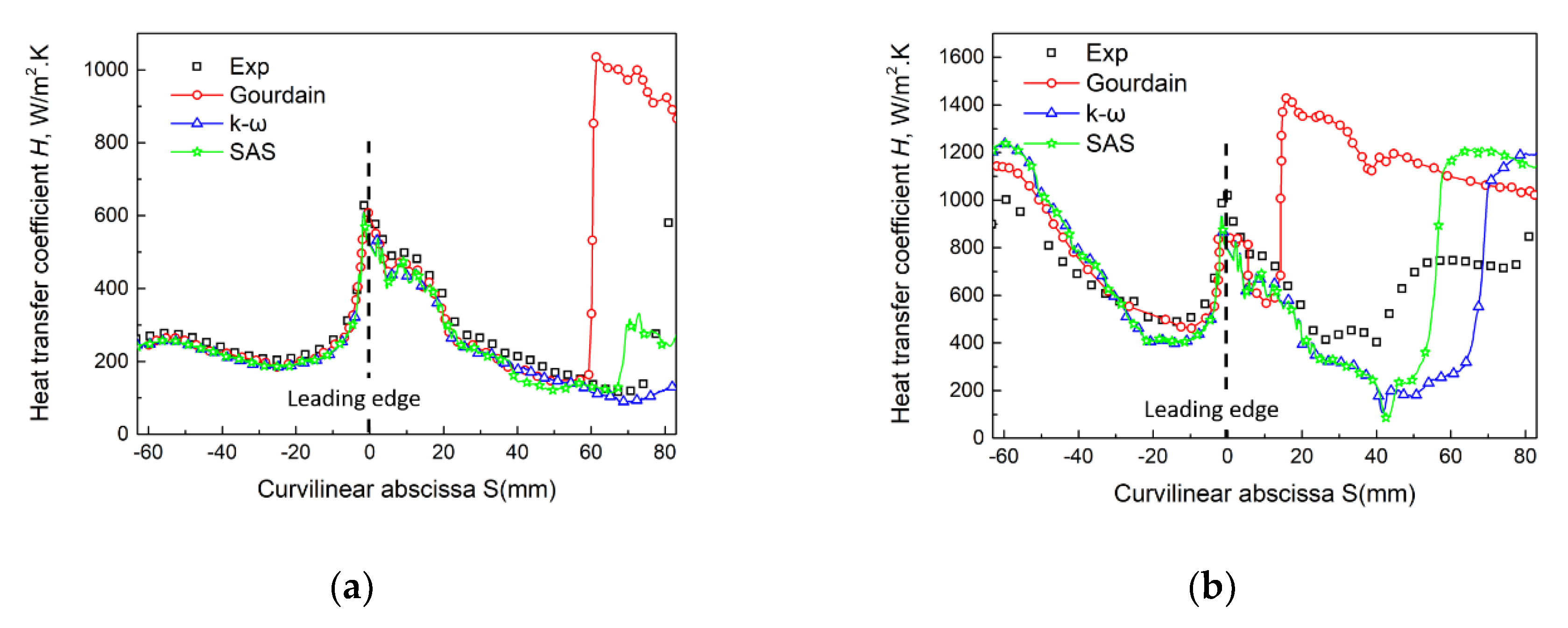
3.1. Case without Entropy Wave
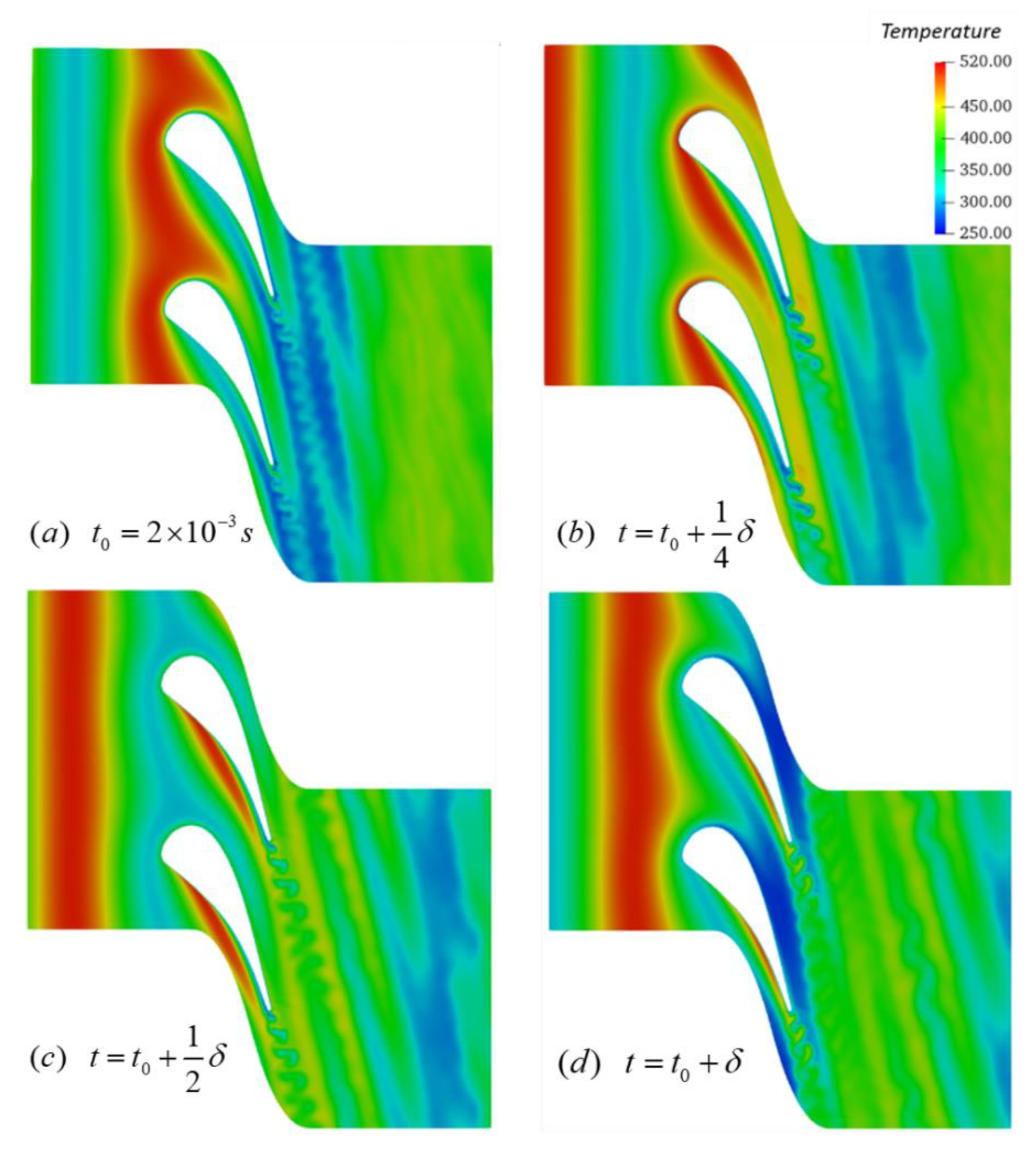
3.2. Case with Entropy Wave
3.2.1. Heat Transfer on the Vane Surface
3.2.2. Downstream Acoustic Field
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nesbitt, E. Towards a quieter low pressure turbine: Design characteristics and prediction needs. Int. J. Aeroacoustics 2010, 10, 1–15. [Google Scholar] [CrossRef]
- Candel, S. Analytical Studies of Some Acoustic Problems of Jet Engines. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1972. [Google Scholar]
- Marble, F.; Candel, S. Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 1977, 55, 225–243. [Google Scholar] [CrossRef]
- Cumpsty, N.; Marble, F. The interaction of entropy fluctuations with turbine blade rows; a mechanism of turbojet engine noise. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 357, 323–344. [Google Scholar]
- Yoon, M. The entropy wave generation in a heated one-dimensional duct. J. Fluid Mech. 2019, 883, A44. [Google Scholar] [CrossRef]
- Morgans, A.S.; Duran, I. Entropy noise: A review of theory, progress and challenges. Int. J. Spray Combust. Dyn. 2016, 8, 285–298. [Google Scholar] [CrossRef]
- Moreau, S.; Duran, I. (Eds.) Analytical and Numerical Study of the Entropy Wave Generator Experiment on Indirect Combustion Noise. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2011. [Google Scholar]
- Bake, F.; Kings, N.; Fischer, A. Experimental investigation of the entropy noise mechanism in aero-engines. Int. J. Aeroacoustics 2009, 8, 125–141. [Google Scholar] [CrossRef]
- Leyko, M.; Nicoud, F.; Moreau, S. Numerical and analytical investigation of the indirect combustion noise in a nozzl. Comptes Rendus Mécanique 2009, 337, 415–425. [Google Scholar] [CrossRef]
- Duran, I.; Moreau, S. Study of the Attenuation of Waves Propagating through Fixed and Rotating Turbine Blades. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012. [Google Scholar]
- Wang, G.; Sanjose, M.; Moreau, S.; Papadogiannis, D.; Duchaine, F.; Gicquel, L. Noise mechanisms in a transonic high-pressure turbine stage. Int. J. Aeroacoustics 2016, 15, 144–161. [Google Scholar] [CrossRef]
- Papadogiannis, D.; Wang, G.; Moreau, S.; Duchaine, F.; Gicquel, L.; Nicoud, F. Assessment of the indirect combustion noise generated in a transonic high-pressure turbine stage. J. Eng. Gas Turbines Power 2016, 138, 041503. [Google Scholar] [CrossRef]
- Ceci, A.; Gojon, R.; Mihaescu, M. Large Eddy Simulations for Indirect Combustion Noise Assessment in a Nozzle Guide Vane Passage. Flow, Turbul. Combust. 2019, 102, 299–311. [Google Scholar] [CrossRef]
- Becerril, C.; Moreau, S.; Gicquel, L. (Eds.) Study of Combustion Noise Generation in a Realistic Turbine Stage Configuration. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Wheeler, A.P.; Sandberg, R.D.; Sandham, N.D.; Pichler, R.; Michelassi, V.; Laskowski, G. Direct numerical simulations of a high-pressure turbine vane. J. Turbomach. 2016, 138, 071003. [Google Scholar] [CrossRef]
- Morata, E.C.; Gourdain, N.; Duchaine, F.; Gicquel, L. Effects of free-stream turbulence on high pressure turbine blade heat transfer predicted by structured and unstructured LES. Int. J. Heat Mass Transf. 2012, 55, 5754–5768. [Google Scholar] [CrossRef]
- Gourdain, N.; Gicquel, L.Y.; Collado, E. Comparison of RANS and LES for prediction of wall heat transfer in a highly loaded turbine guide vane. J. Propuls. Power 2012, 28, 423–433. [Google Scholar] [CrossRef]
- Phan, H.M.; Duan, P.H.; Dinh, C.T. Numerical aero-thermal study of high-pressure turbine nozzle guide vane: Effects of inflow conditions. Phys. Fluids 2020, 32, 034111. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Bender, R. A Scale-Adaptive Simulation Model for Turbulent Flow Predictions. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Antares Development Team, Antares Documentation Release 1.14.0. Available online: https://cerfacs.fr/antares/ (accessed on 3 June 2020).
- Consigny, H.; Richards, B. Short duration measurements of heat-transfer rate to a gas turbine rotor blade. J. Eng. Power 1982, 104, 542–550. [Google Scholar] [CrossRef]
- Arts, T.; Lambertderouvroit, M.; Rutherford, A. Aero-Thermal Investigation of a Highly Loaded Transonic Linear Turbine Guide Vane Cascade; Technical Note 174. Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 1990. [Google Scholar]
- Pouangu, A.F.; Sanjos, M.; Moreau, S. Subsonic Jet Noise Simulations Using Both Structured and Unstructured Grids. AIAA J. 2015, 53, 55–69. [Google Scholar] [CrossRef]
- Hiller, S.; Seitz, P. Interaction Between a Fluidic Actuator and Main Flow Using SAS Turbulence Modelling. In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Winkler, C.; Dorgan, A.; Mani, M. Scale Adaptive Simulations of Turbulent Flows on Unstructured Grids. In Proceedings of the 20th AIAA Computational Fluid Dynamics Conference, Honolulu, GA, USA, 27–30 June 2011. [Google Scholar]
- Wang, Y.; Liu, K.; Song, W.-P. Scale-Adaptive Simulations of Unsteady Flow around NACA0021 Airfoil at 60° angle of attack. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Menter, F.R. A Correlation-Based Transition Model Using Local Variables—Part I: Model Formulation. ASME J. Turbomach. 2006, 128, 413–42230. [Google Scholar] [CrossRef]
- Ansys CFX. CFX User Manual. Ansys Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Leyko, M.; Duran, I.; Moreau, S. Simulation and modelling of the waves transmission and generation in a stator blade row in a combustion-noise framework. J. Sound Vib. 2014, 333, 6090–6106. [Google Scholar] [CrossRef]



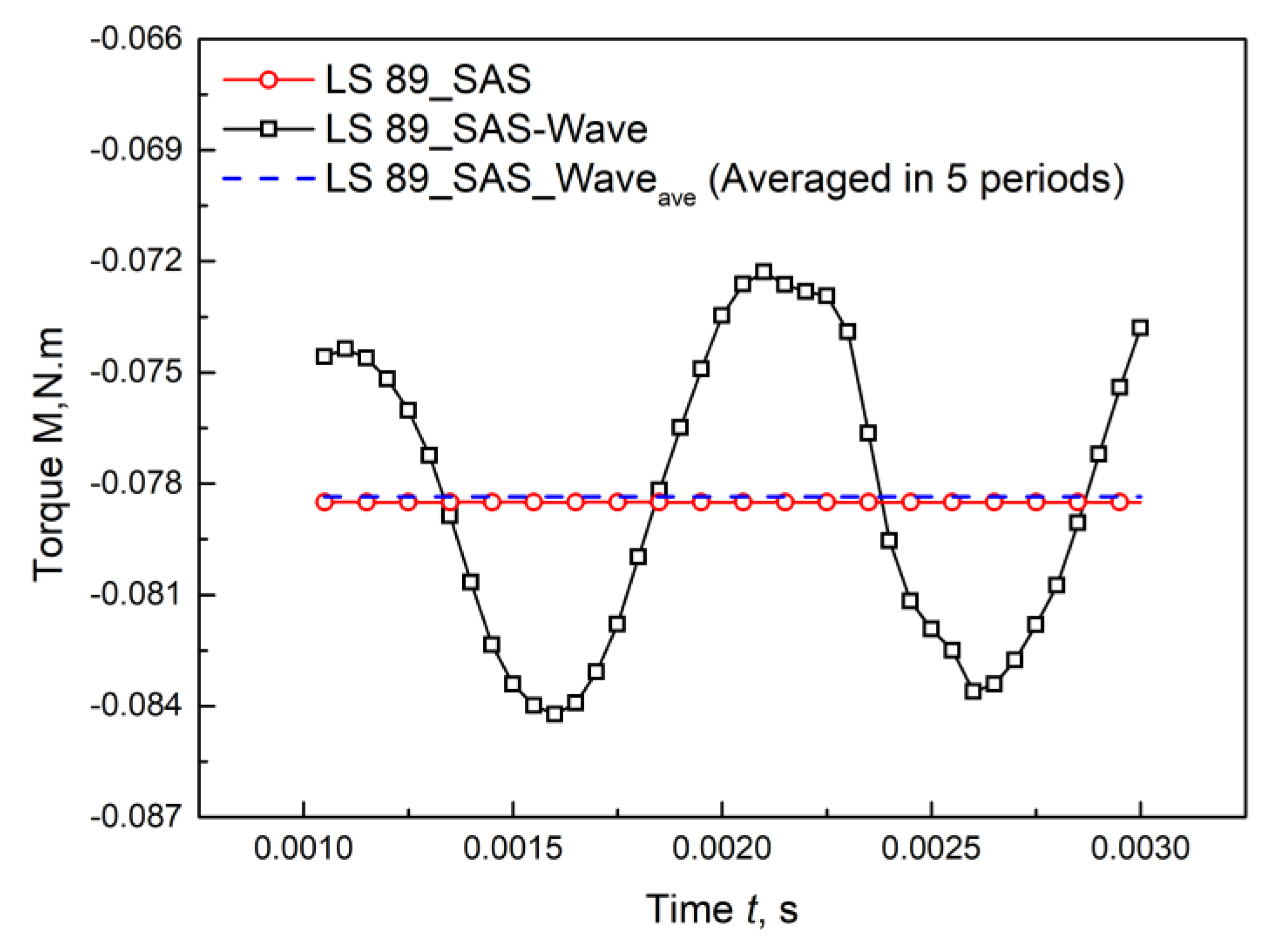

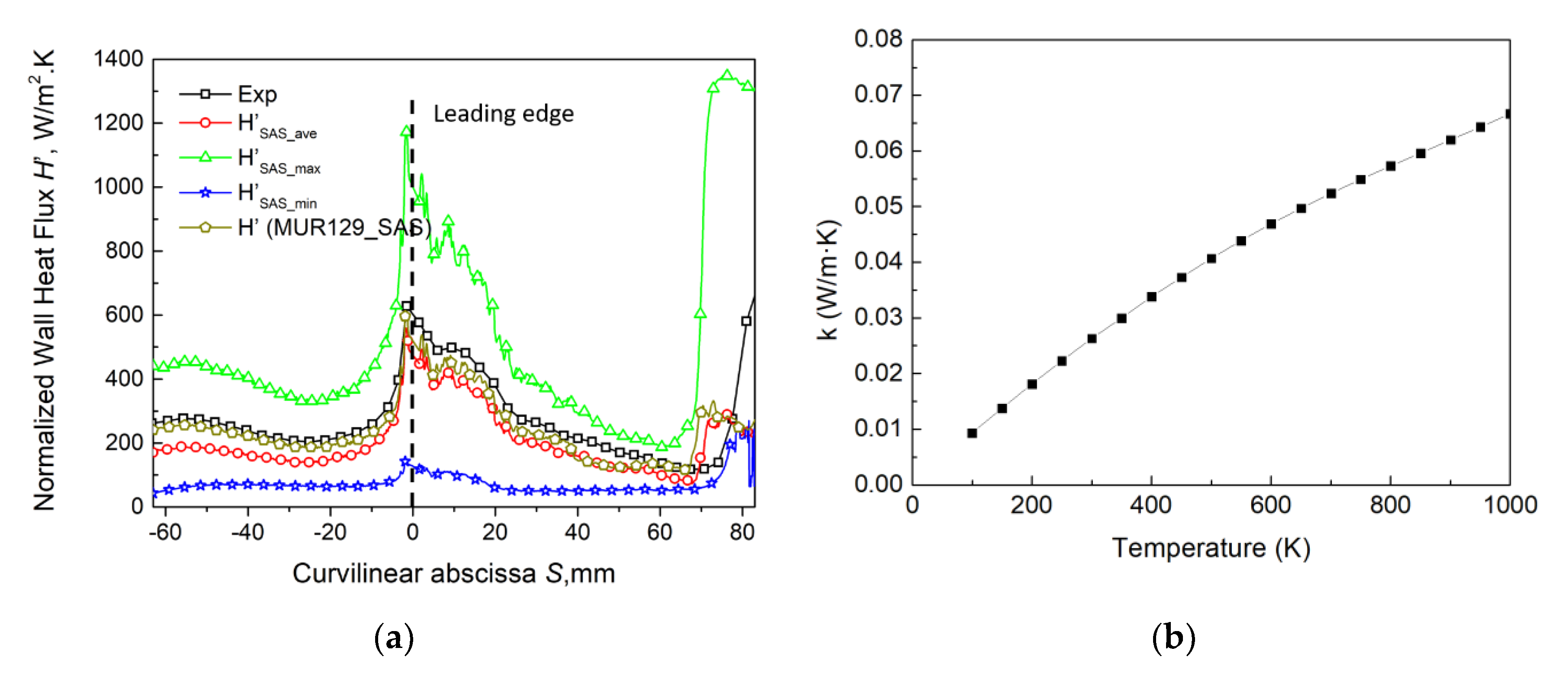
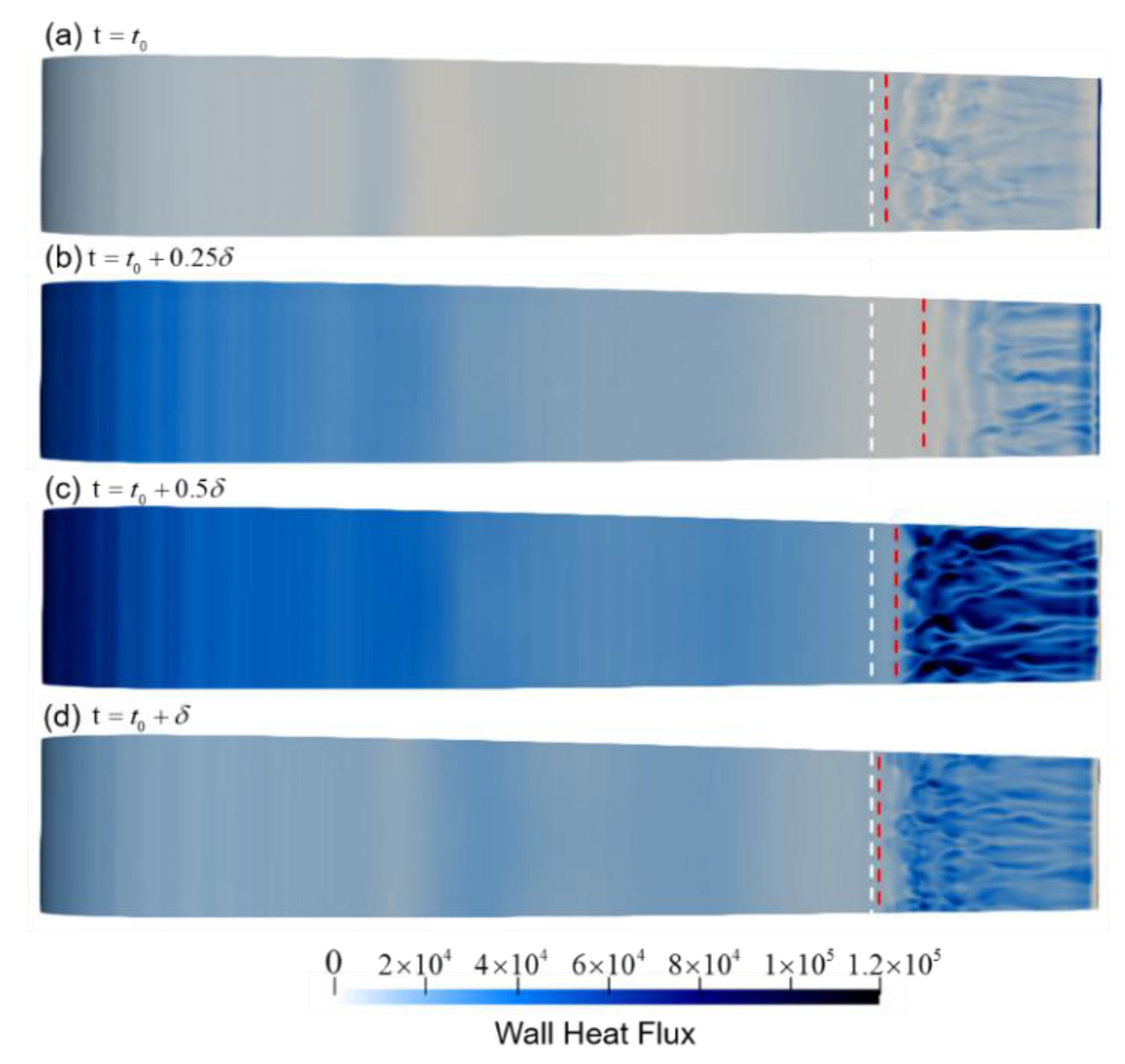

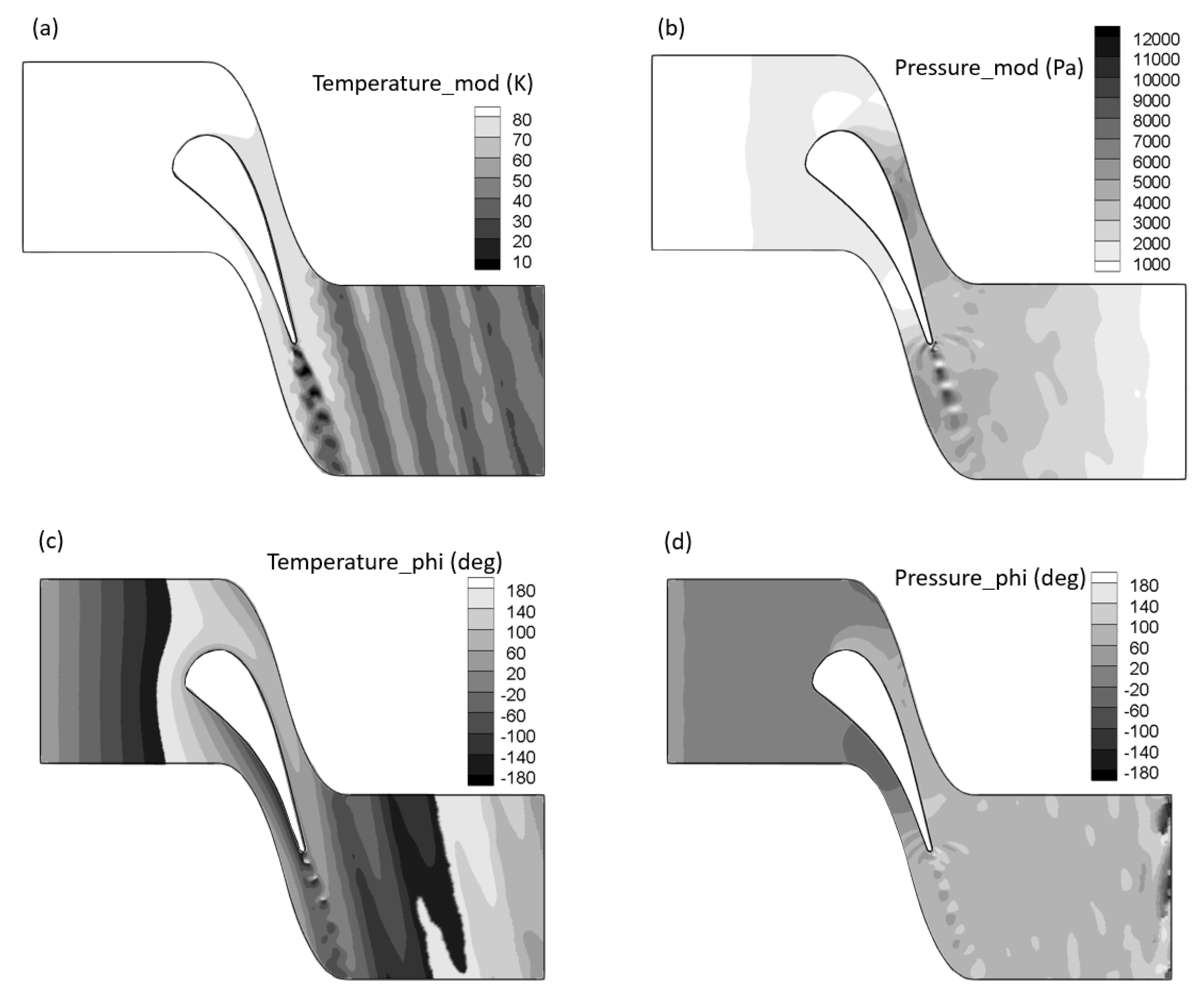
| Case | Twall (K) | Pi,0 (Mpa) a | P2 (Mpa) b | Ti,0 (K) c |
|---|---|---|---|---|
| MUR129_k-ω | 297.75 | 0.1849 | 0.1165 | 409.20 |
| MUR241_k-ω | 299.75 | 3.2570 | 1.5470 | 416.40 |
| MUR129_SAS | 297.75 | 0.1849 | 0.1165 | 409.20 |
| MUR241_SAS | 299.75 | 3.2570 | 1.5470 | 416.40 |
| MUR129_SAS_Wave | 297.75 | 0.1849 | 0.1165 | T1(t)c |
| Case | Calculation | Theory |
|---|---|---|
| 0.6360 | 1 | |
| 0.0554 | 0.0617 | |
| 0.0166 | 0.0064 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Fang, Y.; Zheng, Y.; Wang, G.; Moreau, S. Numerical Investigation of Influence of Entropy Wave on the Acoustic and Wall Heat Transfer Characteristics of a High-Pressure Turbine Guide Vane. Acoustics 2020, 2, 524-538. https://doi.org/10.3390/acoustics2030028
Hu K, Fang Y, Zheng Y, Wang G, Moreau S. Numerical Investigation of Influence of Entropy Wave on the Acoustic and Wall Heat Transfer Characteristics of a High-Pressure Turbine Guide Vane. Acoustics. 2020; 2(3):524-538. https://doi.org/10.3390/acoustics2030028
Chicago/Turabian StyleHu, Keqi, Yuanqi Fang, Yao Zheng, Gaofeng Wang, and Stéphane Moreau. 2020. "Numerical Investigation of Influence of Entropy Wave on the Acoustic and Wall Heat Transfer Characteristics of a High-Pressure Turbine Guide Vane" Acoustics 2, no. 3: 524-538. https://doi.org/10.3390/acoustics2030028
APA StyleHu, K., Fang, Y., Zheng, Y., Wang, G., & Moreau, S. (2020). Numerical Investigation of Influence of Entropy Wave on the Acoustic and Wall Heat Transfer Characteristics of a High-Pressure Turbine Guide Vane. Acoustics, 2(3), 524-538. https://doi.org/10.3390/acoustics2030028







