Liver Backscatter and the Hepatic Vasculature’s Autocorrelation Function
Abstract
:1. Introduction
2. Theory of Scattering Applied to Fractal Branching Networks
2.1. General Theory
2.2. The Long Vessel
3. Methods
3.1. Experimental Animals
3.2. Micro-CT
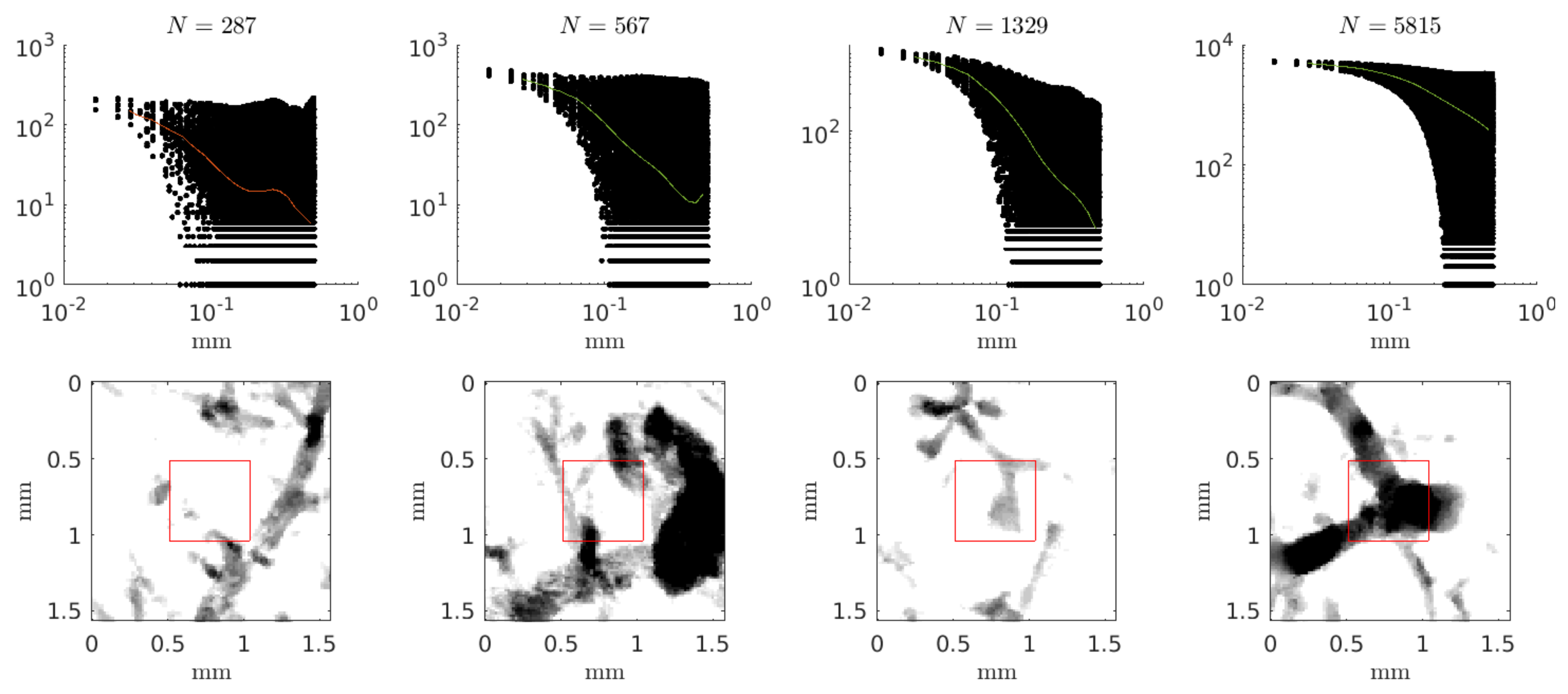
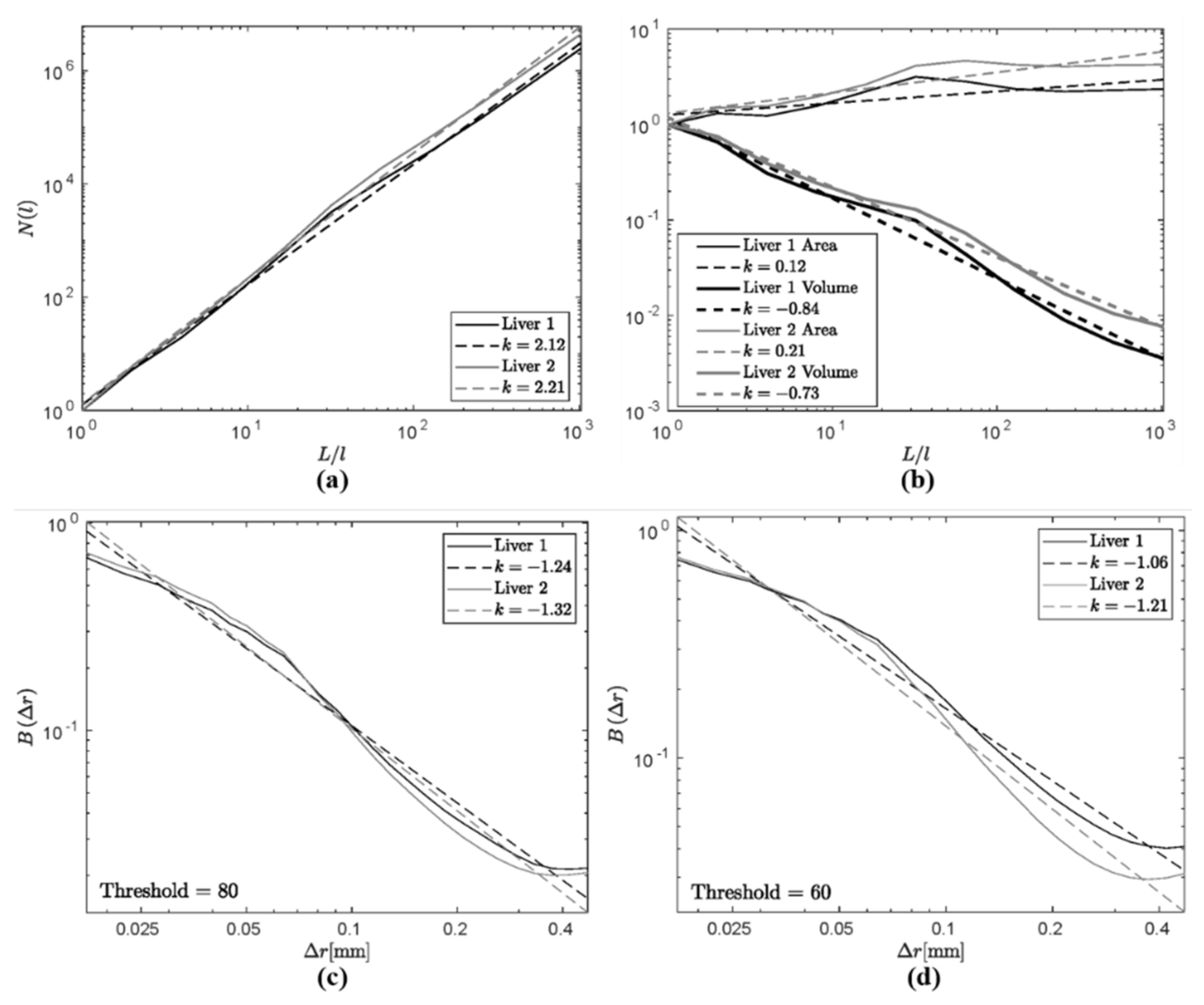
4. Results
5. Discussion
5.1. Comparison of Measures
5.2. Implications for Scattering from Liver
5.3. Resolving Uncertainties and Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Debye, P.; Bueche, A.M. Scattering by an inhomogeneous solid. J. Appl. Phys. 1949, 20, 518–525. [Google Scholar] [CrossRef]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; Chapter 8; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Parker, K.J. Shapes and distributions of soft tissue scatterers. Phys. Med. Biol. 2019, 64, 175022. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; W.H. Freeman: San Francisco, CA, USA, 1977; pp. 1–365. [Google Scholar]
- Bassingthwaighte, J.B.; Bever, R.P. Fractal correlation in heterogeneous systems. Physica D 1991, 53, 71–84. [Google Scholar] [CrossRef]
- Glenny, R.W.; Robertson, H.T.; Yamashiro, S.; Bassingthwaighte, J.B. Applications of fractal analysis to physiology. J. Appl. Physiol. 1991, 70, 2351–2367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, M.Y.; Lindsay, H.M.; Weitz, D.A.; Ball, R.C.; Klein, R. Universality of fractal aggregates as probed by light scattering. Proc. R. Soc. Lond. A Math. Phys. Sci. 1989, 423, 71–87. [Google Scholar]
- Javanaud, C. The application of a fractal model to the scattering of ultrasound in biological media. J. Acoust. Soc. Am. 1989, 86, 493–496. [Google Scholar] [CrossRef]
- Shapiro, S.A. Elastic waves scattering and radiation by fractal inhomogeneity of a medium. Geophys. J. Int. 1992, 110, 591–600. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Connolly, T.J. Imaging of random surfaces. J. Mod. Opt. 1995, 42, 861–881. [Google Scholar] [CrossRef]
- Lambert, S.A.; Nasholm, S.P.; Nordsletten, D.; Michler, C.; Juge, L.; Sinkus, R.; Serfaty, J.M. Bridging three orders of magnitude: Multiple scattered waves sense fractal microscopic structures via dispersion. Phys. Rev. Lett. 2015, 115, 094301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Posnansky, O.; Guo, J.; Hirsch, S.; Papazoglou, S.; Braun, J.; Sack, I. Fractal network dimension and viscoelastic powerlaw behavior: I. A modeling approach based on a coarse-graining procedure combined with shear oscillatory rheometry. Phys. Med. Biol. 2012, 57, 4023–4040. [Google Scholar] [CrossRef] [Green Version]
- Insana, M.F.; Wagner, R.F.; Brown, D.G.; Hall, T.J. Describing small-scale structure in random media using pulse-echo ultrasound. J. Acoust. Soc. Am. 1990, 87, 179–192. [Google Scholar] [CrossRef] [PubMed]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978; Volume 2, pp. 1–572. [Google Scholar]
- Campbell, J.A.; Waag, R.C. Ultrasonic scattering properties of three random media with implications for tissue characterization. J. Acoust. Soc. Am. 1984, 75, 1879–1886. [Google Scholar] [CrossRef] [PubMed]
- Parker, K.J. Hermite scatterers in an ultraviolet sky. Phys. Lett. A 2017, 381, 3845–3848. [Google Scholar] [CrossRef]
- Bracewell, R.N. The Fourier Transform and its Applications; Chapter 12; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Baddour, N. Operational and convolution properties of three-dimensional Fourier transforms in spherical polar coordinates. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2010, 27, 2144–2155. [Google Scholar] [CrossRef] [PubMed]
- Erdélyi, A.; Bateman, H. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 2. [Google Scholar]
- Krenz, G.S.; Linehan, J.H.; Dawson, C.A. A fractal continuum model of the pulmonary arterial tree. J. Appl. Physiol. 1992, 72, 2225–2237. [Google Scholar] [CrossRef]
- Vicsek, T. Fractal Growth Phenomena, 2nd ed.; World Scientific: Singapore, 1992. [Google Scholar]
- Parker, K.J.; Carroll-Nellenback, J.J.; Wood, R.W. The 3D spatial autocorrelation of the branching fractal vasculature. Acoustics 2019, 1, 20. [Google Scholar] [CrossRef] [Green Version]
- Guyton, A.C. Textbook of Medical Physiology, 4th ed.; Saunders: Philadelphia, PA, USA, 1971; pp. 1–1032. [Google Scholar]
- Campbell, J.A.; Waag, R.C. Measurements of calf liver ultrasonic differential and total scattering cross sections. J. Acoust. Soc. Am. 1984, 75, 603–611. [Google Scholar] [CrossRef]
- Bamber, J.C.; Hill, C.R. Acoustic properties of normal and cancerous human liver—I. Dependence on pathological condition. Ultrasound Med. Biol. 1981, 7, 121–133. [Google Scholar] [CrossRef]
- Nicholas, D. Evaluation of backscattering coefficients for excised human tissues: Results, interpretation and associated measurements. Ultrasound Med. Biol. 1982, 8, 17–28. [Google Scholar] [CrossRef]
- Lizzi, F.L.; Greenebaum, M.; Feleppa, E.J.; Elbaum, M.; Coleman, D.J. Theoretical framework for spectrum analysis in ultrasonic tissue characterization. J. Acoust. Soc. Am. 1983, 73, 1366–1373. [Google Scholar] [CrossRef]
- D’Astous, F.T.; Foster, F.S. Frequency dependence of ultrasound attenuation and backscatter in breast tissue. Ultrasound Med. Biol. 1986, 12, 795–808. [Google Scholar] [CrossRef]
- Reid, J.M.; Shung, K.K. Quantitative measurements of scattering of ultrasound by heart and liver. Ultrason. Tissue Charact. II 1979, 2, 153–156. [Google Scholar]
- Ghoshal, G.; Lavarello, R.J.; Kemmerer, J.P.; Miller, R.J.; Oelze, M.L. Ex Vivo study of quantitative ultrasound parameters in fatty rabbit livers. Ultrasound Med. Biol. 2012, 38, 2238–2248. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.F.; Zagzebski, J.A.; Lee, F.T. Ultrasound backscatter and attenuation in human liver with diffuse disease. Ultrasound Med. Biol. 1999, 25, 1047–1054. [Google Scholar] [CrossRef]
- Oelze, M.L.; Zachary, J.F. Examination of cancer in mouse models using high-frequency quantitative ultrasound. Ultrasound Med. Biol. 2006, 32, 1639–1648. [Google Scholar] [CrossRef] [PubMed]
- Rouyer, J.; Cueva, T.; Yamamoto, T.; Portal, A.; Lavarello, R.J. In Vivo estimation of attenuation and backscatter coefficients from human thyroids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1253–1261. [Google Scholar] [CrossRef]
- Schmitt, J.M.; Kumar, G. Turbulent nature of refractive-index variations in biological tissue. Opt. Lett. 1996, 21, 1310–1312. [Google Scholar] [CrossRef]
- Risser, L.; Plouraboue, F.; Steyer, A.; Cloetens, P.; le Duc, G.; Fonta, C. From homogeneous to fractal normal and tumorous microvascular networks in the brain. J. Cereb. Blood Flow Metab. 2007, 27, 293–303. [Google Scholar] [CrossRef]
- Parker, K.J.; Ormachea, J.; McAleavey, S.A.; Wood, R.W.; Carroll-Nellenback, J.J.; Miller, R.K. Shear wave dispersion behaviors of soft, vascularized tissues from the microchannel flow model. Phys. Med. Biol. 2016, 61, 4890. [Google Scholar] [CrossRef]

| Name | Symbol | Equation | Notes |
|---|---|---|---|
| Fractal dimension | |||
| Autocorrelation | |||
| 3D spherical Fourier transform | |||
| Scattering differential cross section |
| Liver | Threshold | N, Lower Bound | N, Upper Bound | Power Law | Regions |
|---|---|---|---|---|---|
| 1 | 60 | 10 | 100 | −0.91 | 49 |
| 60 | 100 | 1000 | −1.09 | 172 | |
| 60 | 1000 | 10000 | −0.79 | 279 | |
| 80 | 10 | 100 | −1.28 | 104 | |
| 80 | 100 | 1000 | −1.23 | 210 | |
| 80 | 1000 | 10000 | −0.84 | 126 | |
| 2 | 60 | 10 | 100 | −1.16 | 50 |
| 60 | 100 | 1000 | −1.22 | 187 | |
| 60 | 1000 | 10000 | −0.87 | 253 | |
| 80 | 10 | 100 | −1.28 | 80 | |
| 80 | 100 | 1000 | −1.32 | 219 | |
| 80 | 1000 | 10000 | −0.87 | 137 |
| Method | Dependence | Estimates |
|---|---|---|
| Autocorrelation | D = 3 − γ | 2.2 > D > 1.8 |
| Surface area | D = 2 + γ | 2.1 |
| Volume | D = 3 + γ | 2.2 |
| Box counting | D = γ | 2.2 |
| Backscatter (predicted) | ∼k4−D | k1.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carroll-Nellenback, J.J.; White, R.J.; Wood, R.W.; Parker, K.J. Liver Backscatter and the Hepatic Vasculature’s Autocorrelation Function. Acoustics 2020, 2, 3-12. https://doi.org/10.3390/acoustics2010002
Carroll-Nellenback JJ, White RJ, Wood RW, Parker KJ. Liver Backscatter and the Hepatic Vasculature’s Autocorrelation Function. Acoustics. 2020; 2(1):3-12. https://doi.org/10.3390/acoustics2010002
Chicago/Turabian StyleCarroll-Nellenback, Jonathan J., R. James White, Ronald W. Wood, and Kevin J. Parker. 2020. "Liver Backscatter and the Hepatic Vasculature’s Autocorrelation Function" Acoustics 2, no. 1: 3-12. https://doi.org/10.3390/acoustics2010002
APA StyleCarroll-Nellenback, J. J., White, R. J., Wood, R. W., & Parker, K. J. (2020). Liver Backscatter and the Hepatic Vasculature’s Autocorrelation Function. Acoustics, 2(1), 3-12. https://doi.org/10.3390/acoustics2010002