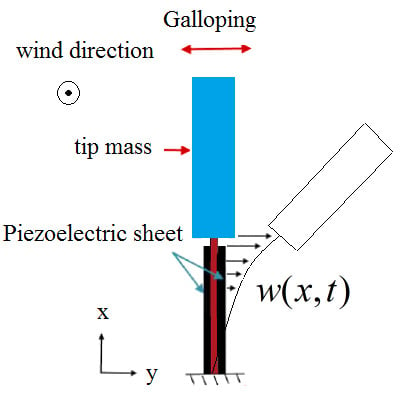
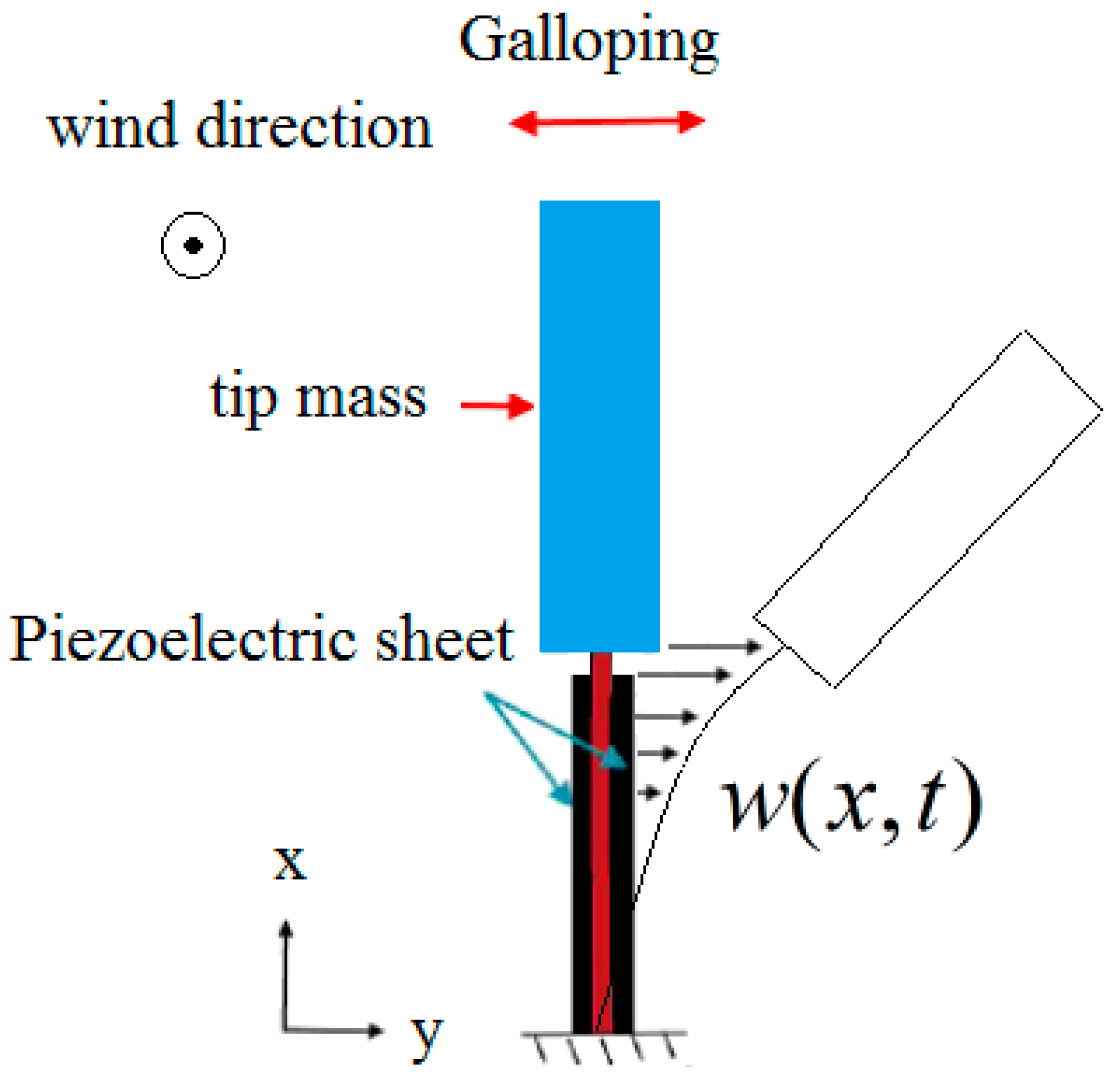
Effect of Tip Mass Length Ratio on Low Amplitude Galloping Piezoelectric Energy Harvesting
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Beam Modeling
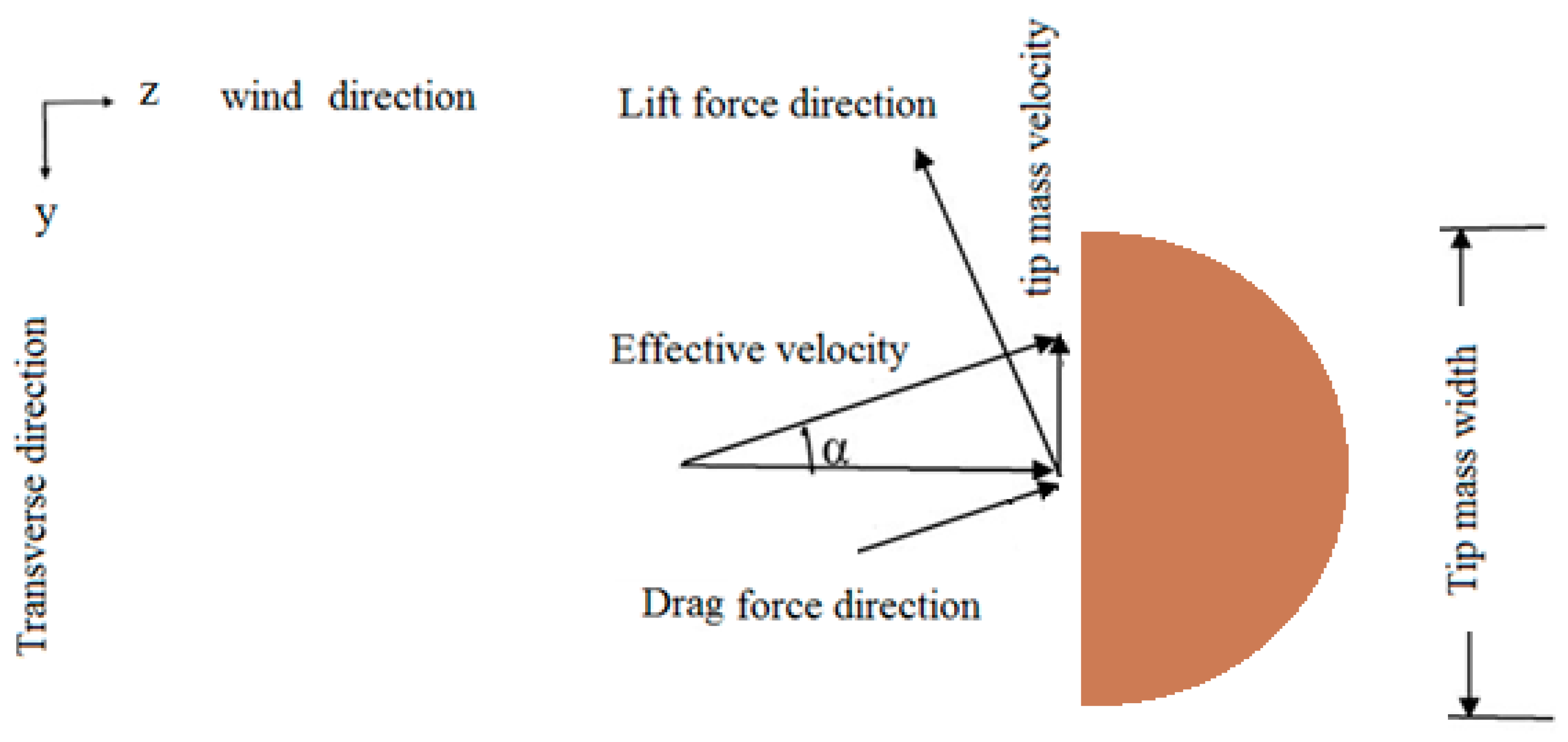
2.2. Aerodynamic Modeling
2.3. Piezoelectric Modeling
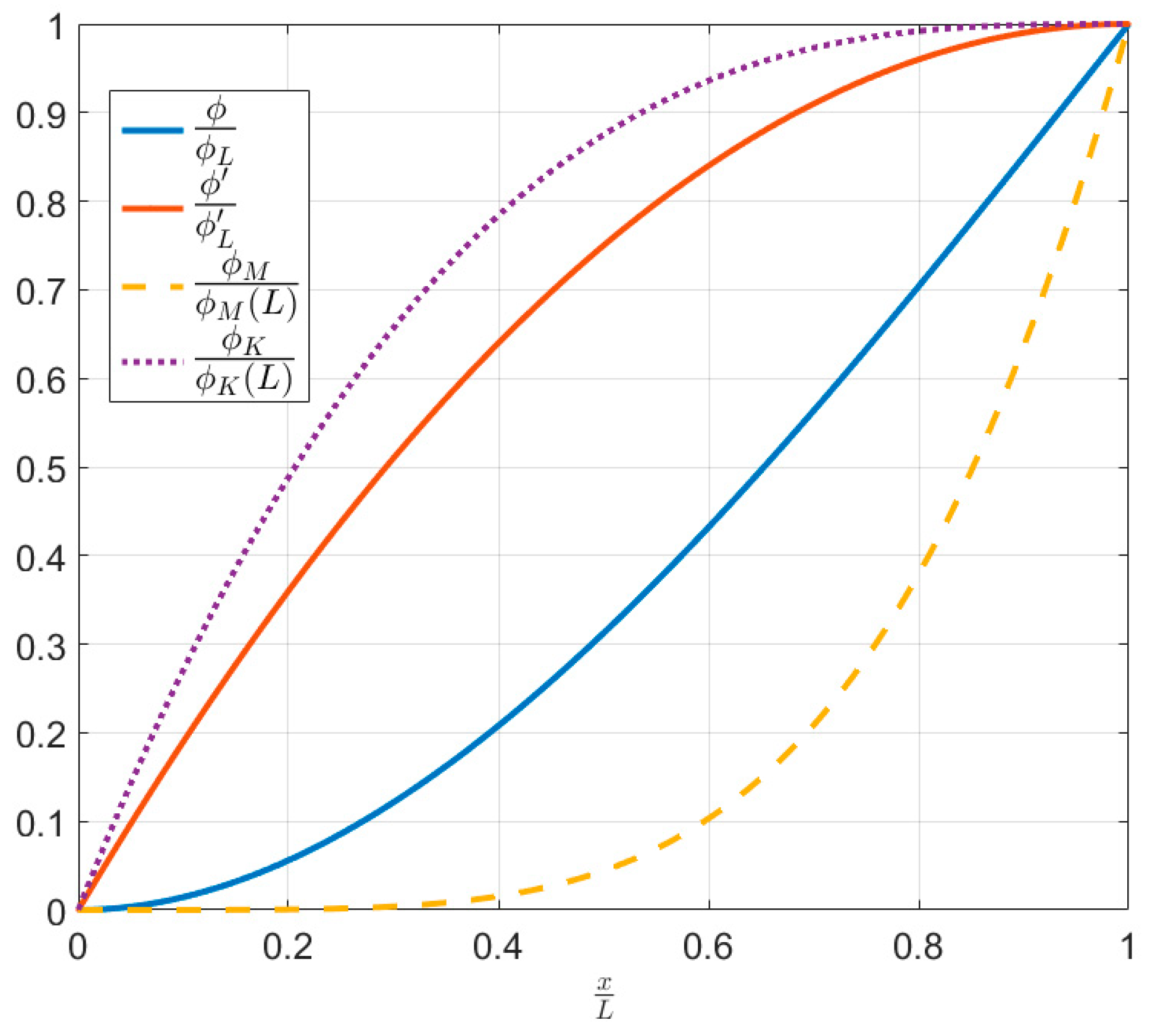
2.4. Approximate Method
2.5. Analytical Solution
2.6. A Note on Coupling Term
3. Results and Discussion
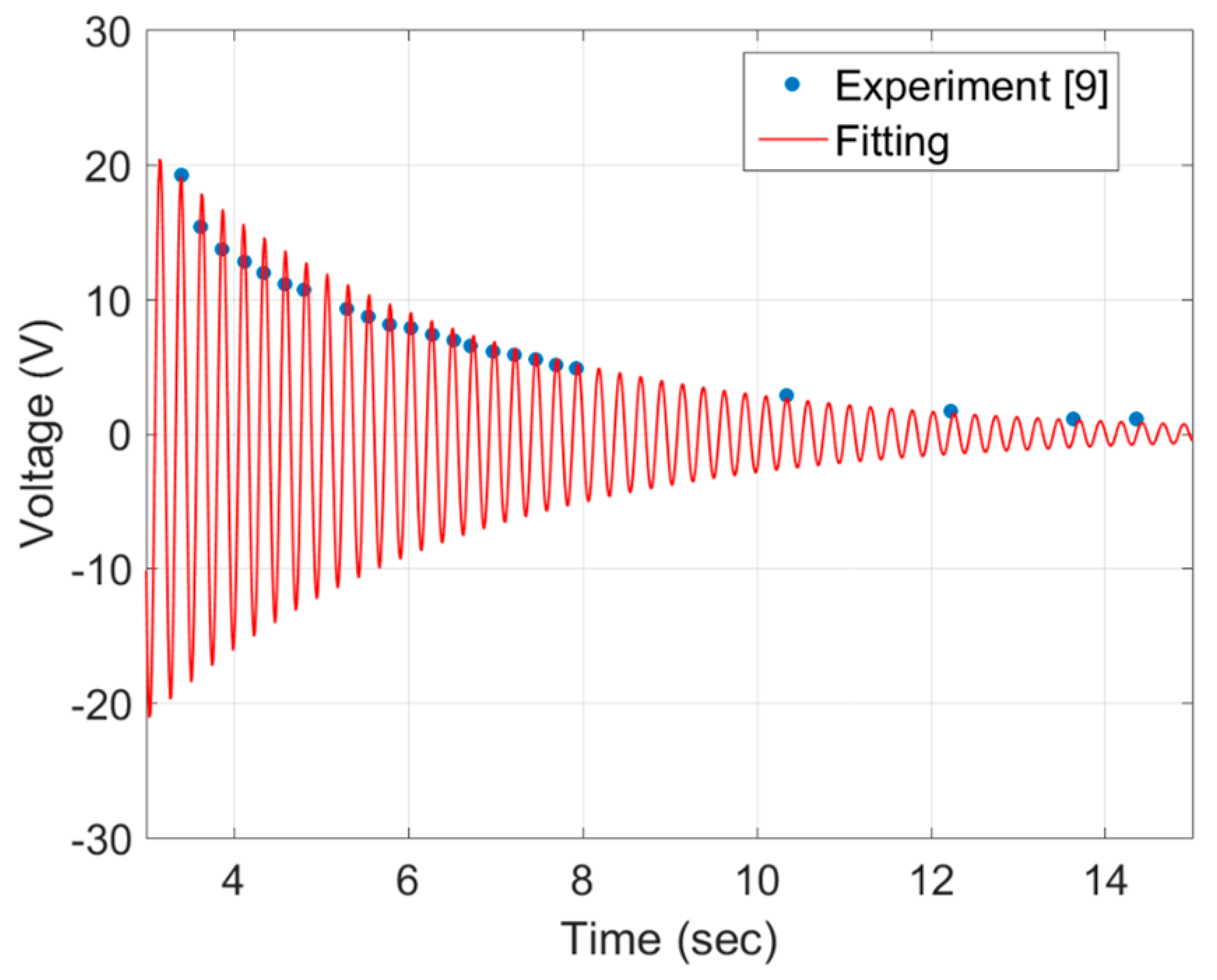
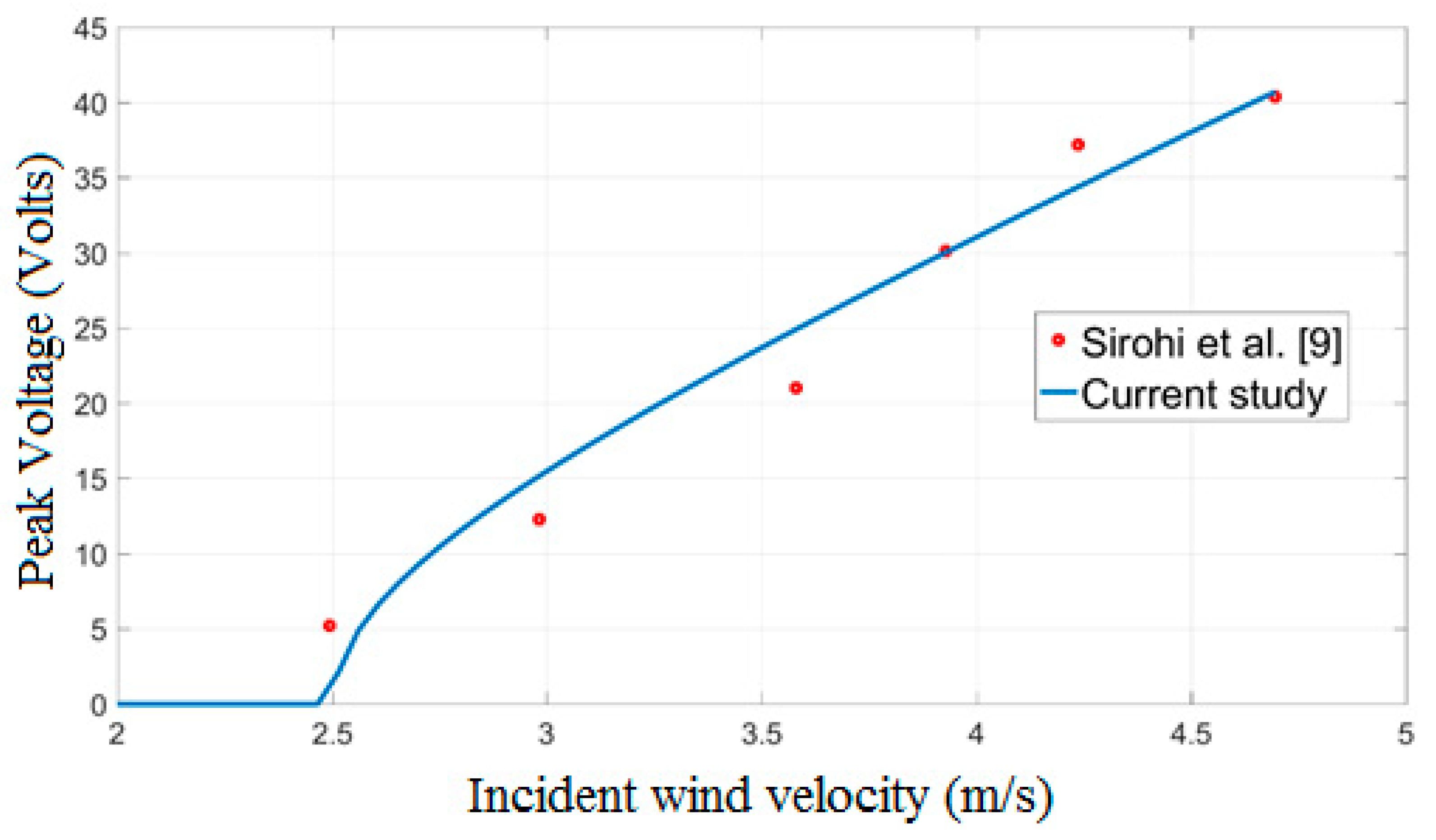
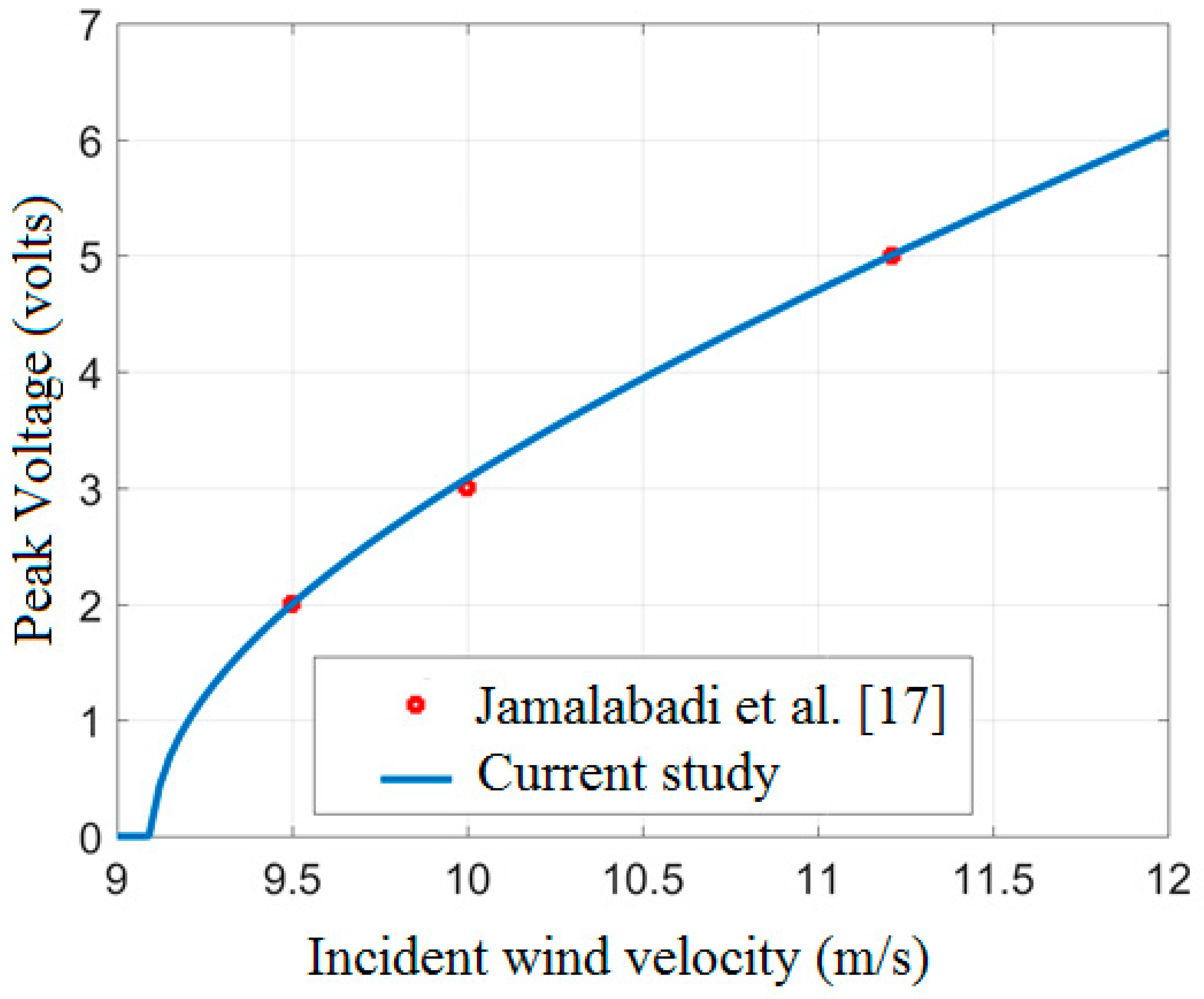
3.1. Validation by Experimental Results
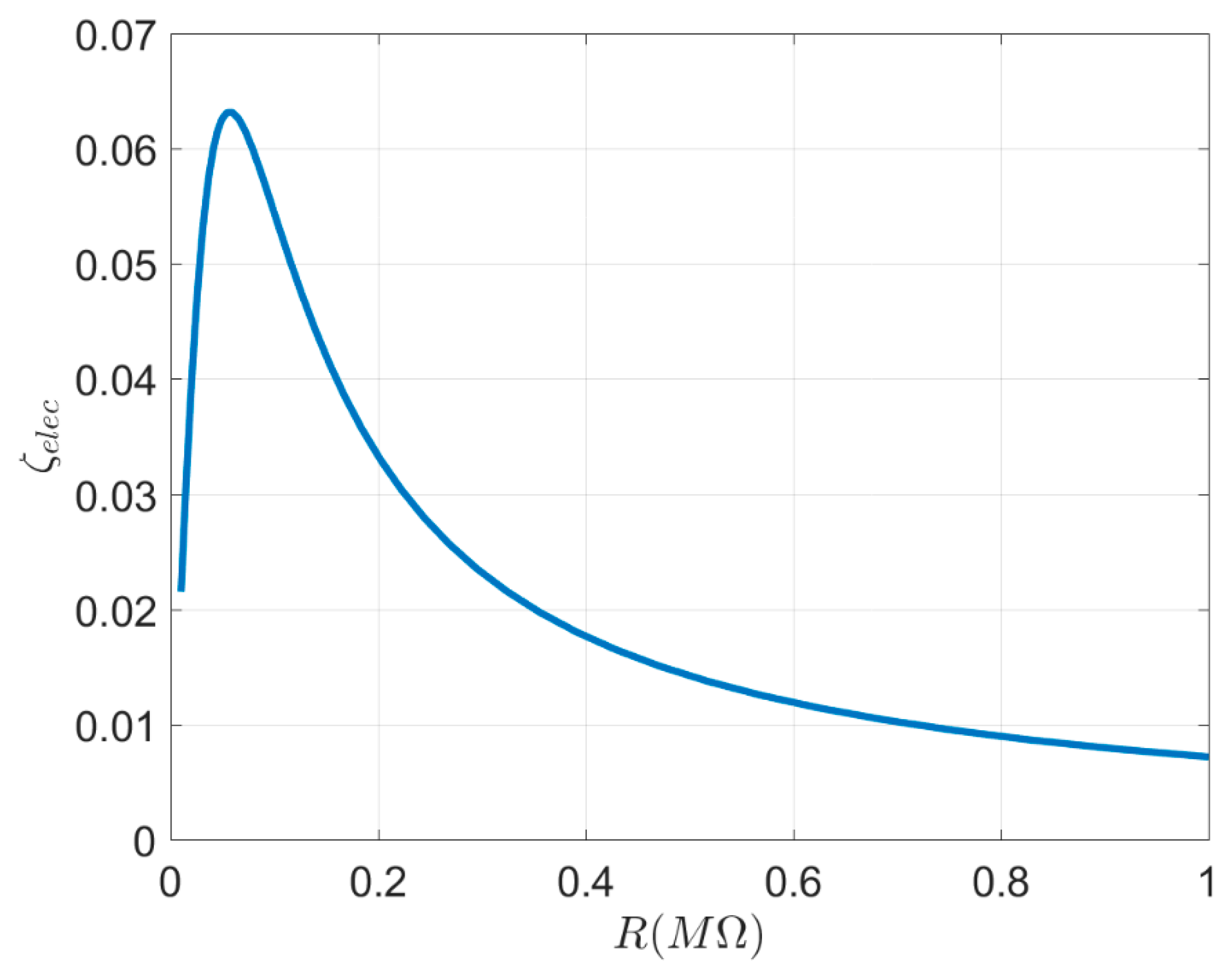
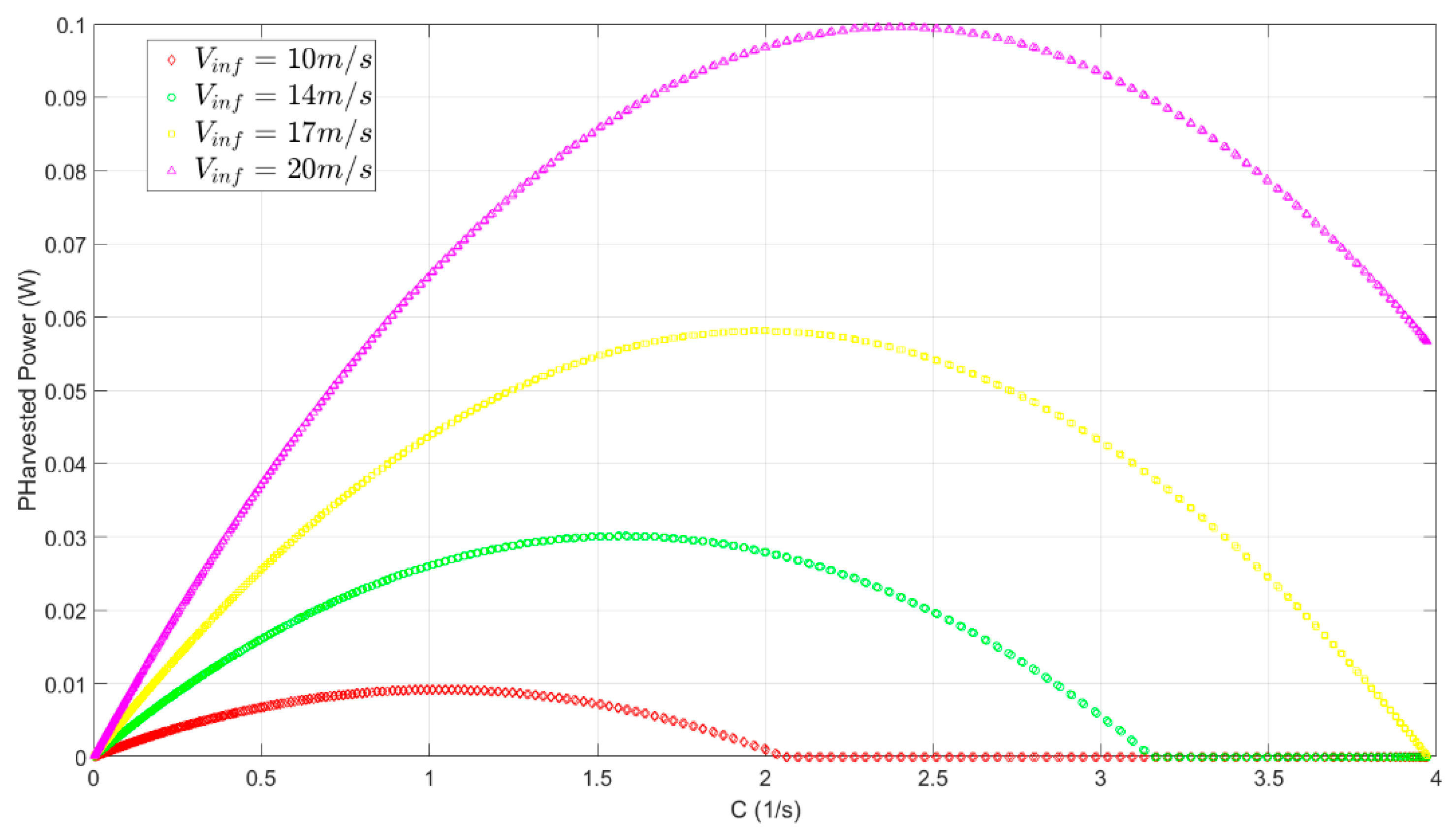
3.2. Effects of the Load Resistance and Tip Mass Length Ratio on the Harvester′s Response
4. Conclusions
- In this study, a simple analytical model is used to encounter the effect of a tip mass which could be used by engineers for design of energy harvesting devices with piezoelectric materials.
- The dimensionless functions for calculation of effective mass, effective stiffness, and electromechanical coupling coefficient were presented.
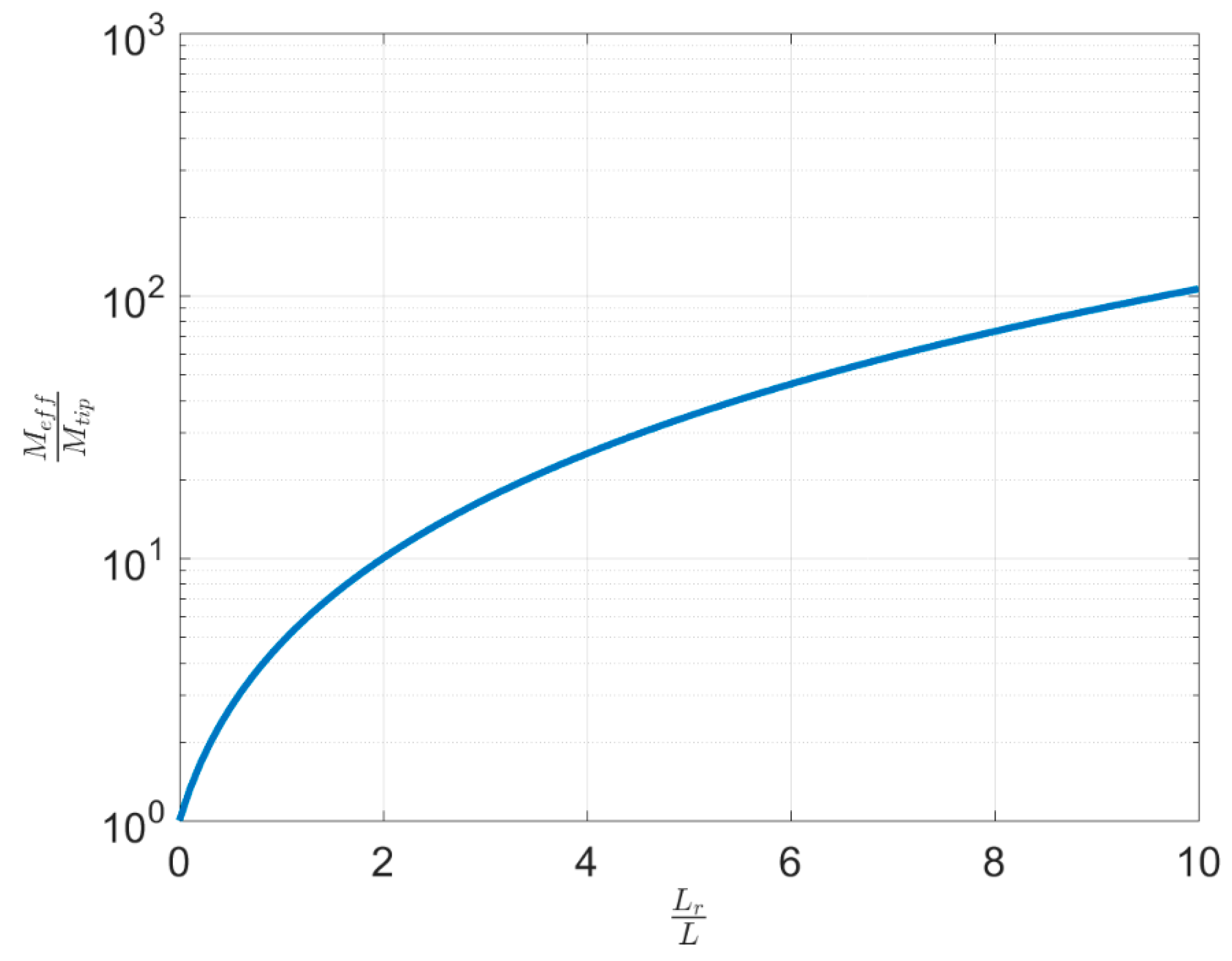
- The effect of tip mass length on effective mass was developed.
- The onset of galloping for the system was predicted analytically.
- The current aerodynamic coefficient in the literature causes great numerical errors.
- The equivalent damping ratio of the electrical load impedance as a function of load impedance was calculated.
- The effect of tip mass on the analytical solution of the concentrated mass was calculated.
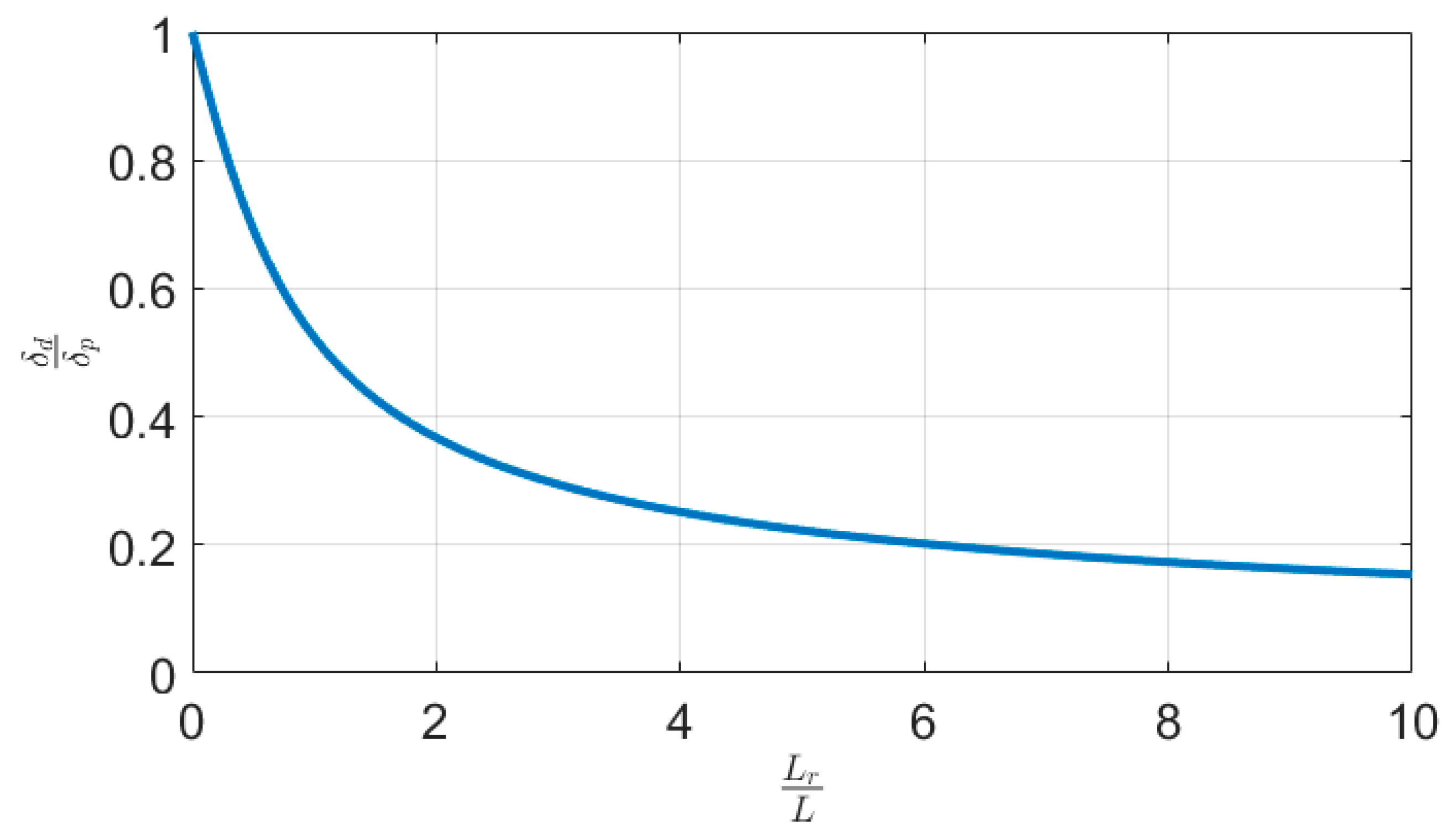
- The effect of tip mass is a decrease in the tip displacement in comparison with the point mass.
- The results are fitted on the analytical solution, and the new aerodynamics coefficients included the effect of tip mass.
- As shown by increases of the length of tip mass for the constant beam and piezoelectric length, the inertia of the system increases while the tip displacement and onset of galloping decrease.
Conflicts of Interest
Nomenclature
| ρa | Air density (kg·m−3) |
| mt | Tip mass (g) |
| Lr | Length of the tip body (mm) |
| D | Width of the tip body (mm) |
| V∞ | Wind velocity (m/s) |
| L | Length of the beam (mm) |
| wb | Width of the beam material layer (mm) |
| tb | Beam material layer thickness (mm) |
| Eb | Beam material Young′s modulus (GN·m−2) |
| ρb | Beam material density (kg m−3) |
| xp | Start of the piezoelectric sheets (mm) |
| Lp | Length of the piezoelectric sheets (mm) |
| wp | Width of the piezoelectric layer (mm) |
| tp | Piezoelectric layer thickness (mm) |
| Ep | Piezoelectric material Young’s modulus (GN m−2) |
| ρp | Piezoelectric material density (kg m−3) |
| d31 | Strain coefficient of the piezoelectric layer (pC N−1) |
| ε33 | Permittivity component at constant strain (nF m−1) |
| mb | Beam mass (g) |
| mp | Piezoelectric sheet mass (g) |
| meff | Total mass (g) |
| kb | Beam stiffness (N/m) |
| kp | Piezoelectric sheet stiffness (N/m) |
| keff | Total stiffness (N/m) |
| fn | Natural frequency (1/s) |
| fexp | Experimental natural frequency (1/s) |
| Cp | Total capacitance of the piezoelectric layers (nF) |
| χ | Coupling factor (mmCm−1·kg−1/2) |
| Vm | Voltage of the piezoelectric layers (V) |
| w | Tip displacement of the beam (m) |
| vonset | Onset of the galloping velocity (ms−1) |
Appendix A
Appendix A1. Find the Effective Stiffness of the System
Appendix A2. Find the Effective Mass of the System
Appendix A3. Find the Second-Order Governing Equation of Motion of the System
Appendix A4. Find the Piezoelectric Effect on the Governing Equation of Motion of the System
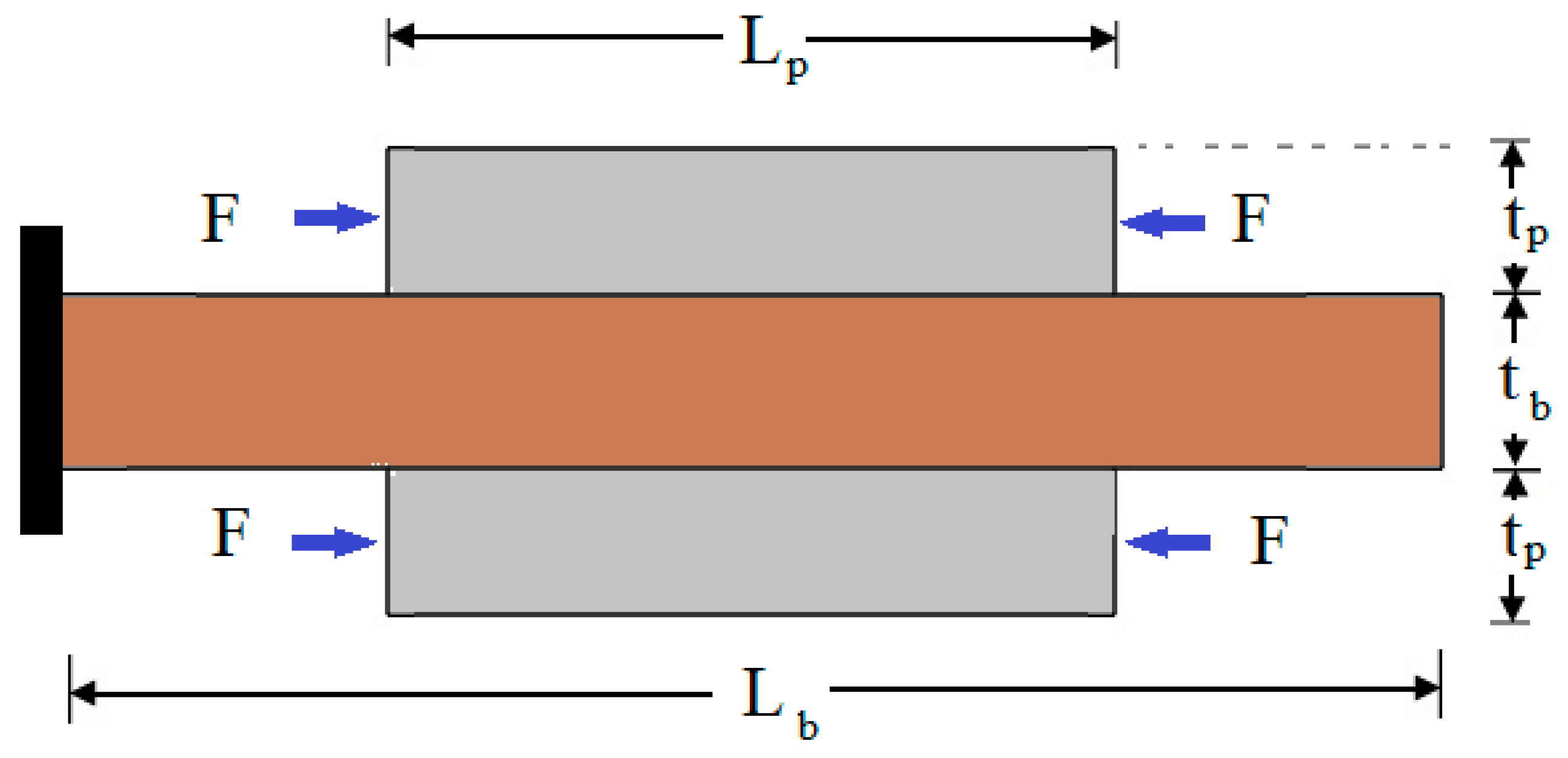
Appendix A5. Find the Relation of Piezoelectric Voltage and Tip Displacement
References
- Saadon, S.; Sidek, O. A review of vibration-based MEMS piezoelectric energy harvesters. Energy Convers. Manag. 2011, 52, 500–504. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Ilyas, M.A.; Swingler, J. Piezoelectric energy harvesting from raindrop impacts. Energy 2015, 90, 796–806. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Ahmadi, E. Design, Construction and Testing of a Dragon Wave Energy Converter. Am. J. Nav. Archit. Mar. Eng. 2016, 1, 7–15. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Ahmadi, E. Experimental study on overtopping performance of a circular ramp wave energy converter. Rev. Energy Technol. Policy Res. 2017, 3, 1–16. [Google Scholar]
- Tan, T.; Yan, Z. Electromechanical decoupled model for cantilever-beam piezoelectric energy harvesters with inductive-resistive circuits and its application in galloping mode. Smart Mater. Struct. 2017, 26, 035062. [Google Scholar] [CrossRef]
- Barrero-Gil, A.; Alonso, G.; Sanz-Andres, A. Energy harvesting from transverse galloping. J. Sound Vib. 2010, 329, 2873–2883. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Piezoelectric wind energy harvester for low-power sensors. J. Intell. Mater. Syst. Struct. 2011, 22, 2215–2228. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Harvesting wind energy using a galloping piezoelectric beam. J. Vib. Acoust. 2012, 134, 011009. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Yan, Z.; Hajj, M. Modeling and nonlinear analysis of piezoelectric energy harvesting from transverse galloping. Smart Mater. Struct. 2013, 22, 025016. [Google Scholar] [CrossRef]
- Bibo, A.; Daqaq, M.F. On the optimal performance and universal design curves of galloping energy harvesters. Appl. Phys. Lett. 2014, 104, 023901. [Google Scholar] [CrossRef]
- Tan, T.; Yan, Z.; Hajj, M. Electromechanical decoupled model for cantilever-beam piezoelectric energy harvesters. Appl. Phys. Lett. 2016, 109, 101908. [Google Scholar] [CrossRef]
- Tan, T.; Yan, Z. Analytical solution and optimal design for galloping-based piezoelectric energy harvesters. Appl. Phys. Lett. 2016, 109, 253902. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Yan, Z.; Hajj, M.R. Performance analysis of galloping-based piezoaeroelastic energy harvesters with different cross-section geometries. J. Intell. Mater. Syst. Struct. 2014, 25, 246–256. [Google Scholar] [CrossRef]
- Kazakevich, M.I.; Vasilenko, A.G. Closed Analytical Solution for Galloping Aeroelastic Self-Oscillations. J. Wind Eng. Ind. Aerodyn. 1996, 65, 353–360. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Harvesting Wind Energy Using a Galloping Piezoelectric Beam. In Proceedings of the ASME 2009 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Oxnard, CA, USA, 21–23 September 2009; pp. 443–450. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Kwak, K.M.; Hwan, S.J. Galloping modeling of a cantilever beam with piezoelectric wafers. In Proceedings of the Joint Conference by KSNVE, ASK and KSME(DC), Gwangju, Korea, 26–18 April 2017; Volume 4, p. 478. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Kwak, K.M.; Hwan, S.J. Flow-induced vibration of Piezoelectric D-shape Beam Wind Energy Harvesters. Proc. KSNVE Annu. Autumn Conf. 2016, 10, 54. [Google Scholar]
- Kim, M.; Hoegen, M.; Dugundji, J.; Wardle, B.L. Modeling and experimental verification of proof mass effects on vibration energy harvester performance. Smart Mater. Struct. 2010, 19, 045023. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, L.; Tang, L. Comparative study of tip cross-sections for efficient galloping energy harvesting. Appl. Phys. Lett. 2013, 102, 064105. [Google Scholar] [CrossRef]
- Bearman, P.W.; Gartshore, I.S.; Maull, D.J.; Parkinson, G.V. Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1987, 1, 19–34. [Google Scholar] [CrossRef]
- Corless, R.M.; Parkinson, G.V. A model of the combined effects of vortex-induced oscillation and galloping. J. Fluids Struct. 1988, 3, 203–220. [Google Scholar] [CrossRef]
- Corless, R.M.; Parkinson, G.V. Mathematical modelling of the combined effects of vortex-induced vibration and galloping. Part II. In Proceedings International Symposium Flow-Induced Vibration and Noise, Bluff-Body/Fluid and Hydraulic Machine Interactions; Pa¨ıdoussis, M.P., Dalton, C., Weaver, D.S., Eds.; ASME: New York, NY, USA, 1992; Volume 6, pp. 39–63. [Google Scholar]
- Corless, R.M.; Parkinson, G.V. Mathematical modelling of the combined effects of vortex-induced vibration and galloping. Part II. J. Fluids Struct. 1993, 7, 825–848. [Google Scholar] [CrossRef]
- Laneville, A.; Parkinson, G.V. Effects of Turbulence on Galloping of Bluff Cylinders. Ph.D Thesis, University of British Columbia, Vancouver, BC, Canada.
- Parkinson, G.V. Wind-induced instability of structures. Philos. Trans. R. Soc. 1971, 269, 395–409. [Google Scholar] [CrossRef]
- Parkinson, G.V. Mathematical models of flow-induced vibrations of bluff bodies. In Flow-Induced Structural Vibrations; Naudascher, E., Ed.; Springer: Berlin, Germany, 1974; pp. 81–127. [Google Scholar]
- Parkinson, G.V. Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 1989, 26, 169–224. [Google Scholar] [CrossRef]
- Parkinson, G.V.; Brooks, N.P.H. On the aeroelastic instability of bluff cylinders. J. Appl. Mech. 1961, 28, 252–258. [Google Scholar] [CrossRef]
- Parkinson, G.V.; Jandali, T. A wake source model for bluff body potential flow. J. Fluid Mech. 1969, 40, 577–596. [Google Scholar] [CrossRef]
- Parkinson, G.V.; Smith, J.D. The square prism as an aeroelastic non-linear oscillator. Q. J. Mech. Appl. Math. 1964, 17, 225–239. [Google Scholar] [CrossRef]
- Parkinson, G.V.; Sullivan, P.P. Galloping response of towers. J. Ind. Aerodyn. 1979, 4, 253–260. [Google Scholar] [CrossRef]
- Parkinson, G.V.; Wawzonek, M.A. Some considerations of the combined effects of galloping and vortex resonance. J. Wind Eng. Ind. Aerodyn. 1981, 8, 135–143. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Transmission line vibration due to sleet. Trans. Am. Soc. Electr. Eng. 1932, 51, 1075–1076. [Google Scholar] [CrossRef]
- Novak, M. Aeroelastic galloping of prismatic bodies. ASCE J. Eng. Mech. 1969, 95, 115–142. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Kwak, M.K. Dynamic modeling of a galloping structure equipped with piezoelectric wafers and energy harvesting. Noise Control Eng. J. 2019, 67, 142–154. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Scanlon, J.M.; McDowell, E.; Hajj, M.R. Performance enhancement of piezoelectric energy harvesters from wake galloping. Appl. Phys. Lett. 2013, 103, 033903. [Google Scholar] [CrossRef]
- Ewere, F.; Wang, G. Performance of galloping piezoelectric energy harvesters. J. Intell. Mater. Syst. Struct. 2014, 25, 1693–1704. [Google Scholar] [CrossRef]
- Rostami, A.B.; Fernandes, A.C. The effect of inertia and flap on autorotation applied for hydrokinetic energy harvesting. Appl. Energy 2015, 143, 312–323. [Google Scholar] [CrossRef][Green Version]
| Symbol | Description and Unit | Value |
|---|---|---|
| ρa | Air density (kg·m−3) | 1.225 |
| mt | Tip mass (g) | 65 |
| Lr | Length of the tip body (mm) | 235 |
| D | Width of the tip body (mm) | 30 |
| V∞ | Wind velocity (m/s) | 4.02 |
| L | Length of the beam (mm) | 90 |
| wb | Width of the beam material layer (mm) | 38 |
| tb | Beam material layer thickness (mm) | 0.635 |
| Eb | Beam material Young’s modulus (GN·m−2) | 70 |
| ρb | Beam material density (kg·m−3) | 2700 |
| Lp | Length of the piezoelectric sheets (mm) | 72.2 |
| wp | Width of the piezoelectric layer (mm) | 36.2 |
| tp | Piezoelectric layer thickness (mm) | 0.267 |
| Ep | Piezoelectric material Young’s modulus (GN·m−2) | 62 |
| ρp | Piezoelectric material density (kg·m−3) | 7800 |
| d31 | Strain coefficient of the piezoelectric layer (pC N−1) | −320 |
| ε33 | Permittivity component at constant strain (nF·m−1) | 33.6 |
| R | Load resistance (MΩ) | 0.7 |
| Isosceles 30° | D-section | Isosceles 53° | Square | |
|---|---|---|---|---|
| a1 | 2.9 | 0.79 | 1.9 | 2.3 |
| a3 | −6.2 | −0.19 | −6.7 | −18 |
| Symbol | Description and Unit | Value |
|---|---|---|
| mb | Beam mass (g) | 5.9 |
| mp | Piezoelectric sheet mass (g) | 5.4 |
| meff | Total mass (g) | 654 |
| kb | Beam stiffness (N/m) | 77.9 |
| kp | Piezoelectric sheet stiffness (N/m) | 69.3 |
| keff | Total stiffness (N/m) | 646.3 |
| fn | Natural frequency (1/s) | 5 |
| fexp | Experimental natural frequency (1/s) | 4.167 |
| Cp | Total capacitance of the piezoelectric layers (nF) | 658.7 |
| χ | Coupling factor (mmCm−1 ·kg−1/2) | −12.8 |
| Voltage to tip displacement of the system (Vmm−1) | 0.57 | |
| R | Load resistance (MΩ) | 0.7 |
| Rmax | Optimal resistance (kΩ) | 57 |
| vonset | Onset of the galloping velocity in open circuit Condition (ms−1) | 22.79 |
| vonset | Onset velocity in load resistance of 0.7 MΩ (ms−1) | 40.95 |
| Symbol | Description and Unit | Value |
|---|---|---|
| ρa | Air density (kg·m−3) | 1.225 |
| mt | Tip mass (g) | 31.6 |
| Lr | Length of the tip body (mm) | 70 |
| D | Width of the tip body (mm) | 60 |
| V∞ | Wind velocity (m/s) | 9–11 |
| L | Length of the beam (mm) | 210 |
| wb | Width of the beam material layer (mm) | 50 |
| tb | Beam material layer thickness (mm) | 1 |
| Eb | Beam material Young’s modulus (GN·m−2) | 69 |
| ρb | Beam material density (kg·m−3) | 3067 |
| xp | Start of the piezoelectric sheets (mm) | 5 |
| Lp | Length of the piezoelectric sheets (mm) | 30 |
| wp | Width of the piezoelectric layer (mm) | 40 |
| tp | Piezoelectric layer thickness (mm) | 0.5 |
| Ep | Piezoelectric material Young’s modulus (GN·m−2) | 61 |
| ρp | Piezoelectric material density (kg·m−3) | 8148 |
| d31 | Strain coefficient of the piezoelectric layer (pC·N−1) | −310 |
| ε33 | Permittivity component at constant strain (nF·m−1) | 38.3 |
| Symbol | Description and Unit | Value |
|---|---|---|
| mb | Beam mass (g) | 32.2 |
| mp | Piezoelectric sheet mass (g) | 4.4 |
| meff | Total mass (g) | 57.6 |
| kb | Beam stiffness (N/m) | 31.0 |
| kp | Piezoelectric sheet stiffness (N/m) | 27.7 |
| keff | Total stiffness (N/m) | 122.35 |
| fn | Natural frequency (1/s) | 7.33 |
| fexp | Experimental natural frequency (1/s) | 7.5 |
| Cp | Total capacitance of the piezoelectric layers (nF) | 92 |
| Coupling factor (mmCm−1·kg−1/2) | −9 | |
| Voltage to tip displacement of the system (Vmm−1) | 0.467 | |
| Voltage to tip displacement of the system (Vmm−1) | 0.444 | |
| vonset | Onset of the galloping velocity in open circuit condition (ms−1) | 27.8 |
| vonset | Onset velocity in load resistance of 0.7 MΩ (ms−1) | 148.8 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdollahzadeh Jamalabadi, M.Y. Effect of Tip Mass Length Ratio on Low Amplitude Galloping Piezoelectric Energy Harvesting. Acoustics 2019, 1, 763-793. https://doi.org/10.3390/acoustics1040045
Abdollahzadeh Jamalabadi MY. Effect of Tip Mass Length Ratio on Low Amplitude Galloping Piezoelectric Energy Harvesting. Acoustics. 2019; 1(4):763-793. https://doi.org/10.3390/acoustics1040045
Chicago/Turabian StyleAbdollahzadeh Jamalabadi, Mohammad Yaghoub. 2019. "Effect of Tip Mass Length Ratio on Low Amplitude Galloping Piezoelectric Energy Harvesting" Acoustics 1, no. 4: 763-793. https://doi.org/10.3390/acoustics1040045
APA StyleAbdollahzadeh Jamalabadi, M. Y. (2019). Effect of Tip Mass Length Ratio on Low Amplitude Galloping Piezoelectric Energy Harvesting. Acoustics, 1(4), 763-793. https://doi.org/10.3390/acoustics1040045