Abstract
This report acquaints the reader with an extra two new shear-horizontal surface acoustic waves (SH-SAWs). These new SH-SAWs can propagate along the free surface of the transversely isotropic (6 mm) magnetoelectroelastic materials. These (composite) materials can simultaneously possess the piezoelectric, piezomagnetic, and magnetoelectric effects. Some competition among these effects can lead to suitable solutions found for the following three possible coupling mechanisms: eα – hε, eµ – hα, εµ – α2. Here, the mechanically free interface between the solid and a vacuum was considered. This report discovers the twelfth (thirteenth) new SH-SAW for the magnetically closed (electrically open) case and continuity of both the normal component of the electrical (magnetic) displacement and the electrical (magnetic) potential when the coupling mechanism eα – hε (eµ – hα) works. The propagation velocities were obtained in explicit forms that take into account the contribution of the vacuum material parameters. The discovered waves were then graphically studied for the purpose of disclosing the dissipation phenomenon (the propagation velocity becomes imaginary) caused by the coupling with the vacuum properties. The obtained results can be useful for further investigations of interfacial and plate SH-waves, constitution of technical devices, nondestructive testing and evaluation, and application of some gravitational phenomena.
1. Introduction
According to their book [], Landau and Lifshits have predicted the existence of the linear magnetoelectric (ME) effect in 1956. Landau has demonstrated the problem of the existence of the ME effect in solids for Dsyaloshinskii. The latter has theoretically found and reported in a 1959 paper [] that antiferromagnetic Cr2O3 can possess the ME effect. One year later, Astrov [] experimentally confirmed the existence of this effect in Cr2O3. The ME effect can be found in a class of ME solids called piezoelectromagnetics (PEMs), also known as magnetoelectroelastics (MEEs). These continuous media can possess both the piezoelectric and piezomagnetic effects resulting in the existence of the ME effect. The ME solids relate to smart materials because any change in the magnetic subsystem can cause some change in the electrical subsystem via the mechanical subsystem, or vice versa. Up to today, various ME materials (composites) were found (created) and they were then investigated both experimentally and theoretically. However, only a few are suitable for commercial use. Some recent reviews on the ME materials and their applications are listed in References [,,,,]. The reader can also find about one hundred reviews on the subject in the literature because the smart ME materials can be used for different applications including spintronics, i.e., the future electronics without free charge carriers.
The linear ME effect characterized by the nonsymmetric second-rank tensor of the electromagnetic constants is quite small. Therefore, creation of two-phase piezoelectric-piezomagnetic composites is commercially required in order to enhance the value of the electromagnetic constant and to have samples with stronger ME effect. Concerning the ME composites, Scott has stated in his recent review [] that the outstanding PEM composite PZT–Terfenol-D is competitive with some respects to SQUID superconducting devices [] because such multiferroic composites have already accomplished the level of commercial technical devices, for instance, weak magnetic field sensors. Also, it is worth noting that some created composite devices [] can cost as much as a one cent coin and have linear dimensions significantly smaller than the coin radius. The ME effect of the composites can be even several orders stronger than that for the ME monocrystals. Concerning the ME monocrystals, a recent review by Kimura [] has stated that the unique monocrystal Sr3Co2Fe24O41 was discovered in 2010. This Z-type hexagonal ferrite actually possesses the realizable ME effect appropriate for practical and commercial employments.
The piezoelectric, piezomagnetic, and magnetoelectric properties can be found simultaneously in piezoelectromagnetic composites or metamaterials. The metamaterials cannot be found in nature and represent special class of magnetoelectric composite materials. Extensive investigations of their properties begun at the beginning of the 21st century []. A handbook [] combines review articles on physics and applications of metamaterials by authors from many international research centers. Such smart materials are already used today in medicine [] and optical nanoantennas []. Also, smart piezoelectromagnetic composites can be used instead of conventional piezoelectric materials. The exploitation of piezoelectromagnetics instead of piezoelectrics is more preferable to experimentally generate anti-plane polarized (surface) acoustic waves with noncontact methods. For this purpose, the electromagnetic acoustic transducers (EMATs) as the famous noncontact method [,,] can be used.
Today there is a single review paper written by the author and published in 2013 []. This review touches upon the acoustic waves’ propagation with the anti-plane polarization along the free surface of hexagonal (6 mm) PEM solids. The propagation of these shear-horizontal surface acoustic waves (SH-SAWs) is studied when the ME effect is taken into account. Also, extra four new SH-SAWs were recently discovered [,]. Some of the new waves studied [] can have a dramatic dependence on the ME effect. These four new SH-SAWs must be added to the known seven new SH-SAWs discovered by the author in a 2010 book [] and three SH-SAWs by Melkumyan introduced in his 2007 paper []. The latter three SH-SAWs were also studied in [,]. They are naturally called the piezoelectric exchange surface Melkumyan (PEESM) wave, the piezomagnetic exchange surface Melkumyan (PMESM) wave, and the surface Bleustein-Gulyaev-Melkumyan (BGM) wave for convenience. The latter Melkumyan SH-SAW was called the BGM wave in order to have an association with the well-known BG-wave [,] existing in purely piezoelectric (or purely piezomagnetic) materials of class 6 mm. However, Bleustein and Gulyaev did not study any wave propagation in a PEM continuum possessing the ME effect. Note that according to Zakharenko, A.A. [], theoretical work [,] has also confirmed the existence of the aforementioned three Melkumyan SH-SAWs.
In 2003, Chapter 7 of dissertational work [] by Darinskii has discussed the wave existence in piezoelectric-piezomagnetic solids (piezoelectromagnetics). Chapter 7 was written following the theoretical investigations published in 1992 [] and 1994 [], respectively. Following the discussions [], it is expected that at least two SAWs, namely one in-plane polarized wave and one anti-plane polarized wave can propagate in piezoelectromagnetics. This is similar to the wave propagation in the pure piezoelectrics or the pure piezomagnetics. Darinskii has also assumed that more than two SAWs can propagate in such media possessing the aforementioned three effects due to a competition among the effects. However, he has written down that such possibility was not recorded. As an example, a propagation velocity was obtained in an explicit form for the case of the mechanically clamped surface. This final result depends on the coefficient of the magnetoelectromechanical coupling (CMEMC) when the dependence on the electromagnetic constant was neglected, i.e., the ME effect was not taken into account. It is obvious that the problem of wave propagation in such smart piezoelectromagnetic materials relates to synergetics that studies various complex systems.
In comparison, the theory developed by the author of this report utilizes the CMEMC depending on the electromagnetic constant α. It is obvious that this material constantly participates in three possible CMEMC coupling mechanisms such as eα – hε, eµ – hα, and εµ – α2. Besides the mass density ρ there are the following material constants for a piezoelectromagnetics: the elastic stiffness constant C, piezoelectric constant e, piezomagnetic coefficient h, dielectric permittivity coefficient ε, magnetic permeability coefficient μ, and aforementioned electromagnetic constant α. It is obvious that two first aforementioned CMEMC coupling mechanisms represent some exchange mechanisms and do not pertain entirely to one of three effects mentioned above. It is possible to assume that only the third mechanism is relevant to the ME effect. Exploiting one of the coupling mechanisms, suitable solutions can be found. This was discussed in reference []. This theoretical report investigates the SH-wave propagation in the transversely isotropic (6 mm) PEM solids and adds the twelfth and thirteenth new SH-SAWs to the family of already known eleven SH-SAWs briefly discussed above. To obtain the explicit forms for the new SH-wave velocities is the main purpose of the following three sections.
2. Theory Leading to an Extra Two New Results
Consider a bulk PEM monocrystal or composite possessing the hexagonal symmetry of class 6 mm. Let us study the wave propagation in such transversely isotropic ME medium exploiting the rectangular coordinate system {x1, x2, x3} also known as the Cartesian coordinate system invented by Descartes, the famous mathematician. First of all, it is necessary to choose proper propagation direction in order to deal with the pure SH-wave coupled with both the electrical (φ) and magnetic (ψ) potentials. The fitting propagation direction for the 6 mm solid is described in reference []. For this purpose, the propagation direction is managed along the x1-axis and perpendicular to the 6-fold symmetry axis. The x2-axis is directed along the 6-fold symmetry axis and the x3-axis is managed along the normal to the free surface of the ME material. The coordinate beginning is situated at the interface between the solid and a vacuum and the x3-axis negative values are managed towards the depth of the piezoelectromagnetics. It is very important to state that the problem of acoustic wave propagation coupled with both the electrical and magnetic potentials is treated. Therefore, the quasi-static approximation must be used here because the speed of any acoustic wave is five orders slower than the speed of the electromagnetic wave in a vacuum or solid.
As a result of the chosen propagation direction, the differential form of the coupled equations of motion [,,,,,] written in the common form can be separated into two independent sets of equations of motion. The first set is for the purely mechanical wave with the in-plane polarization coupling two mechanical displacements U1 and U3 along the x1-axis and x3-axis, respectively. Besides, the second set is for the mechanical SH-wave possessing the mechanical displacement U2 coupled with both the electrical and magnetic potentials. This theoretical report has an interest in the study of the second case. So, the differential form of the coupled equations of motion representing the partial differential equations of the second order can be composed as follows:
In coupled Equation (1), the material parameters such as ρ, C, e, h, ε, μ, and α are defined in the previous section, the mechanical displacement along the x2-axis is U = U2, and t is time. It is natural to write down the solutions of Equation (1) in the following plane wave form:
In Equation (2), the index I can be equal to 2, 4, 5. It is necessary to keep in mind that the electrical potential is φ = U4 and the magnetic potential is ψ = U5. The unknown coefficients U0, φ0, and ψ0 must be determined. The imaginary unity is defined by j = (– 1)1/2 and ω is the angular frequency. The wavevector components are written as follows: {k1,k2,k3} = k{n1,n2,n3}, where k is the wavenumber in the propagation direction because the directional cosines are n1 = 1, n2 = 0, and n3 ≡ n3. A substitution of solutions (2) into Equation (1) leads to the tensor form of the coupled equations of motion known as the Green-Christoffel equation. The tensor form then reads:
In Equations’ set (3), Vph = ω/k stands for the phase velocity, Vt4 = (C/ρ)1/2 denotes the purely mechanical bulk acoustic wave (BAW) with the shear-horizontal (SH) polarization, and . All the suitable eigenvalues n3 must be determined and the corresponding eigenvector components U0, φ0, and ψ0 must be also obtained by resolving the set of three homogeneous Equations (3). For this purpose, an expansion of the determinant of the coefficient matrix in Equation (3) leads to a sixth order polynomial in one indeterminate n3. Therefore, six suitable eigenvalues n3 must be found. They read as follows:
where
In Equation (6), Vtem represents the velocity of the SH-BAW coupled with both the electrical and magnetic potentials via the following coefficient of the magnetoelectromechanical coupling (CMEMC):
In Equation (7), it is convenient to distinguish the following three CMEMC coupling mechanisms discussed in reference []:
For the study of the surface wave propagation in the solid, it is necessary to leave only three suitable polynomial roots of six to deal with the wave damping towards the depth of the piezoelectromagnetics. For the coordinate system described above at the beginning of this section, the suitable values of n3 must have a negative sign. Let us use the first, third, and fifth eigenvalues as the suitable ones. Therefore, it is necessary to find now the eigenvector components by substituting the suitable eigenvalues into Equation (3). The problem of the suitability of the eigenvectors was also recently discussed in reference []. The reader can do the same and find the following forms of the first set of the eigenvector components:
because
In eigenvector components (12), the nondimensional parameter is defined by Equation (15) and combines the terms with the electromagnetic constant α in the CMEMC. Also, the other nondimensional parameter called the coefficient of the electromechanical coupling (CEMC) is defined by Equation (16). The reader can also find the common factors before the eigenvector components in Equation (12). It is necessary to leave them because the dimension of corresponding eigenvector components of different eigenvectors must be the same and they can play a crucial role for some final results of obtaining propagation velocity. Indeed, Equation (12) demonstrates three different forms of the eigenvector. However, they are actually identical. It is thought that it is convenient to utilize the first form when different determinants of the boundary conditions are constructed. They will be used in the following sections. The second form of the eigenvector in Equation (12) uses the nondimensional parameters , , and defined above that can demonstrate a physical sense of the components. The third form already utilizes the CMEMC coupling mechanisms introduced after the CMEMC (7). Other different forms of the eigenvector components are discussed in reference [] stating that forms (12) are preferable. It is possible to briefly note here that eigenvectors (11) are in general uncertain. To resolve this uncertainty, the nonzero eigenvector components (11) can be connected with the corresponding eigenvector components (12) because eigenvector (12) is certain.
So, one has to be familiar that there is the connection among the corresponding eigenvector components via the first CMEMC coupling mechanism. This reads as follows:
There is also the second set of the eigenvector components for the same eigenvalues defined by Equations (4) and (5). These components can be introduced as follows:
where
In eigenvector components (19) there is the nondimensional parameter called the coefficient of the magnetomechanical coupling (CMMC) defined by Equation (21). The connection of the corresponding eigenvector components is plausible through the following second CMEMC coupling mechanism:
Using Equation (2) and the found eigenvalues with the eigenvector components, the complete parameters such as the complete mechanical displacement (), complete electrical potential (), and complete magnetic potential () can be naturally written as follows:
where the index I runs its values of 2, 4, 5.
It is possible to finally state that the studied case relates to the three-partial wave problem because each complete parameter (23) depends on three terms with the weight factors F(1), F(3), and F(5). Let us further use F1, F2, and F3 instead of F(1), F(3), and F(5), respectively. Also, it is natural to further exploit F = F1 + F2 because there are two identical eigenvalues (4) that give two identical eigenvectors (11) or (18).
Exploiting complete parameters (23), various determinants of the boundary conditions can be composed. The possible forms of such determinants depend on the mechanical, electrical, and magnetic boundary conditions at the interface between a vacuum and the piezoelectromagnetic solid. Several decades ago Al’shits, Darinskii, and Lothe [] perfectly described possible boundary conditions for the treated case of the wave propagation along the surface of the piezoelectromagnetics. The used mechanical boundary condition at the interface relates to the normal component of the stress tensor: σ32 = 0. The electrical boundary conditions can be the continuity of the normal component of the electrical displacement D3, continuity of the electrical potential φ, D3 = 0, or φ = 0. Besides, the possible magnetic boundary conditions are the continuity of the normal component of the magnetic displacement B3, continuity of the magnetic potential ψ, B3 = 0, or ψ = 0. It is reasonable that all the boundary conditions will not be given in this report in their explicit final forms because the reader can find them in book [] and open access publication [,].
Also, the reader must be familiar with the following vacuum parameters: the dielectric permittivity constant is ε0 = 10−7/(4πCL2) = 8.854187817 × 10−12 (F/m), where CL = 2.99782458 × 108 (m/s) is the speed of light in a vacuum. The magnetic permeability constant is μ0 = 4π × 10−7 (H/m) = 12.5663706144 × 10−7 (H/m). The constant ε0 is the proportionality coefficient between the electric induction Df and the electric field Ef: Df = ε0Ef, where the superscript “f” is used for the free space (vacuum) and the electric field components can be defined as follows: Efi = − ∂φf/xi. Similarly, the constant μ0 is the proportionality coefficient between the vacuum magnetic induction Bf and the vacuum magnetic field Hf: Bf = μ0Hf, where the magnetic field components can be defined as follows: Hfi = − ∂ψf/xi. So, Laplace’s equations such as Δφf = 0 and Δψf = 0 can be used for the potentials in a vacuum. It is also required that both the potentials must exponentially vanish in a vacuum far from the free surface of the piezoelectromagnetics. Utilizing the vacuum parameters, let’s treat some additional new cases that were not recorded in book [] and reference [,,]. This is the main purpose of the following two sections.
3. The New Results for the Case of B3 = 0 and Continuity of Both D3 and φ
This is the case of the continuity of the electric displacement D3. Therefore, the vacuum electric constant ε0 introduced in the previous section must be included in the further calculations. Using the first set of the eigenvector components given in Equations (11) and (12), the coupled three equations for this case (Equations (188), (189), and (190) in book []) are then rewritten as follows:
where
It is necessary here to state that the set of Equations (24) already embodies three consistent equations in two unknowns because the third equation is the main equation and represents a sum of the rest two. It is unnecessary to acquaint the reader with all the relatively complicated mathematics leading to final Equations’ set (24). The reader can read book [] because the case of this section was treated in Chapter XIII of the book. Therefore, Equations’ set (24) epitomizes Equations (188), (189), and (190) in the book chapter when the vacuum electric constant ε0 is taken into account.
Therefore, the resulting propagation velocity exemplifies the velocity Vnew5 of the fifth new SH-SAW discovered in book []:
In Equation (26), the parameter bn5 already includes the vacuum electric constant ε0 that is missing in the book. Therefore, this parameter can be expressed as follows:
Setting ε0 = 0, this parameter can be simplified and written similar to the result obtained in book [] and studied in reference []:
where VEM = (εμ)−1/2 and Vα = 1/α stand for the electromagnetic wave speed and the exchange speed, respectively.
Also, it is crucial to state that final results (27) and (28) relate to the third coupling mechanism of the CMEMC defined by Equation (10). One can also check that result (28) is also true for the following electrical and magnetic boundary conditions: φ = 0 and ψ = 0 that also supports the propagation of the surface Bleustein-Gulyaev-Melkumyan wave mentioned above in Introduction. It is obvious that zero electromagnetic constant, α = 0, provides bn5 = 0 in Equations (27) and (28) and Vnew5 = Vtem occurs in Equation (26). This means that the magnetoelectric effect is vital for the existence of the fifth new SH-SAW. Indeed, as soon as α <> 0, the fifth new SH-SAW can propagate. This is similar to the eighth and tenth new SH-SAWs discovered in reference [,], respectively, and studied in reference []. However, the existence conditions for the latter two new SH-SAWs are more complicated. These SH-SAWs cannot propagate in some PEM (composite) solids of class 6 mm [] and require large enough value of the electromagnetic constant α. Generally, the value of the α is very small for real piezoelectromagnetics that are available today for commercial aims.
Next, it is possible to treat a new possible case that was not recorded in previous work [,,]. This new case pertains to the first coupling mechanism (8) of the CMEMC. Consequently, one has to fittingly reform Equations’ set (24). To get the suitable new set of three consistent equations, the following corresponding factors must be employed for three Equations (24): , , and . In the reformed Equations (24) with the factors, the first equation is already the main equation that represents a sum of the rest two. As a result, a successive subtraction of the last two equations from the first one leads to the following equation for propagation velocity of the twelfth new SH-SAW:
where
If one does not want to use the vacuum electric constant ε0 in calculations setting ε0 = 0, Equation (30) reduces to the following form:
It is indispensable to briefly discuss that in this case, α = 0 does not ban the SH-SAW existence. Using Equation (7) for and (15) for , the reader can check this statement. Indeed, parameter bn12(α = 0) reduces to the following form:
4. The New Results for the Case of D3 = 0 and Continuity of Both B3 and ψ
For this case, the continuity condition for the magnetic displacement B3 allows one to include the vacuum magnetic constant µ0. Using the second set of the eigenvector components given in Equations (18) and (19), the three coupled equations (namely, Equations (185), (186), and (187) from book []) can be rewritten in the following forms:
In Equations’ set (33), the second equation represents the main equation that can be formed by a sum of the first and third equations. Taking into account the vacuum parameter µ0, the velocity Vnew5 of the fifth new SH-SAW defined by Equation (26) depends on the parameter bn5. This parameter bn5 already includes the vacuum magnetic constant µ0 instead of ε0. So, the parameter bn5 reads:
To obtain the extra new result, it is necessary to multiply the three equations in set (33) by the following factors: , , and , respectively. This transformation of three Equations (33) sets the first equation as the main equation. Therefore, the second and third transformed equations must be successively subtracted from the first. This leads to the existence of the thirteenth new result, namely the velocity Vnew13 of the thirteenth new SH-SAW that can be written as follows:
where
If the reader does not take into account the small vacuum parameter µ0 in (36), the parameter bn13 reduces to the following form:
It is also possible to inspect the limit case for the electromagnetic constant α = 0. With α = 0 in Equations (36) and (37), the parameter bn13 reduces to the following form:
Thus, it is possible to conclude that the magnetoelectric effect does not play a vital role in the existence of the 12th and 13th new SH-SAWs because α = 0 does not lead to the lack of the instability of the SH-BAW: Vnew12 ≠ Vtem due to bn12(α = 0) ≠ 0 in Equation (32) and Vnew13 ≠ Vtem due to bn13(α = 0) ≠ 0 in Equation (38). It is obvious that some graphical investigations of the new results obtained in both this section and the previous sections are required. Also, it is possible to demonstrate the influence of the inclusion of the corresponding vacuum parameter (ε0 or µ0) in the calculations. This is the main purpose of the following section.
5. Numerical Results and Discussion
It is necessary to numerically investigate the theoretical results obtained in the previous two sections. The obtained explicit forms for the new SH-SAW velocities are quite complicated. Therefore, they can be studied numerically with discussion in this section below. Obtained Equations (29) and (35) in the third and fourth sections, respectively, are final and have suitable forms for further numerical study. For the calculations, the material parameters can be borrowed from reference [,,,]. Let us use the material parameters for two piezoelectromagnetic materials (composites BaTiO3–CoFe2O4 and PZT-5H–Terfenol-D) given in references [,]. The PZT-5H–Terfenol-D material parameters are: C = 1.45 × 1010 (N/m2), e = 8.5 [C/m2], h = 83.8 (T), ε = 75.0 × 10−10 (F/m), μ = 2.61 × 10−6 (N/A2), ρ = 8500 (kg/m3). This composite is known as one of the strongest piezoelectromagnetics. The composite material BaTiO3–CoFe2O4 possesses significantly weaker piezoelectromagnetic properties. Therefore, the reader has a contrast for comparison and better understanding of the problem of the SH-wave propagation in the piezoelectromagnetic materials. The BaTiO3–CoFe2O4 material parameters are: C = 4.4 × 1010 (N/m2), e = 5.8 (C/m2), h = 275.0 (T), ε = 56.4 × 10−10 (F/m), μ = 81.0 × 10−6 (N/A2), ρ = 5730 (kg/m3).
First of all, it is natural to contemplate the velocity Vnew5 of the fifth new SH-SAW given by Equation (26) and discovered in book [] several years ago. It depends on the parameter bn5 defined by Equations (27), (28), and (34). Equations (27) and (34) contain the constants ε0 and µ0, respectively. Figure 1 shows the dependence of the normalized velocity Vnew5/Vtem on the electromagnetic constant α, namely on the normalized parameter α2/εµ. It is obvious that the value of Vnew5/Vtem must be smaller than unity because one deals here with one of the surface acoustic waves. Also, the value of the α2/εµ must be confined between zero and unity to satisfy the limitation condition such as α2 < εµ [,]. The insertion in Figure 1 demonstrates that at α = 0 (i.e., α2/εµ = 0) there is Vnew5 = Vtem and then for the larger values of the α2/εµ, the SH-SAW speed Vnew5 is slightly slower than the SH-BAW speed Vtem. However there is Vnew5 = Vtem anew at α2/εµ ~ 0.1565 for BaTiO3–CoFe2O4 and at α2/εµ ~ 0.2793 for PZT-5H–Terfenol-D symbolizing the fact that there is no instability of the SH-BAW at such large enough values of α2/εµ. Indeed, Vnew5 = Vtem can occur when bn5 changes its sign at some certain value of α2/εµ > 0 given above for both the studied solids. One can also read paper [] on the study of the fifth new SH-SAW, in which the parameter Δ = Vtem – Vnew5 was used instead of Vnew5/Vtem. For α2 → εµ there is Vtem → ∞ due to and therefore, Vtem >> Vnew5 occurs resulting in Vnew5/Vtem → 0.
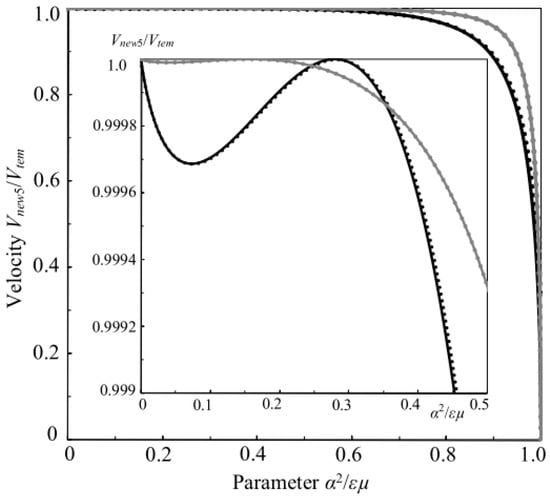
Figure 1.
The influence of the inclusion of the vacuum parameters ε0 and µ0 in the dependence of the normalized velocity Vnew5/Vtem on the electromagnetic constant α, i.e., on the nondimensional parameter α2/εµ. With Equation (26) using (28), the gray and black lines are calculated for BaTiO3–CoFe2O4 and PZT-5H–Terfenol-D, respectively. The dotted lines are calculated by using (27) with ε0 and (34) with µ0. Note that all three cases (27), (28), and (34) coincide which is clearly seen in the inclusion.
For the twelfth new SH-SAW defined by Equations (29), (30), and (31) there can occur more complicated dependence of the normalized velocity Vnew12/Vtem on the parameter α2/εµ. This is shown in Figure 2. For the case of result (29) with (30) when the parameter ε0 is included in the calculations, the velocity Vnew12 touches the SH-BAW speed Vtem at the same nonzero value of α2/εµ that is given in the context above for the case of Vnew5 = Vtem. After that right away, the speed Vnew12 rapidly decreases down to zero and then even becomes imaginary, illuminating the dissipation phenomenon. The velocity Vnew12 stays imaginary for the values of α2/εµ in the narrow α-range between α2/εµ ~ 0.1569 and ~0.1571 for BaTiO3–CoFe2O4 and between ~ 0.27975 and ~ 0.28046 for PZT-5H–Terfenol-D. These are quite narrow α-ranges for the existence of the dissipation phenomenon due to taking into account the vacuum electric constant ε0. It is expected that a narrow α-range for the dissipation phenomenon can exist even for a very weak PEM material and this α-range can be naturally shifted towards smaller values of the normalized parameter α2/εµ.
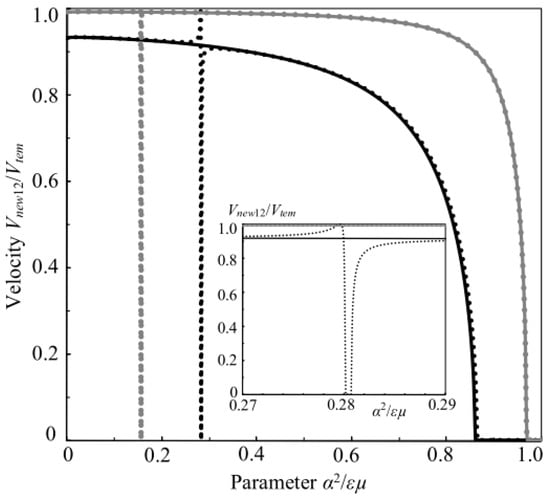
Figure 2.
The normalized velocity Vnew12/Vtem versus the nondimensional parameter α2/εµ. The gray and black lines are for BaTiO3–CoFe2O4 and PZT-5H–Terfenol-D, respectively. Using Equation (29), the dotted and solid lines are for the cases with the parameter ε0 in Equation (30) and without ε0 in Equation (31), respectively. The insertion shows the dissipation phenomenon by the dotted black line at α2/εµ ~ 0.28 for PZT-5H–Terfenol-D.
Using the dotted black line for PZT-5H–Terfenol-D shown in the insertion of Figure 2, it is possible to note that Vnew12 = Vtem occurs when bn12 = 0, i.e., bn12 defined by Equation (30) changes its sign. Indeed, the value of bn12 rapidly approaches an infinity and also quickly returns from an infinity already with the changed sign. It is clearly seen in Figure 2 that these peculiarities of Vnew12 = Vtem and the imaginary velocity Vnew12 within the narrow α-range are absent for the case of Equation (29) with (31). Also, both cases (30) and (31) have the imaginary values of the velocity Vnew12 at some large values of α2/εµ due to large values of (bn12)2 > 1: α2/εµ > ~ 0.96826 for BaTiO3–CoFe2O4 and α2/εµ > ~ 0.85933 for PZT-5H–Terfenol-D. Note that for the case without ε0 shown by the solid lines in Figure 2, this dissipation commences at slightly larger value of α2/εµ for PZT-5H–Terfenol-D. Such small discrepancy was not recorded for the weaker PEM composite BaTiO3–CoFe2O4.
It is also necessary to mention that the dissipation phenomenon can exist at very small values of α2/εµ that are smaller than some threshold value (α2/εµ)th for the 8th and 10th new SH-SAWs discovered in references [,], respectively. Some propagation peculiarities of the 8th and 10th new SH-SAWs were studied in reference []. If α2/εµ > (α2/εµ)th, the 8th and 10th new SH-SAWs can propagate. The value of the electromagnetic constant α is very small for real piezoelectromagnetic monocrystals and even composite materials. Therefore, the existence condition of α2/εµ > (α2/εµ)th for the 8th and 10th new SH-SAWs is extremely important. Also, the existence of the dissipation phenomenon with the imaginary propagation velocity at a narrow α-range, 0 < α2/εµ < (α2/εµ)th, is caused by the corresponding vacuum parameter, ε0 or µ0. Theoretical work [] also states that the 8th and 10th new SH-SAWs are apt for constitution of technical devices to study (to sense) the magnetoelectric effect.
Figure 3 shows the behavior of the normalized velocity Vnew13/Vtem in dependence on the nondimensional parameter α2/εµ for composite materials BaTiO3–CoFe2O4 and PZT-5H–Terfenol-D. The figure insertion illuminates the dependence of Vnew13(α) for small values of α2/εµ. It is clearly seen for one of the strongest PEM composites such as PZT-5H–Terfenol-D that the inclusion of the vacuum parameter µ0 in the calculations with Equations (35) and (36) can result in disappearance of the dissipation phenomenon existing at the large values of α2/εµ ~ 1. For the significantly weaker PEM composite such as BaTiO3–CoFe2O4, this phenomenon cannot exist. Also, the insertion clearly demonstrates that at the very small values of α2/εµ, the speed Vnew13(α → 0) is slower for the case of Equations (35) and (37) without the vacuum parameter µ0 in comparison with the case of Equations (35) and (36). This means that the penetration depth for the 13th new SH-SAW is larger for the latter case.
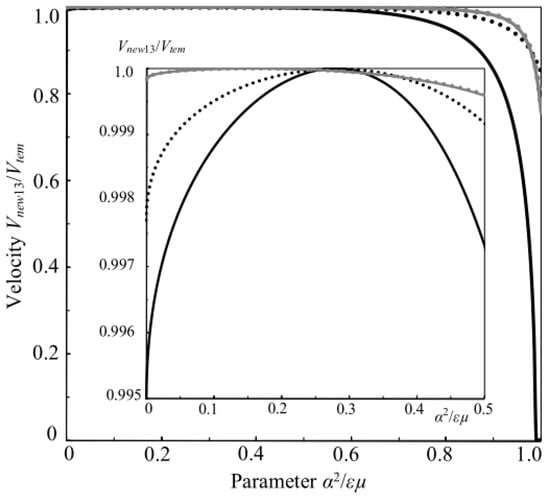
Figure 3.
The normalized velocity Vnew13/Vtem versus the nondimensional parameter α2/εµ. The gray and black lines are for BaTiO3–CoFe2O4 and PZT-5H–Terfenol-D, respectively. The dotted lines correspond to the calculations with Equation (35) when the parameter µ0 is included in Equation (36). The solid lines are for case (37) without the parameter µ0. The insertion shows the dependence for small values of α2/εµ.
It is well-known that experimentally measured values of the electromagnetic constant α are very small, α2 << εµ [] and []. This means that the aforementioned dissipation phenomenon cannot be reachable for all known PEM monocrystals and composites. Indeed, this research is primary and allows the further theoretical investigations of various SH-waves in PEM plates. In general, the plate waves have the following peculiarity: at large values of the plate thickness the speed of the plate SH-wave must approach the speed of the corresponding SH-SAW. Therefore, it is helpful to know the characteristics of SAWs before development of any theory of SH-wave propagation in plates. It is well-known that plates are used for further miniaturization of various technical devices with a higher level of integration. Also, various SH-waves such as SH-SAWs and plate SH-waves can be significantly more sensitive to various chemicals. This fact is called for implementation in sensor technologies. These SH-waves can be also used in nondestructive testing and evaluation of the certain surfaces of various PEM solids.
Finally, it is necessary here to mention the recently developed theory concerning the coexistence of the electromagnetic and gravitational phenomena [,]. It is obvious that the obtained Equations (29) and (35) for the calculation of the 12th and 13th new SH-SAWs can be also true for the case when gravitational phenomena are exploited instead of the electromagnetic phenomena. Indeed, it is possible to use the material parameters corresponding to the purely gravitational case. In this case, speeds (29) and (35) will depend on the gravitational wave speed VGC = (γη)−1/2, where γ and η are the gravitic constant and cogravitic constant, respectively, instead of the electromagnetic wave speed VEM = (εμ)−1/2. For the purely electromagnetic case, it is also possible to state that speeds (29) and (35) depend on the speed of light in a vacuum, CL = (ε0μ0)−1/2 because ε0 = 1/(μ0CL2) and μ0 = 1/(ε0CL2). In the purely gravitational case, there are the vacuum gravitic constant γ0 = 1/(η0CL2) and the vacuum cogravitic constant η0 = 1/(γ0CL2) due to CL = (γ0η0)−1/2. However, it is expected that sound experimental verifications of some gravitational phenomena can be released only in several decades. For instance, the theoretically predicted existence of gravitational waves by Albert Einstein in 1916 [] was verified only in 2016 [] with very expensive experiments carried out by an international group consisting of over 1000 researchers. This happens due to the weakness of the gravitational phenomena. However, these phenomena are extremely important. Therefore, it is expected that it is preferable for the first time to deal with the electromagnetic phenomena regarding the experimental proof. In the case of the acoustic wave propagation in solids, taking into account both the gravitational and the electromagnetic phenomena can result in the dependence of the acoustic wave velocity on both the speeds VEM and VGC as well as on the speeds of the new fast waves that can propagate in both solids and a vacuum. In both continuous media the propagation speeds of the new fast waves can be thirteen orders faster than the speed of light. The propagation of these new fast waves [,] in a vacuum represents a great interest due to a possibility to develop the instant interplanetary communication []. For this purpose, it is necessary to focus on solutions of many theoretical, mathematical, experimental, and engineering problems that can lead to the development of perfect infrastructures for the instant interplanetary communication.
6. Conclusions
This theoretical study has obtained the explicit forms for the propagation velocities of the 12th and 13th new SH-SAWs that can propagate in the transversely isotropic piezoelectromagnetics of symmetry class 6 mm. The discovered new SH-waves correspond to different electrical and magnetic boundary conditions for the electrical and magnetic potentials and the normal components of the electrical and magnetic inductions. This investigation also has an interest in the record of the influence of the inclusion of the corresponding vacuum parameter, ε0 or µ0, on the propagation velocity of the new SH-SAWs. For the fifth new SH-SAW discovered in book [], it was found that the influence of the inclusion of the ε0 or µ0 is not significant and these vacuum parameters can be neglected in calculations. However, this is not true for the 12th and 13th new SH-SAWs discovered in this paper.
It was found that with the vacuum electric constant ε0 for the 12th new SH-SAW there can be found one extra narrow α-range for α2/εµ << 1, in which the propagation velocity becomes imaginary, i.e., there is some dissipation. This dissipation phenomenon can also exist at large values of the nondimensional parameter α2/εµ < ~ 1. For the 13th new SH-SAW there is the other picture: the presence of the vacuum magnetic constant µ0 can result in the disappearance of the dissipation phenomenon for the values of the α2/εµ being just below unity. This was found only for PZT-5H–Terfenol-D representing one of the strongest PEM solids. The obtained theoretical results can be useful for the further investigations of the SH-wave propagation in PEM plates, nondestructive testing and evaluation, constitution of various technical devices based on PEM SH-SAWs. Also, some gravitational phenomena discussed in recently developed theory [] and [] can be applied as a supplementary to the electromagnetic properties or instead of them.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics. Electrodynamics of Continuous Media, 1st ed.; Gostekhizdat: Moscow, Russia, 1957; Volume 8, p. 532. [Google Scholar]
- Dzyaloshinskii, I.E. On the magneto-electrical effects in antiferromagnetics. Sov. Phys. J. Exp. Theor. Phys. 1960, 10, 628–629. [Google Scholar]
- Astrov, D.N. The magnetoelectric effect in antiferromagnets. Sov. Phys. J. Exp. Theor. Phys. 1960, 11, 708–709. [Google Scholar]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123–R152. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.; Morkoç, H. Microwave ferrites, Part 2: Passive components and electrical tuning. J. Mater. Sci. Mater. Electron. 2009, 20, 911–952. [Google Scholar] [CrossRef]
- Kimura, T. Magnetoelectric hexaferrites. Annu. Rev. Condens. Matter Phys. 2012, 3, 93–110. [Google Scholar] [CrossRef]
- Scott, J.F. Prospects for ferroelectrics: 2012–2022. ISRN Mater. Sci. 2013, 2013, 24. [Google Scholar] [CrossRef]
- Zakharenko, A.A. Piezoelectromagnetic SH-SAWs: A review. Can. J. Pure Appl. Sci. 2013, 7, 2227–2240. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Israel, C.; Mathur, N.D.; Scott, J.F. A one-cent room-temperature magnetoelectric sensor. Nat. Mater. 2008, 7, 93–94. [Google Scholar] [CrossRef] [PubMed]
- Vendik, I.B.; Vendik, O.G. Metamaterials and their utilization in techniques of ultrahigh frequencies: A review. J. Tech. Phys. 2013, 83, 3–28. [Google Scholar]
- Capolino, F. (Ed.) Phenomena and Theory of Metamaterials; CRC Press: Boca Raton, FL, USA, 2009; Volume 1, p. 926. [Google Scholar]
- Radu, X.; Garray, D.; Craeye, C. Toward a wire medium endoscope for MRI imaging. Metamaterials 2009, 3, 90–99. [Google Scholar] [CrossRef]
- Filonov, D.S.; Krasnok, A.E.; Slobozhanyuk, A.P.; Kapitanova, P.V.; Nenasheva, E.A.; Kivshar, Y.S.; Belov, P.A. Experimental verification of the concept of all-dielectric nanoantennas. Appl. Phys. Lett. 2012, 100, 2011131. [Google Scholar] [CrossRef]
- Thompson, R.B. Physical principles of measurements with EMAT transducers. In Physical Acoustics; Mason, W.P., Thurston, R.N., Eds.; Academic Press: New York, NY, USA, 1990; Volume 19, pp. 157–200. [Google Scholar]
- Hirao, M.; Ogi, H. EMATs for Science and Industry: Noncontacting Ultrasonic Measurements; Kuwer Academic: Boston, MA, USA, 2003. [Google Scholar]
- Ribichini, R.; Cegla, F.; Nagy, P.B.; Cawley, P. Quantitative modeling of the transduction of electromagnetic acoustic transducers operating on ferromagnetic media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2808–2817. [Google Scholar] [CrossRef] [PubMed]
- Zakharenko, A.A. New nondispersive SH-SAWs guided by the surface of piezoelectromagnetics. Can. J. Pure Appl. Sci. 2013, 7, 2557–2570. [Google Scholar] [CrossRef]
- Zakharenko, A.A. A study of new nondispersive SH-SAWs in magnetoelectroelastic medium of symmetry class 6 mm. Open J. Acoust. 2015, 5, 95–111. [Google Scholar] [CrossRef][Green Version]
- Zakharenko, A.A. Dramatic influence of the magnetoelectric effect on the existence of the new SH-SAWs propagating in magnetoelectroelastic composites. Open J. Acoust. 2015, 5, 73–87. [Google Scholar] [CrossRef][Green Version]
- Zakharenko, A.A. Propagation of Seven New SH-SAWs in Piezoelectromagnetics of Class 6 mm; Lambert Academic Publishing (LAP): Riga, Latvia, 2010; p. 84. [Google Scholar]
- Melkumyan, A. Twelve shear surface waves guided by clamped/free boundaries in magneto-electro-elastic materials. Int. J. Solids Struct. 2007, 44, 3594–3599. [Google Scholar] [CrossRef]
- Zakharenko, A.A. On wave characteristics of piezoelectromagnetics. Pramana J. Phys. 2012, 79, 275–285. [Google Scholar] [CrossRef]
- Zakharenko, A.A. Analytical investigation of surface wave characteristics of piezoelectromagnetics of class 6 mm. ISRN Appl. Math. 2011, 2011, 8. [Google Scholar] [CrossRef]
- Gulyaev, Y.V. Electroacoustic surface waves in solids. Sov. Phys. J. Exp. Theor. Phys. Lett. 1969, 9, 37–38. [Google Scholar]
- Bleustein, J.L. A new surface wave in piezoelectric materials. Appl. Phys. Lett. 1968, 13, 412–413. [Google Scholar] [CrossRef]
- Wei, W.-Y.; Liu, J.-X.; Fang, D.-N. Existence of shear horizontal surface waves in a magneto-electro-elastic material. Chin. Phys. Lett. 2009, 26, 3. [Google Scholar] [CrossRef]
- Darinskii, A.N. Waves in Finite Homogeneous and Layered Inhomogeneous Media with Arbitrary Anisotropy. Ph.D. Thesis, Institute of Crystallography, Russian Academy of Sciences, Moscow, Russia, 2003; pp. 127–148. (In Russian). [Google Scholar]
- Al’shits, V.I.; Darinskii, A.N.; Lothe, J. On the existence of surface waves in half-infinite anisotropic elastic media with piezoelectric and piezomagnetic properties. Wave Motion 1992, 16, 265–283. [Google Scholar] [CrossRef]
- Al’shits, V.I.; Darinskii, A.N.; Lothe, J.; Lyubimov, V.N. Surface acoustic waves in piezocrystals: An example of surface wave existence with clamped boundary. Wave Motion 1994, 19, 113–123. [Google Scholar] [CrossRef]
- Zakharenko, A.A. Peculiarities study of acoustic waves’ propagation in piezoelectromagnetic (composite) materials. Can. J. Pure Appl. Sci. 2013, 7, 2459–2461. [Google Scholar] [CrossRef]
- Gulyaev, Y.V. Review of shear surface acoustic waves in solids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998, 45, 935–938. [Google Scholar] [CrossRef] [PubMed]
- Zakharenko, A.A. Thirty Two New SH-Waves Propagating in PEM Plates of Class 6 mm; Lambert Academic Publishing (LAP): Riga, Latvia, 2012; p. 162. [Google Scholar]
- Pan, E. Exact solution for simply supported and multilayered magneto-electro-elastic plates. J. Appl. Mech. 2001, 68, 608–618. [Google Scholar] [CrossRef]
- Annigeri, A.R.; Ganesan, N.; Swarnamani, S. Free vibrations of simply supported layered and multiphase magneto-electro-elastic cylindrical shells. Smart Mater. Struct. 2006, 15, 459–467. [Google Scholar] [CrossRef]
- Zakharenko, A.A. Twenty Two New Interfacial SH-Waves in Dissimilar PEMs; Lambert Academic Publishing (LAP): Riga, Latvia, 2012; p. 148. [Google Scholar] [CrossRef]
- Berlincourt, D.A.; Curran, D.R.; Jaffe, H. Piezoelectric and piezomagnetic materials and their function in transducers. In Physical Acoustics; Mason, W.P., Ed.; Academic Press: New York, NY, USA, 1964; Volume 1A, pp. 169–270. [Google Scholar]
- Zakharenko, A.A. Some problems of finding of eigenvalues and eigenvectors for SH-wave propagation in transversely isotropic piezoelectromagnetics. Can. J. Pure Appl. Sci. 2014, 8, 2783–2787. [Google Scholar] [CrossRef]
- Zakharenko, A.A. Investigation of SH-wave fundamental modes in piezoelectromagnetic plate: Electrically closed and magnetically closed boundary conditions. Open J. Acoust. 2014, 4, 90–97. [Google Scholar] [CrossRef]
- Zakharenko, A.A. Consideration of SH-wave fundamental modes in piezoelectromagnetic plate: Electrically open and magnetically open boundary conditions. Waves Random Complex Media 2013, 23, 373–382. [Google Scholar] [CrossRef]
- Wang, B.-L.; Mai, Y.-W. Applicability of the crack-face electromagnetic boundary conditions for fracture of magnetoelectroelastic materials. Int. J. Solids Struct. 2007, 44, 387–398. [Google Scholar] [CrossRef]
- Liu, T.J.-C.; Chue, C.-H. On the singularities in a bimaterial magneto-electro-elastic composite wedge under antiplane deformation. Compos. Struct. 2006, 72, 254–265. [Google Scholar] [CrossRef]
- Zakharenko, A.A. On piezogravitocogravitoelectromagnetic shear-horizontal acoustic waves. Can. J. Pure Appl. Sci. 2016, 10, 4011–4028. [Google Scholar] [CrossRef]
- Zakharenko, A.A. The problem of finding of eigenvectors for 4P-SH-SAW propagation in 6 mm media. Can. J. Pure Appl. Sci. 2017, 11, 4103–4119. [Google Scholar] [CrossRef]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Ann. Phys. 1916, 4, 284. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 16. [Google Scholar] [CrossRef] [PubMed]
- Zakharenko, A.A. On necessity of development of instant interplanetary telecommunication based on some gravitational phenomena for remote medical diagnostics and treatment. Can. J. Pure Appl. Sci. 2018, 12, 4481–4487. [Google Scholar] [CrossRef]
- Zakharenko, A.A. On separation of exchange terms for four-potential acoustic SH-wave case with dependence on gravitational parameters. Hadron. J. 2018, 41, 349–370. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).