Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study
Abstract
1. Introduction
2. Fundamentals of Ultrasonic Waves
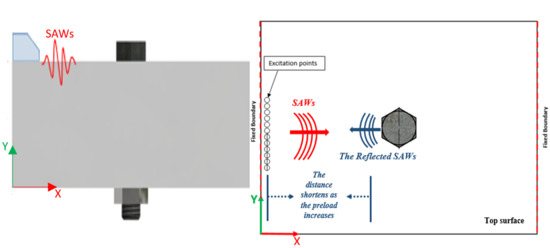
3. Simulation Work
3.1. Initial Simulation Studies
3.2. Preload Analysis
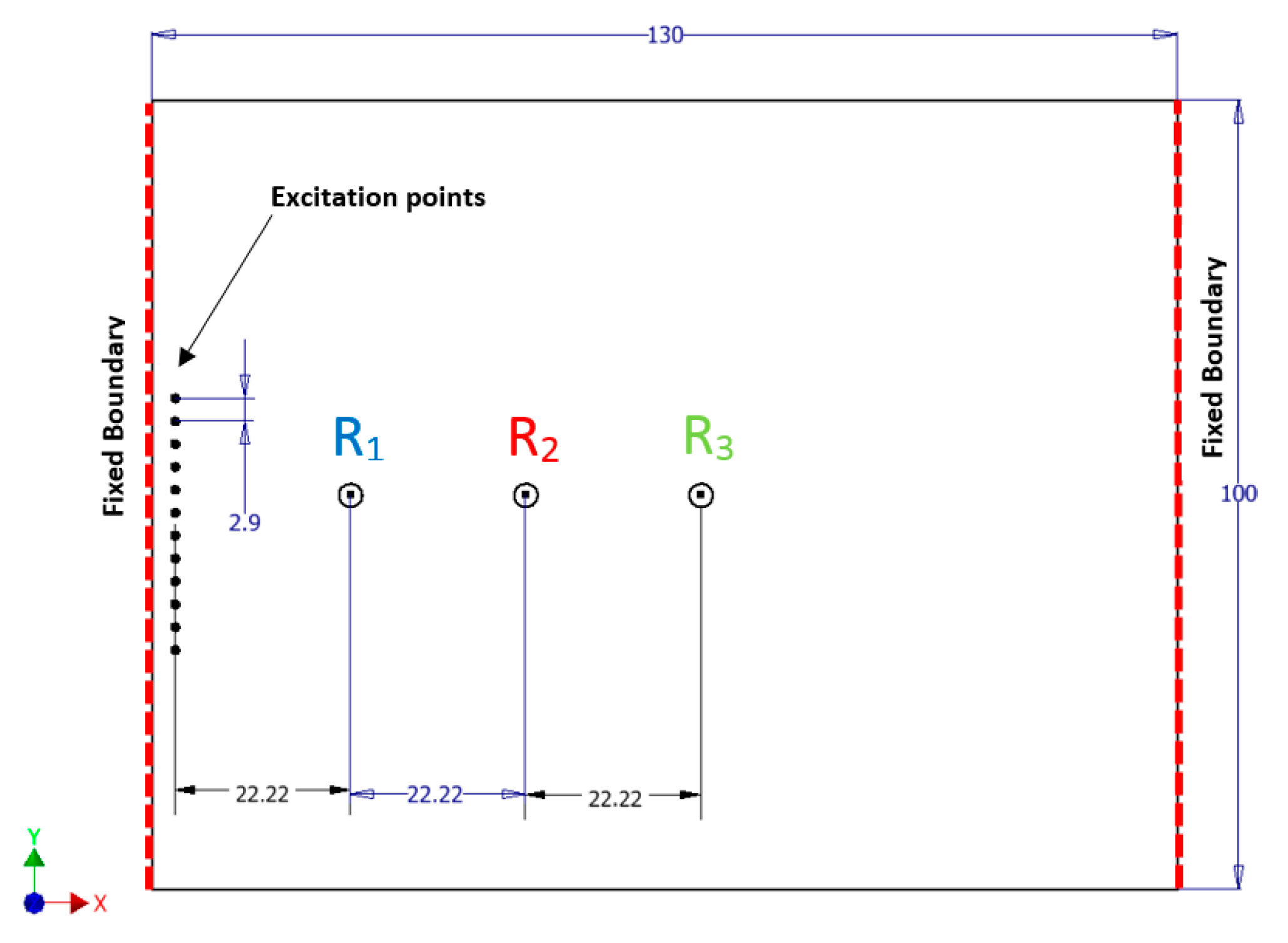
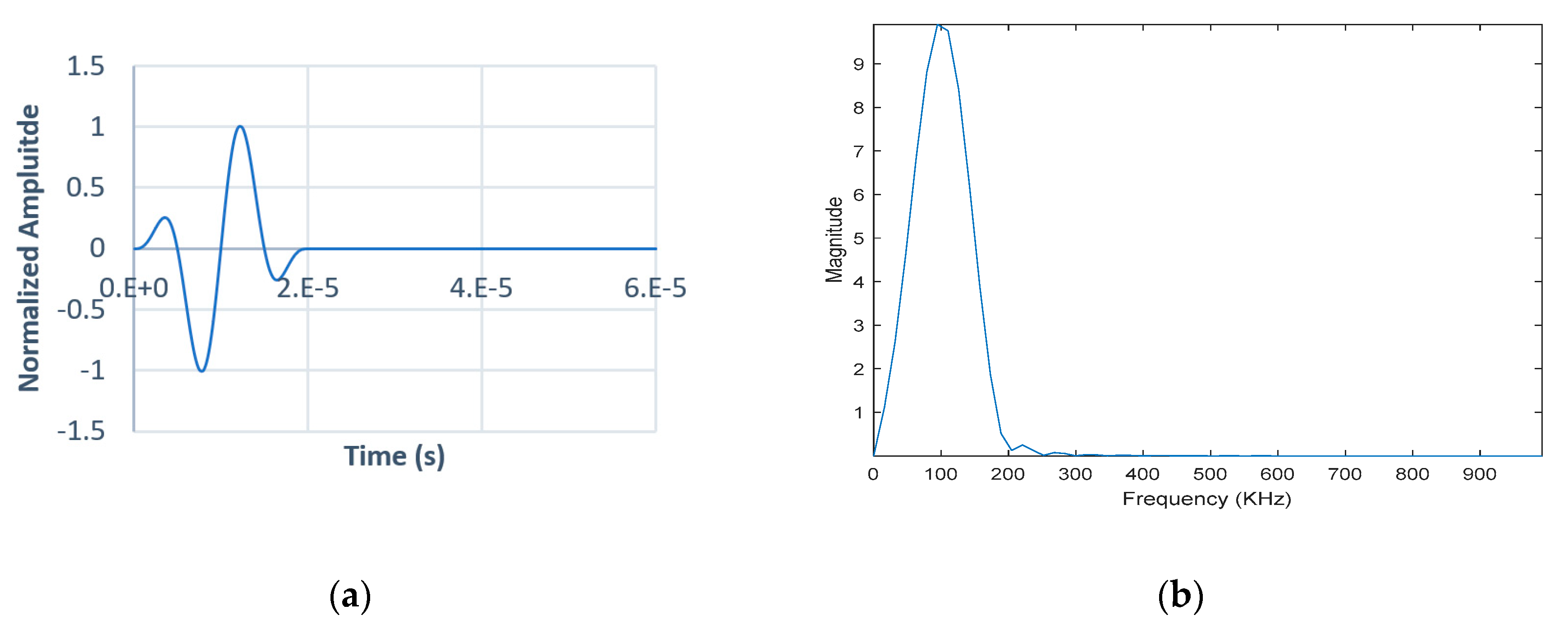
3.3. Transient Simulations
4. Results and Discussion
4.1. Verification Studies
4.2. A Comparison Between No Hole and Fully-Loosened Bolt
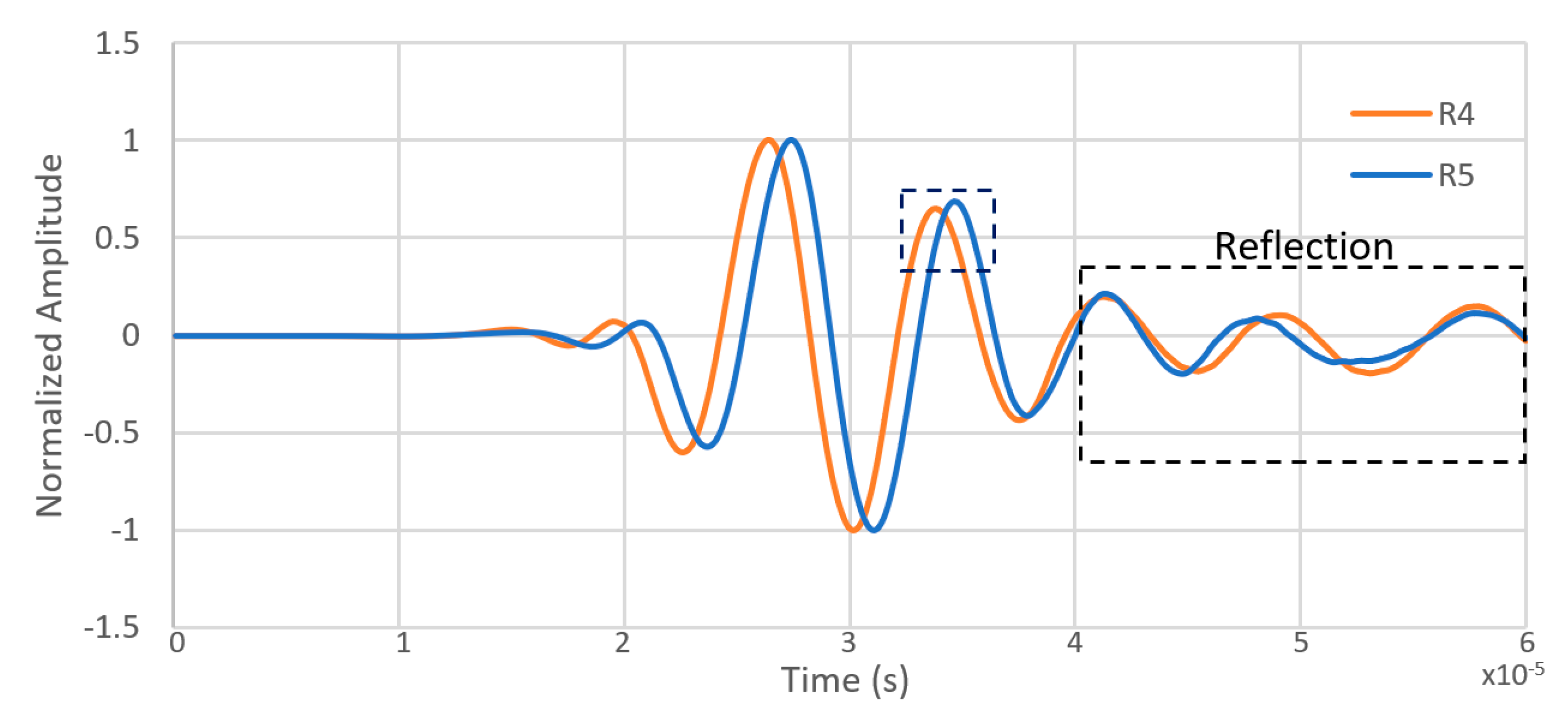
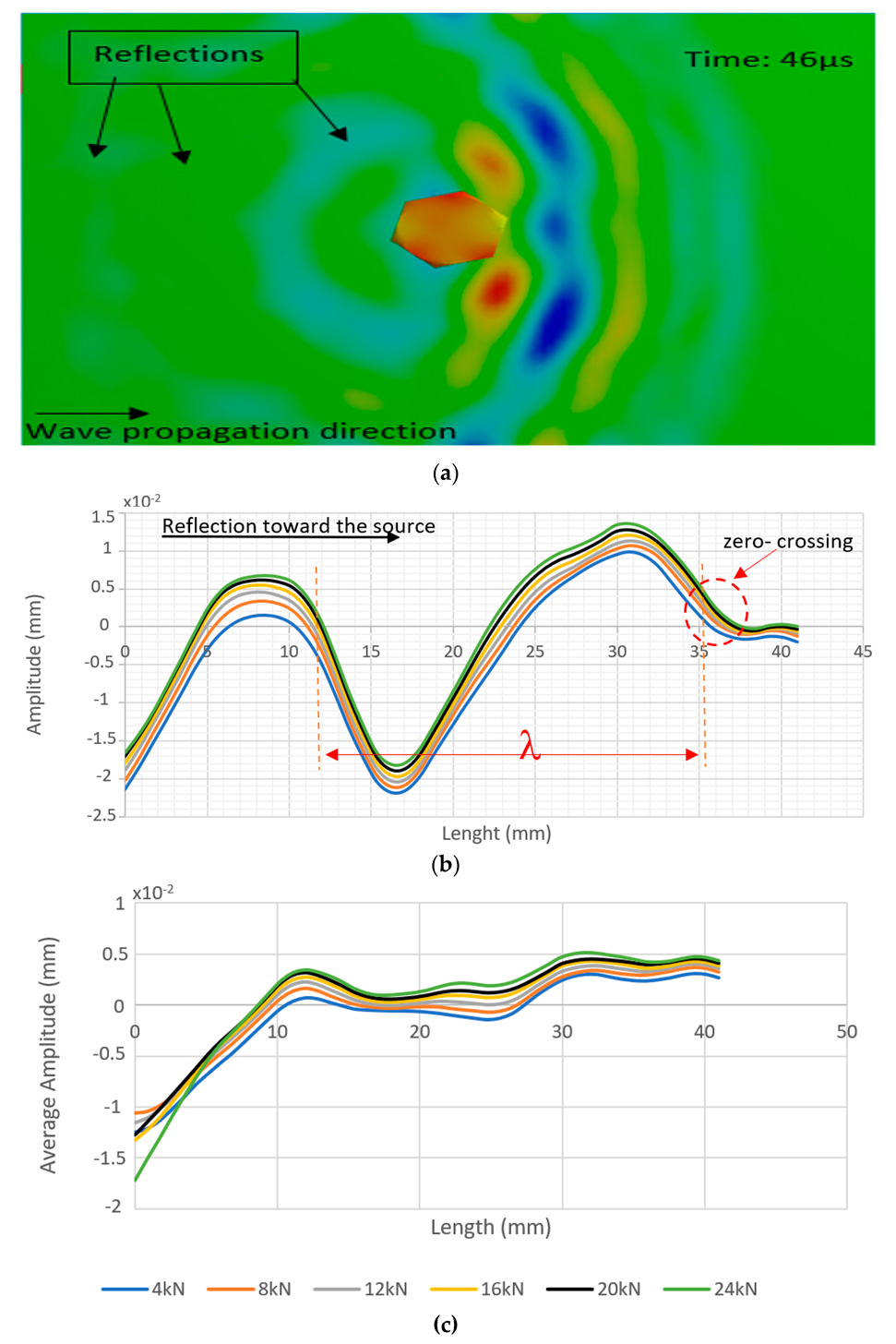
4.3. Detection of Wave Reflection
4.4. Particle Motion Along the Reflected Wave Propagation Path
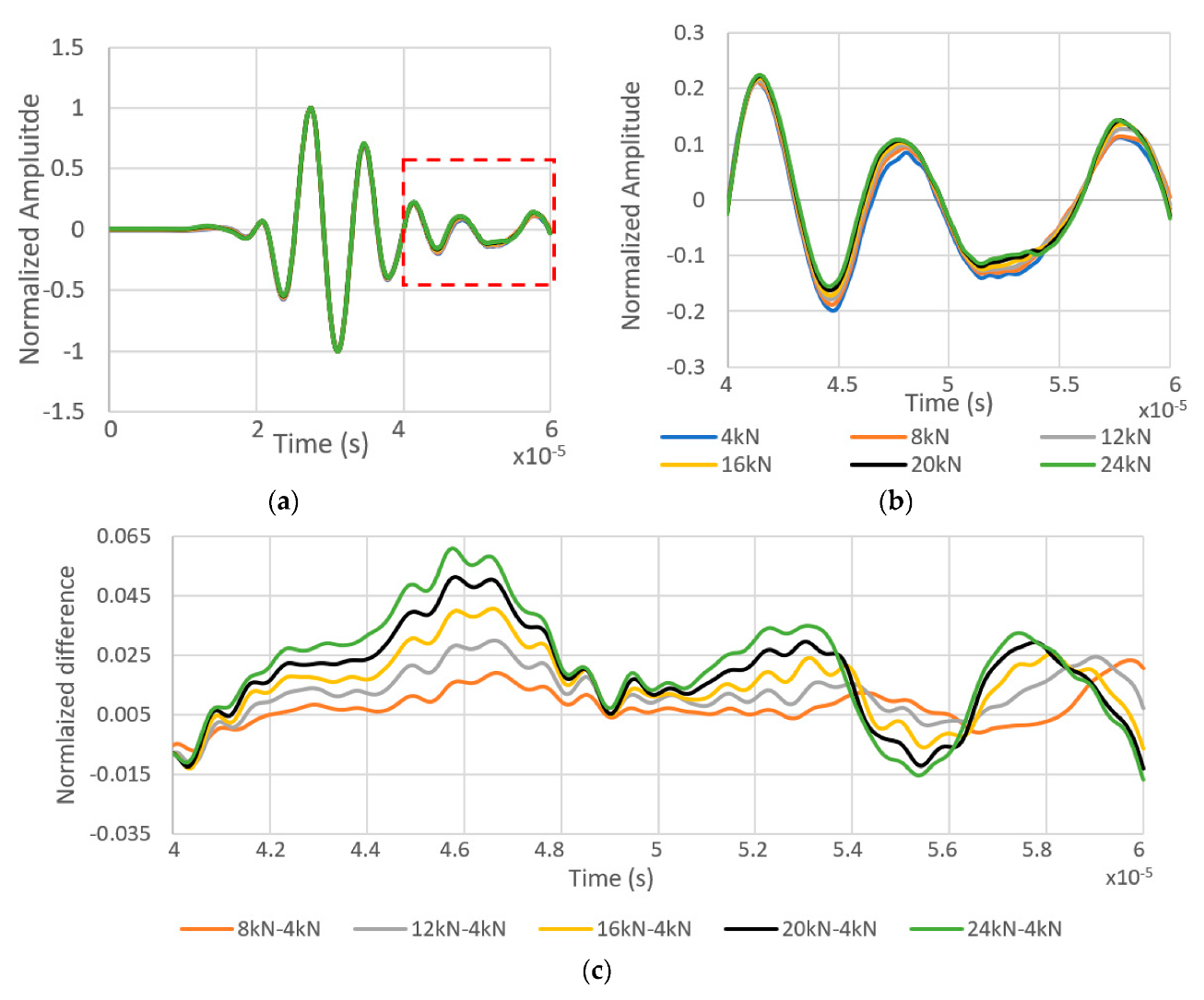
4.5. Time History of the Reflected Wave Near the Bolt
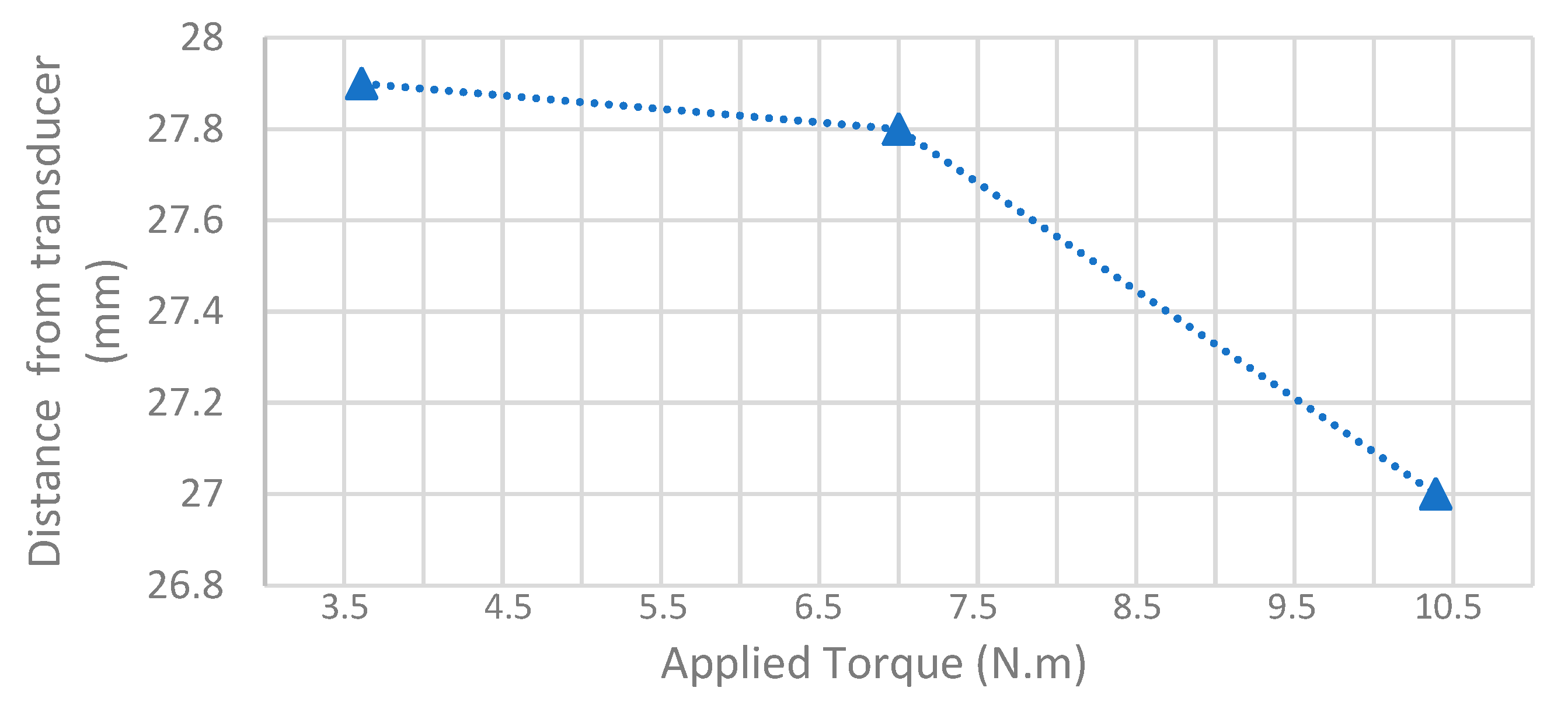
4.6. Simulation and Experimental Comparison
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sakai, T. Bolted Joint Engineering: Fundamentals and Applications; Beuth Verlag: Berlin, Germany, 2008. [Google Scholar]
- Jhang, K.-Y.; Quan, H.-H.; Ha, J.; Kim, N.-Y. Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement. Ultrasonics 2006, 44, e1339–e1342. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Song, G.; Liu, S.; Li, Y.; Xiao, H. Review of bolted connection monitoring. Int. J. Distrib. Sens. Netw. 2013, 9, 871213. [Google Scholar] [CrossRef]
- Chaki, S.; Corneloup, G.; Lillamand, I.; Walaszek, H. Combination of longitudinal and transverse ultrasonic waves for in situ control of the tightening of bolts. J. Press. Vessel Technol. 2007, 129, 383–390. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.; Wang, Z.; Li, Y. Proof-of-concept study of monitoring bolt connection status using a piezoelectric based active sensing method. Smart Mater. Struct. 2013, 22, 087001. [Google Scholar] [CrossRef]
- Martinez, J.; Sisman, A.; Onen, O.; Velasquez, D.; Guldiken, R. A synthetic phased array surface acoustic wave sensor for quantifying bolt tension. Sensors 2012, 12, 12265–12278. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors: With Piezoelectric Wafer Active Sensors; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- White, R.M. Surface elastic waves. Proc. IEEE 1970, 58, 1238–1276. [Google Scholar] [CrossRef]
- ANSYS®. Academic Research Mechanical Release 18.1, Static Structural, Engineering Data; ANSYS, Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Padilla, S.; Tufekcioglu, E.; Guldiken, R. Simulation and verification of polydimethylsiloxane (PDMS) channels on acoustic microfluidic devices. Microsyst. Technol. 2018, 24, 3503–3512. [Google Scholar] [CrossRef]
- Duan, W.; Niu, X.; Gan, T.-H.; Kanfoud, J.; Chen, H.-P. A Numerical Study on the Excitation of Guided Waves in Rectangular Plates Using Multiple Point Sources. Metals 2017, 7, 552. [Google Scholar] [CrossRef]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2008; Volume 8. [Google Scholar]
- Fastenal Technical Reference Guide. Available online: https://www.fastenal.com/content/documents/FastenalTechnicalReferenceGuide.pdf. (accessed on 13 March 2019).
- Vandermaat, D. Factors Affecting Pre-Tension and Load Carrying Capacity in Rockbolts—A Review of Fastener Design. In Proceedings of the 18th Coal Operators’ Conference, Wollongong, Australia, 7–8 February 2018. [Google Scholar]
- ANSYS®. Academic Research Mechanical, Products/Structures/Strength Analysis/Simulating Bolted Assemblies; ANSYS Inc.: Canonsburg, PA, USA, 2019; Available online: https://www.ansys.com/products/structures/strength-analysis/simulating-bolted-assemblies (accessed on 20 March 2019).
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. J. Acoust. Soc. Am. 1991, 89, 1159–1168. [Google Scholar] [CrossRef]
- Yasuda, T.; Pang, B.; Nishino, H.; Yoshida, K. Dynamic behavior evaluation of martensitic transformation in Cu-Al-Ni shape memory alloy using acoustic emission simulation by FEM. Mater. Trans. 2011, 52, 397–405. [Google Scholar] [CrossRef]
- Balvantín, A.J.; Diosdado-De-la-Peña, J.A.; Limon-Leyva, P.A.; Hernández-Rodríguez, E. Study of guided wave propagation on a plate between two solid bodies with imperfect contact conditions. Ultrasonics 2018, 83, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Fierro, G.P.M.; Ciampa, F.; Ginzburg, D.; Onder, E.; Meo, M. Nonlinear ultrasound modeling and validation of fatigue damage. J. Sound Vib. 2015, 343, 121–130. [Google Scholar] [CrossRef]
- Shen, Y.; Giurgiutiu, V. Effective non-reflective boundary for Lamb waves: Theory, finite element implementation, and applications. Wave Motion 2015, 58, 22–41. [Google Scholar] [CrossRef]
- Aiello, G.; Dilettoso, E.; Salerno, N. Finite element analysis of elastic transient ultrasonic wave propagation for NDT applications. In Proceedings of the 5th WSEAS/IASME International Conference on Systems Theory and Scientific Computation, Malta, 15–17 September 2005; World Scientific and Engineering Academy and Society (WSEAS): Stevens Point, WI, USA; pp. 114–119. [Google Scholar]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Draudviliene, L.; Aider, H.A.; Tumsys, O.; Mazeika, L. The Lamb waves phase velocity dispersion evaluation using an hybrid measurement technique. Compos. Struct. 2018, 184, 1156–1164. [Google Scholar] [CrossRef]
- Mažeika, L.; Draudvilienė, L. Analysis of the zero-crossing technique in relation to measurements of phase velocities of the Lamb waves. Ultragarsas Ultrasound 2010, 65, 7–12. [Google Scholar]
- Lynch, K.M.; Marchuk, N.; Elwin, M.L. Chapter 22—Digital Signal Processing. In Embedded Computing and Mechatronics with the PIC32; Lynch, K.M., Marchuk, N., Elwin, M.L., Eds.; Newnes: Oxford, UK, 2016; pp. 341–374. [Google Scholar]



| Target Surface | Source Surface | Contact Type |
|---|---|---|
| Clearance Hole | The Bolt Body | Frictional with Cf = 0.2 |
| Top Surface of the Plate | Bottom Surface of the Bolt Head | Frictional with Cf = 0.2 |
| The Bolt Body | The Nut Inner Surface | Bonded |
| Bottom Surface of the Plate | Top Surface of the Nut | Frictional with Cf = 0.2 |
| Theoretical Value (m/s) | Simulated Value (m/s) | Error (%) | |
|---|---|---|---|
| R1&R2 | 2917.58 | 2905.6 | −0.4 |
| R2&R3 | 2917.58 | 2926.48 | 0.3 |
| R1&R3 | 2917.58 | 2916.01 | −0.05 |
| Preload (kN) Torque (N.m) | 4 7.2 | 8 14.4 | 12 21.6 | 16 28.8 | 20 36 | 24 43.3 |
|---|---|---|---|---|---|---|
| Distance from the source | 17.4 | 16.7 | 16.4 | 16.2 | 15.9 | 15.5 |
| Wavelength (λ) | 22.31 | 22.25 | 25.23 | 25.12 | 25.23 | 25.5 |
| 34% | 67% | 100% | |
|---|---|---|---|
| Simulated shift from the max. allowable (mm) | 1.2 | 0.7 | 0 |
| Experimental shift from the max. allowable (mm) | 0.9 | 0.8 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhazmi, H.; Guldiken, R. Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study. Acoustics 2019, 1, 794-807. https://doi.org/10.3390/acoustics1040046
Alhazmi H, Guldiken R. Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study. Acoustics. 2019; 1(4):794-807. https://doi.org/10.3390/acoustics1040046
Chicago/Turabian StyleAlhazmi, Hani, and Rasim Guldiken. 2019. "Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study" Acoustics 1, no. 4: 794-807. https://doi.org/10.3390/acoustics1040046
APA StyleAlhazmi, H., & Guldiken, R. (2019). Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study. Acoustics, 1(4), 794-807. https://doi.org/10.3390/acoustics1040046