Effects of Nonlinear Propagation of Focused Ultrasound on the Stable Cavitation of a Single Bubble
Abstract
:1. Introduction
2. Theoretical Models
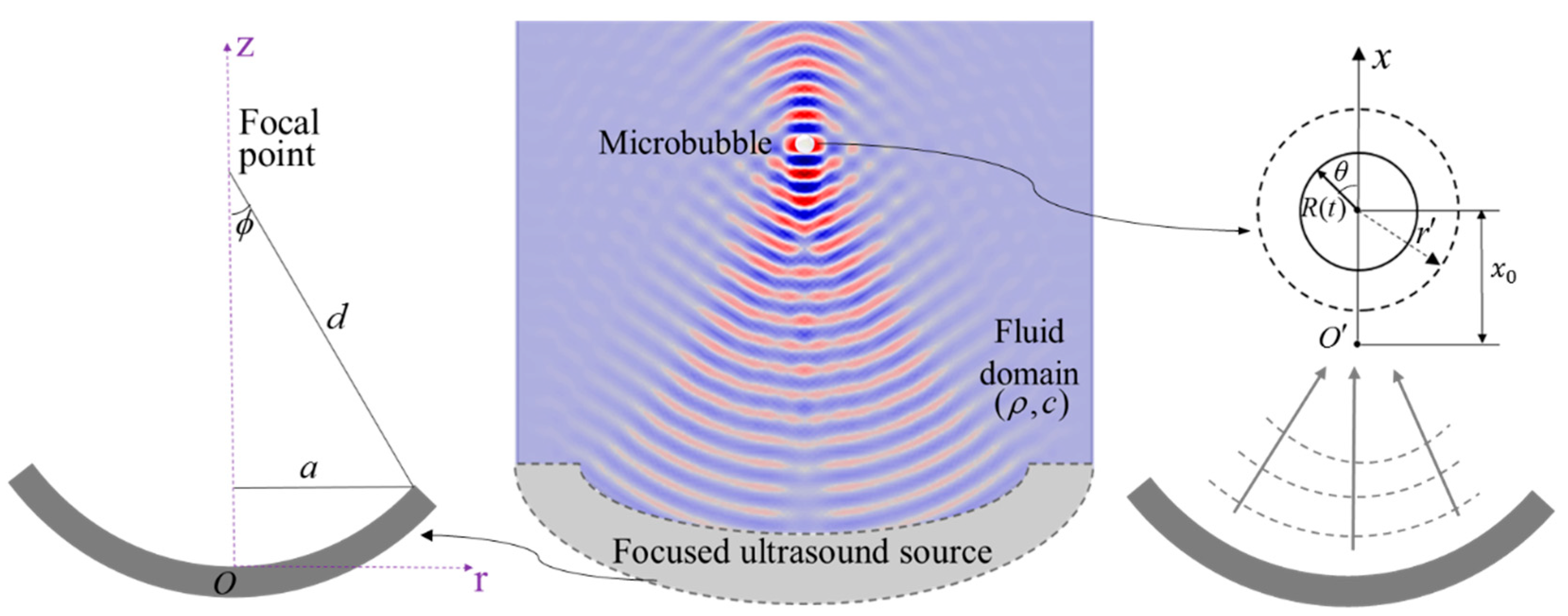
2.1. Nonlinear Acoustic Pressure from FU Transducer
2.2. Single-Bubble Dynamics in a FU Field
3. Numerical Results
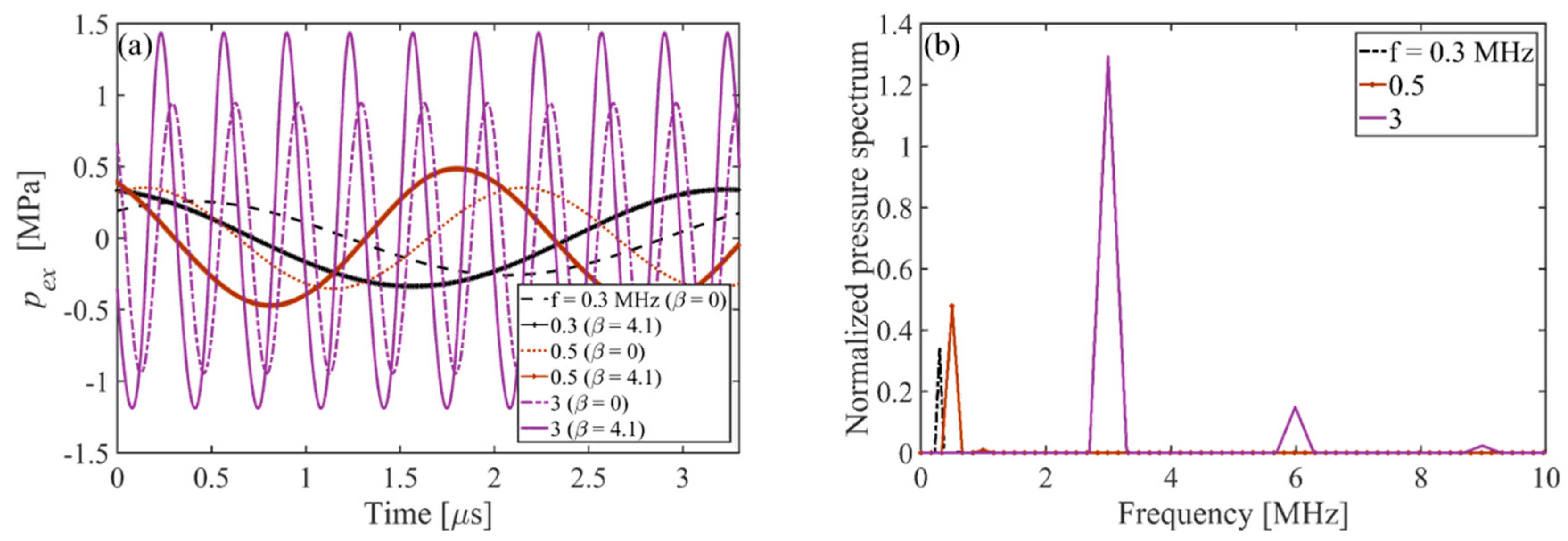
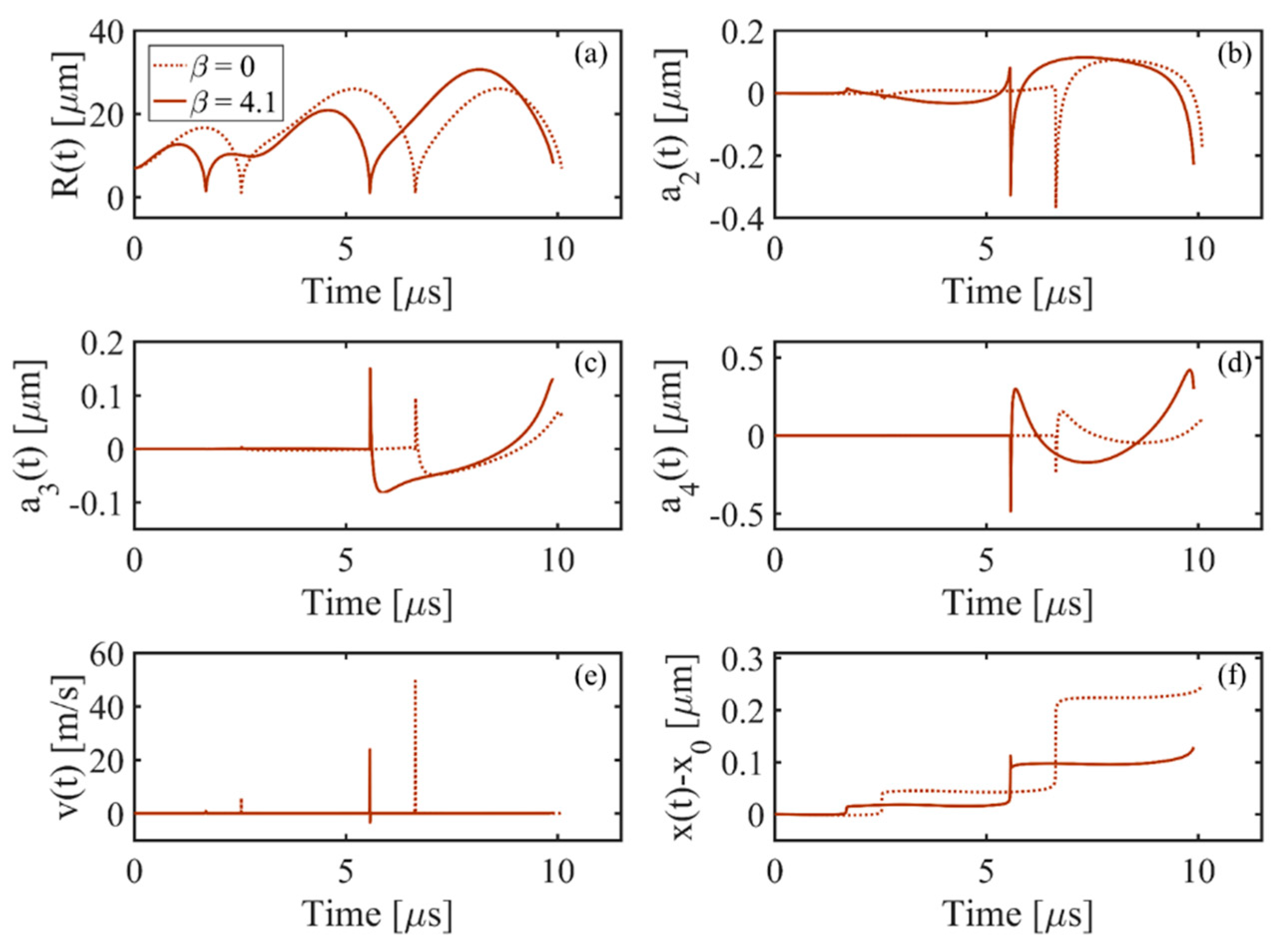
3.1. Effects of Excitation Frequency on Bubble Dynamics
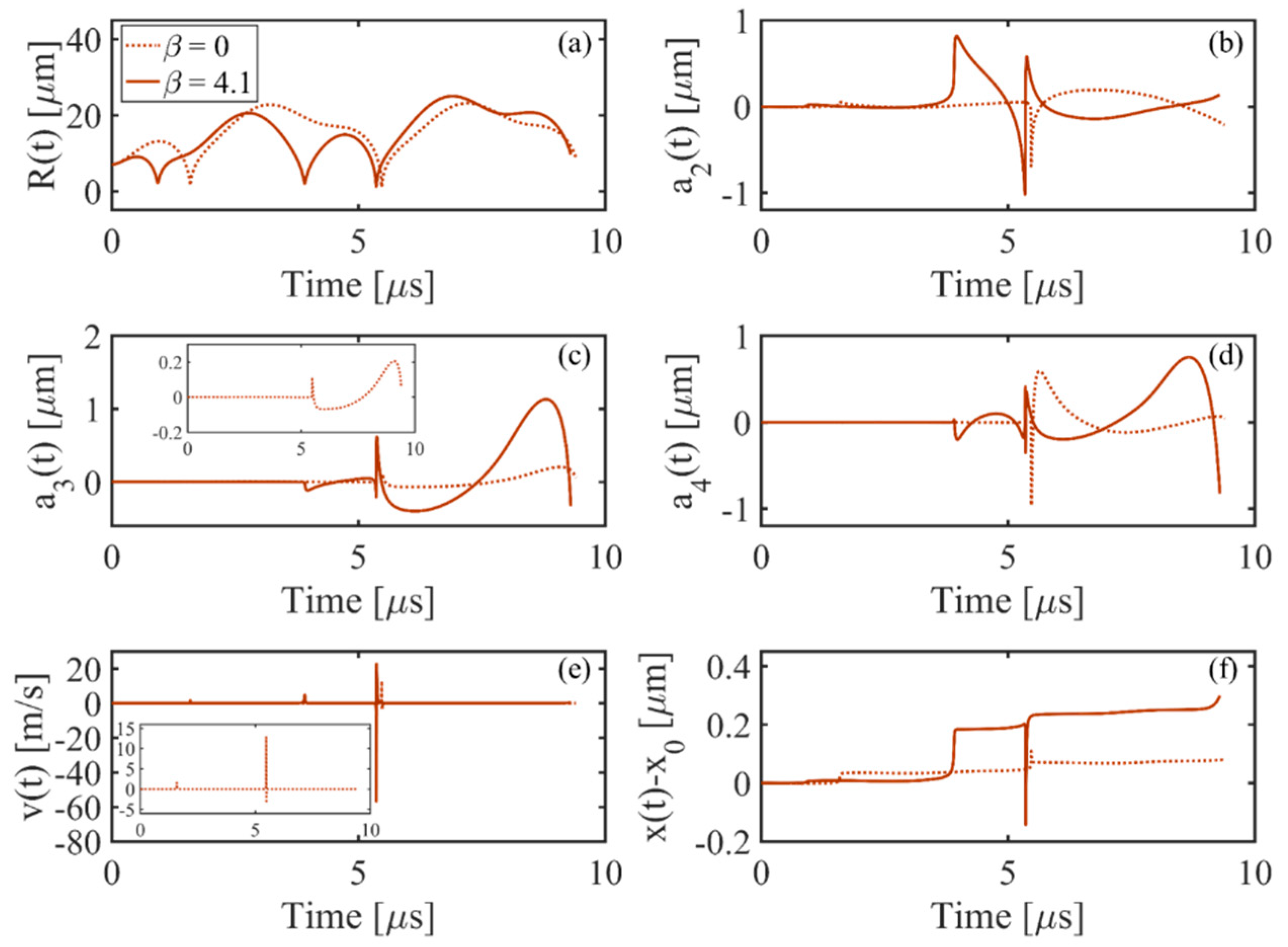
3.2. Effects of Acoustic Pressure (Input Power to the Transducer) on Bubble Dynamics
4. Conclusions
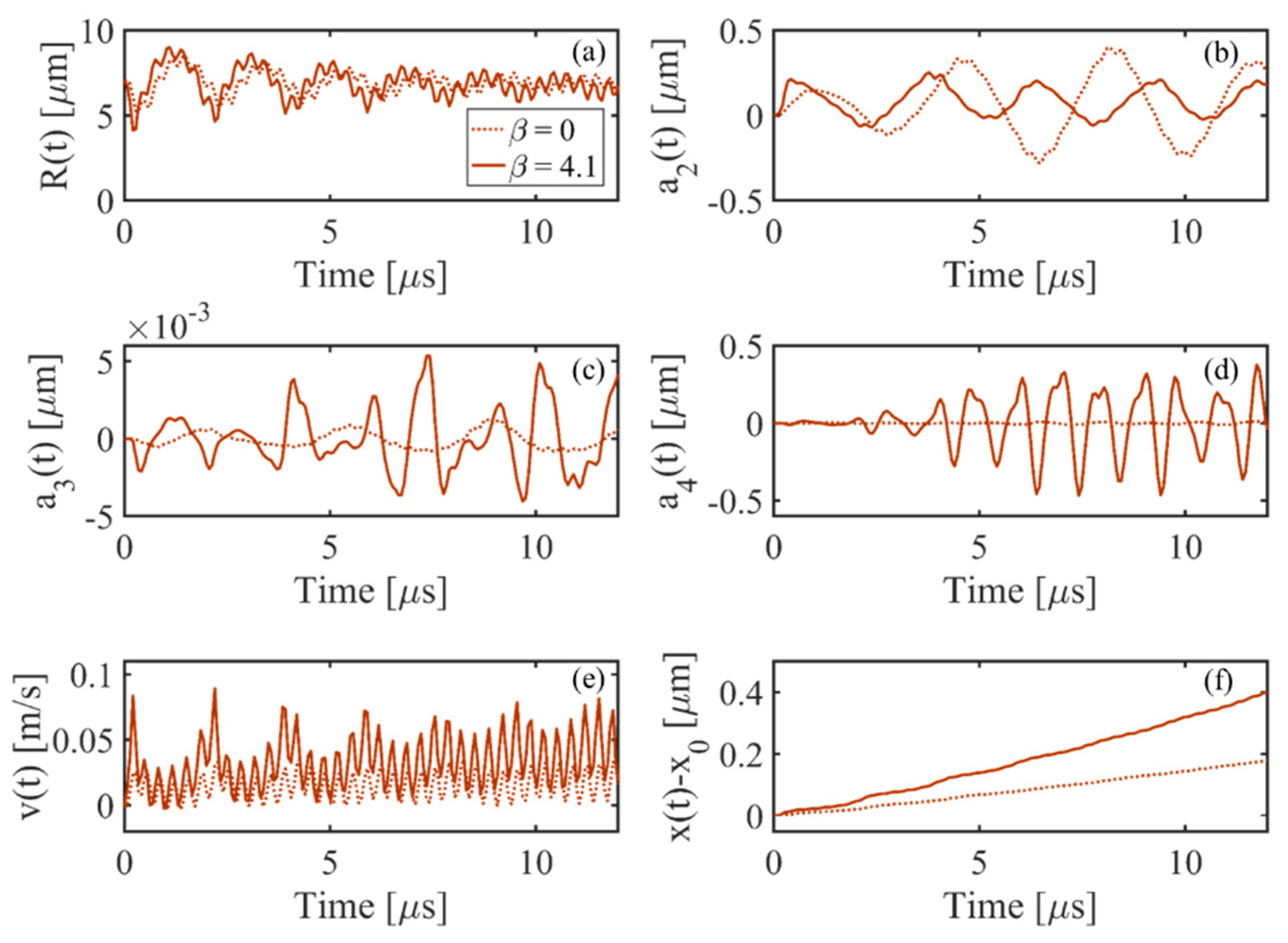
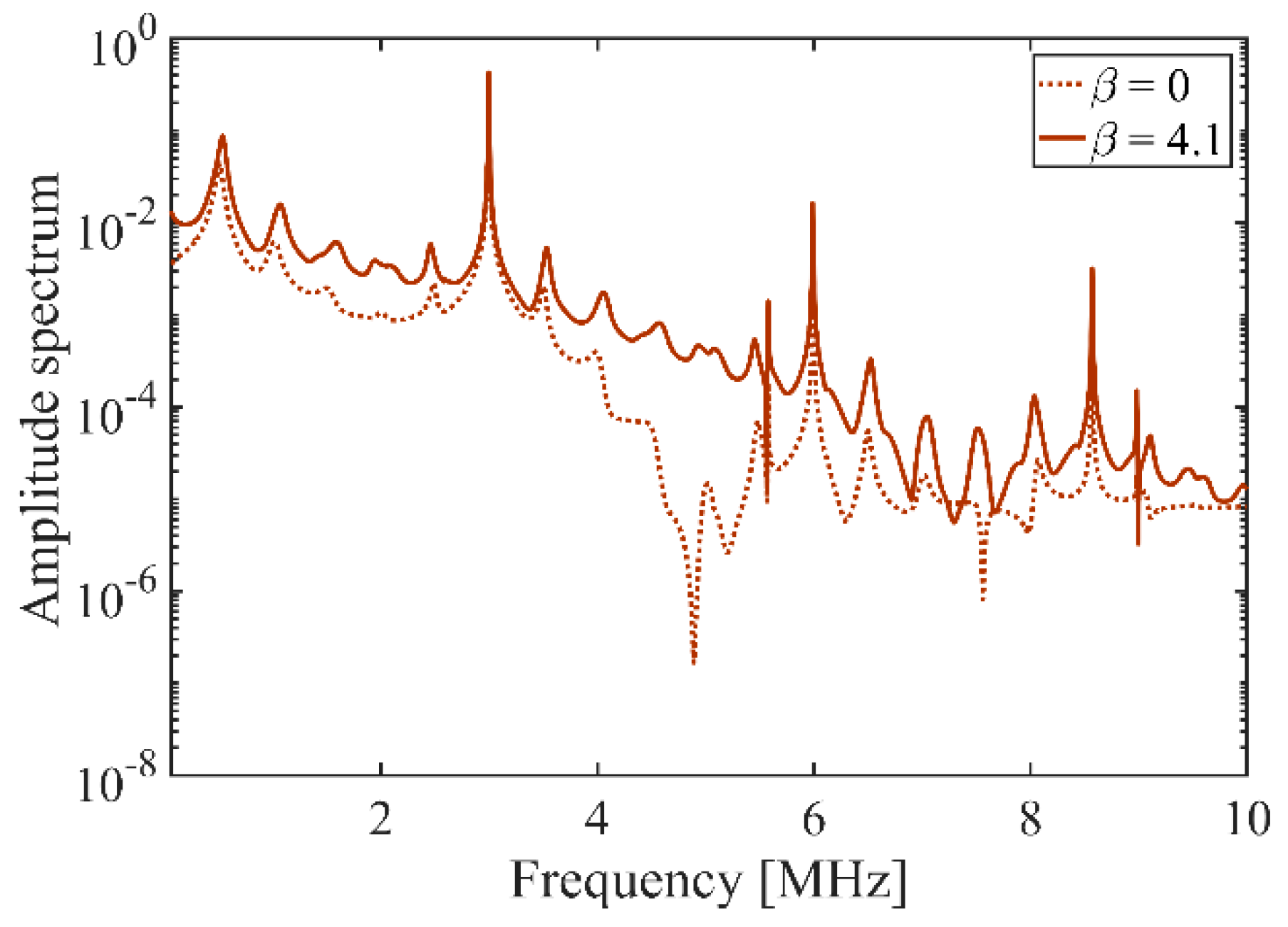
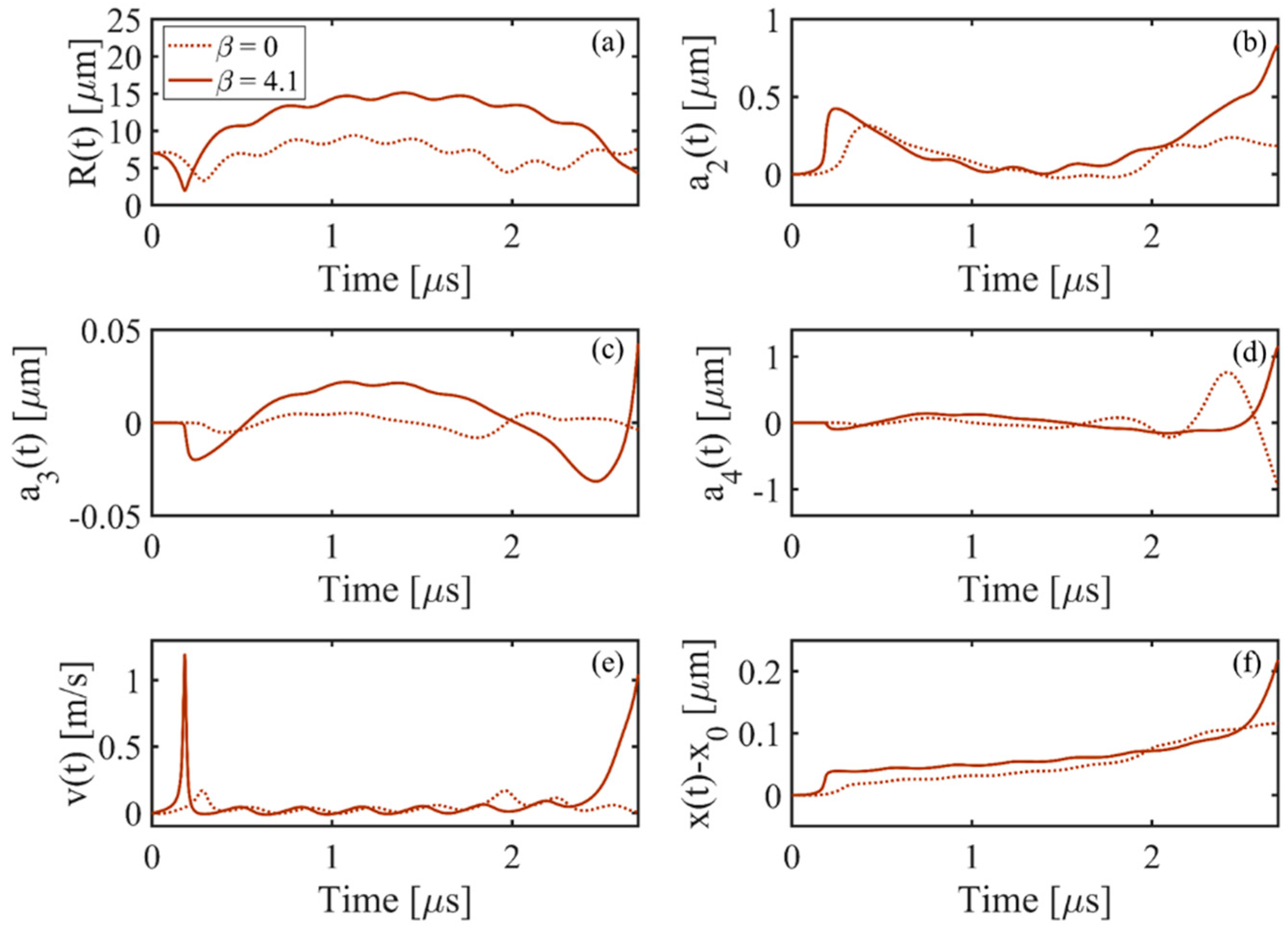
- The results show the dynamical motions of the bubble in the FU field generated by the focused transducer at three different range of frequencies (including the resonance and off-resonance cases). Effects of the change of excitation frequency are investigated and it is shown that in all the frequency ranges, the nonlinearity expedites and amplifies the radial growth and translational motion of the bubble where the indication of the translational instability is observed by a steep rise in the translational velocity of the bubble. It is seen that the initiation of the erratic dancing motion of the bubble in the acoustic field is well-matched with the time of instability of other modes. Moreover, acoustic nonlinearity amplifies almost all the shape oscillations and the instability of the modes. Among the three ranges of frequency investigated in this study, the results show that the changes in the dynamical behavior of the bubble and the translational instability due to nonlinear effects are more significant for higher frequencies, which must be taken into account while investigating an erratic translational (dancing) motion of the bubble. However, a momentous effect of nonlinearity on the translational motion of the bubble is seen at resonance frequency where the bubble initially moves away from the pressure antinode and then makes the translation jumps around the antinode. It is seen that as the excitation frequency increases, the inertial (unstable) cavitation occurs earlier in the nonlinear acoustic field; the nonlinear excitation causes more energy deposition at higher harmonics at the focal point (where the bubble is located); therefore, the radius growth of the bubble is more pronounced at higher frequencies. Accordingly, studying nonlinear acoustics in bubble dynamics is essential for inertial cavitation prediction in biomedically enhanced delivery of drugs into tissue [65] as well as the prediction of the induced impact pressure as a shock loading to a structure, which might even cause mechanical destruction [68].
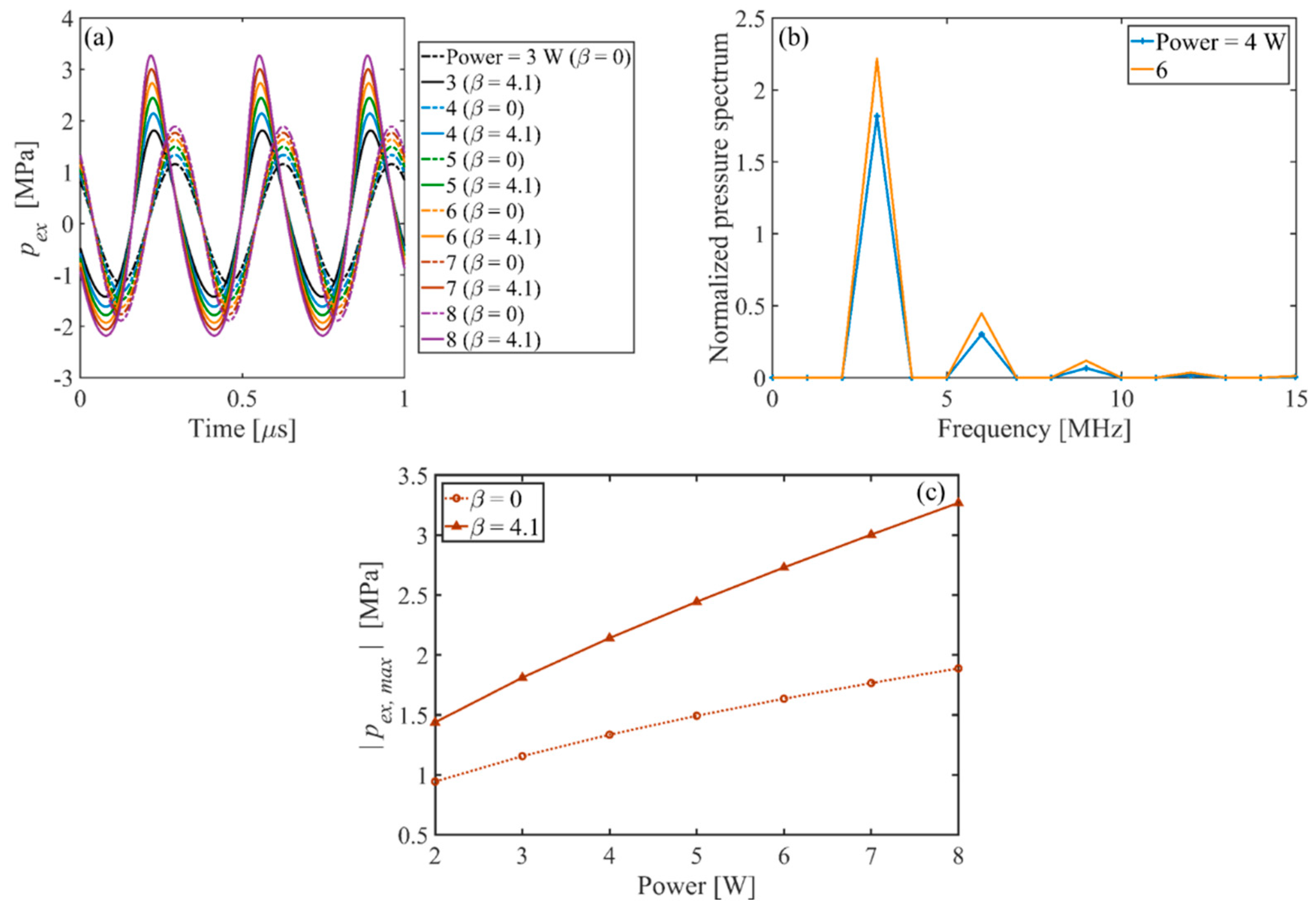
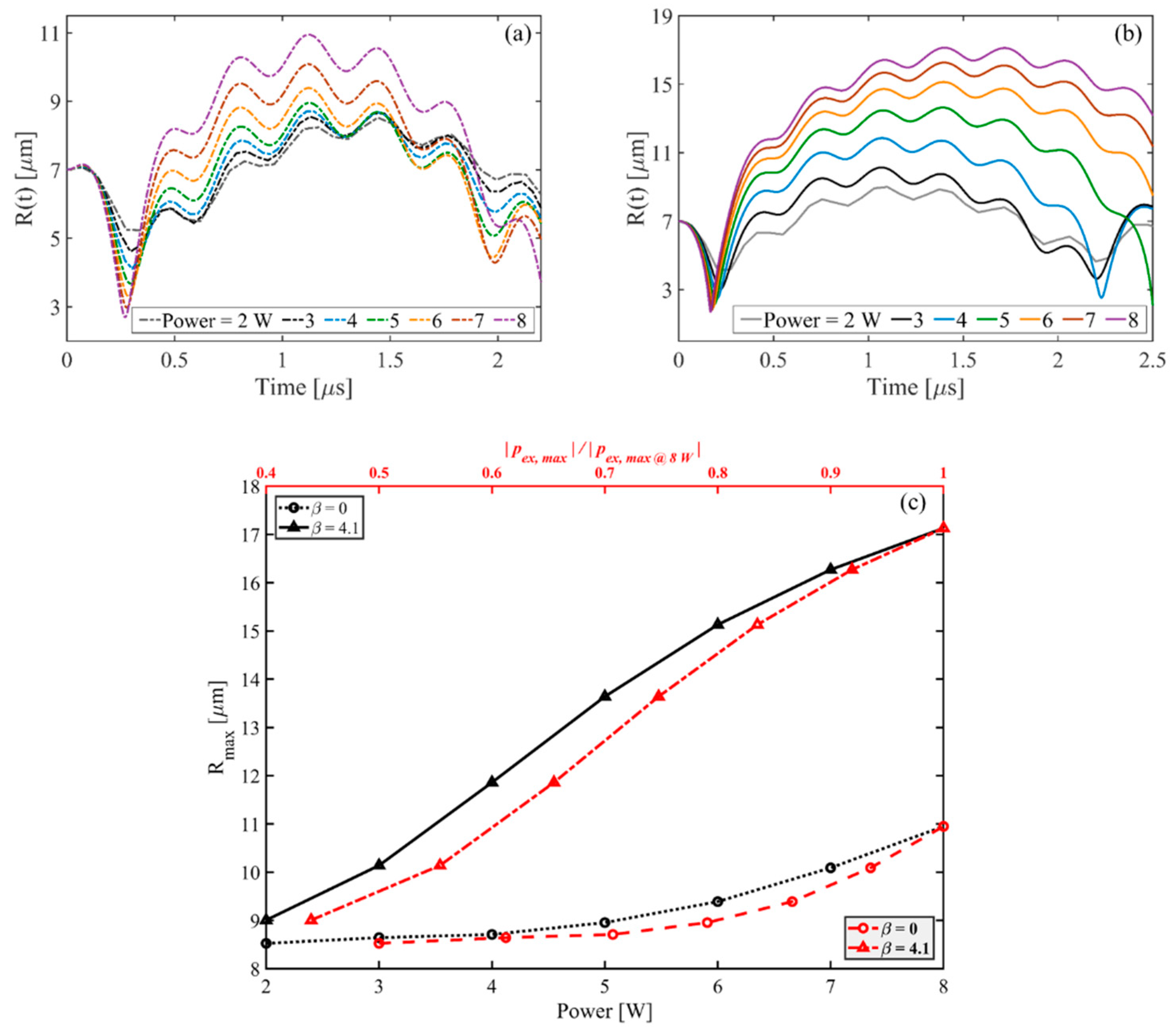
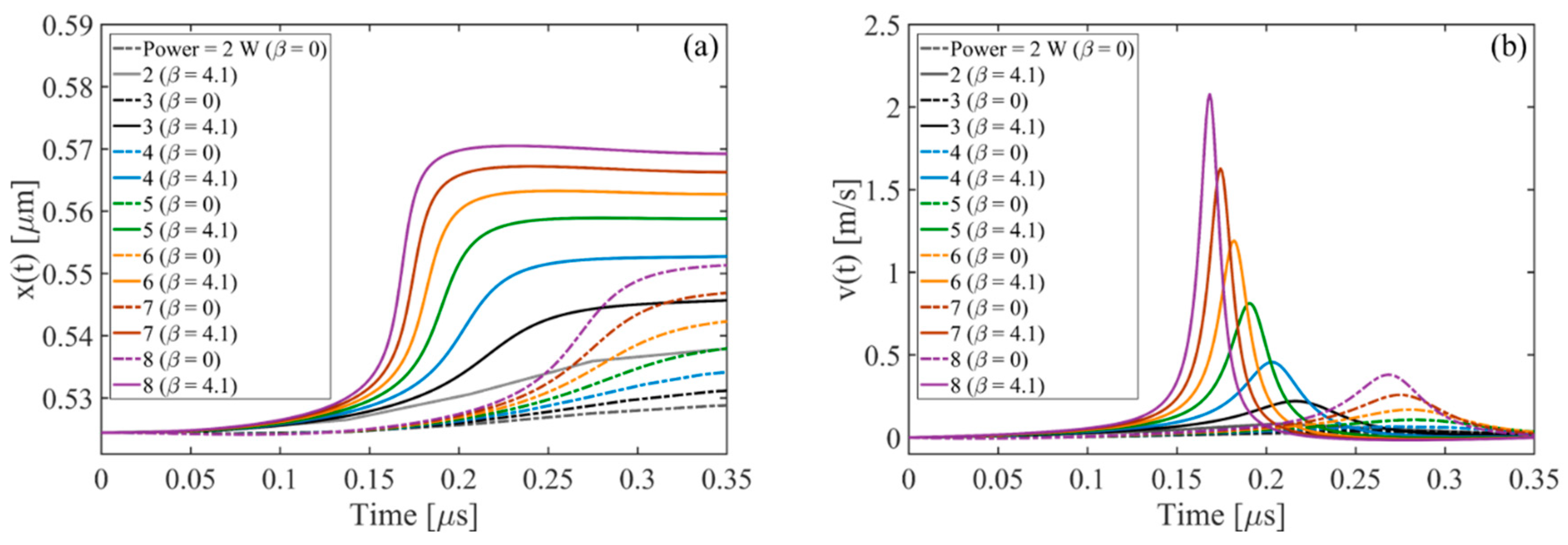
- As the input power is increased, the amplitudes of all the harmonics increase. Comparing the bubble dynamics for two equal pressure amplitudes in linear and nonlinear cases show significant differences in the shape modes and translational instability of the bubble. This confirms that the radial growth and onset of the erratic motion of the bubble in a focused ultrasound field are reliant on both pressure amplitude and the harmonic components of the excitation. It is seen that when the applied pressure increases, the results of the linear model give up to 56% error for predicting the threshold for unstable cavitation (maximum radius of the bubble). In nonlinear acoustics, when the input power increases, the bubble may collapse and shows unstable cavitation as well as the amplified and accelerated translational instability.
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Mitragotri, S. Healing sound: The use of ultrasound in drug delivery and other therapeutic applications. Nat. Rev. Drug Discov. 2005, 4, 255–260. [Google Scholar] [CrossRef]
- Bazan-Peregrino, M.; Rifai, B.; Carlisle, R.C.; Choi, J.; Arvanitis, C.D.; Seymour, L.W.; Coussios, C.C. Cavitation-enhanced delivery of a replicating oncolytic adenovirus to tumors using focused ultrasound. J. Control. Release 2013, 169, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Bader, K.B.; Holland, C.K. Gauging the likelihood of stable cavitation from ultrasound contrast agents. Phys. Med. Biol. 2012, 58, 127–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thomas, C.R.; Farny, C.H.; Coussios, C.C.; Roy, R.A.; Holt, R.G. Dynamics and control of cavitation during high-intensity focused ultrasound application. Acoust. Res. Lett. Online 2005, 6, 182–187. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.-H.; Ting, C.-Y.; Chang, Y.-C.; Wei, K.-C.; Liu, H.-L.; Yeh, C.-K. Drug-loaded bubbles with matched focused ultrasound excitation for concurrent blood–brain barrier opening and brain-tumor drug delivery. Acta Biomater. 2015, 15, 89–101. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.-H.; Liu, H.-L.; Ting, C.-Y.; Lee, Y.-H.; Huang, C.-Y.; Ma, Y.-J.; Wei, K.-C.; Yen, T.-C.; Yeh, C.-K. Submicron-bubble-enhanced focused ultrasound for blood–brain barrier disruption and improved cns drug delivery. PLoS ONE 2014, 9, e96327. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Samiotaki, G.; Olumolade, O.; Feshitan, J.A.; Konofagou, E.E. Microbubble type and distribution dependence of focused ultrasound-induced blood–brain barrier opening. Ultrasound Med. Biol. 2014, 40, 130–137. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Rhim, H.; Choi, M.J.; Lim, H.K.; Choi, D. High-intensity focused ultrasound therapy: An overview for radiologists. Korean J. Radiol. 2008, 9, 291–302. [Google Scholar] [CrossRef]
- Kennedy, J.E. High-intensity focused ultrasound in the treatment of solid tumours. Nat. Rev. Cancer 2005, 5, 321–327. [Google Scholar] [CrossRef]
- Bailey, M.; Khokhlova, V.; Sapozhnikov, O.; Kargl, S.; Crum, L. Physical mechanisms of the therapeutic effect of ultrasound (a review). Acoust. Phys. 2003, 49, 369–388. [Google Scholar] [CrossRef]
- Barber, B.P.; Putterman, S.J. Observation of synchronous picosecond sonoluminescence. Nature 1991, 352, 318–320. [Google Scholar] [CrossRef]
- Gaitan, D.F.; Crum, L.A.; Church, C.C.; Roy, R.A. Sonoluminescence and bubble dynamics for a single, stable, cavitation bubble. J. Acoust. Soc. Am. 1992, 91, 3166–3183. [Google Scholar] [CrossRef]
- Rabaud, D.; Thibault, P.; Mathieu, M.; Marmottant, P. Acoustically bound microfluidic bubble crystals. Phys. Rev. Lett. 2011, 106, 134501. [Google Scholar] [CrossRef] [PubMed]
- Shields, C.W., IV; Reyes, C.D.; López, G.P. Microfluidic cell sorting: A review of the advances in the separation of cells from debulking to rare cell isolation. Lab Chip 2015, 15, 1230–1249. [Google Scholar] [CrossRef] [PubMed]
- Augustsson, P.; Karlsen, J.T.; Su, H.-W.; Bruus, H.; Voldman, J. Iso-acoustic focusing of cells for size-insensitive acousto-mechanical phenotyping. Nat. Commun. 2016, 7, 11556. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaines, N. A magnetostriction oscillator producing intense audible sound and some effects obtained. Physics 1932, 3, 209–229. [Google Scholar] [CrossRef]
- Kornfeld, M.; Suvorov, L. On the destructive action of cavitation. J. Appl. Phys. 1944, 15, 495–506. [Google Scholar] [CrossRef]
- Eller, A.I.; Crum, L.A. Instability of the motion of a pulsating bubble in a sound field. J. Acoust. Soc. Am. 1970, 47, 762–767. [Google Scholar] [CrossRef]
- Mettin, R.; Doinikov, A.A. Translational instability of a spherical bubble in a standing ultrasound wave. Appl. Acoust. 2009, 70, 1330–1339. [Google Scholar] [CrossRef]
- Doinikov, A.A. Translational motion of a spherical bubble in an acoustic standing wave of high intensity. Phys. Fluids 2002, 14, 1420–1425. [Google Scholar] [CrossRef]
- Doinikov, A.A. Translational motion of a bubble undergoing shape oscillations. J. Fluid Mech. 2004, 501, 1–24. [Google Scholar] [CrossRef]
- Eckart, C. Vortices and streams caused by sound waves. Phys. Rev. 1948, 73, 68. [Google Scholar] [CrossRef]
- Hallez, L.; Touyeras, F.; Hihn, J.-Y.; Bailly, Y. Characterization of hifu transducers designed for sonochemistry application: Acoustic streaming. Ultrason. Sonochem. 2016, 29, 420–427. [Google Scholar] [CrossRef] [PubMed]
- Kreider, W.; Crum, L.A.; Bailey, M.R.; Sapozhnikov, O.A. A reduced-order, single-bubble cavitation model with applications to therapeutic ultrasound. J. Acoust. Soc. Am. 2011, 130, 3511–3530. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Roy, R.A.; Holt, R.G. Bubble dynamics and size distributions during focused ultrasound insonation. J. Acoust. Soc. Am. 2004, 116, 3423–3431. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Dayton, P.A.; Caskey, C.; Zhao, S.; Qin, S.; Ferrara, K.W. Ultrasound-driven microbubble oscillation and translation within small phantom vessels. Ultrasound Med. Biol. 2007, 33, 1978–1987. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Li, X.; Wan, M. Spatial–temporal dynamics of cavitation bubble clouds in 1.2 mhz focused ultrasound field. Ultrason. Sonochem. 2006, 13, 480–486. [Google Scholar] [CrossRef]
- Bhargava, A.; Peng, K.; Stieg, J.; Mirzaeifar, R.; Shahab, S. Focused ultrasound actuation of shape memory polymers; acoustic-thermoelastic modeling and testing. RSC Adv. 2017, 7, 45452–45469. [Google Scholar] [CrossRef] [Green Version]
- Rozanova-Pierrat, A. Mathematical Analysis of Khokhlov-Zabolotskaya-Kuznetsov (KZK) Equation. 2006. Available online: https://hal.archives-ouvertes.fr/hal-00112147 (accessed on 5 December 2018).
- Hamilton, M.F.; Blackstock, D.T. Nonlinear Acoustic; Academic Press: San Diego, CA, USA, 1998; Volume 1. [Google Scholar]
- Jing, Y.; Shen, D.; Clement, G.T. Verification of the westervelt equation for focused transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1091–1101. [Google Scholar]
- Tavakkoli, J.; Cathignol, D.; Souchon, R.; Sapozhnikov, O.A. Modeling of pulsed finite-amplitude focused sound beams in time domain. J. Acoust. Soc. Am. 1998, 104, 2061–2072. [Google Scholar] [CrossRef]
- Bakhtiari-Nejad, M.; Elnahhas, A.; Jung, S.; Shahab, S. Ultrasound acoustic energy for microbubble manipulation. In Active and Passive Smart Structures and Integrated Systems 2017; International Society for Optics and Photonics: Washington, DC, USA, 2017; p. 101642H. [Google Scholar]
- Bakhtiari-Nejad, M.; Shahab, S. Investigation of bubble dynamics in nonlinear acoustic field. In Active and Passive Smart Structures and Integrated Systems XII, 2018; International Society for Optics and Photonics: Washington, DC, USA, 2018; p. 105951D. [Google Scholar]
- Zabolotskaya, E. Quasiplane waves in the nonlinear acoustics of confined beams. Sov. Phys. Acoust. 1969, 15, 35–40. [Google Scholar]
- Kuznetsov, V. Equation of nonlinear acoustics. Sov. Phys. Acoust. 1971, 16, 467–470. [Google Scholar]
- Bakhvalov, N.; Zhileĭkin, I.A.K.M.; Zabolotskaiai, E.A.A. Nonlinear Theory of Sound Beams; Amer Inst of Physics: New York, NY, USA, 1987. [Google Scholar]
- Lee, Y.S.; Hamilton, M.F. Time-domain modeling of pulsed finite-amplitude sound beams. J. Acoust. Soc. Am. 1995, 97, 906–917. [Google Scholar] [CrossRef]
- Hart, T.S.; Hamilton, M.F. Nonlinear effects in focused sound beams. J. Acoust. Soc. Am. 1988, 84, 1488–1496. [Google Scholar] [CrossRef]
- Lucas, B.G.; Muir, T.G. The field of a focusing source. J. Acoust. Soc. Am. 1982, 72, 1289–1296. [Google Scholar] [CrossRef]
- Waters, K.R.; Hughes, M.S.; Mobley, J.; Brandenburger, G.H.; Miller, J.G. On the applicability of kramers–krönig relations for ultrasonic attenuation obeying a frequency power law. J. Acoust. Soc. Am. 2000, 108, 556–563. [Google Scholar] [CrossRef]
- Jiménez, N.; Camarena, F.; Redondo, J.; Sánchez-Morcillo, V.; Hou, Y.; Konofagou, E.E. Time-domain simulation of ultrasound propagation in a tissue-like medium based on the resolution of the nonlinear acoustic constitutive relations. Acta Acustica United Acustica 2016, 102, 876–892. [Google Scholar] [CrossRef]
- Lee, Y.-S. Numerical solution of the KZK equation for pulsed finite amplitude sound beams in thermoviscous fluids. Acoust. Eng. Mech. 1993, 54, 6246. [Google Scholar]
- Soneson, J.E. A user-friendly software package for hifu simulation. In AIP Conference Proceedings; AIP: Melville, NY, USA, 2009; pp. 165–169. [Google Scholar]
- Soneson, J.E.; Myers, M.R. Thresholds for nonlinear effects in high-intensity focused ultrasound propagation and tissue heating. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2450–2459. [Google Scholar] [CrossRef]
- Soneson, J.E.; Myers, M.R. Gaussian representation of high-intensity focused ultrasound beams. J. Acoust. Soc. Am. 2007, 122, 2526–2531. [Google Scholar] [CrossRef]
- O’Donnell, M.; Jaynes, E.; Miller, J. Kramers–kronig relationship between ultrasonic attenuation and phase velocity. J. Acoust. Soc. Am. 1981, 69, 696–701. [Google Scholar] [CrossRef]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations; Siam: Philadelphia, PA, USA, 1998; Volume 61. [Google Scholar]
- Plesset, M. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 277–282. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef] [Green Version]
- Hay, T.A.; Ilinskii, Y.A.; Zabolotskaya, E.A.; Hamilton, M.F. Model for the dynamics of a spherical bubble undergoing small shape oscillations between parallel soft elastic layers. J. Acoust. Soc. Am. 2013, 134, 1454–1462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doinikov, A.A.; Bouakaz, A. Theoretical model for coupled radial and translational motion of two bubbles at arbitrary separation distances. Phys. Rev. E 2015, 92, 043001. [Google Scholar] [CrossRef] [PubMed]
- Azhari, H. Appendix A: Typical acoustic properties of tissues. In Basics of Biomedical Ultrasound for Engineers; Wiley: Hoboken, NJ, USA, 2010; pp. 313–314. [Google Scholar]
- Wells, P.N. Ultrasonic imaging of the human body. Rep. Prog. Phys. 1999, 62, 671. [Google Scholar] [CrossRef]
- Soneson, J. Hifu Simulator v1. 2 User’s Manual; FDA: Silver Spring, MD, USA, 2011.
- Longuet-Higgins, M.S. Monopole emission of sound by asymmetric bubble oscillations. Part 1. Normal modes. J. Fluid Mech. 1989, 201, 525–541. [Google Scholar] [CrossRef]
- Mei, C.C.; Zhou, X. Parametric resonance of a spherical bubble. J. Fluid Mech. 1991, 229, 29–50. [Google Scholar] [CrossRef]
- Rosina, J.; Kvasnak, E.; Suta, D.; Kolarova, H.; Malek, J.; Krajci, L. Temperature dependence of blood surface tension. Physiol. Res. 2007, 56, S93. [Google Scholar]
- Elert, G. Viscosity-the Physics Hypertextbook. The Physics Hypertextbook. Available online: http://physics.info/viscosity/ (accessed on 5 December 2018).
- Eller, A. Force on a bubble in a standing acoustic wave. J. Acoust. Soc. Am. 1968, 43, 170–171. [Google Scholar] [CrossRef]
- Apfel, R. Acoustic cavitation prediction. J. Acoust. Soc. Am. 1981, 69, 1624–1633. [Google Scholar] [CrossRef]
- Apfel, R.E.; Holland, C.K. Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound. Ultrasound Med. Biol. 1991, 17, 179–185. [Google Scholar] [CrossRef]
- Holland, C.K.; Apfel, R.E. An improved theory for the prediction of microcavitation thresholds. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1989, 36, 204–208. [Google Scholar] [CrossRef] [PubMed]
- Basude, R.; Wheatley, M.A. Generation of ultraharmonics in surfactant based ultrasound contrast agents: Use and advantages. Ultrasonics 2001, 39, 437–444. [Google Scholar] [CrossRef]
- Schoellhammer, C.M.; Schroeder, A.; Maa, R.; Lauwers, G.Y.; Swiston, A.; Zervas, M.; Barman, R.; DiCiccio, A.M.; Brugge, W.R.; Anderson, D.G. Ultrasound-mediated gastrointestinal drug delivery. Sci. Transl. Med. 2015, 7, 310ra168. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Peng, Z.; Lin, S.-C.S.; Geri, M.; Li, S.; Li, P.; Chen, Y.; Dao, M.; Suresh, S.; Huang, T.J. Cell separation using tilted-angle standing surface acoustic waves. Proc. Natl. Acad. Sci. USA 2014, 111, 12992–12997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Segers, T.; Versluis, M. Acoustic bubble sorting for ultrasound contrast agent enrichment. Lab Chip 2014, 14, 1705–1714. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, O.; Bakhtiari-Nejad, M.; Yazdandoost, F.; Shahab, S.; Mirzaeifar, R. Dissipation of cavitation-induced shock waves energy through phase transformation in niti alloys. Int. J. Mech. Sci. 2018, 137, 304–314. [Google Scholar] [CrossRef]
| Attenuation Parameter, (dB/(m·MHz)) | 20 |
| Attenuation parameter, | 1.3 |
| Coefficient of nonlinearity, | 4.1 |
| Density, (kg/m3) | 1055 |
| Sound speed, (m/s) | 1570 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhtiari-Nejad, M.; Shahab, S. Effects of Nonlinear Propagation of Focused Ultrasound on the Stable Cavitation of a Single Bubble. Acoustics 2019, 1, 14-34. https://doi.org/10.3390/acoustics1010003
Bakhtiari-Nejad M, Shahab S. Effects of Nonlinear Propagation of Focused Ultrasound on the Stable Cavitation of a Single Bubble. Acoustics. 2019; 1(1):14-34. https://doi.org/10.3390/acoustics1010003
Chicago/Turabian StyleBakhtiari-Nejad, Marjan, and Shima Shahab. 2019. "Effects of Nonlinear Propagation of Focused Ultrasound on the Stable Cavitation of a Single Bubble" Acoustics 1, no. 1: 14-34. https://doi.org/10.3390/acoustics1010003
APA StyleBakhtiari-Nejad, M., & Shahab, S. (2019). Effects of Nonlinear Propagation of Focused Ultrasound on the Stable Cavitation of a Single Bubble. Acoustics, 1(1), 14-34. https://doi.org/10.3390/acoustics1010003





