Previous Article in Journal
Interplay Between Membrane Adhesion and Distribution of Lipid Rafts
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Surfaces
Volume 8
Issue 3
10.3390/surfaces8030063
surfaces-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Adsorption of Lanthanide Atoms on a Graphene Cluster Model Incorporating Stone–Wales Defect

by
Vladimir A. Basiuk
1,* and
Elena V. Basiuk
2
1
Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Circuito Exterior C.U., Ciudad de México 04510, Mexico
2
Instituto de Ciencias Aplicadas y Tecnología, Universidad Nacional Autónoma de México, Circuito Exterior C.U., Ciudad de México 04510, Mexico
*
Author to whom correspondence should be addressed.
Surfaces 2025, 8(3), 63; https://doi.org/10.3390/surfaces8030063
Submission received: 31 July 2025 / Revised: 24 August 2025 / Accepted: 27 August 2025 / Published: 29 August 2025
(This article belongs to the Special Issue Nanocarbons: Advances and Innovations)
Browse Figures
Versions Notes

Abstract

To study the adsorption of lanthanide (Ln) atoms on graphene containing a Stone–Wales defect, we used a cluster model (SWG) and performed calculations at the PBE-D2/DNP level of the density functional theory. Our previous study, where the above combination was complemented with the ECP pseudopotentials, was only partially successful due to the impossibility of calculating terbium-containing systems and a serious error found for the SWG complex with dysprosium. In the present study we employed the DSPP pseudopotentials and completely eliminated the latter two failures. We analyzed the optimized geometries of the full series of fifteen SWG + Ln complexes, along with their formation energies and electronic parameters, such as frontier orbital energies, atomic charges, and spins. In many regards, the two series of calculations show qualitatively similar features, such as roughly M-shaped curves of the adsorption energies and trends in the changes in charge and spin of the adsorbed Ln atoms, as well as the spin density plots. However, the quantitative results can differ significantly. For most characteristics we found no evident correlation with the lanthanide contraction. The only dataset where this phenomenon apparently manifests itself (albeit to a limited and irregular degree) is the changes in the closest Ln…C approaches.

1. Introduction

The constantly growing broad variety of applications of graphene and its potentially useful properties (for recent reviews, see, for example, [1,2,3]) results from its quasi-infinite 2D backbone composed of aromatic hexagonal rings. The degree to which this idealized honeycomb structure dominates depends on the particular approach employed for generating graphene sheets: real-world graphene always contains different kinds of structural defects [4,5,6,7,8,9,10,11,12], comprising vacancies, atomic dopants, isolated pentagonal and heptagonal rings, and their combinations, the most important of which are Stone–Wales (SW; more correctly, but rarely, referred to as Stone–Thrower–Wales) defects [13,14,15,16]. The presence of all of the above structural elements has to be taken into account when physical (especially electronic), chemical, and other properties of graphene-based materials are analyzed. Among them, it is the SW defects that deserve special attention. The first reason is that this type of structural imperfection does not imply removal of C atoms (as in the case of vacancies) from or adding other atoms (heteroatoms like B, N, etc.) to the hexagonal network. Instead, the SW defect generation results from a simple C-C bond rotation by 90° in the plane of the graphene backbone, which alters the atomic order and topology of the latter to a minimal degree.
At the same time, the incorporation of SW defects can produce more or less significant effects on the physical and especially on the chemical properties of graphene [15], compared to those of the ideal pristine structure, and this is the second reason why the number of related studies (which can be exemplified by the reports [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]) constantly grows. It was demonstrated, in particular, that incorporation of SW defects can modify the electronic [32,33,41,43,45,47], magnetic [18], and mechanical characteristics of graphene [26,27,29,35]. In the context of graphene’s chemical behavior, one should mention the research reports on its lithium doping and hydrogen storage [24,25,30,37], adsorption and chemisorption of the main-group and transition metals [19,22,23,28,38,44], lanthanide atoms [34,49], as well as from simple ambient and organic molecules [17,19,20,21,22,31,36,38,46,48] to such extended hyperconjugated coordination compounds as 3d-metal monophthalocyanines [39] and rare-earth double-decker phthalocyanines [40,42].
When one analyzes the related literature (including the references mentioned above), it immediately becomes obvious that the main source of information on the interaction of diverse chemical species with SW defects in graphene was and remains quantum chemical calculations in the framework of density functional theory (DFT). The reason is clear: even though experimental observations of isolated SW defects in graphene are documented, they require very expensive high-resolution transmission electron microscopy (HR-TEM) [7,50] and scanning tunneling microscopy (STM) [51] equipment, the measurements are very time- and labor-consuming, and the final micrographs obtained (after additional image processing) might seem rather ambiguous [51]. Furthermore, no direct observations of SW (or any other) defects interacting with chemical species of any nature are possible in principle, since the latter would totally obscure the interaction site. Needless to say, no crucial characteristics (such as interaction energies, interatomic distances, frontier orbitals, spin distribution, etc.) are obtainable.
Within the entire area of DFT calculations on SW defect-containing graphene (hereafter referred to as SWG) interacting with atomic, radical, and molecular species, the most challenging task turns out to be treating highly degenerate systems containing 4f elements—that is, lanthanides (Ln). A series of our previous reports [34,40,42,49,52] can serve as the most illustrative (and as a matter of fact, unique) examples of such calculations. To simulate quasi-infinite 2D systems such as graphene sheets, two general choices of model are possible: periodic or cluster-type. This choice is made based on a particular goal, since each of these models has its advantages/disadvantages and applicability. A particular advantage of periodic calculations (which are based on such physical concepts and parameters as plane waves, k-points, etc.) is that they can provide the information on band structure and density of states, crucial for the characterization of electronic properties of materials. On the other hand, the cluster models offer a broader versatility, since they are able to account for such a changeable chemical environment as peripheral atoms (H, O, etc.) and functional groups (carbonyl, phenol, carboxylic, etc.). Even though the presence of the latter groups is not considered, it is impossible to anticipate which selection of the model would yield more reliable and realistic parameters. The most optimal and rigorous solution would be to perform both series of computations in parallel, and then to compare the results obtained.
It is this strategy that we attempted to pursue. First, it was tested for the defect-free graphene models. Specifically, the interaction of single Ln atoms with the defect-free quasi-infinite graphene sheet was modeled by using a 4 × 4 supercell (32 C atoms) in the periodic calculations [53], and with a supercoronene model containing peripheral H atoms (general formula C54H18) for the posterior cluster calculations [54]. For the sake of as valid a comparison as possible, we employed the same combination of the functional and the dispersion correction in both works. Nevertheless, the results obtained differed considerably, especially in terms of the graphene model geometry: while the periodic model remained essentially planar, the supercoronene model suffered bending distortion, the degree of which varied depending on a particular Ln atom.
More recently, we attempted to make a similar comparison for the SW defect-containing graphene models: again, one was periodic [49], versus a somewhat larger (compared to [54]) cluster model with the general formula C66H20 [52]. This time, the results of the two studies were rather consistent in many regards (including the trends in geometry distortion and bonding strength), despite the theoretical tools used being very different: the periodic calculations employed plane waves, whereas the cluster approach relied upon localized basis sets. Unfortunately, two important observations prevent qualifying the results of the cluster computations [52] as totally successful: first, for an unknown reason, the dysprosium (Dy) atom acquired a negative charge in its complex with the SWG model; and second, it was impossible to obtain the data for terbium (Tb), as in the previous works [54,55]. Both of the latter studies employed the ECP pseudopotentials: this is one of the two options available in the DMol3 module of the Materials Studio package; the other is DSPP, which was used in our other studies involving lanthanide-containing molecules [42] (although they did not contain Tb).
Accordingly, the main goal of the present work was an attempt to achieve more complete and reliable characterization of the adsorption of the full series of 15 lanthanide atoms on the graphene cluster model incorporating a Stone–Wales defect [55], in terms of the optimized geometries and formation energies of SWG + Ln complexes, as well as selected electronic parameters (including the energies of frontier orbitals, Ln atomic charges and spins, and the corresponding plots).

2. Computational Methodology

We followed the same general computational methodology as in the previous study [52], using the DMol3 numerical-based DFT module [56,57,58,59] of the Materials Studio package. Within the module, we employed the Perdew–Burke–Ernzerhof (PBE) general gradient approximation (GGA) functional [60] complemented with the empirical dispersion correction developed by Grimme [61] (that is, PBE-D2 combination), in conjunction with the double-numerical basis set DNP, which has a polarization d-function added on all non-H atoms, plus a polarization p-function added on H atoms (usually compared to the 6-31G (d,p) Pople-type basis set). When studying the noncovalent interactions of diverse chemical species with carbon nanoclusters, the PBE-D2 methodology is usually the preferred choice over, for example, the widely used hybrid functional B3LYP [62].
As mentioned above, the DMol3 module offers two types of pseudopotentials to treat heavy elements including lanthanides: the quasi-relativistic effective core potentials (ECPs) [63,64], and the norm-conserving DFT semi-core pseudopotentials (DSPPs; more recent and developed specifically for use within DMol3), which implement relativistic effects and spin–orbit coupling. In addition to the previously observed failures when characterizing the interaction of Tb atoms with the cluster models of graphene [52,54,55], we found that the inclusion of ECPs prevents even single-point calculations on an isolated Tb atom—unlike DSPPs [65]. So, in the present work, we decided to test the latter pseudopotentials (even though they exhibit certain imperfections, such as a very strong frontier orbital inversion in the case of Gd atoms, resulting in a negative HOMO–LUMO gap value [65]).
The convergence criteria in the full geometry optimization and calculations of electronic parameters were set to ‘fine’, which implies the following threshold values: energy change, 10−5 Ha; maximum force, 0.002 Ha/Å; maximum displacement, 0.005 Å; SCF tolerance, 10−6 Ha. The global orbital cutoff [66], dictated by the presence of Ln species, was as high as 5.8 Å. In the past, we attempted to tighten the energy convergence criterion by one order of magnitude, to 10−6 Ha, in the calculations on similar carbon nanosystems [67,68], but the results obtained differed insignificantly compared to those calculated with the default energy change value of 10−5 Ha.
The main difficulty in our calculations was achieving the self-consistent field (SCF) convergence. The presence of 4f orbitals in the Ln species implies the existence of a number of very close degenerate states near the Fermi level, which, as a general rule, makes reaching SCF convergence impossible without appealing to the thermal (or Fermi) smearing protocol. Previous publications [49,52,53,54,55,69,70,71] illustrate how to use it correctly. In brief, higher smearing values facilitate convergence, at the cost of allowing unrealistic fractional orbital populations and altering the total energies, geometries, and many electronic parameters [69,70,71]. The final (after a series of auxiliary) calculations at a smearing value as low as 0.0001 Ha (equivalent temperature of 31.6 K) yield stable and consistent results for most Ln-containing systems. Thus, all of the data reported in this study were obtained at the latter value of thermal smearing.

3. Results and Discussion

For a valid comparison with the results of calculations using ECP pseudopotentials [52], in the present study we employed the same SWG model (general formula C66H20) shown in Figure 1. The SW defect adsorption site, containing two pentagonal and two heptagonal fused rings, is highlighted in yellow (Figure 1a). When calculated with ECP pseudopotentials [52], it was noticed that the SWG model is not completely planar, as opposed to the common defect-free graphene models, but suffers slight ‘sigmoid’ bending. In the present series of computations, some distortion can be appreciated as well (Figure 1b), but it is of a spherical type. The origin of this difference is not clear, since the core electrons are frozen only for the elements starting with scandium (Sc), whereas C and H are treated as in the all-electron case: that is, in the same way with ECP and DSPP.
First of all, we would like to summarize that the DSPP calculations were successfully completed for all fifteen elements (from La to Lu), including the ‘difficult’ Tb [52,54,55,65]. The bending of SWG + Ln complexes [49,52] was observed for all lanthanides, which is exemplified in Figure 1c for the SWG + Lu complex: by comparing with Figure 1b, one can see that this bending is much stronger than for the isolated SWG model. To characterize both the bending degree and optimized geometries of the SWG + Ln adsorption sites, we kept using the same set of parameters as in the previous works [49,52]. As explained in Figure 1d, these characteristics include the length of the C–C bond (dC–C) in the (7,7) junction, the two closest approaches Ln…C (dLn…C), and the dihedral angle θ.
But first, we will analyze the energies of formation of SWG + Ln complexes. The formation energy (=binding energy = bonding strength, etc.) is the most important parameter that characterizes covalent or noncovalent interactions between two chemical species. The most common general expression for the interacting species A and B forming an AB complex or molecule is Equation (1):
ΔEAB = EAB − (EA + EB)
where Ei is the total energy of the species i.
The present case of Ln complexes with graphene models turns out to be considerably more complicated. The reason for this is that a significant distortion of the normally planar (or close to planar) polycyclic aromatic network (due to stretching of some C–C bonds and shortening of others, as well as changes in C–C–C angles), with [49,52] or without [54,55] SW defect, dramatically increases its energy. This increment (denoted as ΔEdist) can be quantified by calculating the difference between the total energy of the fully relaxed isolated graphene nanocluster (for example, the one shown in Figure 1a,b) and the single-point energy of the graphene model retrieved from the optimized complex graphene + Ln (that is, after the removal of the Ln atom). In the case of SW defect-containing graphene models [49,52], the full formation energy ΔEfull for the SWG + Ln complexes can be computed by using the standard approach (Equation (1)):
ΔEfull = ESWG + Ln − (ELn + ESWG)
and it is a sum of two components, namely,
ΔEfull = ΔEdist + ΔEbond
where ΔEbond is the energy contribution exclusively due to the interaction between the Ln atom and SWG model. Accordingly, it can be calculated as follows:
ΔEbond = ΔEfull − ΔEdist
Table 1 summarizes the ΔEfull, ΔEdist, and ΔEbond values calculated for the fifteen SWG + Ln adsorption complexes. The corresponding trends can be more conveniently appreciated from Figure 2a. For none of the complexes did we detect a positive formation energy ΔEfull, as happened in the previous cluster calculations for SWG + Er (7.8 kcal/mol [52]), as well as for the Gd atom adsorbed on the supercoronene model (16.4 kcal/mol [54]). As in all other cases [49,52,54,55], the ΔEfull and ΔEbond curves have a similar irregular M-like shape. In this work, the ΔEfull values span from −109.4 kcal/mol for SWG + La to −21.3 kcal/mol for SWG + Pm; similarly, the ΔEbond values vary between −131.7 and −41.8 kcal for the same complexes. After the first increase from La to Pm, both energies drop to a minimum for Gd, with ΔEfull of −91.7 kcal/mol and ΔEbond of −112.7 kcal/mol (the steady fall is interrupted with the points corresponding to Sm and Eu), then increase again to the second maximum for Yb (−27.6 and −49.4 kcal/mol, respectively), and then dramatically decrease for Lu (−80.4 and −102.8 kcal/mol, respectively). Thus, the strongest interaction is observed for La, Gd, and Lu, which have correspondingly totally empty, half-filled, and totally filled 4f shells, respectively. At the same time, the values of the ΔEdist component vary in a very narrow range, from 19.8 (SWG + Sm complex) to 22.8 kcal/mol (the complexes of Ce and Tm). There are no indications that the bonding trends observed correlate somehow with the phenomenon of lanthanide contraction (likewise in the previous studies [49,52,54,55]).
In terms of geometry, as expected and observed previously [49,52], the dC–C bond length in the (7,7) junction of 1.344 Å for the isolated optimized SWG model always increases: to a minimum degree (1.414 Å) for SWG + Gd, and to a maximum degree (1.425 Å) for SWG + Tm (Table 2). In principle, this contrasts with the value of 1.381 Å found for SWG + Dy previously [52] (in the present work, it is 1.423 Å), but the behavior of this complex was found to deviate significantly from the expected behavior when using the ECP pseudopotentials. Most unambiguously, the distortion of the SWG model is characterized by the dihedral (or torsion) angle θ, which is 178.3° in the absence of Ln atoms, when calculated using DSPP pseudopotentials. As mentioned above (Figure 1c), the strongest distortion with the smallest θ angle of 144.4° (Table 2) was obtained for the SWG + Lu complex, and the largest one of 148.0° was obtained for SWG + Sm. The corresponding M-like curve (Figure 2b) has two branches, separated by the minimum at the SWG + Gd point (θ angle of 145.2°). The latter correlates with the minima in the ΔEfull and ΔEbond curves (Figure 2a), as well as with the shortest (1.414 Å) dC–C bond length. Furthermore, the point corresponding to SWG + Gd divides the dLn…C curve (Figure 2b) into two branches as well, even though the closest Ln…C approaches for this complex (2.365 and 2.366 Å; Table 2) are not the smallest of all. In the ‘earlier lanthanides’ branch, the closest dLn…C approaches span from 2.441 and 2.458 Å for SWG + Nd to 2.473 and 2.480 Å for SWG + La. In the ‘later lanthanides’ branch, they are considerably smaller, from 2.319 and 2.322 Å for SWG + Lu to 2.392 Å (both distances) for SWG + Dy. This is the only dataset where the lanthanide contraction manifests itself, albeit to a limited and irregular degree. One can only generalize that, for example, the dLn…C distances for La to Sm are notably longer, by roughly 0.1 Å, when compared to those for the series of Tb to Lu.
We would like to note that the dLn…C distances reported here are roughly 0.07 Å shorter than the coordination bonds dLn–N, which we were able to calculate at the same level of DFT theory for a limited number of lanthanide bisphthalocyanines (LnPc2): for example, 2.548–2.554 Å for LaPc2 and 2.387–2.390 Å for LuPc2 [71]. In other words, the observed values of dLn…C distances are consistent with their interpretation as coordination bonds.
The charge and spin of lanthanide species in their complexes with the SWG model were retrieved from the Mulliken population analysis, usually preferred for Ln-containing carbon nanoclusters; see, for example, [72,73]. One should note that the only alternative to this scheme within DMol3 is the Hirshfeld population analysis. Our choice originated not only from the fact that the Mulliken scheme is usually preferred for the carbon nanoclusters interacting with lanthanide species [72,73], but also from the recent critical assessment [74] of 25 charge assignment methods, which ranked it higher than the Hirshfeld analysis. The hyperconjugated aromatic system of SWG acts as an electron acceptor with respect to all Ln atoms, so that the latter acquire some positive charge. As can be seen from Table 2, it can reach 1.077 e for Ce (also exceeding 1 e for Sm, Eu, and Ho), with the smallest value of 0.674 e calculated for Lu. For Dy, it is 0.998 e; in other words, the use of DSPP pseudopotentials helps to avoid artifacts such as a negative charge for this species [52]. The positive charge acquired by the Tb atom is very similar, at 0.999 e. In other regards, the Ln charge curve (the red dataset in Figure 2c) looks rather similar to the one reported for the ECP calculations [52], without exhibiting a clear trend.
A similar parallel with the previous case [52] can be drawn for the spin behavior of adsorbed Ln atoms: their absolute values closely correlate with those for the isolated lanthanide atoms in their ground state (Figure 2c; the blue dataset). As one can see from Table 2, the spin values obtained are mostly positive (spin-up orientation, the most common in DFT calculations); the exceptions are Nd, Gd, Dy, Er, and Yb (spin-down orientation; this difference is unimportant in the absence of an external field). Even though the absolute values for the adsorbed lanthanide species closely correlate with those typical for the isolated Ln atoms in their ground state, they never coincide with the latter, due to either spin gain or depletion as a result of the interaction with the SWG cluster. In the ECP calculations [52], the spin gain was more common, except for La, Ce, Pr, and Lu. In the present work, the spin gain was observed for Pm, Sm, Eu, Tb, Dy, Ho, Er, Tm, and Yb—that is, for nine of the fifteen elements. Its extent varied from only 0.002 e for Yb (totally filled 4f shell; no unpaired electrons) to 0.191 e for Tb. On the other hand, the degree of spin depletion ranged from 0.030 e for Lu (totally filled 4f shell) to 0.399 e for Ce.
A useful graphical complement to the calculated spin values of the adsorbed Ln atoms is spin density plots: they not only allow for visualizing the shape of unpaired electron clouds on lanthanides but can also reveal spin distribution on the graphene carbon atoms. For the sake of an easier comparison with the results reported previously by employing the DMol3 module (for example, in the reports [34,39,40,42,52,54,55,65]), we usually report the spin isosurfaces at 0.02 a.u. The ones obtained in the present DSPP calculations are shown in Figure 3. As a matter of fact, they turn out to be very similar to those computed with the ECP pseudopotentials [52]: apparently, the determining factor is not the type of pseudopotentials applied but the same combination of functional (PBE) and basis set (DNP). The least important difference is an inverted spin orientation for Ce, Nd, and Er. In the cases of La, Ce, and Gd (with relatively high degrees of spin depletion: 0.366, 0.399, and 0.214 e, respectively), one can see a noticeable unpaired electron density (with the same spin orientation) on the C atoms of the SWG cluster. The new plot calculated for Tb (spin-up), which is reminiscent of those observed for most Ln atoms (Pr to Eu, and Dy to Er), does not exhibit the latter feature at the 0.02 a.u. isosurface, but additional minor lobes (with spin-down orientation, due to a significant spin gain of 0.191 e by Tb) become visible when increasing the isovalue to 0.01 a.u. (see the Graphical Abstract to this paper). Logically, no lobes can be seen in the case of the SWG + Yb complex, since the ytterbium atom keeps its essentially closed-shell configuration, with a negligible spin gain of 0.002 e.
The frontier orbital energies and spatial distribution were another set of important electronic parameters that we analyzed. Table 1 summarizes the energies for HOMO, LUMO, and HOMO–LUMO gap for the fifteen SWG + Ln complexes (for comparison, the corresponding energies for the isolated lanthanide atoms and SWG model are listed in Table S1 of the Supplementary Materials). For the SWG cluster model, we calculated the HOMO–LUMO energy of 0.889 eV, very close to the 0.893 eV reported for ECP [52]. The corresponding values for the isolated Ln atoms spanned from 0.223 eV for La to 2.485 eV for Lu, with the two artifacts reported previously [65], which had to be excluded from the analysis: the negative values of –0.223 and –0.690 eV for Sm and Gd, respectively, due to HOMO/LUMO inversion. The HOMO–LUMO energies for SWG + Ln complexes never presented similar anomalies, and they behaved rather uniformly: the smallest value of 0.028 eV was obtained for SWG + Gd, and the largest one of 0.987 eV was obtained for SWG + Eu; for comparison, the values calculated with ECP varied from 0.225 eV for SWG + La to 0.995 eV for SWG + Eu [52]. For the Tb complex, the HOMO–LUMO gap computed was 0.283 eV.
As for the HOMO–LUMO plots (Figure 4), for some complexes they exhibit obvious similarities with those reported in the previous study [52]; for others, significant differences were found. Close similarities can be seen for the complexes of La, Pr, Nd, Pm, Sm, Eu, Ho, Er, Yb, and Lu. In the present DSPP calculations, with some degree of simplification, the HOMO–LUMO distribution (for the isosurfaces at 0.03 a.u.) can be classified into the following categories:
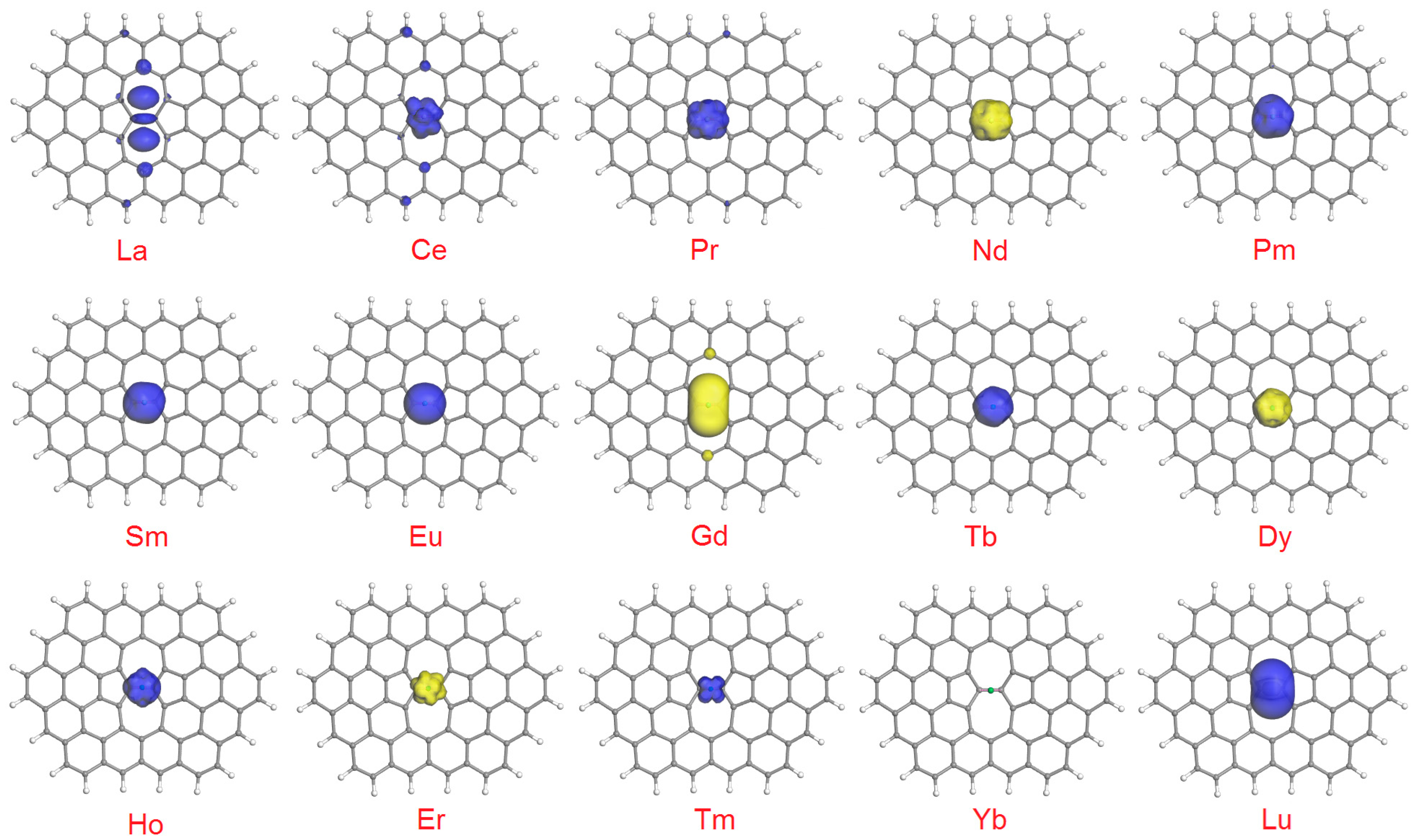
(1)
Both HOMO and LUMO are found exclusively on the Ln atom: the cases of Sm and Tm;
(2)
Both HOMO and LUMO are found on the Ln atom, but LUMO also extends to the carbon atoms of SWG: this is observed for Tb, Dy, and Ho;
(3)
Both HOMO and LUMO are found on the Ln atom, plus minor lobes can be found on the C atoms (usually in proximity to the adsorption site): the cases of Ce, Nd, Eu, Er, Yb, and Lu;
(4)
HOMO is found exclusively (Pr and Pm) or mostly (La) on the Ln atom, but LUMO extends to the carbon atoms only;
(5)
LUMO is found solely on the lanthanide, and HOMO on Ln plus on (mainly adjacent) carbon atoms.

4. Conclusions

Contrary to the previous calculations employing the ECP pseudopotentials within the DMol3 module [52], the use of DSPP allowed us to characterize the adsorption of all fifteen (including Tb) lanthanides on the SW defect-containing graphene cluster model. No artifacts, like a negative charge acquired by the Dy atom, were detected.
In many other regards, the two series of calculations show qualitatively similar features, such as the roughly M-shaped curves of the ΔEfull and ΔEbond energies, trends in the changes in charge (except for Dy) and spin values of the adsorbed Ln atoms, and the spin density plots. In quantitative terms, however, the results can differ (sometimes very) significantly.
Like in the previous studies [49,52,54,55], for most characteristics we found no clear correlation with the lanthanide contraction. The only dataset where this phenomenon apparently manifests itself (albeit to a limited and irregular degree) is the changes in the closest Ln…C approaches.

5. Outlook

During the review process of this paper, both the reviewers and the editor touched upon a series of important issues (apart from the questions that were expected to be explicitly answered) related to the very complex area of lanthanide species interacting with carbon nanomaterials.
One of them is the prospect of bridging theory and experiments. As we already mentioned in the Introduction, even though experimental observations of isolated SW defects in graphene were documented, they require very expensive HR-TEM [7,50] and STM [51] equipment, the measurements are very time- and labor-consuming, and the final micrographs obtained (after additional image processing) might seem rather ambiguous [51]. Furthermore, no direct observations of SW (or any other) defects interacting with chemical species of any nature are possible in principle, since the latter would totally obscure the interaction site. Needless to say, no crucial characteristics (such as interaction energies, interatomic distances, frontier orbitals, spin distribution, etc.) are obtainable. Reports on the use of STM for observing lanthanides on graphene surfaces do exist (see, for example, [75]), but the precision of the imaging does not allow for characterizing finer details than the formation and growth of the Ln islands. At best, one can differentiate between crystalline and fractal-like islands, as well as suggesting that Gd–graphene interactions are stronger compared to those between Eu atoms and the graphene surface [75]. It should be mentioned that scanning electron microscopy and atomic force microscopy (SEM and AFM, respectively) have even coarser resolution. Likewise, speaking about such microanalysis techniques as X-ray photoelectron spectroscopy (XPS) and X-ray absorption spectroscopy (XAS), they are very far from the necessary atomic resolution. Thus, the theoretical calculations in the framework of DFT (as described here and in the works by other research groups [75,76]) will remain the only source of information on the possible geometries, adsorption energies, and electronic states of the adsorbed Ln atoms—at least for a very long time.
When highlighting possible applications of the Ln species adsorbed on graphene-derived materials, it is rather common to make references to single-atom magnets, spintronic devices, quantum technologies, sensors, etc. However, in the present work, we did not consider those materials in general but focused on the adsorption sites with a very particular structure: Stone–Wales defects. In principle, it is difficult (if possible at all) to contemplate an application of what is essentially a point object. Nevertheless, in one of our previous reports [49], we did suggest some practical implications of the related calculation results. Specifically, since local curvature can enhance the reactivity and catalytic activity of graphene sheets [77,78,79,80,81,82,83,84,85], and because SW defects must be common in real-world graphene, the generation of curvature by adsorption of Ln species offers a relatively simple way to enhance chemical activity. In addition, the combination of graphene-derived supports with gadolinium compounds was critically analyzed in the context of carbon nanomaterials for high-resolution magnetic resonance imaging [86].
Finally, similar theoretical studies involving lanthanide species can be extended to other nanocarbon systems, including carbon nanotubes and fullerenes. Here, we are not referring to endohedral fullerenes, since this area is already very well explored (as some examples, one can mention the works [72,73,87] and references therein), and a plethora of new data are constantly published, but the information on the exohedral lanthanide–fullerene interactions remains very limited.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/surfaces8030063/s1: Table S1: The total energies E, HOMO, LUMO, and HOMO–LUMO gap energies for the isolated components (Ln atoms and SWG model) and their SWG + Ln complexes, as well as single-point energies of the distorted SWG clusters after removing Ln atoms (SWG + Ln − Ln).

Author Contributions

Conceptualization, E.V.B.; methodology, V.A.B.; validation, V.A.B.; formal analysis, V.A.B.; investigation, V.A.B.; resources, E.V.B.; data curation, V.A.B.; writing—original draft preparation, V.A.B.; writing—review and editing, E.V.B. and V.A.B.; funding acquisition, E.V.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Autonomous University of Mexico (UNAM), grant number [DGAPA-IG100125].

Data Availability Statement

Data are contained within the article or Supplementary Materials.

Conflicts of Interest

The authors have no competing interests to declare.

References

  1. Izquierdo-García, P.; Fernández-García, J.M.; Martín, N. Twenty years of graphene: From pristine to chemically engineered nano-sized flakes. J. Am. Chem. Soc. 2024, 146, 32222–32234. [Google Scholar] [CrossRef]
  2. Dutta, T.; Chaturvedi, P.; Thakur, A.; Mishra, S.K. Review and outlook of graphene-based catalysis: Revolutionizing water splitting for sustainable hydrogen production. Energy Fuels 2025, 39, 8827–8870. [Google Scholar] [CrossRef]
  3. Elizalde-Herrera, F.J.; Flores-Soto, P.A.; Mora-Cortes, L.F.; González, F.J.; Soria-Arguello, G.; Avalos-Belmontes, F.; Narro-Céspedes, R.I.; Hoyos, M. Recent development of graphene-based composites for electronics, energy storage, and biomedical applications: A review. J. Compos. Sci. 2024, 8, 481. [Google Scholar] [CrossRef]
  4. Hashimoto, A.; Suenaga, K.; Gloter, A.; Urita, K.; Iijima, S. Direct evidence for atomic defects in graphene layers. Nature 2004, 430, 870–873. [Google Scholar] [CrossRef]
  5. Rutter, G.M.; Crain, J.N.; Guisinger, N.P.; Li, T.; First, P.N.; Stroscio, J.A. Scattering and interference in epitaxial graphene. Science 2007, 317, 219–222. [Google Scholar] [CrossRef]
  6. Gass, M.H.; Bangert, U.; Bleloch, A.L.; Wang, P.; Nair, R.R.; Geim, A.K. Free-standing graphene at atomic resolution. Nat. Nanotechnol. 2008, 3, 676–681. [Google Scholar] [CrossRef] [PubMed]
  7. Meyer, J.C.; Kisielowski, C.; Erni, R.; Rossell, M.D.; Crommie, M.F.; Zettl, A. Direct imaging of lattice atoms and topological defects in graphene membranes. Nano Lett. 2008, 8, 3582–3586. [Google Scholar] [CrossRef] [PubMed]
  8. Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
  9. Robertson, A.W.; Allen, C.S.; Wu, Y.A.; He, K.; Olivier, J.; Neethling, J.; Kirkland, A.I.; Warner, J.H. Spatial control of defect creation in graphene at the nanoscale. Nat. Commun. 2012, 3, 1144. [Google Scholar] [CrossRef]
  10. Wei, Y.; Wu, J.; Yin, H.; Shi, X.; Yang, R.; Dresselhaus, M. The nature of strength enhancement and weakening by pentagon–heptagon defects in graphene. Nat. Mater. 2012, 11, 759–763. [Google Scholar] [CrossRef]
  11. Lee, G.-D.; Yoon, E.; He, K.; Robertson, A.W.; Warner, J.H. Detailed formation processes of stable dislocations in graphene. Nanoscale 2014, 6, 14836–14844. [Google Scholar] [CrossRef]
  12. Bhatt, M.D.; Kim, H.; Kim, G. Various defects in graphene: A review. RSC Adv. 2022, 12, 21520–21547. [Google Scholar] [CrossRef]
  13. Thrower, P.A. The study of defects in graphite by transmission electron microscopy. Chem. Phys. Carbon 1969, 5, 217–319. [Google Scholar]
  14. Stone, A.J.; Wales, D.J. Theoretical studies of icosahedral C60 and some related structures. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar]
  15. Tiwari, S.K.; Pandey, S.K.; Pandey, R.; Wang, N.; Bystrzejewski, M.; Mishra, Y.K.; Zhu, Y. Stone–Wales defect in graphene. Small 2023, 19, 2303340. [Google Scholar] [CrossRef]
  16. Chen, M.; Han, X.; Tang, K. Topological regulations of Stone–Wales graphene. Carbon 2024, 226, 119163. [Google Scholar] [CrossRef]
  17. Yang, F.O.; Huang, B.; Li, Z.; Xiao, J.; Wang, H.; Xu, H. Chemical functionalization of graphene nanoribbons by carboxyl groups on Stone–Wales defects. J. Phys. Chem. C 2008, 112, 12003–12007. [Google Scholar] [CrossRef]
  18. Chen, L.; Ouyang, Y.; Wang, Y.; Sun, Y.; Pan, H. The influence of Stone–Wales defects on magnetic properties in graphene. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 43, 593–597. [Google Scholar] [CrossRef]
  19. Qin, X.; Meng, Q.; Zhao, W. Effects of Stone–Wales defect upon adsorption of formaldehyde on graphene sheet with or without Al dopant: A first principle study. Surf. Sci. 2011, 605, 930–933. [Google Scholar] [CrossRef]
  20. Chen, L.; Li, J.; Li, D.; Wei, M.; Wang, X. Chemical functionalization of graphene by H adsorption on Stone-Thrower-Wales defects. Solid State Commun. 2012, 152, 1985–1989. [Google Scholar] [CrossRef]
  21. Guang, H.; Aoki, M.; Tanaka, S.; Kohyama, M. Hole doping by adsorption of oxygen on a Stone–Thrower–Wales defect in graphene. Solid State Commun. 2013, 174, 10–15. [Google Scholar] [CrossRef]
  22. Zhou, Q.; Wang, C.; Fu, Z.; Tang, Y.; Zhang, H. Adsorption of formaldehyde molecule on Stone–Wales defected graphene doped with Cr, Mn, and Co: A theoretical study. Comp. Mater. Sci. 2014, 83, 398–402. [Google Scholar] [CrossRef]
  23. Harman, A.J.; Raelynn, L. Density functional theory study of metal adatoms at or near a Stone–Wales defect in graphene. Procedia Eng. 2014, 93, 2–7. [Google Scholar] [CrossRef]
  24. Kim, D.; Lee, S.; Hwang, Y.; Yun, K.-H.; Chung, Y.-C. Hydrogen storage in Li dispersed graphene with Stone–Wales defects: A first-principles study. Int. J. Hydrog. Energy 2014, 39, 13189–13194. [Google Scholar] [CrossRef]
  25. Yildirim, H.; Kinaci, A.; Zhao, Z.-J.; Chan, M.K.Y.; Greeley, J.P. First-principles analysis of defect-mediated Li adsorption on graphene. ACS Appl. Mater. Interfaces 2014, 6, 21141–21150. [Google Scholar] [CrossRef]
  26. Long, X.J.; Zhao, F.P.; Liu, H.K.; Huang, J.Y.; Lin, Y.; Zhu, J.; Luo, S.N. Anisotropic shock response of Stone–Wales defects in graphene. J. Phys. Chem. C 2015, 119, 7453–7460. [Google Scholar] [CrossRef]
  27. Ebrahimi, S. Influence of Stone–Wales defects orientations on stability of graphene nanoribbons under a uniaxial compression strain. Solid State Commun. 2015, 220, 17–20. [Google Scholar] [CrossRef]
  28. Zhou, Q.; Fu, Z.; Wang, C.; Tang, Y.; Zhang, H.; Yuan, L.; Yang, X. The electronic and magnetic properties of B-doping Stone–Wales defected graphene decorated with transition-metal atoms. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 73, 257–261. [Google Scholar] [CrossRef]
  29. Fu, Y.; Ragab, T.; Basaran, C. The effect of Stone–Wales defects on the mechanical behavior of graphene nano-ribbons. Comp. Mater. Sci. 2016, 124, 142–150. [Google Scholar] [CrossRef]
  30. Zhang, X.; Tang, C.; Jiang, Q. Electric field induced enhancement of hydrogen storage capacity for Li atom decorated graphene with Stone–Wales defects. Int. J. Hydrog. Energy 2016, 41, 10776–10785. [Google Scholar] [CrossRef]
  31. Wang, Y.; Sun, X.; He, F.; Li, K.; Wu, Z. Haeckelite and N-doped haeckelite as catalysts for oxygen reduction reaction: Theoretical studies. J. Phys. Chem. C 2017, 121, 28339–28347. [Google Scholar] [CrossRef]
  32. Zaminpayma, E.; Razavi, M.E.; Nayebi, P. Electronic properties of graphene with single vacancy and Stone–Wales defects. Appl. Surf. Sci. 2017, 414, 101–106. [Google Scholar] [CrossRef]
  33. Rudi, S.G.; Faez, R.; Moravvej-Farshi, M.K.; Saghafi, K. Effect of Stone–Wales defect on an armchair graphene nanoribbon-based photodetector. Superlattices Microstruct. 2019, 130, 127–138. [Google Scholar] [CrossRef]
  34. Basiuk, V.A.; Kakazey, M.; Vlasova, M.; Basiuk, E.V. Effect of structural defects on the strength of adsorption of La and Lu species on graphene. Diam. Relat. Mater. 2019, 100, 107597. [Google Scholar] [CrossRef]
  35. Sadeghzadeh, S.; Ghojavand, M.; Mahmoudi, J. Influence of Stone–Wales defects on the mechanical properties of graphene-like polyaniline (PANI) C3N nanosheets. Diam. Relat. Mater. 2020, 101, 107555. [Google Scholar] [CrossRef]
  36. Kumar, J.; Ansh; Shrivastava, M. Stone–Wales defect and vacancy-assisted enhanced atomic orbital interactions between graphene and ambient gases: A first-principles insight. ACS Omega 2020, 5, 31281–31288. [Google Scholar] [CrossRef] [PubMed]
  37. Arokiyanathan, A.L.; Panjulingam, N.; Lakshmipathi, S. Chemical properties of lithium cluster (Lix, x = 2–8) on Stone–Wales defect graphene sheet: A DFT study. J. Phys. Chem. C 2020, 124, 7229–7237. [Google Scholar] [CrossRef]
  38. Yang, S.; Qian, X.; Xu, H.; Xiong, J.; Wang, Z.; Gu, H. The improved CO adsorption/sensing performance of Stone–Wales defected graphene doped with Fe: A DFT study. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 128, 114603. [Google Scholar] [CrossRef]
  39. Mendoza-Domínguez, C.U.; Basiuk, V.A. Distortion and bonding strength of phthalocyanine molecules adsorbed on topological defects in graphene. Mater. Chem. Phys. 2021, 271, 124963. [Google Scholar] [CrossRef]
  40. Mendoza-Domínguez, C.U.; Basiuk, V.A. Adsorption of yttrium bisphthalocyanine on pristine and defect-contaning graphene models: A DFT study. Diam. Relat. Mater. 2022, 126, 109051. [Google Scholar] [CrossRef]
  41. Rudi, S.G.; Soleimani-Amiri, S. Bilayer armchair graphene nanoribbon photodetector with Stone–Wales defect: A computational study. Mater. Sci. Semicond. Proc. 2022, 150, 106918. [Google Scholar] [CrossRef]
  42. Mendoza-Domínguez, C.U.; Bolivar-Pineda, L.M.; Basiuk, V.A. Effect of structural defects in graphene on the geometry and electronic properties of adsorbed lanthanide bisphthalocyanines: A DFT analysis. Comp. Theor. Chem. 2023, 1225, 114152. [Google Scholar] [CrossRef]
  43. Oliveira, T.A.; Silva, P.V.; Meunier, V.; Girão, E.C. Tuning the carrier mobility and electronic structure of graphene nanoribbons using Stone–Wales defects. Carbon 2023, 201, 222–233. [Google Scholar] [CrossRef]
  44. Jovanović, A.Z.; Dobrota, A.S.; Skorodumova, N.V.; Pašti, I.A. Reactivity of Stone–Wales defect in graphene lattice—DFT study. FlatChem 2023, 42, 100573. [Google Scholar] [CrossRef]
  45. Wang, S.F.; Xue, D.; Liang, J.; Chen, L.Y.; Xie, Y.; Zhang, J.M. The synergistic regulation effect on the structure and electronic properties of graphene by methane plasma, Stone–Wales defect and equibiaxial strain. Diam. Relat. Mater. 2023, 140, 110426. [Google Scholar] [CrossRef]
  46. An, Y. Barrier height breakpoint in employing the Arrhenius equation to proton isotope permeation through Stone–Wales graphene. J. Phys. Chem. Lett. 2023, 14, 10779–10783. [Google Scholar] [CrossRef] [PubMed]
  47. Ghosh, M.; Chowdhury, S.; Majumdar, A.; Jana, D. Stone–Wales decorated phagraphene: A potential candidate for supercapacitor electrodes and thermal transport. ACS Appl. Electr. Mater. 2023, 5, 6725–6737. [Google Scholar] [CrossRef]
  48. Yuan, P.; Li, C.; Zhang, J.; Wang, F.; Chen, X. The special activity of Stone–Wales defect graphene for the oxygen reduction reaction: A comparison study between the charge-neutral model and the constant potential model calculated by density functional theory. J. Phys. Chem. C 2024, 128, 3250–3259. [Google Scholar] [CrossRef]
  49. Basiuk, V.A.; Wu, Y.; Prezhdo, O.V.; Basiuk, E.V. Lanthanide atoms induce strong graphene sheet distortion when adsorbed on Stone–Wales defects. J. Phys. Chem. Lett. 2024, 15, 9706–9713. [Google Scholar] [CrossRef]
  50. Kotakoski, J.; Meyer, J.C.; Kurasch, S.; Santos-Cottin, D.; Kaiser, U.; Krasheninnikov, A.V. Stone-Wales-type transformations in carbon nanostructures driven by electron irradiation. Phys. Rev. B 2011, 83, 245420. [Google Scholar] [CrossRef]
  51. Bandyopadhyay, D.; Sun, Y.; Griffin, R.; Lee, L.Y. Advancing graphene imaging for clear identification of lattice defects: The application of revolve sphere levelling to scanning tunnelling microscopy images. ACS Omega 2024, 9, 43447–43452. [Google Scholar] [CrossRef]
  52. Basiuk, V.A.; Basiuk, E.V. The coordination of lanthanide atoms with Stone–Wales defects on graphene: A cluster DFT analysis using ECP pseudopotentials. Surfaces 2025, 8, 32. [Google Scholar] [CrossRef]
  53. Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Adsorption of lanthanide atoms on graphene: Similar, yet different. J. Phys. Chem. Lett. 2022, 13, 6042–6047. [Google Scholar] [CrossRef] [PubMed]
  54. Basiuk, E.V.; Prezhdo, O.V.; Basiuk, V.A. Strong bending distortion of supercoronene graphene model upon adsorption of lanthanide atoms. J. Phys. Chem. Lett. 2023, 14, 2910–2916. [Google Scholar] [CrossRef]
  55. Basiuk, V.A.; Acevedo-Guzmán, D.A.; Meza-Laguna, V.; Álvarez-Zauco, E.; Huerta, L.; Serrano, M.; Kakazey, M.; Basiuk, E.V. High-energy ball-milling preparation and characterization of Ln2O3−graphite nanocomposites. Mater. Today Commun. 2021, 26, 102030. [Google Scholar] [CrossRef]
  56. Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
  57. Delley, B. Fast calculation of electrostatics in crystals and large molecules. J. Phys. Chem. 1996, 100, 6107–6110. [Google Scholar] [CrossRef]
  58. Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
  59. Delley, B.; Ellis, D.; Freeman, A.; Baerends, E.; Post, D. Binding energy and electronic structure of small copper particles. Phys. Rev. B 1983, 27, 2132–2144. [Google Scholar] [CrossRef]
  60. Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  61. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  62. Basiuk, V.A. Interaction of tetraaza[14]annulenes with single-walled carbon nanotubes: A DFT study. J. Phys. Chem. B 2004, 108, 19990–19994. [Google Scholar] [CrossRef]
  63. Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 1987, 86, 866. [Google Scholar] [CrossRef]
  64. Bergner, A.; Dolg, M.; Kuechle, W.; Stoll, H.; Preuss, H. Ab initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
  65. Basiuk, V.A. DFT calculations on single lanthanide atoms: Is the task as simple as it seems? Comp. Theor. Chem. 2025, 1248, 115170. [Google Scholar] [CrossRef]
  66. Basiuk, V.A.; Henao-Holguín, L.V. Effects of orbital cutoff in DMol3 DFT calculations: A case study of meso-tetraphenylporphine−C60 complex. J. Comput. Theor. Nanosci. 2013, 10, 1266–1272. [Google Scholar] [CrossRef]
  67. Chávez-Colorado, E.; Basiuk, V.A. Noncovalent interactions of free-base phthalocyanine with elongated fullerenes as carbon nanotube models. Struct. Chem. 2017, 28, 1765–1773. [Google Scholar] [CrossRef]
  68. Basiuk, V.A.; Chávez-Colorado, E. Adsorption of free-base phthalocyanine on Stone-Wales defect-containing carbon nanotubes: A DFT study. Diam. Relat. Mater. 2019, 97, 107443. [Google Scholar] [CrossRef]
  69. Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Thermal smearing in DFT calculations: How small is really small? A case of La and Lu atoms adsorbed on graphene. Mater. Today Commun. 2020, 25, 101595. [Google Scholar] [CrossRef]
  70. Basiuk, V.A. Electron smearing in DFT calculations: A case study of doxorubicin interaction with single-walled carbon nanotubes. Int. J. Quantum Chem. 2011, 111, 4197–4205. [Google Scholar] [CrossRef]
  71. Martínez-Flores, C.; Bolivar-Pineda, L.M.; Basiuk, V.A. Lanthanide bisphthalocyanine single-molecule magnets: A DFT survey of their geometries and electronic properties from lanthanum to lutetium. Mater. Chem. Phys. 2022, 287, 126271. [Google Scholar] [CrossRef]
  72. Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Computational modeling of the Ce@C82 metallofullerene isomeric composition. ECS J. Solid State Sci. Technol. 2019, 8, M118–M121. [Google Scholar] [CrossRef]
  73. Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated relative thermodynamic stabilities of the Gd@C82 isomers. ECS J. Solid State Sci. Technol. 2021, 10, 071013. [Google Scholar] [CrossRef]
  74. Manz, T.A. Apples to apples comparison of standardized to unstandardized principal component analysis of methods that assign partial atomic charges in molecules. RSC Adv. 2022, 12, 31617. [Google Scholar] [CrossRef] [PubMed]
  75. Liu, X.; Wang, C.Z.; Hupalo, M.; Yao, Y.X.; Tringides, M.C.; Lu, W.C.; Ho, K.M. Adsorption and growth morphology of rare-earth metals on graphene studied by ab initio calculations and scanning tunneling microscopy. Phys. Rev. B 2010, 82, 245408. [Google Scholar] [CrossRef]
  76. Luo, H.; Xu, K.; Gong, Z.; Li, N.; Zhang, K.; Wu, W. NH3, PH3, AsH3 adsorption and sensing on rare earth metal doped graphene: DFT insights. Appl. Surf. Sci. 2021, 566, 150390. [Google Scholar] [CrossRef]
  77. Bissett, M.A.; Konabe, S.; Okada, S.; Tsuji, M.; Ago, H. Enhanced chemical reactivity of graphene induced by mechanical strain. ACS Nano 2013, 7, 10335–10343. [Google Scholar] [CrossRef] [PubMed]
  78. Wu, Q.; Wu, Y.; Hao, Y.; Geng, J.; Charlton, M.; Chen, S.; Ren, Y.; Ji, H.; Li, H.; Boukhvalov, D.W.; et al. Selective surface functionalization at regions of high local curvature in graphene. Chem. Commun. 2013, 49, 677–679. [Google Scholar] [CrossRef] [PubMed]
  79. Qu, Y.; Ke, Y.; Shao, Y.; Chen, W.; Kwok, C.T.; Shi, X.; Pan, H. Effect of curvature on the hydrogen evolution reaction of graphene. J. Phys. Chem. C 2018, 122, 25331–25338. [Google Scholar] [CrossRef]
  80. Basiuk, V.A.; Bolivar-Pineda, L.M.; Meza-Laguna, V.; Rybak-Akimova, E.V.; Basiuk, E.V. Carbon nanotubes and graphene promote pyrolysis of free-base phthalocyanine. J. Phys. Chem. Lett. 2018, 9, 4420–4427. [Google Scholar] [CrossRef]
  81. Kosmala, T.; Baby, A.; Lunardon, M.; Perilli, D.; Liu, H.; Durante, C.; Di Valentin, C.; Agnoli, S.; Granozzi, G. Operando Visualization of the hydrogen evolution reaction with atomic-scale precision at different metal–graphene interfaces. Nat. Catal. 2021, 4, 850–859. [Google Scholar] [CrossRef]
  82. Banerjee, S.; Rappe, A.M. Mechanochemical molecular migration on graphene. J. Am. Chem. Soc. 2022, 144, 7181–7188. [Google Scholar] [CrossRef]
  83. Hawthorne, N.; Banerjee, S.; Moore, Q.; Rappe, A.M.; Batteas, J.D. Studies of the reactivity of graphene driven by mechanical distortions. J. Phys. Chem. C 2022, 126, 17569–17578. [Google Scholar] [CrossRef]
  84. Kim, C.-E.; Lee, J.; Walsh, A.; Lordi, V.; Bahr, D.F. Role of ripples in altering the electronic and chemical properties of graphene. J. Chem. Phys. 2022, 156, 054708. [Google Scholar] [CrossRef]
  85. Sun, P.Z.; Xiong, W.Q.; Bera, A.; Timokhin, I.; Wu, Z.F.; Mishchenko, A.; Sellers, M.C.; Liu, B.L.; Cheng, H.M.; Janzen, E.; et al. Unexpected catalytic activity of nanorippled graphene. Proc. Natl. Acad. Sci. USA 2023, 120, e2300481120. [Google Scholar] [CrossRef]
  86. Rodríguez-Galván, A.; Rivera, M.; García-López, P.; Medina, L.A.; Basiuk, V.A. Gadolinium-containing carbon nanomaterials for magnetic resonance imaging: Trends and challenges. J. Cell. Mol. Med. 2020, 24, 3779–3794. [Google Scholar] [CrossRef] [PubMed]
  87. Martínez-Flores, C.; Basiuk, V.A. Ln@C60 endohedral fullerenes: A DFT analysis for the complete series from lanthanum to lutetium. Comp. Theor. Chem. 2022, 1217, 113878. [Google Scholar] [CrossRef]
Surfaces 08 00063 g001
Figure 1. The graphene cluster model for incorporating a Stone–Wales defect at its center (SWG; general formula C66H20). (a) A top view, in which the SW defect is highlighted in yellow. (b) A side view of the SWG model, where its slight bending is evident. (c) A side view of the bent geometry typical for the SWG + Ln complexes (a particular example of SWG + Lu, for which the strongest distortion was found). (d) Isolated SW defect with an adsorbed Ln atom, explaining the most important geometric parameters: the C–C bond length (dC–C) in the (7,7) junction, the closest Ln…C approaches (dLn…C), and the dihedral angle θ.
Figure 1. The graphene cluster model for incorporating a Stone–Wales defect at its center (SWG; general formula C66H20). (a) A top view, in which the SW defect is highlighted in yellow. (b) A side view of the SWG model, where its slight bending is evident. (c) A side view of the bent geometry typical for the SWG + Ln complexes (a particular example of SWG + Lu, for which the strongest distortion was found). (d) Isolated SW defect with an adsorbed Ln atom, explaining the most important geometric parameters: the C–C bond length (dC–C) in the (7,7) junction, the closest Ln…C approaches (dLn…C), and the dihedral angle θ.
Surfaces 08 00063 g001
Surfaces 08 00063 g002
Figure 2. (a) Changes in the ΔEfull, ΔEdist, and ΔEbond energies (in kcal/mol) for the fifteen SWG + Ln adsorption complexes, from La to Lu. (b) Changes in the dihedral angles θ for SWG + Ln complexes (dataset in pink) and in the corresponding Ln…C distances (dataset in green). (c) Changes in charge (dataset in red) and spin (dataset in blue; absolute values) of the lanthanide atoms in SWG + Ln complexes, retrieved from the Mulliken population analysis.
Figure 2. (a) Changes in the ΔEfull, ΔEdist, and ΔEbond energies (in kcal/mol) for the fifteen SWG + Ln adsorption complexes, from La to Lu. (b) Changes in the dihedral angles θ for SWG + Ln complexes (dataset in pink) and in the corresponding Ln…C distances (dataset in green). (c) Changes in charge (dataset in red) and spin (dataset in blue; absolute values) of the lanthanide atoms in SWG + Ln complexes, retrieved from the Mulliken population analysis.
Surfaces 08 00063 g002
Surfaces 08 00063 g003
Figure 3. Spin density distribution plotted at 0.02 a.u. isosurfaces for the fifteen SWG + Ln adsorption complexes. Blue and yellow lobes correspond to spin-up and spin-down unpaired electrons, respectively. Additional visualization of how the spin density plots look when reducing the isosurface value can be found in the Graphical Abstract, as exemplified for 0.01 a.u.
Figure 3. Spin density distribution plotted at 0.02 a.u. isosurfaces for the fifteen SWG + Ln adsorption complexes. Blue and yellow lobes correspond to spin-up and spin-down unpaired electrons, respectively. Additional visualization of how the spin density plots look when reducing the isosurface value can be found in the Graphical Abstract, as exemplified for 0.01 a.u.
Surfaces 08 00063 g003
Surfaces 08 00063 g004
Figure 4. HOMO and LUMO distribution plotted at 0.03 a.u. isosurfaces for the fifteen SWG + Ln adsorption complexes.
Figure 4. HOMO and LUMO distribution plotted at 0.03 a.u. isosurfaces for the fifteen SWG + Ln adsorption complexes.
Surfaces 08 00063 g004
Table 1. The ΔEfull, ΔEdist, and ΔEbond energies, along with HOMO, LUMO, and HOMO–LUMO gap energies, for the fifteen SWG + Ln adsorption complexes.
Table 1. The ΔEfull, ΔEdist, and ΔEbond energies, along with HOMO, LUMO, and HOMO–LUMO gap energies, for the fifteen SWG + Ln adsorption complexes.
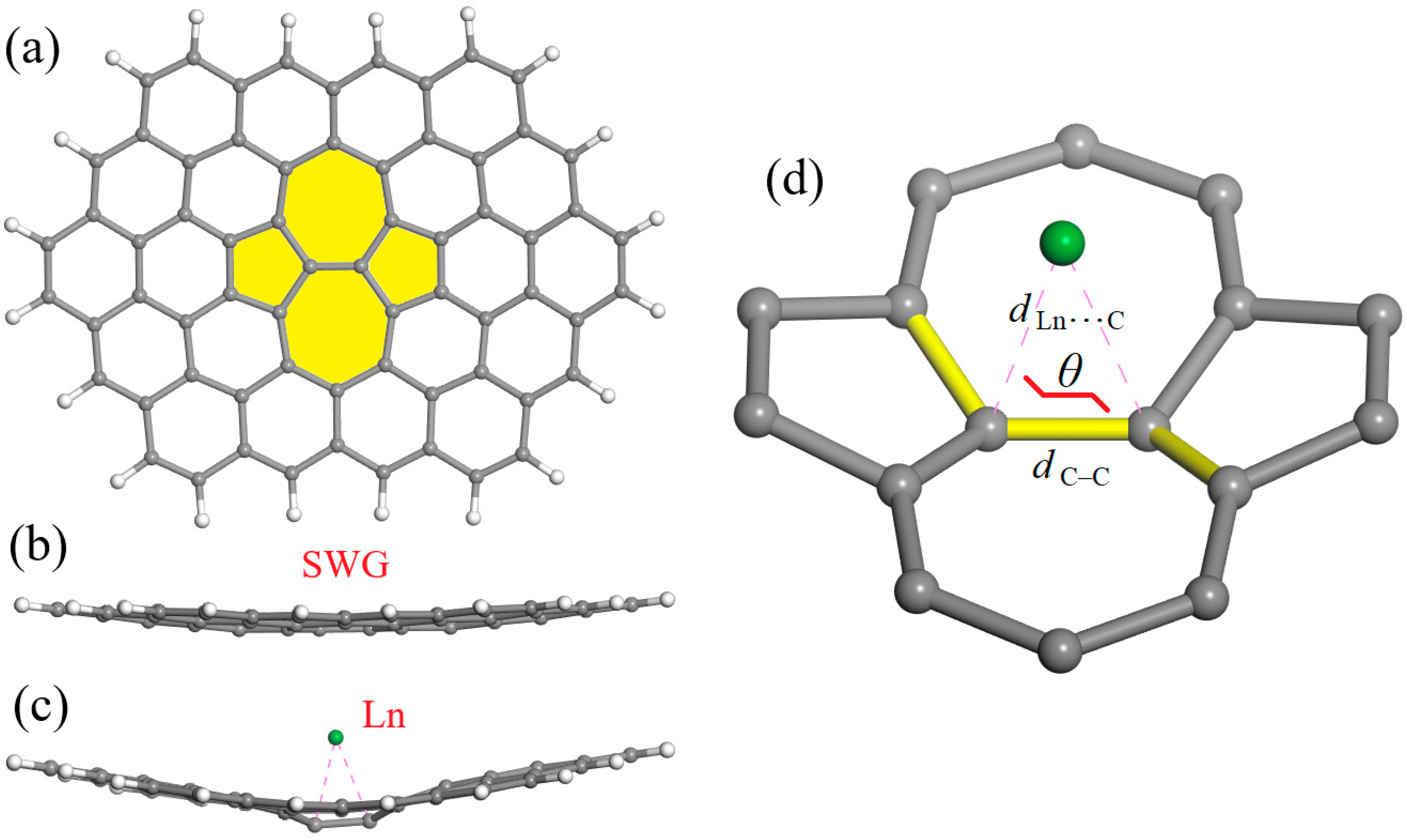
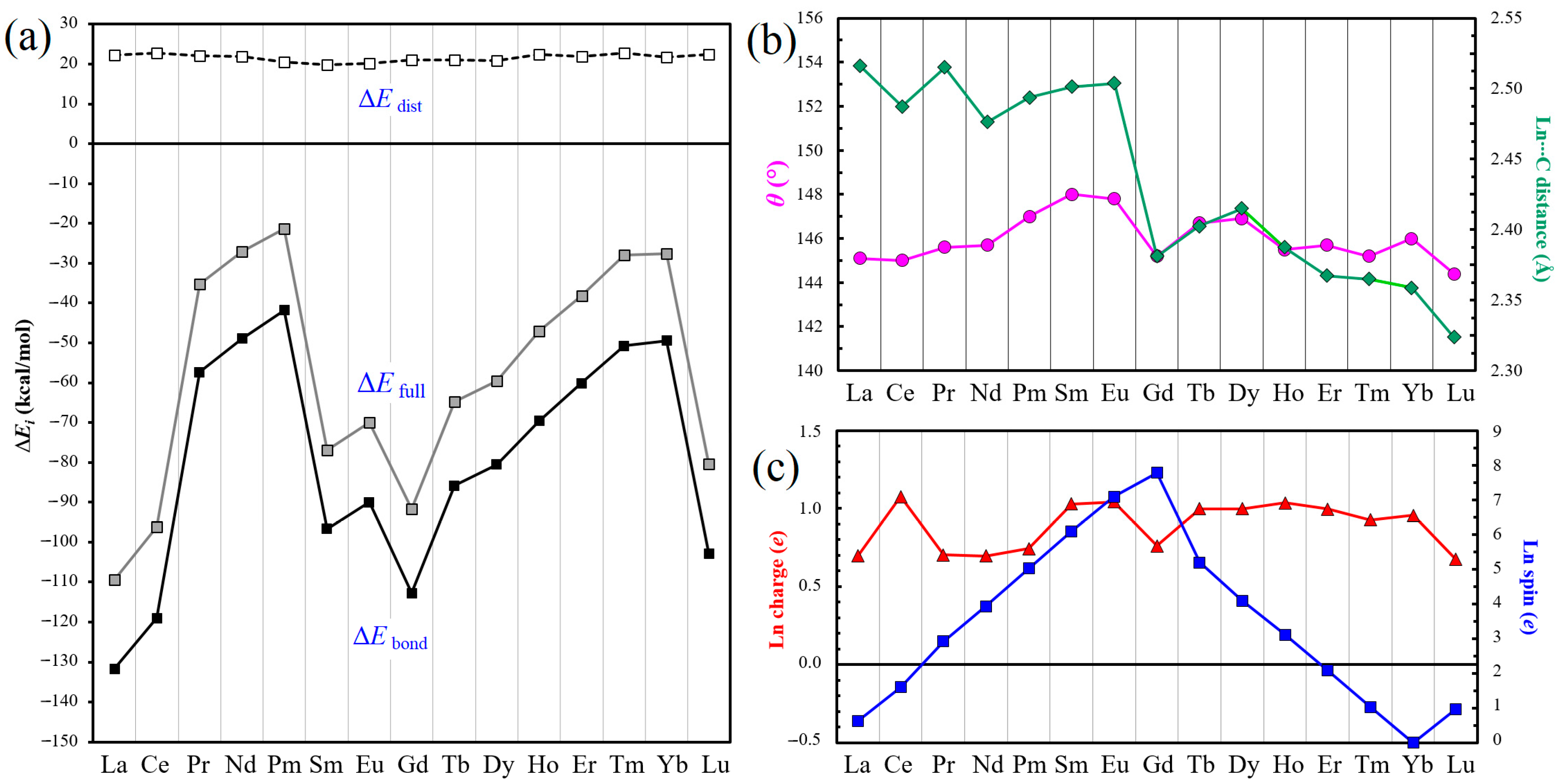
Atomic NumberLnΔEfull (kcal/mol)ΔEdist (kcal/mol)ΔEbond (kcal/mol)HOMO (eV)LUMO (eV)HOMO–LUMO Gap (eV)
57La−109.422.3−131.7−3.387−3.1340.253
58Ce−96.222.8−119.0−3.287−3.1100.177
59Pr−35.222.1−57.3−3.290−3.1060.184
60Nd−27.021.9−48.9−3.431−3.1070.324
61Pm−21.320.5−41.8−3.279−3.1010.178
62Sm−76.919.8−96.7−3.574−3.3100.264
63Eu−69.920.1−90.0−4.102−3.1150.987
64Gd−91.721.0−112.7−3.687−3.6590.028
65Tb−64.821.0−85.8−3.483−3.2000.283
66Dy−59.620.9−80.5−3.750−3.2110.539
67Ho−47.122.5−69.6−3.623−3.2730.350
68Er−38.221.9−60.1−3.482−3.2970.185
69Tm−27.922.8−50.7−3.718−3.3330.385
70Yb−27.621.8−49.4−4.054−3.3870.667
71Lu−80.422.4−102.8−4.249−3.5680.681
Table 2. The geometric parameters (explained in Figure 1d), including the shortest distances dLn…C, the length of the C–C bond in the (7,7) junction, and the dihedral angle θ, as well as the charge and spin of Ln species, in the fifteen SWG + Ln adsorption complexes, retrieved from the Mulliken population analysis.
Table 2. The geometric parameters (explained in Figure 1d), including the shortest distances dLn…C, the length of the C–C bond in the (7,7) junction, and the dihedral angle θ, as well as the charge and spin of Ln species, in the fifteen SWG + Ln adsorption complexes, retrieved from the Mulliken population analysis.
Atomic NumberLndLn…C (Å)dC–C (Å)θ (°)Ln Charge (e)Ln Spin (e)
57La2.473, 2.4801.419145.10.6990.634
58Ce2.450, 2.4601.420145.01.0771.601
59Pr2.472, 2.4841.423145.60.7032.923
60Nd2.441, 2.4581.422145.70.696−3.933
61Pm2.455, 2.4691.421147.00.7435.019
62Sm2.461, 2.4641.421148.01.0296.093
63Eu2.463, 2.4651.422147.81.0437.093
64Gd2.365, 2.3661.414145.20.760−7.786
65Tb2.382, 2.3821.422146.70.9995.191
66Dy2.392, 2.3921.423146.90.998−4.096
67Ho2.370, 2.3791.424145.51.0373.115
68Er2.354, 2.3701.423145.70.997−2.080
69Tm2.352, 2.3541.425145.20.9281.039
70Yb2.347, 2.3491.424146.00.956−0.002
71Lu2.319, 2.3221.420144.40.6740.970
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Basiuk, V.A.; Basiuk, E.V. Adsorption of Lanthanide Atoms on a Graphene Cluster Model Incorporating Stone–Wales Defect. Surfaces 2025, 8, 63. https://doi.org/10.3390/surfaces8030063

AMA Style

Basiuk VA, Basiuk EV. Adsorption of Lanthanide Atoms on a Graphene Cluster Model Incorporating Stone–Wales Defect. Surfaces. 2025; 8(3):63. https://doi.org/10.3390/surfaces8030063

Chicago/Turabian Style

Basiuk, Vladimir A., and Elena V. Basiuk. 2025. "Adsorption of Lanthanide Atoms on a Graphene Cluster Model Incorporating Stone–Wales Defect" Surfaces 8, no. 3: 63. https://doi.org/10.3390/surfaces8030063

APA Style

Basiuk, V. A., & Basiuk, E. V. (2025). Adsorption of Lanthanide Atoms on a Graphene Cluster Model Incorporating Stone–Wales Defect. Surfaces, 8(3), 63. https://doi.org/10.3390/surfaces8030063

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop