Abstract
Adhesion of cell membranes is relevant to many biological processes and arises from the specific binding of membrane-anchored receptor proteins to their ligands present in the apposing membrane. Here, we employ a statistical–mechanical model and perform Monte Carlo simulations to study a system of adhered membranes in which the receptor and ligand proteins exhibit affinity for association with so-called lipid rafts, which are fluctuating nanoscale molecular clusters enriched in sphingolipid and cholesterol. We focus on equilibrium properties of the adhered membranes in the mixed phase, where both the membrane-anchored proteins and lipid rafts are distributed more-or-less uniformly within the membranes. Our simulation results show that lateral attraction between lipid rafts enhances the receptor–ligand binding, affecting the adhesion of the membranes. On the other hand, the receptor–ligand binding causes lipid rafts to be distributed less uniformly within the membranes and, simultaneously, leads to an increased co-localization of the membrane-anchored proteins with lipid rafts. We quantify and discuss all these effects, providing a detailed picture of the complex interplay between the adhesion of the membranes and the lateral distribution of the membrane-anchored proteins and lipid rafts. Our results broaden the understanding of the physical mechanisms that determine the supra-molecular organization of lipid rafts and membrane receptors in cell membranes. This understanding may help to elucidate how lipid rafts function in biological processes such as cell signaling and immune responses.
1. Introduction
Any eukaryotic cell is enclosed by a membrane that separates the intracellular fluids and organelles from the extracellular environment [1]. The cell membrane is composed of diverse macromolecules—primarily lipids and proteins of various types—which govern numerous biological processes, including immune responses, tissue formation and repair, nutrient uptake, drug efflux, and neuronal communication. The spatial distribution of these macromolecules in the cell membrane is non-uniform, dynamic, and responsive to changes in the environment. In particular, physical contact of apposing cells can cause significant changes in the spatial distribution of membrane proteins, as evidenced by the example of the immunological synapse [2].
Diverse biological processes involve changes in the cell membrane shape, which are accompanied by spatial reorganization of molecular components of the cell membrane. Among the major challenges of contemporary biophysics is to explain how dynamic rearrangements of cell membranes—which typically occur at the length scale of micrometers—are induced by such molecular events as protein–protein binding or protein–lipid association, which take place within the cell membrane at the length scales of angstroms and nanometers [3,4,5]. Here, we employ physics-based modeling that captures relevant length scales—ranging from angstroms to micrometers—to investigate an interplay of specific interactions between apposing cell membranes, shape fluctuations of the membranes, and spatial organization of membrane components.
Cell membranes contain fluctuating nanoscale molecular clusters, or domains, enriched in sphingolipid, cholesterol, and proteins [6]. These nanodomains are commonly termed lipid rafts [6]. They form platforms, functioning in such biological processes as cell signaling, immune responses, and membrane trafficking [6,7,8]. A central question is how lipid rafts respond to physical interactions between cells. It has been shown recently that suppression of membrane conformational fluctuations upon membrane adhesion can cause an effective stabilization and enhanced coalescence of lipid rafts [9,10]. Here, we extend these studies and investigate how membrane adhesion affects the spatial distribution of lipid rafts and their co-localization with adhesion receptors.
Adhesion of cell membranes arises from the specific binding of membrane-anchored receptor proteins to their ligands present in the apposing membrane, as illustrated in the cartoon in Figure 1A. The receptor–ligand binding in the adhesion zone is determined not only by the direct interactions between the receptor and ligand molecules but also by other factors, including the elastic properties of the adhering membranes and the flexibility of the membrane-anchoring segments of the adhesion proteins [11,12,13]. For this reason, the so-called two-dimensional binding affinity, , is difficult to measure in the membrane environment [14,15]. Moreover, the binding of the receptor and ligand molecules anchored in the apposing membranes is a cooperative process, which can be explained as follows: The formation of the receptor–ligand complexes suppresses fluctuations in the separation between the two membranes. The suppression of membrane fluctuations, in turn, facilitates formation of additional receptor–ligand complexes between the adhering membranes. The feedback between the suppression of membrane fluctuations and the formation of receptor–ligand complexes leads to an effect of fluctuation-induced cooperative binding [11,16,17], which has been demonstrated in fluorescence microscopy experiments in the biologically relevant context of immune cell adhesion [18].
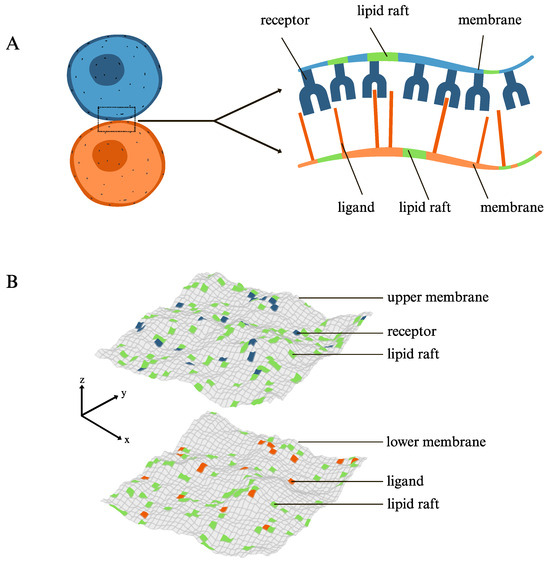
Figure 1.
(A) Cartoon of the system under study. The upper membrane contains receptors (blue) that bind in 1:1 stichometry to their ligands (orange) anchored in the lower membrane. The specific receptor–ligand binding results in adhesion of the two membranes. The receptor and ligand molecules are mobile and exhibit affinity for association with lipid rafts (green) present each of the membranes. (B) Snapshot from MC simulations of the lattice-based mesoscale model for membrane adhesion. Each of the membranes is modeled as a discretized surface, with ”patches” representing either the membrane matrix (gray) or lipid rafts (green). Any patch of the upper membrane can only accommodate one receptor (blue) and any patch of the lower membrane can only be occupied by one ligand (orange). One receptor only binds one ligand if they are located at apposing membrane patches and if the distance between these two patches is within a specific range. The lattice-based mesoscale model is described concisely in Section 2, with further details given in the Supporting Information.
Adhesion-induced phase separation within bio-membranes has been studied both theoretically [19] and experimentally [20,21] in many distinct contexts. For example, adhesion of multi-component membranes to chemically patterned surfaces has been shown to induce phase separation within the membranes under suitable conditions [22]. Interplay between specific attractive and generic repulsive interactions between the apposing membranes has been shown to be sufficient to cause lateral phase separation [23]. Adhesion-induced phase separation has been shown to occur in membranes containing several types of receptor and ligand molecules of different lengths [24,25], and also in membranes with only one type of receptor and ligand, provided that direct receptor–receptor or ligand–ligand attraction is sufficiently strong [26]. Other recent studies on adhesion-induced phase separation [9,10,27,28] have focused on yet a different type of system, namely, membranes in which the receptor and ligand molecules exhibit affinity for lipid rafts, as illustrated in the cartoon in Figure 1A. The latter studies have been motivated by evidence that association of cell adhesion receptors with lipid rafts is a common and biologically relevant process—especially in the context of immune system cells—as it has been reported in experiments both in vitro and in vivo [29,30,31].
There have been computational studies on adhesion of multi-component membranes containing static lipid rafts that have a predefined size, no propensity to coalesce, and some affinity for the membrane-anchored receptor and ligand proteins which mediate the membrane adhesion [27]. These studies have show that the presence of the static lipid rafts enhances the two-dimensional affinity for the receptor–ligand binding, which is consistent with experimental observations that lipid rafts facilitate the formation of the TCR-pMHC protein complex [29,31]. This enhancement in results from an effective increase in local concentrations of the receptor and ligand proteins within lipid rafts, which increases the on-rate for the receptor–ligand binding and, simultaneously, smoothens out the membranes in the lipid-raft regions, which additionally facilitates the receptor–ligand binding.
In our recent studies on adhesion-induced phase separation [9,10], we have simulated dynamic lipid rafts whose shapes and sizes can evolve in time as a result of diffusion, coalescence, and fission. An important aspect of these studies is that the collective and cooperative behavior of the membrane system is manifested not only in an amplification of but also in enhanced coalescence of lipid rafts into stable clusters containing both the raft-favoring lipids and the membrane-anchored receptor and ligand proteins. Here, in contrast to our recent studies [9,10], we explore the supra-molecular organization of adhered membranes rather than the processes of adhesion-induced membrane separation. In particular, we investigate how membrane adhesion affects the spatial distribution and stability of lipid rafts. We also explore the interplay between the adhesion of the membranes and the association of adhesion receptors with lipid rafts. Elucidation of these generic effects is of importance to detailed understanding of many cellular processes, especially in the context of cell signaling and immunity.
Here, we utilize the lattice-based mesoscale model together with its Monte Carlo (MC) simulation algorithm introduced in our earlier studies on adhesion-induced phase separation [9,10]. We adjust the physical parameters of the model to explore the statistical properties of the adhered membranes in the mixed phase, where both the membrane proteins and lipid rafts are distributed more-or-less uniformly within the membranes. Our results show that lateral attraction between lipid rafts enhances both the affinity and the membrane-mediated cooperativity of the receptor–ligand binding, affecting the adhesion of the membranes. On the other hand, the receptor–ligand binding causes lipid rafts to be distributed less uniformly within the adhered membranes and, simultaneously, leads to an increased co-localization of the receptor and ligand proteins with lipid rafts. The non-uniform distribution of lipid rafts, together with their enrichment in receptor–ligand complexes, causes the inter-membrane distance distribution to broaden. We quantify and discuss all these effects, providing a detailed picture of the complex interplay between the adhesion of the membranes and the distribution of lipid rafts within the membranes. Our results may help to elucidate how lipid rafts function in biological processes involving direct contact and specific interactions between apposing cells, such as cell signaling and immune responses.
2. Theoretical Model and Simulation Methods
Molecular dynamics (MD) simulations with all-atom force fields are commonly used to study conformational fluctuations and concerted motions of single receptor molecules, such as the TCR-CD3 complex embedded in a lipid membrane [32,33]. On the other hand, MD simulations with coarse-grained force fields, neglecting certain molecular details of membrane proteins and lipids, allow one to study adhesion of bio-membranes with a lateral size of up to about 100 nm [11,34,35]. However, the adhesion of cell membranes involves multiple length scales, ranging from angstroms (the specific receptor–ligand binding) to micrometers (the lateral size of a typical cell contact area). Therefore, to deal with the multiscale complexity of adhered cell membranes, it is necessary to use appropriate theoretical models and apply simplifying approximations that capture the essential physics of the system under study [34,36]. Here, we employ a suitable variant of lattice-based mesoscale models that have been widely used to study both equilibrium properties and dynamic behavior of bio-membranes with a lateral size of up to several micrometers [17,18,37]. This class of models is based on representing membranes by two-dimensional surfaces and discretizing these surfaces into “patches” of linear size a, larger than the membrane thickness. Within the framework of such models, the elastic deformations of the membranes are described by the Helfrich Hamiltonian [38].
We extend the lattice-based mesoscale model that we have used in our previous studies on membrane adhesion [16,25,28] to incorporate the essential physical processes occurring in the system under study: (i) elastic deformations of the adhering membranes, (ii) two-dimensional diffusion of the receptor and ligand molecules within the membranes, (iii) specific binding of the receptor molecules to their ligands, and (iv) diffusion, coalescence, and fission of the lipid rafts. In this model—by analogy to lattice-gas models—a patch in one membrane can only accommodate one receptor and a patch in the other membrane can only be occupied by one ligand. To ensure the specific binding, one receptor only binds one ligand if they are located at apposing membrane patches and the distance l between these two patches is within the range for the receptor–ligand binding, i.e., , where is the extension of the receptor–ligand complex and is the width of the binding potential. We consider receptor and ligand molecules with nm and nm, as in our earlier studies [9,10], and assume that the energy of the receptor–ligand binding, , is in the range between 5 and 9 , where and T denote the Boltzmann constant and temperature, respectively.
Lipid rafts are represented in our model as domains, or groups of patches, within each of the membranes. Since we consider adhesion proteins that preferentially partition into lipid rafts, we introduce into our model a coupling energy, , in the following way: If one receptor or one ligand is moved from a lipid raft to the membrane matrix, the energy of the system is increased by . Further, to take account of the hydrophobic mismatch between the membrane matrix and lipid rafts, we introduce a contact energy between the nearest-neighbor raft-type patches. This contact energy is analogous to the interaction energy in the two-dimensional lattice-gas model. The short-range attraction between lipid rafts—as quantified by the parameter U—is the driving force for the coalescence of rafts into larger domains, whereas the entropy of the lattice-gas-type system favors disordered states with many separate rafts. The details of the lattice model are given in the Supporting Information.
Without loss of generality, we assume a symmetry in the composition of the two membranes, i.e., the area concentration of receptors in one membrane is equal to the area concentration of ligands in the other membrane, , and the two membranes have the same area fraction as the raft-type patches. In addition, the bending rigidity of each of the membranes is taken to be [9].
We study the model of adhered membranes within the framework of classical statistical mechanics using MC simulations, as detailed in the Supporting Information. In the MC simulations, the membrane patch length is nm and each of the two membranes consists of patches, resulting in a membrane area of 0.49 m2. The area concentration of adhesion proteins, , is varied between and , corresponding to a range of 250 to 400 molecules per micron square. The membrane fraction of raft-type patches is varied from to . The energy of association of a protein molecule with a lipid raft is set to [10], and the raft–raft contact energy U is varied from 0 up to 1.2 to keep the membranes in the mixed phase.
We performed about 5000 independent simulations using our in-house software deposited on GitHub [39]. In each of the simulations, the values of the model parameters a, , , , , , U, , and were fixed. Initially, the adhesion proteins and lipid rafts were distributed randomly and uniformly. Then, MC cycles were executed for thermal equilibration and a subsequent production run of MC cycles was performed for statistical sampling. Details of the MC algorithm, alongside the simulation code, are provided in our recent publication [39]. We used gnuplot [40] to generate the plots presented in all figures in Section 3.
3. Results and Discussion
3.1. The Lateral Attraction Between Lipid Rafts Enhances Both the Affinity and the Membrane-Mediated Cooperativity of the Receptor–Ligand Binding
The binding of the membrane-anchored receptors to their ligands present in the apposing membrane can be quantified by the two-dimensional affinity =[RL]/[R][L], where [RL], [R], and [L] are the area concentrations of the receptor–ligand complexes, free receptors, and free ligands [16]. For a pair of planar, parallel, and rigid (indeformable) membranes whose separation is equal to the receptor–ligand complex size, , the two-dimensional binding affinity, can be calculated analytically, yielding with , where is the energy of binding of a receptor molecule to its ligand, and a is the linear size of membrane patches in the lattice model [16]. For flexible and fluctuating membranes, the average concentrations [RL], [R], and [L] can be determined in MC simulations, yielding the two-dimensional binding affinity =[RL]/[R][L]. The affinity ratio quantifies how membrane flexibility and thermal fluctuations affect the receptor–ligand binding.
Figure 2 shows the results of MC simulations with the area concentration of adhesion proteins m2 and the fraction of the membrane area covered by lipid rafts . The data points in different colors correspond to different values of the raft–raft contact energy U, ranging from 0 to 1.2 . It can be seen in Figure 2 that , which means that thermal fluctuations of the adhered membranes weaken the receptor–ligand binding. This effect can be attributed to the fact that the local distance between the thermally fluctuating membranes is in the range suitable for the receptor–ligand binding only with a certain probability smaller than 1 [16].
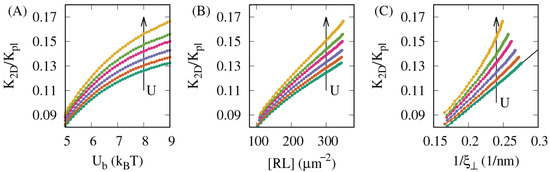
Figure 2.
The lateral short-range attraction between lipid rafts enhances both the affinity and the membrane-mediated cooperativity of the receptor–ligand binding. versus (A), [RL] (B), and (C) for m2; ; and 0 (dark green), 0.5 (orange), 0.8 (blue), (magenta), 1.1 (lime green), and 1.2 (dark yellow). The arrows indicate the increase in U values. The black line in panel C indicates .
The data in Figure 2A show that the affinity ratio increases monotonically with the receptor–ligand binding energy , which can be explained as follows: As the binding energy is increased, the receptor–ligand complexes become more stable, tether the apposing membranes more tightly, and thus effectively dampen fluctuations in the inter-membrane distance, which increases the probability of the local distance between the membranes being in the range suitable for the receptor–ligand binding, which then enhances the binding rate and leads to an increase in . Interestingly, the data in Figure 2A show also that the increase in with becomes more prominent as the raft–raft contact energy U is increased. Thus, the local attraction between lipid rafts, as quantified by the contact energy U, enhances the affinity of the receptor–ligand binding.
The data in Figure 2B show that increases monotonically with the area concentration [RL] of receptor–ligand complexes, which indicates a positive cooperativity in the process of the receptor–ligand binding. This cooperativity results from supersession of membrane fluctuations upon membrane adhesion [11,18]. Importantly, Figure 2B also shows that the increase in with [RL] becomes steeper as the raft–raft contact energy U is increased. Therefore, the local attraction between lipid rafts increases the degree of cooperativity of the receptor–ligand binding.
Another relevant quantity measured in the MC simulations is the thermal roughness of the membranes, , which is defined as the second moment of the inter-membrane distance distribution. The roughness quantifies the magnitude of fluctuations in the local distance between the adhered membranes. The data in Figure 2C show that increases monotonically with , i.e., decreases monotonically with . In the absence of attraction between lipid rafts, i.e., when , the affinity ratio is inversely proportional to the roughness (see the black line and the data points in dark green in Figure 2C), consistent with the theory of membrane-mediated binding cooperativity [11]. However, as the raft–raft contact energy U is increased, the decrease in with becomes progressively steeper than , implying that the local attraction between lipid rafts causes an enhancement in the membrane-mediated cooperativity of the receptor–ligand binding.
Taken together, the data shown in Figure 2 demonstrate that both the affinity and the membrane-mediated cooperativity of the receptor–ligand binding are elevated when the attraction between lipid rafts is increased. This observation is consistent with our earlier findings and can be understood as follows [10,27]: As the contact energy U is increased, lipid rafts have a stronger tendency to merge and grow in size, which leads to an increase in the area concentration of the receptors and ligands associated with these rafts. This effective increase in local concentrations of the receptors and ligands amplifies the receptor–ligand binding rate, which in turn elevates the binding affinity. Moreover, accumulation of the receptor–ligand complexes within the lipid rafts smoothens out the membranes locally, which additionally facilitates the receptor–ligand binding, causing a cooperative effect.
To investigate the influence of the amount of adhesion proteins and lipid rafts on the inter-membrane receptor–ligand binding, we performed additional MC simulations with 250, 300, 350, and 400 molecules per square micron and 0.01, 0.02, 0.05, and 0.1. The results of these simulations are show in Figures S1–S12 in the Supporting Information and demonstrate that lipid rafts have practically no impact on the affinity and cooperativity of the receptor–ligand binding if .
3.2. The Lateral Attraction Between Lipid Rafts Broadens the Inter-Membrane Distance Distribution
To further investigate the influence of the attraction between lipid rafts on membrane adhesion, we analyzed the average distance between the membranes. Figure 3 shows the results of MC simulations with the fraction of the membrane area covered by lipid rafts ; the area concentration of adhesion proteins 200, 250, 300, 350, and 400 m−2; and the receptor–ligand binding energy U between 5 and 9 , resulting in an average area concentration of the receptor–ligand complexes, [RL], in the range from about 50 to 350 m−2. The data points in black, red, and blue in Figure 3 correspond to the raft–raft contact energies 0, 1, and 1.2 . The data in Figure 3A show that the average distance between the membranes, d, decreases monotonically with [RL] down to 15 nm at [RL] of about 350 m−2. This result is intuitively clear, namely, as the area concentration of the receptor–ligand complexes tethering the membranes is increased, the membranes are pulled closer to each other; and at a sufficiently high concentration of the inter-membrane receptor–ligand complexes, the membranes are kept at a distance approaching the length of the receptor–ligand complex. Unexpectedly, however, the decrease in d with [RL] becomes less steep as the contact energy U is increased (compare the lines in black, red, and blue in Figure 3A), meaning that the local attraction between lipid rafts causes an increase in the average distance between the membranes.
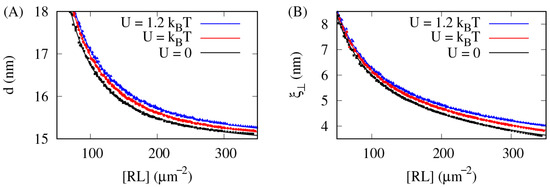
Figure 3.
The lateral short-range attraction between lipid rafts broadens the inter-membrane distance distribution. The average distance d between the membranes (A) and the thermal roughness of the membranes (B) versus the area concentration [RL] of the receptor–ligand complexes for the fraction of the membrane area covered by lipid rafts, , and the raft–raft contact energy 0 (black), (red), and 1.2 (blue).
The data in Figure 3B show that the thermal roughness of the membranes decreases monotonically with [RL], from nm at [RL] m2 to nm at [RL] m2. Clearly, as the area concentration of the inter-membrane receptor–ligand complexes is increased, the membranes become smoother. Unexpectedly, however, the decrease in with [RL] becomes less steep as the contact energy U is increased, which means that the local attraction between lipid rafts makes the membranes effectively rougher.
Taken together, the data shown in Figure 3 demonstrate that both the average inter-membrane distance d and the membrane roughness grow as the raft–raft contact energy U is increased, which may give the impression that the adhesion of the membranes becomes weaker as the attraction between lipid rafts is increased, which in turn is seemingly in contradiction with the data shown in Figure 2 that demonstrate that both the affinity and cooperativity of the receptor–ligand binding are actually elevated as the attraction between lipid rafts is increased. In order to explain this apparent discrepancy between the data shown in Figure 2 and Figure 3, it is useful to determine how lipid rafts and raft-associated proteins are distributed within the membranes, as discussed in the following paragraphs.
3.3. Formation of the Receptor–Ligand Complexes Causes Lipid Rafts to Be Distributed Less Uniformly Within the Adhered Membranes
Within the framework of the lattice model employed in this study, a relevant quantity is the raft coordination number , which is defined as the total number of contacts between the nearest-neighbor raft-type patches of the membranes divided by the total number of the raft-type patches of the membranes. The coordination number is a measure of homogeneity of the spatial distribution of lipid rafts. Namely, when small rafts are distributed uniformly within each of the membranes, then , as illustrated in the simulation snapshots shown in Figure 4A. As the rafts coalesce and grow, then increases, as illustrated in the simulation snapshots in Figure 4B.
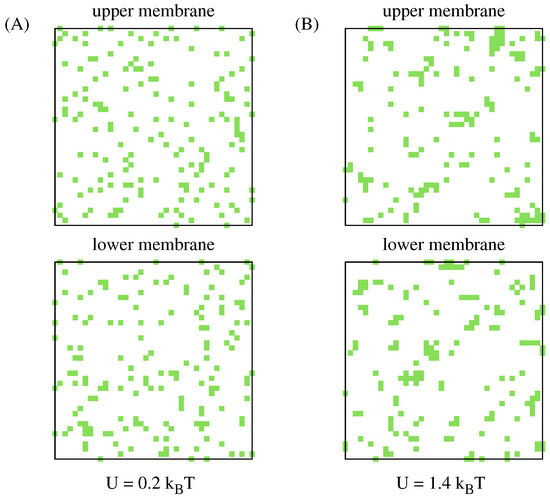
Figure 4.
The raft coordination number is a measure of the homogeneity of the spatial distribution of lipid rafts. Snapshots taken from MC simulations where the receptor–ligand binding energy , the area concentration of adhesion proteins m2, and the fraction of the membrane area covered by lipid rafts . The snapshots show the top view on the upper and lower membranes with lipid rafts marked in green. (A) The raft–raft contact energy , resulting in the coordination number . The lipid rafts are small and distributed rather homogeneously within the membranes. (B) The contact energy , resulting in the coordination number . The lipid rafts are on average larger and distributed less homogeneously than in the snapshots shown in panel A.
Figure 5A shows the results of MC simulations with the raft–raft contact energy and the fraction of the membrane area covered by lipid rafts . The data points in different colors correspond to different area concentrations of the adhesion proteins, , ranging from 200 to 400 m−2. Interestingly, the coordination number is found to increase monotonically with the receptor–ligand binding energy , which implies that lipid rafts join together, thus growing in size, as the receptor–ligand binding becomes stronger. Moreover, this effect becomes more pronounced as the area concentrations of the adhesion proteins is increased.
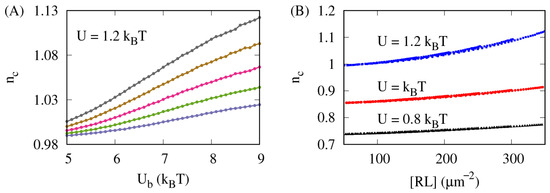
Figure 5.
The receptor–ligand complex formation causes lipid rafts to be distributed less uniformly within the adhered membranes. Results obtained from MC simulations with the fraction of the membrane area covered by lipid rafts . (A) The raft coordination number as a function of the receptor–ligand binding energy U for the raft–raft contact energy and the area concentration of the adhesion proteins: 200 (blue), 250 (green), 300 (magenta), 350 (tan), and 400 m−2 (gray). (B) The coordination number as a function of the average area concentration of the receptor–ligand complexes, [RL], for the raft–raft contact energy (black), (red), and (blue).
Figure 5B shows the results of MC simulations with the raft parameters ; and (data points in black), (data points in red), and (data points in blue). Here, the coordination number is seen to increase monotonically with the average area concentration of the receptor–ligand complexes, [RL], which indicates that formation of the receptor–ligand complexes causes the lipid rafts to redistribute and join together. This effect becomes more prominent as the raft–raft contact energy U is increased.
The data shown in Figure 5 imply that lipid rafts are redistributed and locally coalesce upon formation of the receptor–ligand complexes, which originates from two effects: Firstly, coalescence of lipid rafts is favored by the translational entropy of the receptor–ligand complexes associated with the lipid rafts [9]. Secondly, the receptor–ligand complexes suppress fluctuations of the adhering membranes, which results in an effective, membrane-mediated, lateral attraction between the receptor–ligand complexes [16,41,42]. Since many of the receptors and ligands are associated with lipid rafts, this lateral attraction between the receptor–ligand complexes effectively brings some of the lipid rafts close to one another, facilitating their local coalescence [9]. Thus, the more receptor–ligand complexes are formed, the more lipid rafts are brought together, enhancing their local coalescence and non-uniform distribution.
3.4. Formation of Receptor–Ligand Complexes Enhances Co-Localization of Adhesion Proteins with Lipid Rafts
Another relevant quantity to consider is the average fraction of the adhesion proteins associated with lipid rafts. Figure 6A shows the results of MC simulations with the area concentration of adhesion proteins m2 and the fraction of the membrane area covered by lipid rafts . The lines in different colors correspond to different values of the raft–raft contact energy U, as specified in the figure caption. For , the raft-associated protein fraction is seen to increase monotonically with the receptor–ligand binding energy , indicating that the stronger the receptor–ligand binding is, the more receptors and ligands become associated with lipid rafts. Moreover, the increase in with increasing becomes more pronounced as the raft–raft contact energy U is elevated.
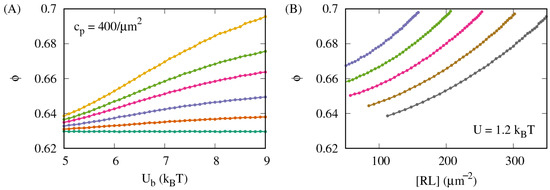
Figure 6.
Receptor–ligand complex formation leads to an enhanced co-localization of the adhesion proteins with lipid rafts. (A) The average fraction of the adhesion proteins associated with lipid rafts versus the receptor–ligand binding energy for m2; ; and 0 (dark green), 0.5 (orange), 0.8 (blue), (magenta), 1.1 (lime green), and 1.2 (dark yellow). (B) The raft-associated protein fraction versus the average area concentration of the receptor–ligand complexes, [RL], for the raft parameters and , and the area concentration of the adhesion proteins 200 (blue), 250 (green), 300 (magenta), 350 (tan), and 400 m−2 (gray).
Figure 6B shows the results of MC simulations with the raft parameters and . The lines in different colors correspond to different area concentrations of the adhesion proteins, as specified in the figure caption. The raft-associated protein fraction is found to increase monotonically with increasing the average area concentration [RL] of the receptor–ligand complexes, which implies that formation of the receptor–ligand complexes effectively enhances co-localization of the adhesion proteins with lipid rafts.
The MC simulation results shown in Figure 6 imply that co-localization of the adhesion proteins with lipid rafts is facilitated by formation of the receptor–ligand complexes linking the apposing membranes. This effect is attributed to the translational entropy of the receptor–ligand complexes associated with lipid rafts.
The data shown in Figure 5 and Figure 6 provide the following picture: Formation of the receptor–ligand complexes promotes both non-uniform distributions of lipid rafts within the membranes and co-localization of the receptor and ligand molecules with lipid rafts. Both of these effects become more pronounced as the energy U of contact between lipid rafts is increased, leading to stabilization of larger rafts enriched in the receptor–ligand complexes that locally restrict the inter-membrane distance. Thus, as the energy U is increased, the receptor–ligand complexes linking the apposing membranes become distributed less homogeneously, causing the inter-membrane distance distribution to broaden, which is reflected in the increase in both the average inter-membrane distance d and the membrane roughness , as seen in Figure 3. This mechanism explains the apparent discrepancy between the MC simulation results shown in Figure 2 and Figure 3.
4. Summary and Conclusions
Cell membranes are not static objects. Instead, they are multi-component and dynamic systems in which diverse processes occur across a broad range of length scales, namely, from angstroms to micrometers. Various species of lipid and protein molecules are distributed non-uniformly within the cell membrane. These distributions are dynamic and influenced by interactions of the cell membrane with its environment. In particular, the supra-molecular architecture of the cell membrane can be affected by the binding of membrane-anchored receptor proteins to their ligands present in an apposing cell membrane (Figure 1), which may contribute to signal transduction across the membrane.
Here, we have employed physics-based modeling together with computer simulations to explore collective and cooperative phenomena in a system of adhered membranes in which both the receptor proteins and their ligands exhibit affinity for association with lipid rafts (Figure 1). Our modeling and simulations provide a detailed picture of the complex interplay between the inter-membrane receptor–ligand binding and the spatial distribution of the receptor–ligand complexes and lipid rafts. On the one hand, lateral attraction between lipid rafts enhances both the affinity and the membrane-mediated cooperativity of the receptor–ligand binding (Figure 2). On the other hand, the receptor–ligand binding causes lipid rafts to be distributed less uniformly within the membranes (Figure 5) and, simultaneously, enhances the tendency of the receptors and ligands to co-localize with lipid rafts (Figure 6). The non-uniform distribution of lipid rafts, together with their enrichment in receptor–ligand complexes, cause the inter-membrane distance distribution to broaden (Figure 3), thus affecting the adhesion of the membranes.
Our findings on the spatial redistribution of lipid rafts upon the inter-membrane receptor–ligand binding bear some similarities to a very recent discovery of lipid raft modulation by polymer adsorbates [43]. Using coarse-grained molecular dynamics simulation and single-molecule-tracking experiments, Gao et al. have shown that adsorption of polymers onto a lipid membrane can induce lipid rafts, which impose dynamic constraints on the adsorbed polymers, leading to an unusual scaling law for polymer diffusion on the membrane surface [43]. These discoveries contribute significantly to the understanding of supra-molecular membrane organization and can help advance membrane-targeted therapeutic approaches.
In contrast to our earlier studies on adhesion-induced phase separation [9,10], a key parameter explored here is the receptor–ligand binding energy . As a matter of fact, here we systematically varied the binding energy and investigated the cooperative receptor–ligand binding (Figure 2), the spatial redistribution of lipid rafts (Figure 5), and the co-localization of the receptor and ligand molecules with lipid rafts (Figure 6). The receptor–ligand binding energy is a biologically relevant parameter that can be modulated and recognized in various cellular processes. For example, the TCR-pMHC binding energy depends sensitively on the amino acid sequence of the peptide exposed by the MHC, which allows the TCRs to discriminate between higher-affinity foreign and lower-affinity self-antigens, enabling T cells to recognize infected or cancerous cells while ignoring normal cells [44].
The results reported here broaden our understanding of the physical mechanisms that determine the spatial organization of lipid rafts and membrane receptors in adhering cell membranes. This understanding may help to elucidate how lipid rafts function in biological processes involving specific interactions between apposing cell membranes, such as cell signaling and immune responses. It is important to acknowledge, however, that the lattice-based mesoscale model employed in this study involves a number of assumptions and bears many limitations. First of all, since the adhesion proteins are represented by single particles with no internal degrees of freedom, physical effects originating from the rotational or conformational entropy of these molecules cannot be captured in the MC simulations. Secondly, the adhered membranes are assumed to bear no tension. It should be noted, however, that sufficiently large tensions applied to the membranes would suppress the membrane-mediated cooperativity of the receptor–ligand binding [16], thus influencing the simulation results reported here. Thirdly, the adhered membranes are assumed to have no spontaneous curvature. Biological membranes, however, are bilayers in which one layer typically has a different molecular composition than the other layer. In addition, the two layers are often exposed to different concentrations of ions or small molecules, which can generate a spontaneous curvature of the bilayer [45]. This spontaneous curvature can undoubtedly influence both the membrane adhesion and the lipid raft distribution. Last but not least, possible effects of molecular crowding at the membranes are not taken into account in our theoretical model. On the one hand, large proteins present in the membrane contact zone could impede the specific receptor–ligand interactions. On the other hand, the molecular crowding could contribute to the spontaneous curvature of the membranes [46]. Despite all these limitations of the lattice-based mesoscale model, we argue that the simulation results reported here could be tested in properly designed experiments using, e.g., super-resolution microscopy [47].
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/surfaces8030062/s1: A detailed description of the lattice-based mesoscale model used in this study, additional information on the Monte Carlo simulations, and twelve figures supporting Figure 2; Figures S1–S4: Analogous to Figure 2A but for different values of parameters and ; Figures S5–S8: Analogous to Figure 2B but for different values of parameters and ; Figures S9–S12: Analogous to Figure 2C but for different values of parameters and .
Author Contributions
I.B.H.T.: conceptualization, data curation, formal analysis, investigation, software, validation, visualization, writing—original draft preparation; B.R.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft preparation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded in whole by the National Science Center of Poland via grant number 2021/40/Q/NZ1/00017.
Data Availability Statement
The original data presented in the study are openly available in Repository for Open Data (RepOD) at https://doi.org/10.18150/FTOBZS.
Acknowledgments
We thank Jinglei Hu for stimulating discussions and useful comments on this manuscript. The numerical simulations were performed using the computing facilities at the Centre of Informatics–Tricity Academic Supercomputer and Network (CI TASK) in Gdansk, Poland.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Alberts, B.; Bray, D.; Hopkin, K.; Johnson, A.D.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Essential Cell Biology; Garland Science: New York, NY, USA, 2015. [Google Scholar]
- Dustin, M.L. The immunological synapse. Cancer Immunol. Res. 2014, 2, 1023–1033. [Google Scholar] [CrossRef]
- Bassereau, P.; Jin, R.; Baumgart, T.; Deserno, M.; Dimova, R.; Frolov, V.A.; Bashkirov, P.V.; Grubmüller, H.; Jahn, R.; Risselada, H.J.; et al. The 2018 biomembrane curvature and remodeling roadmap. J. Phys. D Appl. Phys. 2018, 51, 343001. [Google Scholar] [CrossRef]
- Weikl, T.R. Membrane-mediated cooperativity of proteins. Annu. Rev. Phys. Chem. 2018, 69, 521–539. [Google Scholar] [CrossRef]
- Hurley, J.H.; Boura, E.; Carlson, L.A.; Różycki, B. Membrane budding. Cell 2010, 143, 875–887. [Google Scholar] [CrossRef]
- Lingwood, D.; Simons, K. Lipid rafts as a membrane-organizing principle. Science 2010, 327, 46–50. [Google Scholar] [CrossRef]
- Simons, K.; Sampaio, J.L. Membrane organization and lipid rafts. Cold Spring Harb. Perspect. Biol. 2011, 3, a004697. [Google Scholar] [CrossRef]
- Levental, I.; Veatch, S.L. The continuing mystery of lipid rafts. J. Mol. Biol. 2016, 428, 4749–4764. [Google Scholar] [CrossRef]
- Li, L.; Hu, J.; Różycki, B.; Song, F. Intercellular receptor–ligand binding and thermal fluctuations facilitate receptor aggregation in adhering membranes. Nano Lett. 2020, 20, 722–728. [Google Scholar] [CrossRef]
- Li, L.; Hu, J.; Shi, X.; Różycki, B.; Song, F. Interplay between cooperativity of intercellular receptor–ligand binding and coalescence of nanoscale lipid clusters in adhering membranes. Soft Matter 2021, 17, 1912–1920. [Google Scholar] [CrossRef]
- Hu, J.; Lipowsky, R.; Weikl, T.R. Binding constants of membrane-anchored receptors and ligands depend strongly on the nanoscale roughness of membranes. Proc. Natl. Acad. Sci. USA 2013, 110, 15283–15288. [Google Scholar] [CrossRef]
- Hu, J.; Xu, G.K.; Lipowsky, R.; Weikl, T.R. Binding kinetics of membrane-anchored receptors and ligands: Molecular dynamics simulations and theory. J. Chem. Phys. 2015, 143, 243137. [Google Scholar] [CrossRef]
- Xu, G.K.; Hu, J.; Lipowsky, R.; Weikl, T.R. Binding constants of membrane-anchored receptors and ligands: A general theory corroborated by Monte Carlo simulations. J. Chem. Phys. 2015, 143, 243136. [Google Scholar] [CrossRef]
- Dustin, M.L.; Bromley, S.K.; Davis, M.M.; Zhu, C. Identification of self through two-dimensional chemistry and synapses. Annu. Rev. Cell Dev. Biol. 2001, 17, 133–157. [Google Scholar] [CrossRef]
- Zhu, D.M.; Dustin, M.L.; Cairo, C.W.; Golan, D.E. Analysis of two-dimensional dissociation constant of laterally mobile cell adhesion molecules. Biophys. J. 2007, 92, 1022–1034. [Google Scholar] [CrossRef] [PubMed]
- Krobath, H.; Różycki, B.; Lipowsky, R.; Weikl, T.R. Binding cooperativity of membrane adhesion receptors. Soft Matter 2009, 5, 3354–3361. [Google Scholar] [CrossRef]
- Li, L.; Gui, C.; Hu, J.; Różycki, B. Membrane-mediated cooperative interactions of CD47 and SIRPα. Membranes 2023, 13, 871. [Google Scholar] [CrossRef]
- Steinkühler, J.; Różycki, B.; Alvey, C.; Lipowsky, R.; Weikl, T.R.; Dimova, R.; Discher, D.E. Membrane fluctuations and acidosis regulate cooperative binding of ‘marker of self’protein CD47 with the macrophage checkpoint receptor SIRPα. J. Cell Sci. 2019, 132, jcs216770. [Google Scholar] [CrossRef]
- Weikl, T.R.; Asfaw, M.; Krobath, H.; Różycki, B.; Lipowsky, R. Adhesion of membranes via receptor–ligand complexes: Domain formation, binding cooperativity, and active processes. Soft Matter 2009, 5, 3213–3224. [Google Scholar] [CrossRef]
- Carbone, C.B.; Kern, N.; Fernandes, R.A.; Hui, E.; Su, X.; Garcia, K.C.; Vale, R.D. In vitro reconstitution of T cell receptor-mediated segregation of the CD45 phosphatase. Proc. Natl. Acad. Sci. USA 2017, 114, E9338–E9345. [Google Scholar] [CrossRef]
- Schmid, E.M.; Bakalar, M.H.; Choudhuri, K.; Weichsel, J.; Ann, H.S.; Geissler, P.L.; Dustin, M.L.; Fletcher, D.A. Size-dependent protein segregation at membrane interfaces. Nat. Phys. 2016, 12, 704–711. [Google Scholar] [CrossRef]
- Rouhiparkouhi, T.; Weikl, T.R.; Discher, D.E.; Lipowsky, R. Adhesion-induced phase behavior of two-component membranes and vesicles. Int. J. Mol. Sci. 2013, 14, 2203–2229. [Google Scholar] [CrossRef]
- Weikl, T.R.; Andelman, D.; Komura, S.; Lipowsky, R. Adhesion of membranes with competing specific and generic interactions. Eur. Phys. J. E 2002, 8, 59–66. [Google Scholar] [CrossRef]
- Asfaw, M.; Różycki, B.; Lipowsky, R.; Weikl, T.R. Membrane adhesion via competing receptor/ligand bonds. Europhys. Lett. 2006, 76, 703. [Google Scholar] [CrossRef]
- Różycki, B.; Lipowsky, R.; Weikl, T.R. Segregation of receptor–ligand complexes in cell adhesion zones: Phase diagrams and the role of thermal membrane roughness. New J. Phys. 2010, 12, 095003. [Google Scholar] [CrossRef]
- Weikl, T.R.; Lipowsky, R. Adhesion-induced phase behavior of multicomponent membranes. Phys. Rev. E 2001, 64, 011903. [Google Scholar] [CrossRef]
- Li, L.; Hu, J.; Shi, X.; Shao, Y.; Song, F. Lipid rafts enhance the binding constant of membrane-anchored receptors and ligands. Soft Matter 2017, 13, 4294–4304. [Google Scholar] [CrossRef]
- Li, L.; Hu, J.; Xu, G.; Song, F. Binding constant of cell adhesion receptors and substrate-immobilized ligands depends on the distribution of ligands. Phys. Rev. E 2018, 97, 012405. [Google Scholar] [CrossRef]
- Huang, J.; Zarnitsyna, V.I.; Liu, B.; Edwards, L.J.; Jiang, N.; Evavold, B.D.; Zhu, C. The kinetics of two-dimensional TCR and pMHC interactions determine T-cell responsiveness. Nature 2010, 464, 932–936. [Google Scholar] [CrossRef]
- Murai, T.; Sato, C.; Sato, M.; Nishiyama, H.; Suga, M.; Mio, K.; Kawashima, H. Membrane cholesterol modulates the hyaluronan-binding ability of CD44 in T lymphocytes and controls rolling under shear flow. J. Cell Sci. 2013, 126, 3284–3294. [Google Scholar] [CrossRef]
- Anderson, H.A.; Roche, P.A. MHC class II association with lipid rafts on the antigen presenting cell surface. Biochim. Biophys. Acta (BBA)-Mol. Cell Res. 2015, 1853, 775–780. [Google Scholar] [CrossRef]
- Pandey, P.R.; Różycki, B.; Lipowsky, R.; Weikl, T.R. Structural variability and concerted motions of the T cell receptor–CD3 complex. Elife 2021, 10, e67195. [Google Scholar] [CrossRef]
- Pandey, P.R.; Różycki, B.; Weikl, T.R. Molecular Dynamics Simulations of Immune Receptors and Ligands. In The Immune Synapse: Methods and Protocols; Springer: Berlin/Heidelberg, Germany, 2023; pp. 51–59. [Google Scholar]
- Hou, R.; Ren, S.; Wang, R.; Różycki, B.; Hu, J. Multiscale Simulations of Membrane Adhesion Mediated by CD47-SIRPα Complexes. J. Chem. Theory Comput. 2025, 21, 2030–2042. [Google Scholar] [CrossRef]
- Hou, R.; Gao, J.; Chen, J.; Wang, R.; Różycki, B.; Hu, J. Binding of Soluble Ligands to Membrane Receptors: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2025, 129, 7475–7482. [Google Scholar] [CrossRef]
- Duncan, A.L.; Pezeshkian, W. Mesoscale simulations: An indispensable approach to understand biomembranes. Biophys. J. 2023, 122, 1883–1889. [Google Scholar] [CrossRef]
- Bahrami, A.H.; Weikl, T.R. Curvature-mediated assembly of janus nanoparticles on membrane vesicles. Nano Lett. 2018, 18, 1259–1263. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforschung C 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Li, L.; Gao, J.; Milewski, Ł.; Hu, J.; Różycki, B. Lattice-based mesoscale simulations and mean-field theory of cell membrane adhesion. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2024; Volume 701, pp. 425–455. [Google Scholar]
- Williams, T.; Kelley, C. Gnuplot 5.4: An Interactive Plotting Program. 2020. Available online: http://gnuplot.sourceforge.net/ (accessed on 28 June 2025).
- Speck, T.; Reister, E.; Seifert, U. Specific adhesion of membranes: Mapping to an effective bond lattice gas. Phys. Rev. E 2010, 82, 021923. [Google Scholar] [CrossRef]
- Fenz, S.F.; Bihr, T.; Schmidt, D.; Merkel, R.; Seifert, U.; Sengupta, K.; Smith, A.S. Membrane fluctuations mediate lateral interaction between cadherin bonds. Nat. Phys. 2017, 13, 906–913. [Google Scholar] [CrossRef]
- Gao, J.; Shen, Y.; Komura, S.; Hu, W.; Shen, L.; Hu, J. Polymer sailing on rafts within lipid membranes. Proc. Natl. Acad. Sci. USA 2025, 122, e2503203122. [Google Scholar] [CrossRef]
- Pettmann, J.; Awada, L.; Różycki, B.; Huhn, A.; Faour, S.; Kutuzov, M.; Limozin, L.; Weikl, T.R.; van der Merwe, P.A.; Robert, P.; et al. Mechanical forces impair antigen discrimination by reducing differences in T-cell receptor/peptide–MHC off-rates. EMBO J. 2023, 42, e111841. [Google Scholar] [CrossRef]
- Różycki, B.; Lipowsky, R. Spontaneous curvature of bilayer membranes from molecular simulations: Asymmetric lipid densities and asymmetric adsorption. J. Chem. Phys. 2015, 142, 054101. [Google Scholar] [CrossRef]
- Stachowiak, J.C.; Schmid, E.M.; Ryan, C.J.; Ann, H.S.; Sasaki, D.Y.; Sherman, M.B.; Geissler, P.L.; Fletcher, D.A.; Hayden, C.C. Membrane bending by protein–protein crowding. Nat. Cell Biol. 2012, 14, 944–949. [Google Scholar] [CrossRef]
- Stone, M.B.; Shelby, S.A.; Veatch, S.L. Super-resolution microscopy: Shedding light on the cellular plasma membrane. Chem. Rev. 2017, 117, 7457–7477. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).