Incomplete Wenzel State Induced by Dual-Critical Angles in Regular Square Pyramid Microstructures

Abstract

The array of regular square pyramid microstructures with zero-spacing features is an ideal structural topology for building superhydrophobic functional surfaces due to its excellent anti-wetting performance and low surface adhesion properties. In the framework of existing studies, this microstructured array is usually considered to exist only in two typical wetting states, the stable Cassie state and the Wenzel state. In this study, a third type of wetting state, the incomplete Wenzel state, was discovered for the first time using experimental characterization, and the evolution mechanism of this new wetting state was revealed based on critical contact angle theory and numerical simulation. It is revealed that the faces and edges of the square pyramid microstructures exhibit different tilting angles, and this unique geometrical design endows them with dual critical contact angles. When the intrinsic contact angle of the microstructure is between the critical contact angles for the edges and faces, the wetting behavior of the droplet contact line in the directions parallel to the edges and faces will generate spontaneous and non-spontaneous competition effects, which lead to the formation of the incomplete Wenzel state. The dual-critical-angle theoretical model constructed in this study provides a new perspective for improving the theoretical system of wetting dynamics on pyramid arrays.

1. Introduction

Superhydrophobic surfaces, characterized by a droplet contact angle exceeding 150° and a rolling angle below 10°, exhibit excellent self-cleaning properties and low solid–liquid adhesion [1,2,3,4]. These properties confer significant application value in fields such as fluid drag reduction [5,6], surface antifreezing [7], anti-fogging [8], and microfluidic control [9,10,11,12]. Achieving stabilization of gas–liquid composite interfaces in the Cassie state, which is key to its function, requires the synergistic effect of two performance indicators: low solid–liquid contact area to reduce adhesion and high wetting resistance to prevent Cassie-to-Wenzel state transition [13,14,15,16,17]. However, such surfaces face an intrinsic performance contradiction: to achieve low adhesion, the gas–liquid contact ratio needs to be increased and the solid–liquid contact area reduced [18,19,20,21]; yet interfaces with a high gas–liquid contact ratio are prone to gas-film failure under external loads (e.g., impact [22,23,24,25], compression [26,27], vibration [28,29], evaporation [30,31], and condensation [32,33]), inducing an irreversible Cassie-to-Wenzel state transition [34,35,36]. This contradiction presents a fundamental challenge for synergistically optimizing low adhesion and high wetting resistance on conventional superhydrophobic surfaces.

To resolve this contradiction, current research explores two main directions: first, biomimetic multiscale structure design, which draws on the micro- and nano-composite structures of superhydrophobic biological surfaces, such as lotus leaves and water strider legs, and utilizes nanoscale roughness to enhance capillarity to maintain the stability of the gas–liquid interface [37,38,39,40]. However, this approach faces problems such as complicated preparation processes and insufficient mechanical durability (as nanostructures are easily damaged by shear forces) [41,42]. The second approach is microstructural morphology optimization, including T-shaped [43], hollow pillars [44], and other special geometrical configurations [45,46,47,48,49,50,51]. Although these designs can improve interfacial infiltration resistance to a certain extent, droplets will still undergo an irreversible Cassie-to-Wenzel transition when the external loading pressure exceeds the critical threshold and cannot spontaneously return to the initial Cassie state. In addition, the above engineered designs generally exhibit limited efficacy in modulating interfacial adhesion properties. In conclusion, existing strategies fail to effectively address the core contradiction of simultaneously optimizing low adhesion and high wetting resistance.

Huang et al. have started to study the design of single-scale microstructured superhydrophobic surfaces, aiming to create a surface system that can effectively resist wetting while maintaining low adhesion properties [52,53]. Based on a kinetic analysis framework and numerical simulation, the team conducted a systematic study on a variety of typical single-scale microstructured surfaces. By quantitatively analyzing the effects of the geometrical parameters and contact angles of the microstructures on the critical pressure threshold and surface adhesion behavior, the researchers found that only when the spacing of the regular square pyramid microstructures is zero (zero-spacing) can the surfaces theoretically exhibit infinite wetting resistance and near-zero adhesion, leading to the formation of an ideal superhydrophobic state. In addition, based on the principle of force balance, the study defined a critical contact angle criterion for droplets to maintain the Cassie state. Using this criterion, the study clearly classified the droplet wetting states into two basic types: the stable Cassie state and the Wenzel state.

Building upon the theoretical framework established by Huang et al., this study thoroughly investigates the wetting behavior of zero-spacing regular square pyramid microstructures. By employing 3D-printed arrays of these microstructures combined with a series of wetting experiments, this study observed for the first time a new wetting state—the incomplete Wenzel state—intermediate between the stable Cassie state and the fully wetted Wenzel state. However, we note that existing theoretical models primarily focus on geometric parameters along the edge direction when analyzing wetting transitions, yet they insufficiently account for the anisotropic surface characteristics arising from distinct tilt angles between pyramid faces and edges, which critically govern droplet wetting paths. Theoretical analysis demonstrates that when the intrinsic contact angle lies between the critical contact angles for pyramid faces and edges, the kinetic disparity in wetting along faces versus edges induces the incomplete Wenzel state. Furthermore, numerical simulations corroborate the theoretical model. These findings refine the theoretical criteria for wetting-state transitions in zero-spacing microstructured systems and elucidate how geometric anisotropy drives the surface wetting behavior in pyramidal microstructures.

2. Materials and Methods

The regular square pyramid microstructure array surfaces used in this study were fabricated via 3D printing and soft lithography. The preparation process is illustrated in Figure 1. First, a pyramid microstructure master template was 3D-printed using photosensitive resin (NanoArch P140, Shenzhen MoFang Material Technology, Shenzhen, China). To facilitate demolding, the template surface was hydrophobically modified by vapor deposition of 1H,1H,2H,2H-perfluorodecyltrichlorosilane at 70 °C for 6 h, forming a low-surface-energy perfluorinated layer. Polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning, Midland, MI, USA) was used as the replication material. The PDMS prepolymer and curing agent were mixed at a 10:1 mass ratio and homogenized in a planetary centrifugal mixer (Thinky ARV-310, Thinky, Tokyo, Japan) at 1000 rpm for 5 min, with simultaneous degassing. The mixture was then poured onto the modified template, degassed under vacuum for 30 min to remove interfacial bubbles, and thermally cured at 60 °C for 3 h. After cooling to room temperature, precision demolding yielded a negative replica. Secondary replication of this intermediate mold produced high-fidelity PDMS samples with pyramid microstructures.

In this study, PDMS microstructured arrays were chemically modified via vapor deposition. Samples were placed in a 70 °C vacuum chamber, and surface functionalization was performed using 1H,1H,2H,2H-perfluorodecyltrichlorosilane. By varying deposition time, intrinsic contact angles were continuously tuned from 110° to 130° (Given the non-planar topography and inherent roughness of the printed microstructure surface, the “intrinsic contact angle” referenced in this study represents an effective contact angle exceeding 120°, accounting for surface texture effects). In the geometric parameter design, the bottom edge length was fixed at 300 μm, and the pyramid height was varied from 300 to 700 μm in 100 μm increments, as verified by confocal laser scanning microscopy (CLSM). CLSM characterization confirmed that the “zero-spacing” design was achieved, with adjacent pyramids in direct contact (no lateral gaps) and uniform distribution of heights and base lengths across the array. The chosen dimensions were selected to (i) ensure tilt angles (αₜ) yield distinguishable dual-critical angles, and (ii) facilitate high-fidelity fabrication via 3D printing and PDMS replication (avoiding overly small structures prone to demolding issues). To characterize the wetting behavior, 15 μL deionized water droplets were vertically deposited using a precision micropipette. Equilibrium wetting states were captured with a high-resolution optical microscope.

3. Experimental Characterization of Different Wetting States of Droplets

As shown in Figure 2a, when the pyramid height was 300 μm, droplets maintained a fully wetted Wenzel state even with intrinsic contact angles (θ_in) increasing from 110° to 130° (Figure 2b). This state was characterized by complete liquid infiltration into microstructure interstices and total disappearance of air films. At 400 μm height and 125° contact angle, an incomplete Wenzel state was observed (Figure 2c), exhibiting partial liquid infiltration and residual air films at pyramid bases via optical microscopy. Further increasing the height to 600 μm caused the droplets to transition sequentially from the Wenzel state to an incomplete Wenzel state (contact angle between 110° and 125°), and, finally, to a stable Cassie state at 125° (Figure 2d), where droplets perched atop microstructures with distinct gas–liquid composite interfaces (Figure 2e). To ensure the reliability of wetting state characterization, all sessile droplets were allowed to equilibrate for 300 s before image capture, a duration verified by preliminary tests to ensure stable contact angles and contact areas (no observable changes after 60 s). This standardized equilibration time was maintained across all samples, regardless of wetting state, microstructure height, or intrinsic contact angle. More importantly, the incomplete Wenzel state exhibits stability under static, unperturbed conditions. Experimental observations confirm that this state persists for at least 24 h without transitioning to Wenzel or Cassie states.

To assess the universality of the incomplete Wenzel state beyond deionized water, we performed supplementary wetting experiments using ethanol (surface tension: 22.1 mN/m at 20 °C) and glycerol (surface tension: 63.4 mN/m, viscosity: 1410 mPa·s at 20 °C) on the same microstructured arrays. The results showed that for ethanol, even when the intrinsic contact angle of the microstructure was adjusted to the maximum value (deposition of 1H,1H,2H,2H-perfluorodecyltrichlorosilane was performed for 6 h, H = 700), it only exhibited Wenzel state wetting (Figure 2f), while glycerol showed an incomplete Wenzel state under the same modification conditions (it is in the Wenzel state under all other cases, Figure 2g). In-depth analysis revealed that due to its low surface tension, ethanol could hardly achieve the transition from the incomplete Wenzel state to the Cassie state within the range of experimental parameters; glycerol, on the other hand, did not exhibit the Cassie state due to limitations of its own physical properties (such as high viscosity). Although it was not possible to completely reproduce the three wetting states (Wenzel state, incomplete Wenzel state, and Cassie state) in these two liquid systems, the clearly existing incomplete Wenzel state in glycerol provides strong evidence for the theoretical framework of this study.

Through theoretical analysis and numerical simulation, Huang et al. established that zero-spacing regular square pyramid microstructured arrays exhibit two wetting states: stable Cassie state (gas-film stabilized) and fully wetted Wenzel state, with transition thresholds determined by the tilt angle at a given intrinsic contact angle. While our experimental results validate Huang’s predictions for these classical states, we further reveal a new wetting state—the incomplete Wenzel state—unaccounted for in existing theory. To elucidate its formation mechanism, a theoretical analysis of this state is imperative.

4. Dual-Critical-Angle Theory for Incomplete Wenzel State Formation

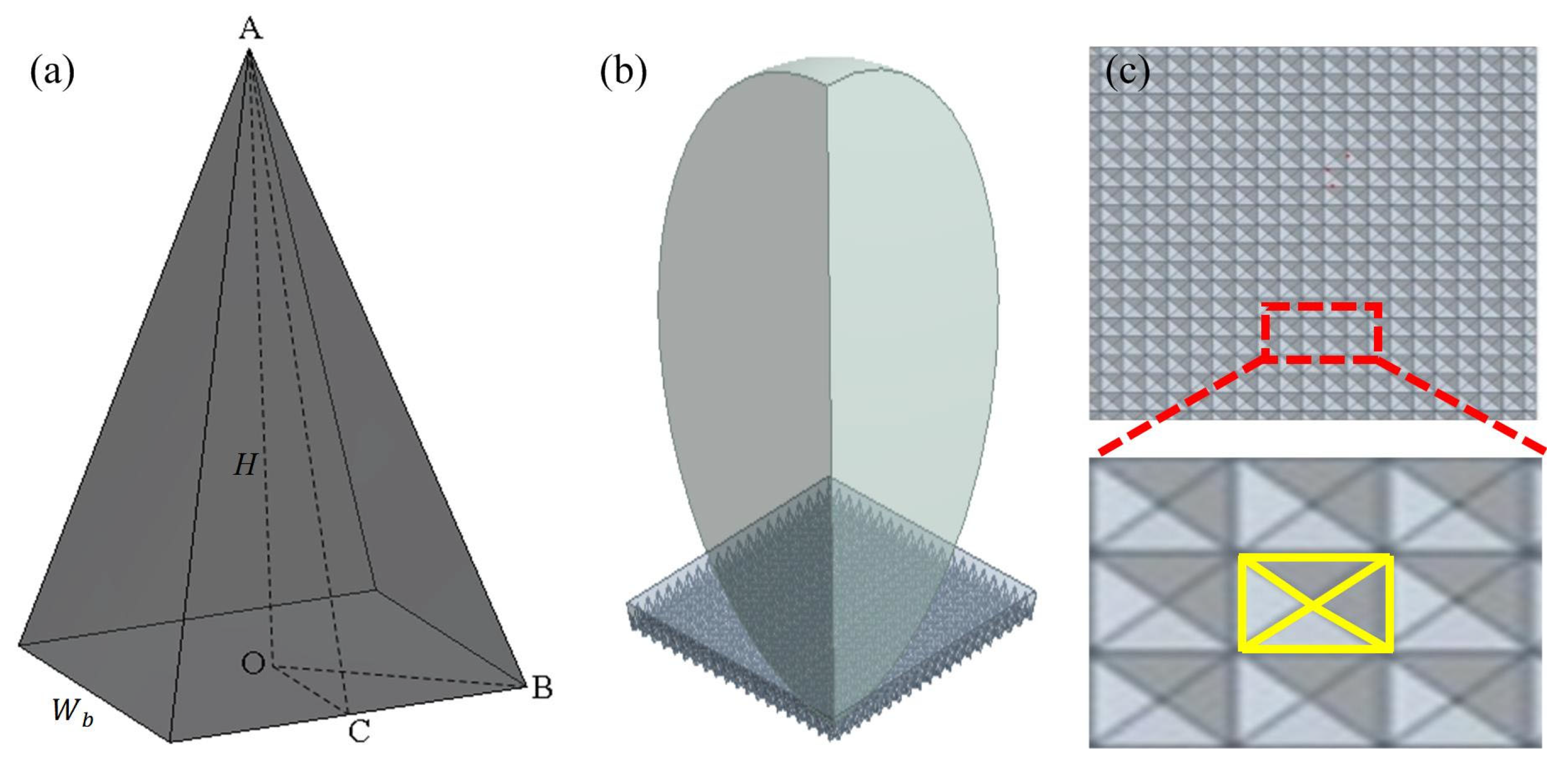
In their study of the wetting mechanism on zero-spacing regular square pyramid arrays, Huang et al. established that when θ_in > θ_cri is satisfied, the droplet maintains a stable Cassie state, whereas transition to the Wenzel state occurs when θ_in < θ_cri. θ_in is the intrinsic contact angle of the microstructure. The theoretical expression for the critical contact angle θ_cri is

$${\theta }_{cri}={\displaystyle \frac{\pi }{2}}+{\alpha }_t$$

(1)

where α_t is the tilt angle along the edge direction (α_t = ∠OAB, Figure 3a), which is given as

$${\alpha }_t=\arctan {\displaystyle \frac{\sqrt{2}{W}_b}{2H}}$$

(2)

W_b is the side length of the base, and H represents the microstructure height (Figure 3a). However, Huang et al. overlooked a key factor: the significant difference in tilt angles between the faces and edges of regular square pyramid microstructures. When defining the face tilt angle as α_t = ∠OAC (Figure 3a), its geometric expression becomes the following:

$${\alpha }_t=\arctan {\displaystyle \frac{W_b}{2H}}$$

(3)

The critical contact angle for the edge direction (∠OAB) is denoted as θ_cri-e, and for the face direction (∠OAC), as θ_cri-f. Geometrically, θ_cri-e > θ_cri-f holds since ∠OAB > ∠OAC. When θ_in > θ_cri-e (implying θ_in > θ_cri-f), non-wetting conditions are satisfied in both directions, yielding a stable Cassie state. When θ_in < θ_cri-f (implying θ_in < θ_cri-e), wetting thresholds are exceeded in all directions, leading to a fully wetted Wenzel state. Crucially, when the intrinsic contact angle lies within the interval θ_cri-f < θ_in < θ_cri-e, edge-directed wetting initiates preferentially due to the satisfied wetting threshold (θ_in < θ_cri-e), while face regions resist wetting as θ_in > θ_cri-f maintains non-wetting conditions. Progressive edge wetting induces droplet deformation, generating capillary-driven surface energy gradients that activate face wetting. This kinetically hindered process culminates in a hybrid state characterized by complete wetting along edges but partial wetting on faces, defining the incomplete Wenzel state. Based on the foregoing analysis, we propose a revised theoretical framework for dual-critical angle:

$$\left\{\begin{array}{l}{\theta }_{in}<{\theta }_{cri-f}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Wenzel\hspace{0.17em}\hspace{0.17em}state\\ \\ {\theta }_{cri-f}<{\theta }_{in}<{\theta }_{cri-e}\hspace{1em}Incomplete\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}Wenzel\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}state\\ \\ {\theta }_{in}>{\theta }_{cri-e}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Cassie\hspace{0.17em}\hspace{0.17em}state\end{array}\right.$$

(4)

Notably, the incomplete Wenzel state is inherently linked to the geometric anisotropy of faceted microstructures (e.g., triangular/hexagonal pyramids), where distinct edge and face tilt angles induce dual critical contact angles. This anisotropy drives the competitive wetting behavior (preferential edge wetting vs. face resistance) that stabilizes the state. For zero-spaced rounded structures (e.g., hemispheres or cylinders), the absence of well-defined edges and faces eliminates such anisotropy, precluding dual-critical angles. Consequently, only Cassie or Wenzel states are expected, as wetting behavior is governed by isotropic parameters like curvature. The incomplete Wenzel state is only observable when the intrinsic contact angle (θ_in) of the material falls within the range defined by the dual-critical angles: θ_cri-f < θ_in < θ_cri-e. This range is determined by the geometric parameters of the pyramid microstructures (Equations (1)–(3)), with θ_cri-f and θ_cri-e typically exceeding 90° for microscale pyramids. For materials with θ_in outside this interval—such as a plain material with θ_in = 35° (far below θ_cri-f)—the wetting threshold for both edges and faces is exceeded, resulting in full infiltration into the microstructure (exclusively the Wenzel state), and the model does not apply. The current study focuses on θ_in = 110–130°, where overlap with the dual-critical angles enables the formation of the incomplete Wenzel state. To validate the reliability of the theoretical analysis and address experimental limitations in resolving droplet wetting dynamics, this study employs simulation-based verification.

5. Computational Validation of the Dual-Critical-Angle Model

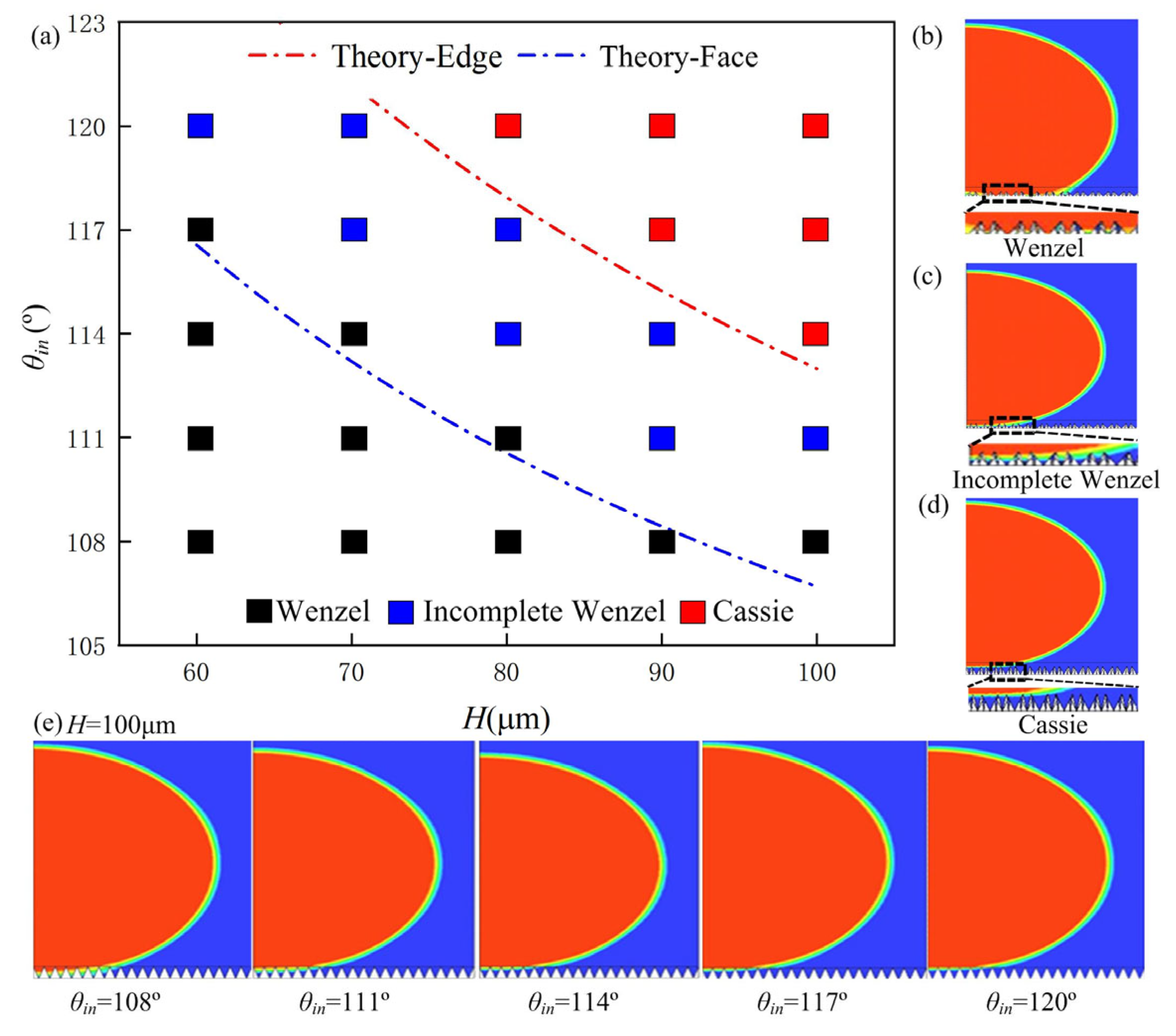
This study established a three-dimensional numerical model using ANSYS Fluent 2023 R1 (finite volume method-based CFD software) to comprehensively validate theoretical predictions. Leveraging the geometric symmetry of regular square pyramid microstructures, a quarter-symmetric computational domain was implemented to maintain physical fidelity while enhancing computational efficiency (Figure 3b,c). Key geometric parameters included a microstructure base side length of 60 μm, pyramid heights ranging from 60 to 100 μm in 10 μm increments (yielding five configurations), and an initial droplet radius of 1 mm. The chosen dimensions were selected to balance computational efficiency in simulations while capturing essential wetting dynamics. A hexahedral-dominant structured mesh system with uniform 20 μm³ elements was adopted. For numerical solution, pressure–velocity coupling employed the PISO algorithm for transient flows with spatial discretization via a second-order upwind scheme. The simulations were conducted under standard ambient conditions (temperature: 293.15 K; pressure: 101,325 Pa) to match the experimental environment. The initial velocity of the droplet was set to 0 m/s, mimicking vertical deposition via a precision micropipette, with subsequent movement driven by surface tension and gravitational forces (maximum liquid–gas interface velocity: ~10⁻³–10⁻² m/s). Contact angle parameterization followed theoretical height–angle correlation (Δθ ≈ 3° per 10 μm height change), with five cases spanning 108–120° at 3° intervals.

Droplets deposited on the microstructure arrays spread under gravity until reaching equilibrium, and numerical simulations reveal that wetting behaviors on zero-spacing regular square pyramid arrays exhibit three characteristic states—Cassie, incomplete Wenzel, and fully wetted Wenzel—dependent on intrinsic contact angle and pyramid height, with state transition boundaries aligning precisely with theoretical predictions (Figure 4a–d). The simulation results show that at a microstructure height of 100 μm, droplet wetting states evolve with increasing intrinsic contact angle, transitioning sequentially from the fully wetted Wenzel state to the incomplete Wenzel state and then to the stable Cassie state (Figure 4e).

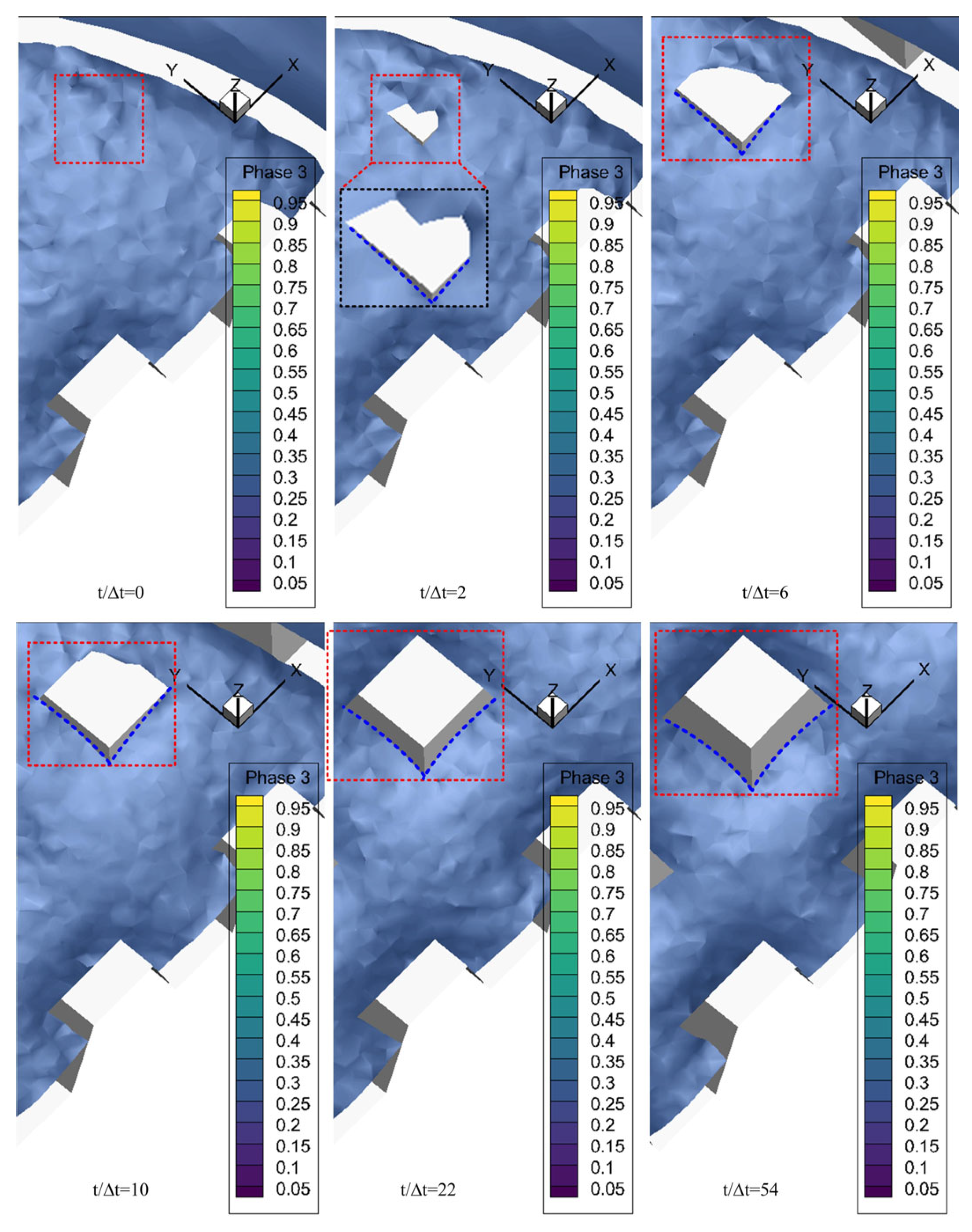
Figure 5 illustrates the dynamics of incomplete Wenzel state formation, where the blue dashed line denotes the contact boundary between the droplet and microstructure. At the initial stage (t/∆t = 2–6), the dashed line adheres closely to the pyramid edges, presenting a narrow-band shape of “extending along the edge lines”—reflecting the characteristic of the droplet preferentially wetting the edge lines. As edge wetting saturates (t/∆t = 10–22), the dashed line broadens and extends from edges toward the center of pyramid faces, indicating progressive face wetting driven by surface tension and interfacial energy. In the final stage (t/∆t = 22–54), the dashed line covers most face areas and stabilizes, outlining the complete contact boundary of the incomplete Wenzel state—partial face coverage without full gap infiltration. In Figure 5, t/∆t denotes dimensionless time, where t is the actual simulation time and ∆t is the numerical time step, facilitating cross-time-scale comparison of wetting dynamics. These results fully validate the dual-critical-angle model, confirming that geometric anisotropy (divergent edge/face tilt angles) governs directional contact line evolution. The model is most reliable for microscale structures (1–1000 μm) where surface tension and geometric anisotropy are the primary drivers, as validated by our experiments and simulations.

6. Potential Applications of Incomplete Wenzel State

The incomplete Wenzel state, with its moderate adhesion (between Cassie and Wenzel states) and controllable wetting behavior, holds potential for practical applications. In microfluidics and biochips, for instance, its tunable adhesion (via adjusting pyramid size or tilt angles) enables precise control over droplet retention and sliding—critical for processes like cell/protein detection. Droplets can be temporarily stabilized in the detection area to complete reactions, then detached with minimal external force, avoiding residue (from high-adhesion Wenzel states) or premature loss (from low-adhesion Cassie states). Such characteristics also make it suitable for adaptive surfaces requiring dynamic wetting adjustment, such as anti-icing or self-cleaning systems.

7. Conclusions

This study addresses the knowledge gap in understanding intermediate wetting states in zero-spacing pyramid microstructures, where geometric anisotropy was previously unaccounted for. Through experiments, theory, and simulations, we report three key findings: First, we discovered the incomplete Wenzel state, bridging Cassie and Wenzel states, filling the theoretical void for partial infiltration in faceted microstructures when θ_in is between edge and face critical angles. Second, we established a dual-critical-angle model showing how geometric anisotropy induces competitive wetting, refining wetting transition criteria beyond the binary Cassie–Wenzel framework. Finally, this resolves the contradiction between low adhesion and high wetting resistance in superhydrophobic surfaces, enabling tunable adhesion design for applications like microfluidics by stabilizing the incomplete Wenzel state. In summary, this advances wetting dynamics understanding in anisotropic microstructures, bridging fundamental theory and practical surface engineering.