General Method for Predicting Interface Bonding at Various Oxide–Metal Interfaces
Abstract
1. Introduction
2. Extension of the Prediction Method
2.1. Interface with Pure Metals including Elemental Semiconductors
− {chemical potential of (M-A-O—) at the standard condition}
− {half of oxygen chemical potential at the standard condition}
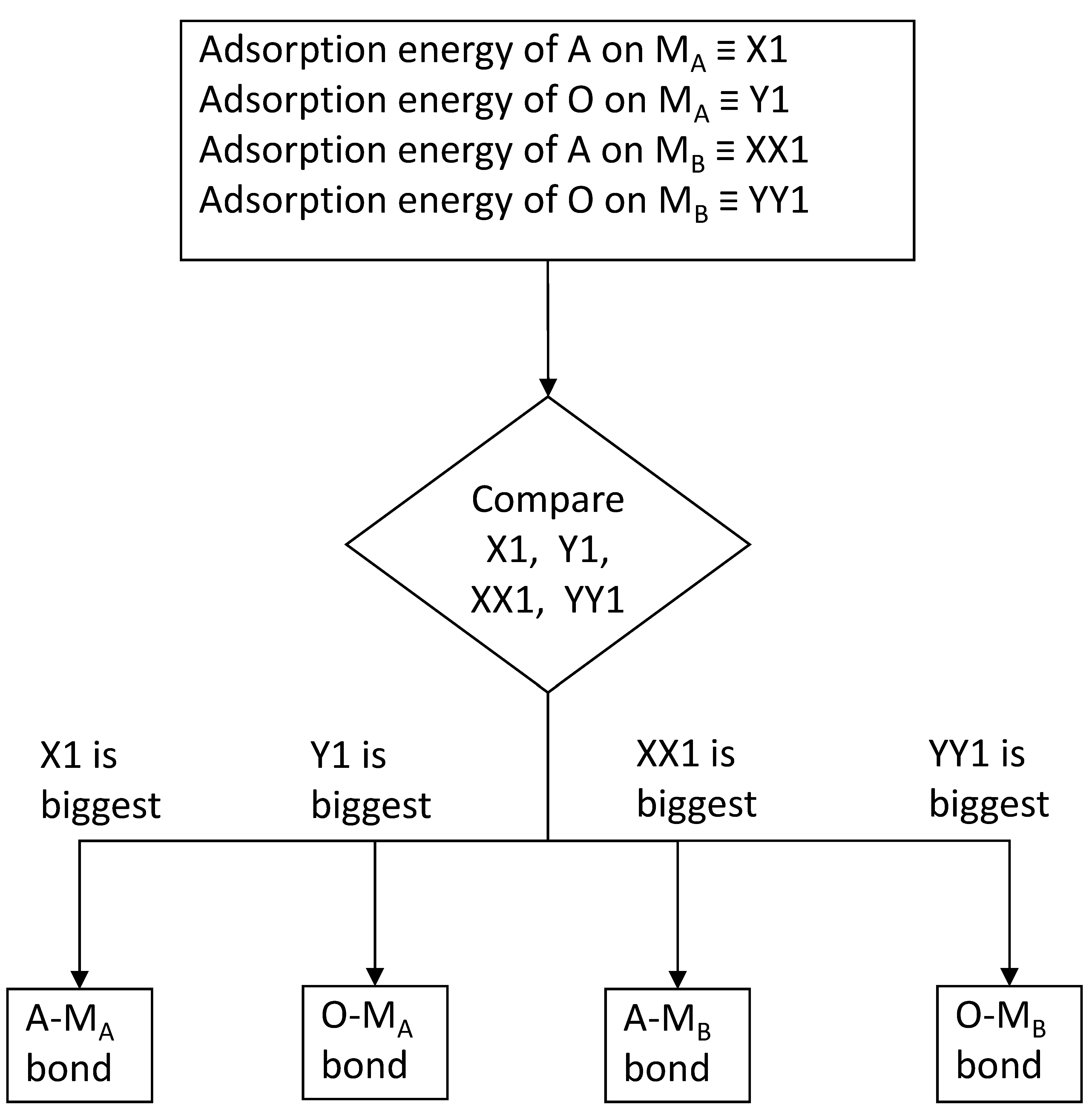
Approx-2: {(A on M) − (M on M)} vs. {(O on M) − 1/2(O2 dissociation energy)} (= X2 vs. Y2),
and {(A on M) − (M on M)} > {(O on M) − 1/2(O2 dissociation energy)},
and {(A on M) − (M on M)} < {(O on M) − 1/2(O2 dissociation energy)},
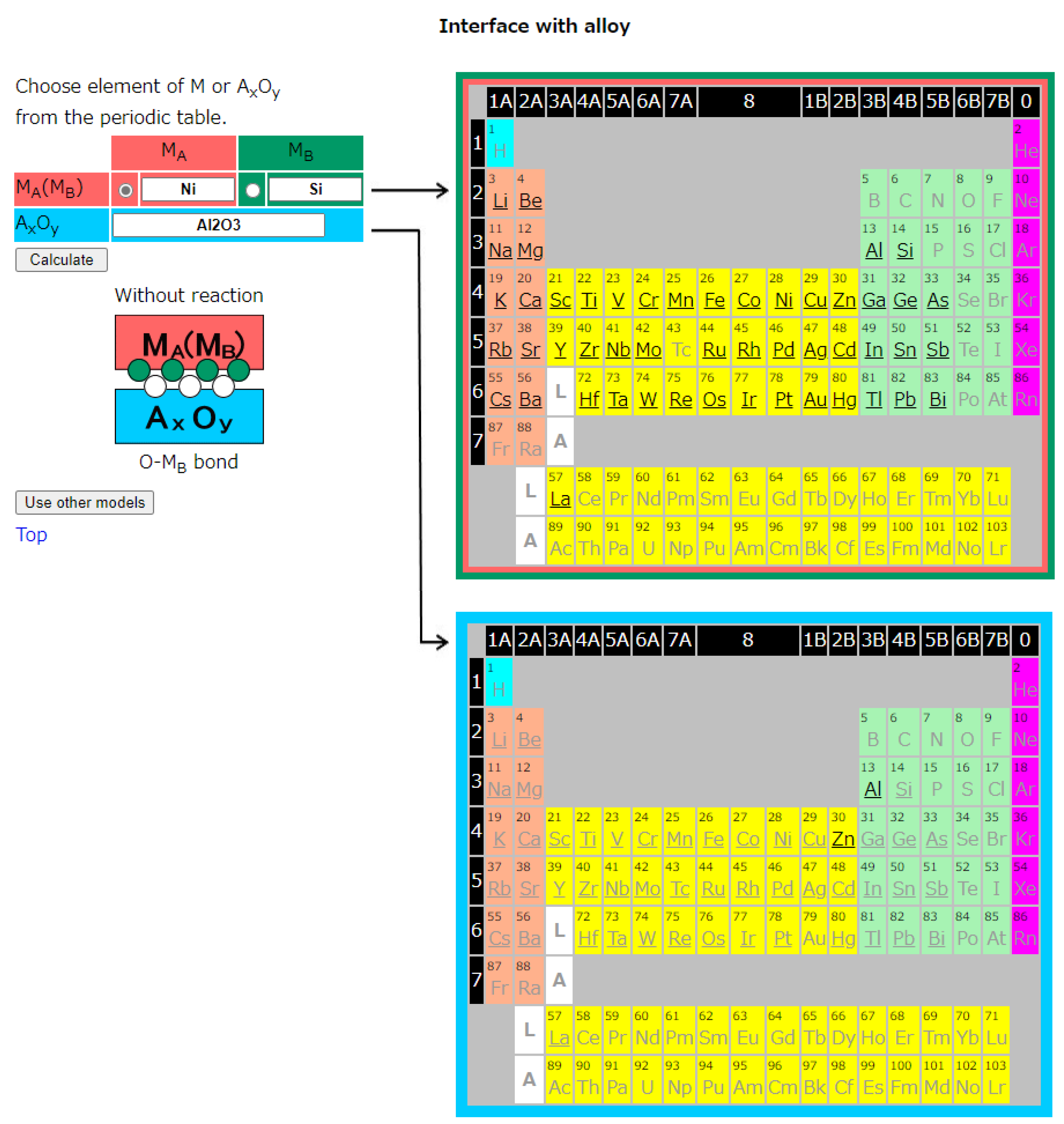
2.2. Interface with Alloys
3. Interface Termination in References
4. Comparison with Predicted Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alber, U.; Mullejans, H.; Ruhle, M. Wetting of copper on α-Al2O3 surfaces depending on the orientation and oxygen partial pressure. Micron 1999, 30, 101–108. [Google Scholar] [CrossRef]
- Merlin, V.; Eustathopoulos, M. Wetting and adhesion of Ni-Al alloys on α-Al2O3 single crystals. J. Mater. Sci. 1995, 30, 3619–3624. [Google Scholar] [CrossRef]
- Chantain, D.; Chabert, F.; Ghetta, V.; Fouletier, J. New Experimental Setup for Wettability Characterization under Monitored Oxygen Activity: II, Wettability of Sapphire by Silver-Oxygen Melts. J. Am. Ceram. Soc. 1994, 77, 197–201. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. First-principles study of the tensile strength and failure of α-Al2O3/Ni(111) interfaces. Phys. Rev. 2007, B76, 075431. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. First-Principles Investigation of the Atomic and Electronic Structures of α-Al2O3/Ni(111) Interfaces. J. Am. Ceram. Soc. 2007, 90, 2429–2440. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. Influence of interface structure on Schottky barrier heights of α-Al2O3 (0001)/Ni (111) interfaces: A first-principles study. Mater. Trans. 2006, 47, 2696–2700. [Google Scholar] [CrossRef]
- Shiraishi, K.; Nakayama, T.; Nakaoka, T.; Ohta, A.; Miyazaki, S. Theory of Metal/Dielectric Interfaces-Breakdown of Schottky Barrier Limits. ECS Trans. 2008, 13, 21–27. [Google Scholar] [CrossRef]
- Nagata, T.; Ahmet, P.; Yoo, Y.Z.; Yamada, K.; Tsutsui, K.; Wada, Y.; Chikyow, T. Schottky metal library for ZNO-based UV photodiode fabricated by the combinatorial ion beam-assisted deposition. Appl. Surf. Sci. 2006, 252, 2503–2506. [Google Scholar] [CrossRef]
- Asthagiri, A.; Niederberger, C.; Francis, A.J.; Porter, L.M.; Salvador, P.A.; Sholl, D.S. Thin Pt films on the polar SrTiO3 (111) surface: An experimental and theoretical study. Surf. Sci. 2003, 537, 134–152. [Google Scholar] [CrossRef]
- Yoshitake, M.; Nemsak, S.; Skala, T.; Tsud, N.; Kim, T.; Matolin, V.; Prince, K.C. Modification of terminating species and band alignment at the interface between alumina films and metal single crystals. Surf. Sci. 2010, 604, 2150–2156. [Google Scholar] [CrossRef]
- Ip, K.; Thaler, G.T.; Yang, H.; Han, S.Y.; Li, Y.; Norton, D.P.; Pearton, S.J.; Jang, S.; Ren, F. Contacts to zno. J. Cryst. Growth 2006, 287, 149–156. [Google Scholar] [CrossRef]
- Young, S.J.; Ji, L.W.; Chang, S.J.; Su, Y.K. ZnO metal–semiconductor–metal ultraviolet sensors with various contact electrodes. J. Cryst. Growth 2006, 293, 43–47. [Google Scholar] [CrossRef]
- Lin, T.K.; Chang, S.J.; Su, Y.K.; Huang, B.R.; Fujita, M.; Horikoshi, Y. ZnO MSM photodetectors with Ru contact electrodes. J. Cryst. Growth 2005, 281, 513–517. [Google Scholar] [CrossRef]
- Yoshitake, M.; Yagyu, S.; Chikyow, T. Novel method for the prediction of an interface bonding species at alumina/metal interfaces. J. Vac. Sci. Technol. 2014, A32, 021102. [Google Scholar] [CrossRef]
- Yoshitake, M.; Yagyu, S.; Chikyow, T. A numerical formula for general prediction of interface bonding between alumina and aluminum-containing alloys. Int. J. Met. 2014, 2014, 120840. [Google Scholar] [CrossRef]
- Yoshitake, M. General method for predicting ZnO–metal interface termination: Extension of the method for Al2O3–metal systems. J. Vac. Sci. Technol. 2021, A39, 063217. [Google Scholar] [CrossRef]
- InterChemBond. Available online: https://interchembond.nims.go.jp (accessed on 23 October 2022).
- Yoshitake, M.; Nemšák, S.; Skála, T.; Tsud, N.; Matolín, V.; Prince, K.C. The influence of Si in Ni on the interface modification and the band alignment between Ni and alumina. Appl. Surf. Sci. 2018, 442, 164–169. [Google Scholar] [CrossRef]
- Yoshitake, M. General method for predicting interface bonding at various oxide-metal interfaces. Jxiv 2022. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 74th ed.; CRC: Boca Raton, FL, USA, 1993–1994. [Google Scholar]
- Brewer, L. The thermodynamic properties of the oxides and their vaporization processes. Chem. Rev. 1953, 52, 1–75. [Google Scholar] [CrossRef]
- Muolo, M.L.; Valenza, F.; Passerone, A.; Passerone, D. Oxygen influence on ceramics wettability by liquid metals: Ag/α-Al2O3—Experiments and modelling. Mater. Sci. Enginnering 2008, A495, 153–158. [Google Scholar] [CrossRef]
- Miedema, A.R.; Dorleijn, J.W.F. Quantitative predictions of the heat of adsorption of metals on metallic substrates. Surf. Sci. 1980, 95, 447–464. [Google Scholar] [CrossRef]
- SurfSeg. Available online: https://surfseg.nims.go.jp (accessed on 3 April 2024).
- Brix, P.; Herzberg, G. Fine structure of the Schumann-Runge bands near the convergence limit and the dissociation energy of the oxygen molecule. Can. J. Phys. 1954, 32, 110–135. [Google Scholar] [CrossRef]
- Green, M.; Kafalas, J.A.; Robinson, P.H. The interaction of oxygen with clean germanium surfaces. In Semiconductor Surface Physics, Proceedings of the Conference on the Physics of Semiconductor Surface, Philadelphia, PA, USA, 4–6 June 1956; Kingston, R.H., Ed.; University of Pennsylvania Press: Philadelphia, PA, USA, 1957; pp. 349–361. [Google Scholar]
- Miedema, A.R.; Chatel, P.F.; Boer, F.R. Cohesion in alloys–fundamentals of a semi-empirical model. Physica 1980, 100B, 1–28. [Google Scholar] [CrossRef]
- Jang, H.; Seidman, D.N.; Merkle, K.L. The chemical composition of a metal/ceramic interface on an atomic scale: The Cu/MgO {111} interface. Interface Sci. 1993, 1, 61–75. [Google Scholar] [CrossRef][Green Version]
- Muller, D.A.; Shashkov, D.A.; Benedek, R.; Yang, L.H.; Silcox, J.; Seidman, D.N. Atomic Scale Observations of Metal-Induced Gap States at {222} MgO/Cu Interfaces. Phys. Rev. Lett. 1998, 80, 4741–4744. [Google Scholar] [CrossRef]
- Chen, F.R.; Chiou, S.K.; Chang, L.; Hong, C.S. High-resolution electron microscopy of Cu/MgO and Pd/MgO interfaces. Ultramicroscopy 1994, 54, 179–191. [Google Scholar] [CrossRef]
- Benedek, R.; Minkoff, M.; Yang, L.H. Adhesive energy and charge transfer for MgO/Cu heterophase interfaces. Phys. Rev. 1996, B54, 7697–7700. [Google Scholar] [CrossRef]
- Shashkov, D.A.; Chisholm, M.F.; Seidman, D.N. Atomic-scale structure and chemistry of ceramic/metal interfaces—I. Atomic structure of {222} MgO/Cu (Ag) interfaces. Acta Mater. 1999, 47, 3939–3951. [Google Scholar] [CrossRef]
- Shashkov, D.A.; Chisholm, M.F.; Seidman, D.N. Atomic-scale structure and chemistry of ceramic/metal interfaces—II. Solute segregation at MgO/Cu (Ag) and CdO/Ag (Au) interfaces. Acta Mater. 1999, 47, 3953–3963. [Google Scholar] [CrossRef]
- Yudanov, I.; Pacchioni, G.; Neyman, K.; Rosch, N. Systematic density functional study of the adsorption of transition metal atoms on the MgO (001) surface. J. Phys. Chem. 1997, B101, 2786–2792. [Google Scholar] [CrossRef]
- Trampert, A.; Ernst, F.; Flynn, C.P.; Fischmeister, H.F.; Ruhle, M. High resolution transmission electron microscopy studies of the Ag/MgO interface. Acta Metall. Mater. 1992, 40, S227–S236. [Google Scholar] [CrossRef]
- Schonberger, U.; Anderson, O.K.; Methfessel, M. Bonding at metal-ceramic interfaces; ab initio density-functional calculations for Ti and Ag on MgO. Acta Metall. Mater. 1992, 40, S1–S10. [Google Scholar] [CrossRef]
- Li, C.; Wu, R.; Freeman, A.J.; Fu, C.L. Energetics, bonding mechanism, and electronic structure of metal-ceramic interfaces: Ag/MgO (001). Phys. Rev. 1993, B48, 8317–8322. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.X.; Chshiev, M.; Dieny, B.; Lee, J.H.; Manchon, A.; Shin, K.H. First-principles investigation of the very large perpendicular magnetic anisotropy at Fe|MgO and Co|MgO interfaces. Phys. Rev. 2011, B84, 054401. [Google Scholar] [CrossRef]
- Bauer, R.S.; Bachrach, R.Z.; Brillson, L.J. Au and Al interface reactions with SiO2. Appl. Phys. Lett. 1980, 37, 1006–1008. [Google Scholar] [CrossRef]
- Hui, L.; Yuping, L.; Caili, Z.; Nan, D.; Aidong, L.; Hongfei, L.; Hongbiao, D.; Peide, H. Effects of aluminum diffusion on the adhesive behavior of the Ni (111)/Cr2O3 (0001) interface: First principle study. Comput. Mater. Sci. 2013, 78, 116–122. [Google Scholar] [CrossRef]
- Hui, L.; Yuping, L.; Caili, Z.; Nan, D.; Hongfei, L.; Hongbiao, D.; Peide, H. The tensile properties and fracture of the Ni/Cr2O3 interface: First principles simulation. Comput. Mater. Sci. 2014, 82, 367–371. [Google Scholar] [CrossRef]
- Aller, H.T.; Yu, X.; Wise, A.; Howell, R.S.; Gellman, A.J.; McGaughey, A.J.H.; Malen, J.A. Chemical Reactions Impede Thermal Transport Across Metal/β-Ga2O3 Interfaces. Nano Lett. 2019, 19, 8533–8538. [Google Scholar] [CrossRef]
- Chu, L.K.; Lee, W.C.; Huang, M.L.; Chang, Y.H.; Tung, L.T.; Chang, C.C.; Lee, Y.J.; Kwo, J.; Hong, M. Metal-oxide-semiconductor devices with molecular beam epitaxy-grown Y2O3 on Ge. J. Cryst. Growth 2009, 311, 2195–2198. [Google Scholar] [CrossRef]
- Sasaki, T.; Matsunaga, K.; Ohta, H.; Hosono, H.; Yamamoto, T.; Ikuhara, Y. Atomic and electronic structures of Ni/YSZ (111) interface. Mater. Trans. 2004, JIM 45, 2137–2143. [Google Scholar] [CrossRef]
- Wang, W.; Guo, H.T.; Gao, J.P.; Dong, X.H.; Qin, Q.X. XPS, UPS and ESR studies on the interfacial interaction in Ni-ZrO2 composite plating. J. Mater. Sci. 2000, 35, 1495–1499. [Google Scholar] [CrossRef]
- Dickey, E.C.; Dravid, V.P.; Nellist, P.D.; Wallis, D.J.; Pennycook, S.J.; Revcolevschi, A. Structure and bonding at Ni–ZrO2 (cubic) interfaces formed by the reduction of a NiO–ZrO2 (cubic) composite. Microsc. Microanal. 1997, 3, 443–450. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Schmauder, S.; Hocker, S.; Kulkova, S.E. Ab-initio investigation of Ni (Fe)/ZrO2 (001) and Ni–Fe/ZrO2 (001) interfaces. Surf. Sci. 2009, 603, 2218–2225. [Google Scholar] [CrossRef]
- Christensen, A.; Carter, E.A. Adhesion of ultrathin ZrO2 (111) films on Ni(111) from first principles. J. Chem. Phys. 2001, 114, 5816–5831. [Google Scholar] [CrossRef]
- Munoz, M.C.; Gallego, S.; Beltran, J.I.; Cerda, J. Adhesion at metal–ZrO2 interfaces. Surf. Sci. Rep. 2006, 61, 303–344. [Google Scholar] [CrossRef]
- Liu, S.-H.; Wang, H.P.; Wang, H.-C.; Yang, Y.W. In situ EXAFS studies of copper on ZrO2 during catalytic hydrogenation of CO2. Electron. Spectrosc. Relat. Phenom. 2005, 144–147, 373–376. [Google Scholar] [CrossRef]
- Ikonomov, J.; Stoychev, D.; Marinova, T. XPS and SEM characterization of electrodeposited transition metals on zirconia. Appl. Surf. Sci. 2000, 161, 94–104. [Google Scholar] [CrossRef]
- Tang, Q.-L.; Hong, Q.-J.; Liu, Z.-P. CO2 fixation into methanol at Cu/ZrO2 interface from first principles kinetic Monte Carlo. J. Catal. 2009, 263, 114–122. [Google Scholar] [CrossRef]
- Guo, Q.; Joyner, R.W. An X-ray photoelectron spectroscopy study of the stability of ZrO2 films on Pd (110). Appl. Surf. Sci. 1999, 144–145, 375–379. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Xu, B.-Q. Remarkable Nanosize Effect of Zirconia in Au/ZrO2 Catalyst for CO Oxidation. J. Phys. Chem. 2005, B109, 9678–9683. [Google Scholar] [CrossRef]
- Peacock, P.W.; Xiong, K.; Tse, K.; Robertson, J. Bonding and interface states of Si:HfO2 and Si:ZrO2 interfaces. Phys. Rev. 2006, B73, 075328. [Google Scholar] [CrossRef]
- Chan, D.K.; Jang, H.; Seidman, D.N.; Merkle, K.L. Initial results on the Ag [vert bar] CdO [222] interface: Atomic scale interfacial chemistry and sequencing of ordered cadmium/oxygen planes. Scri. Metall. Mater. 1993, 29, 1119–1124. [Google Scholar] [CrossRef]
- Rao, F.; Wu, R.; Freeman, A.J. Structure and bonding at metal-ceramic interfaces: Ag/CdO (001). Phys. Rev. 1995, B51, 10052–10056. [Google Scholar] [CrossRef]
- Capodieci, V.; Wiest, F.; Sulima, T.; Schulze, J.; Eisele, I. Examination and evaluation of La2O3 as gate dielectric for sub-100 nm CMOS and DRAM technology. Microelectron. Reliab. 2005, 45, 937–940. [Google Scholar] [CrossRef]
- Ablat, A.; Mamat, M.; Ghupur, Y.; Aimidula, A.; Wu, R.; Baqi, M.A.; Gholam, T.; Wang, J.; Qian, H.; Wu, R.; et al. Electronic structure of La2O3/Si interface by in situ photoemission spectroscopy. Mater. Lett. 2017, 191, 97–100. [Google Scholar] [CrossRef]
- Liu, K.; Ko, E.; Hwang, C.S.; Choi, J.-H. A first-principles study of the structural and electronic properties of the epitaxial Ge (111)/La2O3 (001) heterostructure. J. Phys. D Appl. Phys. 2019, 52, 365101. [Google Scholar] [CrossRef]
- Hobbs, C.C. Hegde. Fermi-Level Pinning at the Polysilicon/Metal Oxide Interface: Part I. IEEE Trans. Electron. Devices 2004, 51, 971–977. [Google Scholar] [CrossRef]
- Hobbs, C.C.; Fonseca, L.R.C.; Knizhnik, A.; Dhandapani, V.; Samavedam, S.B.; Taylor, W.J.; Grant, J.M.; Dip, L.G.; Triyoso, D.H.; Hegde, R.I.; et al. Fermi-level pinning at the polysilicon/metal-oxide interface-Part II. IEEE Trans. Electron. Devices 2004, 51, 978–984. [Google Scholar] [CrossRef]
- Xiong, K.; Peacock, P.W.; Robertson, J. Fermi level pinning and Hf–Si bonds at HfO2: Polycrystalline silicon gate electrode interfaces. Appl. Phys. Lett. 2005, 86, 012904. [Google Scholar] [CrossRef]
- Zhu, H.; Tang, C.; Ramprasad, R. Phase equilibria at Si-HfO2 and Pt-HfO2 interfaces from first principles thermodynamics. Phys. Rev. 2010, B82, 235413. [Google Scholar] [CrossRef]
- Miedema, A.R.; Boom, R.; Boer, F.R. On the heat of formation of solid alloys. J. Less-Common Met. 1975, 41, 283–298. [Google Scholar] [CrossRef]

| Oxide (AO) | Orientation of Oxide | Metal (M) | Interface Termination | ||
|---|---|---|---|---|---|
| Experiment | Theory | References | |||
| MgO | {111} | Cu | O | [28] | |
| {222} | Cu | O | [29] | ||
| (1–11) | Cu | O | [30] | ||
| (111), (100) | Cu | O | [31] | ||
| {222} | Cu(Ag) | O | [32,33] | ||
| (1–11) | Pd | O | [30] | ||
| (001) | Pd | O | [34] | ||
| {100} | Ag | O | [35] | ||
| {100} | Ag | O | [36] | ||
| (001) | Ag | O | [37] | ||
| (100) | Co | O | [38] | ||
| (100) | Fe | O | [38] | ||
| (001) | Ni | O | [34] | ||
| (001) | Pt | O | [34] | ||
| (001) | W | O | [34] | ||
| SiO2 | Al | O | [39] | ||
| Au | Si | [39] | |||
| Cr2O3 | (0001) | Ni | O | [40] | |
| (0001) | Ni | O | [41] | ||
| Ga2O3 | Cr | O | [42] | ||
| Y2O3 | Ge | O | [43] | ||
| ZrO2 | (111) | Ni | O | [44] | |
| Ni | Zr | [45] | |||
| Ni | Zr | [46] | |||
| (001) | Ni | O | [47] | ||
| (111) | Ni | O | [48] | ||
| (100) | Ni | O, Zr | [49] | ||
| Cu | O | [50] | |||
| Cu | O | [51] | |||
| (−111) | Cu | O | [52] | ||
| Co | O | [51] | |||
| Pd | Zr | [53] | |||
| Au | Zr | [54] | |||
| (001) | Fe | O | [47] | ||
| (001) | Si | O | [55] | ||
| CdO | {222} | Ag | O | [56] | |
| (001) | Ag | O | [57] | ||
| {222} | Ag(Au) | Au-seg | [33] | ||
| La2O3 | Si | O | [58] | ||
| Si | O | [59] | |||
| (001) | Ge | O | [60] | ||
| HfO2 | Si | O, Hf | [61,62] | ||
| Si | O, Hf (exp + calc) | [63] | |||
| Si | O | [64] | |||
| Si | O | [65] | |||
| Pt | O, Hf (exp + calc) | [65] | |||
| Oxide | Metal-A | Metal-B | Formation Enthalpy of Oxide [kJ/mol] | Formation Enthalpy of Oxide [kJ/mol-A] | Adsorption Energy [kJ/mol] | Prediction | Experiment | Theory | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AO | MA | MB | A on MA | O on MA | A on MA − MA on MA | O on MA − 493.07/2 | A on MB | O on MB | |||||
| X1 | Y1 | X2 | Y2 | XX1 | YY1 | ||||||||
| MgO | Cu | 601.6 | 601.6 | 223 | 346.47 | −42 | 99.935 | - | - | O | O | O | |
| Cu | Ag | 223 | 346.47 | −42 | 99.935 | 160 | 242.69 | O-Cu | O | ||||
| Pd | 324 | 295.06 | 41 | 48.525 | - | - | Mg, O | O | O | ||||
| Ag | 160 | 242.69 | −62 | −3.845 | - | - | O | O | O | ||||
| Co | 291 | 446.36 | −44 | 199.825 | - | - | O | O | |||||
| Fe | 257 | 528.65 | −59 | 282.115 | - | - | O | O | |||||
| Ni | 295 | 409 | −45 | 162.465 | - | - | O | O | |||||
| Pt | 376 | 329.31 | −72 | 82.775 | - | - | Mg, O | O | |||||
| W | 307 | 836.67 | −388 | 590.135 | - | - | O | O | |||||
| SiO2 | Al | 910.7 | 910.7 | 359 | 833.06 | 89 | 586.525 | - | - | O | O | ||
| Au | 395 | <0 | 102 | <0 | - | - | Si | Si | |||||
| Cr2O3 | Ni | 1139.7 | 569.85 | 313 | 409 | −27 | 162.465 | - | - | O | O; O | ||
| Ga2O3 | Cr | 1089.1 | 544.55 | 363 | 641.44 | 136 | 394.905 | - | - | O | O | ||
| Y2O3 | Ge | 1905.3 | 952.65 | 389 | 648.7 | 92 | 402.165 | - | - | O | O | ||
| ZrO2 | Si | 1094.324 | 1094.324 | 476 | 885.15 | 117 | 638.615 | O | O | ||||
| Fe | 588 | 528.65 | 272 | 282.115 | - | - | Zr, O | O | |||||
| Co | 622 | 446.36 | 287 | 199.825 | - | - | Zr | O | |||||
| Ni | 629 | 409 | 289 | 162.465 | - | - | Zr | O; Zr | Zr, O; O | ||||
| Cu | 529 | 346.47 | 264 | 99.935 | - | - | Zr | O | O | ||||
| Pd | 660 | 295.06 | 377 | 48.525 | - | - | Zr | Zr | |||||
| Au | 566 | <0 | 273 | <0–493.07/2 | Zr | Zr | |||||||
| CdO | Ag | 258.4 | 258.4 | 112 | 242.69 | −110 | −3.845 | - | - | O | O | O | |
| Ag | Au | 112 | 242.69 | −110 | −3.845 | 159 | <0 | Cd-Ag | Au-seg | ||||
| La2O3 | Ge | 1793.7 | 896.85 | 435 | 648.7 | 138 | 402.165 | - | - | O | O | ||
| Si | 459 | 885.15 | 100 | 638.615 | - | - | O | O; O | |||||
| HfO2 | Si | 1144.7 | 1144.7 | 444 | 885.15 | 85 | 638.615 | - | - | O | O, Hf | O | |
| Si | 444 | 885.15 | 85 | 638.615 | - | - | O | Hf, O | |||||
| Pt | 671 | 329.31 | 223 | 82.775 | O | Hf, O | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshitake, M. General Method for Predicting Interface Bonding at Various Oxide–Metal Interfaces. Surfaces 2024, 7, 414-427. https://doi.org/10.3390/surfaces7020026
Yoshitake M. General Method for Predicting Interface Bonding at Various Oxide–Metal Interfaces. Surfaces. 2024; 7(2):414-427. https://doi.org/10.3390/surfaces7020026
Chicago/Turabian StyleYoshitake, Michiko. 2024. "General Method for Predicting Interface Bonding at Various Oxide–Metal Interfaces" Surfaces 7, no. 2: 414-427. https://doi.org/10.3390/surfaces7020026
APA StyleYoshitake, M. (2024). General Method for Predicting Interface Bonding at Various Oxide–Metal Interfaces. Surfaces, 7(2), 414-427. https://doi.org/10.3390/surfaces7020026






