Next Article in Journal
General Method for Predicting Interface Bonding at Various Oxide–Metal Interfaces
Previous Article in Journal
The Use of Plant Extracts as Green Corrosion Inhibitors: A Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Surfaces
Volume 7
Issue 2
10.3390/surfaces7020025
surfaces-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Adsorption of Gadolinium Bisphthalocyanine on Atomically Flat Surfaces: Comparison of Graphene and Hexagonal Boron Nitride from DFT Calculations

by
Vladimir A. Basiuk
1,* and
Elena V. Basiuk
2
1
Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Circuito Exterior C.U., Ciudad de México 04510, Mexico
2
Instituto de Ciencias Aplicadas y Tecnología, Universidad Nacional Autónoma de México, Circuito Exterior C.U., Ciudad de México 04510, Mexico
*
Author to whom correspondence should be addressed.
Surfaces 2024, 7(2), 404-413; https://doi.org/10.3390/surfaces7020025
Submission received: 10 April 2024 / Revised: 14 May 2024 / Accepted: 29 May 2024 / Published: 1 June 2024
Browse Figures
Versions Notes

Abstract

We studied the noncovalent interactions of gadolinium bisphthalocyanine (GdPc2) with cluster models for graphene and hexagonal boron nitride (hBN) of variable size by using the PBE functional of the generalized gradient approximation in conjunction with Grimme’s dispersion correction and a DND double numerical basis set (that is, PBE-D2/DND). We found that in terms of the bonding strength, changes in the Gd-N bond lengths, the charge and spin of the Gd central ion, and the spin of the GdPc2 molecule, the behaviors of the graphene- and hBN-based model systems are rather similar. As expected, when increasing the size of the graphene and hBN cluster models, the strength of the interaction with GdPc2 increases, in which the bonding with the hBN models is usually stronger by a few kcal/mol. One of the main questions addressed in the present work was whether a change in the antiferromagnetic spin alignment to a ferromagnetic one, which is typical for GdPc2, is (at least theoretically) possible, as it has been observed previously for a number of graphene models when a smaller basis set DN was employed. We found that the use of a larger DND basis set dramatically reduces the occurrence of ferromagnetic adsorption complexes but does not exclude this possibility completely.

Graphical Abstract

1. Introduction

The deposition of single-molecule magnets (SMMs) onto solid surfaces and nanomaterials is considered as an essential step for their application in spintronic devices (see, for example, [1,2,3,4,5,6,7,8,9,10]). A special emphasis is placed on graphene (per se, or an upper layer of highly oriented pyrolytic graphite, HOPG) as a solid support [1,2,3,4,5,6,7,8,9,10] as well as on lanthanide bisphthalocyanines (LnPc2, where Ln = Tb, Dy, Er) as representative SMMs [1,2,3,4,5,6,8,9,10].
The popularity of graphene, which is considered one of the most crucial and promising nanomaterials, needs no additional comments or justifications. A rather curious observation in the present context of surface-deposited SMMs is that its ‘sibling’, hexagonal boron nitride (hBN) [11], has received much less attention. This is exemplified by the study of manganese-containing dimers (with ligands other than Pcs) on graphene and hBN [7] and the study [12] in which TbPc2 deposited onto hBN was considered very briefly, for the sake of comparison with MgO-supported bisphthalocyanine.
The interest in TbPc2- and DyPc2-containing systems is quite understandable due to their very complex magnetic behaviors, with very high calculated and experimental magnetic moments [13]. At the same time, their gadolinium analogue GdPc2 [13,14,15,16] deserves attention as well. Formally, it has the highest (of the entire LnPc2 family) number of unpaired electrons: seven on the half-filled 4f shell, plus one π-electron delocalized on the two Pc ligands. However, as a result of strong antiferromagnetic coupling, when the 4f electrons and the π-electron have opposite directions, instead of the theoretical magnetic moment of 7.94 BM, this value decreases to 6.9 BM [13,15].
Experimental measurements are of primary importance in the area of SMMs deposited onto solid supports, but only limited research has been undertaken to complement these with theoretical results [2,4,7]. The latter fact is easily explainable, since, as Marocchi et al. [4] fairly noted, “simulating rare earths within DFT is very tricky, due to the strong electronic correlation effects in 4f-electrons”. We learned this through our own experience when we attempted to study by means of the density functional theory (DFT) the full series (from La to Lu) of lanthanide-containing molecules, such as LnPc2 bisphthalocyanines [17], endohedral fullerenes Ln@C60 [18] and Ln3N@Ih-C80 [19], as well as lanthanide atoms and ions interacting with both cluster [20,21] and periodic [22] graphene models. Nevertheless, along with the serious (sometimes unresolvable) problems of self-consistent field (SCF) convergence for the Tb- and Dy-containing systems, we found that the case of their closest neighbor Gd might be as simple as the cases of La (with a totally empty 4f shell) and Lu (with a completely filled 4f shell), due to the half-filled 4f shell and zero orbital moment. This property allowed us to successfully perform calculations for GdPc2 adsorbed on carbon nanotube [23] and graphene (both pristine and defect-containing) models [24].
In both works [23,24], we focused mostly on the variations in the geometry and interaction strength of GdPc2 with different carbon nanoclusters. At the same time, perhaps the most interesting (from our point of view) result is related to the spin coupling (or alignment) pattern. It was antiferromagnetic only in a limited number of calculations, similar to isolated GdPc2 [13,15,17] with an absolute value for its molecular spin of 6.007e [24], whereas for most adsorption complexes (including those with all graphene models), the coupling became ferromagnetic, reaching absolute spin values of almost 8e [24].
This latter observation served as the foundation for the present study. The previous calculations [24] employed the double-numerical basis set DN, without polarization functions added to any atoms, and thus, the ferromagnetic coupling might have been simply a small basis set-related artifact. In the present work, we added a polarization function to all non-hydrogen atoms (that is, we used a DND basis set) to eliminate this possibility. Our second goal was to compare the behavior of graphene and its ‘sibling’ hBN, in terms of the bonding strength, changes in Gd-N bond lengths, the charge and spin of the Gd central ion, as well as the spin of the GdPc2 molecule. And our third goal was to trace how all the above characteristics change when varying the size of the graphene and hBN cluster model. In this way, we attempted to provide new detailed information to the obviously underexplored area of LnPc2 interactions with nanomaterials such as graphene and especially hBN.

2. Methods

A theoretical analysis of bonding strength, geometries, and electronic parameters of noncovalent complexes of GdPc2 with graphene and hBN cluster models of variable size was performed by employing the numerical-based DFT module DMol3 of the Materials Studio suite [25,26,27,28]. As in all previous related works mentioned above [17,18,19,20,21,22,23,24], the PBE (by Perdew-Burke-Ernzerhof [29]) general gradient approximation function was used in conjunction with the empirical dispersion correction introduced by Grimme [30], that is, the PBE-D2 combination. (One should note that for noncovalent complexes of tetraazaannulenes with carbon nanoclusters, PBE-D2 yields more realistic geometries than, for example, the widely used hybrid functional B3LYP [31].)
As already mentioned in the introduction, the size of the double-numerical basis set (DN in [23,24]) was increased by adding a polarization d-function to all non-H atoms, that is, to DND (which is equivalent to the 6-31G(d) Pople-type basis set). The settings employed for the full geometry optimization and the calculation of the electronic parameters included the use of DFT semi-core pseudopotentials (DSPPs) and a real space (or orbital) cutoff of 5.0 Å, as dictated by the presence of gadolinium atoms. The convergence criteria were as follows: an energy gradient of 2 × 10−5 Ha, maximum force of 0.004 Ha/Å, maximum displacement of 0.005 Å, and SCF tolerance of 10−5 Ha. A special comment has to be added about the use of thermal smearing to facilitate SCF convergence. In the present calculations, we followed the general protocol explained in detail in earlier studies [32,33,34]. In principle, it was found that the use of a very low value of 0.0001 Ha (equivalent temperature of 31.6 K) yields stable and consistent results, which are essentially identical to those afforded by applying Fermi occupancy (that is, zero smearing). Consequently, we usually set 0.0001 Ha as the target value to elaborate on final publishable results [17,18,19,20,21,22,23,24]. While for the derivatives of Tb and some other lanthanides, this value does not allow to achieve SCF convergence and has to be increased, the Gd-containing systems (like the ones incorporating La and Lu atoms) often can be successfully treated at the Fermi occupancy. We took advantage of this possibility in the present paper.
We would like to mention one of the differences in functioning between Gaussian and DMol3 software, which is especially important in the present context of quantum chemical calculations of lanthanide-containing systems. While in the Gaussian software, a total spin of the system has to be assigned in the input (see, for example, references [15,35,36,37]), and it is also possible to specify a particular spin value in DMol3, the option we employed for all calculations was “Use formal spin as initial”. That is, the calculations were unconstrained.
The formation energies ΔEGdPc2+S (or simply ΔE) were calculated by using the following general equation:
ΔEGdPc2+S = EGdPc2+S − (EGdPc2 + ES)
where Ei is the respective absolute energy, and S is surface model.

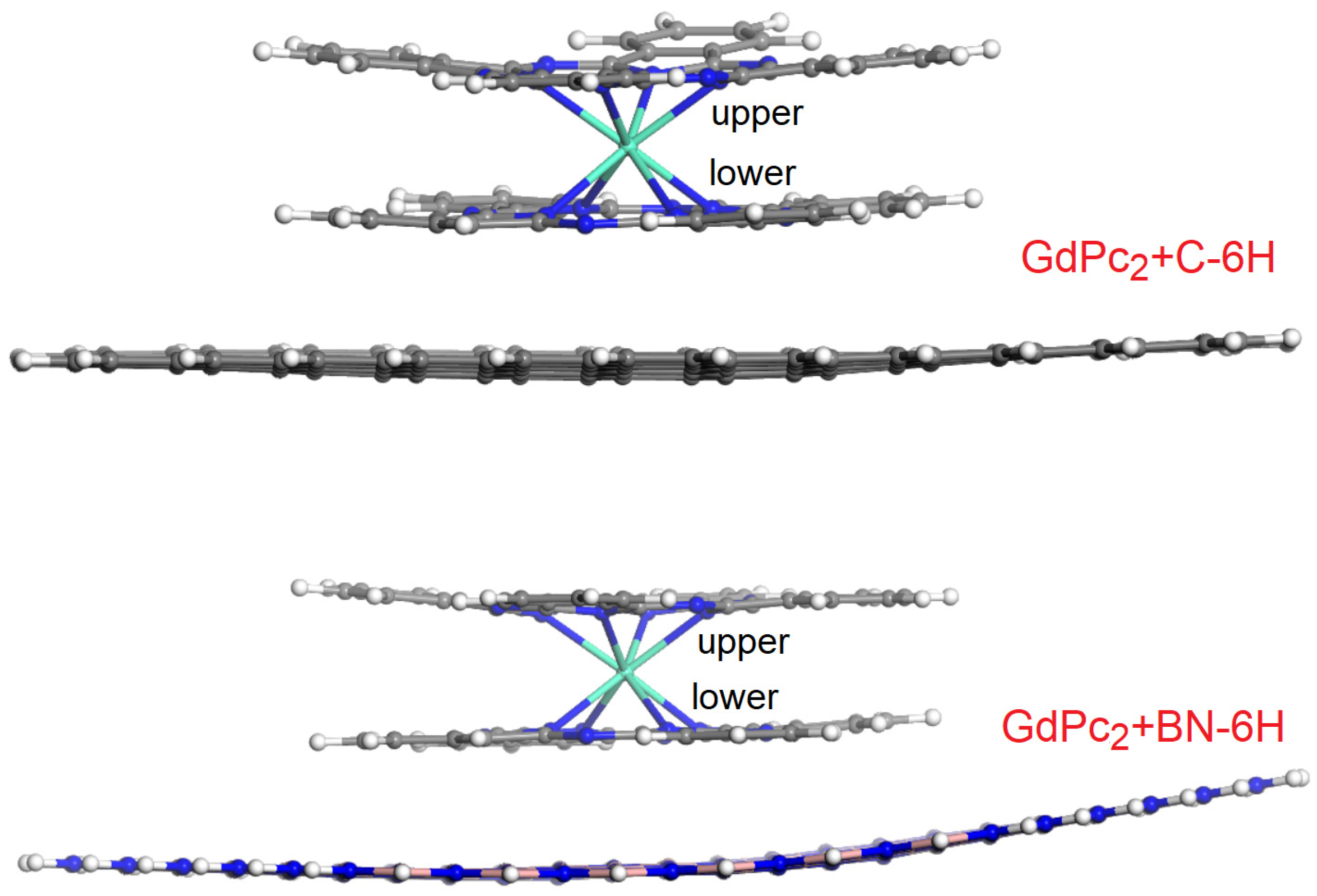
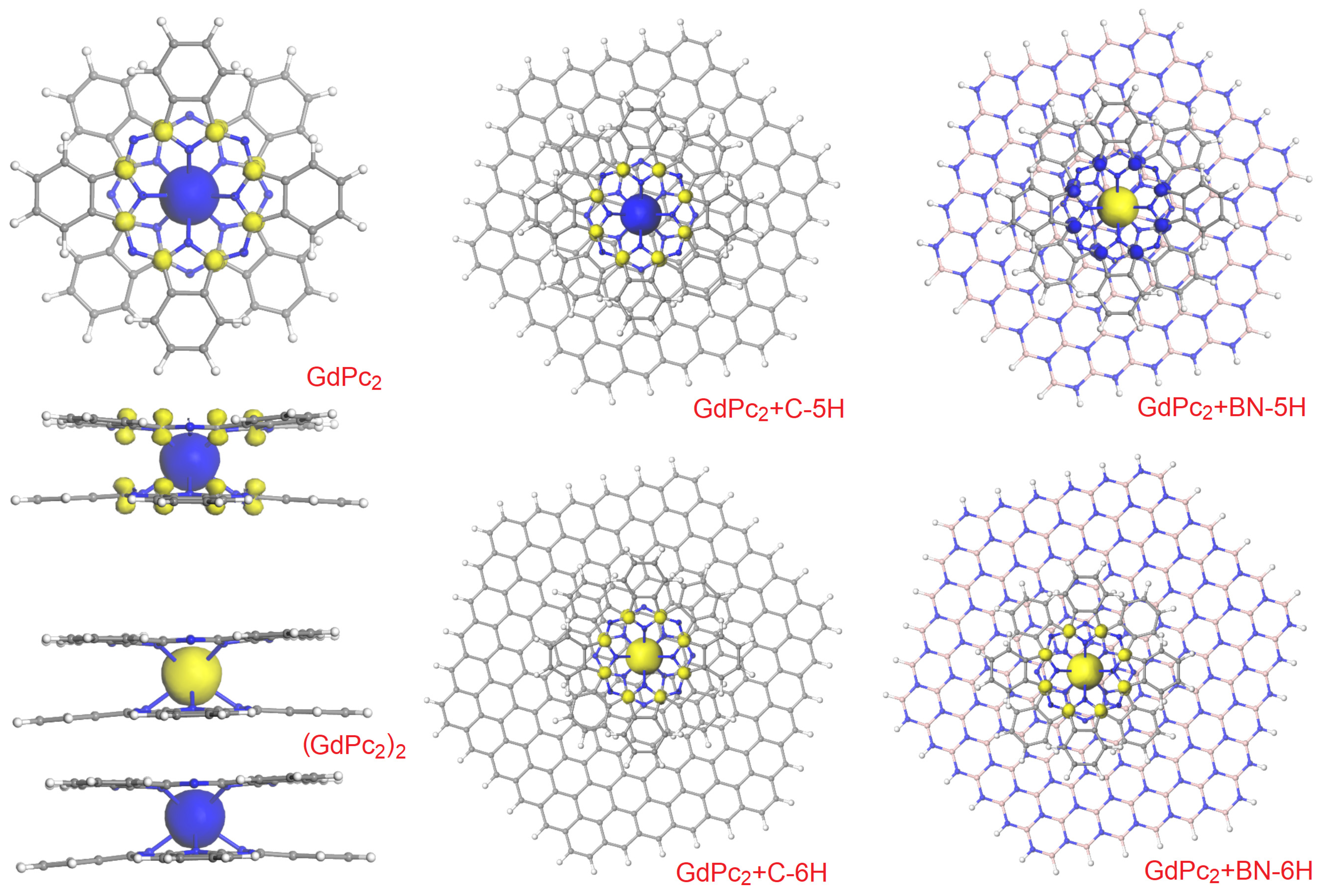
3. Results and Discussion

The cluster models we tested for graphene and hBN, as well as the typical optimized geometry (staggered conformation) for GdPc2, are shown in Figure 1. All the models simulating graphene and hBN are hexagonal. The smallest ones are benzene (C6H6) and borazine (B3N3H6), respectively, in which each side of the hexagon has one H atom. (Strictly speaking, these molecules may not adequately capture the electronic properties of the extended sheets; they were included simply for the completeness of both series.) Using a uniform and easily understood nomenclature, they are denoted as C-1H and BN-1H, respectively. In a similar way, coronene and its BN analogue are referred to as C-2H and BN-2H, respectively; supercoronene and its BN analogue are referred to as C-3H and BN-3H, respectively, and so on. The largest members of the two series are C-7H and BN-7H. Also, within the carbon-based models, we included fullerene C60, for comparison: the planar model closest to this fullerene (in terms of molecular weight) is C-3H, with the chemical formula C54H18. The latter model has a slightly smaller diagonal span (about 14.4 Å) compared to that of GdPc2 (15.2 Å), and the larger graphene models start with C-4H (19.3 Å). In the case of the hBN models BN-3H and BN-4H, the measurements are similar, 14.7 and 19.7 Å, respectively, despite the differences in the bond lengths of C–C and C–H versus B–N, B–H, and N–H. In other words, only starting from C-4H and BN-4H, GdPc2 can fully fit onto the model surface.
Both components undergo a bending distortion, as a result of strong π–π stacking interactions: this is exemplified for the GdPc2 + C-6H and GdPc2 + BN-6H complexes in Figure 2. The surface model tends to ‘embrace’ the GdPc2 molecule, which is more evident here for the latter complex. In turn, the “lower” Pc ligand (the one in contact with the surface) becomes more planar for the same reason, whereas the opposite one (denoted as the “upper” one) does not exhibit visible changes, as compared to the Pc ligands in the isolated bisphthalocyanine.
Among the central questions we addressed is that of the comparative strengths of the GdPc2 interactions for the graphene and hBN models. The numerical results for the corresponding ΔE bonding energies are presented in Table 1, as well as in graphical form in Figure 3a.
In the case of the graphene models, the weakest interaction, of −14.2 kcal/mol, was logically found with the benzene molecule (the smallest C-1H model), reaching −74.4 kcal/mol for the largest nanocluster C-7H. Despite the fact that the molecular weight of C60 fullerene best matches that of the C-3H model, its strong spherical curvature prevents efficient contact between the two components, and the ΔE value of −25.6 kcal/mol for GdPc2 + C60 is actually closer to the one of −28.0 kcal/mol obtained for GdPc2 + C-2H. With the exception of the first member of the hBN models, that is, borazine (ΔE of −9.7 kcal/mol), their bonding with GdPc2 is stronger compared to that of the analogous graphene models, roughly by a few kcal/mol. From Figure 3a, it is more evident that until reaching the complexes with C-4H and BN-4H, the ΔE values tend to decrease almost linearly, then the changes become less apparent. While the lowest ΔE value in the carbon series was obtained for the largest nanocluster C-7H, in the case of the BN series, the bonding strength slightly fluctuates: −76.7, −79.8, and −77.5 kcal/mol for GdPc2 + BN-5H, GdPc2 + BN-6H, and GdPc2 + BN-7H, respectively. That is, the strongest bonding was obtained with the BN-6H model. For comparison, we also calculated the formation energy for the (GdPc2)2 π–π stacking dimer, which is −60.2 kcal/mol, and thus is situated between those obtained for the GdPc2 + X-3H and GdPc2 + X-4H (X = C, BN) noncovalent complexes.
The changes in GdPc2 geometry were estimated in terms of average Gd-N distances, both in the “lower” and in the “upper” phthalocyanine coordination spheres (Table 1 and Figure 3b). In the case of the isolated GdPc2 molecule, their values are equal to 2.450 Å. As a result of the flattening of the “lower” Pc unit, one might expect some shortening of Gd-N coordination bonds compared to the ones found in the “upper” phthalocyanine part. Nevertheless, no such trend can be observed; in some cases, the “lower” Gd-N distances indeed become shorter (the largest difference of 0.018 Å was found in the GdPc2 + C-5H and GdPc2 + BN-6H complexes), in others, they increase (by up to 0.035 Å in GdPc2 + BN-4H). As a whole, from Figure 3b, one can conclude that the shorter Gd-N coordination bonds are associated with the larger graphene and hBN models. However, when considering each of the four series of the Gd-N distances separately, the changes become rather random, without any clear tendency.
One of the electronic parameters analyzed was the (positive) charge of the Gd ion (Table 1). In the isolated GdPc2 molecule, it is 1.300e, with a notable increase to 1.337e on both gadolinium ions in the (GdPc2)2 dimer. Similarly, it increases upon complexation with any graphene or hBN model. In the latter case, the span of Gd charge values is especially wide, from a very minor increase to 1.303e in GdPc2 + BN-7H to a rather high value of 1.408e for the first member of the BN series, GdPc2 + BN-1H. In the graphene series, the corresponding values are found to be between 1.307 e (GdPc2 + C-6H) and 1.367e (GdPc2 + C-1H). At the same time, the spin of the Gd ion is a relatively invariant characteristic, though its direction (up and down, meaning positive and negative values, respectively) is random. In the isolated GdPc2 molecule, it is 7.007e (spin-up, as shown in Figure 4). In the (GdPc2)2 dimer, both absolute Gd spin values are the same of 7.004e, but with opposite signs/directions (Table 1). The lowest absolute value of 7.000e was obtained for the GdPc2 + C-2H complex, and the highest one of 7.008e was obtained for the fullerene derivative GdPc2 + C60.
Now, the most interesting question is related to the possibility of ferromagnetic spin alignment within the GdPc2 molecule. As was mentioned in the introduction, it was antiferromagnetic only in a limited number of the previous calculations with defect-free and defect-containing graphene models, such as in isolated GdPc2, whereas for most adsorption complexes, the coupling became ferromagnetic, reaching absolute spin values of almost 8e [24]. But the previous [24] and the present study employed the double-numerical basis sets of different sizes: DN (with no polarization functions for any atoms) and DND (with a polarization function on all non-H atoms), respectively: the use of the DND basis set is supposed to yield a more realistic picture. All the numerical data obtained are summarized in Table 1, and the most representative spin density plots are shown in Figure 4. The molecular spin of the isolated GdPc2 molecule, as computed with the DND basis set, is 6.011e due to the antiferromagnetic coupling typical for this and some other lanthanide bisphthalocyanines [13,15,17], in which the 4f electrons of the Gd ion and the π-electron have opposite directions (Figure 4). As it could be expected, in the system composed of two GdPc2 molecules (that is, the (GdPc2)2 dimer), the two π-electrons become paired, and no spin density lobes are observed on phthalocyanine ligands; on the other hand, nothing like this can happen to the 4f electrons of the two Gd ions. As a result, the absolute values of the spins of the two GdPc2 molecules are defined by the spins of their Gd ions, which are essentially equal but have opposite signs (7.006 and −7.004e).
In the case of the GdPc2 interacting with the graphene and hBN models, the situation observed previously [24], in which the DN basis set was used, changes quantitatively, but not qualitatively. Now, the dominating pattern of the spin alignment is antiferromagnetic, as in the isolated GdPc2 molecule; this is exemplified in Figure 4 for the GdPc2 + C-5H and GdPc2 + BN-5H complexes. The spin directions (spin-up and spin-down) of the the 4f electrons of the Gd ion and the π-electron of Pc can invert, which does not imply any changes in properties in the absence of an external field. We obtained a ferromagnetic alignment in only two complexes, GdPc2 + C-6H and GdPc2 + BN-6H, though we cannot offer an explanation why this was observed specifically for C-6H and BN-6H, but not for smaller or larger models. The corresponding GdPc2 molecular spins are −7.974e and −7.982e (all the electrons are spin-down); that is, their absolute values almost reach 8e [24]. For all of the remaining antiferromagnetic cases, the absolute values of the GdPc2 molecular spin fluctuate insignificantly: for the graphene models, between 6.010e (GdPc2 + C-1H) and 6.096e (GdPc2 + C-2H) and for hBN models, between 6.008e (GdPc2 + BN-1H) and 6.028e (GdPc2 + BN-4H). In other words, no spin transfer is observed from the GdPc2 to the surface model, and no spin density lobes can be detected on the latter in the spin density plots (Figure 4).

4. Conclusions

In terms of the bonding strength, changes in the Gd-N bond lengths, the charge and spin of the Gd central ion, and the spin of the GdPc2 molecule, the behaviors of graphene- and hBN-based model systems are rather similar. When increasing the size of the graphene and hBN cluster models, the strength of interactions with GdPc2 naturally increases, and the bonding with the hBN model is usually stronger by a few kcal/mol.
One of the main questions addressed in the present work was whether the change in antiferromagnetic spin alignment, which is typical for gadolinium bisphthalocyanine, to a ferromagnetic one is (at least theoretically) possible or it is just an artifact associated with a smaller basis set DN (equivalent to 6-31G) [24]. In this regard, we found that the use of the larger DND basis set dramatically reduces the occurrence of ferromagnetic adsorption complexes, but does not exclude this possibility completely. It would be highly desirable to have an explanation for why these changes occur specifically with certain cluster sizes or structures. Unfortunately, one of the necessary steps this entails would be to explore a much broader variety of graphene and hBN models, for example, in terms of nanocluster size and geometry. However, this would entail increased computational cost and effort, which goes beyond our capabilities at present.

Author Contributions

Conceptualization, V.A.B. and E.V.B.; methodology, V.A.B. and E.V.B.; formal analysis, V.A.B. and E.V.B.; resources, V.A.B.; data curation, V.A.B. and E.V.B.; writing—original draft preparation, V.A.B.; writing—review and editing, V.A.B. and E.V.B.; visualization, V.A.B. and E.V.B.; supervision, V.A.B.; project administration, V.A.B.; funding acquisition, V.A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Autonomous University of Mexico (UNAM), grant DGAPA-IN103622, project title “Efectos topológicos en las interacciones de las especies de “tierras raras” con nanomateriales de carbono de baja dimensionalidad”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Candini, A.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Affronte, M. Graphene spintronic devices with molecular nanomagnets. Nano Lett. 2011, 11, 2634–2639. [Google Scholar] [CrossRef] [PubMed]
  2. Gonidec, M.; Biagi, R.; Corradini, V.; Moro, F.; De Renzi, V.; del Pennino, U.; Summa, D.; Muccioli, L.; Zannoni, C.; Amabilino, D.B.; et al. Surface supramolecular organization of a terbium(III) double-decker complex on graphite and its single molecule magnet behavior. J. Am. Chem. Soc. 2011, 133, 6603–6612. [Google Scholar] [CrossRef] [PubMed]
  3. Klar, D.; Candini, A.; Joly, L.; Klyatskaya, S.; Krumme, B.; Ohresser, P.; Kappler, J.-P.; Ruben, M.; Wende, H. Hysteretic behaviour in a vacuum deposited submonolayer of single ion magnets. Dalton Trans. 2014, 43, 10686–10689. [Google Scholar] [CrossRef] [PubMed]
  4. Marocchi, S.; Candini, A.; Klar, D.; Van den Heuvel, W.; Huang, H.; Troiani, F.; Corradini, V.; Biagi, R.; De Renzi, V.; Klyatskaya, S.; et al. Relay-like exchange mechanism through a spin radical between TbPc2 molecules and graphene/Ni(111) substrates. ACS Nano 2016, 10, 9353–9360. [Google Scholar] [CrossRef] [PubMed]
  5. Corradini, V.; Candini, A.; Klar, D.; Biagi, R.; De Renzi, V.; Lodi Rizzini, A.; Cavani, N.; del Pennino, U.; Klyatskaya, S.; Ruben, M.; et al. Probing magnetic coupling between LnPc2 (Ln = Tb, Er) molecules and the graphene/Ni(111) substrate with and without Au-intercalation: Role of the dipolar field. Nanoscale 2018, 10, 277–283. [Google Scholar] [CrossRef] [PubMed]
  6. Serrano, G.; Velez-Fort, E.; Cimatti, I.; Cortigiani, B.; Malavolti, L.; Betto, D.; Ouerghi, A.; Brookes, N.B.; Mannini, M.; Sessoli, R. Magnetic bistability of a TbPc2 submonolayer on a graphene/SiC(0001) conductive electrode. Nanoscale 2018, 10, 2715–2720. [Google Scholar] [CrossRef] [PubMed]
  7. Berkley, R.S.; Hooshmand, Z.; Jiang, T.; Le, D.; Hebard, A.F.; Rahman, T.S. Characteristics of single-molecule magnet dimers ([Mn3]2) on graphene and h-BN. J. Phys. Chem. C 2020, 124, 28186–28200. [Google Scholar] [CrossRef]
  8. Yin, X.; Deng, L.; Ruan, L.; Wu, Y.; Luo, F.; Qin, G.; Han, X.; Zhang, X. Recent progress for single-molecule magnets based on rare earth elements. Materials 2023, 16, 3568. [Google Scholar] [CrossRef]
  9. Liu, S.; Zhu, Z.; Zhang, P.; Tang, J. Chemisorption of lanthanide single-molecule magnets on surfaces. Fundam. Res. 2023. [Google Scholar] [CrossRef]
  10. Gabarró-Riera, G.; Aromí, G.; Sañudo, E.C. Magnetic molecules on surfaces: SMMs and beyond. Coord. Chem. Rev. 2023, 475, 214858. [Google Scholar] [CrossRef]
  11. Auwärter, W. Hexagonal boron nitride monolayers on metal supports: Versatile templates for atoms, molecules and nanostructures. Surf. Sci. Rep. 2019, 74, 1–95. [Google Scholar]
  12. Wäckerlin, C.; Donati, F.; Singha, A.; Baltic, R.; Rusponi, S.; Diller, K.; Patthey, F.; Pivetta, M.; Lan, Y.; Klyatskaya, S.; et al. Giant hysteresis of single-molecule magnets adsorbed on a nonmagnetic insulator. Adv. Mater. 2016, 28, 5195–5199. [Google Scholar] [CrossRef]
  13. Trojan, K.L.; Kendall, J.L.; Kepler, K.D.; Hatfield, W.E. Strong exchange coupling between the lanthanide ions and the phthalocyaninato ligand radical in bis(phthalocyaninato)lanthanide sandwich compounds. Inorg. Chim. Acta 1992, 198–200, 795–803. [Google Scholar] [CrossRef]
  14. Korolev, V.V.; Lomova, T.N.; Ramazanova, A.G.; Korolev, D.V.; Mozhzhukhina, E.G. Phthalocyanine-based molecular paramagnets. Effect of double-decker structure on magnetothermal properties of gadolinium complexes. J. Organometal. Chem. 2016, 819, 209–215. [Google Scholar] [CrossRef]
  15. Kratochvílová, I.; Šebera, J.; Paruzel, B.; Pfleger, J.; Toman, P.; Marešová, E.; Havlová, Š.; Hubík, P.; Buryi, M.; Vrňata, M.; et al. Electronic functionality of Gd-bisphthalocyanine: Charge carrier concentration, charge mobility, and influence of local magnetic field. Synth. Met. 2018, 236, 68–78. [Google Scholar] [CrossRef]
  16. Taran, G.; Moreno-Pineda, E.; Schulze, M.; Bonet, E.; Ruben, M.; Wernsdorfer, W. Direct determination of high-order transverse ligand field parameters via μSQUID-EPR in a Et4N [160GdPc2] SMM. Nat. Commun. 2023, 14, 3361. [Google Scholar] [CrossRef] [PubMed]
  17. Martínez-Flores, C.; Bolivar-Pineda, L.M.; Basiuk, V.A. Lanthanide bisphthalocyanine single-molecule magnets: A DFT survey of their geometries and electronic properties from lanthanum to lutetium. Mater. Chem. Phys. 2022, 287, 126271. [Google Scholar] [CrossRef]
  18. Martínez-Flores, C.; Basiuk, V.A. Ln@C60 endohedral fullerenes: A DFT analysis for the complete series from lanthanum to lutetium. Comp. Theor. Chem. 2022, 1217, 113878. [Google Scholar] [CrossRef]
  19. Martínez-Flores, C.; Basiuk, V.A. DFT analysis of the electronic and structural properties of lanthanide nitride cluster fullerenes Ln3N@C80. Inorganics 2023, 11, 223. [Google Scholar] [CrossRef]
  20. Basiuk, V.A.; Acevedo-Guzmán, D.A.; Meza-Laguna, V.; Álvarez-Zauco, E.; Huerta, L.; Serrano, M.; Kakazey, M.; Basiuk, E.V. High-energy ball-milling preparation and characterization of Ln2O3−graphite nanocomposites. Mater. Today Commun. 2021, 26, 102030. [Google Scholar] [CrossRef]
  21. Basiuk, E.V.; Prezhdo, O.V.; Basiuk, V.A. Strong bending distortion of supercoronene graphene model upon adsorption of lanthanide atoms. J. Phys. Chem. Lett. 2023, 14, 2910–2916. [Google Scholar] [CrossRef] [PubMed]
  22. Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Adsorption of lanthanide atoms on graphene: Similar, yet different. J. Phys. Chem. Lett. 2022, 13, 6042–6047. [Google Scholar] [CrossRef] [PubMed]
  23. Bolivar-Pineda, L.M.; Mendoza-Domínguez, C.U.; Basiuk, V.A. Adsorption of lanthanide double-decker phthalocyanines on single-walled carbon nanotubes: Structural changes and electronic properties as studied by density functional theory. J. Mol. Model. 2023, 29, 158. [Google Scholar] [CrossRef] [PubMed]
  24. Mendoza-Domínguez, C.U.; Bolivar-Pineda, L.M.; Basiuk, V.A. Effect of structural defects in graphene on the geometry and electronic properties of adsorbed lanthanide bisphthalocyanines: A DFT analysis. Comp. Theor. Chem. 2023, 1225, 114152. [Google Scholar] [CrossRef]
  25. Delley, B.; Ellis, D.E.; Freeman, A.J.; Baerends, E.J.; Post, D. Binding energy and electronic structure of small copper particles. Phys. Rev. B 1983, 27, 2132–2144. [Google Scholar] [CrossRef]
  26. Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
  27. Delley, B. Fast calculation of electrostatics in crystals and large molecules. J. Phys. Chem. 1996, 100, 6107–6110. [Google Scholar] [CrossRef]
  28. Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
  29. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  30. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  31. Basiuk, V.A. Interaction of tetraaza[14]annulenes with single-walled carbon nanotubes: A DFT study. J. Phys. Chem. B 2004, 108, 19990–19994. [Google Scholar] [CrossRef]
  32. Michelini, M.C.; Pis Diez, R.; Jubert, A.H. A density functional study of small nickel clusters. Int. J. Quantum Chem. 1998, 70, 693–701. [Google Scholar] [CrossRef]
  33. Migliore, A.; Sit, P.H.-L.; Klein, M.L. Evaluation of electronic coupling in transition-metal systems using DFT: Application to the hexa-aquo ferric−ferrous redox couple. J. Chem. Theory Comput. 2009, 5, 307–323. [Google Scholar] [CrossRef] [PubMed]
  34. Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Thermal smearing in DFT calculations: How small is really small? A case of La and Lu atoms adsorbed on graphene. Mater. Today Commun. 2020, 25, 101595. [Google Scholar] [CrossRef]
  35. Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Computational modeling of the Ce@C82 metallofullerene isomeric composition. ECS J. Solid State Sci. Technol. 2019, 8, M118–M121. [Google Scholar] [CrossRef]
  36. Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated relative thermodynamic stabilities of the Gd@C82 isomers. ECS J. Solid State Sci. Technol. 2021, 10, 071013. [Google Scholar] [CrossRef]
  37. Uhlík, F.; Slanina, Z.; Bao, L.; Akasaka, T.; Lu, X.; Adamowicz, L. Eu@C88 isomers: Calculated relative populations. ECS J. Solid State Sci. Technol. 2022, 11, 101008. [Google Scholar] [CrossRef]
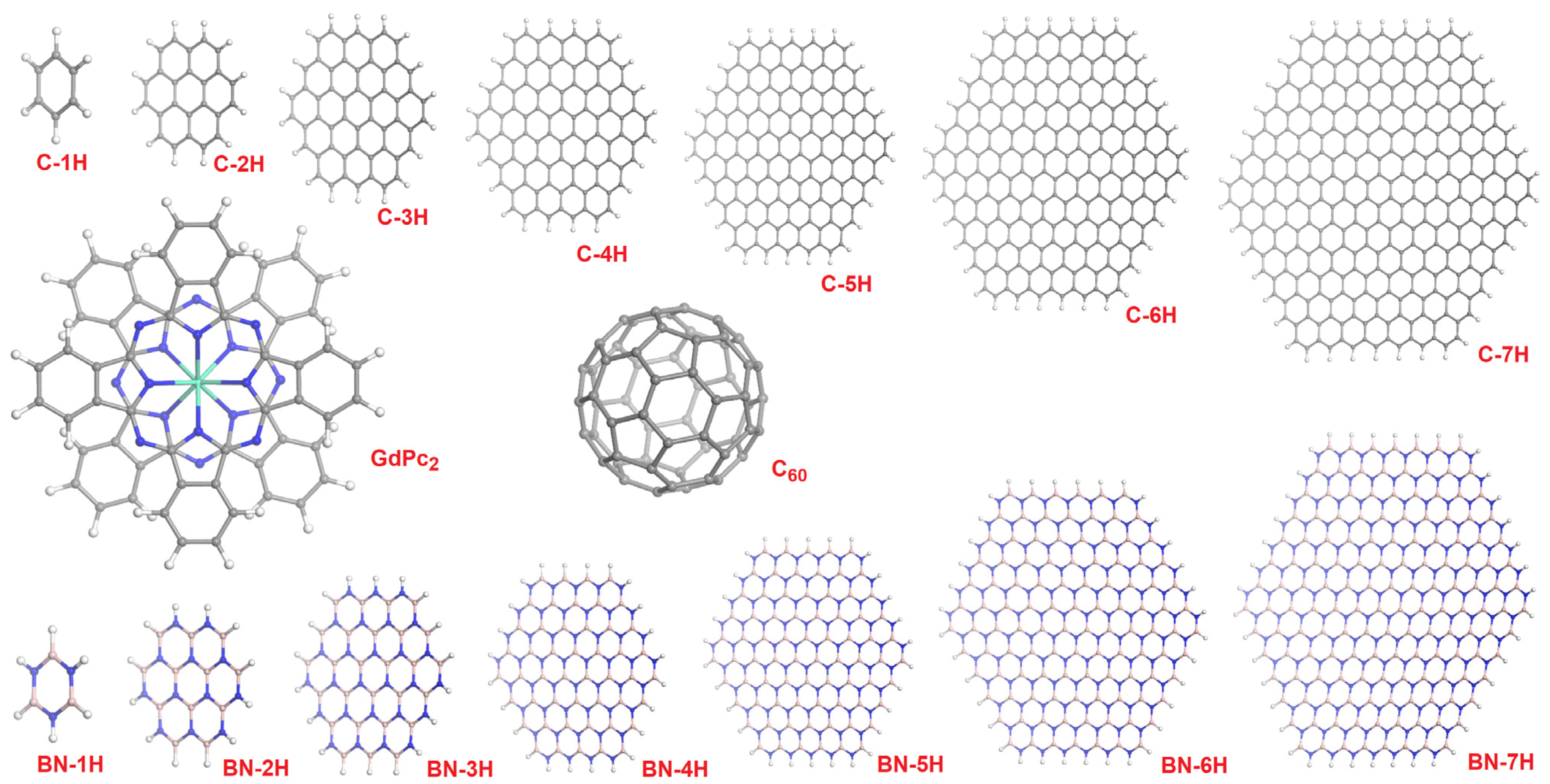
Surfaces 07 00025 g001
Figure 1. The models employed in our cluster calculations. Atom colors: grey, carbon; white, hydrogen; deep blue, nitrogen; pink, boron; light blue green, gadolinium.
Figure 1. The models employed in our cluster calculations. Atom colors: grey, carbon; white, hydrogen; deep blue, nitrogen; pink, boron; light blue green, gadolinium.
Surfaces 07 00025 g001
Surfaces 07 00025 g002
Figure 2. Representative geometries of GdPc2 + C-nH and GdPc2 + BN-nH complexes (exemplified for n = 6, that is, C-6H and BN-6H in Figure 1). Pc ligands are denoted as “upper” or “lower”.
Figure 2. Representative geometries of GdPc2 + C-nH and GdPc2 + BN-nH complexes (exemplified for n = 6, that is, C-6H and BN-6H in Figure 1). Pc ligands are denoted as “upper” or “lower”.
Surfaces 07 00025 g002
Surfaces 07 00025 g003
Figure 3. Graphical representation of the changes in the energy of complex formation (a) and the average Gd-N distance (b) depending on the size of C-nH and BN-nH cluster model. The case of C60 is not included.
Figure 3. Graphical representation of the changes in the energy of complex formation (a) and the average Gd-N distance (b) depending on the size of C-nH and BN-nH cluster model. The case of C60 is not included.
Surfaces 07 00025 g003
Surfaces 07 00025 g004
Figure 4. Different observed patterns of spin density distribution (isosurfaces at 0.02 a.u.) exemplified by isolated GdPc2, noncovalent dimer (GdPc2)2, and GdPc2 adsorption complexes with C-5H, C-6H, BN-5H, and BN-6H models. Lobe colors: blue, spin-up electrons; yellow, spin-down electrons.
Figure 4. Different observed patterns of spin density distribution (isosurfaces at 0.02 a.u.) exemplified by isolated GdPc2, noncovalent dimer (GdPc2)2, and GdPc2 adsorption complexes with C-5H, C-6H, BN-5H, and BN-6H models. Lobe colors: blue, spin-up electrons; yellow, spin-down electrons.
Surfaces 07 00025 g004
Table 1. Total energies (E) for all isolated components and the corresponding noncovalent complexes, formation energies (ΔE) for noncovalent complexes of GdPc2 with carbon- and boron nitride-based models, average Gd-N bond lengths, as well as charge and spin of Gd ion, along with the total spin of GdPc2 molecule, obtained from the Mulliken population analysis.
Table 1. Total energies (E) for all isolated components and the corresponding noncovalent complexes, formation energies (ΔE) for noncovalent complexes of GdPc2 with carbon- and boron nitride-based models, average Gd-N bond lengths, as well as charge and spin of Gd ion, along with the total spin of GdPc2 molecule, obtained from the Mulliken population analysis.
Etotal (Ha)ΔE (kcal/mol)Gd-Nlower (Å) aGd-Nupper (Å)Gd Charge (e)Gd Spin (e)GdPc2 Spin (e)
GdPc2−3528.7468834 2.4502.4501.3007.0076.011
C-1H−232.0208765
C-2H−921.0808194
C-3H−2067.1815845
C-4H−3670.3260780
C-5H−5730.5170328
C-6H−8247.7564282
C-7H−11,222.0439594
C60−2284.4334844
BN-1H−242.4167720
BN-2H−962.7988404
BN-3H−2161.1563381
BN-4H−3837.4911698
BN-5H−5991.8039867
BN-6H−8624.0947660
BN-7H−11,734.3621054
GdPc2 + C-1H−3760.7904162−14.22.4472.4531.367−7.006−6.010
GdPc2 + C-2H−4449.8723439−28.02.4872.4731.364−7.000−6.096
GdPc2 + C-3H−5596.0080928−50.02.4292.4391.3447.0056.038
GdPc2 + C-4H−7199.1737356−63.22.4392.4261.353−7.004−6.065
GdPc2 + C-5H−9259.3781214−71.72.4272.4451.3247.0046.041
GdPc2 + C-6H−11,776.6182309−72.12.4202.4201.307−7.002−7.974
GdPc2 + C-7H−14,750.9094551−74.42.4292.4461.3207.0046.034
GdPc2 + C60−5813.2211513−25.62.4242.4401.3337.0086.014
GdPc2 + BN-1H−3771.1790578−9.72.4922.4931.4087.0036.008
GdPc2 + BN-2H−4491.6012679−34.92.4522.4621.3507.0026.020
GdPc2 + BN-3H−5689.9869344−52.52.4432.4271.3287.0056.019
GdPc2 + BN-4H−7366.3531079−72.22.4672.4321.335−7.004−6.028
GdPc2 + BN-5H−9520.6731475−76.72.4292.4241.316−7.005−6.019
GdPc2 + BN-6H−12,152.9688187−79.82.4152.4331.307−7.002−7.982
GdPc2 + BN-7H−15,263.2324587−77.52.4342.4101.303−7.007−6.024
(GdPc2)2−7057.5896494−60.22.4272.4291.337, 1.3377.004, −7.0047.006, −7.004
a Lower, indicating Pc ligand is in contact with the surface in carbon- and boron nitride-based model; upper, for opposite Pc ligand (Figure 2). Equivalent for isolated GdPc2.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Basiuk, V.A.; Basiuk, E.V. Adsorption of Gadolinium Bisphthalocyanine on Atomically Flat Surfaces: Comparison of Graphene and Hexagonal Boron Nitride from DFT Calculations. Surfaces 2024, 7, 404-413. https://doi.org/10.3390/surfaces7020025

AMA Style

Basiuk VA, Basiuk EV. Adsorption of Gadolinium Bisphthalocyanine on Atomically Flat Surfaces: Comparison of Graphene and Hexagonal Boron Nitride from DFT Calculations. Surfaces. 2024; 7(2):404-413. https://doi.org/10.3390/surfaces7020025

Chicago/Turabian Style

Basiuk, Vladimir A., and Elena V. Basiuk. 2024. "Adsorption of Gadolinium Bisphthalocyanine on Atomically Flat Surfaces: Comparison of Graphene and Hexagonal Boron Nitride from DFT Calculations" Surfaces 7, no. 2: 404-413. https://doi.org/10.3390/surfaces7020025

APA Style

Basiuk, V. A., & Basiuk, E. V. (2024). Adsorption of Gadolinium Bisphthalocyanine on Atomically Flat Surfaces: Comparison of Graphene and Hexagonal Boron Nitride from DFT Calculations. Surfaces, 7(2), 404-413. https://doi.org/10.3390/surfaces7020025

Article Metrics

Back to TopTop