Load Testing of Cultural Heritage Structures and Sculptures: Unconventional Methods for Assessing Safety
Abstract
1. Introduction
2. Load Tests on Bronze Sculptures
2.1. Structural and Material Data
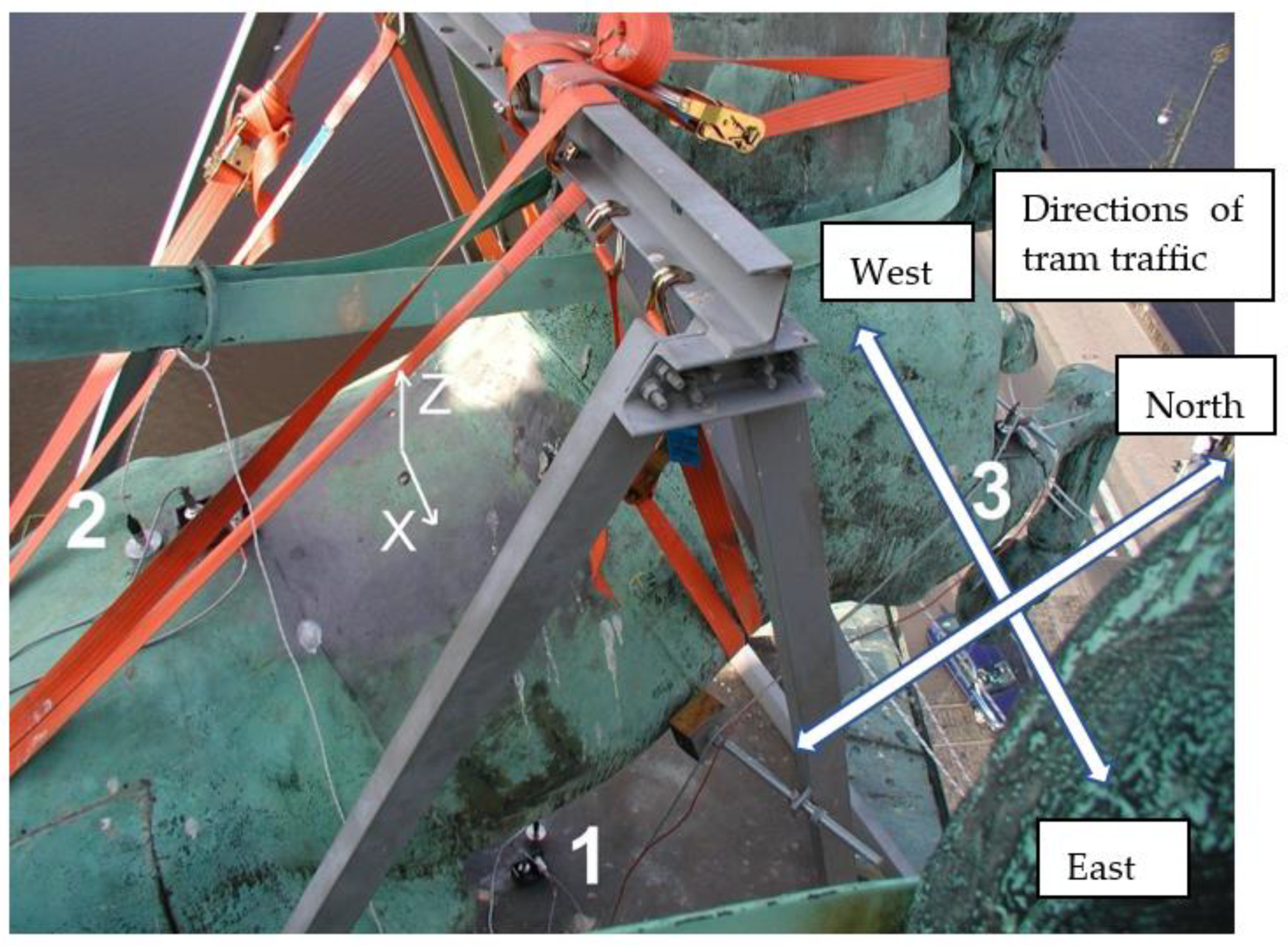
2.2. In Situ Static Load Test Arrangement
2.3. Dynamic Response Measurements
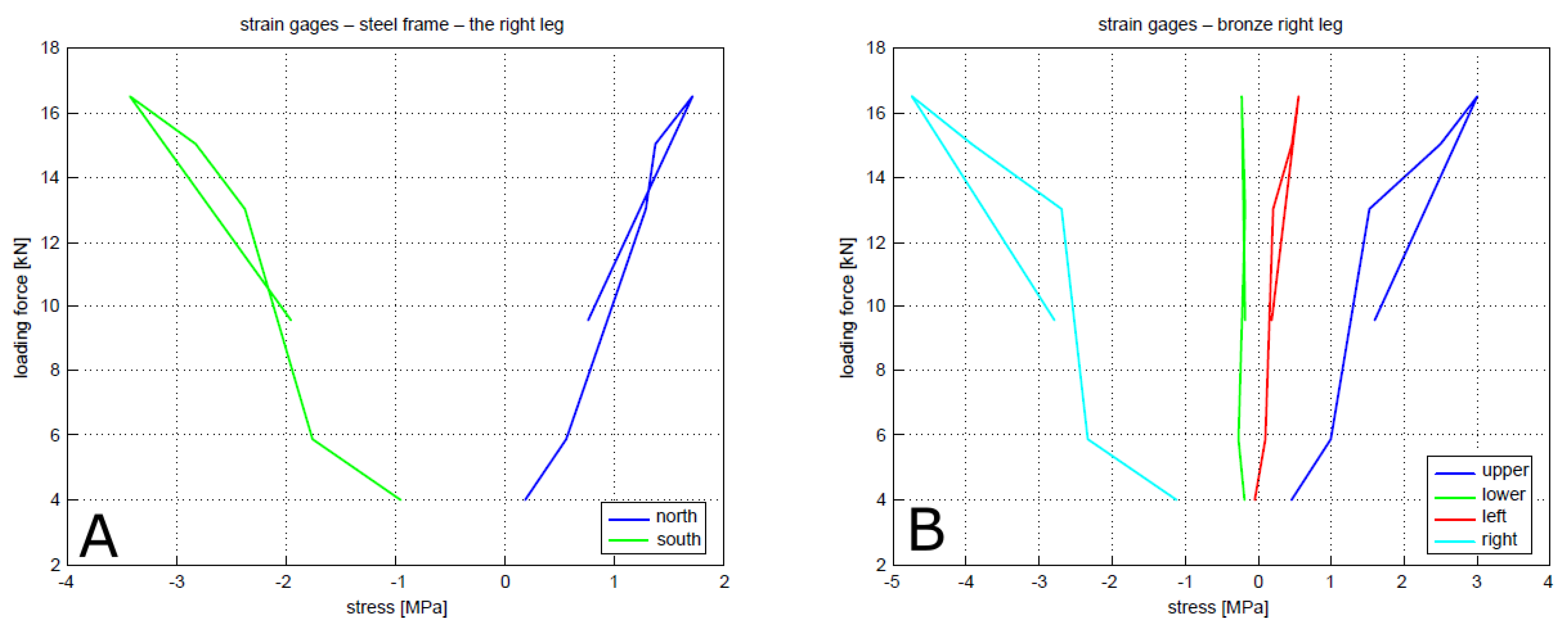
2.4. Static Test Results and Discussion
2.5. Dynamic Response and Comments
3. Assessment of a Renaissance Brick Vault Ceiling
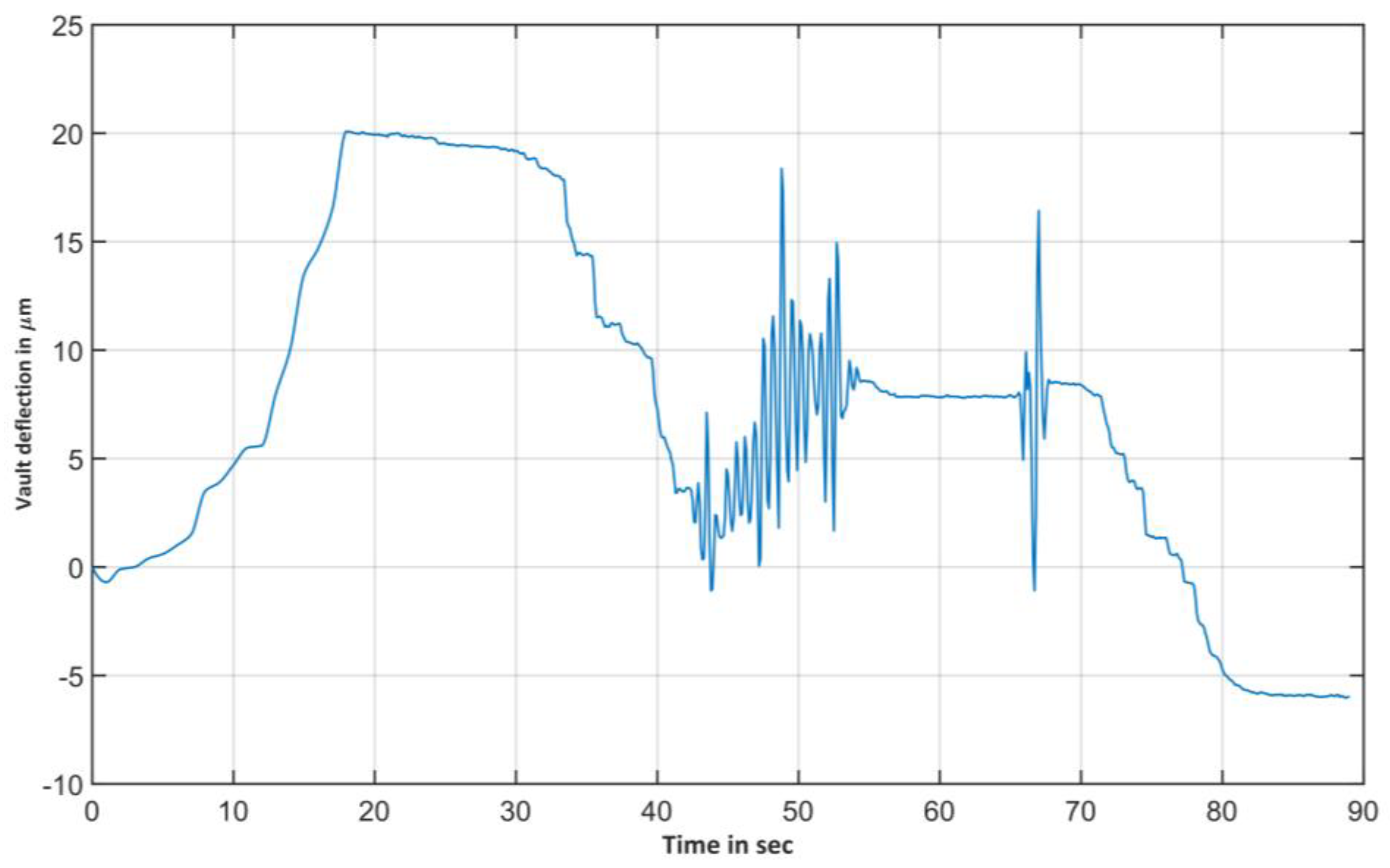
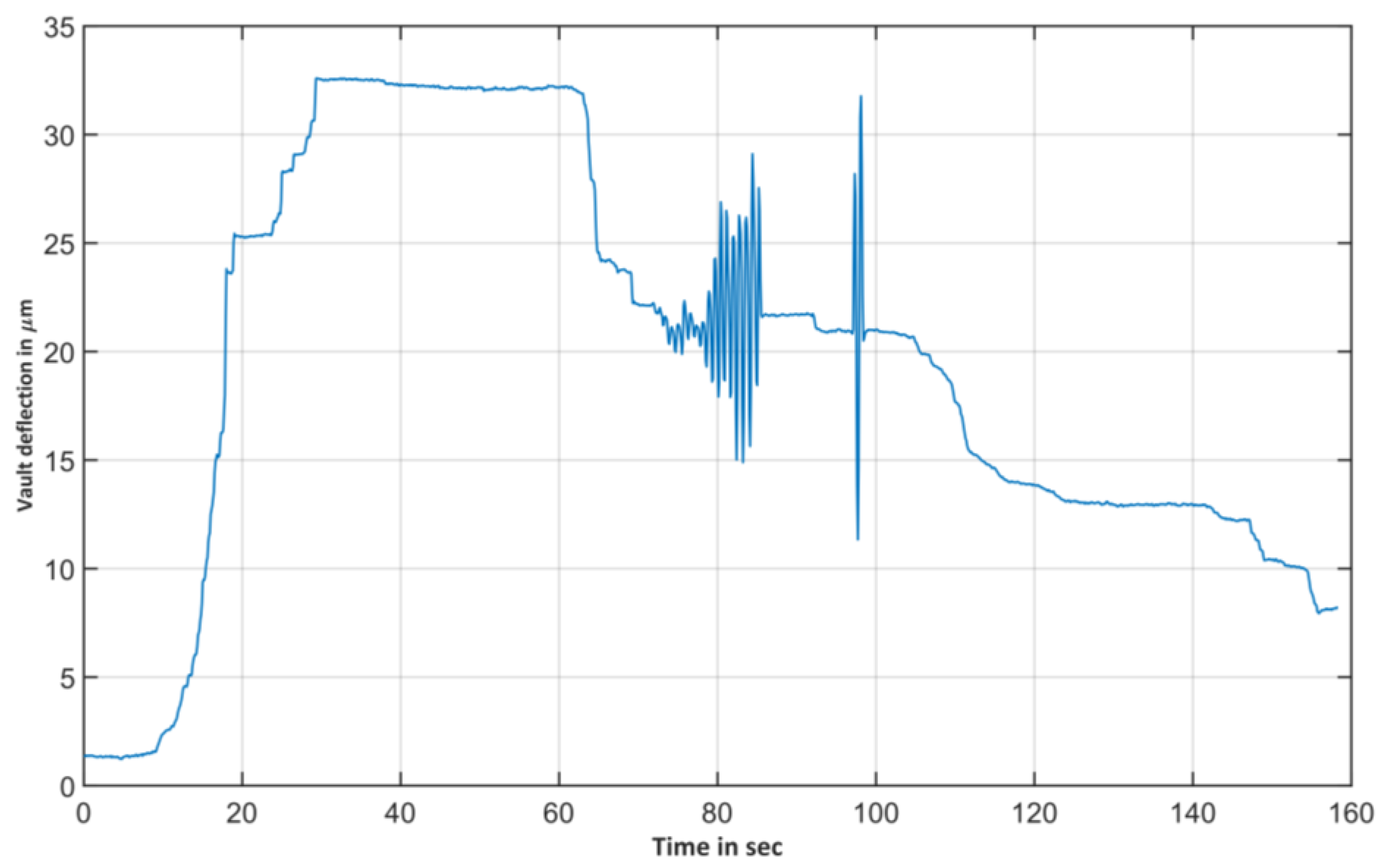
3.1. Load Test Arrangement and Results
3.2. Load Test Findings
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schueremans, L.; Van Gemert, D. Assessing the safety of existing structures: Reliability based assessment framework, examples and application. J. Civ. Eng. Manag. 2004, 10, 131–141. [Google Scholar] [CrossRef]
- Gutermann, M.; Malgut, W. Experimentell gestützter Tragsicherheitsnachweis–Erfahrungen, Potenzial und Grenzen am Beispiel von Hochbauwerken im Bestand. Tagungsband 1. Fachkongress Konstruktiver Ingenieurbau; TAE: Esslingen, Germany, 2022; pp. 53–61. [Google Scholar]
- Steffens, K.; Gutermann, M. Guide to the Load Test of Masonry Arch Bridges; UIC Report; UIC: Paris, France, 2006. [Google Scholar]
- Proske, D.; Sykora, M.; Gutermann, M. Verringerung der Versagenswahrscheinlichkeit von Brücken durch experimentelle Traglastversuche. Bautechnik 2020, 98, 80–92. [Google Scholar] [CrossRef]
- Jing, S.; Nishizawa, H. Experimental Study on the Structural Behavior of the Oldest Timber Frame in China. Buildings 2022, 12, 1860. [Google Scholar] [CrossRef]
- Meng, X.; Li, T.; Yang, Q. Experimental study on the seismic mechanism of a full-scale traditional Chinese timber structure. Eng. Struct. 2018, 180, 484–493. [Google Scholar] [CrossRef]
- Drdácký, M. Historical structures—Inspiration from concepts through details to forms. IABSE Symp. Rep. 2015, 104, 1–8. [Google Scholar] [CrossRef]
- Matysek, P.; Witkowski, M. Compressive Tests of Historical Brick Masonry—Case Study of the Archduke Rudolf Caserns Buildings in Cracow. Int. J. Arch. Herit. 2019, 15, 1364–1374. [Google Scholar] [CrossRef]
- Drdácký, M.; Kasal, B. Testing historic materials for redesign purposes. In Proceedings of the 10th International Conference on “Structural Analysis of Historic Construction—Anamnesis, Diagnosis, Therapy, Controls”, SAHC 2016, Leuven, Belgium, 13–15 September 2016; Van Balen, K., Verstrynge, E., Eds.; CRC Press: Boca Raton, FL, USA; Balkema, Taylor & Francis Group: Leiden, The Netherlands, 2016; pp. 585–591. [Google Scholar]
- de Boer, A.; Ha, L.; Quansah, A. Assessment by in situ load tests of historical steel-concrete bridge decks. In Book: Computational Modelling of Concrete and Concrete Structures; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Vienna, Austria, 2022; pp. 712–719. [Google Scholar] [CrossRef]
- Dilek, U.; Sorenson, M.L.; Chandler, D.B. Load Testing of Historic Cast Iron Stairs at Cape Hatteras Lighthouse. J. Perform. Constr. Facil. 2005, 19, 36–41. [Google Scholar] [CrossRef]
- Gutermann, M.; Malgut, W. In-situ load test of an historic stair rail made of lime stone. In Proceedings of the Conference Proceedings “Structural Faults + Repair”, London, UK, 19 November 2014. [Google Scholar] [CrossRef]
- Urushadze, S.; Pirner, M. The Influence of Bell’s Swaying on Neo-Gothic Cathedral. Structural Analysis of Historical Constructions. An Interdisciplinary Approach; Aguilar, R., Torrealva, D., Moreira, S., Pando, M., Ramos, L., Eds.; RILEM Bookseries, 18. Municipal and Structural Engineering; Springer: Amsterdam, The Netherlands, 2019; pp. 2170–2178. ISBN 978-3-319-99440-6. [Google Scholar] [CrossRef]
- Available online: http://vocab.getty.edu/page/aat/300184603 (accessed on 15 July 2023).
- Cohen, E.; Dinapoli, P.; Vellozzi, J. An engineering view of the Statue of Liberty restoration. IABSE Rep. 1993, 70, 621. [Google Scholar]
- Hacar, B. Bronze sculpture of Jan Žižka of Trocnov at Vítkov and its reinforce concrete frame (Bronzová socha Jana Žižky z Trocnova na Vítkově a její železobetonová výztuha—In Czech). Sborník 21, ČVUT Praha.
- Bayer, J.; Drdácký, M.; Válek, J. Survey and Assessment of a Baroque Vault for Refurbishment and Retrofitting Planning; ALFA: Bratislava, Slovak Republic, 2023; in print. [Google Scholar]
- Watts, G.R. Case Studies of the Effects of Traffic Induced Vibrations on Heritage Buildings; Transport and Road Research Laboratory: Crowthorne, UK, 1988; p. 56. [Google Scholar]
- Crispino, M.; D’Apuzzo, M. Measurement and prediction of traffic-induced vibrations in a heritage building. J. Sound Vib. 2001, 246, 319–335. [Google Scholar] [CrossRef]
- Hunaidi, O.; Tremblay, M. Traffic-induced building vibrations in Montreal. Can. J. Civ. Eng. 1997, 24, 736–753. [Google Scholar] [CrossRef]
- Atamturktur, S.; Bornn, L.; Hemez, F. Vibration characteristics of vaulted masonry monuments undergoing differential support settlement. Eng. Struct. 2011, 33, 2472–2484. [Google Scholar] [CrossRef]
- Bayraktar, A.; Türker, T.; Sevım, B.; Altunişik, A.C.; Yildirim, F. Modal Parameter Identification of Hagia Sophia Bell-Tower via Ambient Vibration Test. J. Nondestruct. Eval. 2009, 28, 37–47. [Google Scholar] [CrossRef]
- Brenchich, A.; Sabia, D. Experimental identification of a multi-span masonry bridge: The Tanaro bridge. Constr. Build. Mater. 2008, 22, 2087–2099. [Google Scholar] [CrossRef]
- Casciati, S.; Al-Saleh, R. Dynamic behavior of a masonry civic belfry under operational conditions. Acta Mech. 2010, 215, 211–224. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á. Explaining operational modal analysis with data from an arch bridge. Mech. Syst. Signal Process. 2011, 25, 1431–1450. [Google Scholar] [CrossRef]
- Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J. Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef]
- Arangjelovski, T.; Gramatikov, K.; Docevska, M. Assessment of damaged timber structures using proof load test—Experience from case studies. Constr. Build. Mater. 2015, 101, 1271–1277. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Karanikoloudis, G.; Greco, F. In situ testing and modeling of cultural heritage buildings in Peru. In “Structural Analysis of Historical Constructions: Anamnesis, Diagnosis, Therapy, Controls”, Proceedings of the 10th International Conference on Structural Analysis of Historical Constructions, SAHC, Leuven, Belgium, 13–15 September 2016; Van Balen, K., Verstrynge, E., Eds.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]


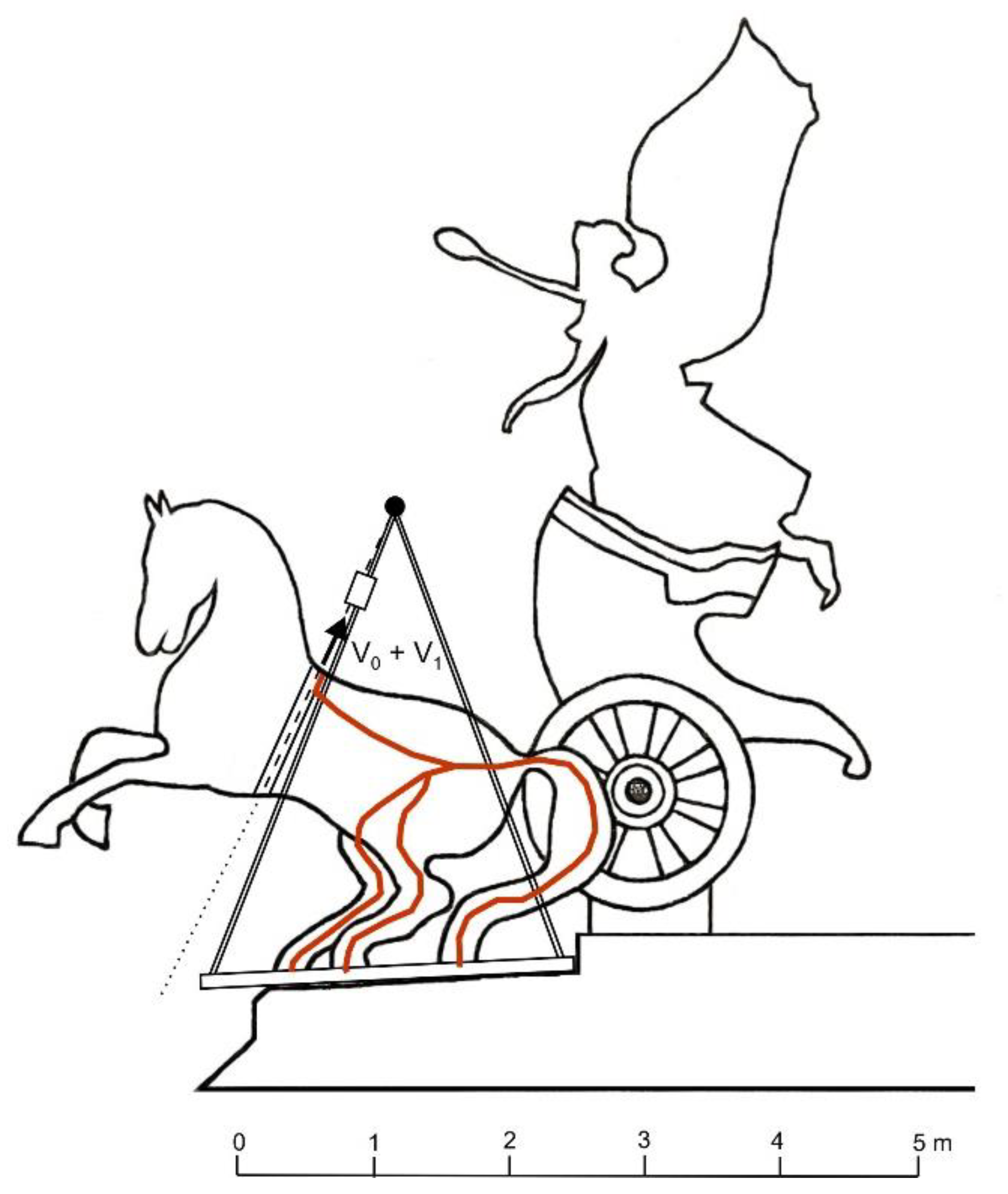



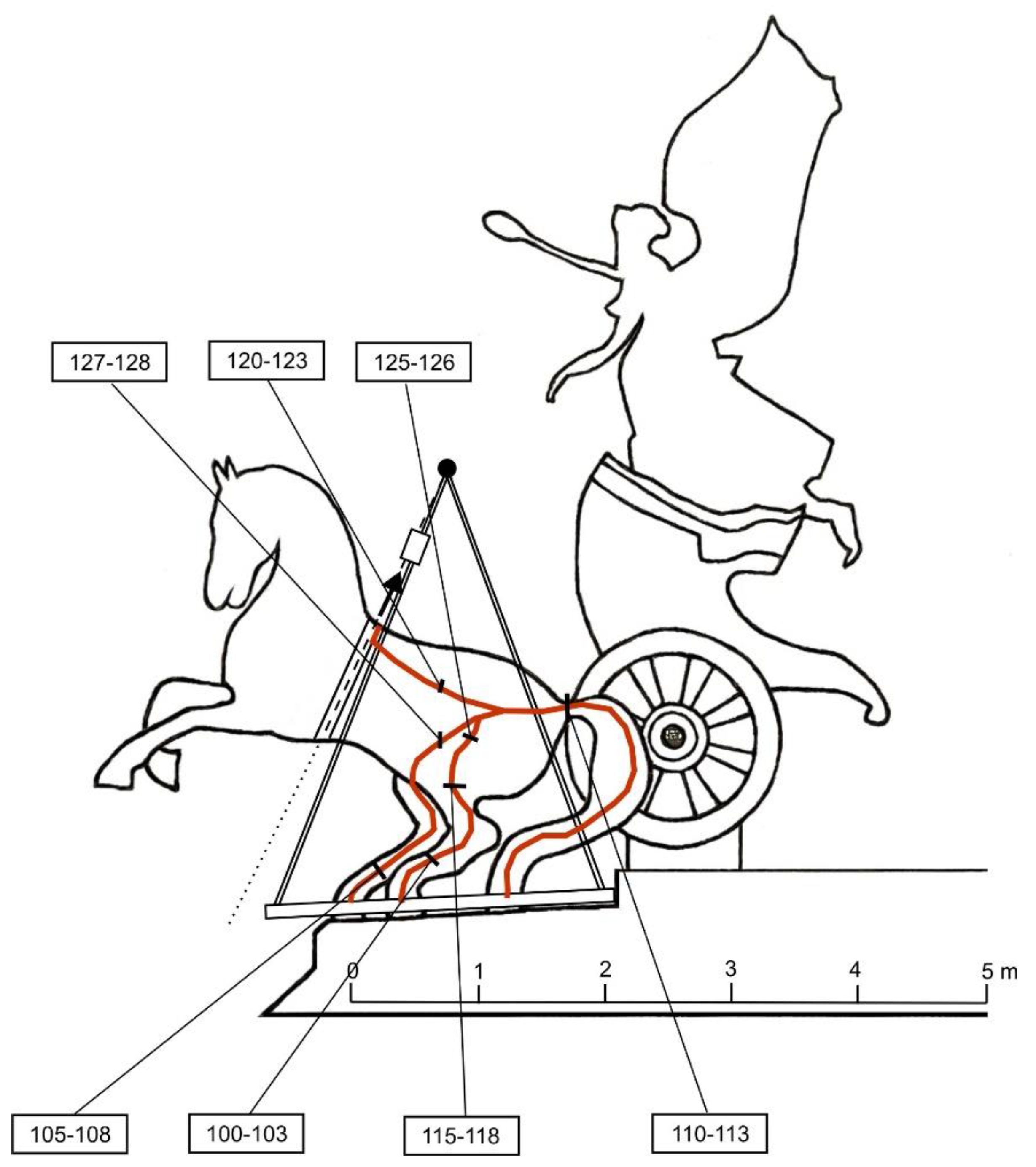
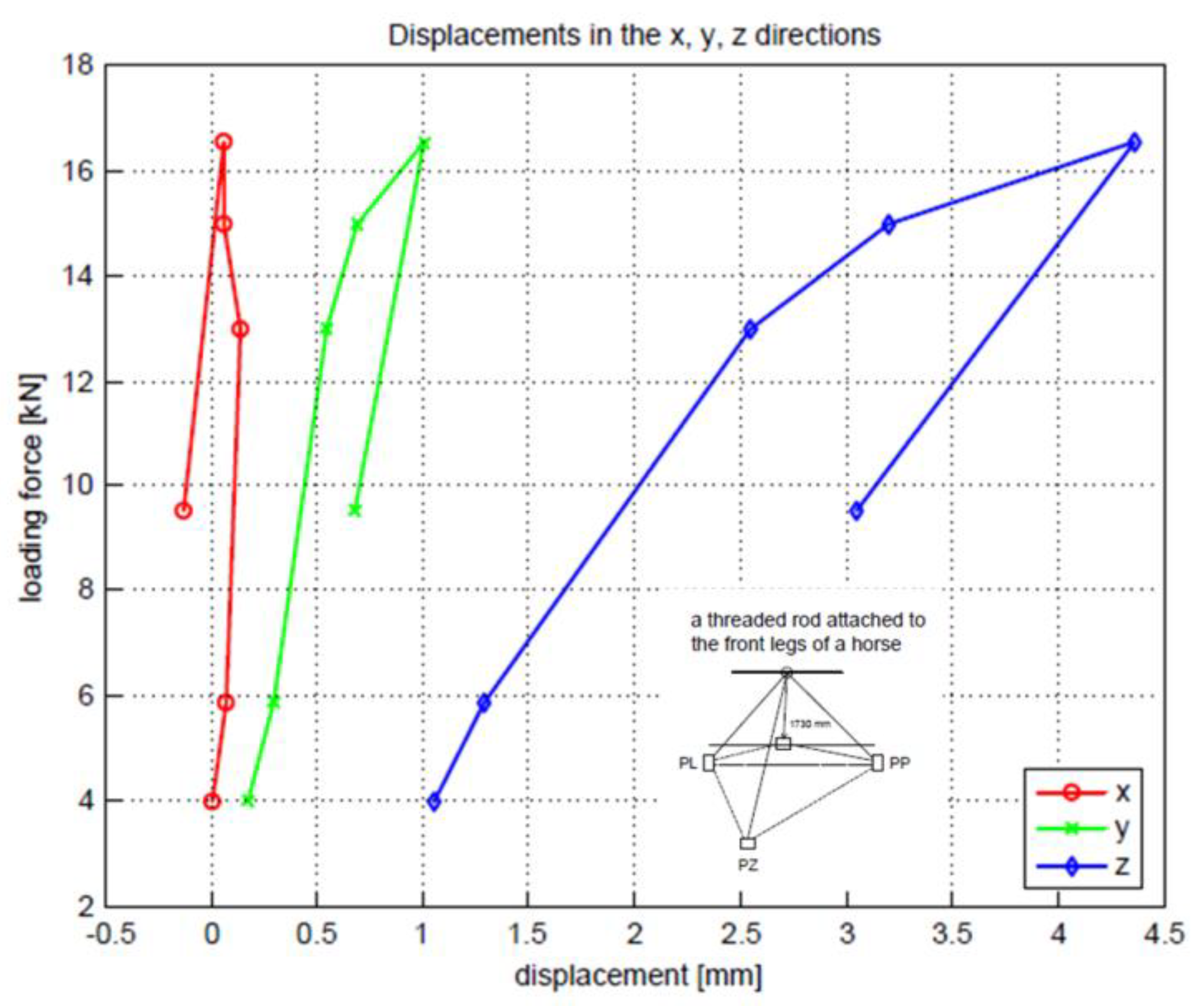




| Specimen | Ductility A5.65 [%] | Strength in Tension Rm [MPa] | Upper Yield Strength ReH [MPa] | Lower Yield Strength ReL [MPa] | Modululus of Elasticity in Tension E [GPa] | |
|---|---|---|---|---|---|---|
| steel | 1 | 17.5 | 422 | 363 | 338 | 83 |
| 2 | 26.5 | 465 | 382 | 375 | 102 | |
| 3 | 27.5 | 422 | 338 | 335 | 108 | |
| Average | 23.8 | 436 | 361 | 349 | 98 | |
| σn-1 | 5.5 | 25 | 22 | 22 | 13 | |
| Specimen | Ductility A5.65 [%] | Strength in Tension Rm [MPa] | Yield Strength Rp0.2 [MPa] | Modululus of Elasticity in Tension E [GPa] | |
|---|---|---|---|---|---|
| bronze | TGZB1 | 23.4 | 240 | 121 | 49 |
| TGZB2 * | 8.5 | 159 | 108 | 43 | |
| TGVB1 | 1.5 | 205 | n.a. | n.a. | |
| TGVB2 * | 0.4 | 152 | n.a. | n.a. | |
| TGVB3 * | 0.4 | 164 | n.a. | n.a. | |
| File Nr. | Street Traffic Excitation | File Nr. | Street Traffic Excitation |
|---|---|---|---|
| 1 | Tram W-E | 16 | No traffic. Wind 2–4 ms−1. |
| 2 | Tram E-W | 17 | Tram E-W (one wagon). Tram W-E follows. |
| 3 | Tram W-E at the beginning of recording. Tram N-E at the end of recording. | 18 | Tram along the river N-S. |
| 4 | Tram W-E at the beginning of recording. Tram E-W follows. | 19 | Tram W-E. |
| 5 | Tram E-N | 20 | Tram W-E at the beginning of recording. Tram along the river S-N follows. |
| 6 | Tram E-W in the middle of recording. Tram E-N at the end of recording | 21 | Tram W-E. |
| 7 | Tram W-E | 22 | Tram W-E at the beginning of recording. Tram E-W follows. |
| 8 | Tram W-E at the beginning of recording. Tram E-W follows. | 23 | No traffic. |
| 9 | Tram W-E | 24 | No traffic. |
| 10 | No traffic. Tram E-W at the end of recording | 25 | Cyclic manual excitation in horizontal direction. |
| 11 | Tram W-E at the beginning of recording. Tram E-W follows. | Shock loading | |
| 12 | Tram along the river S-N. | 26 | Shock load in horizontal direction. |
| 13 | Tram E-W in the middle of recording. Tram W-E follows. | 27 | Shock load in horizontal direction. |
| 14 | No traffic. Tram W-E at the end of recording. | 28 | Shock load in vertical direction. |
| 15 | No traffic. Wind 2–4 ms−1. | 29 | Shock load in vertical direction. |
| No. of Rec. | Response in a Point [RMS] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Velocity [mm/s1] | Deflection [mm] | Acceleration [mm/s2] | ||||||||
| 1 | 2 | 3 | 1 | 2 | ||||||
| z | x | z | x | z | x | z | x | z | z | |
| Street traffic | ||||||||||
| 1 | 0.06012 | 0.06313 | 0.19176 | 0.22987 | 0.39743 | 0.12503 | 0.00350 | 0.00158 | 9.75610 | 26.07900 |
| 2 | 0.04860 | 0.04509 | 0.17434 | 0.18739 | 0.35291 | 0.09556 | 0.00314 | 0.00151 | 8.14330 | 23.46400 |
| 3 | 0.05110 | 0.05145 | 0.15941 | 0.27838 | 0.32168 | 0.11730 | 0.00281 | 0.00184 | 9.37850 | 22.18700 |
| 4 | 0.05579 | 0.05414 | 0.15374 | 0.23414 | 0.29965 | 0.10527 | 0.00275 | 0.00123 | 9.32040 | 21.80100 |
| 5 | 0.02261 | 0.04063 | 0.05824 | 0.08076 | 0.11924 | 0.04915 | 0.00121 | 0.00129 | 3.05160 | 7.83420 |
| 6 | 0.05284 | 0.06366 | 0.17375 | 0.26503 | 0.36874 | 0.10406 | 0.00329 | 0.00157 | 8.07680 | 22.94600 |
| 7 | 0.05687 | 0.06207 | 0.13641 | 0.20267 | 0.27011 | 0.10326 | 0.00238 | 0.00192 | 8.95600 | 19.18300 |
| 8 | 0.06048 | 0.06695 | 0.14606 | 0.24646 | 0.29635 | 0.10504 | 0.00278 | 0.00113 | 9.71150 | 20.32800 |
| 9 | 0.04147 | 0.04616 | 0.14043 | 0.18291 | 0.28687 | 0.08626 | 0.00254 | 0.00188 | 7.40440 | 19.38400 |
| 10 | 0.00480 | 0.02751 | 0.01626 | 0.02955 | 0.03883 | 0.03147 | 0.00066 | 0.00113 | 0.60418 | 1.80610 |
| 11 | 0.05952 | 0.06037 | 0.14246 | 0.21298 | 0.29291 | 0.10127 | 0.00253 | 0.00136 | 10.16800 | 20.83700 |
| 12 | 0.03869 | 0.05061 | 0.09165 | 0.16293 | 0.18645 | 0.09277 | 0.00186 | 0.00106 | 6.72200 | 13.51100 |
| 13 | 0.05437 | 0.05228 | 0.23018 | 0.22794 | 0.46664 | 0.11135 | 0.00413 | 0.00217 | 9.06750 | 30.82400 |
| 14 | 0.04906 | 0.04863 | 0.15614 | 0.18311 | 0.30854 | 0.09235 | 0.00272 | 0.00156 | 9.08660 | 22.12000 |
| 15 | 0.01148 | 0.03053 | 0.04048 | 0.04555 | 0.08603 | 0.04352 | 0.00090 | 0.00141 | 1.48770 | 5.67540 |
| 16 | 0.00417 | 0.02585 | 0.01106 | 0.05029 | 0.03246 | 0.08530 | 0.00054 | 0.00278 | 0.54676 | 1.70420 |
| 17 | 0.05698 | 0.05840 | 0.13207 | 0.20537 | 0.24795 | 0.09966 | 0.00239 | 0.00135 | 9.41030 | 18.74400 |
| 18 | 0.03044 | 0.04898 | 0.08060 | 0.12025 | 0.16473 | 0.07906 | 0.00156 | 0.00231 | 4.23280 | 11.19100 |
| 19 | 0.06574 | 0.06215 | 0.18553 | 0.24812 | 0.37103 | 0.12215 | 0.00342 | 0.00194 | 10.99500 | 25.96400 |
| 20 | 0.05071 | 0.05574 | 0.15407 | 0.17043 | 0.30785 | 0.08738 | 0.00279 | 0.00162 | 7.44600 | 20.76400 |
| 21 | 0.06626 | 0.06983 | 0.20016 | 0.23668 | 0.39737 | 0.13394 | 0.00348 | 0.00230 | 10.78300 | 27.95700 |
| 22 | 0.05822 | 0.05461 | 0.18642 | 0.29360 | 0.37949 | 0.12073 | 0.00326 | 0.00181 | 10.30200 | 26.35400 |
| 23 | 0.00596 | 0.02662 | 0.01441 | 0.03568 | 0.03207 | 0.05057 | 0.00040 | 0.00165 | 0.74264 | 2.06560 |
| 24 | 0.00491 | 0.02622 | 0.01355 | 0.03142 | 0.03316 | 0.03909 | 0.00047 | 0.00130 | 0.62152 | 2.10400 |
| 25 | 0.05919 | 0.04836 | 0.24439 | 0.26570 | 0.51258 | 0.39817 | 0.00464 | 0.01241 | 10.49400 | 33.54000 |
| Shock load | ||||||||||
| 26 | 0.00989 | 0.03376 | 0.30787 | 5.67980 | 0.24440 | 10.54600 | 0.00959 | 0.33906 | 0.79278 | 18.01200 |
| 27 | 0.01231 | 0.02508 | 0.20358 | 3.62420 | 0.27197 | 7.44010 | 0.00945 | 0.24262 | 1.50940 | 12.96900 |
| 28 | 0.04603 | 0.04386 | 0.12893 | 0.16853 | 0.25875 | 0.13993 | 0.00231 | 0.00409 | 7.17240 | 18.00100 |
| 29 | 0.01425 | 0.02746 | 0.13575 | 2.37780 | 0.63979 | 3.99050 | 0.02506 | 0.13805 | 1.93780 | 8.43150 |
| No. of Rec. | Response in a Point [Amplitude] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Velocity [mm/s1] | Defelection [mm] | Acceleration [mm/s2] | ||||||||
| 1 | 2 | 3 | 1 | 2 | ||||||
| z | x | z | x | z | x | z | x | z | z | |
| Street traffic | ||||||||||
| 1 | 0.27550 | 0.22123 | 0.74732 | 0.88624 | 1.49680 | 0.42697 | 0.01296 | 0.00505 | 44.05900 | 114.31000 |
| 2 | 0.18610 | 0.20494 | 0.62057 | 0.62168 | 1.17980 | 0.33838 | 0.01067 | 0.00452 | 33.42000 | 87.90800 |
| 3 | 0.24146 | 0.18397 | 0.59798 | 0.90583 | 1.12040 | 0.35117 | 0.00982 | 0.00608 | 38.56500 | 80.71500 |
| 4 | 0.19794 | 0.19189 | 0.46360 | 0.79628 | 0.89868 | 0.36466 | 0.00967 | 0.00400 | 37.03300 | 76.79900 |
| 5 | 0.08751 | 0.12943 | 0.22631 | 0.27103 | 0.53129 | 0.15891 | 0.00540 | 0.00384 | 11.11400 | 31.69900 |
| 6 | 0.21366 | 0.22515 | 0.64071 | 0.99242 | 1.24790 | 0.36586 | 0.01162 | 0.00441 | 30.97000 | 83.74100 |
| 7 | 0.22312 | 0.22202 | 0.47187 | 0.69147 | 0.86857 | 0.35325 | 0.00794 | 0.00548 | 34.68000 | 69.79300 |
| 8 | 0.27533 | 0.26591 | 0.56046 | 0.94398 | 1.12830 | 0.38450 | 0.00982 | 0.00393 | 48.25900 | 73.55500 |
| 9 | 0.15710 | 0.17336 | 0.47362 | 0.73061 | 0.95044 | 0.29646 | 0.00828 | 0.00464 | 30.47700 | 74.80000 |
| 10 | 0.01796 | 0.08123 | 0.11966 | 0.12728 | 0.12201 | 0.10512 | 0.00198 | 0.00367 | 2.65640 | 6.85250 |
| 11 | 0.23639 | 0.23856 | 0.55385 | 0.72714 | 1.04230 | 0.32458 | 0.00865 | 0.00399 | 38.47500 | 83.93800 |
| 12 | 0.15356 | 0.18138 | 0.37587 | 0.59500 | 0.70544 | 0.31870 | 0.00634 | 0.00326 | 31.26400 | 52.93500 |
| 13 | 0.21928 | 0.19607 | 0.81123 | 0.91937 | 1.62810 | 0.38866 | 0.01421 | 0.00572 | 41.50100 | 110.19000 |
| 14 | 0.20233 | 0.16715 | 0.54805 | 0.61969 | 1.06990 | 0.26420 | 0.00851 | 0.00414 | 37.88600 | 87.45900 |
| 15 | 0.04632 | 0.10846 | 0.13877 | 0.20922 | 0.33286 | 0.12359 | 0.00352 | 0.00431 | 6.31260 | 21.56700 |
| 16 | 0.01405 | 0.06697 | 0.04331 | 0.13427 | 0.11760 | 0.15755 | 0.00162 | 0.00515 | 1.93630 | 7.29540 |
| 17 | 0.23273 | 0.21990 | 0.45250 | 0.69074 | 0.80873 | 0.34246 | 0.00734 | 0.00401 | 42.43200 | 68.65400 |
| 18 | 0.12082 | 0.16000 | 0.34344 | 0.49640 | 0.58452 | 0.22713 | 0.00513 | 0.00604 | 17.30900 | 46.14300 |
| 19 | 0.23784 | 0.22892 | 0.61138 | 0.96369 | 1.22040 | 0.46838 | 0.01047 | 0.00487 | 41.75900 | 93.42100 |
| 20 | 0.19011 | 0.19266 | 0.47005 | 0.58252 | 0.88432 | 0.25976 | 0.00775 | 0.00485 | 25.99600 | 73.04700 |
| 21 | 0.26669 | 0.25391 | 0.70868 | 0.85744 | 1.26480 | 0.49415 | 0.01248 | 0.00650 | 36.37800 | 112.22000 |
| 22 | 0.21982 | 0.18971 | 0.60219 | 0.92357 | 1.37490 | 0.40847 | 0.01169 | 0.00499 | 40.45400 | 93.65400 |
| 23 | 0.02062 | 0.07200 | 0.04664 | 0.10972 | 0.10833 | 0.11672 | 0.00136 | 0.00394 | 2.72280 | 6.93760 |
| 24 | 0.01776 | 0.06716 | 0.04563 | 0.11359 | 0.11044 | 0.08844 | 0.00147 | 0.00299 | 2.17550 | 8.19280 |
| 25 | 0.21883 | 0.19149 | 0.72082 | 1.04510 | 1.44970 | 1.73000 | 0.01571 | 0.06493 | 40.45000 | 109.99000 |
| Shock load | ||||||||||
| 26 | 0.02281 | 0.07369 | 0.62688 | 10.96500 | 0.54518 | 20.55300 | 0.01925 | 0.65392 | 4.78180 | 37.87300 |
| 27 | 0.05109 | 0.06916 | 0.49448 | 7.99920 | 0.71822 | 16.18200 | 0.02494 | 0.53874 | 5.21830 | 39.84200 |
| 28 | 0.20480 | 0.13551 | 0.47439 | 0.62417 | 0.99862 | 0.37091 | 0.00846 | 0.00892 | 29.36100 | 77.30400 |
| 29 | 0.06439 | 0.10829 | 0.31212 | 4.94160 | 2.63100 | 8.43620 | 0.09511 | 0.31036 | 7.00100 | 23.16800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drdácký, M.; Urushadze, S. Load Testing of Cultural Heritage Structures and Sculptures: Unconventional Methods for Assessing Safety. Heritage 2023, 6, 5538-5558. https://doi.org/10.3390/heritage6070292
Drdácký M, Urushadze S. Load Testing of Cultural Heritage Structures and Sculptures: Unconventional Methods for Assessing Safety. Heritage. 2023; 6(7):5538-5558. https://doi.org/10.3390/heritage6070292
Chicago/Turabian StyleDrdácký, Miloš, and Shota Urushadze. 2023. "Load Testing of Cultural Heritage Structures and Sculptures: Unconventional Methods for Assessing Safety" Heritage 6, no. 7: 5538-5558. https://doi.org/10.3390/heritage6070292
APA StyleDrdácký, M., & Urushadze, S. (2023). Load Testing of Cultural Heritage Structures and Sculptures: Unconventional Methods for Assessing Safety. Heritage, 6(7), 5538-5558. https://doi.org/10.3390/heritage6070292









