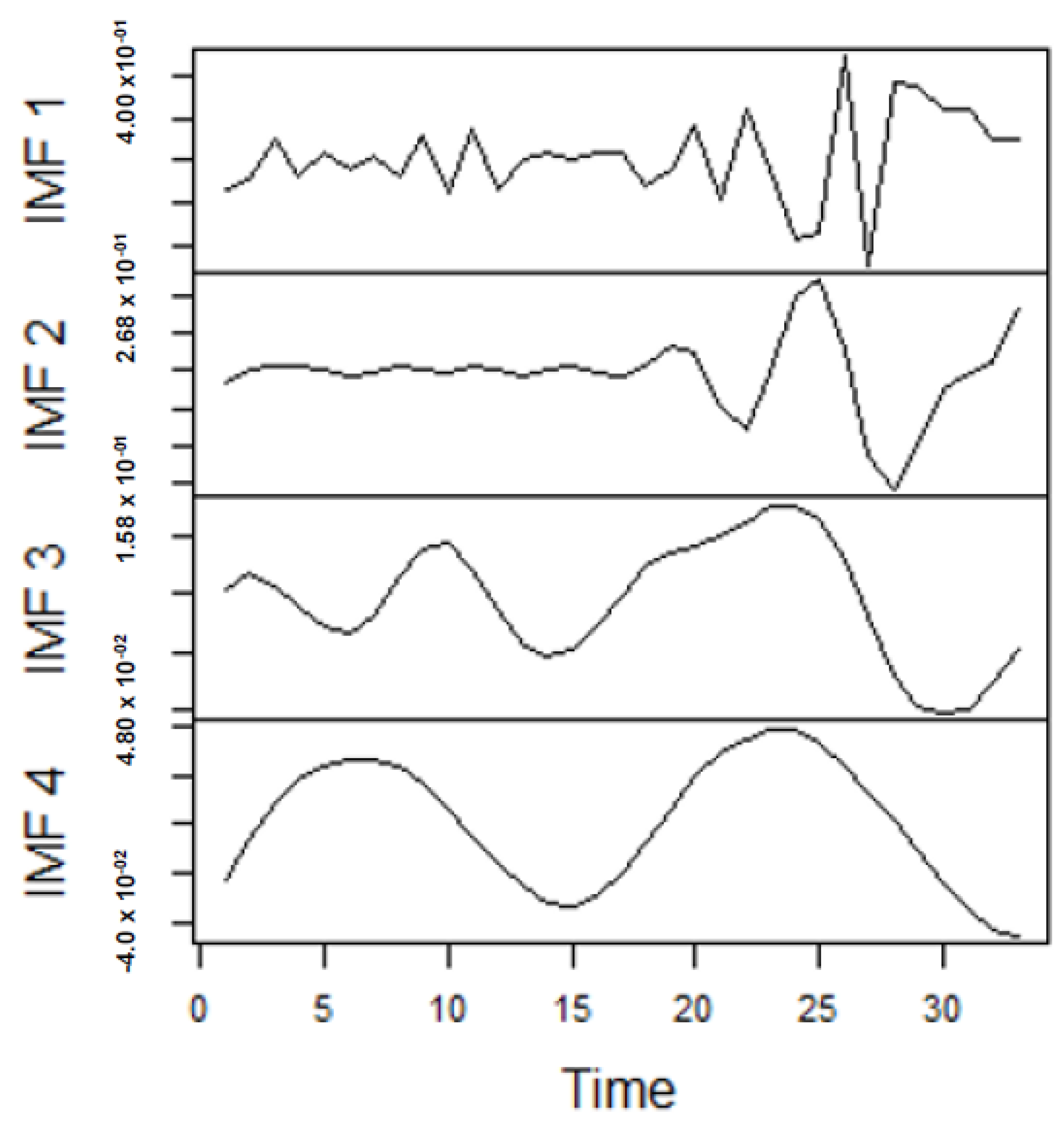
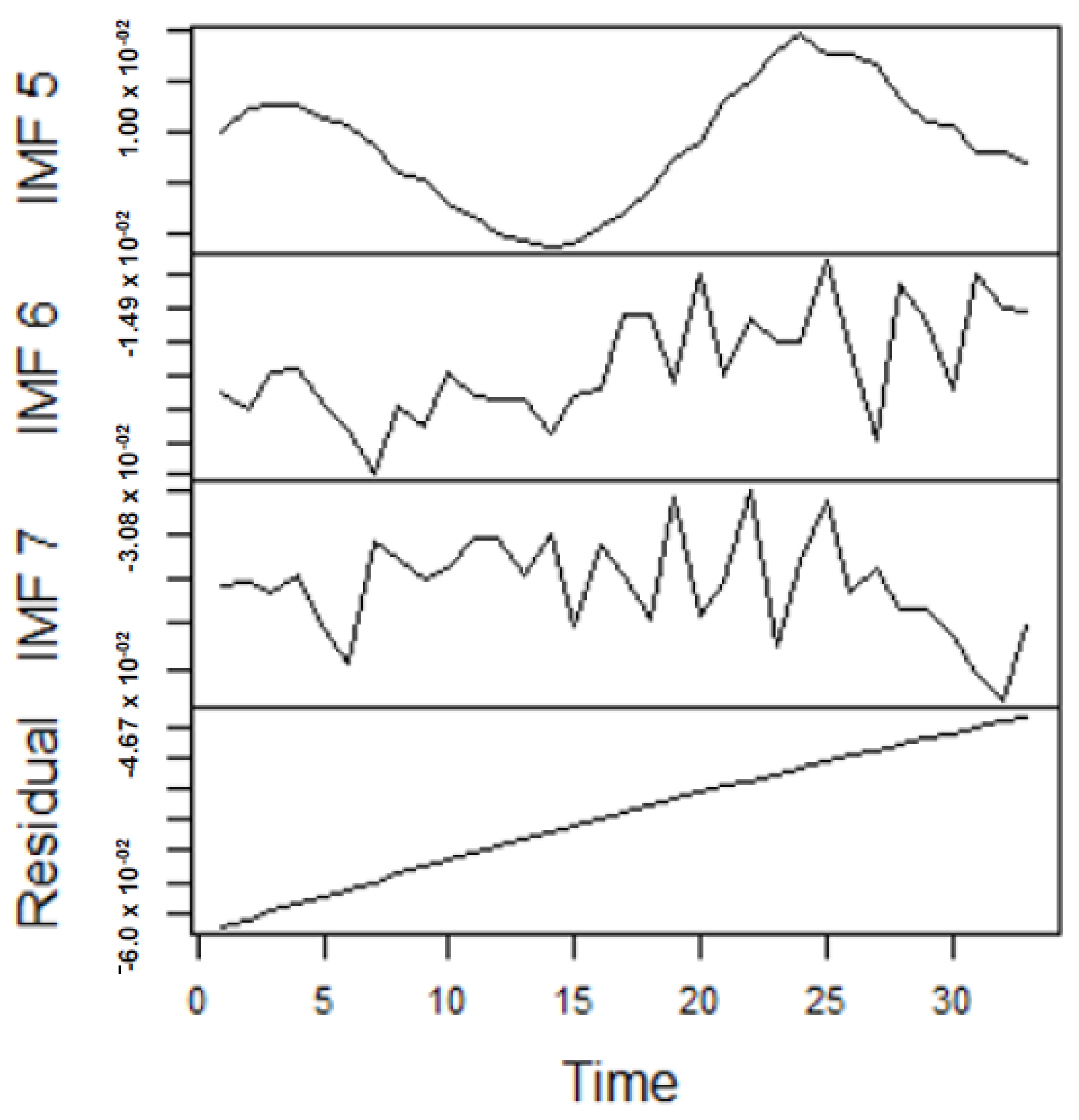
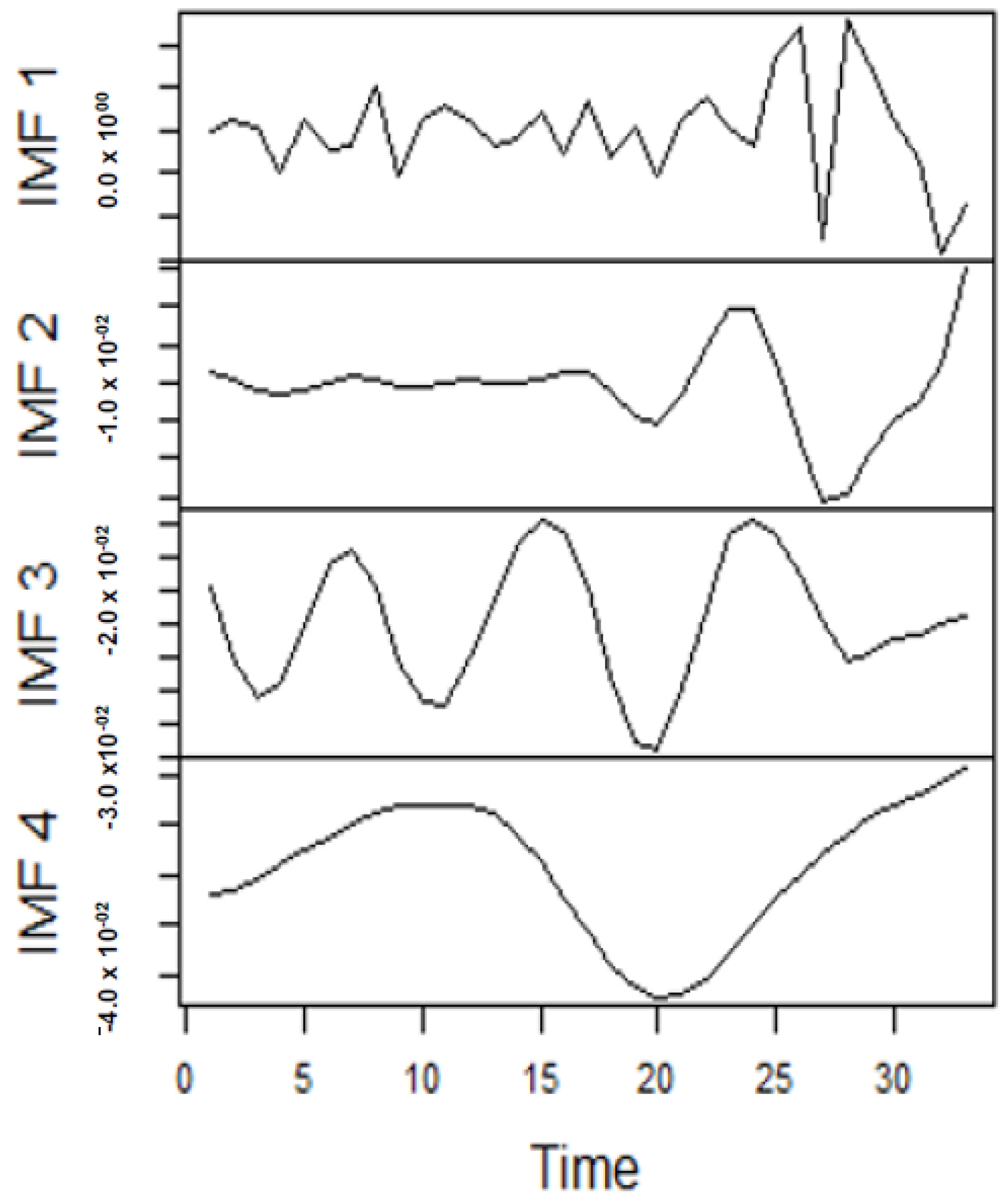
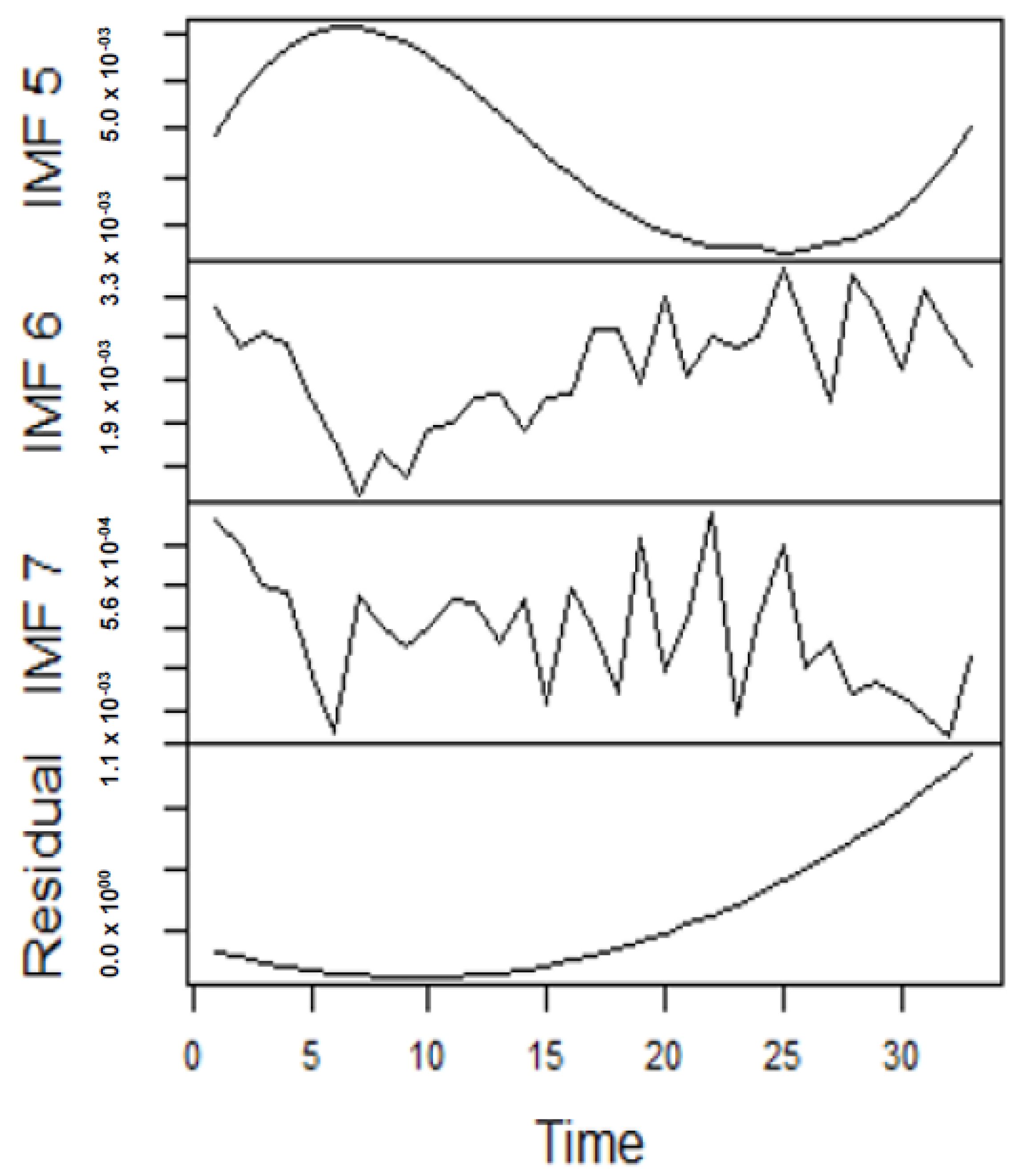
Forecasting Results
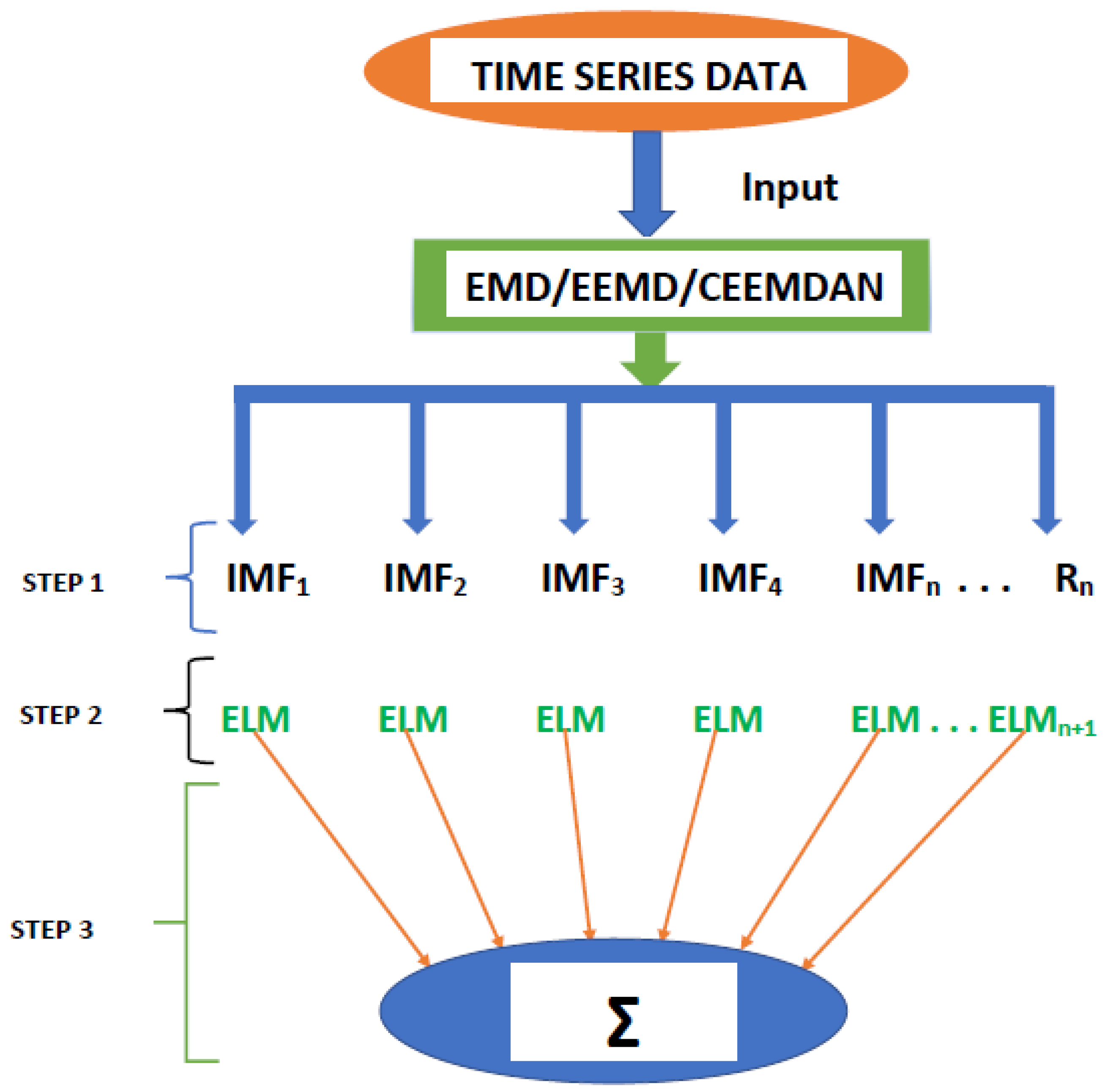
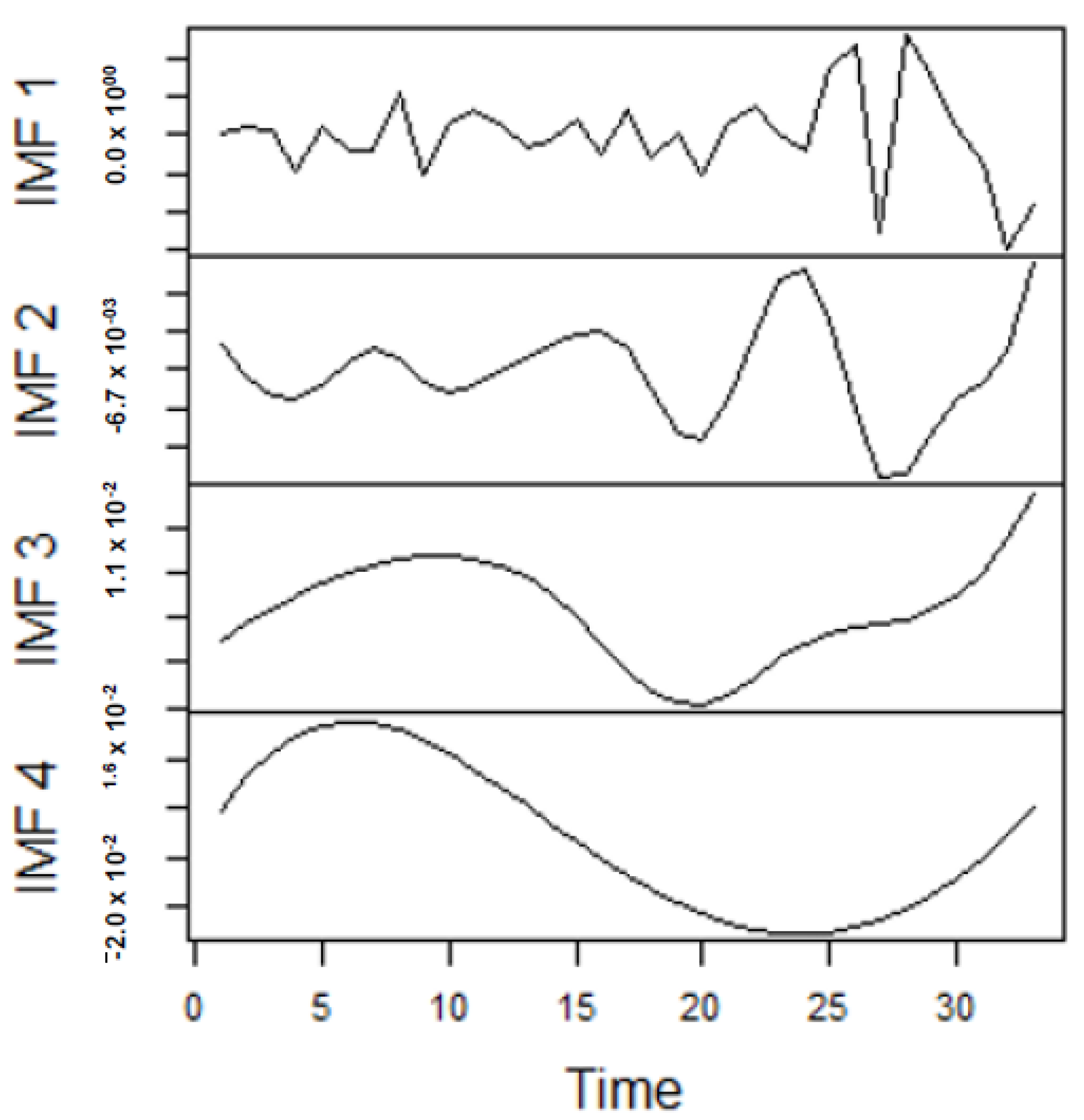
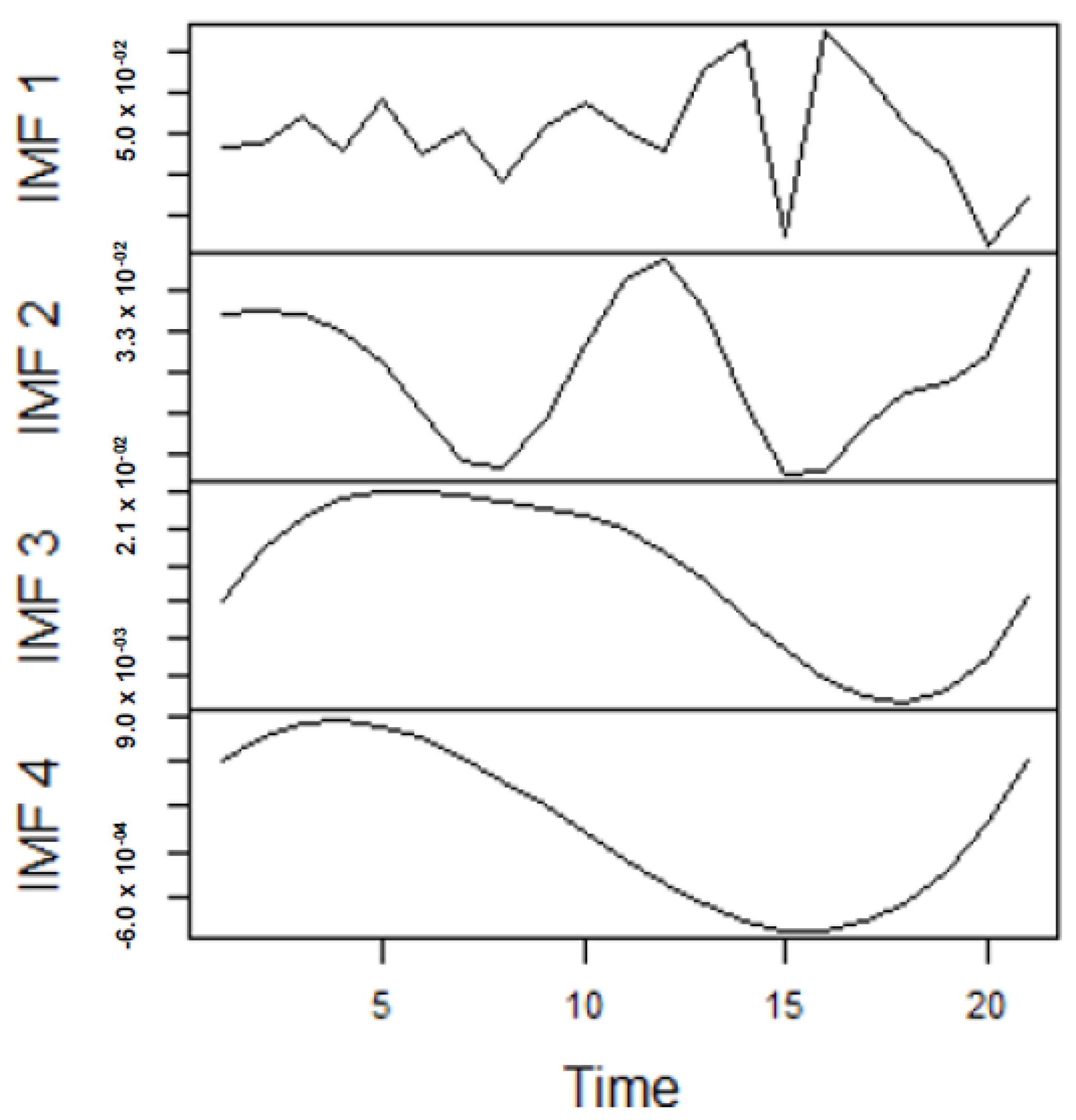
As earlier mentioned, the performance of the EEMD is worsened by some of the IMFs. However, this situation is overcome by the CEEMDAN-ELM, which results in fewer IMFs. Considering this, employing the CEEMDAN-ELM, we conduct various forecasting activities that result in a combination of forecast values of all individual IMFs. An example of this IMFs decomposition for UGAS and JGAS based on CEEMDAN-ELM in the pre-COVID era and stressful paradigm are reported in
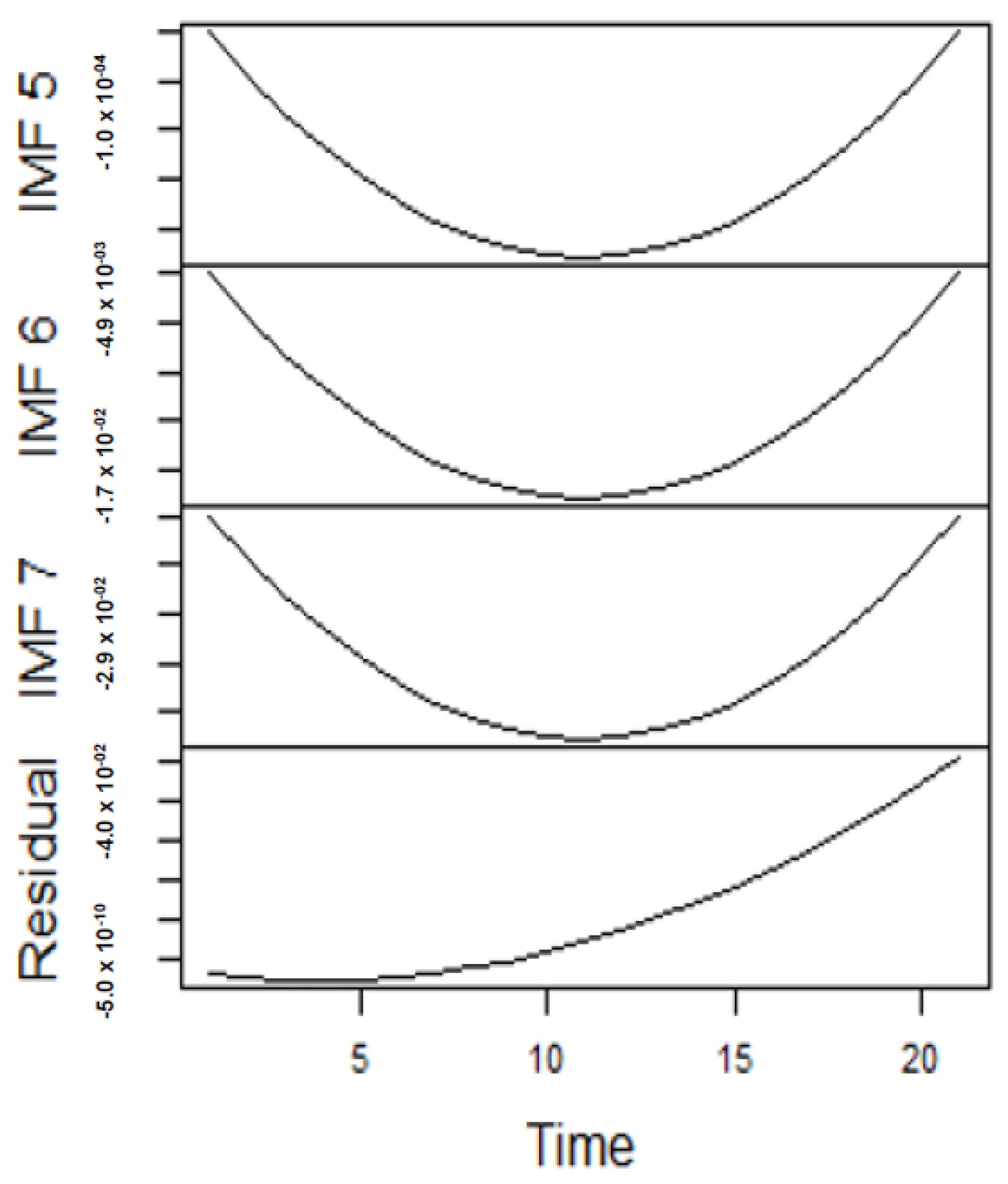
Figure 5,
Figure 6,
Figure 7 and
Figure 8.
Figure 5 and
Figure 6 forms a complete set, however, it has been split for clarity of display. A similar situation applies to
Figure 7 and
Figure 8.
On the other hand, the EEMD seeks to reduce the change of mode mixing, which is an improvement on EMD as already discussed. Hence, extending this to extreme learning machines does lead to an improved forecasting performance. From this viewpoint, of forecasting the generated IMFs, we deduce the combination of forecast values for all individual IMFs, which are reported in
Table 4 and
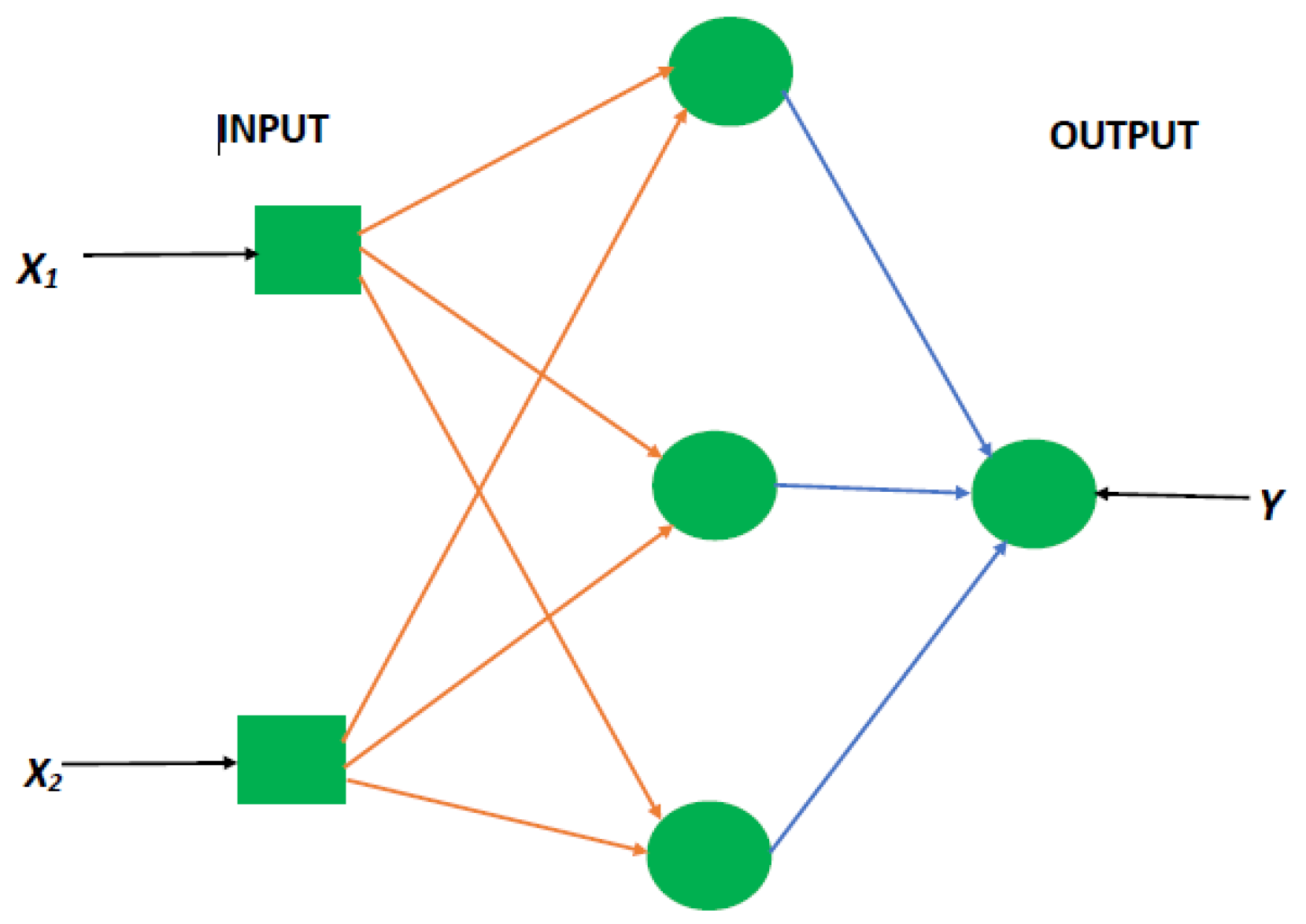
Table 5. In consequence, we employ the EMD-based ELM in a similar framework, which entails decomposing the original series followed by the application of ELM to forecast the individual IMFs generated and finally deducing the combined forecast. In effect, the accuracy of these forecasts is derived based on the individual model-specific framework, that is, for the EMD-ELM, we have the Mean Absolute Error (MAE) for EMD-ELM model (MAE-EMD-ELM), the Mean Absolute Percentage Error (MAPE) for EMD-ELM model (MAPE-EMD-ELM), and Root Mean Square Error (RMSE) for EMD-ELM model (RMSE-EMD-ELM).
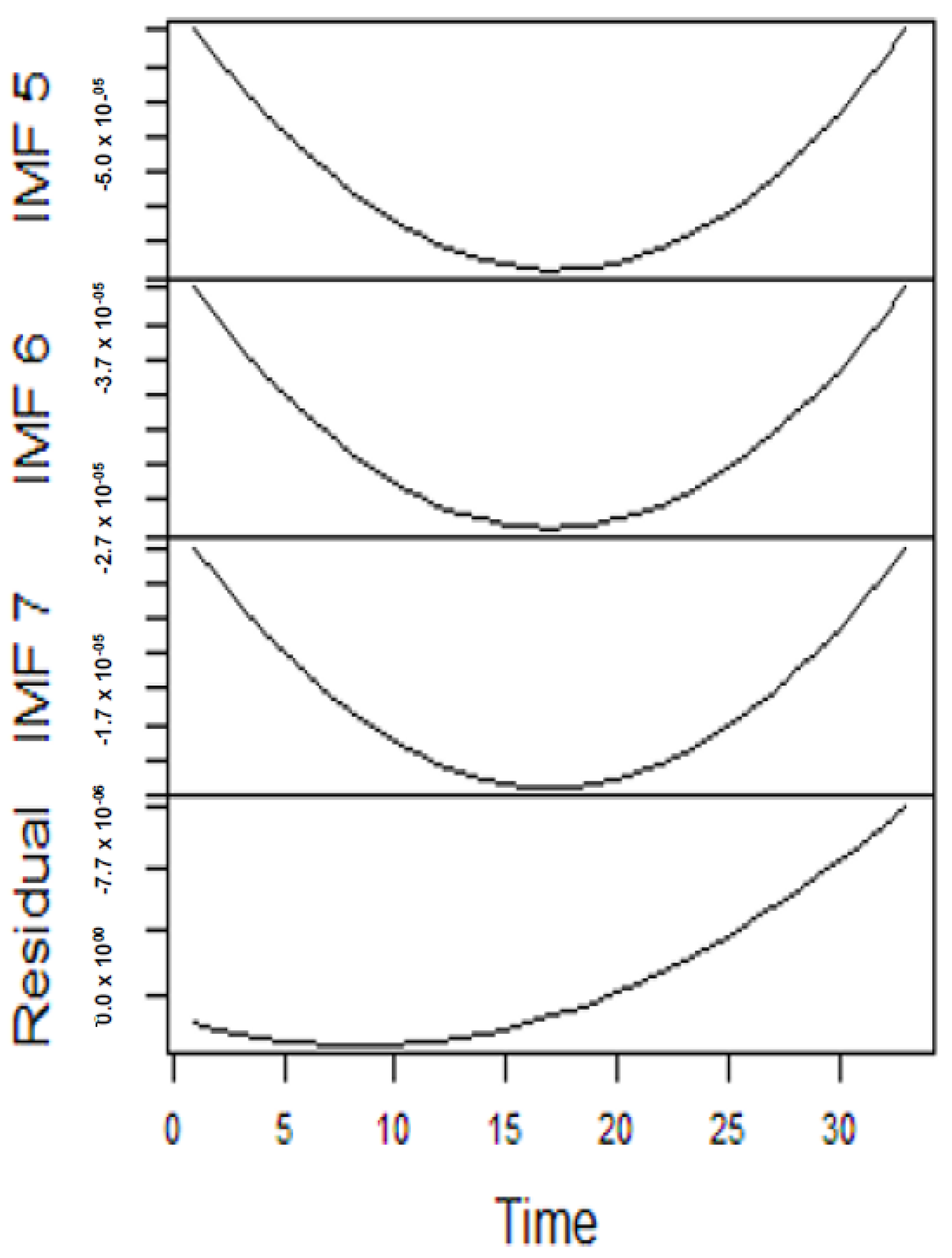
From the lenses of the sifting process, we obtain 7 IMFs in addition to one residual for all the energy price series. It is worth noting that all the IMFs deduced ranges from the highest frequency to the lowest frequency. The residuals show a varying movement toward the long-term average. Using our research methodology, the forecast experiment conducted using the energy commodity time series data exhibit varying dynamics. After the decomposition, as illustrated, for example in
Figure 9,
Figure 10,
Figure 11 and
Figure 12 (
Figure 9 is a continuation of
Figure 10 and similarly
Figure 11 is again continuation of
Figure 12. We split the diagrams for clarity of the graphical display, which depicts the IMFs and the residuals produced), the ELM coupled with the iterated strategy is used to forecast the extracted IMFs and the remaining components. In consequence, the prediction outcome of a 12-month horizon is considered for all the energy commodity series among the decomposition-based extreme learning machines in relation to the benchmark model. For each scenario, we separate the data into two parts, which are the training and the test data set. Specifically, for the first scenario, which depicts the pre-COVID period, we consider January 2005 to December 2018 as in-sample data and January 2019 to December 2019 as the out-of-sample data. Shifting the aforementioned dataset over 12 months leads to the second scenario, which has January 2005 to December 2019 as the in-sample data, and January 2020 to December 2020 as the out of sample data with the specific purpose of comparing normal times, indicative of the non-COVID period and the COVID-period itself.
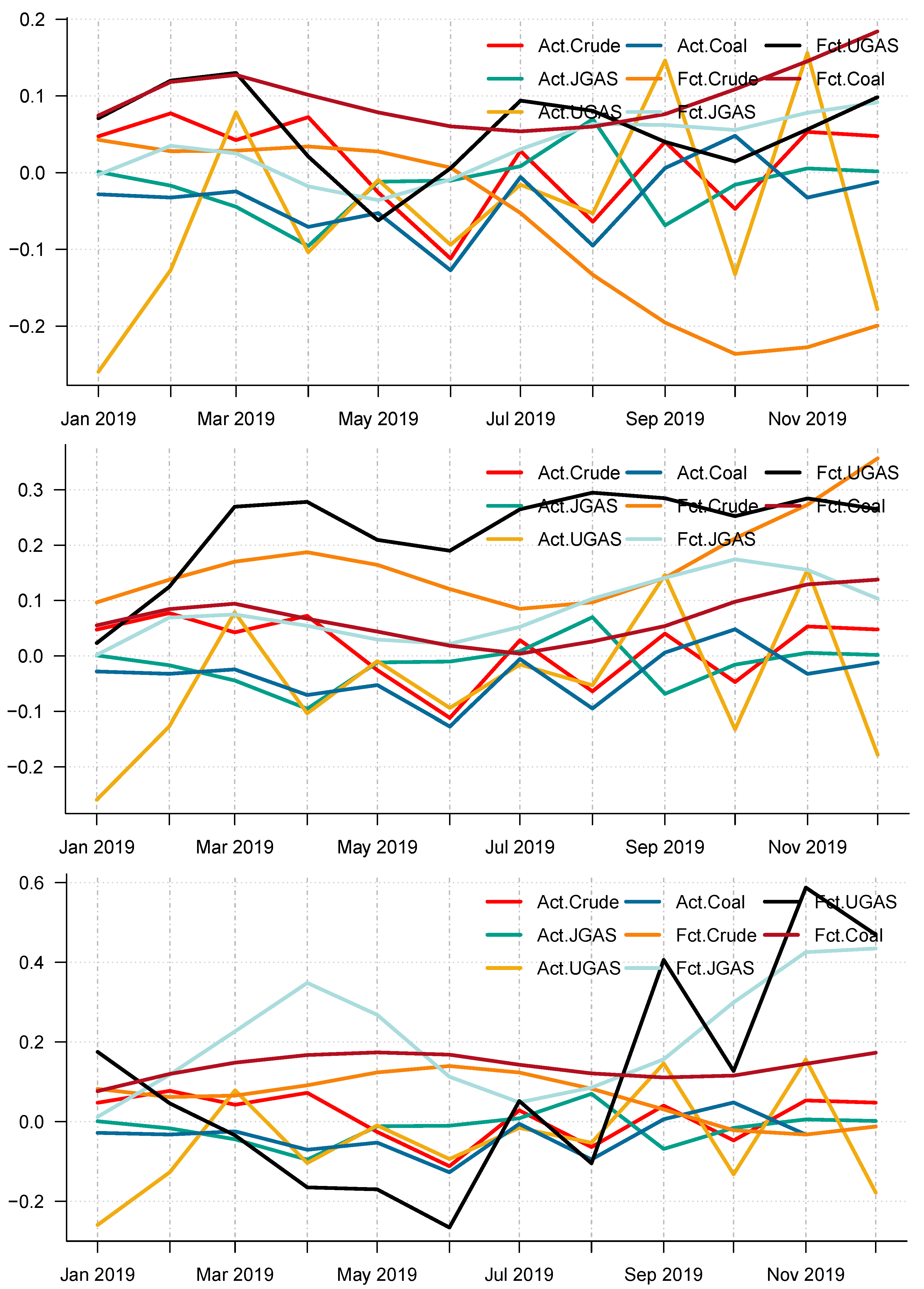
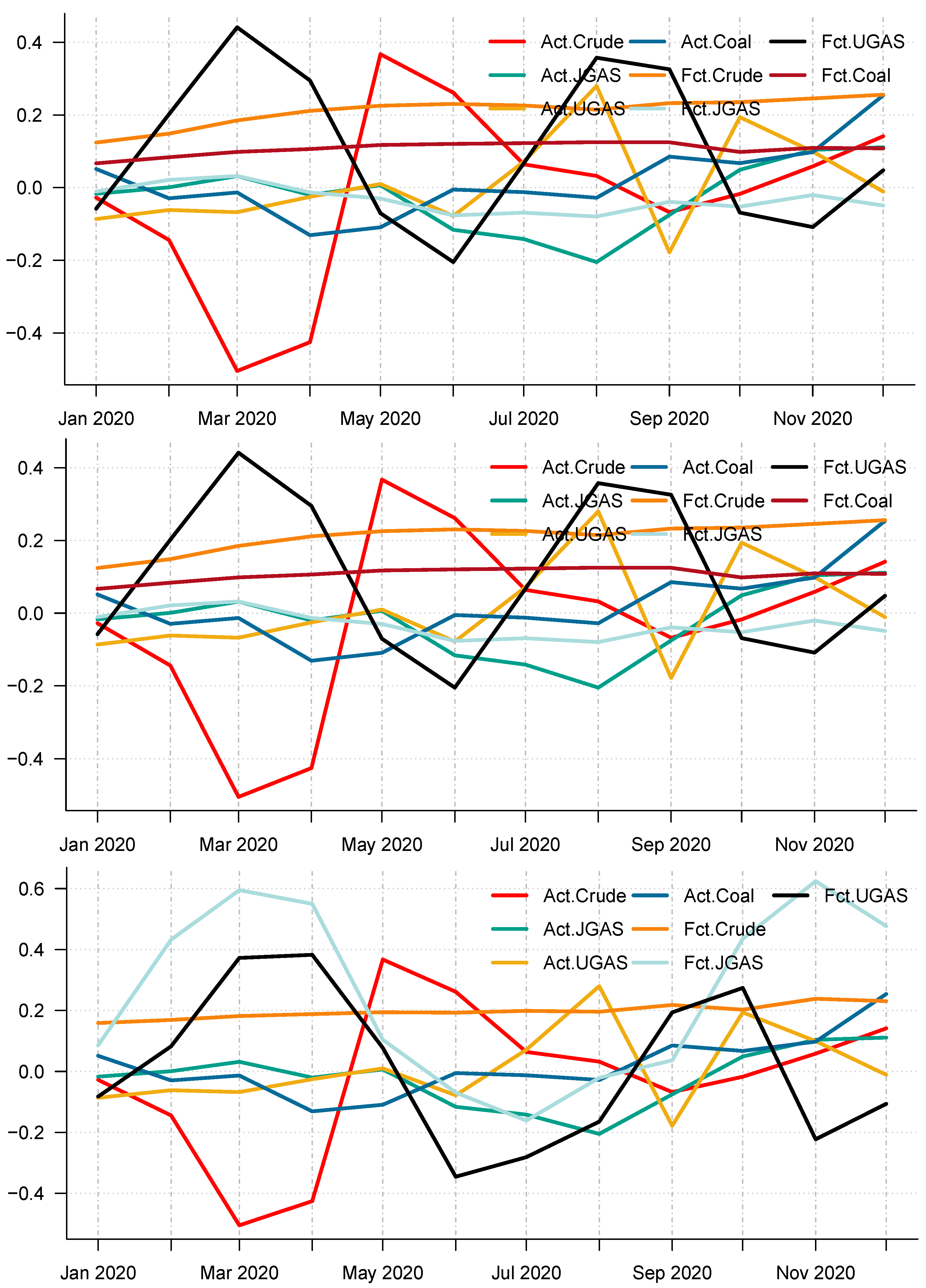
Moreover, using the different accuracy forecast measures, it is obvious that CEEMDAN-ELM is best suitable for forecasting UGAS in the pre-crisis periods based on model-specific forecasting measures, which can be inferred from
Table 4 with the combined forecast final values for all the IMFs reported in Panel A of
Figure 13. However, this is not the case during the COVID-19 outbreak. The CEEMDAN-ELM provides the best forecast for Coal instead in this period. On the other hand, the EEMD-ELM provides an accurate forecast for JGAS in the pre-COVID-19 era whereas the crude oil is the best forecast using the EMD-ELM based on all the three forecasts accuracy measures. One interesting observation is that coal, crude oil, and JGAS strives with EEMD-ELM and appears to be useful for forecasting purposes during the crisis period. Unlike the normal era, which is the period before the COVID-19, coal could not survive the test for EMD-ELM during the stressful periods, which is in our case; the COVID-19 dispensation. All in all, it is evident that EEMD-ELM exhibit some degree of resilience in providing an accurate forecast in both paradigms. The plot of the actual series and the forecast series also reveals the dynamics of the predictions of the different modeling frameworks See
Figure 13 and
Figure 14 for an overview.
Figure 13 and
Figure 14 display the forecast of the various models. In effect, a complete overview of the two eras shows that the models utilized are capable of capturing various dynamics in the data. On the whole, we consider a 12-month forecast horizon for the two scenarios under consideration. The scenarios described above are observed based solely on the decomposition-based extreme learning machine models. However, the above dynamics changed with the introduction of a benchmark model; namely the autoregressive integrated moving average model (ARIMA). The complete model framework is depicted in ARIMA (
), where
p is the order of the autoregressive part,
d, represents the number of differencing required to make the time series stationary, and
q depicts the order of the moving average part.
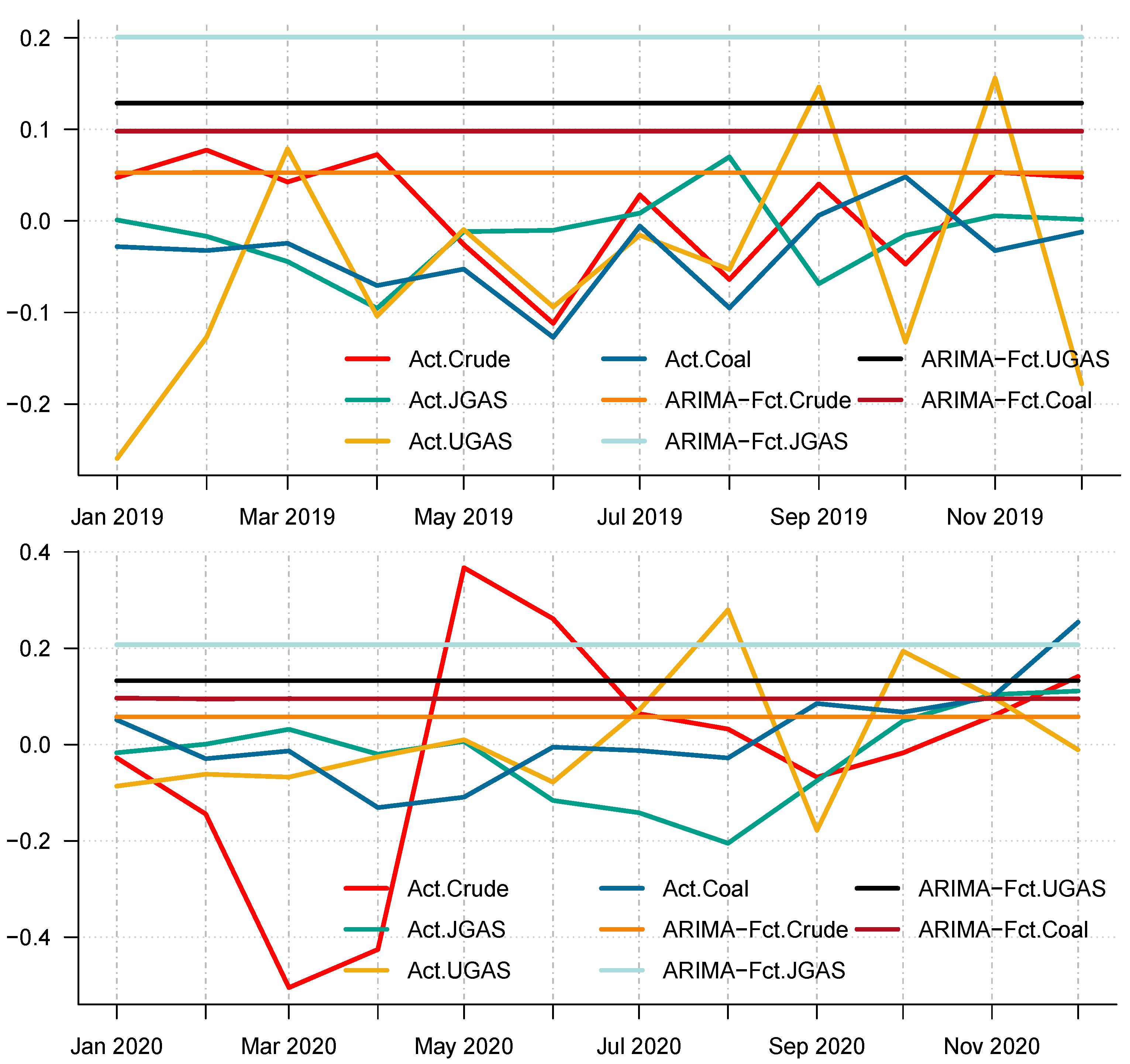
In particular, we employ the autoregressive integrated moving average, which is a commonly used technique to fit most time series data and for forecasting purposes. After all the necessary checks and balances in terms of the autocorrelation function (ACF) and the partial autocorrelation function (PACF), the series shows that AR (1) is appropriate to use on the energy commodity time series data because the ACF tail off and the PACF cuts in the first lag. As such, we apply the ARIMA (1,1,0) to model the energy commodity price changes, whose forecasts could be observed in the different panels of
Figure 13 and
Figure 14. Surprisingly, comparing the benchmark model with the decomposition-based extreme learning machine models based on model-specific forecast error measures (i.e. minimum values of ARIMA-MAE and ARIMA-RMSE) shows that the ARIMA model outperforms the other models in favor of the JGAS and the UGAS markets in both two scenarios, which the before COVID-19 and during COVID-19 periods.
Furthermore, to check the superiority of our modeling framework, this paper utilizes the model confidence set (MCS) pioneered by [
40] to select a set of superior models in the scenarios under consideration (A package in R to evaluate the MCS has been written by [
40]). A MCS is a representation of the construction of a set of models such that it selects only the best models with a given level of confidence. The MCS accommodates various limitations of the data, in which case, if the data is not informative, it yields an MCS with many models. Otherwise, if it is informative enough, it yields an MCS with only a few models. It is worth noting that the MCS method does not assume that a particular model is the true model and therefore can be applied without loss of generalization. We, therefore, apply the MCS to our models including the benchmark model. One characterization of the MCS is that a model is discarded only if it is found to be significantly inferior to another model. A competitive advantage of the MCS in comparison with other selection procedures is that the MCS acknowledges the limits to the information contained in the data. In effect, the MCS procedure yields a set of models that summarizes key sample information. The differences in the forecasting performances of all these approaches have been compared and tested by means of the MCS. The details of the outcome of the MCS evaluation is reported for the two scenarios in
Table 6 and
Table 7 respectively. Some important results emerge. Based on each commodity, we have rankings that depict the model that performs best. For example, in 2019, CEEMDAN-ELM favors crude oil, JGAS, and UGAS only, whilst the MCS captures UGAS and Coal for EEMD-ELM. These dynamics, however, changed in 2020 with EMD-ELM featuring in the MCS for all the commodities, except Coal, which resulted in CEEMDAN-ELM after the MCS evaluation. One unique observation based on the MCS is that all the decomposition-based extreme learning machine framework is captured by the MCS in favor of UGAS. Nonetheless, it is worth noting that the ARIMA is completely absent from the MCS, which already shows that the decomposition-based extreme learning machines outperform the ARIMA modeling framework. In this case, the decomposition-based extreme learning machine models appear to be the more superior models. The inferiority of the benchmark is due to the fact that it cannot capture the non-linearity (see
Figure 15 for a reference) as compared to the other three models, which are the CEEMDAN-ELM, EEMD-ELM, and the EMD-ELM models that exhibit various non-linear dynamics. This is evident in the pre-COVID-19 era as well as during the COVID-19 dispensation.
An alternative to the MCS is the possibility of using a statistical test that distinguishes between the predictive accuracy of two sets of forecasts. This is based on the principles of the Kolmogorov-Smirnov (KS) test, which is referred to as the KS Predictive Accuracy (KSPA) test. As indicated by [
41], a small number of observations result in an accurate KSPA test establishing a statistically significant difference between the forecasts. The KSPA test comes along with another competitive advantage in that it can compare the empirical cumulative distribution function of the errors from two forecasting models because of the nature of these computations. On the other hand, it is non-parametric, which implies that it makes no assumption based on the characterizations of the underlying errors. In a similar viewpoint, since our forecast horizon is 12-months, employing the KSPA test resulted in a statistically significant difference between the pairwise comparisons. However, in a multi-commodity framework, these comparisons become a daunting task as pointed out by [
41], hence we propose that the MCS might be a suitable choice in this sense. Nonetheless, with some extensions of the KSPA to a multivariate fashion, it might be an ideal choice for these types of analysis. As an illustration,
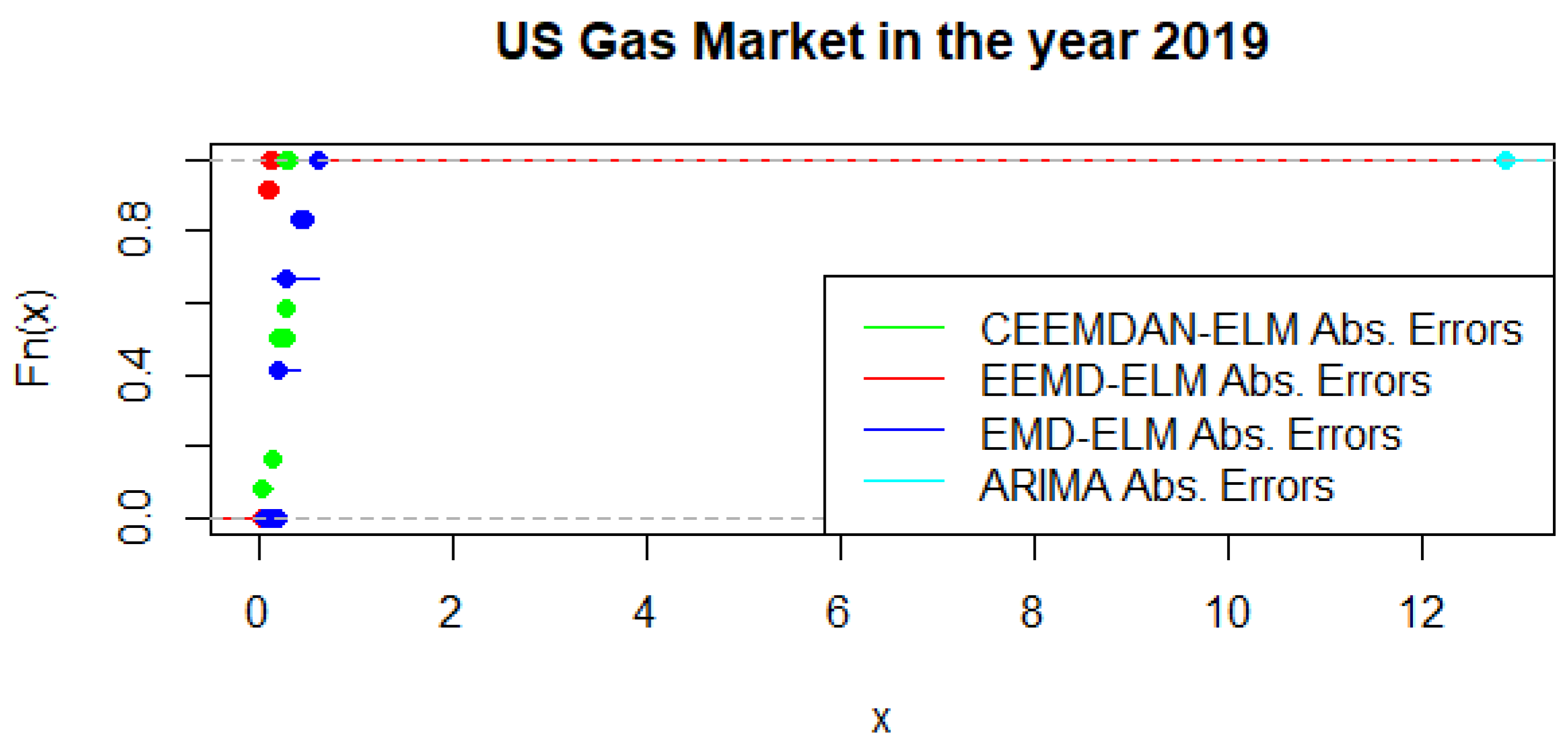
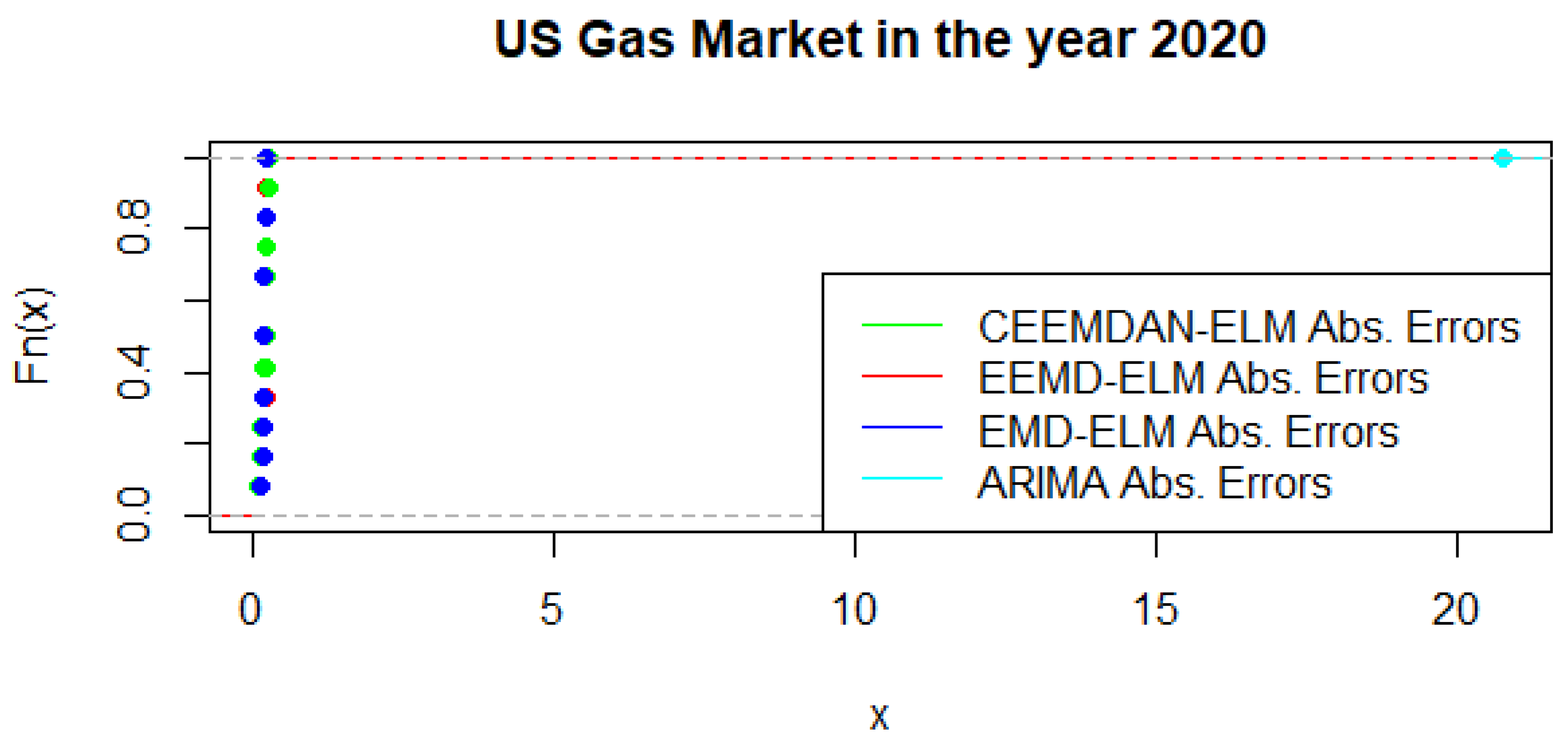
Figure 16 present a graphical display of the cumulative distribution function of UGAS forecast errors, which shows various variation among the different modeling framework. CEEMDAN-ELM followed by EEMD-ELM represent better random variations in the sense that the smaller the error deviation the better the forecast accuracy; a result which is not far from the relative accomplishment of the MCS comparatively. Nonetheless, a slight variation could be observed in the US gas market in 2020 as displayed in
Figure 17. This is evident between EMD-ELM and EEMD-ELM as well as between CEEMDAN-ELM and EEMD-ELM errors. However, the ARIMA errors exhibit the largest variations in 2019 and 2020.