Estimating Path Choice Models through Floating Car Data

Abstract

The path choice models play a key role in transportation engineering, especially when coupled with an assignment procedure allowing link flows to be obtained. Their implementation could be complex and resource-consuming. In particular, such a task consists of several stages, including (1) the collection of a large set of data from surveys to infer users’ path choices and (2) the definition of a model able to reproduce users’ choice behaviors. Nowadays, stage (1) can be improved using floating car data (FCD), which allow one to obtain a reliable dataset of paths. In relation to stage (2), different structures of models are available; however, a compromise has to be found between the model’s ability to reproduce the observed paths (including the ability to forecast the future path choices) and its applicability in real contexts (in addition to guaranteeing the robustness of the assignment procedure). Therefore, the aim of this paper is to explore the opportunities offered by FCD to calibrate a path/route choice model to be included in a general procedure for scenario assessment. The proposed methodology is applied to passenger and freight transport case studies. Significant results are obtained showing the opportunities offered by FCD in supporting path choice simulation. Moreover, the characteristics of the model make it easily applicable and exportable to other contexts.

1. Introduction

In the last few years, in Europe, passengers and freight transport have increased: in 2019, approximately 83% of passengers moved by car and approximately 77% of freight was transported by road [1]. A similar trend can be observed in Italy, where passenger road transport represents approximately 81% of the sector [1] while freight road transport represents around 62% [2]. The European Commission has adopted some policies to make the transport field more sustainable [3], and then new scenarios were promoted, which need to be assessed in order to evaluate the effects on the transport system ([4,5,6]).

The simulation of a transport system requires one to solve an assignment problem deriving from the interaction between demand and supply [7]. In this task, the path/route choice models play a key role, evaluating the route chosen by users in relation to the perceived utility (generalized travel cost) and consequently influencing the road network load. It is also for this reason that research in route choice models is a topic that is extensively discussed in the literature, to try to develop models that make it possible to reproduce the choices made by users. In general, to capture the user perception in path/route choice, the problem is often tackled by considering first the choice set generation (containing the routes perceived by the user) and then route choice among the routes belonging to the choice set [8]. This requires a database that compiles the users’ route choice preferences; traditionally, a survey is designed to collect the desired data, with a high cost in terms of time and resources and, often, the number of interviews is low and unreliable. However, nowadays, the availability of floating car data (FCD) allows us to collect the data in a different way and, in the case of routes, make available some data (e.g., speed, stop time) that are difficult to collect using traditional surveys. Furthermore, it is possible to ensure the certainty of the routes followed by users (which can be visualized on a map).

Thus, the aim of this paper is to explore the opportunities offered by FCD to calibrate a path/route choice model to be included in a general procedure for scenario assessment.

The rest of the paper is structured as follows. Section 2 presents a literature review on route choice models. Section 3 reports the proposed method, by describing a general procedure for scenario assessment and the approach for route choice simulation. In Section 4, the results of the proposed procedure for model calibration are reported. Finally, Section 5 discusses the results obtained in terms of policy indications, while Section 6 draws conclusions and considers the road ahead.

2. Literature Review

Several approaches have been developed over the years for route choice ([9,10]), which can be classified into three main groups: random utility models (RUMs), fuzzy utility models (FUMs), and quantum utility models (QUMs).

Focusing on RUMs, two further aspects can be considered: models with (e.g., multinomial logit) or without (e.g., Probit and Gammit) a closed form for calculating choice probabilities. The RUMs are among the most used models, because of their analytical tractability. Regarding logit models [11], a weakness that must be underlined is the assumption that the random residuals are independently and identically distributed (IIA property) as Gumbel random variables with zero mean [7]. This implies the impossibility of considering the similarities between different routes [9]. To overcome the drawbacks of multinomial logit, several types of models have been proposed [12]. Cascetta et al. [13] proposed a modification in the utility function by introducing a commonality factor (C-Logit) able to measure the overlap among the paths and reduce the utility of similar routes. Similarly, Ben-Akiva and Bierlaire [14] proposed the path size logit; in this case, a correction term was also introduced in the utility function. The cross nested logit ([15,16]) was also used in route choice simulation, the basic assumption being that the nests coincide with the road network links. The idea behind the paired combinatorial logit ([15,16]) is that the routes are chosen by considering them as pairs; the route choice probability is the product between the probability to choose a pair and the probability to choose the route within the pair. Another way to overcome the IIA while maintaining the closed form in probability calculation is to assume a distribution for random residuals that differs from Gumbel. Castillo et al. [17] introduced the Weibit model by assuming that the random residuals are distributed as Weibull variables. In contrast to the case of logit, in the Weibit model, the variance is a function of the route cost, and this means that the route costs are independent. However, as with logit, the Weibit model does not consider the route overlapping; thus, some authors [18] developed C-Weibit by defining a commonality factor that reduces the utility of similar routes. An alternative approach is to eliminate the calculation of the probability in closed form and use a Probit [19] or a Gammit model [20] (these models consider a covariance among routes).

The FUMs were introduced in route choice simulation to consider the uncertainty in the choice by the users [21]. These models can be classified into two main groups [22]: models based on fuzzy rules (e.g., [21,23]) and models based on assuming the path cost as the core of a fuzzy number (e.g., [24,25]). Peeta and Yu [26] used fuzzy rules to simulate the en-route driver behavior under real-time information. Arslan and Khisty [27] proposed a heuristic approach by using a set of rules able to represent the decision-making process to estimate the preference among the available routes. A choice function based on fuzzy preference was proposed by Ridwan [28] that also considers the case in which the users do not maximize their utility in route choice. The approach was tested in a traffic assignment framework. Binetti et al. [29] proposed an approach where the imprecision in route cost perception was modeled by means of some parameters for cost definition and route classification (considering, in addition, the overlapping among different paths). A comparison between FUMs and RUMs is reported in [30], where the route choice model is defined as a three-level model (route generation, route perception, and route choice). Hawas [31] developed an approach to route choice simulation to capture the user’s capability to perceive the route attributes and their variability. An analysis on the effects given by the implementation of different route choice models based on random utility theory (logit, Probit, Weibit, and Gammit) is reported in [32].

The QUMs were recently applied in route choice simulation. The main idea is to introduce an interference term that is added to the covariance. Vitetta [33] uses this model to simulate different levels of perception of the users in the case in which pre-trip choices are possible. The role of the interference term in route choice is further examined in Di Gangi and Vitetta [34,35], where the route choice model is embedded inside an assignment algorithm.

For calibration, the previous models require a set of data [7], which requires the design and implementation of a highly resource-consuming survey [36]. Recent approaches exploit the floating car data (FCD), particularly global positioning system (GPS) data, to calibrate the route choice models [37,38,39]. The FCD allows one to evaluate the route choice (e.g., whether the observed route is the shortest route) [40,41] and, in some studies, it is used to investigate the traveler’s behavior [42,43,44]. The use of FCD was also applied to other classes of users, such as taxi drivers [45], pedestrians [46], and bicyclists [47]. Some preliminary steps may be required to use this type of data. For example, Marchal et al. [48] and Bierlaire et al. [49] proposed a map matching algorithm to identify the routes followed by users. The same problem is tackled in Du and Aultman-Hall [50] and in Chung and Shalaby [51], which proposed some algorithms able to identify the routes and their origin and destination.

Some authors in the literature proposed the calibration of route choice models by using floating car data. While not exhaustive, below, some papers grouped by the type of model calibrated are recalled. Bwambale and Choudhury [52] proposed a method for analyzing the users’ route choice starting from phone tracking data and calibrated some models based on the logit structure (multinomial, C-Logit, and path size). Freijinger and Bierlaire [53] and Montini et al. [54] calibrated a path size logit model by using GPS data relying on travel in an urban area. Similarly, Dhakar and Srinivasan [55] calibrated a path size logit model from GPS data and considered different cases obtained by varying the size of the choice set. Duncan et al. [56] and Hess et al. [57] proposed some modifications in the path size logit model and evaluated them by using GPS data. Sobhani et al. [58] adapted C-Logit to simulate the route choices of bicyclists, while Huang et al. [59] developed a procedure for identifying routes through cell tower IDs.

The above literature review shows that a large amount of work has been carried out in path choice modeling; however, further work needs to be performed in this field, especially when data need to be collected for calibration. Given the desirability of a calibration procedure that uses large and easy-to-obtain data, this paper presents a calibration procedure that uses FCD.

3. Proposed Method

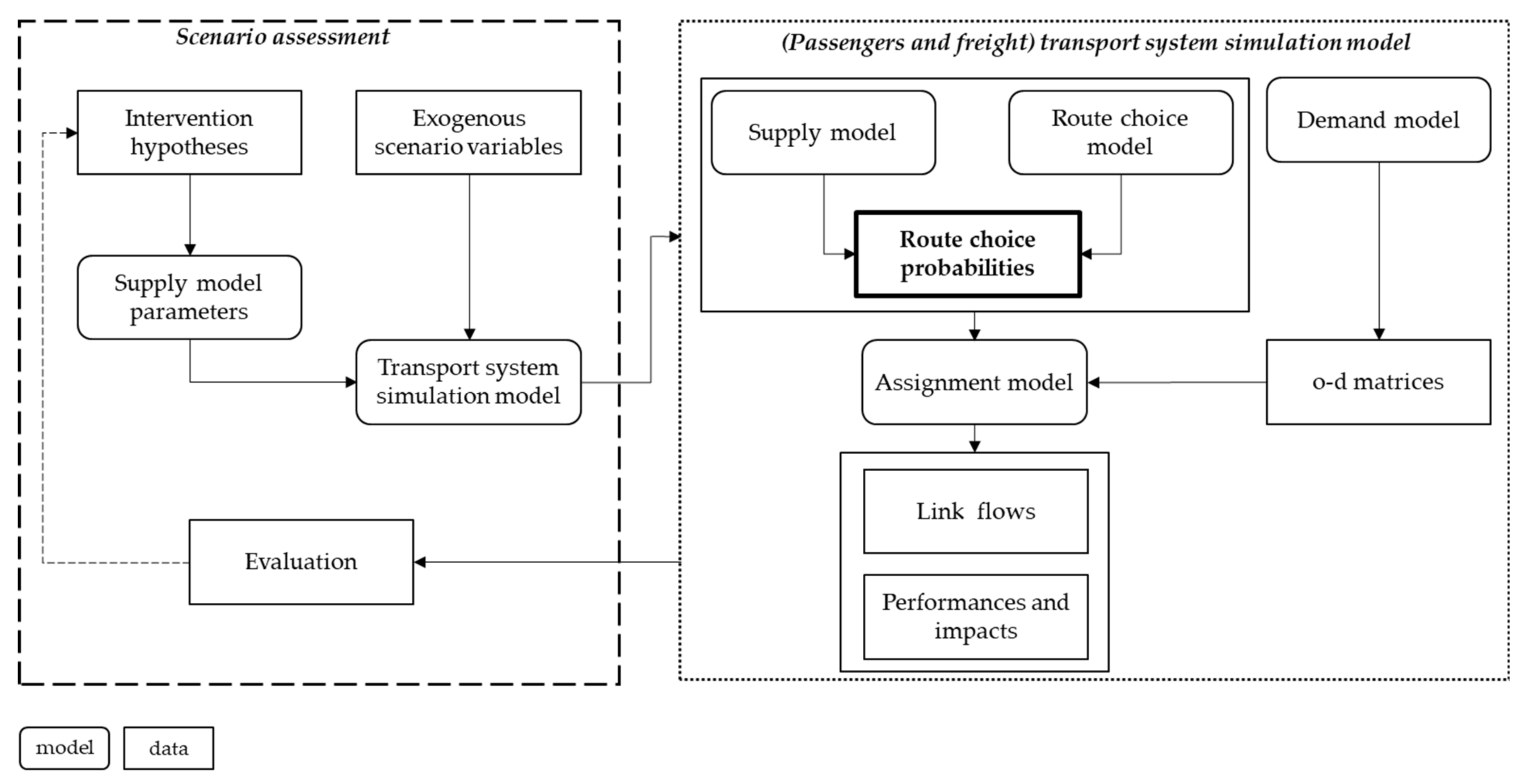
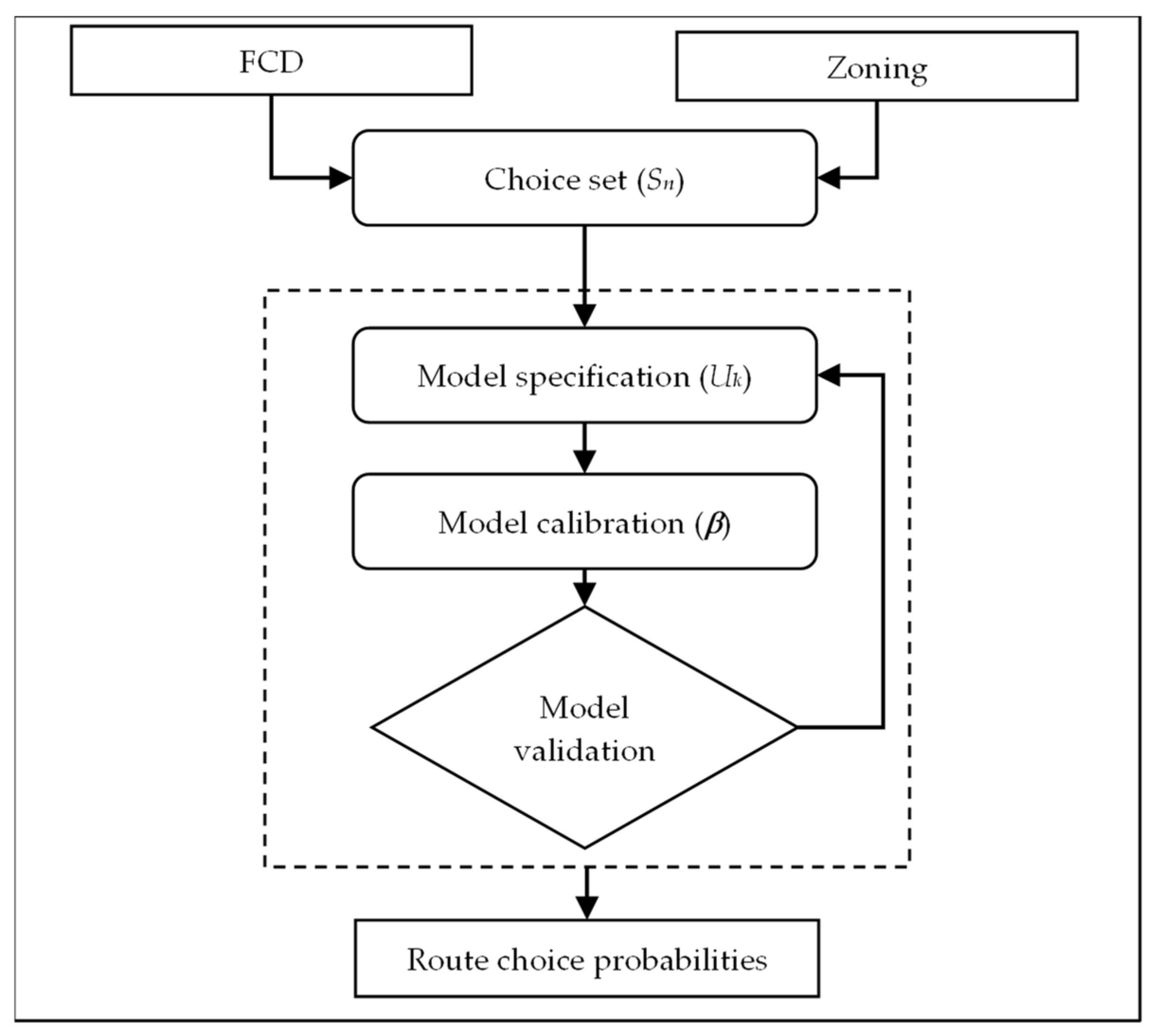
3.1. General Procedure

A general procedure for scenario assessment should be applied when, because of some interventions, a transport system is subject to modifications. In the schematic approach reported in Figure 1, a set of intervention hypotheses cause changes in the transport system: in the simulation, this means a change in the supply model parameters that are the input for the transport simulation model. Moreover, some exogenous scenario variables (in general, context-dependent variables) can be considered as the input of the simulation model. The transport simulation model (for freight and passengers) requires a demand model and a supply model accompanied by a route choice model: in the specific case treated in this paper, the demand model allows one to obtain the o-d matrices for passengers and freight, while the combination between the supply model and the route choice model (see Section 3.2) gives as output the route choice probabilities. Then, the assignment model gives as output the link flows. This allows one to calculate the performance and impacts of the scenario and their evaluation allows (if it is the case) us to modify the initial hypotheses.

3.2. Route Choice Probabilities

Focusing on the route choice probabilities, one possible procedure to evaluate them starting from FCD is reported in Figure 2. The inputs are the FCD and the zoning of the study area. They allow us to individuate the choice set (the assumption is that the choice set is constituted by all observed routes in a considerable and long time period) for each origin–destination pair (indicated with n in Figure 2) and for each type of vehicle. This procedure has the advantage that by explicitly specifying the set of available routes, we can examine actual used paths and reduce the computational time by not generating unrealistic routes. The set of routes followed by users is the output of a matching procedure, able to associate the GPS points with the road links. Figure 3a reports an example of matching among GPS points and road links: only the points within a buffer around the link are considered in the route analysis. This approach, suitable for extra-urban travel, must be improved in the urban case, where the graph density makes it unreliable. Another issue to solve is related to the origin–destination of the routes. According to the scope of this research (e.g., to avoid the case in which the route/path investigated differs from the starting and/or ending links due to different real starting/ending locations, albeit belonging to the same traffic zone), for each origin–destination pair, close locations were considered. Moreover, the vehicle travel time was obtained by comparing the arrival time and the departure time of each vehicle, obtained via the timestamps associated with each GPS datum. The route travel time was the average value, calculated on the basis of investigated vehicle trips and paying the due to attention to possible outliers.

With a finite, known choice set, we can apply theoretically based corrections for route overlapping, if needed. As shown in [60], the first step in route choice simulation is the definition of the choice set S_n. Considering all the available routes between an origin and a destination, they can be grouped into subsets (I_n) referring to a specific criterion (e.g., travel time, travel distance). Two different cases can arise: only one subset (mono-set approach) or more than one subset (multi-set approach). In both situations, an exhaustive or a selective approach can be used to select the routes to place in the subset(s). The former considers all the available routes, and the latter considers only the routes that respect some rules. With each choice set, we associate a probability (equal to one in the case of the mono-set approach) that represents the probability that the user considers it in his/her choice. Once the choice set has been identified, the probability of each element (route) in the choice set can be calculated. Following Manski [8] and Quattrone and Vitetta [25], the probability of choosing a route k can be evaluated as:

$$p[k/S_n]={\displaystyle \sum _{I_n\in S_n}{p}_n[I_n/S_n]}\cdot p_n[k/I_n]\hspace{1em}\hspace{1em}{S}_n\ne \varnothing$$

where:

• p_n(I_n/S_n) is the conditioned probability to choose the subset I_n belonging to S_n;
• p_n(k/I_n) is the conditioned probability to choose the route k belonging to I_n.

The next step is the model specification (i.e., the definition of the functional form of the model) by considering the available attributes for path k (X_k). This refers to the definition, for each route k, of the utility U_k. Considering the random utility theory, the user associates with each route k a perceived utility U_k as follows:

U_k = V_k + ε_k

where:

• V_k is the systematic utility;
• ε_k is the random residual.

The type of RUM used depends on the probability distribution of ε_k. In this paper, the focus is on multinomial logit (MNL). The use of this model is due to different considerations. First, although there are more precise models (such as C-Logit or path size) that allow us to better reproduce the route choice made by users, none of them are considered sufficiently valid for the assignment [61], which is a relevant element in scenario assessment. Second, the dataset used from calibration relies on the travel of vehicles (heavy goods vehicles and private cars) at a regional level and, in most observed cases, the overlapping among different routes is low. This implies that the i.i.d. property of multinomial logit can be considered valid (no covariance between alternative routes).

Defining the systematic utility as [7]

V_k = ^Tβ X_k,

and assuming I_n = S_n, the route choice probability will be

$$p[k/I_n]=\frac{\exp (V_k)}{{\displaystyle \sum _{h\in I_n}\exp (V_h)}}$$

The model calibration allows the parameter vector β associated with the attributes to be estimated. The method used for calibration is the maximum likelihood (ML). Calibration of the coefficients occurs through the maximization of natural logarithm of the likelihood function, formed by the sum of the natural logarithm of the probability of the chosen alternative (k’) of each user i:

$$\ln L\left(\beta ,\theta \right)={\displaystyle \sum _i\ln p^i\left[k\prime /I_n\right]}$$

The last step in model calibration is the model validation, to establish the model’s capability to reproduce the observed choices. The choice model is the output of a loop procedure where the specification, calibration, and validation are repeated until a good model (a model whose parameters have passed validation) is obtained.

4. Results

This section reports an application where a route choice model is estimated by using a set of floating car data in two different case studies and two different study areas: case study 1 relies considers the travels of a sample of goods freight vehicles (laden weight greater than 18 tons) and the study area is the Veneto region (Northern Italy), while case study 2 considers the travels of a sample of cars and the study area is the Lazio region (Central Italy). In Section 4.1, we provide a brief presentation of the available data in relation to the study area, while, in Section 4.2, the developed models are reported.

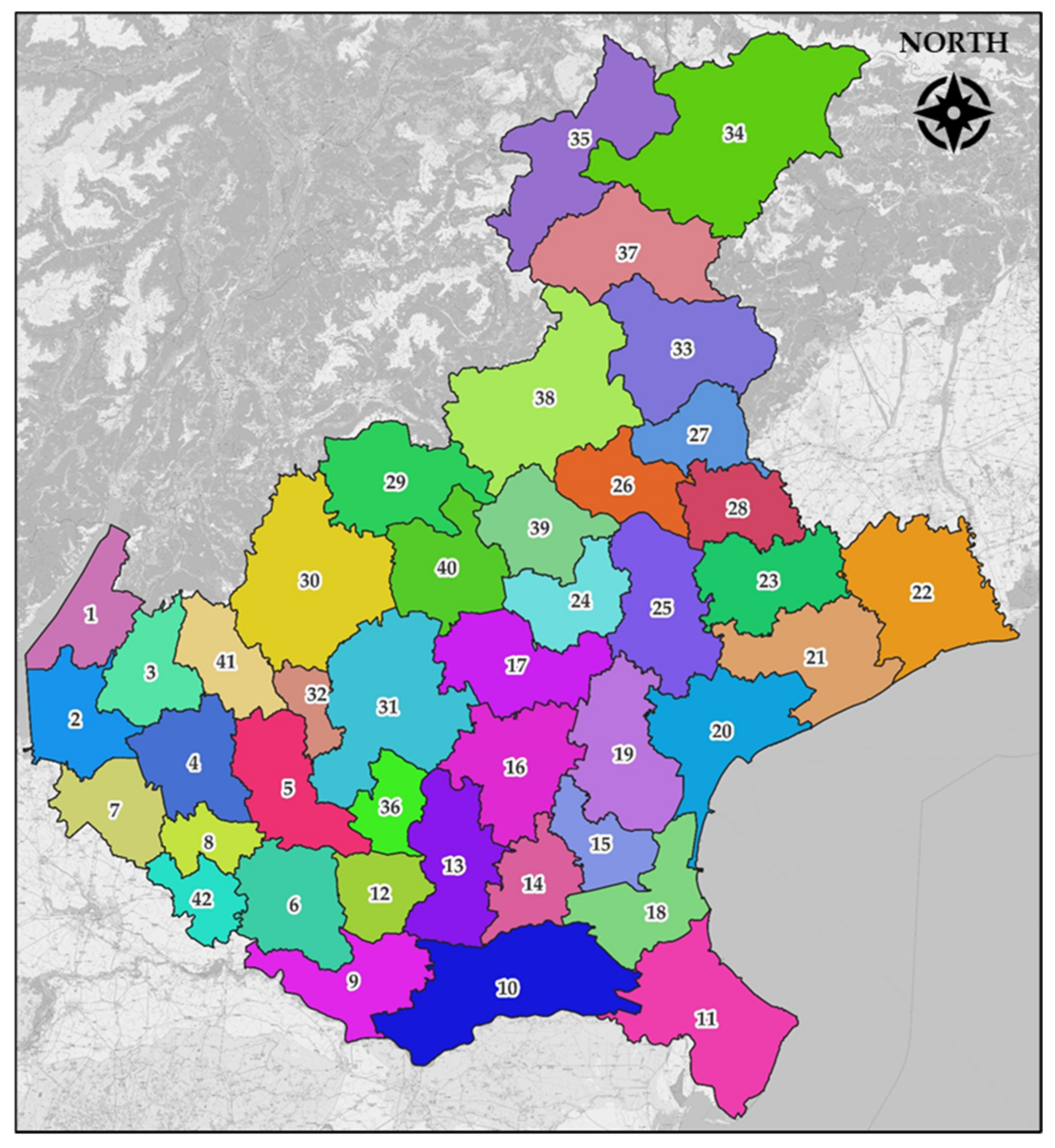
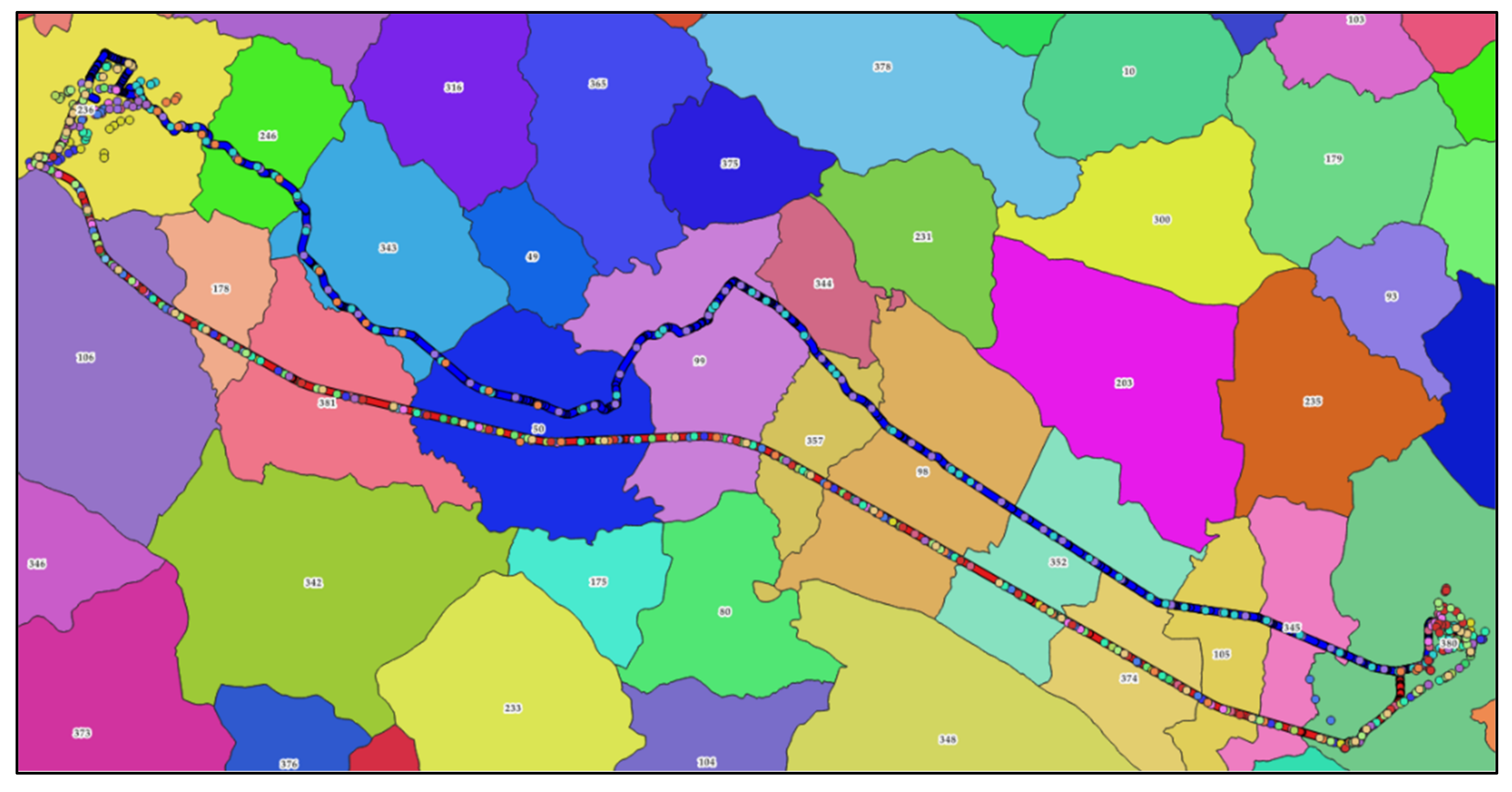
4.1. Study Areas and Available Data

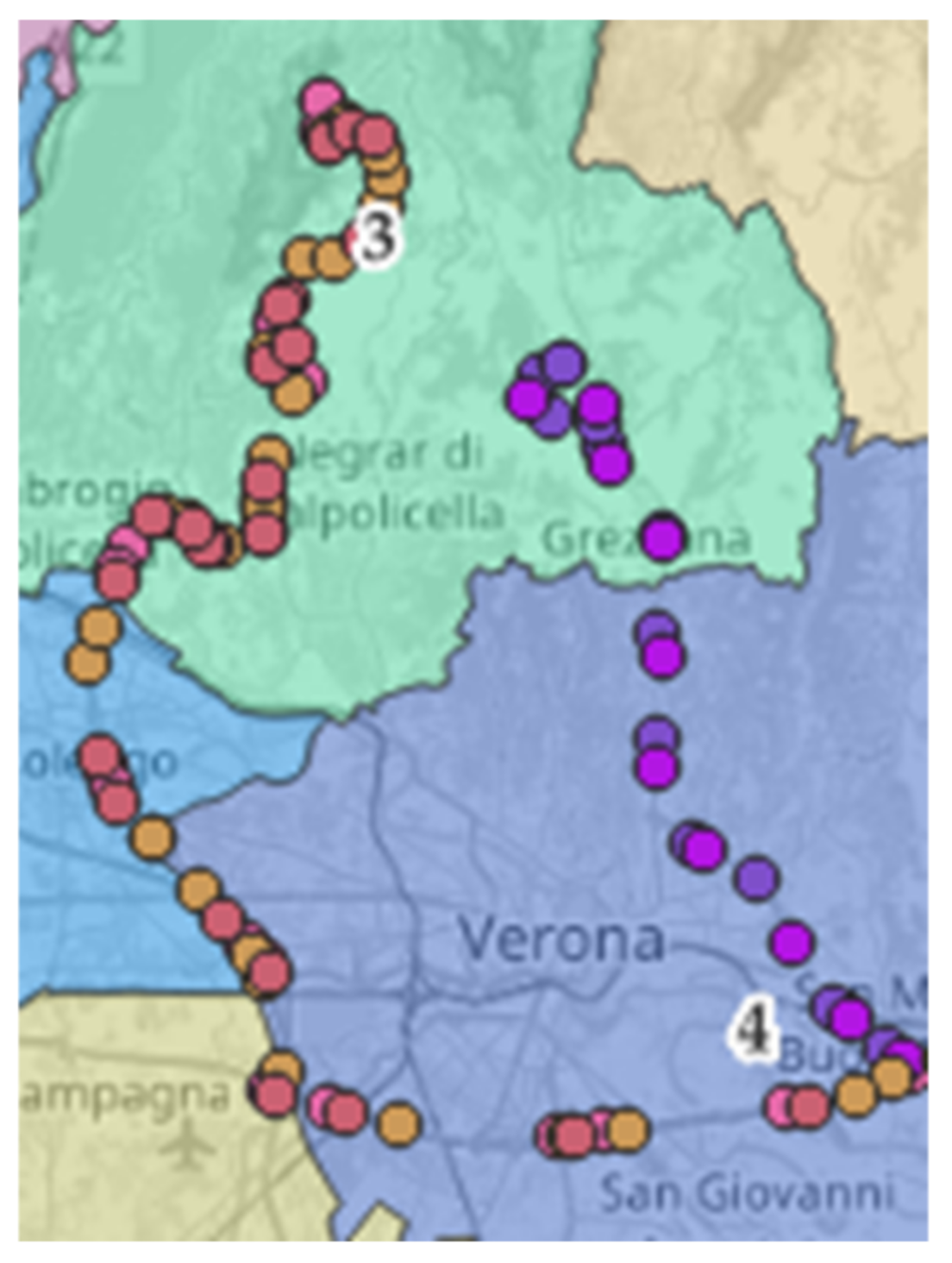
4.1.1. Case Study 1: Veneto Region

This case study considers the calibration of a route choice model for freight vehicles, considering as the study area the Veneto region. This Italian region has an area of approximately 18,400 square kilometers, with around 5 million inhabitants and around 2.1 million of employees. The study area consists of seven administrative zones and, for the purpose of this work, was divided into 42 traffic zones (Figure 4). Some data on the movements of heavy goods vehicles operating in the Veneto region were analyzed to identify the route followed for each origin–destination pair. The database [62] consists of sixty working-day observations, spread over six months (from January 2018 to June 2018). For each surveyed vehicle, basic information on the vehicle (class, brand, model, gross weight) is available. All trips undertaken can be identified by date (i.e., date and time are logged) and geographical location (i.e., latitude and longitude). In total, 5330 vehicles were analyzed, for a total of 9,071,331 trips in the observation period. The analysis of the trips allows the identification of the origin and destination zones, and the route followed. Following the travel pattern definition (as in [63,64]), the trips of the heavy goods vehicles in the sample can be assigned to the case of single direct travel (i.e., if the same vehicle performs more than one trip in the same day, each trip is independent of the previous one and does not influence the next one).

To calibrate the route choice model, since the objective was to establish a model at a regional level, all trips with a length greater than 50 km were selected. In the case of freight vehicles, the database consisted of 59,226 trips performed by 3618 heavy goods vehicles.

Figure 5 shows an example of routes from origin 3 and destination 4. Note that the number of vehicles following the same route can be more than one.

4.1.2. Case Study 2: Lazio Region

This case study considers the calibration of a route choice model for cars, considering as the study area the Lazio region. This Italian region has an area of approximately 17,240 square kilometers, around 5.7 million inhabitants, and around 2.3 million employees. The study area consists of five administrative zones and, for the purpose of this work, was divided into 456 traffic zones (Figure 6). The database consists of five working-day observations in February 2017. For each surveyed vehicle, basic information on the vehicle (class, brand, model) is available, similarly to the freight vehicles. In total, 49,105 vehicles were analyzed for a total of 231,958 trips in the investigation period.

Figure 7 reports an example of two different routes from origin 380 and destination 236, followed by different cars.

4.2. Models

A route choice model (Section 2) requires the individuation of the choice set: this task should be carried out by defining a set of criteria [23] and then finding the routes for each criterion. The use of floating car data can help to simplify this aspect: the assumption is that the choice set is constituted by all the observed routes followed by the vehicles in the sample. Moreover, in choice set formation, the mono-set approach is used.

Aiming to develop an easy-to-apply route choice model, the attributes used in the utility specification were those that would be available to any technician and were the most relevant, as shown by the literature review in Section 2: the travel time (t_k), the toll costs (c_k), and the percentage of the route on the highway (h_k). Then, the systematic utility is

Vⁱ_k = βⁱ₁∙t_k + βⁱ₂∙h_k + βⁱ₃∙c_k

where i indicates the type of vehicle (freight vehicle or car).

The calibrated parameters are reported in

Table 1. Calibrated parameters.

		β1 [1/h]	β2 [1/€]	β3 [1/€]
Heavy goods vehicles	Value	−0.744	2.133	−0.031
	t-Student	−3.51	3.70	−1.41
	ρ2 = 0.26           %-of-right = 84%
Cars	Value	−12.84		−1.345
	t-Student	−2.16		−3.35
	ρ2 = 0.39           %-of-right = 92%

. All the calibrated parameters were statistically significant and correct in signs. The value of time (VOT) for heavy goods vehicles was approximately 24 €/h (similar to the ones reported in Stinson et al. [65] and Nuzzolo et al. [66]), while the value of time for cars was approximately 10 €/h, similar to the one reported in [7]. The statistic ρ² is, in value, similar to those reported in the literature (e.g., see [13]). The %-of-right statistics revealed the good capacity of the models to reproduce the observed choices.

5. Discussion

This study approached the calibration of route choice models using floating car data. Route choice model calibration is a topic generally treated in the literature from the point of view of the functional form (e.g., multinomial logit and its variants, Probit, others), recognizing the importance of input data, obtained with ad-hoc surveys but often limited in number. The floating car data allow us to overcome this aspect, but at the cost of losing some socio-economic attributes of drivers, which can be obtained through interviews.

The results of this study deal with the problem of calibrating a route choice model for a large-scale network where the overlapping issues can be neglected. The approach of the paper was to first generate a choice set and use this choice set to estimate the model parameters. In particular, the innovation derives from the exploitation of opportunities offered by FCD (big data). According to the literature, the choice set generation method proposed falls within the class of deterministic methods. The advantage of such a method is that it can be applied for any network with existing resources. The case studies presented also show how the multinomial logit model was adapted to model route choices for a large problem, both for passengers and freight transport. This base formulation appears to have significant explanatory power regarding how travelers perceive the alternative paths in a road network.

In fact, the FCD used in this paper allowed us to estimate a route choice model for two classes of vehicles, by considering the routes’ attributes in terms of monetary costs and travel times. The analysis of the available FCD allowed us not only to obtain the route attributes, but also to simplify some tasks with respect to the case where traditional surveys were used. For example, with a traditional survey, the analyst has to reconstruct each route from the answers of the users (eventually considering the reliability of the information), while the FCD allows us to immediately visualize the followed route on a map (this also affects the evaluation of the overlap among routes, helping the analyst in the choice of the model’s functional form) and, in large-scale networks, to easily identify the road links actually used.

The results obtained in this work, certainly improvable, indicate that FCD is a useful approach for estimating route choice models, guaranteeing the feasibility of data collection and their reliability.

6. Conclusions

In this paper, route model calibration was tackled by using as input floating car data. The most used approaches in the literature for route choice calibration require a set of surveys, which can be limited both in the quantity of collected data and data reliability. Approaches using floating car data are increasing because of the ease of finding them and the accuracy of the GPS features. The data used in the calibrations proposed in this paper were related to two different study areas and to two classes of vehicles: freight vehicles and cars. In the case of freight vehicles, a database containing trips related to more than 5000 vehicles was considered. The observations (approximately 9 million trips) were distributed in the first six months of 2017. Similarly, for the car database, the data were related to approximately 49,000 cars for 232,000 trips in five days. The model calibration followed two steps: the definition of the choice set and then the evaluation of the route choice model. In relation to the choice set definition, the characteristics of floating car data allowed us to simplify the procedure: in traditional approaches, the analyst must define some criteria and make assumptions on the route choice made by users, whereas with this type of data, it was possible to assume that the choice set was constituted by all observed paths (this implies that the procedure of path generation is neglected).

The route choice models were estimated within the random utility theory, and one model for freight vehicles and one for cars was obtained. The validation of the models showed good values of statistics and reliable values of VOT.

Consequently, the objective of exploring the opportunities offered by FCD to calibrate a route choice model has been achieved as follows:

• two sets of FCD have been analyzed in order to individuate the routes followed by users and, consequently, to obtain a reasonable choice set to use in model calibration;
• two classes of route choice models have been calibrated, for cars and freight vehicles.

The proposed procedure for route choice model calibration could be used in real applications in order to reduce the workload due to traditional data collection and improve the quality of the obtained models. Of course, this is achieved at the cost of neglecting drivers’ preferences and attitudes.

Further developments could include the calibration of the models for other vehicle classes (e.g., light and medium freight vehicles) and the comparison of the results of FCD with those of traditional surveys.