Farlie–Gumbel–Morgenstern Bivariate Moment Exponential Distribution and Its Inferences Based on Concomitants of Order Statistics

Abstract

In this research, we design the Farlie–Gumbel–Morgenstern bivariate moment exponential distribution, a bivariate analogue of the moment exponential distribution, using the Farlie–Gumbel–Morgenstern approach. With the analysis of real-life data, the competitiveness of the Farlie–Gumbel–Morgenstern bivariate moment exponential distribution in comparison with the other Farlie–Gumbel–Morgenstern distributions is discussed. Based on the Farlie–Gumbel–Morgenstern bivariate moment exponential distribution, we develop the distribution theory of concomitants of order statistics and derive the best linear unbiased estimator of the parameter associated with the variable of primary interest (study variable). Evaluations are also conducted regarding the efficiency comparison of the best linear unbiased estimator relative to the respective unbiased estimator. Additionally, empirical illustrations of the best linear unbiased estimator with respect to the unbiased estimator are performed.

1. Introduction

The authors in [1] introduced the moment exponential (ME) distribution by assigning linear weights to the exponential distribution. With the scale parameter $\sigma$, the probability density function (pdf) of the ME distribution can be expressed as follows:

$$\begin{array}{c}\hfill f(x;\sigma )=\left\{\begin{array}{c}{\displaystyle \frac{x}{{\sigma }^2}{e}^{-\frac{x}{\sigma }},x>0,\sigma >0}\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(1)

The corresponding cumulative distribution function (cdf) is given by

$$F(x;\sigma )=1-\left(1+\frac{x}{\sigma }\right)e^{-\frac{x}{\sigma }},x>0,\sigma >0.$$

(2)

The moment-generating function (mgf) of the ME distribution is obtained as

$$M\left(t\right)={(1-\sigma t)}^{-2},t\ge 0.$$

(3)

Many researchers are drawn to the ME distribution, and they further study it because of its simplicity and superiority to the exponential distribution. The authors in [2] have proposed an exponentiated ME distribution and discussed its significance in detail. Different estimators for the pdf and cdf of the exponentiated ME distribution were provided in [3]. The Topp–Leone ME distribution was developed in  [4], where its competence in comparison with other well-known models in the literature is also discussed. The authors in [5] provided narration for the ME distribution’s slashed version. The authors in [6] explained the Weibull-ME distribution and its significance. Another development of the ME distribution, known as the BurrXII-ME distribution, and its properties were recently proposed in [7]. Another generalization, the alpha power ME distribution, and its applications to biomedical science, was taken into consideration in [8]. The so-called Poisson-moment exponential distribution was introduced in [9] as an alternative to the ME-distribution-based model for count data modeling. The aforementioned literature ought to demonstrate that the ME distribution is a very alluring generalization of the exponential distribution and has a wide range of applications. To our knowledge, no statistician has proposed any of the ME distribution’s bivariate versions, despite the fact that its competence has been thoroughly established in the body of existing literature. This provided us with a strong motivation to propose a bivariate version of the ME distribution utilizing the Farlie–Gumbel–Morgenstern (FGM) technique.

When conducting research on a bivariate population, two types of statistical situations commonly arise: In the former scenario, it is possible to determine the shape of the bivariate population distribution, making it easier to develop subsequent procedures for modeling and analyzing the data that result from it. In the latter scenario, since the bivariate population distribution’s shape will not be known in advance, the problems that result are complex, and modeling the parent bivariate distribution becomes obviously critical. In univariate cases, a parent distribution can be modeled using a variety of techniques. Nevertheless, one way of designing a bivariate model is to use the FGM technique if prior information is available in the form of the marginal distribution of random variables.

The authors in [10] proposed a family of bivariate distributions, called the FGM family, with a cdf of the following form:

$$H(x,y)=F\left(x\right)G\left(y\right)\{1+\xi [1-F\left(x\right)\left]\right[1-G\left(y\right)\left]\right\},$$

(4)

where $F\left(x\right)$ and $G\left(y\right)$ are two univariate cdfs, and the association parameter $\xi$ lies in the interval $[-1,1]$. If the cdfs $F\left(x\right)$ and $G\left(y\right)$ are absolutely continuous with pdfs $f\left(x\right)$ and $g\left(y\right)$, respectively, the joint pdf of $H(x,y)$ is given by

$$h(x,y)=f\left(x\right)g\left(y\right)\{1+\xi [1-2F\left(x\right)\left]\right[1-2G\left(y\right)\left]\right\}.$$

(5)

By substituting the expression of any desired set of marginal distributions of random vector $(X,Y)$, members of the family can be derived.

Theoretical and practical advancements in concomitants of order statistics (COS) pave the way for a fresh look at the analysis of data resulting from bivariate distributions. Let $(X_i,Y_i),i=1,2,\dots ,n$, be n independent and identically distributed random vectors arising from the random vector $(X,Y)$, which follows an arbitrary absolutely continuous bivariate distribution with cdf $F(x,y)$ and pdf $f(x,y)$. If the components in the sample associated to X (i.e., the $X_i$’s), are ordered as $X_{1:n},X_{2:n},\dots ,X_{n:n}$, then the component associated to Y (i.e., the $Y_i$’s), accompanying with the $r^{\mathrm{th}}$ order statistic $X_{r:n}$, that is, the corresponding ordered pair of $X_{r:n}$ is called the concomitant of the $r^{\mathrm{th}}$ order statistic, and it is denoted as $Y_{[r:n]}$. One can refer to [11] to learn more about the early theoretical development of the COS. The most significant COS application is based on challenges with biological selection problems. For example, if the top k of n rams are selected for breeding based on their genetic makeup, $Y_{[n-k+1:n]},\dots ,Y_{[n:n]}$ could be a representation of the wool quality of one of their female offspring. A geneticist is more likely to select the best set of offspring in such experiments with fewer trials than in ones where all trials are carried out, which is much more difficult, expensive, and time-consuming. One can find examples of these applications in [12]. In many engineering situations, when developing structural designs, a statistical solution based on concomitant extremes is needed for the quantification of the risk of failure arising due to extreme levels of some environmental processes. These are also notable challenging applications of the COS, and examples can be found in [13,14].

In the literature, the ordering of $X_i^{\prime }s$, particularly distributions originating from the FGM family, allowed for the COS to be used to estimate the parameters associated with the distribution of the variable Y of primary interest. The inferential aspects of the FGM-type bivariate logistic distributions with equal coefficients of variation by the COS were studied in [15]. From the FGM-type bivariate Lindley distribution, the authors in [16] developed the COS distribution theory and proposed the estimator of the parameter associated with the variable Y. The FGM-type bivariate Bilal distribution was proposed in [17], who studied the estimation problem in detail by COS. Additionally, the authors in [18] elucidated some properties and applications of FGM bivariate generalized exponential distribution based on the COS.

Consequently, this work has many goals, which are listed below:

• To propose a bivariate version of the ME distribution using the FGM approach and study its competency compared with the other FGM bivariate distributions.
• To reveal the commendable theoretical flexibility of the proposed FGM bivariate moment exponential (FGMBME) distribution.
• To develop the distribution theory of the FGMBME distribution based on the COS and study the estimation problem in detail.
• To demonstrate the compactness of the FGMBME distributional aspect based on the COS.
• To demonstrate the successful establishment of the proposed estimator theoretically, as well as empirically.

The remaining part of this paper is consolidated as follows: In Section 2, we propose the FGMBME distribution and discuss its main properties. Section 3 reveals the inferential aspects of the proposed distribution. The distributional aspects of the COS arising from the FGMBME distribution are obtained in Section 4. In Section 5, we derive the best linear unbiased estimator (BLUE) of the parameter associated with the study variate involved in the FGMBME distribution using the COS. This section also considers a moment-type estimator for the association parameter $\xi$. The efficiency of the BLUE with respect to the respective unbiased estimator is also compared. Section 6 is devoted to comparing the proposed estimator using real-life data. The research study is then fully fledged with the concluding remarks in Section 7.

2. Farlie–Gumbel–Morgenstern Bivariate Moment Exponential Distribution

2.1. Presentation

The joint pdf $f(x,y)$ of the FGMBME distribution is obtained by incorporating the pdfs $f(x;{\sigma }_1)=\frac{x}{{\sigma }_1^2}{e}^{-\frac{x}{{\sigma }_1}},g(y;{\sigma }_2)=\frac{y}{{\sigma }_2^2}{e}^{-\frac{y}{{\sigma }_2}}$ and cdfs $F(x;{\sigma }_1)=1-\left(1+\frac{x}{{\sigma }_1}\right)e^{-\frac{x}{{\sigma }_1}},G(y;{\sigma }_2)=1-\left(1+\frac{y}{{\sigma }_2}\right)e^{-\frac{y}{{\sigma }_2}}$ of two univariate ME distributions in (5). Thus, the joint pdf $f(x,y)$ of the FGMBME distribution is obtained as

$$f(x,y)=\left\{\begin{array}{c}\begin{array}{c}\frac{xy}{{\sigma }_1^2{\sigma }_2^2}{e}^{-\frac{x}{{\sigma }_1}}{e}^{-\frac{y}{{\sigma }_2}}\hfill \\ \times \left[1+\xi \left(2e^{-\frac{x}{{\sigma }_1}}\left\{1+\frac{x}{{\sigma }_1}\right\}-1\right)\left(2e^{-\frac{y}{{\sigma }_2}}\left\{1+\frac{y}{{\sigma }_2}\right\}-1\right)\right],\hfill \\ x>0,y>0;{\sigma }_1>0,{\sigma }_2>0;-1\le \xi \le 1,\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

(6)

The corresponding cdf is indicated as

$$F(x,y)=\left\{\begin{array}{c}\begin{array}{c}\left[1-\left(1+\frac{x}{{\sigma }_1}\right)2e^{-\frac{x}{{\sigma }_1}}\right]\left[1-\left(1+\frac{y}{{\sigma }_2}\right)2e^{-\frac{y}{{\sigma }_2}}\right]\times \hfill \\ \left\{1+\xi \left(1+\frac{x}{{\sigma }_1}\right)e^{-\frac{x}{{\sigma }_1}}\left(1+\frac{y}{{\sigma }_2}\right)e^{-\frac{y}{{\sigma }_2}}\right\},\hfill \\ x>0,y>0;{\sigma }_1>0,{\sigma }_2>0;-1\le \xi \le 1,\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

(7)

Figure 1 displays the pdfs for several arbitrary values of the parameters. As shown in this figure, the FGMBME distribution has a variety of shapes, making it useful for analyzing bivariate data.

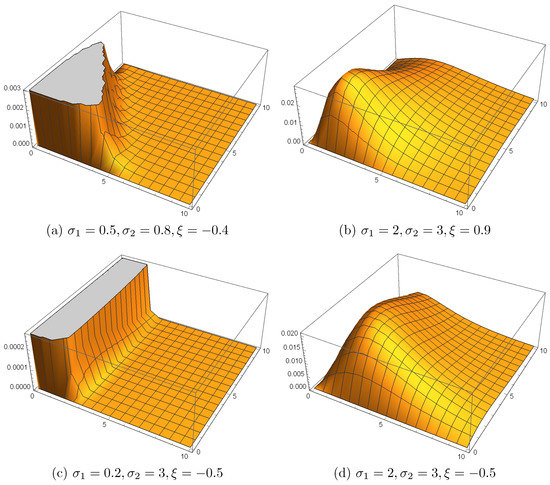
Figure 1. Pdf plots for varying values of parameters.

Let $(X,Y)$ be a random vector that follows the FGMBME distribution. Evidently, we have

$$E\left(X\right)=2{\sigma }_1,Var\left(X\right)=2{\sigma }_1^2,$$

$$E\left(Y\right)=2{\sigma }_2,Var\left(Y\right)=2{\sigma }_2^2,$$

and, with more integral developments, we obtain

$$E\left(XY\right)={\sigma }_1{\sigma }_2\left(4+\frac{9}{16}\xi \right).$$

The correlation coefficient $\rho$ between X and Y is given by

$$\rho =\frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{Var\left(X\right)Var\left(Y\right)}}=\frac{9}{32}\xi ,$$

(8)

such that $\rho \in [-0.28125,0.28125]$, corresponding to a moderately negative or positive correlation.

2.2. Moment-Generating Function and Moments

In this section, the mgf, moments, and the conditional moments of the FGMBME distribution are derived. In full generality, the mgf of a random vector $(X,Y)$ with a distribution from the FGM family is given by

$$\begin{array}{cc}\hfill & M_{(X,Y)}(t_1,t_2)=E\left(e^{t_{1}X+t_{2}Y}\right)=M_X\left(t_1\right)M_Y\left(t_2\right)+\hfill \\ & \xi \left[\left(M_X\left(t_1\right)-2{\int }_0^{\infty }F\left(x\right)f\left(x\right)e^{t_{1}x}dx\right)\left(M_Y\left(t_2\right)-2{\int }_0^{\infty }G\left(y\right)g\left(y\right)e^{t_{2}y}dy\right)\right],\hfill \end{array}$$

(9)

where $M_X\left(t_1\right)$ and $M_Y\left(t_2\right)$ are the mgfs of X and Y, respectively. Thus, the mgf of a random vector $(X,Y)$ that follows the FGMBME distribution is obtained as

$$\begin{array}{cc}\hfill M_{(X,Y)}(t_1,t_2)=& \frac{1}{\left(1-{\sigma }_1{t}_1\right){}^2{\left(1-{\sigma }_2{t}_2\right)}^2}+\xi \left[\{4{(2-{\sigma }_1{t}_1)}^{-3}+2{(2-{\sigma }_1{t}_1)}^{-2}-{(1-{\sigma }_1{t}_1)}^{-2}\}\right.\hfill \\ \hfill & \left.\times \{4{(2-{\sigma }_2{t}_2)}^{-3}+2{(2-{\sigma }_2{t}_2)}^{-2}-{(1-{\sigma }_2{t}_2)}^{-2}\}\right].\hfill \end{array}$$

(10)

In this setting, the $(r,s)$-th moment of $(X,Y)$ is obtained as

$$\begin{array}{cc}\hfill E\left(X^r{Y}^s\right)={\sigma }_1^r{\sigma }_2^s(r+1)!(s+1)!& \left[1+\xi \left\{\frac{1}{2^{r+s+2}}+\frac{s+r+4}{2^{r+s+3}}-\frac{1}{2^{r+1}}\right.\right.+\hfill \\ & \left.\left.\frac{(r+2)(s+2)}{2^{r+s+4}}-\frac{r+2}{2^{r+2}}-\frac{1}{2^{s+1}}-\frac{s+2}{2^{s+2}}+1\right\}\right].\hfill \end{array}$$

(11)

In full generality, for a random vector $(X,Y)$ with a distribution into the FGM family, the conditional pdf of $Y\mid X=x$ is given by

$$h(y\mid X=x)=g\left(y\right)\{1+\xi [1-2F\left(x\right)\left]\right[1-2G\left(y\right)\left]\right\},-1\le \xi \le 1.$$

(12)

By using (12), the conditional pdf of $Y\mid X=x$ with $x>0$, where $(X,Y)$, a random vector that follows the FGMBME distribution, is given by

$$f(y\mid X=x)=\frac{y}{{\sigma }_2^2}{e}^{-\frac{y}{{\sigma }_2}}\left[1+\xi \left(2e^{-\frac{x}{{\sigma }_1}}\left\{1+\frac{x}{{\sigma }_1}\right\}-1\right)\left(2e^{-\frac{y}{{\sigma }_2}}\left\{1+\frac{y}{{\sigma }_2}\right\}-1\right)\right],y>0.$$

Therefore, the conditional mean of $Y\mid X=x$ is obtained as

$$E(Y\mid X=x)=\frac{1}{4}{\sigma }_2\left[3\xi -\frac{6\xi e^{-\frac{x}{{\sigma }_1}}\left({\sigma }_1+x\right)}{{\sigma }_1}+8\right].$$

3. Estimation and Inference

3.1. Estimation Method

Let $(x_i,y_i),i=1,2,\cdots ,n$ be observations from a random sample of size n from the FGMBME distribution with unknown parameters ${\sigma }_1,{\sigma }_2,$ and $\xi$. Using the pdf of the FGMBME distribution, the log-likelihood function is obtained as

$$\begin{array}{cc}\hfill logL=\sum _{i=1}^{n}log{x}_i+& \sum _{i=1}^{n}log{y}_i-\frac{1}{{\sigma }_1}\sum _{i=1}^n{x}_i-\frac{1}{{\sigma }_2}\sum _{i=1}^n{y}_i\hfill \\ \hfill +& \sum _{i=1}^{n}log{A}_i-2nlog{\sigma }_1-2nlog{\sigma }_2,\hfill \end{array}$$

(13)

where

$$A_i=1+\xi \left[2e^{-\frac{x_i}{{\sigma }_1}}\left(1+\frac{x_i}{{\sigma }_1}\right)-1\right]\left[2e^{-\frac{y_i}{{\sigma }_2}}\left(1+\frac{y_i}{{\sigma }_2}\right)-1\right].$$

The maximum likelihood (ML) estimates ${\widehat{\sigma }}_1$, ${\widehat{\sigma }}_2$, and $\widehat{\xi }$ of ${\sigma }_1$, ${\sigma }_2$, and $\xi$, respectively, are obtained by maximizing $logL$. To this end, the system of partial derivatives of $logL$ with respect to each parameter set equal to zero is given by

$$\begin{array}{cc}\hfill \frac{\partial logL}{\partial {\sigma }_1}& =\frac{1}{{{\sigma }_1}^2}\sum _{i=1}^n{x}_i-\sum _{i=1}^n\frac{B_i}{A_i}-\frac{2n}{{\sigma }_1}=0,\hfill \\ \hfill \frac{\partial logL}{\partial {\sigma }_2}& =\frac{1}{{{\sigma }_2}^2}\sum _{i=1}^n{y}_i-\sum _{i=1}^n\frac{C_i}{A_i}-\frac{2n}{{\sigma }_2}=0,\mathrm{and}\hfill \\ \hfill \frac{\partial logL}{\partial \xi }& =\sum _{i=1}^n\frac{D_i}{A_i}=0,\hfill \end{array}$$

(14)

where

$$B_i=\frac{2\xi x_i}{{{\sigma }_1}^2}{e}^{-\frac{x_i}{{\sigma }_1}}\left(\frac{2x_i}{{\sigma }_1}{e}^{-\frac{y_i}{{\sigma }_2}}+\frac{2x_i{y}_i}{{\sigma }_1{\sigma }_2}{e}^{-\frac{y_i}{{\sigma }_2}}-\frac{x_i}{{\sigma }_1}\right),$$

$$C_i=\frac{2\xi y_i}{{{\sigma }_2}^2}{e}^{-\frac{y_i}{{\sigma }_2}}\left(\frac{2y_i}{{\sigma }_2}{e}^{-\frac{x_i}{{\sigma }_1}}+\frac{2x_i{y}_i}{{\sigma }_1{\sigma }_2}{e}^{-\frac{x_i}{{\sigma }_1}}-\frac{y_i}{{\sigma }_2}\right),$$

and

$$D_i=\left[2e^{-\frac{x_i}{{\sigma }_1}}\left(1+\frac{x_i}{{\sigma }_1}\right)-1\right]\left[2e^{-\frac{y_i}{{\sigma }_2}}\left(1+\frac{y_i}{{\sigma }_2}\right)-1\right].$$

As the system of Equation (14) does not have explicit solutions, in order to obtain the ML estimates, we maximize the log-likelihood function for numerical optimization. In this study, we determine the ML estimates numerically using the constrOptim function in the built-in stats package of the R software.

3.2. Application of Real-Life Data

For some variety of real-life datasets, the FGMBME distribution serves as one of the most accurate and reliable models. For example, consider the real-life data from [19], which includes mineral content measurements of bones in 25 elderly women’s dominant ulna (X) and ulna (Y). The FGMBME distribution is fitted to the data, and the results are compared with two other FGM distributions, namely the FGM bivariate exponential (FGMBE) (see [20]) and the FGM bivariate Bilal (FGMBB) (see [17]). Along with the ML estimates, the negative of log-likelihood function ($-logL$), Akaike information criterion (AIC), and Bayesian information criterion (BIC) are computed. They are provided in Table 1. For all three distributions, the ML estimate of $\xi$ is $\widehat{\xi }=1$. Based on the $-logL$, AIC, and BIC values given in Table 1, it can be concluded that the FGMBME distribution provides better performance than the FGMBE and FGMBB distributions.

Table 1. ML estimates, $-logL$, AIC and BIC values of the considered models.

Model	Association Parameter	Other Parameters	$-log\mathit{L}$	AIC	BIC
FGMBE	$\widehat{\xi }$ = 1	${\widehat{\sigma }}_1$ = 0.566, ${\widehat{\sigma }}_2$ = 0.557	29.321	62.643	65.080
FGMBB	$\widehat{\xi }$ = 1	${\widehat{\sigma }}_1$ = 0.750, ${\widehat{\sigma }}_2$ = 0.739	12.314	28.629	31.067
FGMBME	$\widehat{\xi }$ = 1	${\widehat{\sigma }}_1$ = 0.308, ${\widehat{\sigma }}_2$ = 0.304	11.575	27.150	29.588

Secondly, we consider the real-life data from [19], which includes, the tail length (X) and wing length (Y) in millimeters for a sample of size $n=45$ of female hook-billed kites. For the above data, we computed the ML estimates of the parameters of the FGMBE, FGMBB, and FGMBME distributions, and the $-logL$, AIC, and BIC values are given in Table 2. Here, also, the ML estimates of $\xi$ are obtained as $\widehat{\xi }=1$ for all the distributions. Based on $-logL$, AIC, and BIC values given in Table 2, it can be concluded that the FGMBME distribution provides better performance than the FGMBE and FGMBB distributions.

Table 2. ML estimates, $-logL$, AIC, and BIC values of the considered models.

Model	Association Parameter	Other Parameters	$-log\mathit{L}$	AIC	BIC
FGMBE	$\widehat{\xi }$ = 1	${\widehat{\sigma }}_1$ = 153.734, ${\widehat{\sigma }}_2$ = 222.239	575.388	1154.776	1157.214
FGMBB	$\widehat{\xi }$ = 1	${\widehat{\sigma }}_1$ = 202.629, ${\widehat{\sigma }}_2$ = 292.903	544.198	1092.396	1094.834
FGMBME	$\widehat{\xi }$ = 1	${\widehat{\sigma }}_1$ = 83.360, ${\widehat{\sigma }}_2$ = 120.401	542.795	1089.590	1092.027

4. Distribution Theory of the COS Arising from the FGMBME Distribution

In this section, we perform the distribution theory of the COS derived from the FGMBME distribution. Let $(X_i,Y_i),i=1,2,\dots ,n$, be n independent and identically distributed random vectors from the FGMBME distribution. Let $Y_{[r:n]}$ be the concomitant of the $r^{\mathrm{th}}$-order statistic $X_{r:n}$ arising from (6). Then, using the expression for the distribution of the COS given in [21], the pdf $f_{[r:n]}\left(y\right)$ of $Y_{[r:n]}$ and the joint pdf $f_{[r,s:n]}(y_1,y_2)$ of $(Y_{[r:n]},Y_{[s:n]})$ are obtained as follows:

For $1\le r\le n$, we have

$$f_{[r:n]}\left(y\right)=\frac{y}{{\sigma }_2^2}{e}^{-\frac{y}{{\sigma }_2}}\left[1+\xi G_r\left(2e^{-\frac{y}{{\sigma }_2}}\left\{1+\frac{y}{{\sigma }_2}\right\}-1\right)\right],y>0,$$

(15)

and, for $1\le r<s\le n$,

$$\begin{array}{cc}\hfill f_{[r,s:n]}(y_1,y_2)=& \frac{y_1{y}_2}{{\sigma }_1^2{\sigma }_2^2}{e}^{-\frac{y_1}{{\sigma }_1}}{e}^{-\frac{y_2}{{\sigma }_2}}\left[1+\xi G_r\left(2e^{-\frac{y_1}{{\sigma }_1}}\left\{1+\frac{y_1}{{\sigma }_1}\right\}-1\right)\right.\hfill \\ \hfill & +\xi G_s\left(2e^{-\frac{y_2}{{\sigma }_2}}\left\{1+\frac{y_2}{{\sigma }_2}\right\}-1\right)+{\xi }^2\left(G_s-G_{rs}\right)\hfill \\ \hfill & \left.\times \left(2e^{-\frac{y_1}{{\sigma }_1}}\left\{1+\frac{y_1}{{\sigma }_1}\right\}-1\right)\left(2e^{-\frac{y_2}{{\sigma }_2}}\left\{1+\frac{y_2}{{\sigma }_2}\right\}-1\right)\right],y_1,y_2>0,\hfill \end{array}$$

(16)

where $G_r=\frac{n-2r+1}{n+1}$, $G_s=\frac{n-2s+1}{n+1}$, and $G_{rs}=\frac{2r(n-2s)}{(n+1)(n+2)}$. The expression for the $k^{th}$ moment of the concomitant $Y_{[r:n]}$ is obtained as

$$E\left[Y_{[r:n]}^k\right]={\sigma }_2^k(k+1)!\left[1+\xi G_r\left\{-1+\frac{1}{2^{k+1}}+\frac{k+2}{2^{k+2}}\right\}\right]$$

(17)

and the product moment of $Y_{[r:n]}$ and $Y_{[s:n]}$ is indicated as

$$E\left[Y_{[r:n]}{Y}_{[s:n]}\right]={\sigma }_2^2\left[4-3\xi \frac{\{n-(r+s)+1\}}{(n+1)}+\frac{9{\xi }^2}{16}\{G_s-G_{rs}\}\right].$$

(18)

From (17), we obtain the mean and variance of $Y_{[r:n]}$ as

$$E\left[Y_{[r:n]}\right]={\sigma }_2\left[2-\frac{3}{4}\xi G_r\right]$$

(19)

and

$$Var\left[Y_{[r:n]}\right]={\sigma }_2^2\left[2-\frac{3}{4}\xi G_r-\frac{9}{16}{\xi }^2{G_r}^2\right],$$

(20)

respectively.

By virtue of (18) and (19), we obtain the covariance between the $r$ and $s$ COS, and it is given by

$$Cov[Y_{[r:n]},Y_{[s:n]}]={\sigma }_2^2\frac{9}{16}{\xi }^{2}2r\left[\frac{n-2s+1}{{(n+1)}^2}-\frac{(n-2s)}{(n+1)(n+2)}\right].$$

(21)

Let us set

$${\kappa }_r=2-\frac{3}{4}\xi G_r,$$

(22)

$${\varrho }_{r,r}=2-\frac{3}{4}\xi G_r-\frac{9}{16}{\xi }^2{G_r}^2$$

(23)

and

$${\varrho }_{r,s}=\frac{9}{16}{\xi }^{2}2r\left[\frac{n-2s+1}{{(n+1)}^2}-\frac{(n-2s)}{(n+1)(n+2)}\right].$$

(24)

Then, from (22)–(24), the following results hold: For $1\le r\le n$, we have

$$E\left[Y_{[r:n]}\right]={\sigma }_2{\kappa }_r,$$

(25)

$$Var\left[Y_{[r:n]}\right]={\sigma }_2^2{\varrho }_{r,r}$$

(26)

and, for $1\le r<s\le n,$

$$Cov[Y_{[r:m]},Y_{[s:n]}]={\sigma }_2^2{\varrho }_{r,s}.$$

(27)

5. BLUE of ${\mathbf{\sigma }}_{\mathbf{2}}$ Using the COS

In this section, using the COS, we obtain the BLUE of the parameter ${\sigma }_2$ involved in the FGMBME distribution. Let $Y_{[r:n]}$, $r=1,2,\dots ,n$, be the COS arising from the FGMBME distribution defined in (16). Let $Y_{\left[n\right]}={(Y_{[1:n]},Y_{[2:n]},\dots ,Y_{[n:n]})}^{\prime }$ denote the vector of COS. Then, from (25)–(27), we can write

$$E\left[Y_{\left[n\right]}\right]={\sigma }_2\kappa ,$$

(28)

where $\kappa ={({\kappa }_1,{\kappa }_2,\dots ,{\kappa }_n)}^{\prime }$, and the dispersion matrix of $Y_{\left[n\right]}$ is indicated as

$$D\left(Y_{\left[n\right]}\right)={\sigma }_2^2\Lambda ,$$

(29)

with $\Lambda =\left[\left[{\varrho }_{r,s}\right]\right]$. If $\xi$ is contained in $\kappa$, and $\Lambda$ are known, then the combination of (28) and (29) allows to apply the generalized Gauss–Markov theorem on the linear model $(Y_{\left[n\right]},{\sigma }_2\kappa ,{\sigma }_2^2\Lambda )$ (see [11]). According to [22], the BLUE of ${\sigma }_2$ is then given by

$${\tilde{\sigma }}_2={\left({\kappa }^{\prime }{\Lambda }^{-1}\kappa \right)}^{-1}{\kappa }^{\prime }{\Lambda }^{-1}{Y}_{\left[n\right]}.$$

(30)

Furthermore, the variance of ${\tilde{\sigma }}_2$ is given by

$$Var\left({\tilde{\sigma }}_2\right)={\left({\kappa }^{\prime }{\Lambda }^{-1}\kappa \right)}^{-1}{\sigma }_2^2.$$

(31)

From (30), it is clear that ${\tilde{\sigma }}_2$ is a linear function of $Y_{[r:n]}$, $r=1,2,\dots ,n$. Thus, ${\tilde{\sigma }}_2$ can be written as

$${\displaystyle {\tilde{\sigma }}_2=\sum _{r=1}^n{b}_r{Y}_{[r:n]},}$$

where $b_r,r=1,2,\dots ,n$, are constants. It should be noted that the interval $[-1,1]$ contains all possible values of $\xi$. If the estimate ${\tilde{\sigma }}_2$ of ${\sigma }_2$ for a given $\xi ={\xi }_0\in [-1,1]$ is evaluated, then one need not compute the estimate of ${\sigma }_2$ for $\xi =-{\xi }_0$, as the coefficients of the COS in the estimate for this case can be obtained from the coefficients of ${\tilde{\sigma }}_2$ for $\xi ={\xi }_0$, as proved in the next result.

Theorem 1.

Concerning a specific association parameter $\xi ={\xi }_0\in [-1,1]$, let $Y_{[r:n]}$, $r=1,2,\dots ,n$, represent theCOSof a random sample $(X_i,Y_i)$, $i=1,2,\dots ,n$, obtained from theFGMBMEdistribution with the pdf defined in (6). Let ${\displaystyle {\tilde{\sigma }}_2\left({\xi }_0\right)=\sum _{r=1}^n{\omega }_r{Y}_{[r:n]}}$ represent theBLUEof ${\sigma }_2$ for a given ${\xi }_0$ based on theCOS$Y_{[r:n]}$, $r=1,2,\dots ,n$. In this case, theBLUEof ${\sigma }_2$ when $\xi =-{\xi }_0$ is given by ${\displaystyle {\tilde{\sigma }}_2(-{\xi }_0)=\sum _{r=1}^n{\omega }_{n-r+1}{Y}_{[r:n]}}$ with $Var\left[{\tilde{\sigma }}_2(-{\xi }_0)\right]=Var\left[{\tilde{\sigma }}_2\left({\xi }_0\right)\right]$.

Proof. 

Let $Y_{\left[n\right]}\left({\xi }_0\right)$ be the vector of the COS of a random sample of size n drawn from a population with pdf defined in (6) for a given ${\xi }_0$. Then, from (28) and (29), we can write the mean vector and dispersion matrix of $Y_{\left[n\right]}\left({\xi }_0\right)$ as

$$\begin{array}{cc}\hfill E\left[Y_{\left[n\right]}\left({\xi }_0\right)\right]& ={\sigma }_2\kappa \left({\xi }_0\right)={\sigma }_2{[{\kappa }_1\left({\xi }_0\right),{\kappa }_2\left({\xi }_0\right),\dots ,{\kappa }_n\left({\xi }_0\right)]}^{\prime },\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill D\left[Y_{\left[n\right]}\left({\xi }_0\right)\right]& ={\sigma }_2^2\Lambda \left({\xi }_0\right)={\sigma }_2^2\left(\left({\varrho }_{r,s}\left({\xi }_0\right)\right)\right),\hfill \end{array}$$

respectively, where

$${\kappa }_r\left({\xi }_0\right)=2-\frac{3}{4}{\xi }_0{G}_r,$$

(32)

$${\varrho }_{r,r}\left({\xi }_0\right)=2-\frac{3}{4}{\xi }_0{G}_r-\frac{9}{16}{\xi }_0^2{G_r}^2,1\le r\le n,$$

(33)

and

$${\varrho }_{r,s}\left({\xi }_0\right)=\frac{9}{16}{\xi }_0^{2}2r\left[\frac{n-2s+1}{{(n+1)}^2}-\frac{(n-2s)}{(n+1)(n+2)}\right],r\ne s.$$

(34)

By virtue of Equations (32)–(34), we obtain

$${\kappa }_r\left({\xi }_0\right)={\kappa }_{n-r+1}(-{\xi }_0),$$

(35)

$${\varrho }_{r,r}\left({\xi }_0\right)={\varrho }_{n-r+1,n-r+1}(-{\xi }_0),$$

(36)

$${\varrho }_{r,s}\left({\xi }_0\right)={\varrho }_{r,s}(-{\xi }_0)$$

(37)

and

$${\varrho }_{r,s}\left({\xi }_0\right)={\varrho }_{n-s+1,n-r+1}\left({\xi }_0\right),1\le r<s\le n.$$

(38)

Using (30), we obtain the BLUE of ${\sigma }_2$ as

$${\tilde{\sigma }}_2\left({\xi }_0\right)={\left\{{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }{[\Lambda \left({\xi }_0\right)]}^{-1}\kappa \left({\xi }_0\right)\right\}}^{-1}{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }{[\Lambda \left({\xi }_0\right)]}^{-1}{Y}_{\left[n\right]}\left({\xi }_0\right)$$

(39)

and the variance of ${\tilde{\sigma }}_2\left({\xi }_0\right)$ is

$$Var\left[{\tilde{\sigma }}_2\left({\xi }_0\right)\right]={\left\{{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }{[\Lambda \left({\xi }_0\right)]}^{-1}\kappa \left({\xi }_0\right)\right\}}^{-1}{\sigma }_2^2.$$

(40)

Clearly, (39) is a linear function of $Y_{[r:n]},r=1,2,\dots ,n$, and hence, it can be written as

$${\displaystyle {\tilde{\sigma }}_2\left({\xi }_0\right)=\sum _{r=1}^n{b}_r{Y}_{[r:n]}.}$$

Let S be an $n\times n$ matrix defined as

$$S=\left[\begin{array}{cccc}0& \cdots & 0& 1\\ \\ 0& \cdots & 1& 0\\ \\ ⋮& ⋮& \cdots & ⋮\\ \\ 1& \cdots & 0& 0\end{array}\right].$$

(41)

Hence, we have $S{Y}_{\left[n\right]}\left({\xi }_0\right)={(Y_{[n:n]},\dots ,Y_{[1:n]})}^{\prime }$.

From (35) to (38), we obtain

$$\begin{array}{c}\hfill E\left[Y_{\left[n\right]}(-{\xi }_0)\right]={\sigma }_2\kappa (-{\xi }_0)={\sigma }_{2}S\kappa \left({\xi }_0\right).\end{array}$$

Since the difference between $D\left[Y_{\left[n\right]}(-{\xi }_0)\right]$ and $D\left[Y_{\left[n\right]}\left({\xi }_0\right)\right]$ is only by the order of the elements along the diagonal element, we have

$$D\left[Y_{\left[n\right]}(-{\xi }_0)\right]={\sigma }_2^2\Lambda (-{\xi }_0)={\sigma }_2^{2}S\Lambda \left({\xi }_0\right)S.$$

Therefore, the BLUE of ${\sigma }_2$ is

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_2(-{\xi }_0)& =& {\left\{{\left[\kappa (-{\xi }_0)\right]}^{\prime }{[\Lambda (-{\xi }_0)]}^{-1}\kappa (-{\xi }_0)\right\}}^{-1}{\left[\kappa (-{\xi }_0)\right]}^{\prime }{[\Lambda (-{\xi }_0)]}^{-1}{Y}_{\left[n\right]}(-{\xi }_0)\hfill \\ & =& {\left\{{\left[S\kappa \left({\xi }_0\right)\right]}^{\prime }{[S\Lambda \left({\xi }_0\right)S]}^{-1}S\kappa \left({\xi }_0\right)\right\}}^{-1}{\left[S\kappa \left({\xi }_0\right)\right]}^{\prime }{[S\Lambda \left({\xi }_0\right)S]}^{-1}{Y}_{\left[n\right]}(-{\xi }_0)\hfill \\ & =& {\left\{{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }SS{[\Lambda \left({\xi }_0\right)]}^{-1}SS\kappa \left({\xi }_0\right)\right\}}^{-1}{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }SS{[\Lambda \left({\xi }_0\right)]}^{-1}S{Y}_{\left[n\right]}(-{\xi }_0).\hfill \end{array}$$

Using the result $SS=I$, we have

$${\tilde{\sigma }}_2(-{\xi }_0)={\left\{{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }{[\Lambda \left({\xi }_0\right)]}^{-1}\kappa \left({\xi }_0\right)\right\}}^{-1}{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }{[\Lambda \left({\xi }_0\right)]}^{-1}S{Y}_{\left[n\right]}(-{\xi }_0).$$

(42)

In (42), $S{Y}_{\left[n\right]}(-{\xi }_0)$ is ${(Y_{[n:n]},Y_{[n-1:n]}\dots ,Y_{[1:n]})}^{\prime }$, and the coefficients of $S{Y}_{\left[n\right]}\left({\xi }_0\right)$ in (39) and those of $Y_{\left[n\right]}(-{\xi }_0)$ in (42) are exactly same. Thus, we have ${\displaystyle {\tilde{\sigma }}_2\left({\xi }_0\right)=\sum _{r=1}^n{b}_r{Y}_{[r:n]}}$ and ${\displaystyle {\tilde{\sigma }}_2(-{\xi }_0)=\sum _{r=1}^n{b}_{n-r+1}{Y}_{[r:n]}}$.

Moreover, from (40), we have

$$\begin{array}{ccc}\hfill Var\left[{\tilde{\sigma }}_2(-{\xi }_0)\right]& =& {\left\{{\left[\kappa (-{\xi }_0)\right]}^{\prime }{[\Lambda (-{\xi }_0)]}^{-1}\kappa (-{\xi }_0)\right\}}^{-1}{\sigma }_2^2\hfill \\ & =& {\left\{{\left[S\kappa \left({\xi }_0\right)\right]}^{\prime }{[S\Lambda \left({\xi }_0\right)S]}^{-1}S\kappa \left({\xi }_0\right)\right\}}^{-1}{\sigma }_2^2\hfill \\ & =& {\left\{{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }SS{[\Lambda \left({\xi }_0\right)]}^{-1}SS\kappa \left({\xi }_0\right)\right\}}^{-1}{\sigma }_2^2\hfill \\ & =& {\left\{{\left[\kappa \left({\xi }_0\right)\right]}^{\prime }{[\Lambda \left({\xi }_0\right)]}^{-1}\kappa \left({\xi }_0\right)\right\}}^{-1}{\sigma }_2^2\hfill \\ & =& Var\left[{\tilde{\sigma }}_2\left({\xi }_0\right)\right].\hfill \end{array}$$

This ends the proof.    □

In order to illustrate our findings, we compute the coefficients $b_r$ of $Y_{[r:n]}$, $r=1,2,\dots ,n$, in ${\tilde{\sigma }}_2$ and $Var\left({\tilde{\sigma }}_2\right)$ for $n=2,3,\dots ,10$, and $\xi =0.25,0.50,0.75,1.00$. The results are given in Table 3 and Table 4. By using Theorem 1, one can also use Table 3 and Table 4 to obtain the coefficients $b_r$ of $Y_{[r:n]}$, $r=1,2,\dots ,n$, in ${\tilde{\sigma }}_2$, and $Var\left({\tilde{\sigma }}_2\right)$ for $n=2,3,\dots ,10$, and $\xi =-1.00,-0.75,-0.50,-0.25$.

Table 3. The coefficients $b_r$, $r=1,2,\dots ,n$, in the BLUE, $V_1=\frac{Var\left({\tilde{\sigma }}_2\right)}{{\sigma }_2^2}$, $V_2=\frac{Var\left({\widehat{\sigma }}_2\right)}{{\sigma }_2^2}$, and the efficiency $E_1=\frac{V_2}{V_1}$ of ${\tilde{\sigma }}_2$ relative to ${\widehat{\sigma }}_2$.

n	$\mathit{\xi }$	Coefficients										${\mathit{V}}_1$	${\mathit{V}}_2$	${\mathit{E}}_1$
		${\mathit{b}}_{\mathbf{1}}$	${\mathit{b}}_{\mathbf{2}}$	${\mathit{b}}_{\mathbf{3}}$	${\mathit{b}}_{\mathbf{4}}$	${\mathit{b}}_{\mathbf{5}}$	${\mathit{b}}_{\mathbf{6}}$	${\mathit{b}}_{\mathbf{7}}$	${\mathit{b}}_{\mathbf{8}}$	${\mathit{b}}_{\mathbf{9}}$	${\mathit{b}}_{\mathbf{10}}$
2	0.25	0.25000	0.25000									0.25000	0.25000	1.00000
	0.50	0.25000	0.25000									0.25000	0.25000	1.00000
3	0.25	0.16698	0.16608	0.16695								0.16667	0.16667	1.00000
	0.50	0.16824	0.16418	0.16764								0.16665	0.16667	1.00012
4	0.25	0.12547	0.12455	0.12457	0.12542							0.12500	0.12500	1.00000
	0.50	0.27030	0.12314	0.12327	0.12660							0.12417	0.12500	1.00024
5	0.25	0.10054	0.09974	0.09950	0.09975	0.10047						0.10000	0.10000	1.00000
	0.50	0.10236	0.09889	0.09796	0.09902	0.10182						0.09997	0.10000	1.00030
6	0.25	0.08390	0.08322	0.08291	0.08292	0.08323	0.08383					0.08333	0.08333	1.00000
	0.50	0.08583	0.08285	0.08158	0.08168	0.08292	0.08522					0.08330	0.08333	1.00036
7	0.25	0.07200	0.07143	0.07111	0.07101	0.07112	0.07143	0.07192				0.07143	0.07143	1.00000
	0.50	0.07395	0.07140	0.07008	0.06973	0.07020	0.07142	0.07331				0.07140	0.07143	1.00042
8	0.25	0.06306	0.06258	0.06227	0.06213	0.06214	0.06229	0.06257	0.06298			0.06250	0.06250	1.00000
	0.50	0.06500	0.06281	0.06153	0.06098	0.06104	0.06164	0.06275	0.06433			0.06247	0.06250	1.00048
9	0.25	0.05610	0.05569	0.05541	0.05525	0.05520	0.05526	0.05542	0.05567	0.05602		0.05555	0.05555	1.00000
	0.50	0.05800	0.05611	0.05491	0.05428	0.05412	0.05437	0.05500	0.05599	0.05733		0.05553	0.05555	1.00054
10	0.25	0.05052	0.05017	0.04992	0.04975	0.04968	0.04968	0.04976	0.04992	0.05015	0.05045	0.05000	0.05000	1.00000
	0.50	0.05238	0.05073	0.04963	0.04897	0.04868	0.04873	0.04907	0.04967	0.05055	0.05171	0.04997	0.05000	1.00060

Table 4. The coefficients $b_r$, $r=1,2,\dots ,n$, in the BLUE, $V_1=\frac{Var\left({\tilde{\sigma }}_2\right)}{{\sigma }_2^2}$, $V_2=\frac{Var\left({\widehat{\sigma }}_2\right)}{{\sigma }_2^2}$, and the efficiency $E_1=\frac{V_2}{V_1}$ of ${\tilde{\sigma }}_2$ relative to ${\widehat{\sigma }}_2$.

n	$\mathit{\xi }$	Coefficients										${\mathit{V}}_1$	${\mathit{V}}_2$	${\mathit{E}}_1$
		${\mathit{b}}_{\mathbf{1}}$	${\mathit{b}}_{\mathbf{2}}$	${\mathit{b}}_{\mathbf{3}}$	${\mathit{b}}_{\mathbf{4}}$	${\mathit{b}}_{\mathbf{5}}$	${\mathit{b}}_{\mathbf{6}}$	${\mathit{b}}_{\mathbf{7}}$	${\mathit{b}}_{\mathbf{8}}$	${\mathit{b}}_{\mathbf{9}}$	${\mathit{b}}_{\mathbf{10}}$
2	0.75	0.25000	0.25000									0.25000	0.25000	1.00000
	1.00	0.25000	0.25000									0.25000	0.25000	1.00000
3	0.75	0.16987	0.16122	0.16903								0.16658	0.16667	1.00054
	1.00	0.17297	0.15672	0.17073								0.16638	0.16667	1.00174
4	0.75	0.13006	0.12062	0.12109	0.12848							0.12487	0.12500	1.00104
	1.00	0.13529	0.11674	0.11790	0.13096							0.12456	0.12500	1.00353
5	0.75	0.10601	0.09731	0.09532	0.09777	0.10393						0.09985	0.10000	1.00150
	1.00	0.11257	0.09472	0.09143	0.09587	0.10672						0.09948	0.10000	1.00523
6	0.75	0.08978	0.08209	0.07925	0.07956	0.08234	0.08740					0.08317	0.08333	1.00192
	1.00	0.09716	0.08071	0.07571	0.07647	0.08137	0.09028					0.08278	0.08333	1.00664
7	0.75	0.07803	0.07130	0.06823	0.06753	0.06864	0.07130	0.07548				0.07126	0.07143	1.00239
	1.00	0.08588	0.07094	0.06530	0.06428	0.06631	0.07096	0.07834				0.07086	0.07143	1.00804
8	0.75	0.06909	0.06320	0.06015	0.05897	0.05918	0.06054	0.06297	0.06646			0.06234	0.06250	1.00257
	1.00	0.07730	0.06375	0.05762	0.05570	0.05651	0.05892	0.06314	0.06933			0.06200	0.06250	1.00806
9	0.75	0.06205	0.05687	0.05396	0.05255	0.05225	0.05286	0.05426	0.05643	0.05939		0.05540	0.05555	1.00289
	1.00	0.07030	0.05803	0.05230	0.04988	0.04949	0.05063	0.05297	0.05686	0.06211		0.05502	0.05555	1.00963
10	0.75	0.05635	0.05177	0.04903	0.04753	0.04694	0.04709	0.04787	0.04923	0.05116	0.05369	0.04985	0.05000	1.00301
	1.00	0.06459	0.05345	0.04791	0.04523	0.04432	0.04468	0.04607	0.04842	0.05179	0.05629	0.04946	0.05000	1.01092

For the purpose of comparison, we compute an unbiased estimator of the parameter ${\sigma }_2$, which is ${\widehat{\sigma }}_2=\frac{\overline{Y}}{2}$, and its variance is obtained as $\frac{{\sigma }_2^2}{2n}$. We also compute the ratio $\frac{Var\left({\widehat{\sigma }}_2\right)}{Var\left({\tilde{\sigma }}_2\right)}$ to measure the efficiency of our estimator ${\tilde{\sigma }}_2$ relative to ${\widehat{\sigma }}_2$ for $n=2,3,\dots ,10$ and $\xi =0.25,0.50,0.75,1.00$. The results are also presented in Table 3 and Table 4. From these tables, one can clearly notice that ${\tilde{\sigma }}_2$ is more efficient than ${\widehat{\sigma }}_2$.

Remark 1.

We took into account the correlation coefficient between the two variables for theFGMBMEdistribution specified in (6), and its expression is obtained as $\rho =\frac{9}{32}\xi$. However, even so, our presumption that ξ is known might be viewed as impractical in some real-life scenarios. As a result, in cases where ξ is unknown, we compute the sample correlation τ from $(X_{r:n},Y_{[r:n]})$ for $r=1,2,\dots ,n$, and hence introduce a moment-type estimator, $\widehat{\xi }$, for ξ, as

$$\begin{array}{c}\hfill \widehat{\xi }=\left\{\begin{array}{c}{\displaystyle -1,if\tau <-\frac{9}{32}}\hfill \\ {\displaystyle \frac{32}{9}\tau ,if-\frac{9}{32}\le \tau \le \frac{9}{32}}\hfill \\ {\displaystyle 1,if\tau >\frac{9}{32}}\hfill \end{array}\right.\end{array}.$$

(43)

6. Empirical Illustration

We empirically compare the efficiency of the estimator ${\tilde{\sigma }}_2$ to the unbiased estimator ${\widehat{\sigma }}_2$ using female hook-billed kite data from Section 3. We start with an $n=10$-sized random sample drawn from observations of X and arranged in ascending order of magnitude. The ordered observations are 178, 179, 186, 186, 188, 189, 196, 197, 200, and 209. The corresponding COS are 268, 257, 262, 266, 280, 262, 285, 285, 272, and 305. Based on this, using (43), the moment-type estimator of $\xi$ is obtained as $\widehat{\xi }=2.94$. Since $-1\le \xi \le 1$, and the estimated value of $\xi$ falls outside of this range, $\widehat{\xi }=1$, the highest permissible value, is chosen for the moment-type estimate of $\xi$. As a result, the BLUE ${\tilde{\sigma }}_2$ is calculated as ${\tilde{\sigma }}_2=137.93$ and its variance as $Var\left({\tilde{\sigma }}_2\right)=0.04$. Again, the value of the unbiased estimator ${\widehat{\sigma }}_2$ is obtained as ${\widehat{\sigma }}_2=137.10$, and its variance is obtained as $Var\left({\widehat{\sigma }}_2\right)=0.50$. As a result, we conclude that ${\tilde{\sigma }}_2$ is a better estimator than ${\widehat{\sigma }}_2$.

7. Conclusions

By utilizing the FGM methodology, a bivariate variant of the ME distribution was derived in this article, and using two real-life data sets, its competitiveness with other well-known FGM distributions was discussed. Furthermore, the distribution theory of the COS arising from the FGMBME distribution was thoroughly studied. The best linear unbiased estimator (BLUE) of the parameter associated with the variable of primary interest was derived. BLUE’s efficacy in comparison with the respective unbiased estimator generated was evaluated. Empirical evidence supports the efficiency of BLUE. In light of this article, we recommend that one should take into account the FGMBME distribution rather than the FGMBE distribution and the FGMBB distribution for modeling some bivariate real-life datasets.