Abstract
Paired outcomes are common in correlated clustered data where the main aim is to compare the distributions of the outcomes in a pair. In such clustered paired data, informative cluster sizes can occur when the number of pairs in a cluster (i.e., a cluster size) is correlated to the paired outcomes or the paired differences. There have been some attempts to develop robust rank-based tests for comparing paired outcomes in such complex clustered data. Most of these existing rank tests developed for paired outcomes in clustered data compare the marginal distributions in a pair and ignore any covariate effect on the outcomes. However, when potentially important covariate data is available in observational studies, ignoring these covariate effects on the outcomes can result in a flawed inference. In this article, using rank based weighted estimating equations, we propose a robust procedure for covariate effect adjusted comparison of paired outcomes in a clustered data that can also address the issue of informative cluster size. Through simulated scenarios and real-life neuroimaging data, we demonstrate the importance of considering covariate effects during paired testing and robust performances of our proposed method in covariate adjusted paired comparisons in complex clustered data settings.
1. Introduction
Paired outcomes are very common in various fields of study. Data with paired observations can often be seen in health and social studies, which include results of the same test before and after an intervention, outcomes from crossover clinical trials where the same subject is assigned two treatment arms at two different time points in the same trial, measurements on the left and right eyes of the same person, and observations from twin studies involving identical or fraternal twins. For comparing the distributions of such paired outcomes, a paired-t test is a widely used approach. However, the strong distributional assumption of a paired-t test makes it unfavorable for non-normal data. As an alternative nonparametric approach, a Wilcoxon signed-rank test is very popular for comparing the paired outcomes.
The Wilcoxon signed-rank test is only valid for independent and identically distributed pairs. In practice, not all data is independently distributed as there can be correlated datasets. One type of correlated data is clustered data where outcomes within a cluster are correlated while outcomes between different clusters may be independent. Several methods have been developed for inference on different types of outcomes from clustered data including comparison of continuous outcomes from independent groups [1,2,3,4], categorical outcomes [5], longitudinal outcomes [6], and censored time-to-event outcomes [7]. Apart from these aforementioned outcomes, another type of outcome which can exist in clustered data is paired outcomes. Such paired outcomes in clustered data can be observed in dental studies involving multiple individuals where measurement of attachment loss in each tooth is carried out at two different locations (e.g., buccal and mesial) of the same tooth. Here, individuals are clusters and attachment loss scores from buccal and mesial site of the same tooth form a paired outcome resulting in many paired observations within each cluster. Paired clustered data can also be obtained from large crossover clinical trials with two treatment arms and a washout period. Here, a trial participant forms a cluster while the outcome measurements before and after a treatment form a pair in that cluster. Since in a crossover trial every participant is allocated to both the competing treatment arms, separated by a washout period to remove prior treatment effects, each cluster has multiple pairs of observations. In these types of clustered paired data, the traditional Wilcoxon signed-rank test do not work as it fails to account for the correlated nature of the data. As a result, there have been a number of attempts in the past to develop signed-rank test for clustered data [8,9,10].
The signed-rank test by Rosner, Glynn, and Lee [10] is one of the earliest signed-rank tests developed for clustered data under the assumption of a common intra-cluster correlation structure across different clusters. Later, Datta and Satten [8] developed a more flexible signed-rank testing approach for clustered data that considers informative cluster size scenarios using the idea of within-cluster resampling [11]. Informative cluster sizes occur when the cluster size (i.e., the number of units (pairs) within a cluster) is correlated with the outcome in that cluster. Such informative cluster sizes can exist in a dental study when comparing the buccal and mesial attachment loss scores in an aged population. This is because the number of teeth (cluster size) in an aged individual (cluster) is indicative of the overall attachment loss (outcome) of that individual. Another example of a potentially informative cluster size can be considered while analyzing neuroimaging data of individuals suffering from dementia or Alzheimer’s disease. In this case, the number of imaging sessions, conducted on a patient, is the cluster size that may be related to the disease severity outcome.
The signed-rank tests discussed above are tests developed for marginal comparison of outcomes in a pair. These tests do not take into account any covariate information while comparing the outcome distributions in a pair. However, in many situations, there may exist potentially important covariate information in the data, which can significantly impact the outcomes and, hence, the paired comparison results. Ignoring available covariate information for marginal analyses of outcomes can lead to incomplete inference and, consequently, can result in inaccurate or biased findings. For example, in longitudinal neuroimaging data, it can be interesting to examine whether certain metrics of cognitive abilities of individuals who are at risk of cognitive impairment have significantly changed over the period of study. This can be obtained through the multiple MRI scans performed during their successive clinic visits. In this case, the data is clustered as each individual represents a cluster while there exists a possibility of informative cluster sizes since the number of visits (cluster size) may be associated with the severity of the impairment. However, it is also known that age impacts cognitive abilities of individuals and the effect of age on cognitive abilities can become significant in older population. Therefore, even if we find some significant changes in cognitive metrics over a certain period of study, those changes cannot be solely attributed to some cognitive disorder as age may have also contributed to the change in those cognitive abilities. Therefore, ignoring the age information during a marginal analysis may leave the effect of the age on the outcome, unadjusted leading to a possibility of biased inference. It becomes essential to adjust for the effect of such important covariates while performing pairwise comparison of outcomes in a clustered data. This highlights the need of a robust approach that can perform hypothesis testing of paired outcomes while incorporating information on and adjusting for the effect of important covariates. Motivated by this need, in this article, we develop a method for the covariate adjusted pairwise comparison of the outcomes in clustered data while maintaining a rank-based approach that is robust to the choice of outcome distribution. We discuss the different scenarios of clustered data, where the cluster sizes can be informative and where they can be uninformative, and how we can apply our covariate adjusted testing approach to address both types of clustered data. We show that the proposed covariate adjusted testing methodology maintains the correct size and has substantial power in different simulated scenarios of clustered data and performs better than the marginal signed rank tests and a standard parametric linear mixed effects method. Through neuroimaging data, we demonstrate the applicability of our method in obtaining meaningful results.
The rest of the article is organized in the following way. In Section 2, we introduce the notations, discuss the different types of marginal hypothesis that can be framed for a clustered data and their implications. We also develop, in this section, our rank-based covariate adjusted testing mechanism for paired comparison that can be used for clustered data when the cluster sizes are informative as well as in situations when the cluster sizes appear to be uninformative. In Section 3, we explore the performances of our covariate adjusted testing methodology through different simulated scenarios of clustered data. In Section 4, we return to the neuroimaging data example for the application of our method. Finally, the article ends with a discussion in Section 5.
2. Methods
2.1. Preliminaries
Let M denote the number of clusters and the number of matched pairs in the ith cluster is Ni. Let Yij denote the pair-specific difference in outcome for the jth pair in the ith cluster, 1 ≤ j ≤ Ni, 1 ≤ i ≤ M. The null hypothesis we considered was that the marginal distribution of the paired difference for a randomly chosen pair in a randomly chosen cluster is symmetric around 0 (i.e., H0:F is symmetric around 0), where is the distribution function of a typical pair-specific outcome difference. This marginal distribution function can be interpreted in different ways for a clustered data. If is the empirical analog of this marginal distribution function, then we can express in one of the following two ways.
where and I is a binary indicator function. Note that in (1) every paired difference contributes equally to the construction of the marginal distribution function. Hence, every paired unit receives equal weight in . However, in (2) contribution of a paired difference to the construction of the marginal distribution function depended on the cluster to which the pair belonged. In , pairs belonging to a typical cluster i received a weight , which was the inverse of its cluster size. Therefore, a pair from a larger cluster received smaller weight than a pair from a smaller cluster. It was important to determine which of the two forms, or , would be the appropriate choice for the empirical version of the marginal distribution function F for a given clustered data. If the cluster size was informative and the number of units within a cluster was correlated with the outcome variable in that cluster, then preferring over would seem more appropriate. On the other hand, if there were no informativeness in cluster sizes, then using would be good enough.
2.2. Proposed Covariate Adjusted Ranked Residual Based Signed Rank Tests for Clustered Data
In this section, our main aim is to develop a signed rank test for marginal hypothesis while accounting for the effects of additional covariate(s) on the outcome variable. For developing such a covariate-adjusted signed rank test in a clustered data, we adopted a robust rank-based regression technique for computing covariate-adjusted residuals and use these residuals, in place of the raw outcomes, for the signed rank testing. The detailed steps for this method are explained in the next two sub-sections.
2.2.1. Rank Based Estimation of Covariate Effects and Residual Formation
At first, we will discuss the process of obtaining covariate-adjusted residuals. There exists a number of approaches for modeling covariate effects in clustered data settings as discussed in [12]. However, instead of extending one of those methods for our setting, we accounted for the effects of the covariates through a rank-based estimating equation approach. In doing this, we maintained a uniform rank-based, distribution-free structure in both covariate effect estimation and hypothesis testing of paired differences in a clustered data.
Let the impact of the covariate vector X on the pair-specific outcome difference variable Y be modeled through the following linear regression model:
Here, Xij is the covariate effect on unit j in cluster i, βT is the regression coefficient vector denoting the impact of the covariate, and ϵij are the model errors for the cluster i. We assumed that the ϵij, which may be correlated for a given cluster i, had a common cluster-specific continuous distribution. Note that the errors were free of any location constraint, which is reflected through the absence of an intercept term in the above model. Our aim was to estimate the unknown parameter β and use this estimate to calculate the residuals which would be free from the effects of the covariate. Subsequently, these residuals would be used as covariate adjusted paired differences for hypothesis testing. For estimating β, we employed a rank-based approach (R-estimation) where we minimized the following weighted score function.
Here, , , and wij is the weight associated with the jth paired difference in the cluster i. The choice of wij can be an important factor in the resulting rank-based inference. We proposed the use of , where any paired difference in outcome from a typical cluster i was given a weight equal to the inverse of its cluster size (Ni). Such a choice addressed the issue of informative cluster sizes by involving (in Section 2.1) and has reasonable performances even if the cluster sizes were not informative, as shown later in Section 3. Suppose is the value (R-estimator) of β that minimizes R(β). The large sample properties of this R-estimator can be obtained through the following theorem:
Theorem 1.
Under H0, as M → ∞, under certain regularity conditions, where , , , , while f and f′ are first and second derivatives of F.
An outline of the proof of Theorem 1 is provided in the Appendix A section.
Once we obtained the R-estimator of β, i.e., , the residuals could be obtained as
This Uij was the modified paired difference, which was free from the effects of the covariates and was used as a proxy for the original paired difference Yij in constructing the marginal signed rank test statistic in the next step. These covariate-adjusted residuals belonged to the category of aligned- residuals, which were constructed to remove any unwanted effects of nuisance variables on the outcome before performing a rank-based test on the outcome. The resulting rank test is, often, known as an aligned rank test [13].
2.2.2. Signed-Rank Test Based on the Covariate-Adjusted Residual
We constructed a signed-rank test for clustered data based on the previously obtained covariate adjusted residuals or aligned residuals of paired differences in Section 2.2.1. For the signed-rank testing, we explored two different approaches:
- (i.)
- The first approach was the signed-rank testing developed by Rosner, Glynn, and Lee [10], which was mainly aimed for comparing marginal distributions under uninformative cluster sizes. This was equivalent to a test involving .
- (ii.)
- The second approach was based on the signed-rank testing developed by Datta and Satten [8], which aimed to compare marginal distributions under informative cluster sizes. This was equivalent to the testing marginal distributions involving .
We will refer the testing approach (i) as uninformative covariate adjusted signed-rank testing (UCAST) and the testing approach (ii) as informative covariate adjusted signed-rank testing (ICAST).
For constructing both ICAST and UCAST, we denoted Rij as the rank of |Uij| among the set of absolute values of the residuals {|Uij|, 1 ≤ j ≤ Nij, 1 ≤ i ≤ M}. Further, we denoted Vij = sign(Uij) and Qij = VijRij. Then, the test statistic for the UCAST approach was obtained as
where , and under the null hypothesis where the variance estimator was obtained assuming a shared correlation coefficient as shown in Rosner, Glynn, and Lee [10]. Under H0, the large sample distribution of the standardized statistic , where was a standard normal distribution under mild regularity conditions as described in Rosner Glynn, and Lee [10].
For describing the ICAST, we denoted , I(.) being a binary indicator function, and . Then, following Datta and Satten [8], the test statistic for ICAST was defined as
where and . The standardized followed a standard normal distribution asymptotically where and .
3. Simulation Studies
We conducted two simulation studies in this section. In the first simulation scenario, the cluster sizes varied among different clusters, but these cluster sizes were uninformative. The second simulation scenario considered clustered data, where the cluster sizes were informative (i.e., the cluster sizes are correlated with the outcome of interest). In each of these simulated scenarios, we evaluated the performances, namely size (type-I error rate) and power, of ICAST and UCAST methods. Moreover, we compared the performances of these methods with the marginal signed-rank tests of both Rosner, Glynn, and Lee [10] and Datta and Satten [8]. We abbreviated these two marginal signed-rank testing methods as RGL and DS, respectively. In addition, we compared the performances of ICAST and UCAST with a parametric linear mixed model (LMM) [14], which involved a fixed effect for covariate and a random cluster effect. The size and power computations for each of the abovementioned testing approaches were based on 500 Monte-Carlo repetitions under a fixed nominal size (type-I error) of 0.05. The empirical size (type-I error rate) and power were calculated as the proportion of total Monte Carlo replicates in which the null hypothesis was rejected. Note that, in this setting, if the empirical size of any method largely exceeded 0.05, then that testing approach was unacceptable for testing these hypotheses irrespective of its power.
3.1. Simulation Scenario 1
In this simulation scenario, we considered clustered data with uninformative cluster size where the marginal distribution of pairwise difference in a cluster did not depend on its cluster size. Extending the simulation settings of Rosner, Glynn, and Lee [10] and Datta and Satten [8], we generated the pairwise differences as
where Xij∼N(0,1), β = 5, ϵij = Rijexp(|Bij|), Bij = Aij + Eij, Ai∼N(0,0.25), Eij∼N(0,0.75), and 1 ≤ j ≤ Ni, 1 ≤ i ≤ M. For generating Rij, we first generated pi, from a Beta(1,b) distribution for each 1 ≤ i ≤ M. If pi ≤ 0.5, then Rij = 1, or else Rij = −1. Here, M was fixed (either 10 or 25), but for each i, Ni was generated as Ni = Ni* + 1 where Ni*∼Binomial(7,0.5). In this scenario, the cluster size Ni, for typical cluster i, was a random variable which was independent of the outcome variable Yij. Note that, b = 1 represented the marginal null hypothesis H0. For power calculations, one could choose any positive value of b other than 1. For our simulations, we chose three different values of b (0.15, 0.3, 0.6) to investigate and compare the power performances of all the methods under consideration.
Table 1 displays the results relating to the performances of all the methods in this simulated scenario. From Table 1, we found that both the covariate-adjusted methods of ICAST and UCAST maintain the nominal size of 0.05 and had similar power performance patterns for both choices of M. The powers of both methods increased with the increase in the number of clusters with the ICAST having slightly increased power in the case of smaller sample size (M = 10). The marginal signed-rank testing methods (i.e., the Datta-Satten (DS) test and the Rosner-Glynn-Lee (RGL) test) maintained the nominal size of 0.05 but have extremely low power compared to ICAST and UCAST for both small and large number of clusters. This showed that there was a substantial loss of power for ignoring the effect of covariates on the outcomes. The parametric LMM approach has a highly inflated empirical size, much higher than the nominal size of 0.05, making them unacceptable for this simulated scenario. This was mainly because the underlying skewed distributions of the outcomes make the standard parametric mixed effects model unsuitable for this analysis. Overall, we observed that both ICAST and UCAST methods were appropriate for this scenario of uninformative cluster sizes and, hence, either of them can be considered for testing the marginal null hypothesis H0 in presence of covariates.

Table 1.
Empirical size (type-I error rate) and power performances of different methods for clustered data with uninformative cluster sizes under Simulation Scenario 1. Here M is the number of clusters and b represents the true effect-size where b = 1 denotes H0 is true and any other value of b denotes H0 is false. The nominal/target size (type-I error rate) is 0.05 and empirical size of any valid test should not exceed 0.05 irrespective of its power.
3.2. Simulation Scenario 2
In this simulation scenario, we considered clustered data with informative cluster size where the marginal distribution of pairwise difference in a cluster was correlated to the cluster size. Here, we generated the pairwise differences through the same model, as in Section 3.1, with the same model parameters except for the generation of cluster size Ni for each 1 ≤ i ≤ M. In this case, Ni = 2 if pi ≤ 0.5 and Ni = 8 if pi > 0.5. Recall that, pi is generated from a Beta(1,b) for each 1 ≤ i ≤ M and contributes to the generation of the paired differences Yij through the quantity ϵij as shown in Section 3.1. Therefore, for a typical cluster i, the cluster size Ni and the paired outcome differences Yij were correlated leading to an informative cluster size scenario. For the size calculation we simulated the data under H0 which was equivalent to choosing b = 1 while for the power calculations we retained the previous set of values of b as (0.15, 0.3, 0.6).
The performances of all the methods in this simulated scenario of informative cluster size are shown in Table 2. ICAST closely maintained the nominal size of 0.05 for both small and large number of clusters and its power increased with the increase in the number of clusters for all choices of b. The performance of UCAST, in this informative cluster size setting, was different from that in the uninformative cluster size scenario. Here, the empirical size of UCAST exceeded the nominal size of 0.05 for both small and large number of clusters indicating that the type-I error rate of UCAST can be higher than expected in case of an informative cluster size. The marginal DS test maintained the nominal size for M = 10 but narrowly exceeded the target size of 0.05 for M = 25. The power performance of DS method was, again, dismal with its power values drastically lower than the power of ICAST even for large number of clusters. The marginal test of RGL, on the other hand, had a grossly inflated empirical size (0.202) compared to the target size of 0.05 when the number of clusters is large. Even the power of RGL became lower than that of the ICAST and UCAST methods when the effect size b shifted further away (b = 0.3 or b = 0.15) from its null value (b = 1). These indicated the unsuitability of marginal RGL test for informative cluster size scenarios. An interesting fact, however, was that applying our proposed covariate effect adjustment technique on the marginal RGL test does lead to a significant reduction of the type-I error rate, as evident from the size value (0.067) of UCAST, although it still exceeded the nominal limit of 0.05 by a considerable margin. The parametric LMM had unacceptably high sizes values, much worse than its size under the uninformative cluster size scenario, due to the added complexity of informative cluster size which the standard LMM does not address. Hence, the standard parametric LMM was inappropriate in presence of informative cluster sizes. Overall, we found that ICAST is the only method that, simultaneously, maintained the empirical size close to the nominal size and had adequate power for the informative cluster size scenario.

Table 2.
Empirical size (type-I error rate) and power performances of different methods for clustered data with informative cluster sizes under Simulation Scenario 2. Here M is the number of clusters and b represents the true effect-size where b = 1 denotes H0 is true and any other value of b denotes H0 is false. The nominal/target size (type-I error rate) is 0.05 and empirical size of any valid test should not exceed 0.05 irrespective of its power.
4. An Application to Open Access Series of Imaging Studies (OASIS) Data
The Open Access Series of Imaging Studies (OASIS) [15] is a collection of neuroimaging data sets that are publicly available and contains magnetic resonance imaging (MRI) data from brains of hundreds of individuals including dementia and Alzheimer patients as well as nondemented individuals. In this section, we focus on a longitudinal data [16] from the OASIS platform that involves MRI data of 150 individuals who have visited the clinic two or more times separated by at least a year. These individuals included 72 subjects who have been classified as non-demented throughout the entire period of study and 78 subjects who were identified as demented and/or suffering from Alzheimer’s Disease (AD) at some point during this study. Among the different variables computed from the MRI scans of brain, a variable of interest is the total intracranial volume (TIV) that has been, in the past, linked to cognitive impairments and development of dementia or AD in certain individuals [17,18]. A normalization factor called atlas scoring factor (ASF) [19], proportional to TIV, is often measured in neuroimaging studies and is available from the OASIS longitudinal data. In this longitudinal study, an interesting question to consider is whether the ASF values, and hence the TIV levels, change over time that may be indicative of the changes or time trends in cognitive abilities of these individuals under study.
To answer this question, we use the change in ASF values, obtained from the MRI scans, during successive visits of an individual as the pairwise difference in the outcome. In that case, a hypothesis of no change over time would be equivalent to the null hypothesis of symmetry (about 0) of the distribution of the paired differences in ASF values. This scenario represents a clustered data where each individual is a cluster, and we have 150 clusters with one or more paired differences since all these individuals have at least two visits for MRI scans during the period of the study. Note that the number of visits vary by individuals, and it is possible that the frequency of visits for individuals suffering from cognitive impairments, e.g., demented individuals and AD patients, may be different from that of the nondemented group of individuals. Figure 1 compares the distributions of number of visits between the demented group and the nondemented group. Combining the numbers from Figure 1, we find that among the demented group of individuals only 23% had three or more visits, while more than 47% of nondemented individuals visited the MRI clinics three or more times. Such discrepancies in the number of visits between the two groups can be related to the fact that demented individuals are more prone to be lost to follow-up due to the severity of their diseases and high mortality. Since every clinic visit generated an MRI scan, a cluster size is directly obtained from total number of visits by an individual. Hence, this situation gives rise to a possibility of an informative cluster size in this clustered data. For the testing of the null hypothesis of no change in ASF values over time in such a clustered data, one can use the marginal testing approach of DS that addresses the issue of informative cluster size. Application of the DS test yields a p-value of 0.0003. We also implement the marginal RGL testing approach that generates a p-value < 0.0001. In both cases the null hypothesis of symmetry appears to be rejected with highly significant p-values indicating that the distribution of paired differences is highly asymmetric around 0 and the ASF values changed over the time period of study.
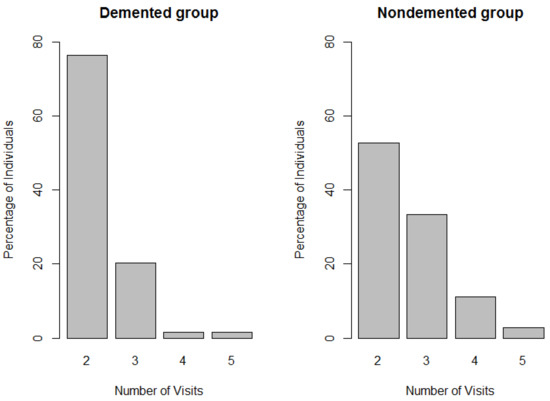
Figure 1.
Plot showing distribution of the number of visits in the demented group and the nondemented group of individuals.
These results, obtained from marginal tests of DS and RGL, do not account for effects of any covariate which may be associated with TIV or ASF values. However, certain covariates, that are available from the data, may have important effects on TIV that needs to be monitored or adjusted for while carrying out the testing of pairwise differences of ASF. One such important covariate is age of an individual. In recent studies [20], it has been found out that age, especially in older individuals, affects the intracranial volume. It would be interesting to see if the conclusion of change in ASF values over time remains consistent after adjusting for the effect of age as this longitudinal study contains many aged individuals. For this analysis, we need to apply the covariate adjusted testing approaches of ICAST and UCAST with age as the adjusted additional covariate. The estimated age coefficient, obtained through the relevant R-estimation of ICAST and UCAST, is −0.008 indicating that higher age is associated with lower ASF values and larger cognitive impairment which is consistent with the findings in other recent studies [20]. The signed-rank tests of ICAST and UCAST produce a p-value of 0.050 and 0.049, respectively. The ICAST and UCAST p-values show that the previously obtained highly significant changes in ASF over time can no longer be concluded once the effect of the age covariate is considered. Rather, the age adjusted ICAST and UCAST results indicate only a marginally significant ASF change, if any, over time at 5% level of significance. Figure 2 shows the weighted histogram of paired differences of ASF values with inverse cluster size weights while Figure 3 shows the unweighted histogram of same paired differences of ASF values. From these figures, it appears that the distribution of paired differences may be only marginally asymmetric supporting the borderline significant p-values of the ICAST and UCAST approaches. Therefore, it is demonstrated that adjusting for the effects of potentially important covariates, while performing marginal hypothesis testing of paired outcome differences, can play important role in obtaining accurate inference.
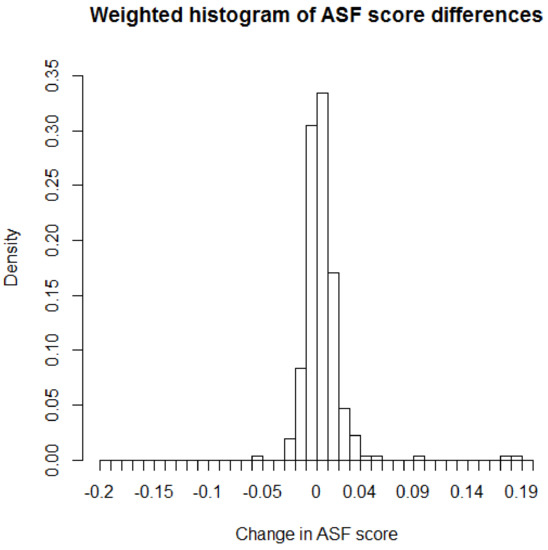
Figure 2.
Plot showing inverse cluster size weighted histogram of ASF score differences.
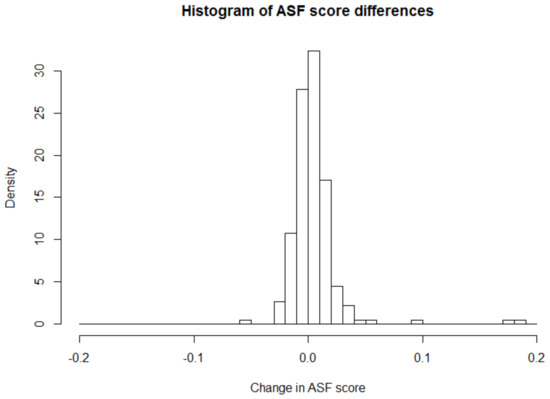
Figure 3.
Plot showing unweighted histogram of ASF score differences.
5. Discussion
Rank based tests are popular nonparametric hypotheses testing approaches when distributions of outcomes tend to be non-normal with the signed rank test being one such test widely used for the comparison of marginal distributions of paired outcomes. Signed rank tests have been extended to different types of clustered data including the ones where the cluster sizes are informative. Most of these existing signed rank tests compare marginal distributions of paired outcomes without considering any additional covariate effect on the outcomes. However, ignoring available covariate information during paired comparisons can result in inaccurate inferences as discussed in Section 1 and evident from the OASIS neuroimaging data analysis in Section 4. Based on this need to develop a hypothesis testing mechanism for paired outcomes that can adjust for the effect of covariates, we proposed a robust rank-based procedure of covariate effect adjustment while carrying out hypothesis testing in a clustered data framework. Our method addresses the issue of informative cluster sizes and performs well even if the cluster sizes are uninformative as presented through the extensive simulation results in Section 3.
In this article we have outlined covariate adjusted signed rank testing procedure for two types of clustered data, namely, a testing procedure in presence of informative cluster size (ICAST) and a testing procedure when the cluster sizes are uninformative (UCAST). The determination of the most appropriate choice between these two testing procedures would depend on the research aim of the investigator and the type of marginal distributions ( or ) to be compared. Note that another deciding factor in this context can be the identification of the primary unit of sampling and inference. In case the primary sampling unit is a cluster, ICAST may be preferred over UCAST as all the clusters receive the same weight under ICAST. On the other hand, if the primary sampling unit is a member within a cluster and the cluster sizes are not expected to be informative, UCAST can be preferred. Following this idea, one can prefer to choose ICAST over UCAST in the OASIS neuroimaging data analysis in Section 4 since the primary unit of inference is a patient undergoing the MRI scans and not the pair of successive MRI scans.
In addition to the potential areas of real-life application mentioned in Section 1 and Section 4, our proposed method can also be applied in analyzing data arising from cluster-randomized trials. In such a trial, the clusters are randomized, and an intervention is administered to a whole cluster (i.e., all the units in a cluster receive the same intervention). If the intervention is a drug under trial while the patients are units within hospitals (clusters), then our method can be applied for testing the drug efficacy. Here, the outcomes obtained for each patient before and after receiving the drug form paired outcomes and we have multiple pairs from multiple patients in a cluster. Then, we can use our proposed method to adjust for the effects of the available covariates in each patient while comparing the pre-intervention and post-intervention outcomes.
In our rank-based covariate adjustment procedure, we have assumed a linear model framework without making any strong distributional assumptions. This type of model is applicable to any continuous response even if the underlying distribution is asymmetric. This rank-based covariate adjustment procedure can be extended to other types of non-continuous responses as well through generalized linear model frameworks (e.g., count model for discrete count responses). We plan to pursue such non-continuous outcome modeling in future. However, a limitation of this type of covariate adjusted rank-based testing is that it cannot be used for binary outcomes due to the infeasibility of ranking in those outcomes. Our proposed method is a two-step procedure where we perform covariate effect adjustment on the outcomes at the first step and then test the distribution of the modified paired differences at the second step. An alternative approach could be to develop a one-step inference procedure that can simultaneously estimate the covariate effects using ranks and perform rank-based testing under informative cluster sizes. Such an approach is an area of potential future research on rank-based inference.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the reviewers for their insightful comments and suggestions which have greatly helped in improving the article.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Outline of the proof of Theorem 1
Without loss of generality, let us assume that true value of the parameter β is 0. The R-estimator of β, i.e., , is obtained as the solution to estimating equation
Then, following the results of Datta and Beck [21], we can get
where ∑ is defined in Section 2.2.1. Next, following the expansions of R-estimators from Chapter 3 of Hettmansperger and McKean [22], we can obtain
in a local neighborhood of 0. Here, τ is the same as defined in Section 2.2.1.
Then, denoting and combining (A1) (where β = 0), (A2), and (A3), we have
References
- Datta, S.; Satten, G.A. Rank-sum tests for clustered data. J. Am. Stat. Assoc. 2005, 100, 908–915. [Google Scholar] [CrossRef]
- Dutta, S.; Datta, S. A rank-sum test for clustered data when the number of subjects in a group within a cluster is informative. Biometrics 2016, 72, 432–440. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Datta, S. Rank-based inference for covariate and group effects in clustered data in presence of informative intra-cluster group size. Stat. Med. 2018, 37, 4807–4822. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B.; Glynn, R.J.; Lee, M.L.T. Incorporation of clustering effects for the Wilcoxon rank sum test: A large-sample approach. Biometrics 2003, 59, 1089–1098. [Google Scholar] [CrossRef] [PubMed]
- Gregg, M.; Datta, S.; Lorenz, D. Variance estimation in tests of clustered categorical data with informative cluster size. Stat. Methods Med. Res. 2020, 29, 3396–3408. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Kong, M.; Datta, S. Inference for marginal linear models for clustered longitudinal data with potentially informative cluster sizes. Stat. Methods Med. Res. 2011, 20, 347–367. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Sun, J. Regression analysis of clustered interval-censored failure time data with informative cluster size. Comput. Stat. Data Anal. 2010, 54, 1817–1823. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Satten, G.A. A signed-rank test for clustered data. Biometrics 2008, 64, 501–507. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Nevalainen, J.; Oja, H. A general class of signed-rank tests for clustered data when the cluster size is potentially informative. J. Nonparametr. Stat. 2012, 24, 797–808. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B.; Glynn, R.J.; Lee, M.L. The Wilcoxon signed rank test for paired comparisons of clustered data. Biometrics 2006, 62, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, E.B.; Sen, P.K.; Weinberg, C.R. Within-cluster resampling. Biometrika 2001, 88, 1121–1134. [Google Scholar] [CrossRef]
- Seaman, S.; Pavlou, M.; Copas, A. Review of methods for handling confounding by cluster and informative cluster size in clustered data. Stat. Med. 2014, 33, 5371–5387. [Google Scholar] [CrossRef] [PubMed]
- Hájek, J.; Šidák, Z.; Sen, P.K. Theory of Rank Tests; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- McCulloch, C.E.; Searle, S.R. Generalized, Linear, and Mixed Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Marcus, D.S.; Wang, T.H.; Parker, J.; Csernansky, J.G.; Morris, J.C.; Buckner, R.L. Open Access Series of Imaging Studies (OASIS): Cross-sectional MRI data in young, middle aged, nondemented, and demented older adults. J. Cognit. Neurosci. 2007, 19, 1498–1507. [Google Scholar] [CrossRef] [PubMed]
- Marcus, D.S.; Fotenos, A.F.; Csernansky, J.G.; Morris, J.C.; Buckner, R.L. Open access series of imaging studies: Longitudinal MRI data in nondemented and demented older adults. J. Cognit. Neurosci. 2010, 22, 2677–2684. [Google Scholar] [CrossRef] [PubMed]
- Schofield, P.W.; Mosesson, R.E.; Stern, Y.; Mayeux, R. The age at onset of Alzheimer’s disease and an intracranial area measurement: A relationship. Arch. Neurol. 1995, 52, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Schofield, P.W.; Logroscino, G.; Andrews, H.F.; Albert, S.; Stern, Y. An association between head circumference and Alzheimer’s disease in a population-based study of aging and dementia. Neurology 1997, 49, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Buckner, R.L.; Head, D.; Parker, J.; Fotenos, A.F.; Marcus, D.; Morris, J.C.; Snyder, A.Z. A unified approach for morphometric and functional data analysis in young, old, and demented adults using automated atlas-based head size normalization: Reliability and validation against manual measurement of total intracranial volume. NeuroImage 2004, 23, 724–738. [Google Scholar] [CrossRef] [PubMed]
- Caspi, Y.; Brouwer, R.M.; Schnack, H.G.; van de Nieuwenhuijzen, M.E.; Cahn, W.; Kahn, R.S.; Niessen, W.J.; van der Lugt, A.; Pol, H.H. Changes in the intracranial volume from early adulthood to the sixth decade of life: A longitudinal study. NeuroImage 2020, 220, 116842. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Beck, J.D. Robust estimation of marginal regression parameters in clustered data. Stat. Modell. 2014, 14, 489–501. [Google Scholar] [CrossRef] [PubMed]
- Hettmansperger, T.P.; McKean, J.W. Robust Nonparametric Statistical Methods, 2nd ed.; Chapman & Hall: New York, NY, USA, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).