Point Cloud Registration via Heuristic Reward Reinforcement Learning
Abstract
:1. Introduction
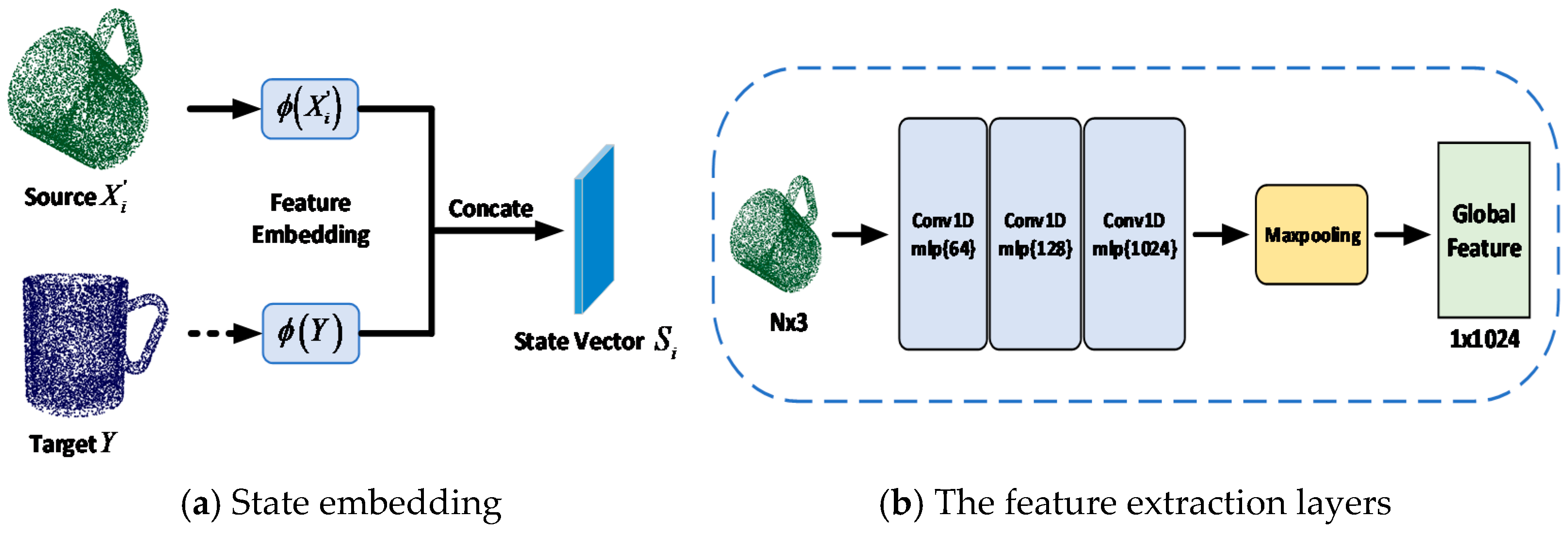
- First, to enrich the encoding process, an improved state-embedding module is proposed. It combines EdgeConv to capture the local features of relative coordinates, reflecting the key information of two point cloud positions among the current state.
- Second, a heuristic reward function is proposed. Unlike the invariable penalty in each step, the newly designed reward function allows aggressive attempts at the beginning when the environment is still unclear.
- Finally, the new method with an improved state-embedding module and the heuristic reward function is evaluated on two public datasets as well as real-world data of train components. The experimental results show that the new method effectively reduces the errors in rotation and translation, and can lead to more precise point cloud registration.
2. Related Work
3. Methodology
3.1. Point Cloud Registration Network and ReAgent
3.2. Feature Extraction and an Improved State-Embedding Module
3.3. Heuristic Reward Function in RL
4. Experimental Results
4.1. Registration on ModelNet40
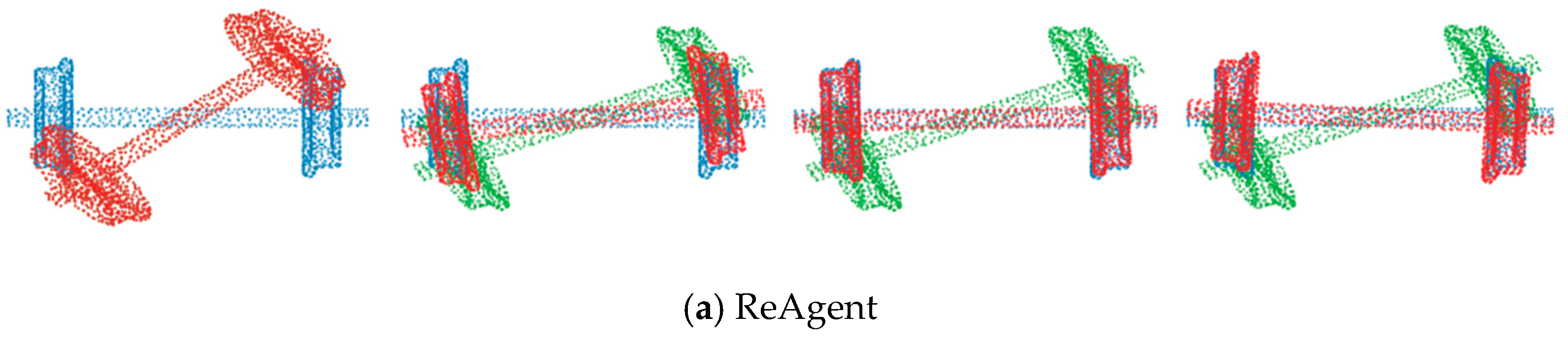
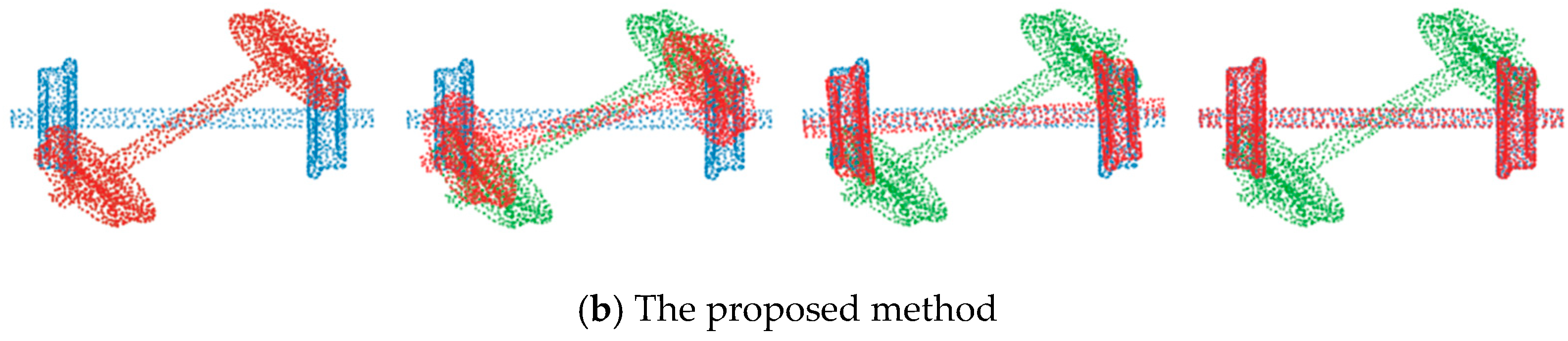
4.2. Robustness Test
4.3. Experiment on ScanobjectNN and Other Real-World Data
5. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Hartley, R. The 3D-3D registration problem revisited. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio De Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Yang, B.; Zang, Y. Automated registration of dense terrestrial laser-scanning point clouds using curves. ISPRS J. Photogramm. Remote Sens. 2014, 95, 109–121. [Google Scholar] [CrossRef]
- He, B.; Lin, Z.; Li, Y.F. An automatic registration algorithm for the scattered point clouds based on the curvature feature. Opt. Laser Technol. 2013, 46, 53–60. [Google Scholar] [CrossRef]
- Bauer, D.; Patten, T.; Vincze, M. Reagent: Point cloud registration using imitation and reinforcement learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14586–14594. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Johnson, A.E. Spin-Images: A Representation for 3-D Surface Matching. Ph.D. Thesis, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, USA, 1997. [Google Scholar]
- Tombari, F.; Salti, S.; Stefano, L.D. Unique signatures of histograms for local surface description. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 356–369. [Google Scholar]
- Oomori, S.; Nishida, T.; Kurogi, S. Point cloud matching using singular value decomposition. Artif. Life Robot. 2016, 21, 149–154. [Google Scholar] [CrossRef]
- Taati, B.; Greenspan, M. Local shape descriptor selection for object recognition in range data. Comput. Vis. Image Underst. 2011, 115, 681–694. [Google Scholar] [CrossRef]
- Papazov, C.; Haddadin, S.; Parusel, S.; Krieger, K.; Burschka, D. Rigid 3D geometry matching for grasping of known objects in cluttered scenes. Int. J. Robot. Res. 2012, 31, 538–553. [Google Scholar] [CrossRef]
- Hong, S.; Ko, H.; Kim, J. VICP: Velocity updating iterative closest point algorithm. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 1893–1898. [Google Scholar]
- Yang, J.; Li, H.; Jia, Y. Go-icp: Solving 3d registration efficiently and globally optimally. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1457–1464. [Google Scholar]
- Censi, A. An ICP variant using a point-to-line metric. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 19–25. [Google Scholar]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. In ACM SIGGRAPH 2008 Papers; ACM: New York, NY, USA, 2008; pp. 1–10. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 2–8 December 2018; Volume 31. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9621–9630. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8895–8904. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3523–3532. [Google Scholar]
- Zhu, T.; Ma, M.H. Deriving the Optimal Strategy for the Two Dice Pig Game via Reinforcement Learning. Stats 2022, 5, 805–818. [Google Scholar] [CrossRef]
- Zhu, T.; Zhu, W. Quantitative trading through random perturbation Q-network with nonlinear transaction costs. Stats 2022, 5, 546–560. [Google Scholar] [CrossRef]
- Liao, R.; Miao, S.; de Tournemire, P.; Grbic, S.; Kamen, A.; Mansi, T.; Comaniciu, D. An artificial agent for robust image registration. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Ma, K.; Wang, J.; Singh, V.; Tamersoy, B.; Chang, Y.J.; Wimmer, A.; Chen, T. Multimodal image registration with deep context reinforcement learning. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2017; pp. 240–248. [Google Scholar]
- Ye, Z.; Xiao, K.; Ge, Y.; Deng, Y. Applying simulated annealing and parallel computing to the mobile sequential recommendation. IEEE Trans. Knowl. Data Eng. 2018, 31, 243–256. [Google Scholar] [CrossRef]
- Ye, Z.; Xiao, K.; Deng, Y. A unified theory of the mobile sequential recommendation problem. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; IEEE: New York, NY, USA, 2018; pp. 1380–1385. [Google Scholar]
- Xiao, K.; Ye, Z.; Zhang, L.; Zhou, W.; Ge, Y.; Deng, Y. Multi-user mobile sequential recommendation for route optimization. ACM Trans. Knowl. Discov. Data 2020, 14, 1–28. [Google Scholar] [CrossRef]
- Guo, P.; Ye, Z.; Xiao, K.; Zhu, W. Weighted aggregating stochastic gradient descent for parallel deep learning. IEEE Trans. Knowl. Data Eng. 2022, 34, 5037–5050. [Google Scholar] [CrossRef]
- Guo, P.; Xiao, K.; Ye, Z.; Zhu, H.; Zhu, W. Intelligent career planning via stochastic subsampling reinforcement learning. Sci. Rep. 2022, 12, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Xiao, K.; Ye, Z.; Zhu, W. Route optimization via environment-aware deep network and reinforcement learning. ACM Trans. Intell. Syst. Technol. 2021, 12, 1–21. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Yew, Z.J.; Lee, G.H. Rpm-net: Robust point matching using learned features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11824–11833. [Google Scholar]
- Uy, M.A.; Pham, Q.H.; Hua, B.S.; Nguyen, T.; Yeung, S.K. Revisiting point cloud classification: A new benchmark dataset and classification model on real-world data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1588–1597. [Google Scholar]
- Li, J.; Chen, B.; Yuan, M.; Zhao, Q.; Luo, L.; Gao, X. Matching Algorithm for 3D Point Cloud Recognition and Registration Based on Multi-Statistics Histogram Descriptors. Sensors 2022, 22, 417. [Google Scholar] [CrossRef] [PubMed]





| The First 20 Categories | The Second 20 Categories | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | ISO | MAE | ISO | T | |||||||
| R | T | R | T | ×0.001 | R | T | R | T | ×0.001 | (ms) | |
| DCP-v2 | 3.876 | 0.032 | 7.826 | 0.071 | 2.81 | 4.912 | 0.038 | 9.138 | 0.079 | 3.95 | 21 |
| PointNetLK | 1.912 | 0.013 | 3.826 | 0.028 | 1.12 | 1.853 | 0.017 | 3.812 | 0.032 | 1.62 | 42 |
| ReAgent IL + RL | 1.783 | 0.011 | 3.189 | 0.024 | 0.76 | 1.760 | 0.011 | 2.996 | 0.023 | 0.99 | 19 |
| Our method IL + RL | 1.588 | 0.011 | 3.134 | 0.024 | 0.78 | 1.557 | 0.010 | 2.897 | 0.022 | 1.00 | 26 |
| MAE | ISO | T | ||||
|---|---|---|---|---|---|---|
| R | T | R | T | ×0.001 | ms | |
| DCP-v2 | 8.760 | 0.081 | 17.320 | 0.163 | 5.08 | 53 |
| PointNetLK | 1.321 | 0.015 | 2.314 | 0.030 | 1.62 | 46 |
| ReAgent IL + RL | 1.449 | 0.012 | 2.789 | 0.025 | 0.75 | 22 |
| Our method IL + RL | 1.153 | 0.012 | 2.276 | 0.022 | 0.68 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B. Point Cloud Registration via Heuristic Reward Reinforcement Learning. Stats 2023, 6, 268-278. https://doi.org/10.3390/stats6010016
Chen B. Point Cloud Registration via Heuristic Reward Reinforcement Learning. Stats. 2023; 6(1):268-278. https://doi.org/10.3390/stats6010016
Chicago/Turabian StyleChen, Bingren. 2023. "Point Cloud Registration via Heuristic Reward Reinforcement Learning" Stats 6, no. 1: 268-278. https://doi.org/10.3390/stats6010016
APA StyleChen, B. (2023). Point Cloud Registration via Heuristic Reward Reinforcement Learning. Stats, 6(1), 268-278. https://doi.org/10.3390/stats6010016






