A New Class of Alternative Bivariate Kumaraswamy-Type Models: Properties and Applications
Abstract
1. Introduction
- Model In this case, we assume the joint density will be of the formwhere D is an appropriate normalizing constant which can be obtained throughSome representative plots of the bivariate density for varying parameter choices are given in Appendix A.In this case, the parametric restrictions are the following: , , and . The parameters and influence the correlation measure between the X and Y components of the distribution. Note that when , the joint density reduces to the product of two independent univariate KW random variables, particularly when and independently. Since the KW distribution has two shape parameters, it appears that the marginals of both X and Y have the same second shape parameter, specifically , but different first shape parameters, which are and , respectively. Potential application of such bivariate probability models can be envisioned in real-life scenarios where, for example, X and Y have data structures such that one characteristic is common to both of them, but the other one is different. The only factor that might work as a deterrent regarding the flexibility of such a model is how a practitioner can guarantee that restrictions such as and would be met in reality. Notice that since and one can easily observe that Additional discussion of the parameters is given in the structural properties section later. However, one may consider appropriate testing of the hypothesis as a part of model fitting regarding whether these parametric constraints are met.In the next section, we consider another bivariate KW-type model that we conjecture to have some flexibility in terms of modeling positively dependent data.
- Model Suppose that the joint density is of the formwhere C is an appropriate normalizing constant. Note that when , the joint density reduces to two independent KW random variables with respective parameters.Noticeably, when it appears that and independently. Therefore, by invoking independence via a linear constraint on the parameters, component-wise, the marginals of both X and Y follow a scaled version of a two-parameter univariate KW distribution with the scale factors and , respectively. Furthermore, this model is significantly different from the first proposed model in the sense that we bring in scale factors to capture the variability of X and and the shape parameters are different. This feature is different from the first model, in which the second shape parameter is the same for both X and Once again, as before, a natural objection that might occur in terms of application in modeling real-life data based on this probability model is how our informed expert can guarantee that for dependence modeling, the linear restriction is not satisfied. One simple strategy would be to simply consider a hypothesis test of independence, which can be written as follows:against the alternativeSome additional discussion on the parameters is given in the structural properties section for this model later.
- (1)
- The Gauss hypergeometric function is defined byIn addition, denotes the ascending factorial.
- (2)
- The series expansion is given by
2. Bivariate KW-Type Model 1 Structural Properties
2.1. Marginal Densities
- Observe that as Thus, the distribution of Y along the vertical boundary of the simplex belongs to a univariate KW distribution with two shape parameters: and The parameter represents the scale variation from a standard KW model.
- Likewise, as Therefore, the distribution of X along the vertical boundary of the simplex belongs to a univariate KW distribution with two shape parameters and The parameter represents the scale variation from a standard KW model.
2.2. Conditional Distributions
2.3. Marginal Moments
2.4. Product Moment
2.5. Distributional Properties
- The bivariate density in Equation (1) is positive regression-dependent (PRD) (i.e.,is decreasing in y for all and similarly, is decreasing in x for all y).
- Furthermore, the property of being PRD will imply that is non-decreasing in x for all y and that is non-increasing in x for all each of which imply that and , namely such that X and Y are positive quadrant-dependent (PQD).
3. Model 2’s Structural Properties
- Observe that as Thus, the distribution of Y along the vertical boundary of the simplex belongs to a univariate KW distribution with two shape parameters and The parameter represents the scale variation from a standard KW model.
- Likewise, as Thus, the distribution of Y along the vertical boundary of the simplex belongs to a univariate KW distribution with two shape parameters and The parameter represents the scale variation from a standard KW model.
Distributional Properties
4. Inference
4.1. Method of Moments Estimation
4.2. Maximum Likelihood Estimation
5. Simulation
- Generate independent Kumaraswamy random variables U and V with shape parameters and respectively.
- Generate a uniform [0, 1] random variable W independent from
- If , then accept as a realization from the bivariate density in Equation (1).
- If then return to step
6. Real Data Application
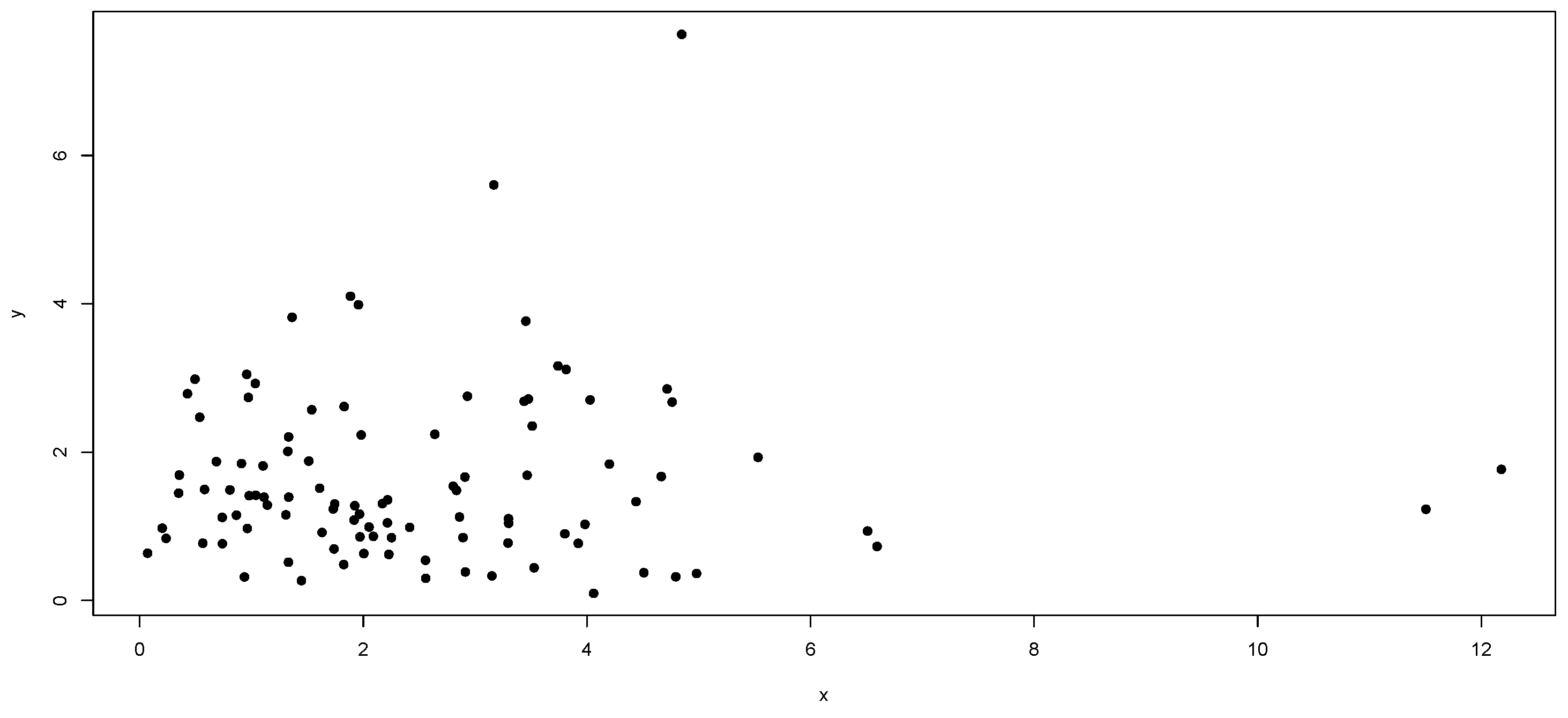
- Data Set I: Earthquakes become major societal risks when they strike vulnerable populations. We consider the data obtained from [7]. Due to the fact that a significant portion of Turkey is subject to frequent earthquakes, destructive mainshocks and their foreshock and aftershock sequences, the area between the longitudes 39 and 42 N and latitudes 26 and 45 E was investigated. In this particular region, 111 mainshocks with surface magnitudes () of five or more occurred in the past 106 years. We define the following random variables. X represents the magnitude of the foreshocks, and Y represents the magnitude of the aftershocks. We fit the data to the following bivariate KW models.
- Data Set II: The data on 45 patients were available from a private clinic in Tennessee regarding the hemoglobin content in blood being prone to type II diabetes. To see the effect of reducing the hemoglobin content in the blood, a special type of treatment was administered to those patients. We define the following variables. X is a random variable which represents the proportion of hemoglobin content in the blood before the treatment, and Y is a random variable which represents the proportion of hemoglobin content in the blood after treatment.
- Model I: Bivariate distribution as defined in Equation (1);
- Model II: Bivariate distribution as defined in Equation (2);
- Model IV: Bivariate Kumaraswamy distribution via conditional specification, according to [5], given bywhere C is an appropriate normalizing constant;
- Model V: Bivariate Kumaraswamy distribution via conditional survival specification, according to Arnold and Ghosh (2016), given by
- Model VI: [11] bivariate ’s beta distribution, given byfor and where C is the normalizing constant.
- Model VII: [12] bivariate generalized beta distribution given byfor and where C is the normalizing constant.
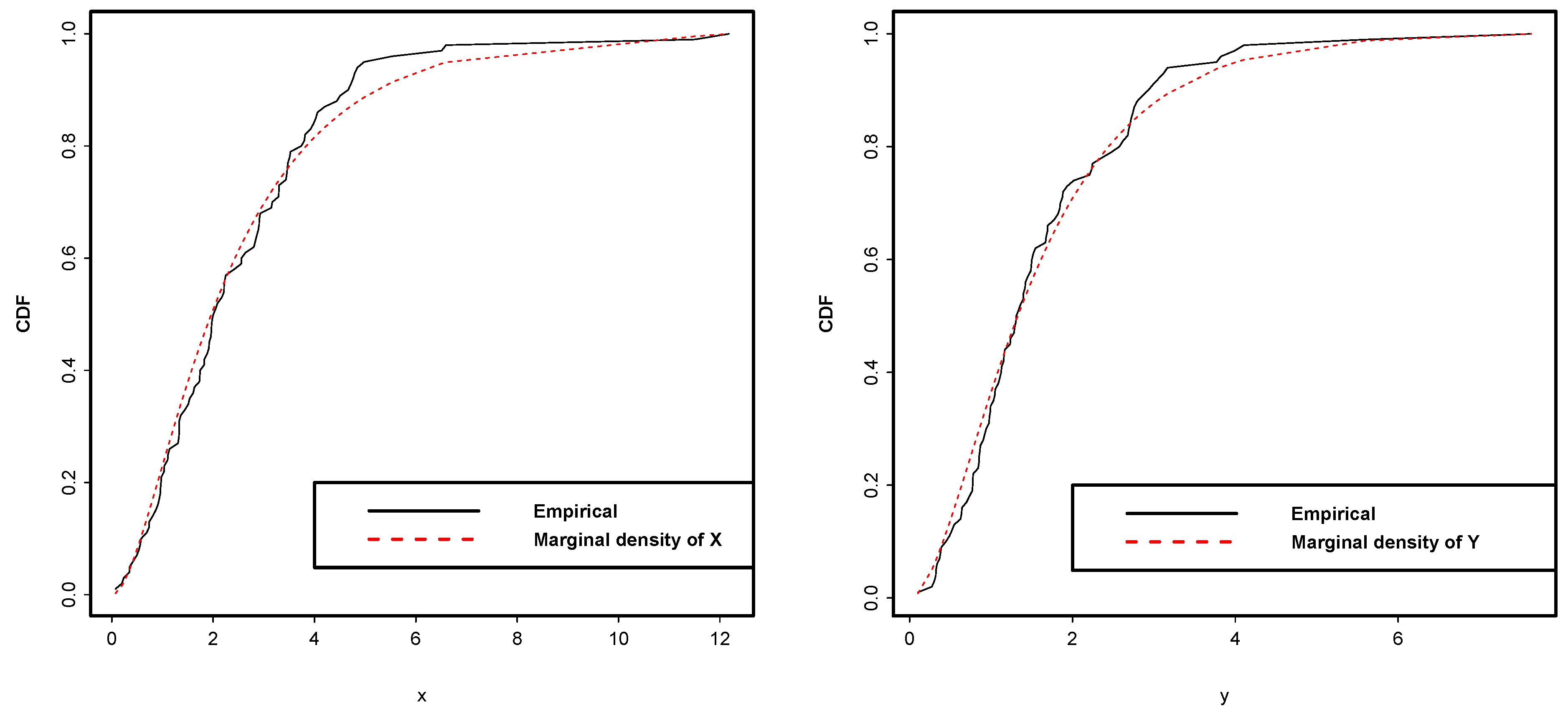
- Here are the results for the K-S goodness of fit for Data Set I:
- For the marginal density of X, K-S value = 0.0648 and K-S p-value = 0.7946.
- For the marginal density of Y, the K-S value = 0.06893 and K-S p-value = 0.8139.
- Here are the results for the K-S goodness of fit for Data Set II:
- For the marginal density of the K-S value = 0.06794 and K-S p-value = 0.8233.
- For the marginal density of the K-S value = 0.06853 and K-S p-value = 0.8394.
7. Concluding Remarks
- which is defined on
- Another such model could bewhich is defined on
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
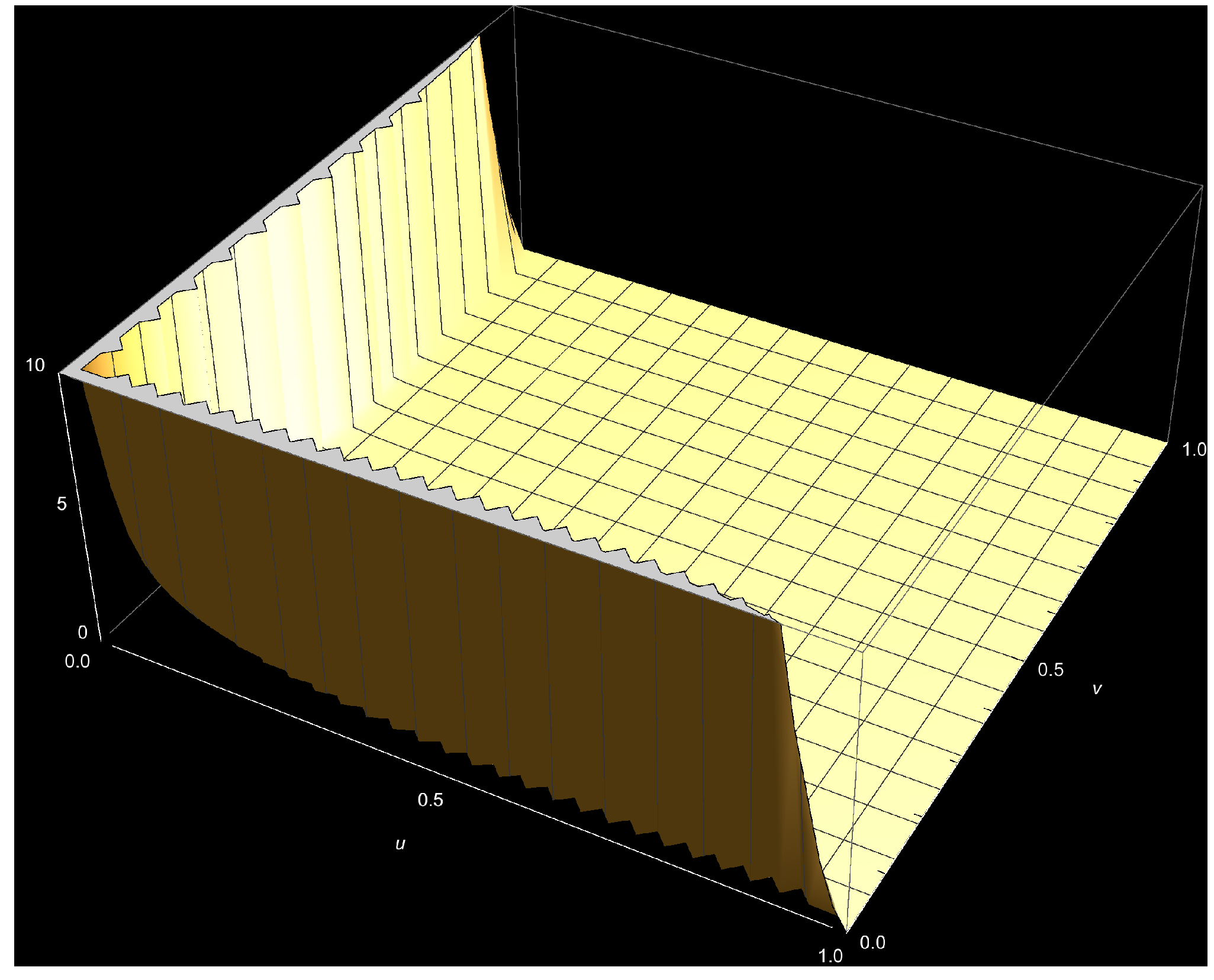
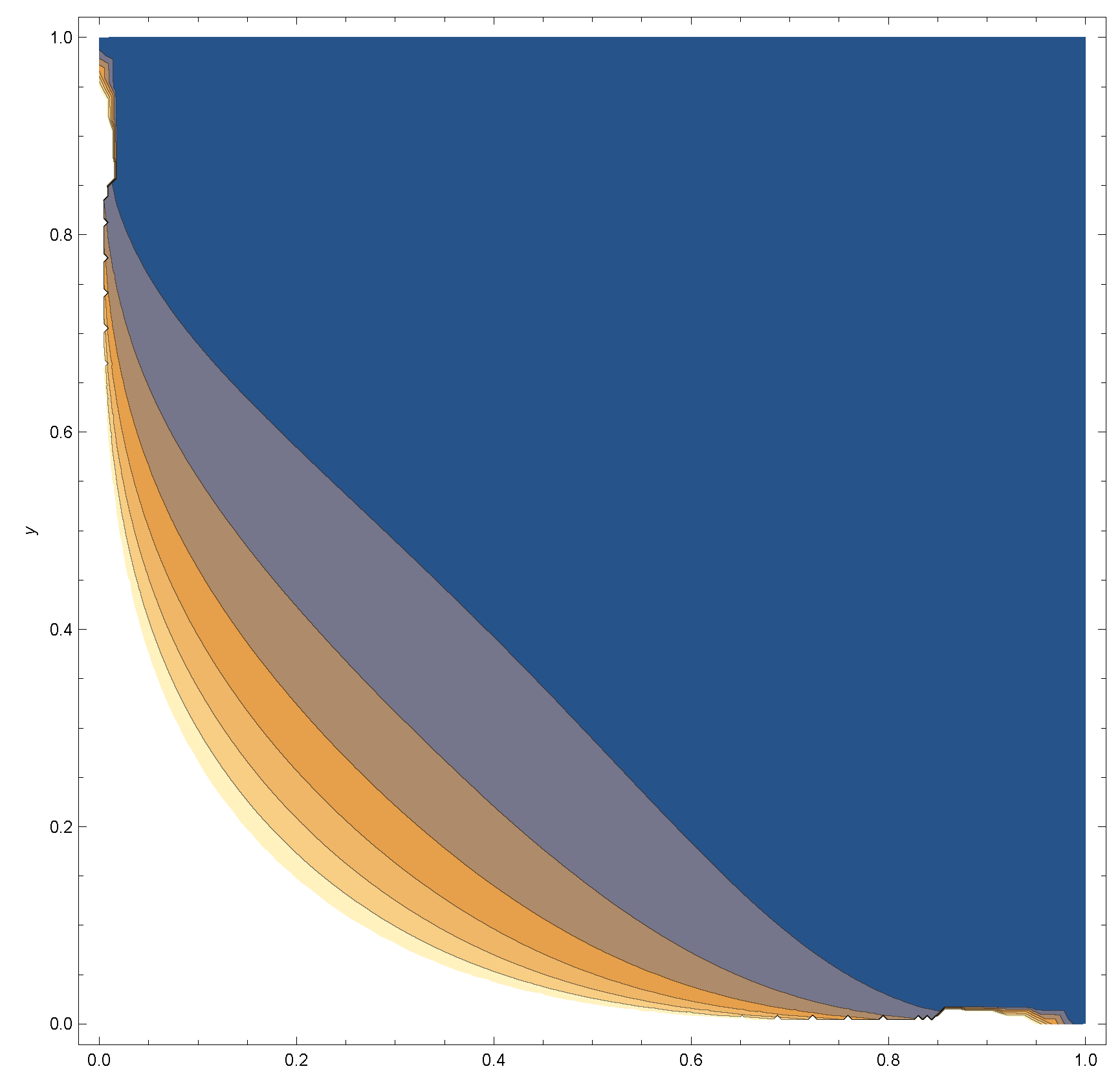
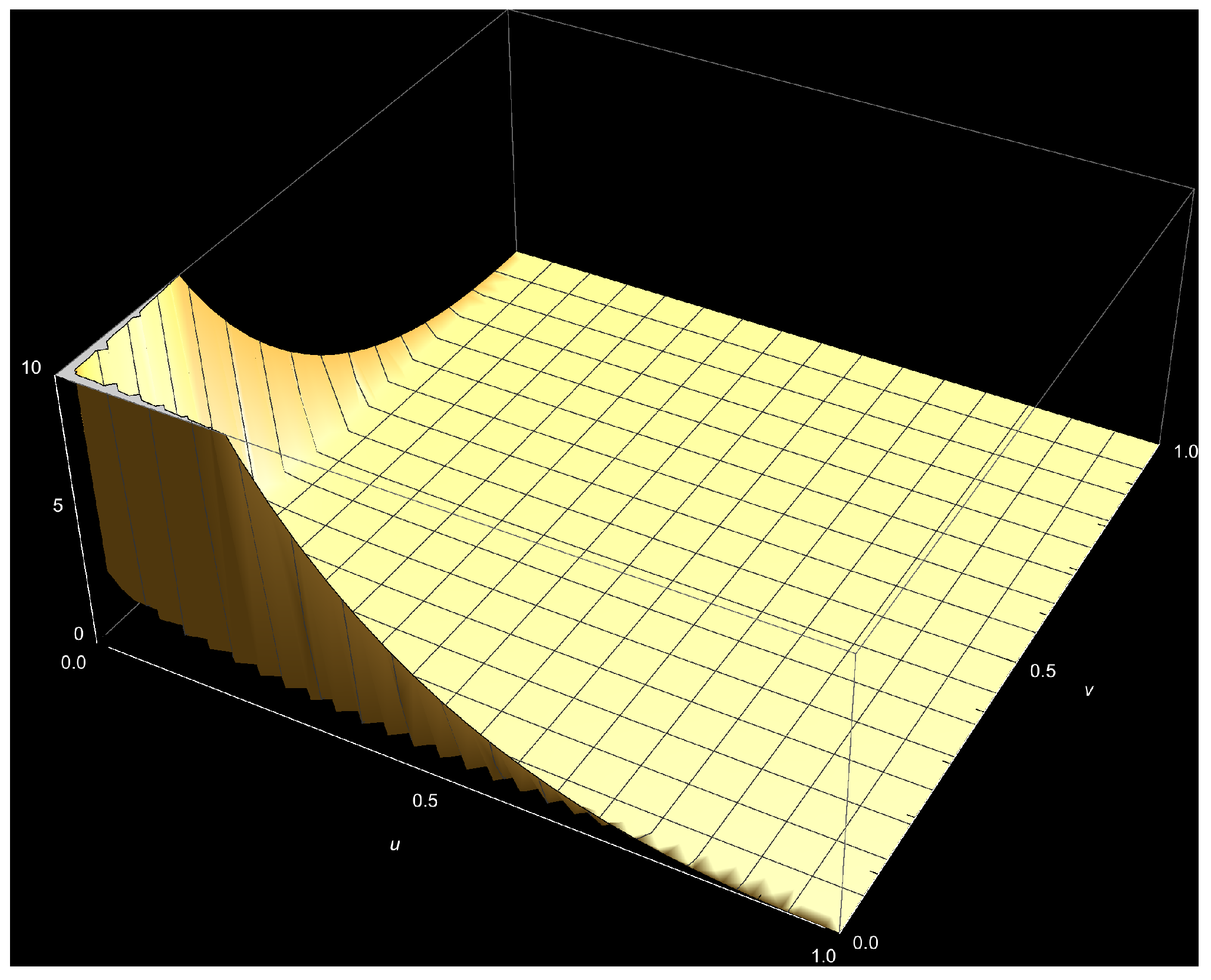
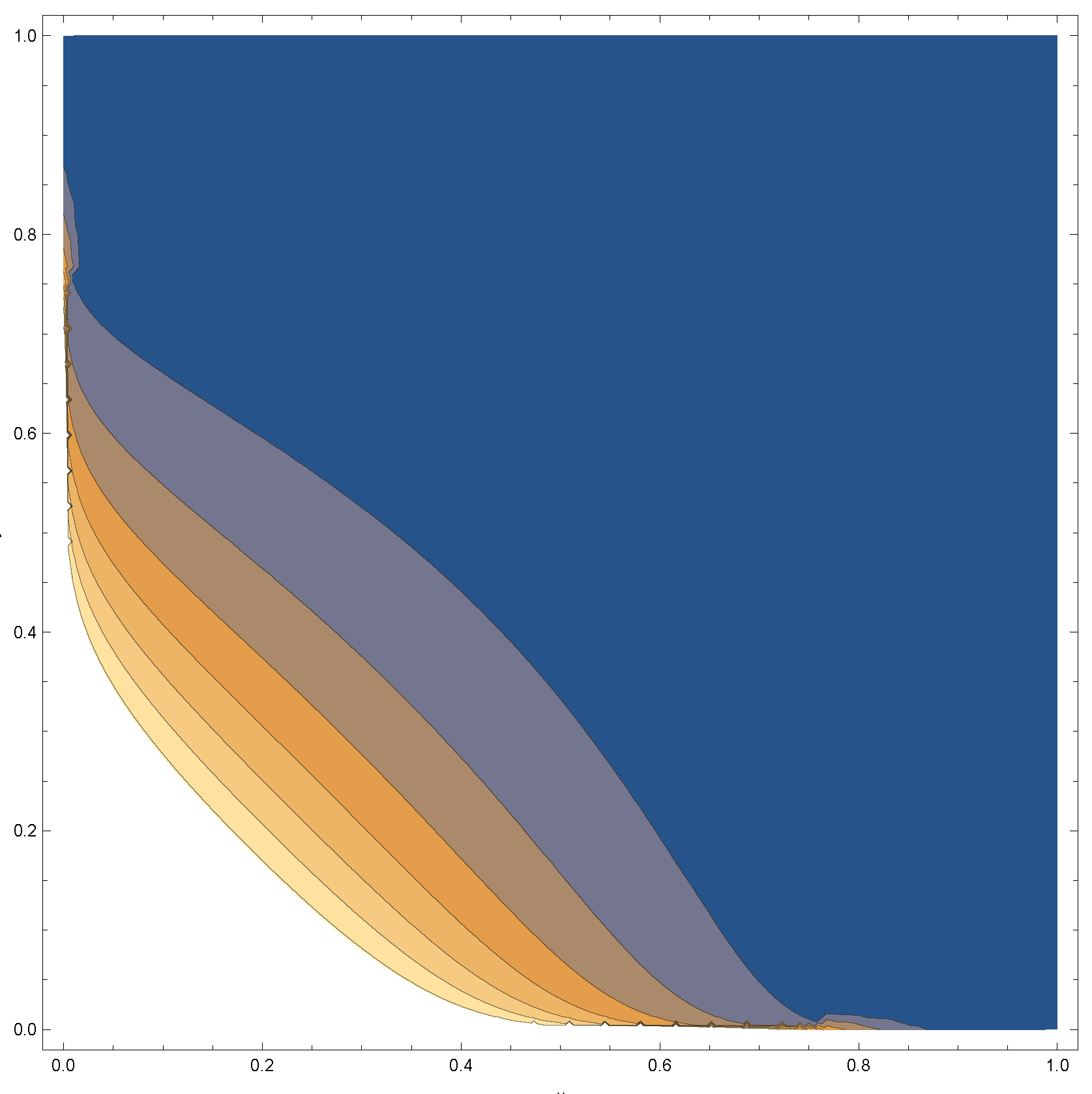
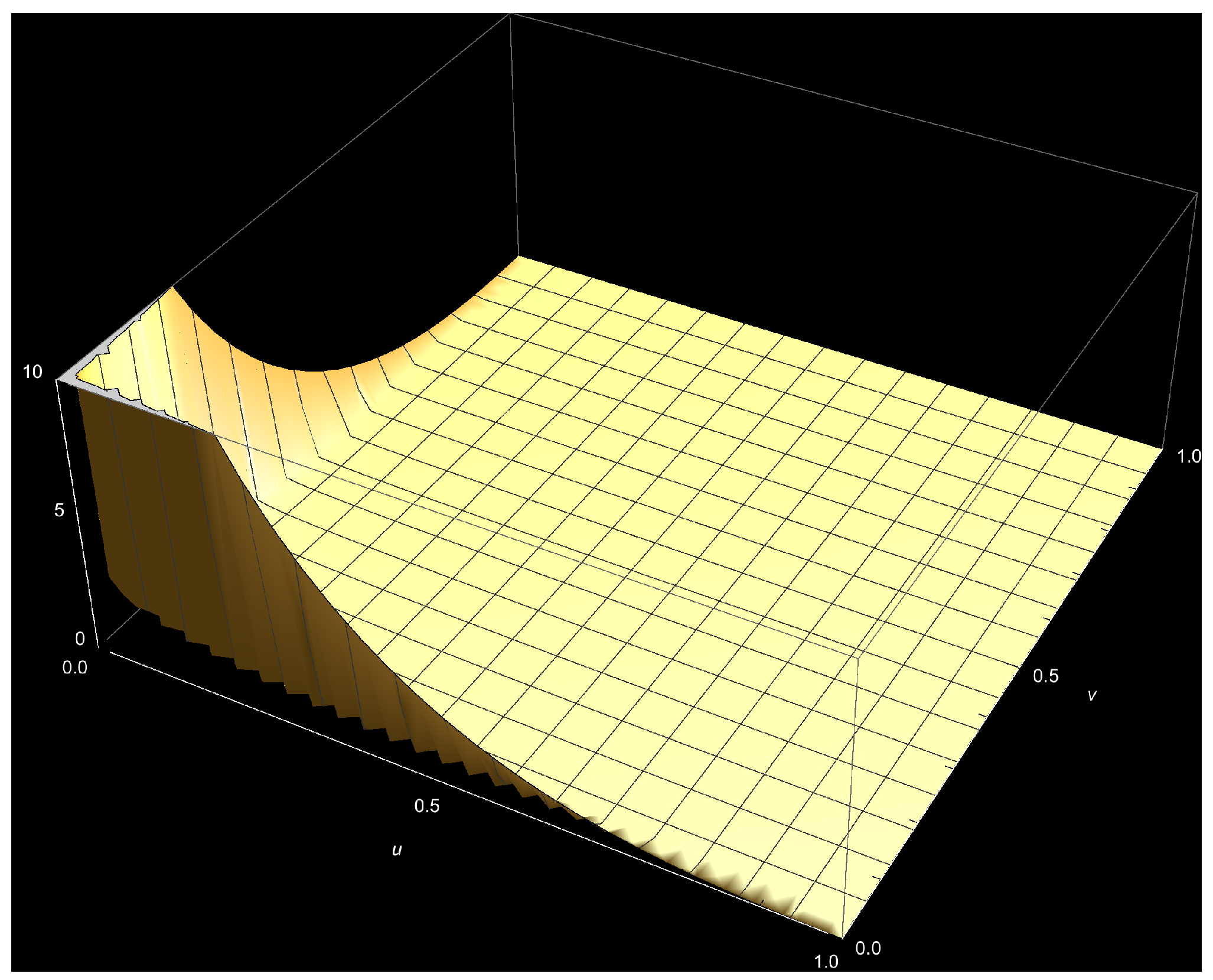

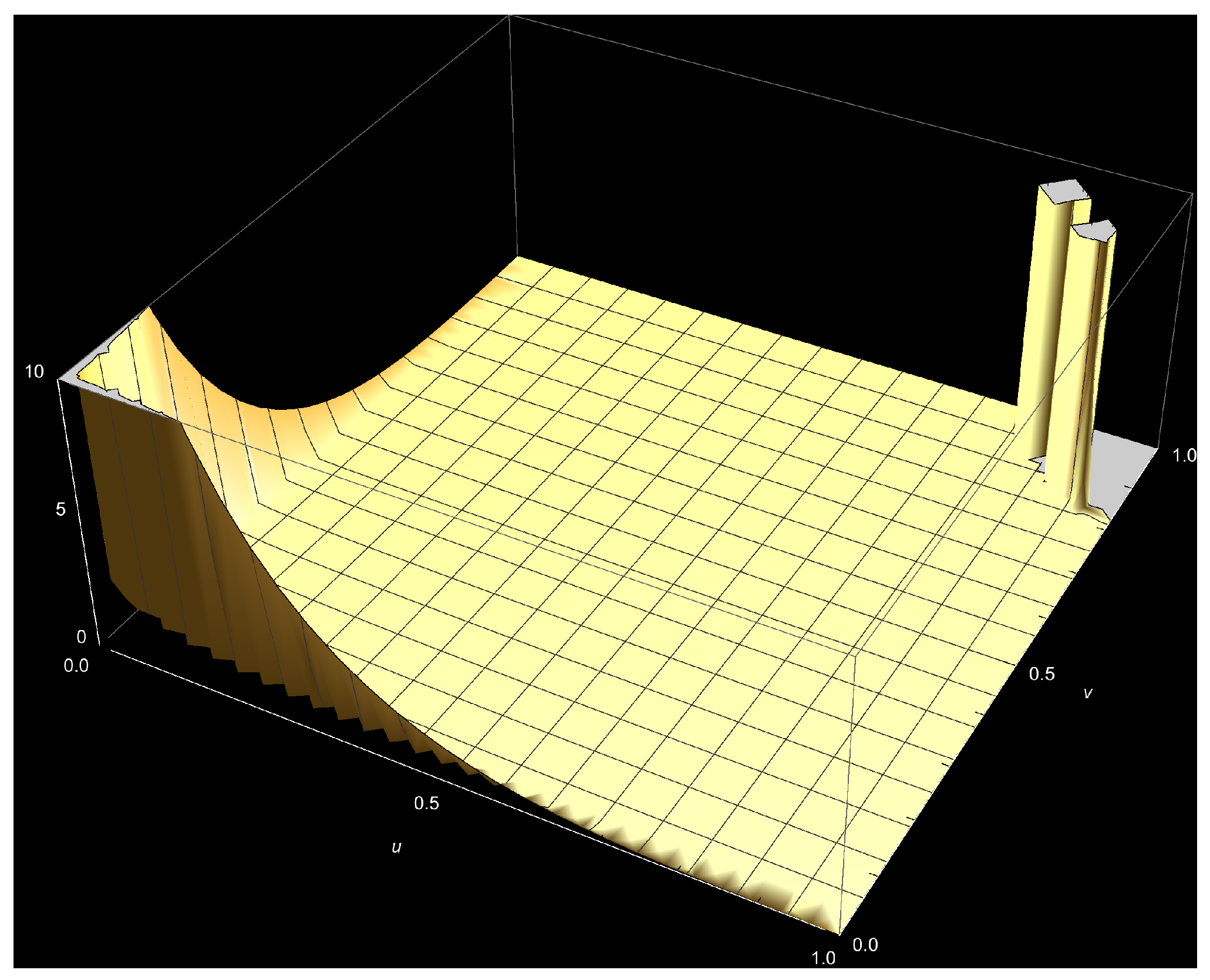
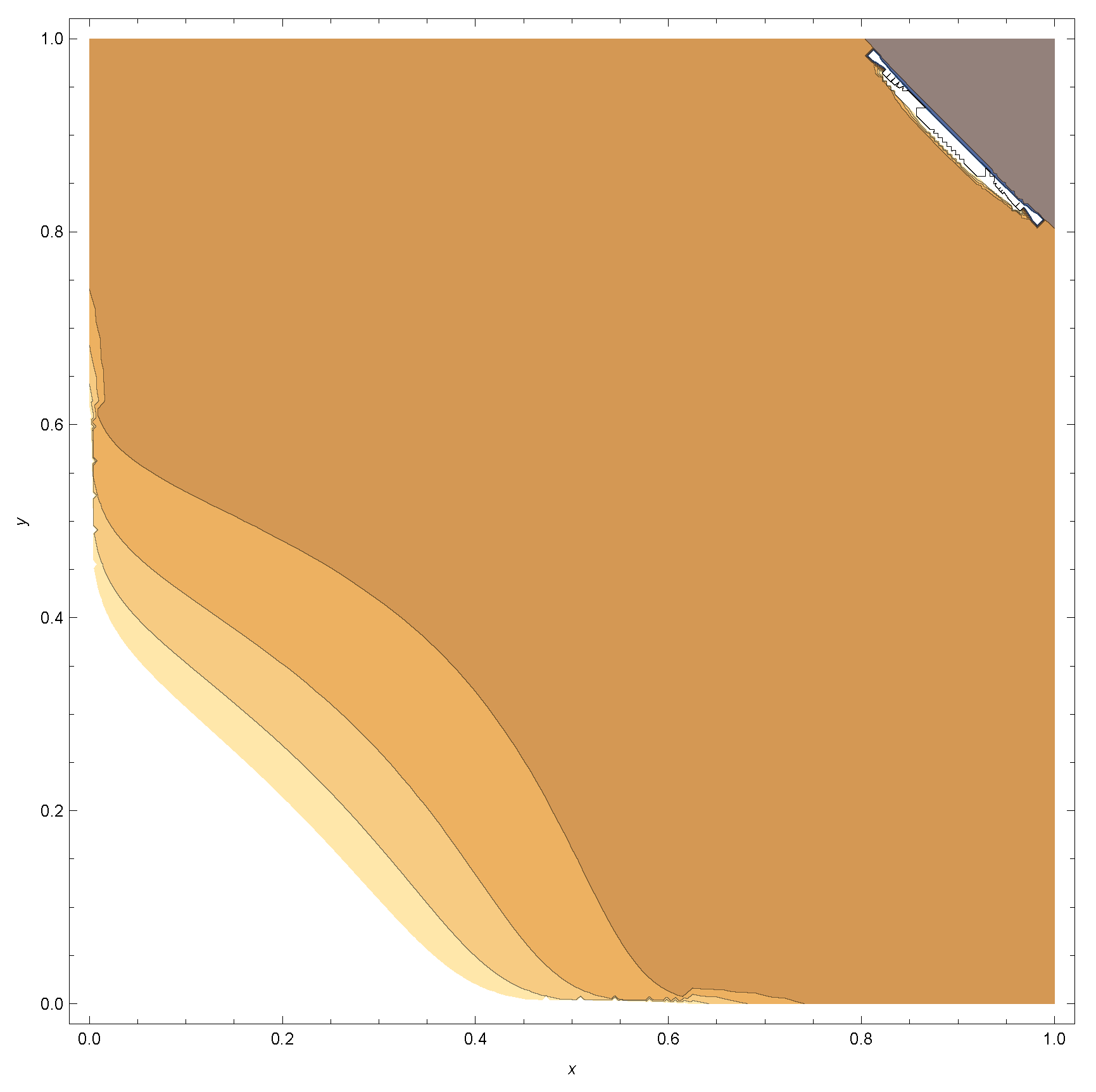
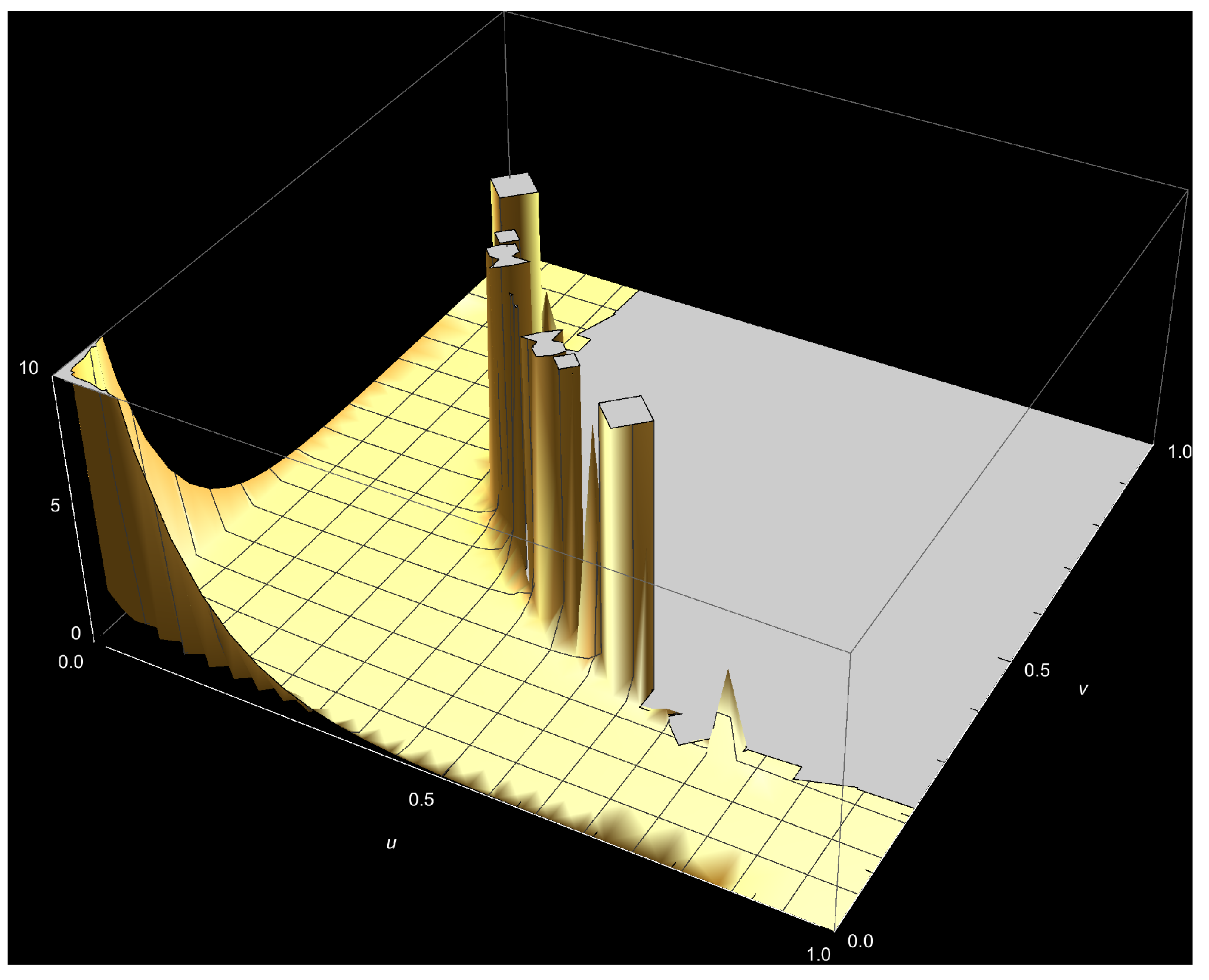


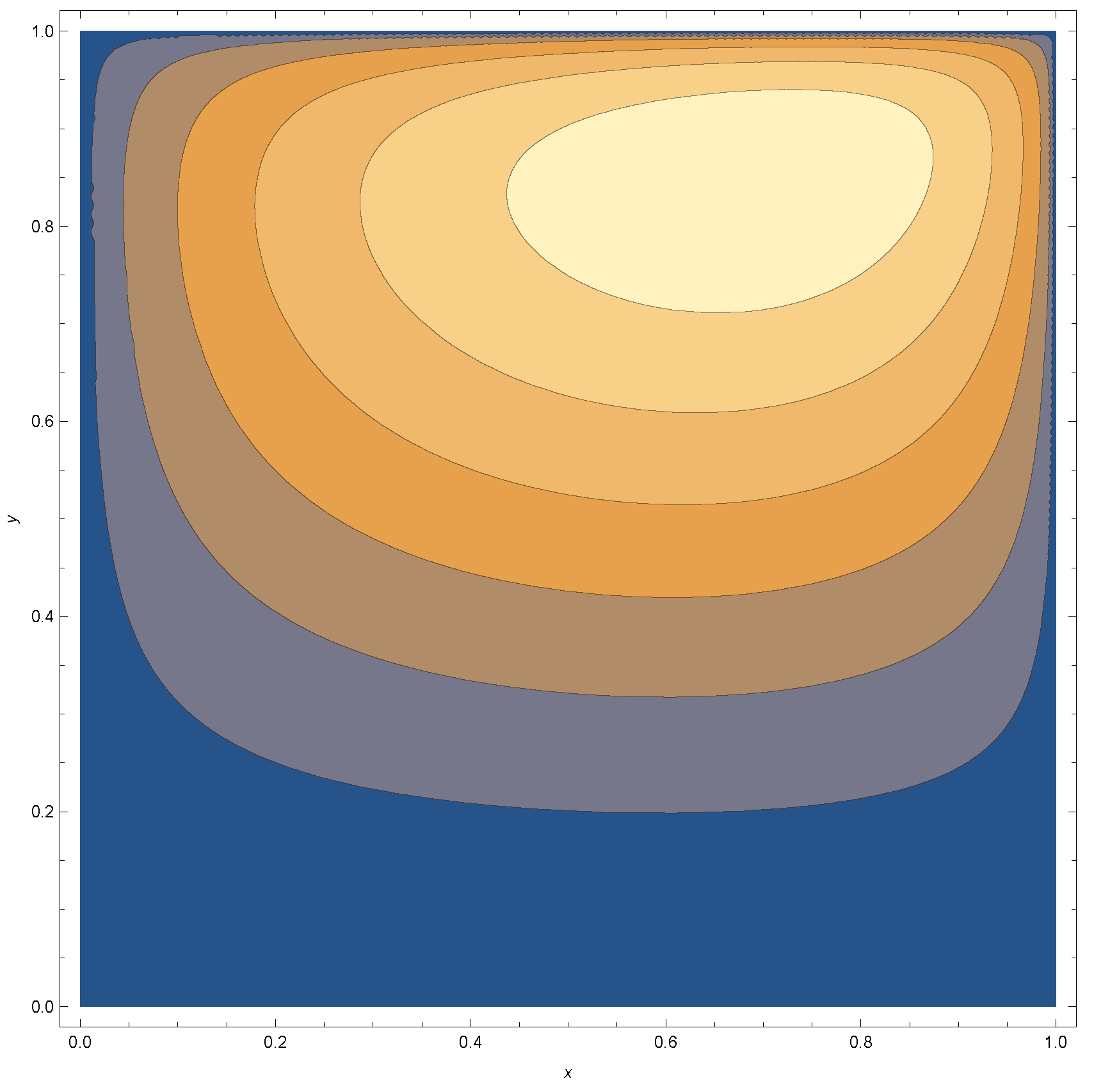

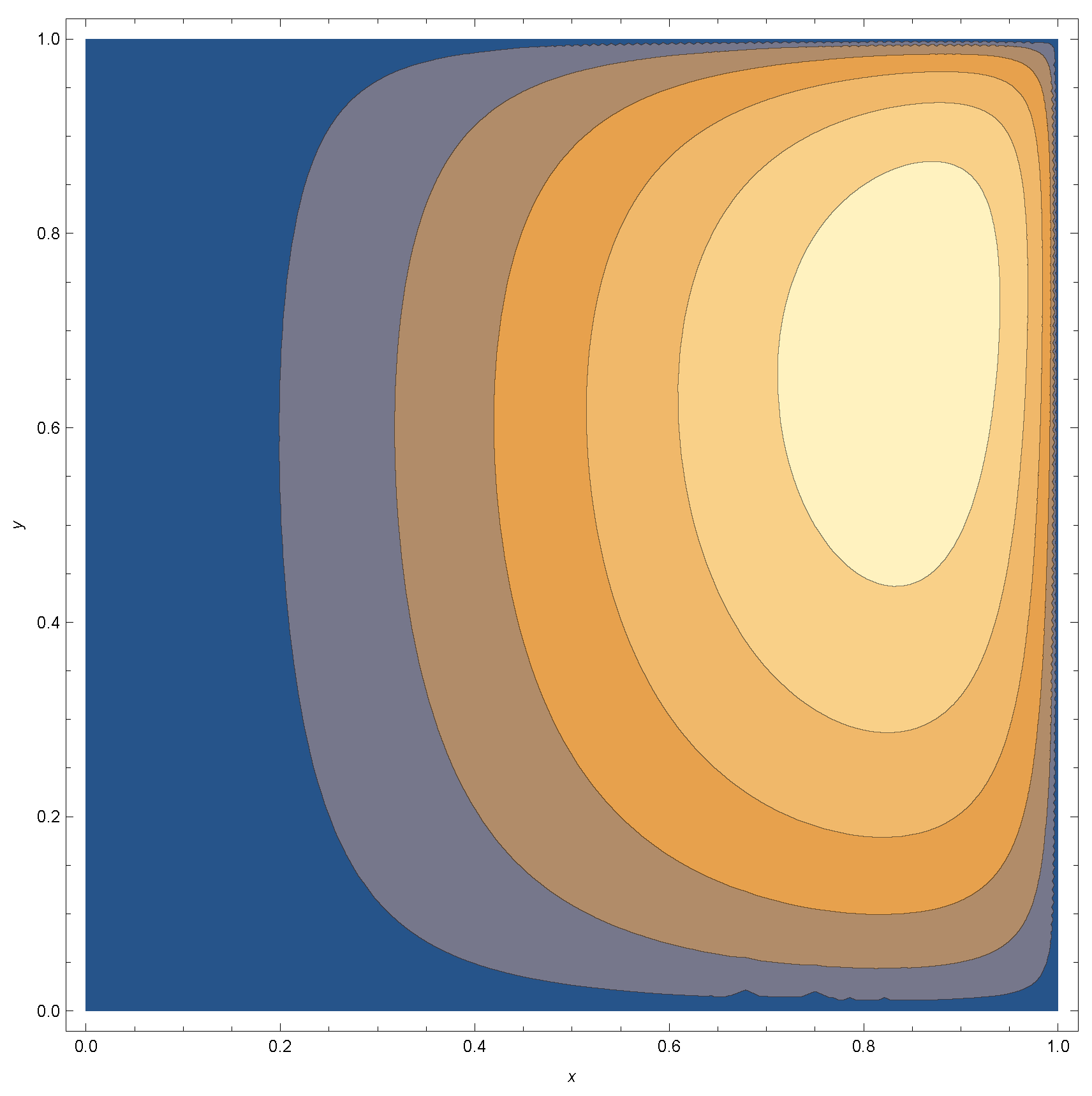
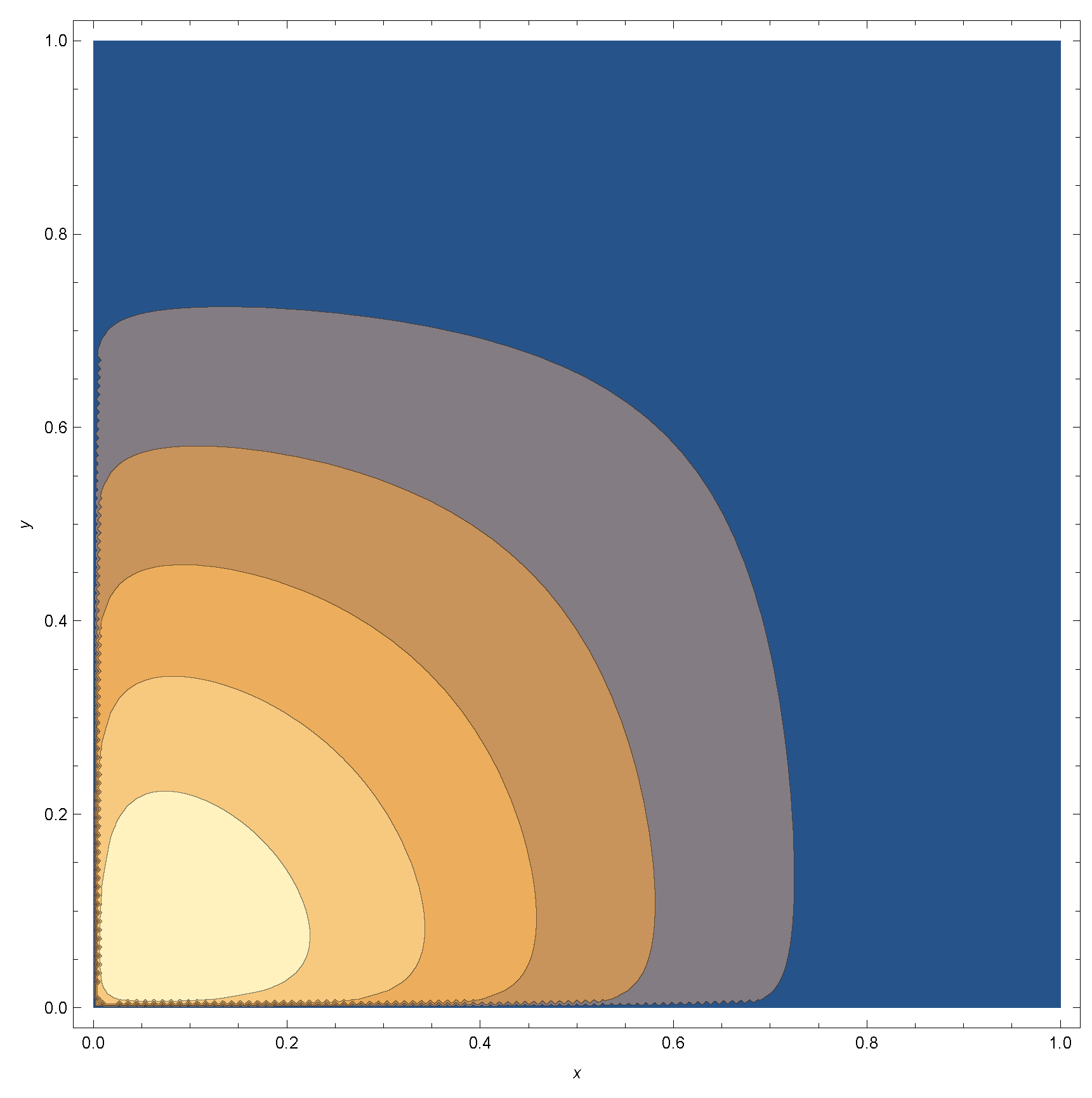

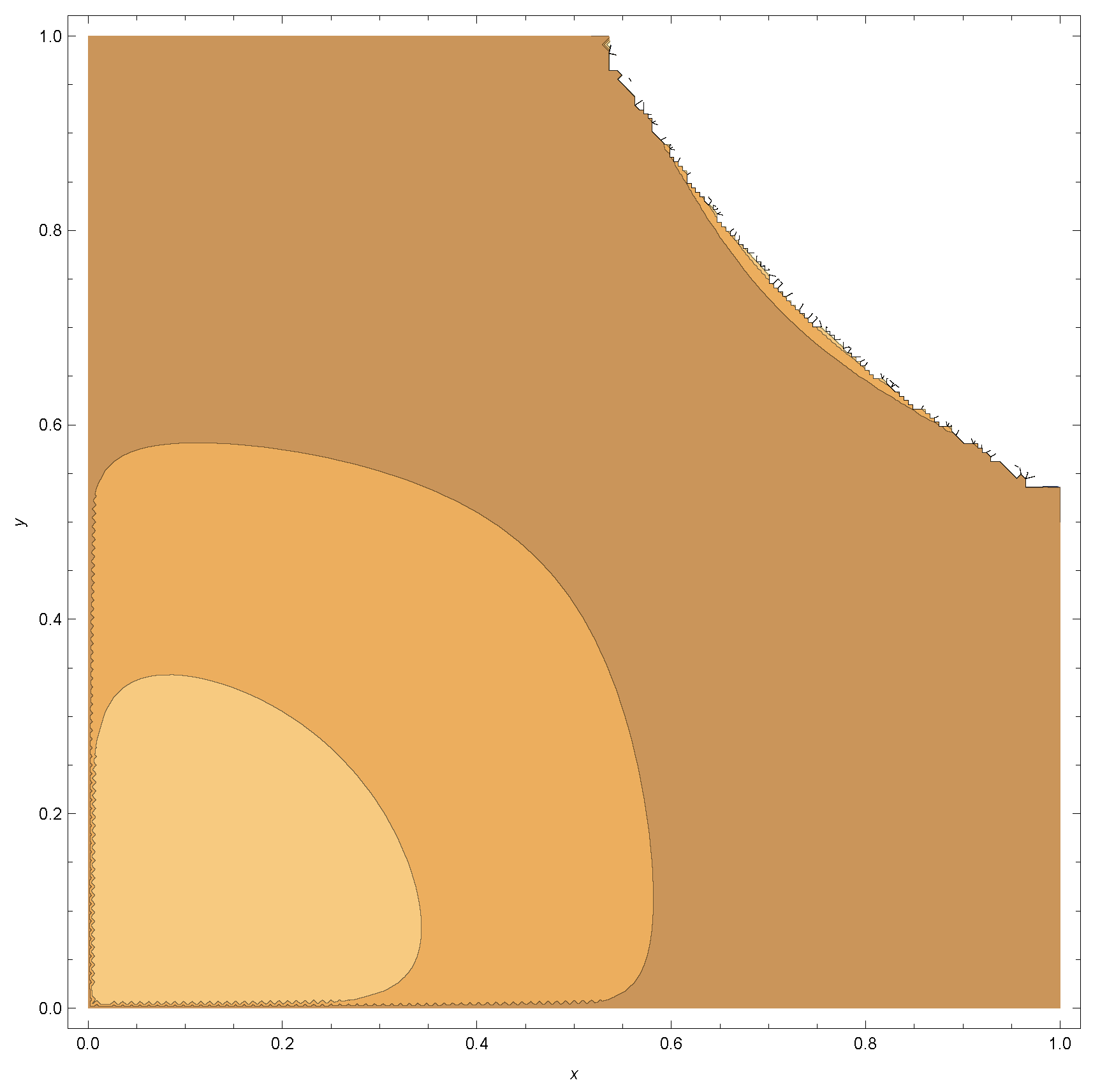
References
- Barreto-Souza, W.; Lemonte, A.J. Bivariate Kumaraswamy distribution: Properties and a new method to generate bivariate classes. Statistics 2013, 47, 1321–1342. [Google Scholar] [CrossRef]
- Ghosh, I. Bivariate and multivariate weighted Kumaraswamy distributions: Theory and applications. J. Stat. Theory Appl. 2019, 18, 198. [Google Scholar] [CrossRef]
- Arnold, B.C.; Ghosh, I. Some alternative bivariate Kumaraswamy models. Commun. Stat.-Theory Methods 2017, 46, 9335–9354. [Google Scholar] [CrossRef]
- Arnold, B.C.; Ng, H.K.T. Flexible bivariate beta distributions. J. Multivariate Anal. 2011, 102, 1194–1202. [Google Scholar] [CrossRef]
- Nadarajah, S.; Cordeiro, G.M.; Ortega, E.M. General results for the Kumaraswamy-G distribution. J. Stat. Comput. Simul. 2012, 82, 951–979. [Google Scholar] [CrossRef]
- Arnold, B.C.; Ghosh, I. Bivariate Kumaraswamy models involving use of Arnold-Ng copulas. J. Appl. Stat. Sci. 2017, 22, 227–241. [Google Scholar]
- Özel, G. Bivariate Kumaraswamy distribution with an application on earthquake data. AIP Conf. Proc. 2014, 1648, 610002. [Google Scholar]
- Chatfield, C. A marketing application of a characterization theorem. In A Modern Course on Distributions in Scientific Work; 2, Model Building and Model Selection; Patil, G.P., Kotz, S., Ord, J.K., Eds.; Reidel: Dordrecht, The Netherlands, 1975; pp. 175–185. [Google Scholar]
- Hoyer, R.W.; Mayer, L.S. The Equivalence of Various Objective Functions in a Stochastic Model of Electoral Competition; Technical Report No. 114, Series 2; Department of Statistics, Princeton University: Princeton, NJ, USA, 1976. [Google Scholar]
- Tong, Y.L. Probability Inequalities in Multivariate Distributions; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Nadarajah, S. The bivariate F3-beta distribution. Commun. Korean Math. Soc. 2006, 21, 363–374. [Google Scholar] [CrossRef]
- Nadarajah, S. A new bivariate beta distribution with application to drought data. Metron 2007, 65, 153–174. [Google Scholar]
| Parameter | Sample Size () | Sample Size () | Sample Size () |
|---|---|---|---|
| 0.1211 (0.3548) | 0.0769 (0.2271) | 0.0451 (0.1718) | |
| −0.0148 (0.03748) | 0.0132 (0.02616) | 0.00118 (0.0135) | |
| 0.0962 (0.0452) | 0.0473 (0.0224) | 0.00945 (0.1154) | |
| 0.1452 (0.1094) | 0.1317 (0.0248) | 0.00438 (0.0176) |
| Model | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Parameter estimates | ||||
| Log likelihood | −234.18 | −242.67 | −265.46 | −274.83 |
| value | 0.1485 | 0.3518 | 1.0678 | 2.1019 |
| AIC | 476.36 | 497.34 | 540.92 | 559.66 |
| BIC | 472.17 | 489.15 | 534.73 | 553.466 |
| Model | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Parameter estimates | ||||
| Log likelihood | −212.17 | −216.32 | −238.49 | −255.38 |
| value | 0.1378 | 0.1416 | 0.5516 | 0.5492 |
| AIC | 432.34 | 444.64 | 486.98 | 520.76 |
| BIC | 429.049 | 437.35 | 481.68 | 515.469 |
| Model | Model V | Model VI | Model VII |
|---|---|---|---|
| Parameter estimates | |||
| Log likelihood | −245.48 | −267.18 | −286.65 |
| value | 0.5237 | 0.6225 | 0.7244 |
| AIC | 501.16 | 544.36 | 581.30 |
| BIC | 494.77 | 538.17 | 577.11 |
| Model | Model V | Model VI | Model VII |
|---|---|---|---|
| Parameter estimates | |||
| Log likelihood | −262.17 | −258.34 | −247.38 |
| value | 0.5632 | 0.4785 | 0.3451 |
| AIC | 534.34 | 526.68 | 502.76 |
| BIC | 529.049 | 521.38 | 499.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, I. A New Class of Alternative Bivariate Kumaraswamy-Type Models: Properties and Applications. Stats 2023, 6, 232-252. https://doi.org/10.3390/stats6010014
Ghosh I. A New Class of Alternative Bivariate Kumaraswamy-Type Models: Properties and Applications. Stats. 2023; 6(1):232-252. https://doi.org/10.3390/stats6010014
Chicago/Turabian StyleGhosh, Indranil. 2023. "A New Class of Alternative Bivariate Kumaraswamy-Type Models: Properties and Applications" Stats 6, no. 1: 232-252. https://doi.org/10.3390/stats6010014
APA StyleGhosh, I. (2023). A New Class of Alternative Bivariate Kumaraswamy-Type Models: Properties and Applications. Stats, 6(1), 232-252. https://doi.org/10.3390/stats6010014






