Detecting Regional Differences in Italian Health Services during Five COVID-19 Waves
Abstract
1. Introduction
2. Time Series Clustering
- Step 1.
- Compute a dissimilarity matrix D based on a given measure;
- Step 2.
- Apply a weighted multidimensional scaling (wMDS) procedure, storing the coordinates of the first two components;
- Step 3.
- Perform cluster analysis on the MDS reduced space to identify groups between the n regions.
2.1. Dissimilarities between Time Series
2.2. Multidimensional Scaling
2.3. Clustering
3. Data and Descriptive Statistics
- Wave 1 (W1):
- days from 24 February to 30 June 2020
- Wave 2 (W2):
- days from 14 September 2020 to 19 February 2021
- Wave 3 (W3):
- days from 20 February to 14 July 2021
- Wave 4 (W4):
- days from 15 July to 21 October 2020
- Wave 5 (W5):
- days from 22 October to 15 March 2022
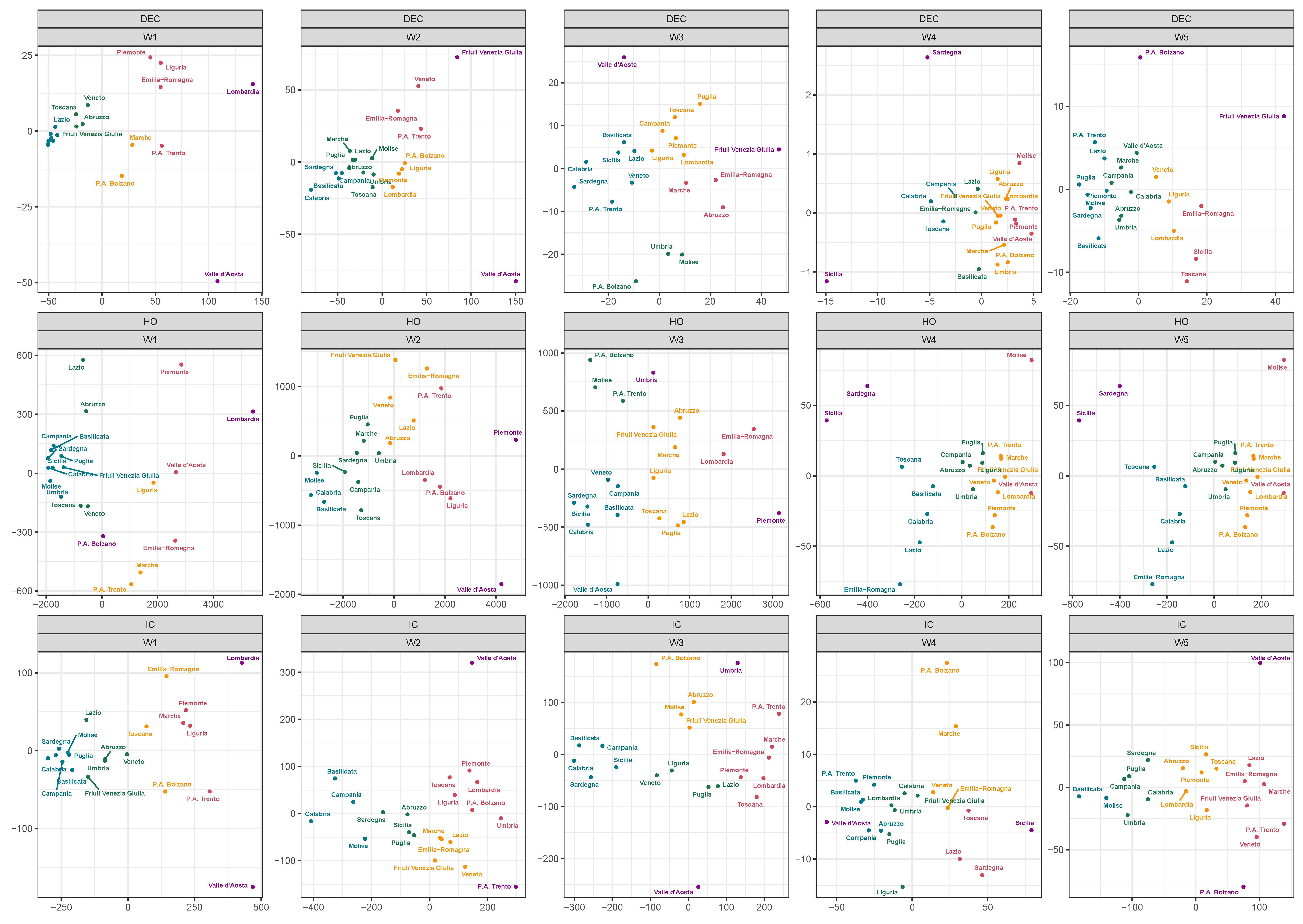
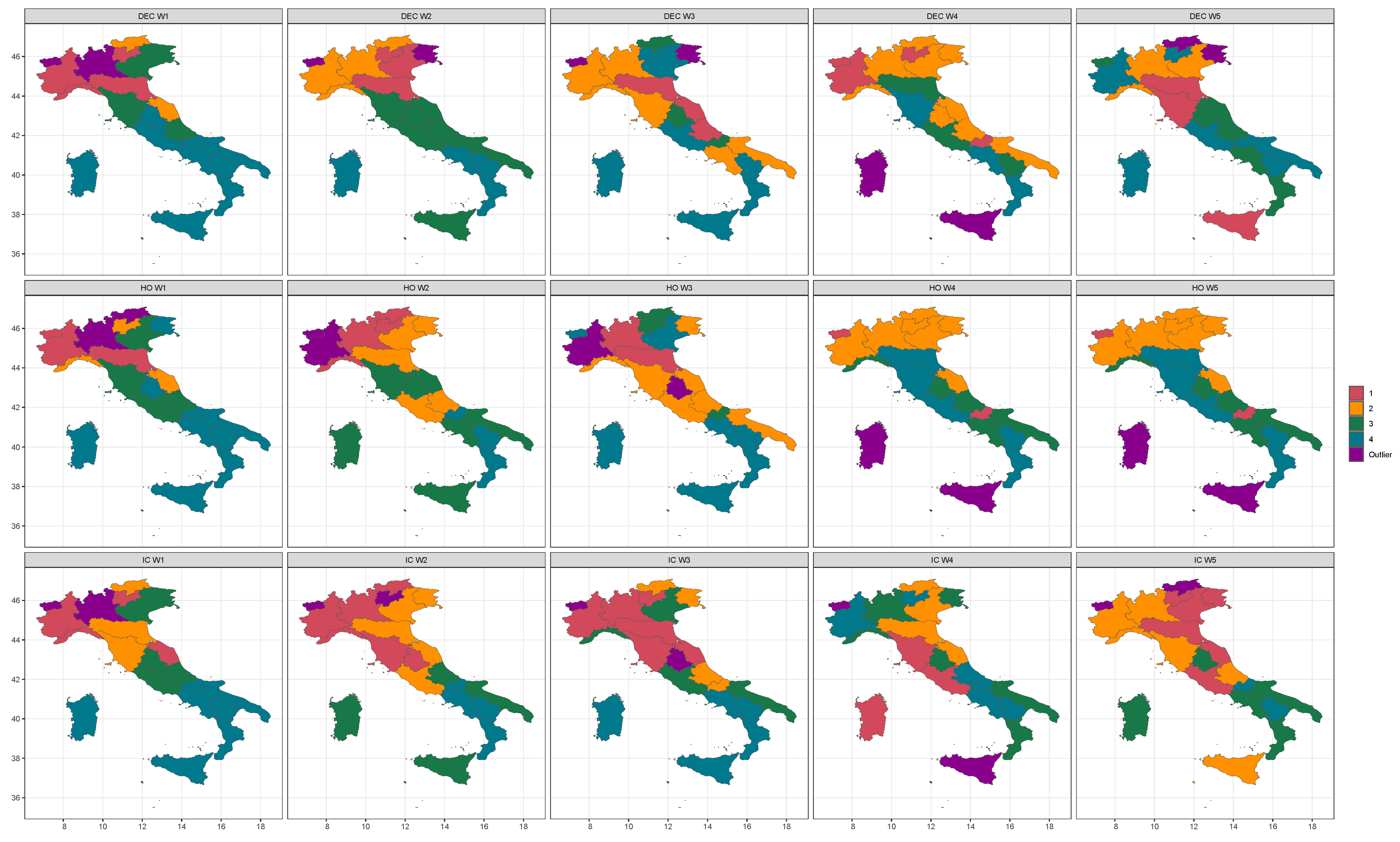
4. Grouping Regions by Clustering and Discussion
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CID | Complexity Invariance Dissimilarity |
| Cor | Pearson’s correlation |
| DEC | Deceased patients |
| DTW | Dynamic Time Warping |
| HO | Hospitalized count |
| IC | Intensive Care count |
| MDS | Multidimensional Scaling |
| NUTS2 | European nomenclature of basic regions for the application of regional policies |
| RHS | Regional Health Services |
| wMDS | Weighted Multidimensional Scaling |
References
- Capolongo, S.; Gola, M.; Brambilla, A.; Morganti, A.; Mosca, E.I.; Barach, P. Covid-19 and Healthcare facilities: A decalogue of design strategies for resilient hospitals. Acta Bio Med. 2020, 91, 50–60. [Google Scholar]
- Pecoraro, F.; Luzi, D.; Clemente, F. Analysis of the different approaches adopted in the Italian regions to care for patients affected by Covid-19. Int. J. Environ. Res. Public Health 2021, 18, 848. [Google Scholar] [PubMed]
- Han, E.; Tan, M.M.J.; Turk, E.; Sridhar, D.; Leung, G.M.; Shibuya, K.; Asgari, N.; Oh, J.; García-Basteiro, A.L.; Hanefeld, J.; et al. Lessons learnt from easing Covid-19 restrictions: An analysis of countries and regions in Asia Pacific and Europe. Lancet 2020, 396, 1525–1534. [Google Scholar] [CrossRef] [PubMed]
- Ascani, A.; Faggian, A.; Montresor, S. The geography of Covid-19 and the structure of local economies: The case of Italy. J. Reg. Sci. 2020, 61, 2. [Google Scholar] [CrossRef]
- Beria, P.; Lunkar, V. Presence and mobility of the population during the first wave of Covid-19 outbreak and lockdown in Italy. Sustain. Cities Soc. 2021, 65, 102616. [Google Scholar]
- Marziano, V.; Guzzetta, G.; Rondinone, B.M.; Boccuni, F.; Riccardo, F.; Bella, A.; Poletti, P.; Trentini, F.; Pezzotti, P.; Brusaferro, S.; et al. Retrospective analysis of the Italian exit strategy from Covid-19 lockdown. Proc. Natl. Acad. Sci. USA 2021, 118, e2019617118. [Google Scholar] [CrossRef]
- Bontempi, E. The Europe second wave of Covid-19 infection and the Italy “strange” situation. Environ. Res. 2021, 193, 110476. [Google Scholar] [CrossRef]
- Boriani, G.; Guerra, F.; De Ponti, R.; D’Onofrio, A.; Accogli, M.; Bertini, M.; Bisignani, G.; Forleo, G.B.; Landolina, M.; Lavalle, C.; et al. Five waves of COVID-19 pandemic in Italy: Results of a national survey evaluating the impact on activities related to arrhythmias, pacing, and electrophysiology promoted by AIAC (Italian Association of Arrhythmology and Cardiac Pacing). Intern. Emerg. Med. 2022, 18, 137–149. [Google Scholar] [CrossRef]
- Pecoraro, F.; Clemente, F.; Luzi, D. The efficiency in the ordinary hospital bed management in Italy: An in-depth analysis of intensive care unit in the areas affected by Covid-19 before the outbreak. PLoS ONE 2020, 15, e0239249. [Google Scholar] [CrossRef]
- Agosto, A.; Giudici, P. A Poisson autoregressive model to understand Covid-19 contagion dynamics. Risks 2020, 8, 77. [Google Scholar] [CrossRef]
- Farcomeni, A.; Maruotti, A.; Divino, F.; Lasinio, G.J.; Lovison, G. An ensemble approach to short-term forecast of Covid-19 intensive care occupancy in Italian Regions. arXiv 2020, arXiv:2005.11975. [Google Scholar] [CrossRef] [PubMed]
- James, N.; Menzies, M. Cluster-based dual evolution for multivariate time series: Analyzing Covid-19. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 061108. [Google Scholar] [CrossRef] [PubMed]
- Rojas, I.; Rojas, F.; Valenzuela, O. Estimation of Covid-19 dynamics in the different states of the United States using Time-Series Clustering. medRxiv 2020. [Google Scholar] [CrossRef]
- Studer, M.; Ritschard, G. What matters in differences between life trajectories: A comparative review of sequence dissimilarity measures. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2016, 179, 481–511. [Google Scholar] [CrossRef]
- Kruskal, J.B. Multidimensional Scaling; Sage: Newcastle upon Tyne, UK, 1978; Number 11. [Google Scholar]
- Mead, A. Review of the development of multidimensional scaling methods. J. R. Stat. Soc. Ser. D (Stat.) 1992, 41, 27–39. [Google Scholar] [CrossRef]
- Górecki, T.; Piasecki, P. A Comprehensive Comparison of Distance Measures for Time Series Classification. In Proceedings of the Workshop on Stochastic Models, Statistics and their Application, Dresden, Germany, 6–8 March 2019; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 409–428. [Google Scholar]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 2020, 139, 110057. [Google Scholar] [CrossRef]
- Piccolo, D. A distance measure for classifying ARIMA models. J. Time Ser. Anal. 1990, 11, 153–164. [Google Scholar] [CrossRef]
- D’Urso, P.; Maharaj, E.A. Autocorrelation-based fuzzy clustering of time series. Fuzzy Sets Syst. 2009, 160, 3565–3589. [Google Scholar] [CrossRef]
- Fenga, L. CoViD–19: An Automatic, Semiparametric Estimation Method for the Population Infected in Italy. PeerJ 2021, 9, e10819. [Google Scholar] [CrossRef]
- Iglesias, F.; Kastner, W. Analysis of similarity measures in times series clustering for the discovery of building energy patterns. Energies 2013, 6, 579–597. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the KDD Workshop, Seattle, WA, USA, 31 July–1 August 1994; Volume 10, pp. 359–370. [Google Scholar]
- Giorgino, T. Computing and visualizing dynamic time warping alignments in R: The dtw package. J. Stat. Softw. 2009, 31, 1–24. [Google Scholar] [CrossRef]
- Montero, P.; Vilar, J.A. TSclust: An R Package for Time Series Clustering. J. Stat. Softw. 2014, 62, 1–43. [Google Scholar] [CrossRef]
- Tormene, P.; Giorgino, T.; Quaglini, S.; Stefanelli, M. Matching incomplete time series with dynamic time warping: An algorithm and an application to post-stroke rehabilitation. Artif. Intell. Med. 2009, 45, 11–34. [Google Scholar] [CrossRef]
- Benkabou, S.E.; Benabdeslem, K.; Canitia, B. Unsupervised outlier detection for time series by entropy and dynamic time warping. Knowl. Inf. Syst. 2018, 54, 463–486. [Google Scholar] [CrossRef]
- Batista, G.E.; Wang, X.; Keogh, E.J. A complexity-invariant distance measure for time series. In Proceedings of the 2011 SIAM International Conference on Data Mining, SIAM, 2011, Mesa, AZ, USA, 28–30 April 2011; pp. 699–710. [Google Scholar]
- Agrawal, R.; Faloutsos, C.; Swami, A. Efficient similarity search in sequence databases. In Proceedings of the International Conference on Foundations of Data Organization and Algorithms, Chicago, IL, USA, 13–15 October 1993; Springer: Berlin/Heidelberg, Germany, 1993; pp. 69–84. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 3. [Google Scholar]
- Torgerson, W.S. Multidimensional scaling: I. Theory and method. Psychometrika 1952, 17, 401–419. [Google Scholar] [CrossRef]
- Saeed, N.; Nam, H.; Haq, M.I.U.; Muhammad Saqib, D.B. A survey on multidimensional scaling. ACM Comput. Surv. (CSUR) 2018, 51, 1–25. [Google Scholar] [CrossRef]
- Piccolo, D. Una rappresentazione multidimensionale per modelli statistici dinamici. Atti Della XXXII Riun. Sci. Della SIS 1984, 2, 149–160. [Google Scholar]
- Tenreiro Machado, J.; Lopes, A.M.; Galhano, A.M. Multidimensional scaling visualization using parametric similarity indices. Entropy 2015, 17, 1775–1794. [Google Scholar] [CrossRef]
- Di Iorio, F.; Triacca, U. Distance Between VARMA Models and Its Application to Spatial Differences Analysis in the Relationship GDP-Unemployment Growth Rate in Europe. In Proceedings of the International Work-Conference on Time Series Analysis, Granada, Spain, 1–20 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 203–215. [Google Scholar]
- He, J.; Shang, P.; Xiong, H. Multidimensional scaling analysis of financial time series based on modified cross-sample entropy methods. Phys. A Stat. Mech. Its Appl. 2018, 500, 210–221. [Google Scholar]
- Mardia, K.V. Some properties of clasical multi-dimesional scaling. Commun. Stat.-Theory Methods 1978, 7, 1233–1241. [Google Scholar] [CrossRef]
- Kent, J.; Bibby, J.; Mardia, K. Multivariate Analysis; Academic Press: Amsterdam, The Netherlands, 1979; Chapter 14. [Google Scholar]
- Greenacre, M. Weighted metric multidimensional scaling. In New Developments in Classification and Data Analysis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 141–149. [Google Scholar]
- Kruskal, J. The relationship between multidimensional scaling and clustering. In Classification and Clustering; Elsevier: Amsterdam, The Netherlands, 1977; pp. 17–44. [Google Scholar]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Giuliani, D.; Dickson, M.M.; Espa, G.; Santi, F. Modelling and predicting the spatio-temporal spread of Covid-19 in Italy. BMC Infect. Dis. 2020, 20, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Cuesta-Albertos, J.A.; Gordaliza, A.; Matrán, C. Trimmed k-means: An attempt to robustify quantizers. Ann. Stat. 1997, 25, 553–576. [Google Scholar] [CrossRef]
- Garcia-Escudero, L.A.; Gordaliza, A. Robustness properties of k-means and trimmed k-means. J. Am. Stat. Assoc. 1999, 94, 956–969. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Least median of squares regression. J. Am. Stat. Assoc. 1984, 79, 871–880. [Google Scholar] [CrossRef]
- Sebastiani, G.; Massa, M.; Riboli, E. Covid-19 epidemic in Italy: Evolution, projections and impact of government measures. Eur. J. Epidemiol. 2020, 35, 341–345. [Google Scholar] [CrossRef]
- Chirico, F.; Sacco, A.; Magnavita, N.; Nucera, G. Coronavirus disease 2019: The second wave in Italy. J. Health Res. 2021, 35, 359–363. [Google Scholar] [CrossRef]
- Pelagatti, M.; Maranzano, P. Assessing the effectiveness of the Italian risk-zones policy during the second wave of COVID-19. Health Policy 2021, 125, 1188–1199. [Google Scholar] [CrossRef]
- Shang, D.; Shang, P.; Liu, L. Multidimensional scaling method for complex time series feature classification based on generalized complexity-invariant distance. Nonlinear Dyn. 2019, 95, 2875–2892. [Google Scholar] [CrossRef]
- D’Urso, P.; De Giovanni, L.; Disegna, M.; Massari, R. Fuzzy clustering with spatial–temporal information. Spat. Stat. 2019, 30, 71–102. [Google Scholar] [CrossRef]

| W1 | W2 | W3 | W4 | W5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DEC | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD |
| Abruzzo | 0.85 | 0.24 | 0.31 | 1.42 | 0.35 | 0.40 | 1.35 | 0.42 | 0.46 | 0.10 | 0.03 | 0.03 | 0.65 | 0.18 | 0.19 |
| Basilicata | 0.23 | 0.06 | 0.00 | 1.14 | 0.26 | 0.28 | 0.89 | 0.23 | 0.23 | 0.15 | 0.04 | 0.04 | 0.71 | 0.21 | 0.21 |
| Calabria | 0.23 | 0.06 | 0.01 | 0.51 | 0.13 | 0.13 | 0.44 | 0.11 | 0.13 | 0.18 | 0.05 | 0.06 | 0.63 | 0.16 | 0.25 |
| Campania | 0.22 | 0.07 | 0.04 | 0.90 | 0.27 | 0.30 | 0.80 | 0.22 | 0.29 | 0.15 | 0.03 | 0.04 | 0.62 | 0.15 | 0.12 |
| Emilia-Romagna | 2.11 | 0.70 | 0.57 | 1.64 | 0.55 | 0.57 | 1.20 | 0.40 | 0.49 | 0.13 | 0.03 | 0.03 | 0.90 | 0.25 | 0.26 |
| Friuli Venezia Giulia | 0.71 | 0.21 | 0.16 | 2.74 | 0.90 | 1.05 | 1.69 | 0.56 | 0.59 | 0.15 | 0.03 | 0.03 | 1.07 | 0.25 | 0.31 |
| Lazio | 0.31 | 0.07 | 0.07 | 0.89 | 0.28 | 0.23 | 0.65 | 0.20 | 0.28 | 0.10 | 0.02 | 0.03 | 0.47 | 0.11 | 0.12 |
| Liguria | 2.02 | 0.66 | 0.70 | 1.78 | 0.47 | 0.51 | 1.02 | 0.26 | 0.26 | 0.10 | 0.02 | 0.01 | 0.80 | 0.23 | 0.31 |
| Lombardia | 4.43 | 1.28 | 0.95 | 2.01 | 0.54 | 0.58 | 0.96 | 0.33 | 0.42 | 0.06 | 0.01 | 0.02 | 0.90 | 0.26 | 0.26 |
| Marche | 2.07 | 0.63 | 0.33 | 0.90 | 0.32 | 0.29 | 0.92 | 0.34 | 0.37 | 0.09 | 0.03 | 0.03 | 0.60 | 0.14 | 0.18 |
| Molise | 0.33 | 0.08 | 0.00 | 1.31 | 0.41 | 0.45 | 1.31 | 0.39 | 0.38 | 0.14 | 0.03 | 0.00 | 0.65 | 0.18 | 0.14 |
| P.A. Bolzano | 2.64 | 0.63 | 0.04 | 2.23 | 0.59 | 0.56 | 1.51 | 0.36 | 0.16 | 0.11 | 0.03 | 0.04 | 0.54 | 0.13 | 0.12 |
| P.A. Trento | 2.85 | 0.86 | 0.27 | 2.14 | 0.69 | 0.94 | 0.63 | 0.19 | 0.20 | 0.11 | 0.03 | 0.04 | 0.53 | 0.13 | 0.16 |
| Piemonte | 2.10 | 0.65 | 0.67 | 1.94 | 0.58 | 0.74 | 0.98 | 0.31 | 0.43 | 0.06 | 0.02 | 0.02 | 0.64 | 0.17 | 0.18 |
| Puglia | 0.37 | 0.10 | 0.07 | 1.01 | 0.31 | 0.28 | 1.05 | 0.32 | 0.35 | 0.10 | 0.02 | 0.03 | 0.48 | 0.14 | 0.12 |
| Sardegna | 0.28 | 0.08 | 0.03 | 0.84 | 0.22 | 0.23 | 0.45 | 0.12 | 0.12 | 0.26 | 0.06 | 0.06 | 0.49 | 0.16 | 0.12 |
| Sicilia | 0.18 | 0.05 | 0.02 | 0.94 | 0.28 | 0.27 | 1.01 | 0.20 | 0.14 | 0.41 | 0.11 | 0.14 | 0.91 | 0.27 | 0.29 |
| Toscana | 0.68 | 0.21 | 0.19 | 1.52 | 0.43 | 0.48 | 0.83 | 0.25 | 0.31 | 0.18 | 0.04 | 0.03 | 0.84 | 0.28 | 0.20 |
| Umbria | 0.29 | 0.09 | 0.05 | 1.31 | 0.41 | 0.48 | 1.31 | 0.34 | 0.26 | 0.11 | 0.04 | 0.05 | 0.65 | 0.19 | 0.18 |
| Valle d’Aosta | 5.46 | 1.43 | 0.34 | 5.23 | 1.45 | 1.01 | 1.71 | 0.38 | 0.17 | 0.11 | 0.03 | 0.00 | 0.91 | 0.22 | 0.17 |
| Veneto | 0.76 | 0.26 | 0.29 | 2.11 | 0.71 | 1.11 | 0.73 | 0.22 | 0.31 | 0.08 | 0.02 | 0.02 | 0.65 | 0.20 | 0.27 |
| W1 | W2 | W3 | W4 | W5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IC | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD |
| Abruzzo | 5.79 | 1.83 | 0.90 | 5.87 | 1.70 | 1.98 | 7.17 | 2.53 | 3.45 | 1.07 | 0.27 | 0.23 | 3.13 | 0.81 | 0.68 |
| Basilicata | 3.38 | 1.07 | 0.26 | 5.33 | 1.41 | 1.05 | 3.02 | 0.98 | 1.05 | 0.71 | 0.25 | 0.26 | 1.24 | 0.32 | 0.26 |
| Calabria | 1.18 | 0.34 | 0.15 | 2.72 | 0.65 | 0.46 | 2.57 | 0.71 | 0.84 | 0.92 | 0.23 | 0.30 | 1.95 | 0.47 | 0.57 |
| Campania | 3.12 | 0.73 | 0.41 | 3.91 | 0.89 | 0.79 | 3.17 | 0.94 | 0.91 | 0.53 | 0.08 | 0.10 | 1.76 | 0.48 | 0.33 |
| Emilia-Romagna | 8.41 | 2.79 | 3.39 | 5.79 | 1.92 | 1.13 | 9.01 | 2.91 | 4.27 | 1.23 | 0.31 | 0.20 | 3.45 | 0.93 | 1.25 |
| Friuli Venezia Giulia | 5.02 | 1.54 | 0.37 | 5.68 | 1.88 | 0.98 | 7.08 | 2.58 | 3.72 | 1.23 | 0.34 | 0.37 | 3.62 | 0.86 | 0.98 |
| Lazio | 3.45 | 1.11 | 1.01 | 6.19 | 1.88 | 1.24 | 6.77 | 1.98 | 2.52 | 1.22 | 0.21 | 0.20 | 3.52 | 0.90 | 1.08 |
| Liguria | 11.54 | 3.80 | 3.16 | 7.93 | 1.90 | 1.48 | 5.61 | 1.62 | 1.58 | 0.97 | 0.19 | 0.19 | 3.10 | 0.76 | 1.05 |
| Lombardia | 13.73 | 4.51 | 4.24 | 9.43 | 2.81 | 3.07 | 8.65 | 2.83 | 4.09 | 0.63 | 0.12 | 0.15 | 2.74 | 0.75 | 1.02 |
| Marche | 11.08 | 3.70 | 3.11 | 6.16 | 2.05 | 1.41 | 10.29 | 3.31 | 4.76 | 1.77 | 0.49 | 0.73 | 4.26 | 1.00 | 1.17 |
| Molise | 2.94 | 0.81 | 0.97 | 4.58 | 1.27 | 0.97 | 8.51 | 2.44 | 3.64 | 0.65 | 0.22 | 0.24 | 1.96 | 0.39 | 0.49 |
| P.A. Bolzano | 12.24 | 3.66 | 1.40 | 8.28 | 2.60 | 2.79 | 7.53 | 2.43 | 1.12 | 1.88 | 0.58 | 0.84 | 4.14 | 1.19 | 1.95 |
| P.A. Trento | 14.97 | 4.84 | 2.19 | 9.79 | 3.55 | 3.84 | 10.16 | 3.43 | 4.66 | 0.92 | 0.26 | 0.27 | 5.17 | 1.64 | 2.47 |
| Piemonte | 10.40 | 3.44 | 3.06 | 9.27 | 2.81 | 2.99 | 8.68 | 2.78 | 3.86 | 0.57 | 0.18 | 0.24 | 3.56 | 1.03 | 0.87 |
| Puglia | 3.95 | 0.88 | 0.70 | 5.63 | 1.71 | 1.21 | 7.10 | 2.34 | 3.11 | 0.77 | 0.13 | 0.11 | 1.74 | 0.47 | 0.37 |
| Sardegna | 1.89 | 0.60 | 0.81 | 4.64 | 0.99 | 1.18 | 3.72 | 1.09 | 1.36 | 1.83 | 0.41 | 0.50 | 2.07 | 0.58 | 0.86 |
| Sicilia | 1.60 | 0.49 | 0.36 | 5.06 | 1.52 | 1.11 | 3.78 | 1.10 | 1.29 | 2.40 | 0.64 | 0.83 | 3.40 | 0.87 | 0.74 |
| Toscana | 7.96 | 2.61 | 2.39 | 7.99 | 2.28 | 2.52 | 7.67 | 2.46 | 3.08 | 1.58 | 0.39 | 0.54 | 3.70 | 0.87 | 0.83 |
| Umbria | 5.44 | 1.84 | 0.67 | 9.64 | 2.75 | 2.86 | 9.75 | 3.33 | 3.87 | 0.91 | 0.25 | 0.34 | 1.59 | 0.24 | 0.25 |
| Valle d’Aosta | 21.49 | 6.68 | 1.18 | 13.53 | 4.01 | 2.36 | 11.94 | 3.74 | 2.36 | 0.80 | 0.11 | 0.00 | 6.37 | 1.82 | 1.18 |
| Veneto | 7.26 | 2.39 | 1.18 | 7.58 | 2.64 | 3.66 | 6.22 | 1.90 | 2.39 | 1.16 | 0.31 | 0.35 | 4.20 | 1.19 | 1.63 |
| W1 | W2 | W3 | W4 | W5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HO | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD | Peak | s.d. | MAD |
| Abruzzo | 27.52 | 9.33 | 14.24 | 54.44 | 15.67 | 13.23 | 52.23 | 18.90 | 29.16 | 6.79 | 1.53 | 1.75 | 40.79 | 11.97 | 12.66 |
| Basilicata | 11.55 | 4.16 | 3.42 | 29.31 | 7.61 | 6.32 | 31.98 | 10.17 | 15.54 | 9.95 | 2.23 | 3.03 | 20.43 | 6.05 | 8.30 |
| Calabria | 9.40 | 2.92 | 2.89 | 22.34 | 6.50 | 6.78 | 24.75 | 7.33 | 9.59 | 9.30 | 2.25 | 3.08 | 22.91 | 6.12 | 8.79 |
| Campania | 10.72 | 3.71 | 5.60 | 40.18 | 9.66 | 7.27 | 27.92 | 9.10 | 6.31 | 6.53 | 1.23 | 1.85 | 24.20 | 7.24 | 6.77 |
| Emilia-Romagna | 88.44 | 30.55 | 23.47 | 65.34 | 22.44 | 18.27 | 83.01 | 27.33 | 40.56 | 10.09 | 2.05 | 1.60 | 60.57 | 17.42 | 21.58 |
| Friuli Venezia Giulia | 19.42 | 5.71 | 7.56 | 57.85 | 21.50 | 18.48 | 55.96 | 18.99 | 24.34 | 4.36 | 1.17 | 1.16 | 42.71 | 10.21 | 11.16 |
| Lazio | 24.97 | 8.77 | 11.70 | 57.97 | 15.87 | 12.24 | 55.54 | 17.07 | 22.58 | 9.15 | 1.86 | 1.55 | 36.50 | 9.79 | 11.31 |
| Liguria | 74.36 | 25.06 | 24.95 | 90.41 | 22.80 | 16.06 | 44.56 | 15.70 | 16.64 | 6.00 | 1.40 | 1.82 | 49.21 | 15.42 | 21.46 |
| Lombardia | 120.04 | 38.94 | 42.15 | 83.40 | 23.88 | 22.40 | 71.35 | 24.15 | 35.60 | 4.35 | 0.87 | 0.76 | 36.97 | 10.42 | 9.84 |
| Marche | 65.63 | 24.45 | 19.25 | 39.21 | 13.84 | 6.71 | 53.24 | 18.94 | 29.65 | 4.52 | 1.08 | 1.17 | 22.75 | 6.30 | 9.43 |
| Molise | 11.45 | 3.62 | 3.88 | 26.18 | 7.83 | 4.85 | 35.67 | 11.66 | 11.89 | 4.25 | 1.20 | 0.97 | 14.72 | 4.00 | 4.37 |
| P.A. Bolzano | 61.18 | 16.90 | 13.12 | 91.68 | 26.38 | 20.93 | 48.76 | 13.29 | 12.42 | 6.02 | 1.42 | 1.54 | 26.17 | 4.01 | 3.77 |
| P.A. Trento | 66.53 | 24.13 | 14.25 | 80.58 | 28.26 | 43.98 | 40.10 | 14.50 | 16.71 | 5.54 | 1.26 | 0.96 | 29.20 | 8.46 | 10.00 |
| Piemonte | 81.56 | 27.56 | 38.12 | 119.94 | 36.15 | 42.06 | 89.27 | 30.11 | 45.98 | 4.77 | 1.16 | 1.11 | 49.12 | 15.70 | 17.78 |
| Puglia | 16.08 | 5.53 | 6.51 | 42.02 | 13.03 | 6.00 | 50.36 | 16.61 | 20.50 | 6.23 | 1.29 | 1.60 | 18.69 | 6.28 | 5.57 |
| Sardegna | 7.68 | 2.63 | 4.16 | 37.88 | 10.09 | 8.95 | 23.05 | 6.59 | 8.18 | 14.64 | 3.96 | 5.29 | 25.19 | 8.07 | 9.31 |
| Sicilia | 11.36 | 4.13 | 3.02 | 32.08 | 8.90 | 8.05 | 25.48 | 7.17 | 9.16 | 17.10 | 4.55 | 6.11 | 29.92 | 8.91 | 13.55 |
| Toscana | 30.81 | 10.74 | 6.96 | 49.12 | 13.82 | 14.33 | 46.22 | 15.40 | 20.87 | 11.37 | 2.86 | 3.16 | 36.84 | 11.28 | 14.89 |
| Umbria | 19.95 | 6.35 | 3.87 | 53.40 | 14.49 | 12.61 | 53.85 | 17.83 | 22.44 | 6.12 | 1.67 | 1.51 | 25.40 | 8.03 | 12.86 |
| Valle d’Aosta | 104.24 | 31.94 | 30.67 | 135.28 | 41.62 | 46.60 | 54.11 | 16.22 | 12.98 | 3.98 | 1.14 | 1.18 | 64.46 | 17.02 | 17.70 |
| Veneto | 35.02 | 12.13 | 9.49 | 55.26 | 19.69 | 28.62 | 35.06 | 11.26 | 16.49 | 4.65 | 1.05 | 0.92 | 32.29 | 9.61 | 11.68 |
| DEC | HO | IC | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W1 | W2 | W3 | W4 | W5 | W1 | W2 | W3 | W4 | W5 | W1 | W2 | W3 | W4 | W5 | |||
| CID | 0.5262 | 0.6510 | 0.7988 | 0.7192 | 0.8241 | 0.5997 | 0.6823 | 0.7537 | 0.7196 | 0.7196 | 0.5211 | 0.8079 | 0.8167 | 0.7649 | 0.7638 | ||
| 0.9969 | 0.9830 | 0.8320 | 0.9411 | 0.7782 | 0.9953 | 0.9671 | 0.9106 | 0.9326 | 0.9326 | 0.9965 | 0.9193 | 0.8648 | 0.9142 | 0.9381 | |||
| Cor | 0.8441 | 0.8237 | 0.8342 | 0.5388 | 0.7939 | 0.9520 | 0.9603 | 0.9811 | 0.9239 | 0.9239 | 0.9110 | 0.9252 | 0.9416 | 0.7199 | 0.8292 | ||
| 0.5825 | 0.6851 | 0.6746 | 0.3491 | 0.5647 | 0.8236 | 0.8424 | 0.9092 | 0.6525 | 0.6525 | 0.7328 | 0.7878 | 0.8113 | 0.5690 | 0.6995 | |||
| DTW | 0.9525 | 0.8975 | 0.8149 | 0.9419 | 0.8085 | 0.9430 | 0.9128 | 0.9024 | 0.9436 | 0.9436 | 0.9264 | 0.9227 | 0.8955 | 0.8916 | 0.8951 | ||
| 0.9852 | 0.8976 | 0.7863 | 0.8332 | 0.7131 | 0.9922 | 0.9016 | 0.9404 | 0.9535 | 0.9535 | 0.9757 | 0.8531 | 0.8635 | 0.8318 | 0.9180 | |||
| Euclidean | 0.9958 | 0.9894 | 0.9507 | 0.9856 | 0.9249 | 0.9985 | 0.9877 | 0.9917 | 0.9951 | 0.9951 | 0.9951 | 0.9552 | 0.9800 | 0.9807 | 0.9791 | ||
| 0.9408 | 0.8642 | 0.7608 | 0.7689 | 0.7176 | 0.9807 | 0.9116 | 0.9544 | 0.9340 | 0.9340 | 0.9542 | 0.8343 | 0.8961 | 0.8601 | 0.8902 | |||
| Fourier | 0.9975 | 0.9930 | 0.9663 | 0.9924 | 0.9611 | 0.9992 | 0.9933 | 0.9951 | 0.9979 | 0.9979 | 0.9970 | 0.9760 | 0.9878 | 0.9904 | 0.9872 | ||
| 0.9584 | 0.8974 | 0.7918 | 0.8533 | 0.7931 | 0.9876 | 0.9394 | 0.9668 | 0.9631 | 0.9631 | 0.9682 | 0.8818 | 0.9234 | 0.9127 | 0.9264 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palazzo, L.; Ievoli, R. Detecting Regional Differences in Italian Health Services during Five COVID-19 Waves. Stats 2023, 6, 506-518. https://doi.org/10.3390/stats6020032
Palazzo L, Ievoli R. Detecting Regional Differences in Italian Health Services during Five COVID-19 Waves. Stats. 2023; 6(2):506-518. https://doi.org/10.3390/stats6020032
Chicago/Turabian StylePalazzo, Lucio, and Riccardo Ievoli. 2023. "Detecting Regional Differences in Italian Health Services during Five COVID-19 Waves" Stats 6, no. 2: 506-518. https://doi.org/10.3390/stats6020032
APA StylePalazzo, L., & Ievoli, R. (2023). Detecting Regional Differences in Italian Health Services during Five COVID-19 Waves. Stats, 6(2), 506-518. https://doi.org/10.3390/stats6020032





