Parametrical T-Gate for Joint Processing of Quantum and Classic Optoelectronic Signals
Abstract
1. Introduction
1.1. Homeostatic Model of Equilibrium in Medicine, Biology and Technique
- The general scheme to sustain internal parameters of live systems in some limited bands.
- The substantial role of feedback mechanisms, including negative and positive ones.
- The joint work of two organ systems necessarily maintains homeostasis at the equilibrium state by means of the regulation of disturbances emerging in the body.
1.2. Possible Logic Platforms for Network Agents
1.3. Specifics of Quantum Schemes, Substantial for the Design of Network Agents
1.4. Heterogeneous Logic Architecture of the Agent for the Integration of Precise, Approximate and Quantum Data
1.5. The goal of the Paper
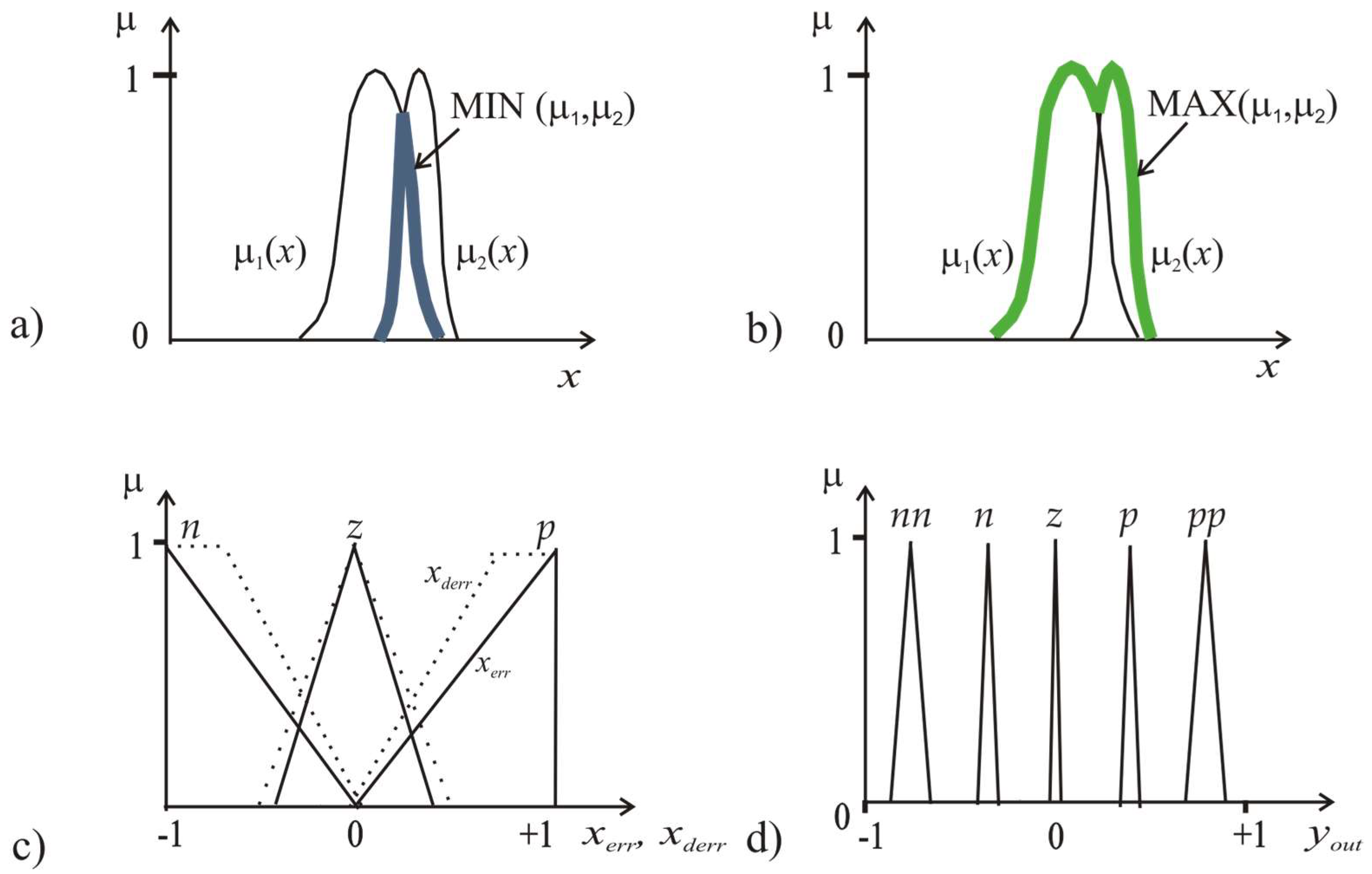
2. Method: Operators MIN/MAX and Parametrical -Norms/-Conorms
2.1. Specifics of Fuzzy Membership Functions and -Norms/-Conorms
2.2. MVL Modelling
3. Results: Parametrical Logic Gate as the Tool for Confidential Control of Classical Signals by Quantum Data
3.1. Confidential Parameter Transfer by Means of Quantum Keys and Simplified Sectret Coding
3.2. Comparison of Confidential Data without Their Disclosing, Based on -Norms and -Conorms
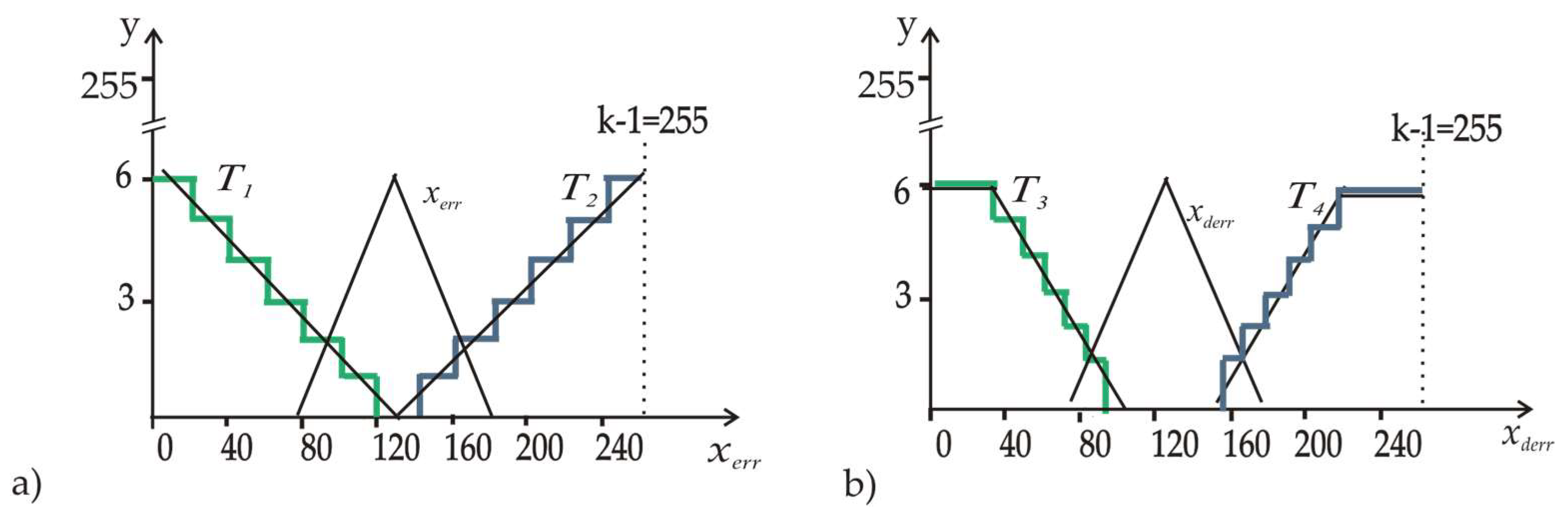
3.3. MVL Emulation of T-Gates for Controllers
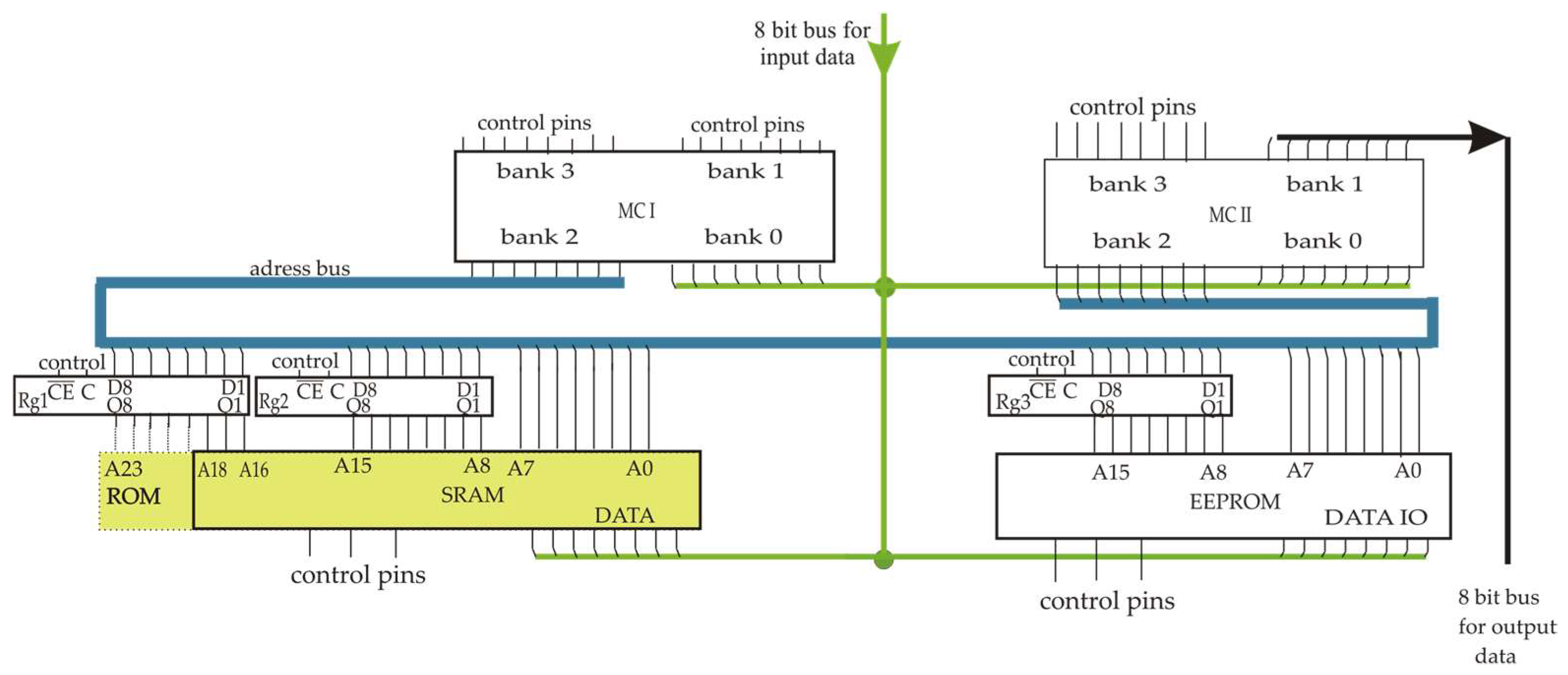
3.4. Specifics of Microassembler Modelling for -Gates
| ). Actual values of variables are written in microcontroller MCI. |
| m R1 R2 |
| 1: TNORM: MOV P2, R0; output of m |
| 2: CLR P1.7; enable Rg1 by |
| 3: SETB P1.4; Rg1 writes #A23-A17 |
| 4: CLR P1.4 |
| 5: SETB P1.7; lock Rg1 to fix m |
| 6: MOV P2,R1; output |
| 7: CLR P1.6; enable Rg2by |
| 8: SETB P1.4; write to Rg2 |
| 9: CLR P1.4 |
| 10: SETB P1.6; lock Rg2 to fix |
| 11: MOV P2,R2; output of |
| 12: CLR P1.3; enable SRAM by |
| 13: CLR P1.1;enables output of SRAM |
| 14: MOV A,P0; read to A |
| 15: SETB P1.1; disable output of SRAM |
| 16: RETI |
| OUTPUT: A→,) for further calculations |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chander, B. Quantum Cryptography Key Distribution: Quantum Computing. In Quantum Cryptography and the Future of Cyber Security 2020; Chaubey, N.K., Prajapati, B.B., Eds.; IGI Global: Hershey, PA, USA, 2020; pp. 84–108. [Google Scholar] [CrossRef]
- Laghari, A.A.; Shah, H.; Laghari, R.A.; Kumar, K.; Waqan, A.A.; Jumani, A.K. A Review on Quantum Computing Trends & Future Perspectives. EAI Endorsed Trans. Cloud Syst. 2022, 7, 1–11. [Google Scholar] [CrossRef]
- Elgazzar, K.; Khalil, H.; Alghamdi, T.; Badr, A.; Abdelkader, G.; Elewah, A.; Buyya, R. Revisiting the internet of things: New trends, opportunities and grand challenges. Front. Internet Things 2022, 1, 7. [Google Scholar] [CrossRef]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Gyanendra Prasad Joshi, G.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Kim, J.; Moon, H.; Jung, H. Drone-Based Parcel Delivery Using the Rooftops of City Buildings: Model and Solution. Appl. Sci. 2020, 10, 4362. [Google Scholar] [CrossRef]
- Zhang, K.; Kang, L.; Chen, X.; He, M.; Zhu, C.; Li, D. A Review of Intelligent Unmanned Mining Current Situation and Development Trend. Energies 2022, 15, 513. [Google Scholar] [CrossRef]
- Denecke, K.; Claude, R.; Baudoin, C.R. A Review of Artificial Intelligence and Robotics in Transformed Health Ecosystems. Front. Med. 2022, 9, 795957. [Google Scholar] [CrossRef]
- Carpentiere, C.D.; Mancuso, I.; Albino, V.; Petruzzelli, A.M.; Panniello, U. Innovative Business Models for the Future Smart City. Resourceedings. 2023, 3, 1–12. [Google Scholar] [CrossRef]
- Bykovsky, A.Y. Heterogeneous network architecture for integration of AI and quantum optics by means of multiple-valued logic. Quantum Rep. 2020, 2, 126–165. [Google Scholar] [CrossRef]
- Barfield, W. A Systems and Control Theory Approach for Law and Artificial Intelligence: Demystifying the “Black-Box”. J 2021, 4, 564–576. [Google Scholar] [CrossRef]
- Guerola-Navarro, V.; Gil-Gomez, H.; Oltra-Badenes, R.; Soto-Acosta, P. Customer relationship management and its impact on entrepreneurial marketing: A literature review. Int. Entrep. Manag. J. 2022, 41. [Google Scholar] [CrossRef]
- Gupta, M.M.; Qi, J. Theory of t-norms and fuzzy inference methods. Fuzzy Sets Syst. 1991, 40, 431–450. [Google Scholar] [CrossRef]
- Bykovsky, A. Multiple-Valued Logic Modelling for Agents Controlled via Optical Networks. Appl. Sci. 2022, 12, 1263. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 4th ed.; Pearson: Hoboken, NJ, USA, 2021. [Google Scholar]
- Gorodetskiy, A.E.; Tarasova, I.L.; Kurbanov, V.G. Situational Control of the Group Interaction of Mobile Robots. In Smart Electromechanical Systems. Studies in Systems, Decision and Control; Gorodetskiy, A., Tarasova, I., Eds.; Springer: Cham, Switzerland, 2020; Volume 261, pp. 91–101. [Google Scholar] [CrossRef]
- Bykovsky, A.Y. Multiple-Valued Logic and Neural Network in the Position-Based Cryptography Scheme. J.Russ. Laser Res. 2021, 42, 618–630. [Google Scholar] [CrossRef]
- Ma, X.; Yuan, X.; Cao, Z.; Qi, B.; Zhang, Z. Quantum random number generation. NPJ Quantum Inf. 2016, 2, 16021. [Google Scholar] [CrossRef]
- Bykovsky, A.Y.; Vasiliev, N.A. Data Verification in the Agent, Combining Blockchain and Quantum Keys by Means of Multiple-Valued Logic. Appl. Syst.Innov. 2023, 6, 51. [Google Scholar] [CrossRef]
- Unruh, D. Quantum Position Verification in the Random Oracle Model. In Advances in Cryptology—CRYPTO 2014; Garay, J.A., Gennaro, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–18. [Google Scholar] [CrossRef]
- Billman, G.E. Homeostasis: The Underappreciated and Far Too Often Ignored Central Organizing Principle of Physiology. Front. Physiol. Sec. Integr. Physiol. 2020, 11, 200. [Google Scholar] [CrossRef] [PubMed]
- Kotas, M.; Medzhitov, R. Homeostasis, inflammation and disease susceptibility. Cell 2015, 160, 816–827. [Google Scholar] [CrossRef]
- Sandler, U.; Tsitolovsky, L. Fuzzy Logic and S-Lagrangian Dynamics of Living Systems: Theory of Homeostasis. In Lagrangian Mechanics; Canbolat, H., Ed.; InTech: London, UK, 2017. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. The Consept of a Linguistic Variable and Its Application to Approximate Reasoning; Elsevier: New York, NY, USA, 1973. [Google Scholar]
- Li, X. The Classical Logic and the Continuous Logic. In Proceedings of the Future Technologies Conference (FTC) 2022, Virtual, 20–21 October 2022; Arai, K., Ed.; Lecture Notes in Networks and Systems. Springer: Cham, Switzerland, 2022; Volume 1, pp. 511–525. [Google Scholar] [CrossRef]
- Bergmann, M. An Introduction to Many-Valued and Fuzzy Logic. In Semantics, Algebras, and Derivation Systems; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Greco, G.; Liang, F.; Palmigiano, A. Kleene algebras, adjunction and structural control. arXiv 2018, arXiv:1805.07583v1. Available online: https://doi.org/10.48550/arXiv.1805.07583 (accessed on 16 April 2023). [CrossRef]
- Le Mézo, T.; Jaulin, L.; Massé, D.; Zerr, B. Kleene Algebra to Compute Invariant Sets of Dynamical Systems. Algorithms 2022, 15, 90. [Google Scholar] [CrossRef]
- Yurenko, K.; Kharchenko, P.; Fandeev, E.; Yurenko, I. Synthesis of a Neuro-Fuzzy Model in the Structure of an Automatic Rolling Stock Control System. In Cyber-Physical Systems: Intelligent Models and Algorithms. Studies in Systems, Decision and Control; Kravets, A.G., Bolshakov, A.A., Shcherbakov, M., Eds.; Springer: Cham, Switzerland, 2022; Volume 417, pp. 121–132. [Google Scholar] [CrossRef]
- Beiu, V. Threshold logic implementations: The early days. In Proceedings of the IEEE 46th Midwest Symposium on Circuits and Systems, Cairo, Egypt, 27–30 December 2003; Volume 3, pp. 1379–1383. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M. Construction and evaluation of a control mechanism for fuzzy fractional-order PID. Appl. Sci. 2022, 12, 6832. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Reznik, L. Fuzzy Controllers. In Newnes; An Imprint of Butterworth-Heinemann Linacre House; Jordan Hill: Oxford, UK, 1997. [Google Scholar]
- Sivanandam, S.N.; Sumathi, S.; Deepa, S.N. Introduction to Fuzzy Logic Using MATLAB; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Hamacher, H. Uber logische verknunpfungenn unssharfer aussagen undderen zugenhorige bewertungsfunktione. Prog. Cybern. Syst. Res. 1978, 3, 267–288. [Google Scholar]
- Hamacher Operations of Intuitionistic Fuzzy Matrices. Available online: https://www.researchgate.net/publication/323385451_Hamacher_Operations_of_Intuitionistic_Fuzzy_Matrices#fullTextFileContent (accessed on 16 April 2023).
- Zhu, J.; Li, Y. Hesitant Fuzzy Linguistic Aggregation Operators Based on the Hamacher t-norm and t-conorm. Symmetry 2018, 10, 189. [Google Scholar] [CrossRef]
- Allen, C.M.; Givone, D.D. The Allen-Givone Implementation Oriented Algebra. In Computer Science and Multiple-Valued Logic: Theory and Applications; Rine, D.C., Ed.; North Holland: Amsterdam, The Netherlands, 1984; pp. 262–283. [Google Scholar]
- Aliseda, A. The Logic of Abduction: An Introduction. In Springer Handbook of Model-Based Science; Magnani, L., Bertolotti, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 219–230. [Google Scholar]
- Non-Monotonic Logic. Revision Apr 20. 2019. Available online: https://plato.stanford.edu/entries/logic-nonmonotonic/ (accessed on 16 April 2023).
- Pigozzi, F.; Medvet, E.; Nenzi, L. Mining Road Traffic Rules with Signal Temporal Logic and Grammar-Based Genetic Programming. Appl. Sci. 2021, 11, 10573. [Google Scholar] [CrossRef]
- Antunes, H.; Carnielli, W.; Kapsner, A.; Rodrigues, A. Kripke-Style Models for Logics of Evidence and Truth. Axioms 2020, 9, 100. [Google Scholar] [CrossRef]
- Zavitsanos, D.; Ntanos, A.; Giannoulis, G.; Avramopoulos, H. On the QKD Integration in Converged Fiber/Wireless Topologies for Secured, Low-Latency 5G/B5G Fronthaul. Appl. Sci. 2020, 10, 5193. [Google Scholar] [CrossRef]
- Wooters, W.K.; Zurek, W.H. A Single Quantum Cannot Be Cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Bykovsky, A.Y.; Kompanets, I.N. Quantum cryptography and combined schemes of quantum cryptography communication networks. Quantum Electron. 2018, 48, 777–801. [Google Scholar] [CrossRef]
- Averkin, A.N.; Batyrshin, I.; Blishun, A.; Silov, V.; Tarasov, V. Fuzzy Sets in Models of Control and Artificial Intelligence; Nauka: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Averkin, A.N.; Bykovsky, A.Y.; Melnik, A.V. Fuzzy and multiple-valued optoelectronic data processing based on MAXIMUM, MIMIMUM and parametrical logical gates. Proc. SPIE 1999, 3733, 392–400. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- NIST SP 800-22 Revision 1a, A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22r1a.pdf (accessed on 16 April 2023).
- Bykovsky, A.Y. Multiple-Valued Logic for The Implementation of Random Oracle and Position-Based Cryptography. J. Russ. Laser Res. 2019, 40, 173–183. [Google Scholar] [CrossRef]
- Predko, M. Programming and Customizing the 8051 Microcontroller; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Simpson, P.A. FPGA Design, Best Practices for Team Based Reuse, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]





| Author | Norm T(x,y) | Conorm T*(x,y) |
|---|---|---|
| L. Zadeh | MIN (x,y) | MAX (x,y) |
| Goguen | xy | x + y − xy |
| - | xy/(x + y − xy) | (x + y−2xy)/(1 − xy) |
| Giles | MIN (x + y, 1) | MAX (x + y−1,0) |
| - | (lxy/(1 − (1 − l) (x + y − xy)) | l(x + y) + xy(1−2l)/l + xy(1 − l)) |
| - | mxy/(1 − (1 − m)(x + y − xy) | (m(x + y) + xy(1−2m))/(m + xy(1 − m)) |
| - | MIN (x + y + mxy,1) | MAX ((1 + m)(x + y-1) − mxy,0) |
| Weber | MIN (x + y + mxy,1) | MAX ((x + y − 1 + mxy)/(1 + m),0) |
| Yandong | MIN (x + y + mxy,1) | MAX ((1 + m)(xy − 1) − mxy,0) |
| Schweizer and Sklar, p ∈ (−∞,+∞) | 1 - max [0, (1 − x) –p + (1 + y)–p − 1)] 1/p | MAX (0, x−p + y–p − 1) −1/p |
| Hamacher, | xy/(m + (1 − m)(x + y − xy)) | (x + y − (2 − m) xy)/xy(1 − (1 − m)xy) |
| Frank, s ∈ (0,+∞) | 1 − logs [1 + (s 1-x − 1)(s1 - y − 1)/s − 1] | logs [1 + (sx − 1)(sy − 1)/s − 1] |
| Yager, w∈(0,+∞) | MIN [1, (xw + yw)1/w] | 1 − MIN [1,(1 − x)w + (1 − y)w)1/w |
| Dubois and Prade, α∈ (0,1) | X + y − xy − MIN(x,y,1 − α)/ MAX (1 − x,1 − y, α) | ab/MAX (x,y,α) |
| Dombi, λ ∈ (0,+∞) | 1/1 + [(1/x − 1)-λ + (1/y − 1) −λ ] −1/λ | 1/1 + [(1/x − l)λ + (1/y − 1)λ]1/λ |
| X2 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | |||||||||||
| 0.1 | 0.0168 | 0.0313 | 0.0437 | 0.0547 | 0.0645 | 0.0732 | 0.0809 | 0.0879 | 0.0938 | 0.1 | |
| 0.2 | 0.0313 | 0.0588 | 0.0833 | 0.1053 | 0.1250 | 0.1428 | 0.1590 | 0.1739 | 0.1875 | 0.2 | |
| 0.3 | 0.0437 | 0.0833 | 0.1192 | 0.1518 | 0.1818 | 0.2093 | 0.2346 | 0.2580 | 0.2798 | 0.3 | |
| 0.4 | 0.0547 | 0.1053 | 0.1518 | 0.1951 | 0.2352 | 0.2727 | 0.3077 | 0.3404 | 0.3711 | 0.4 | |
| 0.5 | 0.0645 | 0.1250 | 0.1818 | 0.2352 | 0.2857 | 0.3333 | 0.3784 | 0.4211 | 0.4615 | 0.5 | |
| 0.6 | 0.0732 | 0.1428 | 0.2093 | 0.2727 | 0.3333 | 0.3913 | 0.4468 | 0.5000 | 0.5510 | 0.6 | |
| 0.7 | 0.0809 | 0.1590 | 0.2346 | 0.3077 | 0.3784 | 0.4468 | 0.5130 | 0.5773 | 0.6396 | 0.7 | |
| 0.8 | 0.0879 | 0.1739 | 0.2580 | 0.3404 | 0.4211 | 0.5000 | 0.5773 | 0.6531 | 0.7273 | 0.8 | |
| 0.9 | 0.0938 | 0.1875 | 0.2798 | 0.3711 | 0.4615 | 0.5510 | 0.6396 | 0.7273 | 0.8140 | 0.9 | |
| 1.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| Alice | Bob | |
|---|---|---|
| Task: | To send confidential byte, e.g., to Bob | |
| Coding resource: Equal sets (or the numbered list) of common quasi-random keys. | = 11001011, , , … | = 11001011, = 01011100, = 10010111, … |
| Steps: | Alice | Bob |
| 1. To write consecutive numbers of positions for bits in , …, which coincide with bits in | Compares: di = 10001110 with = 11001011, = 01011100, … Result: In :Poz = 1,3,4,6; In :Poz = 2,4,5,7. | - |
| 2. Transfer to Bob | : 1,3,4,6; : 2,4,5,7 | - |
| : 1,3,4,6; : 2,4,5,7 | ||
| 3. Reconstruction of confidential byte | - | = 1 1 0 0 1 0 1 1, ↓ ↓↓ ↓ 1 0 0 0 =0 1 0 1 1 1 0 0 ↓ ↓ ↓ ↓ 1 1 1 0 Finally, di = 10001110 |
| Input: ← List of quasi-random keys from QKD line or copies of RO in both agents | ||
| Agent 1 | Agent 2 | |
| 1. | , | - |
| 2. | Calculates T | - |
| 3. | , and T to Agent 2 | - |
| 4. | - | , |
| 5. | - | |
| 6. | - | , and T to Agent 2 |
| 7. | ||
| for comparison are in Agents 1 and 2 | ||
| Total number of involved instructions | 9 | 9 | 202 | 315 |
| Calculation time, work cycles | 10 | 10 | 251 | 409 |
| Emulation of 16-bit calculations by the 8-bit platform | Not used | Not used | + | + |
| Addition | - | - | 2 | 1 |
| 6 Instructions | - | - | 12 | 6 |
| 6 Work cycles | - | - | 12 | 6 |
| Subtraction | - | - | 2 | 4 |
| 7 Instructions | 14 | 28 | ||
| 7 Work cycles | 14 | 28 | ||
| Multiplication | - | - | 3 | 6 |
| 35 Instructions | 105 | 210 | ||
| 50 Work cycles | 150 | 300 | ||
| Division | - | - | 1 | 1 |
| 71 Instructions | 71 | 71 | ||
| 75 Work cycles | 75 | 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bykovsky, A.Y.; Vasiliev, N.A. Parametrical T-Gate for Joint Processing of Quantum and Classic Optoelectronic Signals. J 2023, 6, 384-410. https://doi.org/10.3390/j6030026
Bykovsky AY, Vasiliev NA. Parametrical T-Gate for Joint Processing of Quantum and Classic Optoelectronic Signals. J. 2023; 6(3):384-410. https://doi.org/10.3390/j6030026
Chicago/Turabian StyleBykovsky, Alexey Y., and Nikolay A. Vasiliev. 2023. "Parametrical T-Gate for Joint Processing of Quantum and Classic Optoelectronic Signals" J 6, no. 3: 384-410. https://doi.org/10.3390/j6030026
APA StyleBykovsky, A. Y., & Vasiliev, N. A. (2023). Parametrical T-Gate for Joint Processing of Quantum and Classic Optoelectronic Signals. J, 6(3), 384-410. https://doi.org/10.3390/j6030026





