Abstract
The protonation/deprotonation reaction is one of the most fundamental processes in solutions and biological systems. Compounds with dissociative functional groups change their charge states by protonation/deprotonation. This change not only significantly alters the physical properties of a compound itself, but also has a profound effect on the surrounding molecules. In this paper, we review our recent developments of the methods for predicting the , the equilibrium constant for protonation reactions or acid dissociation reactions. The , which is a logarithm of , is proportional to the reaction Gibbs energy of the protonation reaction, and the reaction free energy can be determined by electronic structure calculations with solvation models. The charge of the compound changes before and after protonation; therefore, the solvent effect plays an important role in determining the reaction Gibbs energy. Here, we review two solvation models: the continuum model, and the integral equation theory of molecular liquids. Furthermore, the reaction Gibbs energy calculations for the protonation reactions require special attention to the handling of dissociated protons. An efficient method for handling the free energy of dissociated protons will also be reviewed.
1. Introduction
The protonation and deprotonation reactions of dissociative functional groups in solvated compounds often play essential roles in chemical and biological processes, such as solvation, protein–ligand binding, and the higher-order structure formation of proteins. Such processes occur in complex environments, where the functional groups are surrounded by other molecules, ions, and water. The equilibrium of the pronation and deprotonation states is governed by the Gibbs energy change of the reaction; thus, it can be stated that the process is fully thermodynamic.
The equilibrium constants of the protonation/deprotonation reaction, or the acid dissociation reaction, , or its logarithm, , can be measured experimentally by titration combined with pH electrode measurement, vibrational spectroscopy, neutron diffraction, and nuclear magnetic resonance. However, experimental values are not always available; hence, highly accurate prediction by computational means is most desirable [1].
Currently, one of the most successful methods for predicting the values of amino acids in proteins is PROPKA, an empirical method based on the three-dimensional (3D) protein structure [2]. The method can estimate the value, or the charged states of the amino acids in target proteins, within a reasonable computational time and with accuracy. However, to understand the mechanism of the protonation reactions and the shifts due to the environment, a nonempirical approach based on molecular theory is effective.
An accurate estimation of the free-energy change in the protonation process is indispensable for quantitative prediction. Therefore, estimating the energy change before and after dissociation using quantum chemistry calculations is a very effective approach.
In this paper, we review our recent developments of the computational methods for predicting pKa values, which are based on quantum chemical electronic structure methods combined with solvation models. Here, we review the methods employed. Specifically, we review two different solvation models: the polarizable continuum model (PCM) and the reference interaction site model (RISM) theories.
Quantum chemical calculations, such as density functional theory (DFT), can often be used to avoid the computational parameter dependence. For the pKa values of small compounds, a number of studies using quantum chemical calculations have been reported, and the details of their accuracy are discussed in a review by Ho and Coote [3]. To estimate reliable values, it is necessary to obtain the solvation free-energy difference of the molecules in aqueous solution, due to acid dissociation, as accurately as possible. Sprik and coworkers proposed a method for obtaining the free-energy profile due to acid dissociation from DFT-based ab initio molecular dynamics (AIMD) simulations and successfully obtained the values of many compounds, including amino acids in aqueous solution [4]. Although this method is highly accurate for pKa prediction, long computation times are required to obtain the solvation free-energy difference, thus indicating that it is only applicable to small molecules. To avoid these high computational costs, it is, therefore, essential to employ solvation free-energy calculation methods that are based on static quantum chemical methods. Recently, combinations of various quantum chemical calculation methods and the PCM have been explored in considering the solvent effects. High-precision solvation free-energy calculations can be used to discuss deprotonation trends in aqueous solutions [5,6,7,8,9,10]. The accuracy is in good agreement with experimental values, as reported by Takano and Houk [11].
However, even in calculations using the static DFT calculations with the PCM model, one often encounters several problems when adopting the conventional methods. One such problem is the choice of methodology (combinations of quantum chemical calculation methods, basis functions, cavity models, and the parameters of the PCM), and the error can vary greatly depending on the choice. An additional problem is that the solvation free energies of similar molecules, having the same chemical groups, tend to have correlations among them, while this rule is not applicable for all molecules. Because of such a methodology and the chemical group dependence, the calculated values scatter toward the corresponding experimental values.
One of the root causes in this complex issue is the treatment of the proton’s solvation free-energy value. Conventional methods adopt some reference value (e.g., values from experimental values) and assume that it is a constant value in the calculation of the for any type of molecule. Unlike an arbitrary molecule, the solvation free energy of one proton (H+), , cannot be directly calculated because the proton has no electrons. Instead, is sometimes calculated from the dissociation of a proton from the hydronium ion, , . The hydronium ion is surrounded by many water molecules and forms a hydrogen-bonding network with them; hence, it is desirable to use larger proton solvation clusters and/or other proton exchange reactions involving protonated/deprotonated compounds, except for clusters. However, the computational costs increase exponentially when the size of the clusters increases because of the vast configurations of the water clusters, as in the AIMD calculations. Therefore, it is extremely difficult to obtain the solvation free energy of the proton with high accuracy, which indicates that, in many cases, it has not been possible to quantitatively reproduce values.
In efforts to address the above, we have developed a methodology- and chemical-group-dependent approach for the evaluation of values using PCM-based methods [12,13,14,15]. This method refers to the experimental data of representative molecules with specific chemical groups, such as COOH, OH (alcohol), OH (phenol), SH, and NH2, among others. As noted earlier, the value depends strongly on the choice of methodology. Thus, the correction terms for the value should be evaluated for each methodology and chemical group considered. Our linear scaling scheme, mentioned in Section 3.2, provided the error within 0.25 units for standard PCM–DFT calculations. The details of this scheme are reported later.
The success of the abovementioned method allows us to adopt other static solvation models that differ from the PCM. The RISM theory is a statistical mechanics integral equation theory of molecular liquids, derived from the density functional derivative of the grand potential under a solute–solvent molecular pair interaction [16,17,18,19]. Unlike the PCM, the theory now allows us to consider molecular interaction, such as hydrogen bonding, which plays an important role in the acid dissociation reaction. In addition, the analytical solvation free-energy formula is known and can be evaluated on the basis of the first-principles approach. Although the computational cost is somewhat higher than that of the PCM, it has, nonetheless, been used to analyze various chemical processes in solution because of the above advantages. An extension of the RISM theory that is applicable to highly complex molecules, such as proteins, is the so-called 3D-RISM theory [20,21,22]. The latter can be derived from the six-dimensional molecular Ornstein–Zernike equation by applying the interaction site model for solvent molecules. The hybrid methods of the RISM, or the 3D-RISM theory with the quantum chemical electronic structure theory, are referred to as the RISM self-consistent field (SCF), or as the 3D-RISM-SCF theories [23,24,25].
In this paper, we review two types of approaches that are based on the RISM-SCF/3D-RISM-SCF theory: namely, the first-principles approach and the data-driven approach. In their pioneering work, Sato and coworkers applied the first-principles approach for measuring the , which is the equilibrium constant of the autoionization reaction of water [26,27]. Their method has been applied to studies of the of various systems in efforts to improve the accuracy. These studies have revealed that the most serious problem to be addressed, namely, improving the accuracy, is the estimation of the free energy of the dissociated protons. As mentioned above, Matsui et al. proposed a method to avoid this difficulty by using a data-driven approach with the PCM method [14]. Fujiki et al. extended their method by combining the 3D-RISM-SCF and Matsui’s method and achieved quantitative accuracy of the predicted values [28].
The organization of this review is as follows: Section 2 provides a general background to computation. In Section 3 and Section 4, theoretical studies, based on the PCM and RISM, respectively, are reviewed. In Section 5, we include a summary and offer some future perspectives pertaining to computational prediction.
2. Basics of pKa Computation
The value is proportional to the Gibbs energy change of the protonation reaction, or the acid dissociation reaction, , given by:
where and denote the gas constant and absolute temperature, respectively. The Gibbs energy change, , is:
where , , and denote the Gibbs energy of the unprotonated and protonated states of an acid, A, and that of a dissociated proton, respectively (See Figure 1). If we consider a thermodynamic cycle of the reaction, Equation (2) can be written as Equation (3), using the gas-phase reaction Gibbs energy, , and the solvation free energy of the , , and , namely, , respectively. These Gibbs energy terms can be evaluated by quantum chemical electronic structure calculations, such as the ab initio molecular orbital (MO) theory, or the Kohn–Sham DFT (KS-DFT). As mentioned earlier, since a compound/an acid, A, rearranges its electronic structure because of the protonation/deprotonation, a precise treatment of the electronic structure of the target compounds is highly anticipated. Furthermore, the solvent environment surrounding the target compounds must be considered. The most popular way to take solvent effects into account is to implement the PCM, one of the implicit solvation models, which is implemented in all the popular quantum chemical software packages, such as Gaussian and GAMESS. The computational methods employing the PCM will be reviewed in Section 3. Other candidates applicable to the consideration of the solvent effects on the electronic structure of solvated molecules are the integral equation theories of molecular liquids, namely, the RISM and 3D-RISM theories, which allow us to treat the solvent effects on the basis of the statistical mechanics theory on the molecular level, unlike the PCM. The computation method based on the RISM/3D-RISM will be reviewed in Section 4.
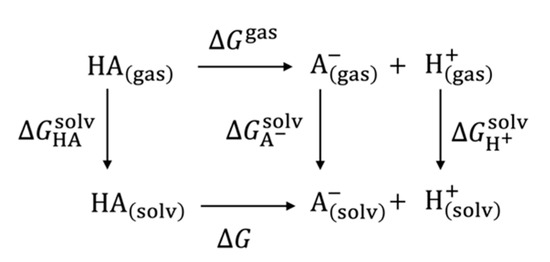
Figure 1.
Schematic description of thermodynamic cycle of the acid dissociation reaction.
3. Polarizable Continuum Model-Based Approach
3.1. Basics of the Polarizable Continuum Model
Among the methods that incorporate solvent effects, the dielectric model is a relatively simple method that is installed in many quantum chemistry program packages. In this section, we present a basic concept of the PCM for describing solvent effects and the results using this model.
In the continuum model, a cavity is created around a molecule filled with a dielectric medium with a dielectric constant, . We refer to the change in properties caused by this effect as the “solvent effect”. This effect can be described as in Equation (4):
In this equation, the latter two terms are obtained by the empirical method obtained from the volume/surface of a solute. For further details, see the following references by Mennucci’s group and the references therein [29,30]. In the dielectric model, consists of two types of potential. One is the electrostatic potential, from . The other is the reaction potential, , generated by the polarization emanating from the solvent molecules:
In the dielectric model, a vacancy in the form of a solute molecule is formed in a continuous dielectric, and the solute molecule is placed in the vacancy, using the polarization surface charge density, , at the boundary of the vacancy. When expresses an area integral, can be written as follows:
This surface integral is obtained by dividing the whole into smaller parts, Ak, and finding the sum of them:
The in Equation (7) depends on the overall charge, which is calculated from the electrostatic potential obtained when the solute molecules are assumed to be in a vacuum. We must consider the following equation to satisfy the boundary condition mentioned earlier:
where is the unit vector of the normal vector at a point, s, on the surface, and the direction is from inside the cavity to the outside. When we define the integral operator, , the above equation can be rewritten as follows:
where I is the unit operator. The conductor-like screening model [5] is based on the idea that the dielectric constant, , is now assumed, but, because of the effect of the solvent–solute interaction, it does not actually shield the charge effect, as per the value of . In this model, the following equation is assumed:
The in the following equation is an artificial function specific to this model:
where there is an arbitrariness in the value of . In the PCM, is used, and the model is referred to as a conductor-like PCM. As an alternative to this type of shielding, one can solve the integral equation by another method, the integral equation formulation of the PCM [7]:
By replacing each of these, we obtain what is called the PCM formation:
Obtaining VR(s) is similar to the SCF calculations performed, where the interaction energy, , is obtained by iteratively calculating and then adding the energy of the vacancy formation, etc., as an empirical value, to obtain the overall energy.
The calculation results are poor in many cases because of the addition of parameters under the assumption of an ideal gas. The solvation model of Truhlar and coworkers improved this term by calling it “cavitation”, “dispersion”, and “solvent structural effects” [31]. The most commonly used model is its density version (SMD, often referred to as “PCM-SMD”). By setting the structural information of a molecule into a parameter, this model reproduces the solvation energy of many types of solvents very well. Although the other parts are based on the derivation method of the PCM, the SMD is the most frequently used solvent model in quantum chemistry calculations.
3.2. The AKB Scheme
We now briefly summarize the “appropriate estimation with benchmark molecules” (AKB) scheme, the details of which were reported previously [14,32,33].
As noted earlier, the difference between the computed and observed values depends on the computational methods, such as the functional of DFT, the basis set, and the cavity of the PCM method; hence, the error should be systematic within similar reactions. In computing the with the AKB scheme, the Gibbs energy difference between the reactant and the product is scaled by s as follows:
The scaling factor, s, corresponds not only to an activity coefficient of the deprotonation reaction, but also to an error correction for a given computational method. We regard and s as constants, both of which depend on the approximation levels. Equation (14) then becomes:
where is defined as . Equation (15) results in an apparent linear correlation between the and values. Therefore, it is possible to compute an unknown by fitting and for reference molecules. We computed for several compounds that have either COOH, OH (phenol), or NH2 (aniline) groups, and plotted it with the experimental values, where linear regression curves were estimated by least-squares analysis (see Figure 2). The calculations by B3LYP/6-31++G(d, p) with the PCM-SMD provide a good result, within units (mean absolute error) in aqueous solution [32]. Note that, here, the slopes ( for the COOH, OH (phenol), and NH2 (aniline) groups differ from each other, indicating that the curves also exhibit the chemical-group dependence. Once the linear regression curve is obtained, from Equation (14), one can estimate the Gibbs energy of the proton in aqueous solution using the slope and the abscissa, as follows:
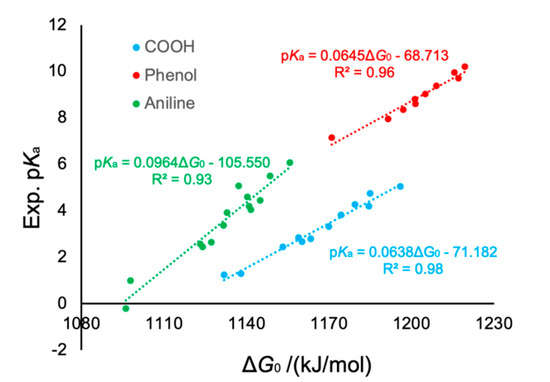
Figure 2.
Example of linear fitting at B3LYP/6-31++G(d, p) + PCM-SMD level. Three chemical groups (COOH, phenol, and aniline) were considered. R2 is the coefficient of determination.
for the COOH, OH (phenol), and NH2 (aniline) groups are 1115.71, 1065.32, and 1094.92 kJ/mol, respectively. This result indicates that, if one adopts the same value for evaluating the values of these compounds, a large error is obtained when using Equation (2). The AKB scheme complements the errors arising from both a difference in the method and the chemical groups, simultaneously.
3.3. Some Applications of the AKB Scheme
The linear scaling method is a very powerful scheme because it enables us to compute the values for many compounds.
3.3.1. Application to Salicylic Acid
Salicylic acid (2-hydroxybenzoic acid) has a COOH group and an OH (phenol) group; hence, two different regioisomers exist (3- and 4-hydroxybenzoic acid) (see Figure 3). Experimentally, the first value of salicylic acid is lower than the values of benzoic acid () and phenol () because the hydrogen bond between the neighboring COO− and OH groups stabilizes the deprotonated compound. This detail is presumed from the structures and experimental results, but it has not yet been accurately confirmed by theory. Although salicylic acid has good analgesic action, it can simultaneously cause the perforation of stomach ulcers as one of its adverse effects because of the low . To reduce the adverse effect while retaining the medicinal action, acetylsalicylic acid (commercially known as aspirin) was synthesized. Here, we examine both the first and second values of the hydroxybenzoic acids, and the value of the acetylsalicylic acid, to clarify the relationship between the and the structure of the conformers.
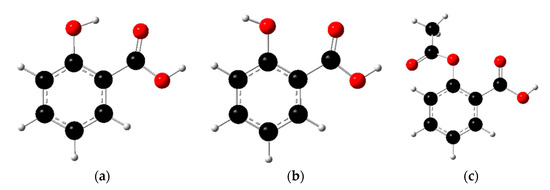
Figure 3.
Two conformers of salicylic acid. Conformer (a) forms a hydrogen bond between a phenol OH and a COOH group (shown by the broken line), conformer (b) does not form a hydrogen bond, and conformer (c) is aspirin. The black, red, and white balls represent carbon, oxygen, and hydrogen atoms, respectively.
For simplicity, we considered two conformations (Figure 3). Conformer (a) has a hydrogen bond between the phenol and carboxyl groups, whereas conformer (b) does not have any hydrogen bonds. Because of this difference, conformer (a) is more stable than conformer (b), by 22.1 kJ/mol, at the computational level. Hence, in the case of the salicylic acid, the existence of (b) is negligibly small, judging from the Boltzmann distribution. Table 1 provides the calculated ΔG and values for each conformer. It was found that both of the values for conformer (a) agree well with the experimental values: 2.97 and 13.4 [34]. However, the values for conformer (b) are similar to those of the benzoic acid () and phenol (). This difference is ascribed to the effect of the presence of a hydrogen bond in conformer (a). Specifically, the first deprotonated compound is stabilized by the hydrogen bond in conformer (a), which decreases the value by 1.5 units in the first deprotonation and increases the value by 2.5 units in the second deprotonation. These results indicate how the hydrogen bond strongly affects the value in small molecules, such as those of the salicylic acid. Furthermore, to understand this effect, we then examined (c) (aspirin), which has no explicit intramolecular interaction (see Figure 3). The corresponding results are also shown in Table 1. Here, the values of the regioisomers differ from the value of the salicylic acid. Because of the absence of an intramolecular hydrogen bond, the values of these isomers are also found to be close to the values of each chemical group. In the case of aspirin, the value is lower than that of the benzoic acid, but higher than that of the salicylic acid. Therefore, the neighboring acetyl group also affects the of the COOH group through a weaker hydrogen bond than that of the salicylic acid, or through a secondary hydrogen bond via water molecules. Our scheme can also consider the effect of the acetylation, compared with the salicylic acid alone, the effect of which is not fully treated in empirical approaches, such as PROPKA and H++. Our results demonstrate that our scheme is safely and accurately applicable to the evaluation of the of arbitrary molecules.

Table 1.
Deprotonation Gibbs energy (in kJ/mol) and estimated in each conformer of salicylic acid. Numbers in parentheses indicate experimental values.
3.3.2. Solvent Dependence
We next investigated the solvent dependencies on using various solvents [35,36,37]. Table 2 shows the results of the fitting and the estimated Gibbs energy of a proton of each solvent molecule. Again, the AKB method provided very good results. Interestingly, the experimental value is very different because of the for acetonitrile and DMSO, which have similar dielectric constants. The same also applies to aniline. The deprotonation Gibbs energy decreases as the dielectric constant decreases. This is why the values in THF are too low, even though the proton affinity of THF and acetonitrile is similar. Conversely, in the case of acids, such as carboxylic acids, the deprotonation Gibbs energy increases as the dielectric constant decreases. Table 2 shows the results for aniline. There are two different experimental results for THF; therefore, two results from the AKB scheme are independently shown. One of the problems associated with the AKB scheme is that we are unable to judge whether the experimental results are reliable or not when there is not much data available.

Table 2.
Solvent dependence on the scaling factor, , Gibbs energy of a proton, and mean absolute error (MAE) in computing for aniline derivatives. indicates the samples of aniline derivatives that have experimental values for the solvents.
4. Integral Equation-Based Approach
In this section, computational methods based on integral equation theories, RISM, and 3D-RISM, are reviewed. A comparison between the PCM-based method and the 3D-RISM-based method will also be discussed.
4.1. Basics of RISM-SCF and 3D-RISM-SCF
In this subsection, the basics of the RISM-SCF and 3D-RISM-SCF methods are explained. Since the formalisms of these two methods are very similar, that of RISM-SCF will be explained first, followed by a brief description of the 3D-RISM-SCF formalism later.
Similar to the PCM, the total free energy of solvated molecules is given by:
where is the free energy of the molecule in an isolated system or gas phase, which is evaluated as an expected value of the gas-phase Hamiltonian with respect to the solvated wave function, . It is noted that the is an eigen function of the solvated Hamiltonian, which includes the solvent electrostatic potential as an external field. is the solvation free energy, expressed by:
where is the number density of the solvent site, . The summations of and are running over the interaction sites in the solute and solvent molecules, respectively. The and are the total and direct correlation functions, evaluated by solving the RISM integral equation. These are the function of the distance between two interaction sites, and . To derive Equation (18), the Kovalenko–Hirata (KH) closure equation is employed [24,38]. If one employs the hypernetted chain (HNC) closure, instead of the KH closure, the Heaviside step function, , is replaced by . The RISM/KH equation is solved under the following solute–solvent interaction potential:
where and are the Lennard–Jones parameters, with the usual meanings. and denote point charges on the solute site, , and solvent site, , respectively. The solute point charge, , is determined to reproduce the electrostatic potential, due to the solute electronic structure, by the least-squares fitting method, known as the “restrained electrostatic potential” method. The solute wave function depends on the solvent distribution, which depends on the solute wave function through the solute–solvent interaction potential. Therefore, the quantum chemical electronic structure and the RISM calculations were performed until the solute wave function and solvent distribution were unchanged iteratively.
In the case of the 3D-RISM-SCF, is given by:
where and are the total and direct correlations in 3D format, respectively. These functions are obtained as the results of the 3D-RISM calculation coupled with the 3D-KH closure. In contrast to the correlation functions of the RISM, the in the 3D-RISM is related to the special distribution of solvent species. The solute–solvent interaction potential is given by:
where is the wave function of a solute molecule, and is the nucleus charge of a solute atom, . Unlike the RISM case, the electrostatic potential, due to the solute molecule, can be evaluated from the solute wave function directory, which is a great advantage of the 3D-RISM-SCF theory over the RISM-SCF theory. Therefore, since the 3D-RISM can incorporate anisotropic solvent distribution under the spatial distribution of solute electron density, it is suitable for handling complex solutes, such as biomolecules.
4.2. First-Principles Calculation of pKa and pKw
The can be determined by first-principles calculations, such as evaluating the free energy of the reactant and the product species of the acid dissociation reaction using RISM-SCF or 3D-RISM-SCF theories.
The pioneering work using the first-principles calculation by the RISM-SCF was performed by Sato et al. [27], who investigated the temperature and density dependences of the , where is an equilibrium constant of the autoionization reaction of water:
They performed the RISM-SCF calculation of the for a wide range of temperatures and densities. Following them, Yoshida et al. [26] extended the range of the applications of the temperature and density by using the KH closure, and also investigated the temperature and density dependences of the , including the supercritical region. Figure 4 shows the RISM-SCF results of the changes in the density and temperature dependences of the , , compared with experimental results. The computational values show a qualitatively similar tendency with the values of the experiments, namely, the decreases with increasing density and temperature, although, quantitatively, there are significant deviations. A detailed analysis of the free-energy components revealed the origin of these monotonical changes. The behavior is essentially determined by the difference in the solvation free energy, which is affected by two major effects: electrostatic stabilization and cavity formation. The balance between them determines the change in the .
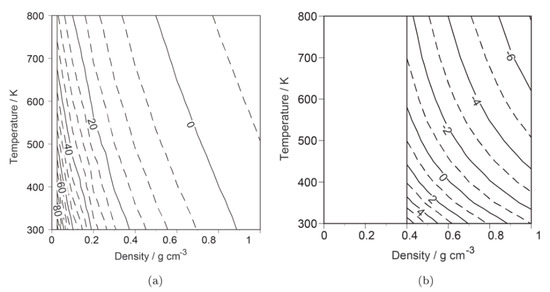
Figure 4.
Density and temperature dependences of , the difference of the from (1.0 g cm−3, 273.15 K). The computational and experimental values are provided in panels (a) and (b), respectively. These figures are reprinted with permission from [26], Copyright 2014, American Chemical Society.
Kido et al. performed first-principles calculations for the of glycine using the RISM-SCF extended to mixed solvent systems [39]. In this calculation, not only water, but also self-dissociated and were considered as solvents, making it possible to analyze the pH-dependent protonation state of glycine. Later, to further improve the accuracy, Kido et al. applied and assessed the RISM-SCF spatial electron density distribution (SEDD) method, which can take into account the spatial distribution of the electron density in the solute–solvent interaction [40]. As shown in Equation (19), the RISM-SCF requires the use of effective point charges for the solute–solvent interaction, which is one of the reasons for errors. The restraint electrostatic potential (RESP) method is usually used to determine the point charges, but it is known that the fitting accuracy of the RESP deteriorates when “rich” basis functions, such as those used in accurate electronic structure calculations, are required. The assessment by Kido et al. reveals that the RISM-SCF-SEDD can perform accurate calculations using “rich” basis functions by considering the spatial charge distribution.
A more straightforward way to consider the spatial charge distribution is to employ the 3D-RISM-SCF. As shown in Equation (21), the 3D-RISM-SCF can take into account the spatial distribution of the electron density derived from the solute wave function in the solute–solvent interaction. Seno et al. [41,42] calculated the of p-carboxybenzeneboronic acid (PCBA), and its complex, with a monosaccharide, using the 3D-RISM-SCF, and clarified the mechanism of a shift due to complex formation. PCBA is a drug candidate used in boron neutron capture therapy for skin cancer. The change is utilized upon the complex formation with monosaccharides to increase solubility.
In aqueous solution at physiological pH, PCBA exists in equilibrium as:
 and under higher pH conditions, the following equilibrium forms:
and under higher pH conditions, the following equilibrium forms:
 where and denote the dissociation constants of the corresponding reactions. The estimated and values are shown in Table 3. The results reveal that the was greatly reduced by the complex formation. Note that the adjusted values provided in Table 3 were evaluated on the basis of:
where is a parameter for calibrating the values. The parameter was determined by performing similar calculations for various carboxylic acids to fit the experimental values. On the basis of the computed , the molar fraction of each species of PCBA and its complex are plotted against the pH in Figure 5. The results indicate that, at physiological pH (≈7.4), the fraction of dissociated species with high solubility increases in the complex.
where and denote the dissociation constants of the corresponding reactions. The estimated and values are shown in Table 3. The results reveal that the was greatly reduced by the complex formation. Note that the adjusted values provided in Table 3 were evaluated on the basis of:
where is a parameter for calibrating the values. The parameter was determined by performing similar calculations for various carboxylic acids to fit the experimental values. On the basis of the computed , the molar fraction of each species of PCBA and its complex are plotted against the pH in Figure 5. The results indicate that, at physiological pH (≈7.4), the fraction of dissociated species with high solubility increases in the complex.
 and under higher pH conditions, the following equilibrium forms:
and under higher pH conditions, the following equilibrium forms:
 where and denote the dissociation constants of the corresponding reactions. The estimated and values are shown in Table 3. The results reveal that the was greatly reduced by the complex formation. Note that the adjusted values provided in Table 3 were evaluated on the basis of:
where and denote the dissociation constants of the corresponding reactions. The estimated and values are shown in Table 3. The results reveal that the was greatly reduced by the complex formation. Note that the adjusted values provided in Table 3 were evaluated on the basis of:
Table 3.
Reaction free energies and values for PCBA and its complex. This table is reprinted with permission from [42], Copyright 2016, Elsevier.
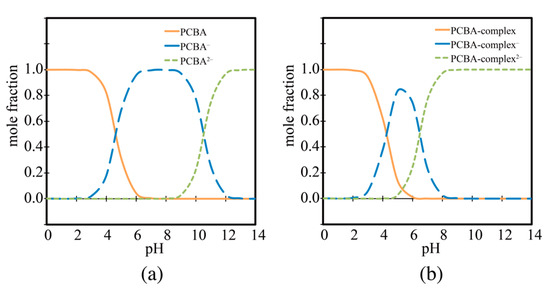
Figure 5.
pH-dependent mole fractions for (a) PCBA, and (b) PCBA-complex. These figures are reprinted with permission from [42], Copyright 2016, Elsevier.
As mentioned above, the RISM-SCF and the 3D-RISM-SCF can be used to calculate the using a first-principles method, and to understand the mechanism at the molecular level. However, accuracy remains at a qualitative level, and corrections are necessary for quantitative discussions.
4.3. Data-Driven Approach for pKa Prediction with 3D-RISM-SCF
As mentioned in the previous subsection, it was difficult to achieve quantitative accuracy in the first-principles calculations of the RISM-SCF and the 3D-RISM-SCF. Possible sources of the error include the accuracy of the empirical parameters used in the Lennard-Jones potential, the functional and basis functions in the electronic structure calculations, and, most seriously, the accuracy of the free-energy values of the dissociated protons.
A data-driven method, to avoid the calculation of the free energy of a proton and to improve the quantitative accuracy, was proposed by Fujiki et al. [28]. This is an extension of the AKB method, proposed by Matsui et al. (explained in Section 3), to use the 3D-RISM-SCF method instead of the PCM [14]. Here, the method of Matsui et al. will be referred to as the linear fitting correction (LFC) method, which is referred to as the AKB method in Section 3. For the LFC method, the is provided by Equation (14).
The parameters introduced here, and , are determined by the data-learning method. In this work, Fujiki et al. employed simple least-square fitting for the experimental values of training molecules. In this way, the free energy of a proton is buried in the parameter, , and only is required by the 3D-RISM-SCF. Furthermore, errors based on functional dependence and basis functions are mitigated by the parameter, , included in and . Fujiki et al. determined these parameters by data learning for each of the following functional groups: alcohol, amine, imidazole, thiol, phenol, and carboxyl. Figure 6 compares the accuracy of the of the LFC/3D-RISM-SCF, with the determined using the first-principles method, as described in the previous subsection. On the one hand, the first-principles method shows a good correlation, qualitatively, but a large error, quantitatively. On the other hand, quantitative accuracy was achieved with the LFC/3D-RISM, enabling highly accurate prediction.
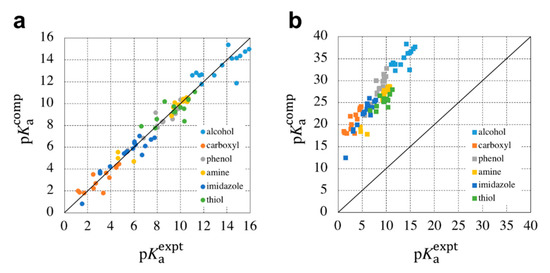
Figure 6.
Comparison of the computed values with the experimental values determined using (a) the LFC/3D-RISM-SCF, and (b) first-principles approach of the 3D-RISM-SCF. These figures are reprinted with permission from [28], Copyright 2018, Royal Society of Chemistry.
The method employing the continuum model introduced in the previous section is also capable of predicting the with high accuracy. However, it is difficult to apply this method to systems with strong heterogeneity, such as the inside of a protein, where it is difficult to define the dielectric constant. By using the 3D-RISM-SCF, the solvent effects in heterogeneous systems can be incorporated with high accuracy. The LFC/3D-RISM-SCF method is, therefore, expected to be applicable to complex biomolecular systems.
5. Summary
This review addresses computational methods used to evaluate values that are based on the first-principles quantum chemical electronic structure theory, coupled with two different solvation models, the PCM and RISM/3D-RISM methods.
The strategy common to the methods presented in this review is the use of quantum chemical electronic structure theory to determine the free-energy change of the deprotonation reaction of a target system. The most serious difficulty associated with achieving quantitative accuracy is the estimation of the free energy of dissociated protons in solution. To avoid this, the free energy of the dissociated proton was replaced by an empirical parameter, using a linear relationship between the free-energy change and the actual value. The method proposed by Matsui et al. [28], which used the PCM as a solvent model, was reviewed in detail. On the one hand, several studies reveal that it has both quantitative accuracy and a reasonable computational cost. Their method was extended to the use of the 3D-RISM as a solvent model by Fujiki et al. [28]. On the other hand, first-principles computational methods that are without empirical parameters are also important. The first-principles approach of the RISM/3D-RISM-SCF allows the qualitative prediction of the in various solution environments, such as with mixed solvents and in supercritical conditions. In the future, it is expected that methods for the quantitative prediction of the in such complex solution environments will be developed on the basis of the approaches reviewed in this paper.
Here, we mainly reviewed examples of research related to prediction by the authors’ group. Further developments of prediction methods or theories are ongoing within the science community, with a variety of approaches being used [1,2,43,44,45,46,47,48]. The conductor-like screening model for real solvents (COSMO-RS) is one such method [49,50]. COSMO-RS-based methods have also been successfully applied to predict the and for various systems, including proteins [51,52,53,54].
The prediction of the is considered important for drug design and for understanding biomolecular functions; thus, computer-aided prediction methods will become increasingly important. In order to predict the pKa of biomolecular systems, the electronic structure theory for large-scale molecules, such as quantum mechanics/molecular mechanics (QM/MM) or fragment molecular orbital (FMO) methods, has been introduced [55,56,57,58]. In addition, it is essential to consider the structural fluctuations of biomolecules, which were not addressed in this review. Indeed, the Boltzmann average of the values are, in principle, evaluated for all possible conformations. However, it is quite time-consuming and rather difficult to explore all of the stable structures for a given molecule, especially for biomolecules. Therefore, an efficient structural sampling method based on molecular simulation is necessary. The constant pH (CpH) MD is one such method, which is widely used and equipped in major program packages [59,60]. By combining the methods described in this review with CpHMD, it is expected that a method will be developed that describes the changes in the electronic structure and that also takes structural fluctuations into account. The development of such a method is in progress in the authors’ group. It is desirable that we continue to improve the methods that can provide accuracy, computational speed, and a detailed molecular picture.
Author Contributions
Funding
We are grateful for the financial support from the Japan Society for the Promotion of Science (JSPS), KAKENHI (Grant Nos. 18K05036 and 19H02677).
Acknowledgments
Norio Yoshida would like to thank Sato (Kyoto University, Japan) and Hirata (Institute for Molecular Science, Japan) for their contributions in writing some of the original papers referred to in this review. We would like to dedicate this work to the late Yukako Kasai (1990–2020) for her significant contributions to the development of the LFC/3D-RISM-SCF method.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Navo, C.D.; Jiménez-Osés, G. Computer Prediction of pKa Values in Small Molecules and Proteins. ACS Med. Chem. Lett. 2021, 12, 1624–1628. [Google Scholar] [CrossRef]
- Li, H.; Robertson, A.D.; Jensen, J.H. Very Fast Empirical Prediction and Rationalization of Protein pKa Values. Proteins Struct. Funct. Genet. 2005, 61, 704–721. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.M.; Coote, M.L. A universal approach for continuum solvent pKa calculations: Are we there yet? Theor. Chem. Acc. 2010, 125, 3–21. [Google Scholar] [CrossRef]
- Mangold, M.; Rolland, L.; Costanzo, F.; Sprik, M.; Sulpizi, M.; Blumberger, J. Absolute pKa Values and Solvation Structure of Amino Acids from Density Functional Based Molecular Dynamics Simulation. J. Chem. Theory Comput. 2011, 7, 1951–1961. [Google Scholar] [CrossRef] [PubMed]
- Klamt, A.; Schuurmann, G. Cosmo—A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc. Perkin Trans. 2 1993, 799–805. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J. Continuum solvation models: A new approach to the problem of solute’s charge distribution and cavity boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
- Foresman, J.B.; Keith, T.A.; Wiberg, K.B.; Snoonian, J.; Frisch, M.J. Solvent effects. 5. Influence of cavity shape, truncation of electrostatics, and electron correlation ab initio reaction field calculations. J. Phys. Chem. 1996, 100, 16098–16104. [Google Scholar] [CrossRef]
- Pliego, J.R.; Riveros, J.M. Gibbs energy of solvation of organic ions in aqueous and dimethyl sulfoxide solutions. Phys. Chem. Chem. Phys. 2002, 4, 1622–1627. [Google Scholar] [CrossRef]
- Takano, Y.; Houk, K.N. Benchmarking the conductor-like polarizable continuum model (CPCM) for aqueous solvation free energies of neutral and ionic organic molecules. J. Chem. Theory Comput. 2005, 1, 70–77. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Oshiyama, A.; Shigeta, Y. A Simple scheme for estimating the pKa values of 5-substituted uracils. Chem. Phys. Lett. 2011, 502, 248–252. [Google Scholar] [CrossRef]
- Matsui, T.; Miyachi, H.; Baba, T.; Shigeta, Y. Theoretical Study on Reaction Scheme of Silver(I) Containing 5-Substituted Uracils Bridge Formation. J. Phys. Chem. A 2011, 115, 8504–8510. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Baba, T.; Kamiya, K.; Shigeta, Y. An accurate density functional theory based estimation of pKa values of polar residues combined with experimental data: From amino acids to minimal proteins. Phys. Chem. Chem. Phys. 2012, 14, 4181. [Google Scholar] [CrossRef]
- Baba, T.; Matsui, T.; Kamiya, K.; Nakano, M.; Shigeta, Y. A Density Functional Study on the pKa of Small Polyprotic Molecules. Int. J. Quantum Chem. 2014, 114, 1128–1134. [Google Scholar] [CrossRef]
- Hirata, F. (Ed.) Molecular Theory of Solvation; Kluwer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Chandler, D.; Andersen, H.C. Optimized Cluster Expansions for Classical Fluids. 2. Theory of Molecular Liquids. J. Chem. Phys. 1972, 57, 1930–1937. [Google Scholar] [CrossRef]
- Andersen, H.; Chandler, D.; Weeks, J. Optimized Cluster Expansions for Classical Fluids. 3. Applications to Ionic Solutions and Simple Liquids. J. Chem. Phys. 1972, 57, 2626–2631. [Google Scholar] [CrossRef]
- Andersen, H.; Chandler, D. Optimized Cluster Expansions for Classical Fluids. 1. General Theory and Variational Formulation of Mean Spherical Model and hard-sphere Percus-Yevick Equations. J. Chem. Phys. 1972, 57, 1918–1929. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. An Integral Equation to Describe the Solvation of Polar Molecules in Liquid Water. J. Phys. Chem. B 1997, 101, 7821–7826. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. Solvation Of Complex Molecules in A Polar Liquid: An Integral Equation Theory. J. Chem. Phys. 1996, 104, 8678–8689. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Three-Dimensional Density Profiles of Water in Contact with A Solute of Arbitrary Shape: A RISM Approach. Chem. Phys. Lett. 1998, 290, 237–244. [Google Scholar] [CrossRef]
- Ten-No, S.; Hirata, F.; Kato, S. A Hybrid Approach for the Solvent Effect on the Electronic Structure of A Solute Based on the RISM and Hartree-Fock Equations. Chem. Phys. Lett. 1993, 214, 391–396. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Self-Consistent Description of A Metal-Water Interface by the Kohn-Sham Density Functional Theory and the Three-Dimensional Reference Interaction Site Model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar] [CrossRef]
- Sato, H.; Kovalenko, A.; Hirata, F. Self-Consistent Field, Ab Initio Molecular Orbital and Three-Dimensional Reference Interaction Site Model Study for Solvation Effect on Carbon Monoxide in Aqueous Solution. J. Chem. Phys. 2000, 112, 9463–9468. [Google Scholar] [CrossRef]
- Yoshida, N.; Ishizuka, R.; Sato, H.; Hirata, F. Ab initio theoretical study of temperature and density dependence of molecular and thermodynamic properties of water in the entire fluid region: Autoionization processes. J. Phys. Chem. B 2006, 110, 8451–8458. [Google Scholar] [CrossRef] [PubMed]
- Sato, H.; Hirata, F. Theoretical study for autoionization of liquid water: Temperature dependence of the ionic product (pKw). J. Phys. Chem. A 1998, 102, 2603–2608. [Google Scholar] [CrossRef]
- Fujiki, R.; Kasai, Y.; Seno, Y.; Matsui, T.; Shigeta, Y.; Yoshida, N.; Nakano, H. A computational scheme of pKa values based on the three-dimensional reference interaction site model self-consistent field theory coupled with the linear fitting correction scheme. Phys. Chem. Chem. Phys 2018, 20, 27272–27279. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Mennucci, B. Polarizable continuum model. WIREs Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Shigeta, Y.; Morihashi, K. Assessment of Methodology and Chemical Group Dependences in the Calculation of the pKa for Several Chemical Groups. J. Chem. Theory Comput. 2017, 13, 4791–4803. [Google Scholar] [CrossRef]
- Hengphasatporn, K.; Matsui, T.; Shigeta, Y. Estimation of Acid Dissociation Constants (pKa) of N-Containing Heterocycles in DMSO and Transferability of Gibbs Free Energy in Different Solvent Conditions. Chem. Lett. 2020, 49, 307–310. [Google Scholar] [CrossRef]
- Dawson, R.M.C.; Elliott, D.C.; Elliott, W.H.; Jones, K.M. Data for Biochemical Research; Clarendon Press: Oxford, UK, 1969; Volume 316. [Google Scholar]
- Kaljurand, I.; Kutt, A.; Soovali, L.; Rodima, T.; Maemets, V.; Leito, I.; Koppel, I.A. Extension of the self-consistent spectrophotometric basicity scale in acetonitrile to a full span of 28 pKa units: Unification of different basicity scales. J. Org. Chem. 2005, 70, 1019–1028. [Google Scholar] [CrossRef]
- Garrido, G.; Roses, M.; Rafols, C.; Bosch, E. Acidity of several anilinium derivatives in pure tetrahydrofuran. J. Solut. Chem. 2008, 37, 689–700. [Google Scholar] [CrossRef]
- Jover, J.; Bosque, R.; Sales, J. QSPR Prediction of pK for Aliphatic Carboxylic Acids and Anilines in Different Solvents. QSAR Comb. Sci. 2008, 27, 1204–1215. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. First-principles realization of a van der Waals-Maxwell theory for water. Chem. Phys. Lett. 2001, 349, 496–502. [Google Scholar] [CrossRef]
- Kido, K.; Sato, H.; Sakaki, S. First Principle Theory for pKa Prediction at Molecular Level: pH Effects Based on Explicit Solvent Model. J. Phys. Chem. B 2009, 113, 10509–10514. [Google Scholar] [CrossRef] [PubMed]
- Kido, K.; Sato, H.; Sakaki, S. Systematic Assessment on Aqueous pKa and pKb of an Amino Acid Base on RISM-SCF-SEDD Method: Toward First Principles Calculations. Int. J. Quantum Chem. 2012, 112, 103–112. [Google Scholar] [CrossRef]
- Islam, T.M.B.; Yoshino, K.; Sasane, A. 11B NMR study of p-carboxybenzeneboronic acid ions for complex formation with some monosaccharides. Anal. Sci. 2003, 19, 455–460. [Google Scholar] [CrossRef][Green Version]
- Seno, Y.; Yoshida, N.; Nakano, H. Theoretical analysis of complex formation of p-carboxybenzeneboronic acid with a monosaccharide. J. Mol. Liq. 2016, 217, 93–98. [Google Scholar] [CrossRef]
- Radak, B.K.; Chipot, C.; Suh, D.; Jo, S.; Jiang, W.; Phillips, J.C.; Schulten, K.; Roux, B. Constant-PH Molecular Dynamics Simulations for Large Biomolecular Systems. J. Chem. Theory Comput. 2017, 13, 5933. [Google Scholar] [CrossRef]
- Tielker, N.; Eberlein, L.; Gussregen, S.; Kast, S.M. The SAMPL6 challenge on predicting aqueous pKa values from EC-RISM theory. J. Comput.-Aided Mol. Des. 2018, 32, 1151–1163. [Google Scholar] [CrossRef]
- Tielker, N.; Tomazic, D.; Heil, J.; Kloss, T.; Ehrhart, S.; Gussregen, S.; Schmidt, K.F.; Kast, S.M. The SAMPL5 challenge for embedded-cluster integral equation theory: Solvation free energies, aqueous pKa, and cyclohexane-water log D. J. Comput.-Aided Mol. Des. 2016, 30, 1035–1044. [Google Scholar] [CrossRef]
- Matos, M.J.; Oliveira, B.L.; Martínez-Sáez, N.; Guerreiro, A.; Cal, P.M.S.D.; Bertoldo, J.; Maneiro, M.; Perkins, E.; Howard, J.; Deery, M.J.; et al. Chemo- and Regioselective Lysine Modification on Native Proteins. J. Am. Chem. Soc. 2018, 140, 4004. [Google Scholar] [CrossRef]
- Işık, M.; Rustenburg, A.S.; Rizzi, A.; Gunner, M.R.; Mobley, D.L.; Chodera, J.D. Overview of the SAMPL6 PKa Challenge: Evaluating Small Molecule Microscopic and Macroscopic PKa Predictions. J. Comput.-Aided Mol. Des. 2021, 35, 131. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Chen, B.; Wu, Y.; Guan, L. Prediction of PKa Values for Neutral and Basic Drugs Based on Hybrid Artificial Intelligence Methods. Sci. Rep. 2018, 8, 3991. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-Like Screening Model for Real Solvents—A New Approach to the Quantitative Calculation of Solvation Phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F.; Diedenhofen, M.; Beck, M.E. First principles calculations of aqueous pKa values for organic and inorganic acids using COSMO-RS reveal an inconsistency in the slope of the pKa scale. J. Phys. Chem. A 2003, 107, 9380–9386. [Google Scholar] [CrossRef] [PubMed]
- Eckert, F.; Klamt, A. Accurate prediction of basicity in aqueous solution with COSMO-RS. J. Comput. Chem. 2006, 27, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Eckert, F.; Leito, I.; Kaljurand, I.; Kutt, A.; Klamt, A.; Diedenhofen, M. Prediction of Acidity in Acetonitrile Solution with COSMO-RS. J. Comput. Chem. 2009, 30, 799–810. [Google Scholar] [CrossRef]
- Toure, O.; Dussap, C.G.; Lebert, A. Comparison of Predicted pKa Values for Some Amino-Acids, Dipeptides and Tripeptides, Using COSMO-RS, ChemAxon and ACD/Labs Methods. Oil Gas Sci. Technol. 2013, 68, 281–297. [Google Scholar] [CrossRef]
- Andersson, M.P.; Jensen, J.H.; Stipp, S.L.S. Predicting pKa for proteins using COSMO-RS. PeerJ 2013, 1, e198. [Google Scholar] [CrossRef] [PubMed]
- Kitaura, K.; Ikeo, E.; Asada, T.; Nakano, T.; Uebayasi, M. Fragment Molecular Orbital Method: An Approximate Computational Method For Large Molecules. Chem. Phys. Lett. 1999, 313, 701–706. [Google Scholar] [CrossRef]
- Fedorov, D.G.; Kitaura, K.; Li, H.; Jensen, J.H.; Gordon, M.S. The Polarizable Continuum Model (PCM) Interfaced With The Fragment Molecular Orbital Method (FMO). J. Comput. Chem. 2006, 27, 976–985. [Google Scholar] [CrossRef]
- Yoshida, N. Efficient implementation of the three-dimensional reference interaction site model method in the fragment molecular orbital method. J. Chem. Phys. 2014, 140, 214118. [Google Scholar] [CrossRef]
- Yoshida, N.; Kiyota, Y.; Hirata, F. The Electronic-Structure Theory Of A Large-Molecular System In Solution: Application to The Intercalation of Proflavine With Solvated DNA. J. Mol. Liq. 2011, 159, 83–92. [Google Scholar] [CrossRef]
- Mongan, J.; Case, D.A.; McCammon, J.A. Constant pH molecular dynamics in generalized born implicit solvent. J. Comput. Chem. 2004, 25, 2038–2048. [Google Scholar] [CrossRef]
- Itoh, S.G.; Damjanovic, A.; Brooks, B.R. pH replica-exchange method based on discrete protonation states. Proteins 2011, 79, 3420–3436. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).